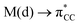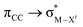Coordination and insertion of alkenes and alkynes in Au^III complexes: nature of the intermediates from a computational perspective

Abstract

The contribution of Au^III species to catalysis is still debated due to the limited number of characterized intermediates with this oxidation state. In particular, the coordination of alkenes and alkynes to Au^III followed by insertion into Au^III–X bonds has been suggested but rarely proven experimentally. Here, these reactions are explored by means of DFT and CCSD(T) calculations considering [AuX₃(L)] and [AuX₂(L)₂]⁺ complexes. In these complexes, L = ethylene and acetylene have been chosen as substrates of high interest and representative of any unsaturated organic substrate, whereas X is Cl, Me or H, as found in metal salts and as model for intermediates involved in catalysis. Isoelectronic Pt^II complexes are also considered for comparison. Ethylene coordination occurs preferentially perpendicular for all X except H, whereas for acetylene, coordination takes place in-plane for all X except Cl. These coordination isomers can represent either minima (intermediates) or saddle points (transition states) on the potential energy surface, depending on X. NBO analysis shows how this variety of structures results from the combination of electronic (M–L donation and back-donation) and steric (cis L–X repulsion) effects. With the sole exception of [AuMe₂(ethylene)₂]⁺, rotation of the unsaturated ligand and insertion into a cis Au–X bond involve low to moderate energy barriers, ΔG^‡ = 2.5 to 23.5 kcal mol⁻¹, and are thermodynamically feasible, ΔG = 4.3 to −47.2 kcal mol⁻¹. The paucity of experimental observations for such reactions should thus be caused by other factors, like the participation of the intermediates and products in competitive side reactions including the reductive elimination of XCH_nCH_nX (n = 1 or 2).

---

Introduction

Isoelectronic metal centres tend to show similar structures and reactivity patterns. This is in agreement with the ability of Au^III and Pt^II to activate unsaturated bonds towards the addition of nucleophiles.^1–3 However, the relative stability of the intermediates that participate in these reactions is significantly different,⁴ in particular the stability of the η²-alkene and -alkyne intermediates.⁵ This is clearly shown by the large number of η²-alkene Pt^II complexes that have been isolated and characterized by NMR and X-ray diffraction.⁶ The first complex of this family to be reported was K[PtCl₃(C₂H₄)], which was synthesized by Zeise in 1825⁷ (Fig. 1). Since then, many other Pt–alkene complexes have been reported.⁵ The scenario is quite different with Au^III for which η²-alkene complexes were unknown until our group obtained the first crystal structure of the Au^III-cod complex in 2013 (Fig. 1).⁸ Independently at the same time, the group of Bochmann isolated and characterized several Au^III –alkene complexes by NMR, including an Au^III–ethylene and an Au^III–cyclopentene complex in addition to the most stable Au^III-norbornene pincer shown in Fig. 1.⁹ Likewise, no Au^III η²-alkyne complexes have yet been characterized while the corresponding complexes are known since 1959 for Pt^II.^10,11

Fig. 1 First isolated alkene and alkyne complexes reported with Pt^II and Au^III.

The X-ray structures of Pt^II–alkene and alkyne complexes show that the η²-coordinated ligand is perpendicular to the PtX₃ plane,^6,11 although rotation of the organic moiety takes place at room temperature.¹² The nature of the Pt–alkene bond in Zeise's complex was first described by using the Dewar–Chatt–Duncanson model in 1953.¹³ Afterwards, computational methods were used to analyse the rotational barrier of L (ethylene and acetylene) in [PtCl₃L]⁻ complexes.^14,15 With Au^III, NMR data on the η²-alkene complexes known to date are consistent with a perpendicular orientation.⁹ The same preference is observed in the crystal structure of [AuMe₂(cod)]⁺, although the two CC double bonds of the cod ligand are not exactly parallel (dihedral angle between alkenes planes of 13.7°) and are probably influenced by the cyclic nature of the cod ligand.⁸ With alkynes, the preferred coordination mode with Au^III can only be inferred computationally. For instance, a DFT study by Pernpointner and Hashmi showed perpendicular orientation of propyne in the coordination to the [PtCl₂(H₂O)] and AuCl₃ moieties.¹⁶

The orientation of the alkene in Au^III complexes is important because it can alter the nature of the reactions taking place in the coordination sphere of the metal centre. For instance, the perpendicular coordination of ethylene in [(tpy)Au(ethylene)(OCOCF₃)]⁺ (tpy = 2-p-tolylpyridine) triggers the intermolecular addition of a free CF₃CO₂⁻ anion to the coordinated ethylene anti to the metal, whereas the in-plane coordination triggers the unexpected intramolecular insertion of the alkene ligand into the Au^III–OCOCF₃ bond (Fig. 2a).¹⁷ Although in this particular case the intermolecular addition is preferred experimentally and computationally, the other pathway cannot be fully excluded in other systems as shown by the insertion of norbornene into Au^III–Me bonds¹⁸ and of allene derivatives into Au^III–H bonds in complexes supported by pincer ligands (Fig. 2b and c respectively).¹⁹ Insertion of ethylene into Au^III–H has also been proposed computationally as an elementary step in the experimentally observed catalytic hydrogenation of ethylene.²⁰ In addition, the insertion of alkynes and allenes into Au^III–Si bonds has been proved experimentally and studied computationally.²¹ To the best of our knowledge, these are the only cases for which an insertion reaction has been established in Au^III species. The scenario is similar with Au^I, in which case few insertion reactions have been reported.²² In line with this, computational studies have shown that insertion of alkenes into Au^I–H bonds has prohibitively high energy barriers.²³ This is in contrast to the demonstrated ability of alkenes to insert into Pt^II–R (R = H, hydrocarbyl) bonds.^24,25

Fig. 2 (a) Coordination modes of ethylene for the inter- and intramolecular reaction of OCOCF₃⁻ anion with Au^III coordinated ethylene. Insertion reactions of alkene into (b) Au^III–Me¹⁸ and (c) Au^III–H¹⁹ bonds.

In this work, we explore with computational methods (DFT/CCSD(T)) the interaction of Au^III with double and triple CC bonds. We analyse the π complexes and the insertion reactions into Au^III–X bonds. The energetics of these systems will shed light on how Au^III catalysts form intermediates and initiate reactions in the presence of unsaturated organic molecules, information which is not available experimentally. For this purpose, we have used ethylene and acetylene due to their high interest as chemical feedstocks and their ability to represent any unsaturated organic substrate. The [LAu^IIIX₃] and [L₂Au^IIIX₂]⁺ complexes (X = Cl, Me, and H; L = ethylene and acetylene) have been studied. X = Cl is considered because [AuCl₃] is the most frequently used Au^III catalyst^1,2 and [AuCl₃L] is analogous to the well-known Pt^II Zeise salt⁷ (Fig. 1); X = Me because Au^III–alkyl species can be catalytic intermediates,²⁶ and X = H because Au^III hydrides are involved in hydrogenation reactions.²⁰ The [Au(ethylene)₂(Me)₂]⁺ complex is used to understand the geometry and electronic structure of [AuMe₂(cod)]⁺, which is to date the only Au^III–alkene complex characterized by X-ray diffraction.⁸ In addition, isoelectronic Pt^II complexes have been used as further reference because of the larger number of isolated related complexes. The insight given by this study can contribute significantly to the isolation of Au^III–alkyne complexes, which is still unprecedented, and the design of new Au^III-catalyzed reactions in which product formation or catalyst deactivation involves insertion steps.

Computational details

Calculations were carried out using Density Functional Theory (DFT) and Coupled-Cluster with Single, Double and perturbative Triple excitations (CCSD(T)) as implemented in the Gaussian09 software package.²⁷ The hybrid PBE0+GD3 functional^28,29 including Grimme's model for dispersion forces was used to optimize the geometries. Benchmark calculations showed that this level of theory slightly outperforms both the PBE0 and B2PLYPD³⁰ functionals, as shown by the root-mean-square-deviations between the DFT-optimized geometries and the crystal structure of the [PtCl₃(CH₂=CH₂)]⁻ anion of the Zeise's salt (Fig. 1). Absolute deviations in bond distances are within a range of 0.004–0.068 Å (see ESI†). Geometries were fully optimized without any geometry or symmetry constraint at the PBE0+GD3 level with the triple-ζ all-electron 6-311G** basis set³¹ for all atoms except the metal centre. Platinum and gold were described with the Stuttgart triple-ζ+polarization basis sets including quasi-relativistic effective core potentials.³² This level of calculations should insure a good representation of all interactions in these systems. All stationary points were characterized as either minima or transition states by analytic calculation of frequencies. The vibrational data were used in combination with intrinsic reaction coordinate (IRC) calculations to connect minima to transition states. Energies were further refined by means of single point CCSD(T) calculations³³ with the cc–pVTZ(–PP) basis set³⁴ on the PBE0+GD3-optimized geometries. Electronic structures were studied by means of Natural Bond Orbital analysis (NBO 6.0).³⁵ This includes second order perturbation theory analysis of the Fock matrix in the localized orbital basis set, which allows for identification of mixing orbitals and quantification of the magnitude of their interactions.³⁶ The interacting orbitals can be ascribed to donor–acceptor interactions, e.g., d → π*, p → σ*, etc., which are confirmed by visual inspection of their isosurfaces. The Gibbs free energies reported in the text were obtained by adding the thermochemistry parameters (zero-point, thermal and entropy energies at the PBE0+GD3 level) calculated in standard conditions (T = 298 K and p = 1 atm) to the CCSD(T) potential energies. Solvent effects in the energy profile for the rotation and insertion of ethylene into the Au–Cl bond of AuCl₃(ethylene) was evaluated by doing single point calculations on the gas phase optimized structures using the continuum SMD model (see ESI†). Comparison of the free energy profiles in gas phase and in solvent (toluene, ε = 2.7, and TFE, ε = 26.7, two solvents which are representative of experimental conditions) shows small variations in the relative energies (1–2 kcal mol⁻¹) depending on the solvent dielectric constant.

Results

[MX₃(ethylene)]ⁿ⁻ and [MX₃(acetylene)]ⁿ⁻ (M = Au, n = 0; M = Pt, n = −1; X = Cl, Me, and H)

The rotation of the unsaturated ligand L around the Au–L bond axis and its insertion into a cis-Au–X bond were studied computationally for M = Au and Pt, X = Cl, Me, and H. These processes yield the species labelled in Fig. 3. Each label is composed by the capital letters A–E, referring to the structure of the system, followed by either -en or -yn, identifying ethylene and acetylene, respectively, and finalized by -X, which identifies the ancillary ligand (Cl, Me, and H). The metal centre of interest in this study is Au^III, but the isolelectronic Pt^II was also considered in selected cases for sake of comparison. Therefore the metal is also added at the beginning; e.g., Au-A-en-Cl stands for the perpendicular Au^III ethylene complex bearing three chloride ligands.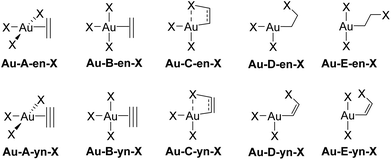

Fig. 3 Structure labelling (A–E) for the rotation and insertion of L = ethylene (en) and acetylene (yn) in [Au^IIIX₃L] complexes (X = Cl, Me, H).

The free energy profiles connecting structures A–E are shown in Fig. 4. For ethylene and X = Cl, the profile depends dramatically on the metal centre. With Pt^II, the in-plane coordinated ethylene, Pt-B-en-Cl is not an energy minimum but rather a bifurcation point associated with the rotation of ethylene in Pt-A-en-Cl, and is connected with the transition state (TS) for the ethylene insertion into a cis-Pt–Cl bond, Pt-C-en-Cl.³⁷ In contrast, for Au^III, both Au-A-en-Cl and Au-B-en-Cl are energy minima connected by a low-energy rotation transition state (not shown in Fig. 4 for clarity; see ESI†).³⁸ The same scenario applies for X = Me with Au^III. Nonetheless, the nature of X also influences strongly the Gibbs free energy profile, because with X = H, Au-A-en-H, which is less stable than Au-B-en-H, is no longer a minimum but the TS for ethylene rotation. The insertion of ethylene into a cis-Pt/Au–X bond involves transition state C and product D, a T-shaped 3-coordinate species in which the two remaining X ligands are cis to each other. The cis–trans isomerization transition state was found to be at lower energy than transition state C (X = Cl, see ESI†) and in the case of X = Me product E is obtained directly from C.³⁹ Therefore, this barrier was not studied further.

Fig. 4 Free Gibbs energy profiles in kcal mol⁻¹ for the rotation and insertion into the M–X bond of L = ethylene (top) and acetylene (bottom) in [AuX₃L] (X = Cl (red), Me (green), H (lilac)) and [PtCl₃L]⁻ (blue). Square bracketed energies are for TS and dotted lines connect minima separated by a single TS, which has been computed for the ethylene rotation from Au-A-en-Cl and Me (ΔG^‡ = 8.8 and 2.8 kcal mol⁻¹, respectively) and for the cis–trans isomerization from Au-D-en-Cl (ΔG^‡ = 5.4 kcal mol⁻¹).

The energy patterns for the rotation and insertion of ethylene are also significantly different for [AuCl₃(ethylene)] and [PtCl₃(ethylene)]⁻ (Fig. 4).⁴⁰ With Au^III, the energy differences between the perpendicular (Au-A-en-X) and the in-plane (Au-B-en-X) isomers are much lower than with Pt^II. The A → B isomerization is endoergic for X = Cl (8.0 kcal mol⁻¹) and Me (1.2 kcal mol⁻¹) showing a preference for the perpendicular isomer. In contrast, with X = H, A becomes the TS for rotation with a low barrier of 7.2 kcal mol⁻¹ above B. The way electronic and steric effects combine to lead to these differences will be discussed below (vide infra). The rotation energy barriers with X = Cl and Me (not shown in Fig. 4 for clarity) are also low, i.e. 8.8 and 2.8 kcal mol⁻¹ respectively. This indicates that facile or essentially free Au–alkene rotation should be expected at room temperature for AuX₃ alkene complexes, at least in the absence of steric hindrance inhibiting the rotation in substituted alkenes.

The TS energies for insertion into the M–X bond (C-en-X) are higher and follow a different trend when compared to rotation. While the stability of the in-plane isomer preceding the insertion TS decreases in the order H > Me > Cl, the insertion barrier decreases in the order Me > Cl > H. For TS C, in contrast to B, the capacity of X to migrate from the metal to the alkene should play a relevant role. This should be a more facile process with the p lone pairs of X = Cl and the spherical electron distribution at H, than with the directionally highly localized sp³ bonding electron pair of X = Me. The direct insertion product is Au-D-en-X for X = Cl and H, whereas X = Me yields Au-E-en-Me. This results from the difference in the trans influence of X (lowest for Cl, highest for H) and the additional non-covalent Au⋯Cl (2.439 Å) and Au⋯H interactions (1.939 Å) that stabilize D and may become repulsive with X = Me.⁴¹ Besides the low energy barriers, insertion is thermodynamically favourable by 4.8 and 6.8 kcal mol⁻¹ with X = Cl and Me. With X = H, Au-B-en-H is the thermodynamic sink, however the moderate free energy difference between B and E, i.e. ΔG^‡ = 8.1 and ΔG = 4.3 kcal mol⁻¹ suggests an equilibrium between both species. In contrast, with Pt^II the insertion has a prohibitive energy barrier of 41.8 kcal mol⁻¹ and is endoergic by 26.5 kcal mol⁻¹. The differences in insertion ability between Au^III and Pt^II–ethylene suggest that this reaction could be involved in decomposition processes of Au^III–alkene complexes, which are not observed with Pt^II, as showed by the high stability of Zeise's salt and analogous [PtCl₃(alkene)]⁻ complexes.^7,11

The energy trends obtained for ethylene rotation and insertion in A–E are also found for acetylene but the energies of all stationary structures are consistently shifted to lower energies relative to A. This is especially pronounced for platinum, where the insertion barrier is lowered from 41.8 to 27.2 kcal mol⁻¹. The latter barrier agrees with the observation of slow acetylene insertion into the Pt–Cl bond in [PtCl₂(N^N)] (N^N = 2,9-dimethyl-1,10-phenanthroline).⁴² For gold, the in-plane coordination of acetylene is preferred not only for X = H, but also for X = Me (Au-B-yn), with energy barriers for rotation (A-yn) of 9.7 and 2.5 kcal mol⁻¹, respectively. For X = Cl, the rotation barrier of acetylene is also very low (3.5 kcal mol⁻¹), with the in-plane coordination structure, Au-B-yn-Cl, being the TS. Taking as a reference point the lowest energy isomer of M–ethylene and acetylene, i.e.A or B, respectively, the insertion barriers are significantly lower for acetylene (19.1, 9.9 and 7.5 kcal mol⁻¹ for X = Me, Cl, and H, respectively) than for ethylene (23.5, 16.3 and 8.1 kcal mol⁻¹ for X = Me, Cl, and H, respectively). The lower energies of C, D, and E with a partially or fully broken π-bond in the case of the alkyne relative to alkene are due to several factors including (i) the lower energy loss for breaking one π bond in a triple bond compared to in a double one, (ii) the weaker coordination of acetylene compared to ethylene (as seen in the isodesmic reactions, eqn (1) and (2), and (iii) the stronger M–C(sp²) bond in the M–vinyl insertion product from acetylene, compared to the M–C(sp³) bond in the M–alkyl insertion product from ethylene.⁴³ In addition, for X = H, the reaction is further thermodynamically driven by the reductive elimination of H₂ yielding Au^I-yn-H₂ (Fig. 4).

These results clearly show that ethylene or acetylene insertion into Au–X bonds (X = Cl, Me, and H) is not encumbered by prohibitive energy barriers or endoergic steps (with the exception of the ethylene insertion into Au–H). These processes may be even faster in polar solvents, as suggested by the ca. 1–2 kcal mol⁻¹ decrease in the energy barriers for coordination, rotation and insertion of ethylene in Au-Cl-en when considering benzene and TFE as solvents (Fig. S2†). Nonetheless, this reaction cannot occur if generation of either A and even more B has a high energy cost that needs to be added to the energetics of the insertion process itself. This may be indeed the case considering the weak coordination of an unsaturated ligand to Au^III relative to Pt^II, as shown for ethylene by the thermochemistry of eqn (3). This is primarily caused by the reduced back-donation from Au (vide infra). There are other factors that may reduce the lifetime of the Au-π adduct and preclude possible insertion processes. For instance, addition of an external nucleophilic molecule (solvent or substrate) to L may be energetically facile.¹⁷ In addition to the transient nature of A or B, the insertion product, E, may be scavenged by protonation⁹ or reductive elimination⁴⁴ processes, which can be promoted by low energy barriers and tunneling effects.⁴⁵ Indeed, at AuH₃, the insertion of acetylene into one Au–H bond proceeds with concomitant reductive elimination of H₂ (Fig. 4). With ethylene, the reductive elimination of XCH₂CH₂X calculated from the trans insertion products (E) has an energy barrier of 7.2 and 23.3 kcal mol⁻¹ for X = Me and Cl, respectively (eqn (4)). The corresponding barriers for the elimination yielding XCH=CHX from the acetylene insertion products are even lower, 0.3 and 11.8 kcal mol⁻¹ for X = Me and Cl, respectively (eqn (5)). The poor stability of Au^III alkene and alkyne complexes, as inferred from these thermodynamic (A/B stability) and kinetic (reductive elimination from E) data, accounts for the limited success attained so far in the isolation and characterization of such species as well as their immediate insertion products.

[MX₂(ethylene)₂]ⁿ⁺ and [MX₂(acetylene)₂]ⁿ⁺ (M = Au, n = 1; M = Pt, n = 0; X = Cl, Me, and H)

The compound [AuMe₂(ethylene)₂]⁺ has been investigated in order to gain further insight into the structure and bonding features of [AuMe₂(cod)]⁺ in the absence of the geometrical restrictions that are imposed by the cyclic cod ligand. Ethylene rotation around the Au–ethylene bond axis and insertion of ethylene into the cis Au–Me bond in [AuMe₂(ethylene)₂]⁺ were also studied to get insight into the partial stability of [AuMe₂(cod)]⁺, which still remains the only Au^III–alkene complex that has been crystallographically characterized.

In the following discussion of ethylene rotation, the rotation angle θ is defined as the angle between the molecular plane of Au and the plane defined by Au and the two C atoms of each ethylene. Thus, for θ = 90° and 0°, the ethylene is perpendicular and in-plane, respectively (see Fig. 5). The optimized geometry of [AuX₂(ethylene)₂]⁺ corresponds to neither of the structures in Fig. 5, since θ = 77° yielding a species labelled Au-F′-en-Me (Fig. 6). A similar deviation from the idealized perpendicular structure was also seen in [AuMe₂(cod)]⁺, with θ = 85°. Surprisingly, the deviation away from the perpendicular structure is even more pronounced in Au-F′-en-Me than in the crystal structure of [AuMe₂(cod)]⁺. Thus, it appears that the deviation from θ = 90° is not only imposed by the constrained cyclic nature of the cod ligand, but rather reflects an intrinsic feature of the Au^III–alkene bond (vide infra).

Fig. 5 Structure labelling (F–K) for the ethylene rotation and insertion into Au–Me bonds. θ is the angle between the square coordination plane of Au and the plane defined by Au and the two C atoms of each ethylene.

Fig. 6 Gibbs free energy profile, in kcal mol⁻¹, for the insertion of ethylene into the Au–Me bond of [AuMe₂(ethylene)₂]⁺. TS energies are given in square brackets. Solid and dotted lines link directly and non-directly connected stationary points, respectively.

In [AuMe₂(ethylene)₂]⁺, rotation of one ethylene ligand has a very low energy barrier of 3.9 kcal mol⁻¹ (Au-G-en-Me, Fig. 6), and should take place even at low temperatures. In contrast, insertion of ethylene into the Au–Me bond has a prohibitively high energy barrier of almost 40 kcal mol⁻¹ (Au-J-en-Me). The dramatic influence of the ligand trans to the Au–Me bond that undergoes insertion becomes apparent when this barrier is compared to that associated with Au-C-en-Me (23.5 kcal mol⁻¹, Fig. 4). In line with these data, no insertion products are observed with [AuMe₂(cod)]⁺.⁸

In order to determine the influence of the X group in [AuX₂(ethylene)₂]⁺ and [AuX₂(acetylene)₂]⁺ on the orientation of the unsaturated ligands from the ideal structures shown in Fig. 5, geometries were optimized for X = Cl and H (Table 1). The related Pt complexes were also considered. With X = Cl, all geometries are almost ideal with two perpendicular oriented double or triple bonds (F), whereas for X = Me, all geometries deviate significantly (F′). In contrast, X = H shows a distinct scenario, with several different structures, including a Au^I dihydrogen complex, [Au(H₂)(ethylene)₂]⁺ (Au^I-en₂-H₂), I′, and G. This structural diversity suggests that the weak bonding of alkenes and alkynes to Au^III allows for multiple structural distortions likely dominated by dispersion forces, including weak H^δ+⋯H^δ−, CH⋯π and CH⋯Cl interactions.

Table 1 Optimized θ values, in degrees^a

	Au		Pt
X	en	yn	en	yn
a Geometry labelled’ indicates that it is not described by the idealized structure shown in Fig. 5. b Au ^I -en 2 -H 2 is used for [Au(H2)(ethylene)2]^+.
Cl	90 (F)	90 (F)	90 (F)	90 (F)
Me^a	77 (F′)	69 (F′)	78 (F′)	87 (F′)
H^a^,^b	0 (Au^I-en2-H2)	39 (I′)	0/90 (G)	12 (I′)

---

Discussion

Coordination of alkenes and alkynes to Au^IIIvs. Pt^II

The results, which have been described above, show that η²-coordinated ethylene and acetylene complexes adopt a large variety of structures and display significant differences in their ability to insert into the cis bond, an important channel for functionalizing the unsaturated ligand but also for controlling the kinetic stability of the η²-complex. The calculations have also indicated that relative stability of the out- and in-plane ethylene/acetylene complexes was an important element in their overall behaviour. The variety of structures and energy pattern of these η²-coordinated complexes is likely to be the result of a subtle interplay between several electronic and steric interactions. To get insight into this point NBO (natural bond orbital) analyses were performed for all perpendicular (A) and in-plane (B) Au^III and Pt^II complexes that are depicted in Fig. 4.⁴⁶ In both A and B, the metal–ethylene/acetylene bonds involve three interactions: (i) π-donation from the π_CC orbital to a trans orbital ( is the out-of-phase Au(d)–X(p(Cl)/sp(Me)/s(H) combination), (ii) π-back-donation from an M(d) lone pair to the orbital, and (iii) donation from an X(p/sp/s) lone pair to the orbital. The stabilization energy (SE), which measures the strength of these donor–acceptor interactions, was computed from second order perturbation analysis.³⁶ The NLMO (natural localized molecular orbital) associated with the strongest interactions, i.e. i and ii, are shown in Fig. 7 for Au-A-en-Cl and Au-B-en-Cl. The stabilization energies given in Fig. 8a show that the strength of these donor–acceptor interactions follows the trend i ≫ ii > iii, with the latter only present in B. The overall SE is higher in A than in B, when the former is the most stable isomer (X = Cl for both Pt^II and Au^III; Fig. 4). In contrast, the SE is very similar in A and B for X = Me, in line with the small energy difference between them in this case. For X = H, the SE is higher with B, which is consistent with A becoming a transition state. Similar trends were observed in the NBO analysis of the acetylene complexes (see ESI†).

Fig. 7 NLMOs associated with donation and back-donation in Au-A-en-Cl (A) and Au-B-en-Cl (B).

Fig. 8 (a) Stabilization energies associated with donation (blue bars), back-donation (red bars), and back-donation (green bars). (b) Steric exchange energies between ethylene and X^c fragments (orange bars) in Au-A-en-X and Au-B-en-X for X = Cl, Me, and H, and in Pt-A-en-Cl and Pt-B-en-Cl. Energies are in kcal mol⁻¹.

The trend observed in the SE () for Au-A-en-X, Cl > Me > H, can be ascribed to the increasing trans influence of these ligands (Cl < Me < H), which raises the energy of the empty 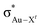orbital in the same order. This effect causes ethylene to coordinate more strongly in Au-A-en-Cl than in Au-A-en-Me and Au-A-en-H (eqn (6) and (7)). In addition to the trans influence of X^t there is a cis influence of X^c, specifically in the geometry of B, which involves donation of electron density from an occupied orbital localized on the ligand (the σ_Au–Xc-bond) to 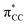. This donation decreases in the order H > Me > Cl as shown by the green bars in Fig. 8a.

The different trend observed in the donation in A (Au–Cl > Au–Me > Au–H) and B (Au–H > Au–Cl > Au–Me) can be understood by considering the steric repulsion between the occupied orbitals of X^c and ethylene by using natural steric analysis.⁴⁷ The steric exchange energies between ethylene and X^c (Fig. 8b)⁴⁸ clearly show a higher steric hindrance in B than in A, which follows the trend H < Me < Cl. In B, the highest exchange energy with X = Cl is mainly due to the interaction between a lone pair on Cl(p) with the CC(π) and the CH bonds of ethylene. This steric hindrance is also reflected in the deviation from 90° of the square planar geometry for Cl^t–Au–Cl^c angle (87.4°) and the Au–ethylene elongation by 0.07 Å when going from A to B (Table 2). In contrast, with X = H and Me, the Au–ethylene distances are shorter in B than in A by 0.04 and 0.13 Å, respectively, in agreement with the higher stabilization energies in the former.

Table 2 Calculated Au–C_ethylene (d) distances (Å) and X^tAuX^c (a) angles (°) for PtCl₃⁻, AuCl₃, AuMe₃ and AuH₃ with ethylene coordinated in parallel (A) and perpendicular (B) orientation

	A		B
	d	a	d	a
a Range of Au–C distances.
PtCl	2.100	90.9	2.170	85.2
AuCl	2.247	91	2.346	87.4
AuMe^a	2.360(3)	88.8	2.321(5)	84.5
AuH	2.391	86.9	2.265	83.2

---

The structural preferences for [MX₂(ethylene)₂]ⁿ⁺ and [MX₂(acetylene)₂]ⁿ⁺ (M = Au, n = 1; M = Pt, n = 0; X = Cl, Me, and H) shown in Table 1 can also be explained by a similar combination of electronic and steric interactions shown in Fig. 7 and 8. In particular, the higher cis influence of hydride (Fig. 8) together with the small size of this atom may account for the geometrical diversity obtained for X = H (Au^I-H₂-en, Au-I′-yn, Pt-G-en, and Pt-I′-yn) compared to X = Cl and Me (F for all X = Cl and F′ for all X = Me). In the latter complexes, both donation and back-donation are involved.⁸ Reduction of the former interaction when moving from Au-F-en-Cl to Au-F′-en-Me (from 130.4 to 70.1 kcal mol⁻¹) due to the highest trans influence of Me is consistent with the longer Au–ethylene distances in Au-F′-en-Me (2.46 Å) compared to Au-F-en-Cl (2.31 Å). The weak interaction of ethylene in Au-E′-en-Me probably explains that distortion from the ideal θ angle, to increase the dispersion forces between the two coordinated ethylenes,⁴⁹ does not imply a loss of energy.

The preference for the perpendicular coordination in [PtCl₃(ethylene)]⁻, [AuX₃(ethylene)], [PtX₂(ethylene)₂], and [AuX₂(ethylene)₂]⁺ for X = Me and Cl obtained in this study (Fig. 4 and Table 1) agree with the observation of this coordination mode in crystal structures of η²-coordinated alkene in mononuclear Pt^II complexes,^6,11 with the crystal structure of [AuMe₂(cod)]^+ 8 and with the NMR characterization of the Au^III-norbornene pincer complex⁹ shown in Scheme 1. According to the present study the two main factors explaining the low success in characterizing η²-alkene complexes of Au compared to Pt are: (1) the weakest Au^III–alkene interaction (eqn (3)), and (2) the lowest energy barrier for inserting the alkene into the Au–X bond in AuX₃L type systems (Fig. 4), which reduce the lifetime of the η²-alkene complexes. The same factors account for the unsuccessful characterization of Au^III-η²-alkyne complexes in which the M–L interaction is even weaker and the insertion energy barrier lower than with alkene. Chelating ligands with larger donor character and steric bulk should thus stabilize these intermediates and facilitate their characterization, due to their ability to strengthen the Au–L interaction and prevent L insertion into Au–X by disfavouring or excluding in-plane coordination. Our X-ray characterized [AuMe₂(cod)]⁺ complex does indeed fall into this category.

Scheme 1 Schematic representation of Au-A-en-Me and Au-F′-en-Me with the Me groups that migrate during the insertion process inside red circles, the ligands trans to them in blue circles, and the nature of the donation in green.

From coordination to insertion

The relation between the coordination mode of L, perpendicular and in-plane, and its reactivity with nucleophiles, intramolecular addition vs. insertion, which was already mentioned in our previous study on the insertion of alkene into [(tpy)Au(OCOCF₃)₂] (Fig. 2a),¹⁷ has been confirmed in this study by showing the direct connection between the in-plane coordination and the TS for the insertion. However, this study shows that the former does not necessarily have to be a real intermediate (energy minimum), but can also be a transition state. In addition, the electronic and steric effects that favour the in-plane coordination (cis effect and low steric bulk) are not the same as the ones favouring the insertion (low directional orbital to facilitate migration) as indicated by the different energy trends of B and C in Fig. 4, e.g. ΔG(Au-B-en-Cl) > ΔG(Au-B-en-Me) while ΔG(Au-C-en-Me) > ΔG(Au-C-en-Cl). Nevertheless with Pt^II, both in-plane coordination of ethylene and its insertion into the Pt–Cl bond are unfavourable, in agreement with experiments showing that the intermolecular addition of nucleophiles is preferred to insertion.⁵⁰

Concerning Au^III, the energy barriers calculated for the insertion of ethylene in [AuX₃(ethylene)] (X = Cl, Me, and H) are 23.5, 16.3 and 8.1 kcal mol⁻¹, respectively. These energies suggest that the insertion process should be feasible at room temperature and may be competitive to intermolecular addition processes. In addition to the nature of the X group, for X = Me, the energy barrier for the insertion process depends on the ligand trans to the Me group that migrates (Scheme 1, blue). Hence, when the trans ligand is Me, i.e. [AuMe₃(ethylene)], the energy barrier is 23.5 kcal mol⁻¹, whereas when this ligand is ethylene, i.e. [AuMe₂(ethylene)₂]⁺, the energy barrier is 39.5 kcal mol⁻¹. This energy difference may be due to the higher trans effect of Me compared to ethylene (Scheme 1, both blue), which weakens the trans Au–Me bond (Scheme 1, red). The lower donation in Au-F′-en-Me (70 kcal mol⁻¹ from the NBO analysis) compared to the 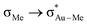donation in Au-A-en-Me (329 kcal mol⁻¹)⁵¹ is also consistent with the difficult migration of the Me group (Scheme 1, red) to ethylene in the former system.

In addition to the trans effect, other factors may determine the preference for an intermolecular nucleophilic addition rather than an insertion process, e.g. the ability of some metal-free ligands to act as external nucleophiles. This would be the case for alcohols, amines, and anions such as CF₃CO₂⁻,^2,17 but not for other anions like alkyl⁻ and H⁻. In the latter case, insertion should be preferred as it has been proposed for the reaction of norbornene with [(P–C)AuMe₂] complex (P–C = cyclometalated diisopropylnaphthylphosphine (Fig. 2b).¹⁸ In this reaction, the cyclometalated system is activated by methyl anion abstraction with B(C₆F₅)₃ prior to norbornene coordination and insertion. To our knowledge, this is the only example in which a product derived from alkene insertion into a Au^III–Me bond has been isolated and characterized. A possible reason for this paucity of precedents is the short-lifetime expected for the insertion products due to fast reductive elimination in tricoodinated Au^III species, as it has been shown in this study (eqn (4) and (5)). This decomposition process is inhibited in the reaction shown in Fig. 2b because of the chelating nature of the ancillary P–C ligand.

Conclusions

Unlike Au^I, the use of Au^III catalysts in organic transformations is still underdeveloped. The main reason for this difference is the higher stability of Au^I complexes compared to Au^III, which are thus known and understood to a lesser extent. In the present work, we have used state-of-the art computational methods in order to shed light onto the coordination of representative unsaturated ligands (L = ethylene and acetylene) to Au^III centres and their subsequent insertions into Au–X bonds (X = Cl, Me, and H). The results showed that the insertion barriers and the π-coordination complexes, which can be either intermediates or transition states, are strongly dependent on the nature of the X ligand. This originates from several stereoelectronic factors, including the donor–acceptor interactions between Au and L and the steric hindrance between X and L. Both rotation and insertion have low- to moderate barriers and the formation of σ-bonded complexes is, in most cases, exoergic. This suggests that these transformations are not prevented by prohibitive thermodynamic or kinetic parameters but rather masked by side reactions, including reductive elimination from the products. This study provides useful insight into the chemistry of the largely used [AuCl₃] catalyst and for the design of new Au^III catalysts with high activity and robustness. Our group is already exploiting these data in the development of Au^III catalyzed alkene and alkyne functionalization.

Acknowledgements

DB, OE, AN, and MT thank the Research Council of Norway for the funding provided through the Centre of Excellence for Theoretical and Computational Chemistry (CTCC; Grant 179568/V30) and for a stipend to AN (Grant 221801/F20), and the Norwegian Metacenter for Computational Science (NOTUR; Grant nn4654k). DB also thanks the EU REA for a Marie Curie Fellowship (Grant CompuWOC/618303).

Notes and references

1. A. Corma, A. Leyva-Pérez and M. Sabater, J. Chem. Rev., 2011, 111, 1657–1712.
2. (a) D. J. Gorin and F. D. Toste, Nature, 2007, 446, 395–403; (b) M. Chiarucci and M. Bandini, Beilstein J. Org. Chem., 2013, 9, 2586–2614.
3. For the first key references of Au^III in homogeneous catalysis see: (a) Y. Fukuda and K. Utimoto, J. Org. Chem., 1991, 56, 3729–3731; (b) A. S. K. Hashmi, L. Schwarz, J.-H. Choi and T. M. Frost, Angew. Chem., Int. Ed., 2000, 39, 2285–2288; (c) A. S. K. Hashmi, T. M. Frost and J. W. Bats, J. Am. Chem. Soc., 2000, 122, 11553–11554.
4. A. S. K. Hashmi, Angew. Chem., Int. Ed., 2010, 49, 5232–5241 . For experimental evidences on in situ reduction of Au^III catalysts: A. S. K. Hashmi, M. C. Blanco, D. Fischer and J. W. Bats, Eur. J. Org. Chem., 2006, 1387–1389.
5. (a) A. Sivaramakrishnaa, H. S. Claytona, M. M. Mogorosi and J. R. Moss, Coord. Chem. Rev., 2010, 254, 2904–2932; (b) H. Schmidbaur and A. Schier, Organometallics, 2010, 29, 2–23; (c) R. E. M. Brooner and R. A. Widenhoefer, Angew. Chem., Int. Ed., 2013, 52, 11714–11724; (d) D.-A. Roşca, J. A. Wright and M. Bochmann, Dalton Trans., 2015, 44, 20785–20807; (e) F. R. Hartley, Compr. Organomet. Chem. III, 1982, 6, 471–762.
6. Recent Pt(II) crystal structures with coordinated ethylene: (a) B. A. McKeown, H. E. Gonzalez, T. B. Gunnoe, T. R. Cundari and M. Sabat, ACS Catal., 2013, 3, 1165–1171; (b) M. Benedetti, C. R. Barone, D. Antonucci, V. M. Vecchio, A. Ienco, L. Maresca, G. Natile and F. P. Fanizzi, Dalton Trans., 2012, 41, 3014–3021; (c) A. Maronna, E. Bindewald, E. Kaifer, H. Wadepohl and H.-J. Himmel, Eur. J. Inorg. Chem., 2011, 1302–1314; (d) P. A. Dub, J.-C. Daran, V. A. Levina, N. V. Belkova, E. S. Shubina and R. Poli, J. Organomet. Chem., 2011, 696, 1174–1183; (e) N. I. Dodoff, M. Lalia-Kantouri, M. Gdaniec, A. Czapik, N. G. Vassilev, L. S. Markova and M. D. Apostolova, J. Coord. Chem., 2012, 65, 688–704.
7. (a) W. C. Zeise, Overs. K. Dan. Vidensk. Selsk. Forh., 1825–1826, 13; (b) W. C. Zeise, Pogg. Ann. Phys., 1827, 9, 632.
8. E. Langseth, M. L. Scheuermann, D. Balcells, W. Kaminsky, K. I. Goldberg, O. Eisenstein, R. H. Heyn and M. Tilset, Angew. Chem., Int. Ed., 2013, 52, 1660–1663.
9. N. Savjani, D.-A. Roşca, M. Schormann and M. Bochmann, Angew. Chem., Int. Ed., 2013, 52, 874–877.
10. (a) J. Chatt, L. A. Duncanson and R. G. Guy, Chem. Indust., 1959, 430; (b) J. Chatt, L. A. Duncanson and R. G. Guy, Nature, 1959, 184, 526–527; (c) G. R. Davies, W. Hewertson, R. H. B. Mais and P. G. Owston, Chem. Commun., 1967, 423.
11. A. König, M. Bette, C. Wagner, R. Lindner and D. Steinborn, Organometallics, 2011, 30, 5919–5927.
12. M. Orchin and P. Schmidt, J. Inorg. Chim. Acta Rev., 1968, 2, 123–135.
13. (a) J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939–2947; (b) G. Leigh, J. Coord. Chem. Rev., 1991, 108, 1–25.
14. T. A. Albright, R. Hoffmann, J. C. Thibeault and D. L. Thorn, J. Am. Chem. Soc., 1979, 101, 3801–3812.
15. (a) K. S. Wheelock, J. H. Nelson, L. C. Cusachs and H. B. Jonassen, J. Am. Chem. Soc., 1970, 92, 5110–5114; (b) P. J. Hay, J. Am. Chem. Soc., 1981, 103, 1390–1393.
16. M. Pernpointner and A. S. K. Hashmi, J. Chem. Theory Comput., 2009, 5, 2717–2725 . For related computational studies, see: M. Lein, M. Rudolph, S. K. Hashmi and P. Schwerdtfeger, Organometallics, 2010, 29, 2206–2210.
17. E. Langseth, A. Nova, E. Aa. Tråseth, F. Rise, S. Øien, R. H. Heyn and M. Tilset, J. Am. Chem. Soc., 2014, 136, 10104–10115.
18. F. Rekhroukh, R. Brousses, A. Amgoune and D. Bourissou, Angew. Chem., Int. Ed., 2015, 54, 1266–1269 . With norbornene a syn-oxyauration has been observed too: M. A. Cinellu, G. Minghetti, F. Cocco, S. Stoccoro, A. Zucca and M. Manassero, Angew. Chem., Int. Ed., 2005, 44, 6892–6895.
19. (a) D. A. Roşca, D. A. Smith, D. L. Hughes and M. Bochmann, Angew. Chem., Int. Ed., 2012, 51, 10643–10646; (b) A. S. K. Hashmi, Angew. Chem., Int. Ed., 2012, 51, 12935–12936.
20. A. Comas-Vives, C. González-Arellano, A. Corma, M. Iglesias, F. Sánchez and G. Ujaque, J. Am. Chem. Soc., 2006, 128, 4756–4765.
21. M. Joost, L. Estevez, S. Mallet-Ladeira, K. Miqueu, A. Amgoune and D. Bourissou, J. Am. Chem. Soc., 2014, 136, 10373–10382.
22. (a) J. A. Akana, K. X. Bhattacharyya, P. Müller and J. P. Sadighi, J. Am. Chem. Soc., 2007, 129, 7736–7737; (b) E. Tsui, P. Müller and J. P. Sadighi, Angew. Chem., Int. Ed., 2008, 47, 8937–8940; (c) M. Joost, P. Gualco, S. Mallet-Ladeira, A. Amgoune and D. Bourissou, Angew. Chem., Int. Ed., 2013, 52, 7160–7163.
23. (a) G. Klatt, R. Xu, M. Pernpointner, L. Molinari, T. Quang Hung, F. Rominger, A. S. K. Hashmi and H. Köppel, Chem. – Eur. J., 2013, 19, 3954–3961; (b) A. Comas-Vives and G. Ujaque, J. Am. Chem. Soc., 2013, 135, 1295–1305.
24. F. R. Hartley, Chem. Rev., 1969, 69, 799–844.
25. B. A. McKeown, H. E. Gonzalez, M. R. Friedfeld, T. B. Gunnoe, T. R. Cundari and M. Sabat, J. Am. Chem. Soc., 2011, 133, 19131–19152 , and references therein.
26. R. Casado, M. Contel, M. Laguna, P. Romero and S. Sanz, J. Am. Chem. Soc., 2003, 125, 11925–11935.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
28. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154123.
30. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406.
31. (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654; (b) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
32. (a) D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244; (b) D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108–164120.
33. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
34. (a) M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123; (b) K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296.
35. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
36. F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor–Acceptor Perspective, Cambridge University Press, Cambridge UK, 2005.
37. IRC calculation from Au-C-en-X finishes with a geometry close to Au-B-en-X. For other examples of connected TSs see: M. Reinhold, J. E. McGrady and R. N. Perutz, J. Am. Chem. Soc., 2004, 126, 5268–5276 , and references therein.
38. The transition states connecting A and B with Cl and Me have the double bond oriented in between perpendicular and parallel.
39. The full geometry optimization of D yields E.
40. The same trend and a bigger difference in energy are found in ref. 5d for the ethylene rotation energy barrier in Au^III and Pt^II with a pincer ligand.
41. Considering δ+⋯δ− versus δ+⋯δ+.
42. (a) F. Canziani, J. Organomet. Chem., 1978, 146, 179–196; (b) M. Benedetti, V. Lamacchia, D. Antonucci, P. Papadia, C. Pacifico, G. Natile and F. P. Fanizzi, Dalton Trans., 2014, 43, 8826–8834.
43. E. Clot, C. Mégret, O. Eisenstein and R. N. Perutz, J. Am. Chem. Soc., 2006, 128, 8350–8357.
44. W. J. Wolf, M. S. Winston and F. D. Toste, Nat. Chem., 2014, 6, 159–164.
45. A. Nijamudheen, S. Karmakar and A. Datta, Chem. – Eur. J., 2014, 20, 14650–14658.
46. In order to compare the NBO results for all A-B systems, the same Lewis structure has been used, in which MX₃(ethylene) is divided in three fragments: MX^cX^t, ethylene and X^c (X^c and X^t are the X in cis and the X in trans to ethylene, respectively).
47. J. K. Badenhoop and F. Weinhold, J. Chem. Phys., 1997, 107, 5406–5421.
48. This analysis has been performed considering the full fragments ethylene and X^c.
49. The ΔG between E′-en-Me and [AuMe₂(ethylene)₂]⁺ with the C^Me-Au-CC dihedral angle frozen at 90° is 0.5 kcal mol⁻¹.
50. A. R. Chianese, S. J. Lee and M. R. Gagné, Angew. Chem., Int. Ed., 2007, 46, 4042–4059.
51. These values should not be taken literally but only in a relative manner.

---

Footnote

† Electronic supplementary information (ESI) available: Further computational details available include: (i) DFT functional benchmarking, (ii) complete energy profiles for [AuX₃(ethylene)] with X = Cl and Me, (iii) NBO analysis with L = acetylene and (iv) optimized coordinates and energies. See DOI: 10.1039/c5dt05014f

---