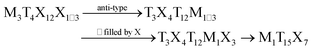AlPd₁₅B₇: a new superconducting cage-compound with an anti-Yb₃Rh₄Sn₁₃-type of structure

Abstract

A new intermetallic compound AlPd₁₅B₇ was synthesized by arc-melting the stoichiometric mixture of the elements. Single crystal X-ray diffraction data of ternary metal-rich boride reveal a new type of structure with the space group Ia3̄d and the lattice parameter a = 16.4466(3) Å. It adopts a filled anti-Yb₃Rh₄Sn₁₃-type structure, where the positions corresponding to 3Yb, 4Rh and 13Sn atoms are occupied by 3Pd, 4B, and 1Al + 12 Pd, respectively and 3B additionally at interstitial sites. Magnetic susceptibility, electrical resistivity, and specific heat measurements reveal bulk superconductivity with a critical temperature T_c ≈ 2.9 K. Electronic structure calculations show that Pd 4d and B 2p states dominate the density of states (DOS) at the Fermi level E_F.

---

Introduction

In the early 1980s, Remeika and co-workers discovered a family of M₃T₄X₁₃ cage-compounds (where M = rare-earth, alkaline-earth, or actinide metal, T = transition metal, and X = In or group-IV elements) crystallizing with a primitive cubic Yb₃Rh₄Sn₁₃-type structure (space group Pm3̄n).^1–4 They became an object of numerous studies, mostly owing to the interesting interplay between magnetic and superconducting properties.^1,5–9 The crystal structures of both Remeika M₃T₄X₁₃ phases and filled-skutterudites^10,11 are derivatives of the simple perovskite-type structure, and show similar arrays of corner-sharing trigonal prisms/antiprisms (octahedra) enclosing icosahedral voids. For more details about their structural relationships, we refer to ref. 12 (and references therein). In recent studies,^12–14 several new cubic, tetragonal, rhombohedral and monoclinic distorted variants of the Remeika prototype with a Pt–Ge framework were reported. In these structures, distortions occur exclusively in the Ge-framework, while M and Pt atoms remain in their original positions. In the M₃T₄X₁₃ structures, twelve X atoms form icosahedra filled by one remaining X atom, T atoms reside in trigonal prisms formed by two neighboring [X₁₂] icosahedra, and M atoms are encapsulated in cubooctahedra built by X atoms (see Fig. S3 in the ESI†). Owing to the variety of M, T, and X elements forming such compounds without major changes in the crystal structures, substitution by elements not only limited to the above mentioned groups should be possible.

In this study, we report the boride AlPd₁₅B₇ with a new type of structure, which is closely related to the Yb₃Rh₄Sn₁₃ prototype. Physical property measurements reveal superconducting behavior of this new boride with T_c ≈ 2.9 K. The thermodynamic properties are compatible with an s-wave energy gap conventional superconductivity and moderate electron–phonon coupling.

Experimental section

Sample preparation

The samples with a nominal composition of AlPd₁₅B₇ were synthesized by arc-melting of aluminum (Chempur, 99.9999 mass%) and palladium (Chempur, 99.9 mass%) foils and crystalline boron powder (Alfa Aesar, 99.999 mass%). The obtained button was remelted several times to obtain a homogeneous sample. The weight loss during arc-melting was less than 0.1 mass%. All above operations were performed inside an argon-filled glove box (p(O₂/H₂O) ≤ 1 ppm). A nearly single phase sample was obtained. The resulting sample is stable in air for long time.

Powder and single-crystal X-ray diffraction

Due to the ductility, stress annealing of ground powders was performed at 840 °C for 1.5 h to obtain powder diffraction patterns with sharper and better resolved diffraction peaks. Powder X-ray diffraction (XRD) data were collected on a HUBER G670 imaging plate Guinier camera (Cu K_α1 radiation, λ = 1.540598 Å). Phase analysis and indexing were performed within the WinXPow program package.¹⁵ Lattice parameters were refined by least-squares fitting with LaB₆ internal standard correction within the program package WinCSD.¹⁶

Single crystals were selected from the stress-annealed crushed sample. Single crystal XRD data were collected on a Rigaku AFC7 diffraction system equipped with a Saturn 724+ CCD detector (Mo K_α radiation, λ = 0.71073 Å). Absorption correction was made using a multi-scan procedure. The crystal structure was solved by a direct phase determination method and refined by a full-matrix least-squares procedure within the program package WinCSD.¹⁶ Details of the single crystal XRD data collection are listed in Table 1.

Table 1 Crystallographic data for AlPd₁₅B₇

Composition	AlPd15B7
Space group	Ia3̄d
Lattice parameters
a (Å)	16.4466(3)
V (Å^3)	4448.7(3)
Formula unit per cell, Z	16
Calculated density (g cm^−3)	10.14
Diffraction system	Rigaku AFC7
Radiation; λ (Å)	Mo Kα; 0.71073 Å
2θmax (°)	67.07
Absorption coefficient (mm^−1)	23.07
N(hkl)measured	18 108
N(hkl)unique	730
N(hkl)observed (Fhkl > 4σ(F))	718
R int/Rσ	0.053/0.037
Refined parameters	32
R F/wRF^2	0.058/0.064
Extinction coefficient	0.00026(2)
Residual electron density (e Å^−3)	+1.1; −0.8

---

Metallography

A small piece of the as-cast AlPd₁₅B₇ sample was embedded in a conductive resin and then subjected to a multistep grinding and polishing process to achieve a high-quality surface. The microstructure observations were performed on an optical microscope (Axioplan 2, Zeiss) as well as on a scanning electron microscope (JSM-7800F, JEOL). The chemical composition of the observed phase was analysed by means of energy dispersive X-ray spectroscopy (EDXS, Quantax 400 EDXS system, Silicon Drift Detector, Bruker) and wavelength dispersive X-ray spectroscopy (WDXS, SX 100, Cameca) using Al K_α, Pd L_α, and B K_α signals with elemental Al and Pd₃B as standards. The Al : Pd atomic ratio of the studied phase from EDXS and its composition from WDXS were measured to be 0.9(1) : 15.0(1) and Al_4.6(2)Pd_66.5(2)B_28.9(1), respectively, in good accordance with the theoretical values (1 : 15 and Al_4.35Pd_65.22B_30.43, respectively).

Physical properties

The magnetization data of a polycrystalline AlPd₁₅B₇ sample were collected in external fields μ₀H ranging from 2 mT to 7 T and temperatures between 1.8 K and 400 K on a SQUID magnetometer (MPMS-XL7, Quantum Design). The electrical resistivity was measured using a four-point ac method between 1.8 K and 320 K (PPMS, Quantum Design) on a small bar (1 mm × 1 mm × 6.5 mm). The heat capacity was measured by means of a relaxation-type calorimeter on a PPMS in external fields μ₀H up to 0.5 T between 0.35 and 320 K.

Electronic structure calculations

The scalar-relativistic band-structure of AlPd₁₅B₇ was calculated within the local-density approximation (LDA) of density functional theory (DFT) using the full-potential local-orbital FPLO code (version 9.01-35).¹⁷ The calculation was performed by employing the exchange-correlation potential of Perdew and Wang¹⁸ and using the experimental structural data from Table 2. The first Brillouin zone was sampled by a mesh of 12 × 12 × 12 (1728) k points.

Table 2 Atomic coordinates and isotropic displacement parameters (in Ų) for AlPd₁₅B₇

Atom	Site	x	y	z	B iso/Beq^a
a B eq = 1/3[a*^2a^2B11 + b*^2b^2B22 + c*^2c^2B33 + 2aba*b*(cos γ)B12 + 2aca*c*(cos β)B13 + 2bcb*c*(cos α)B23].
Al	16a	0	0	0	1.08(8)
Pd1	48g	1/8	0.24484(6)	0.00516(6)	1.23(2)
Pd2	96h	0.00090(6)	0.14693(6)	0.07718(6)	0.99(2)
Pd3	96h	0.10758(6)	0.24514(6)	0.33770(6)	1.13(2)
B1	16b	1/8	1/8	1/8	1.4(5)
B2	48f	0.263(2)	0	1/4	1.5(3)
B3	48g	1/8	0.619(1)	0.631(1)	1.4(3)

---

Results and discussion

Crystal structure determination

As shown in Fig. 1 and Fig. S1 (in the ESI†), the XRD patterns of the ground powders of an as-cast AlPd₁₅B₇ sample with and without stress-annealing reveal no difference between them besides peaks broadening in the latter one. As revealed by Fig. S2 in the ESI,† the content of impurities in the as-cast sample is less than 1 vol%. The strong reflections could be indexed in a simple cubic unit cell with lattice parameter a = 8.2233(2) Å. However, as one can see as an example in the inset of Fig. 1, there are still many reflections that could not be indexed in this unit cell, revealing the appearance of a superstructure. Taking these reflections into account, a body centered cubic unit cell with lattice parameter a = 16.4466(3) Å is obtained. Subsequently, single crystals were selected for XRD experiments.

Fig. 1 Experimental (black circles) and calculated (red line) powder XRD patterns of an as-cast AlPd₁₅B₇ sample after grinding and subsequent stress-annealing at 840 °C for 1.5 h. Peak positions of AlPd₁₅B₇ are given by black ticks; the difference plot is shown as a black line in the bottom. The inset shows the 2θ-range from 45.8° to 52°, where the reflections corresponding to the superstructure are marked by asterisks (see text).

Details on single crystal XRD data collection for AlPd₁₅B₇ are listed in Table 1. Analysis of the reflection intensities and the extinction conditions confirm the appearance of the superstructure, indicating centrosymmetry and only one possible space group Ia3̄d. Positions of the heavy Pd and Al atoms and the light B atoms were acquired by a direct phase determination procedure and from difference Fourier maps, respectively. Anisotropic displacement parameters for all the Al and Pd atoms were refined. Final atomic coordinates and anisotropic atomic displacement parameters are listed in Tables 2 and 3, respectively. Moreover, diffraction data were also collected for single crystals selected from powders of the as-cast sample without stress annealing, and reveal the same structure solution result and only larger residual values due to broadening of the reflections. The acquired composition is in good agreement with the compositions from the EDXS and WDXS analysis.

Table 3 Anisotropic displacement parameters (in Ų) for AlPd₁₅B₇

Atom	B 11	B 22	B 33	B 12	B 13	B 23
Al	1.1(1)	B 11	B 11	−0.06(15)	B 12	B 12
Pd1	1.09(5)	1.31(4)	B 22	−0.11(3)	B 12	0.12(4)
Pd2	0.93(4)	1.09(4)	0.96(4)	0.01(2)	−0.02(2)	0
Pd3	1.26(4)	1.08(4)	1.06(4)	−0.09(3)	−0.02(3)	−0.14(3)

---

Crystal structure

AlPd₁₅B₇ crystallizes with a new type of structure, which can be regarded as a filled anti-Yb₃Rh₄Sn₁₃ structure. The crystal structures of AlPd₁₅B₇ and Yb₃Rh₄Sn₁₃ are shown in Fig. 2a and Fig. S3 in the ESI,† respectively. The group–subgroup relationship between them is shown in Fig. 2b. The crystallographic positions for 3Yb, 4Rh and 13Sn atoms in the Yb₃Rh₄Sn₁₃ structure¹ are now occupied by 3Pd, 4B, and 1Al + 12Pd atoms in the AlPd₁₅B₇ structure, respectively. The octahedra formed by Yb and Sn atoms are empty in the Yb₃Rh₄Sn₁₃-type structure, whereas the corresponding octahedra solely formed by Pd atoms are filled by additional B atoms in the AlPd₁₅B₇ structure. The transformation between these two types of structures can be described as:
where M, T, and X are Yb, Rh, and Sn in Yb₃Rh₄Sn₁₃, and Al, Pd and B in AlPd₁₅B₇. Different from Yb₃Rh₄Sn₁₃, the lattice parameters of AlPd₁₅B₇ are doubled and the space group changes from Pm3̄n to Ia3̄d, due to the shift of the Pd atoms from some special positions. As one can see in Fig. 6 in ref. 13, the relationship between many derivatives of the primitive cubic Yb₃Rh₄Sn₁₃-type of structure (e.g. La₃Rh₄Sn₁₃ (I4₁32), Ca₃Pt_4+xGe_13−y (I2₁3),¹² HT-Y₃Pt₄Ge₁₃ (R3c),¹³ Yb₃Pt₄Ge₁₃ (P4₂cm),¹² and LT-Y₃Pt₄Ge₁₃ (Cc)¹⁴) can be understood within a group–subgroup scheme. AlPd₁₅B₇ crystallizes with the space group Ia3̄d, which links the space groups Pm3̄n and I4₁32 via the indices of k4 (klassengleiche) and t2 (translationengleiche) symmetry reductions, respectively.

Fig. 2 (a) Crystal structure of AlPd₁₅B₇. For a better visualization, only a part of the structure in one unit cell is shown. [Al@Pd₁₂] icosahedra – light gray; distorted [B@Pd₆] trigonal prisms – dark gray; [B@Pd₆] octahedra – blue. (b) group–subgroup relationship between the structures of Yb₃Rh₄Sn₁₃ and AlPd₁₅B₇ (see text). For better visualization the coordinates for AlPd₁₅B₇ are not standardized, like those given in Table 2.

The AlPd₁₅B₇ structure is shown in Fig. 2a, and interatomic distances are listed in Table S1 in the ESI.† In such a structural arrangement, similar to Al residing in [Ni₁₂] icosahedra in the AlNi₉B₈ structure,¹⁹ each Al atom resides in a distorted [Pd₁₂] icosahedron, consisting of 6Pd2 and 6Pd3 atoms, with the Al–Pd and Pd–Pd distances ranging from 2.730 Å to 2.752 Å, and from 2.714 Å to 2.955 Å, respectively. The empty spaces between the icosahedra are occupied by the Pd1, B1, B2 and B3 atoms. Each [Al@Pd₁₂] icosahedron interconnects with 14 neighboring [Al@Pd₁₂] icosahedra via 8 distorted corner-sharing trigonal prisms and 6 distorted octahedra. The two sorts of corner-sharing [Pd₆] trigonal prisms, formed by 6 Pd2 atoms or 2Pd2 and 4Pd3 atoms, are centered by the B1 or B3 atoms, respectively. In a [B1Pd₆] trigonal prism, the Pd2–Pd2 distances are 2.850 Å and 2.942 Å, and the Pd–B distance is 2.217 Å; in a [B3Pd₆] trigonal prism, the Pd–Pd distances are in the range of 2.885 Å to 2.955 Å, the Pd2–B3 distance is 2.139 Å, and the Pd3–B3 distances are 2.157 Å and 2.28 Å. Each [Pd₆] octahedron, formed by 2Pd1, 2Pd2, and 2Pd3 atoms, is centered by a B2 atom, with Pd–Pd distances and Pd–B distances ranging from 2.714 Å to 3.5423 Å and from 2.08 Å to 2.252 Å, respectively. These kinds of metal–atom coordination of boron are commonly observed in borides.^20,21 In Pd₃B (Fe₃C type of structure),²² B resides in trigonal prisms with Pd–B distances of 2.166 Å to 2.180 Å; in Pd₂B (anti-CaCl₂ type of structure),²³ B centers Pd octahedra with Pd–B distances of 2.104 Å to 2.122 Å. In comparison with the sum of atomic radii of pure elements (r_B = 0.83 Å, r_Al = 1.43 Å, and r_Pd = 1.38 Å (ref. 24)), the Al–Pd distances are shorter than the sum of atomic radii of Al and Pd, the Pd–Pd distances obviously deviate from the two-fold atomic radius of Pd, and the shortest and longest Pd–B distances are 6% shorter and ∼3% longer than the sum of atomic radii of Pd and B, respectively. Coordination polyhedra of all the atoms in AlPd₁₅B₇ are shown in Fig. S4 in the ESI.†

Physical properties

The magnetic susceptibility of AlPd₁₅B₇ in an external field of μ₀H = 7 T is shown in the inset of Fig. 3, revealing that it is a diamagnet with an extrapolated value of χ₀ = −2.0 × 10⁻⁴ emu mol⁻¹ at T = 0. The slight upturn towards low temperature is probably due to minor paramagnetic impurities or point defects.

Fig. 3 Magnetic susceptibility for AlPd₁₅B₇ in a field μ₀H = 2 mT measured during warming after zero-field cooling (zfc) and during field cooling (fc). The inset shows the magnetic susceptibility in a field μ₀H = 7 T.

The temperature dependence of the zero-field-cooled (zfc) and field-cooled (fc) magnetic susceptibility of AlPd₁₅B₇ in an external field of μ₀H = 2 mT is given in Fig. 3, indicating a superconducting transition. The transition temperature was determined via a tangent to the steepest slope of χ_zfc(T), resulting in T_c^mag = 2.78 K. Considering the demagnetization correction, the diamagnetic response in zfc is close to complete. The fc signal (Meißner effect) is much weaker, which is due to strong flux line pinning in the type-II superconductor (see below).

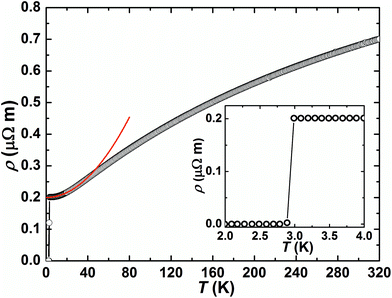
As shown in Fig. 4, the electrical resistivity of AlPd₁₅B₇ increases with increasing temperature in the range of 3.0–320 K, revealing a metallic behavior of this compound. For 4 K < T < 40 K, it can be fitted to ρ₀ + A_FLT² with a residual resistivity ρ₀ = 0.20(1) μΩ m from impurity scattering, and the cross section of quasiparticle–quasiparticle scattering A_FL = 3.96(3) × 10⁻⁵ μΩ m K⁻². The room-temperature resistivity ρ(300 K) is 0.68 μΩ m, and the residual resistivity ratio RRR = 3.4 indicates moderate quality of the investigated polycrystalline sample. As revealed by the inset of Fig. 4, a sharp superconducting transition can be observed, and the resistivity drops to zero at T ^res_c = 2.89 K.

Fig. 4 The temperature-dependent electrical resistivity ρ(T) for AlPd₁₅B₇. The solid line shows a fitting by ρ₀ + A_FLT² in the range of 4 K < T < 40 K; the inset shows a magnification for low temperatures.

The specific heat c_p/T vs. T for AlPd₁₅B₇ in the temperature range 0.35–4.0 K and in various magnetic fields is shown in Fig. 5a. For zero-field, a sizable sharp step-like anomaly confirms the bulk nature of the superconductivity. The normal-state specific heat (Fig. 5b) can be described by c_p,n(T) = γ_totT + βT³ + δT⁵ in the temperature range 0.5–5 K, where γ_tot is the Sommerfeld coefficient of the electronic heat capacity, and βT³ + δT⁵ are the first terms of the harmonic lattice approximation for the phonon contribution. The resulting parameters are γ_tot = 28.3(1) mJ mol⁻¹ K⁻² and β = 1.38(2) mJ mol⁻¹ K⁻⁴, which corresponds to an initial Debye temperature Θ_D(0) = 319 K, and δ = 2.86(6) × 10⁻⁵ mol⁻¹ K⁻⁶.

Fig. 5 (a) Molar specific heat c_p/T of AlPd₁₅B₇ in various magnetic fields; (b) the low-temperature normal-state c_p(T) for AlPd₁₅B₇ together with the fit to c_p = γ_totT + βT³ + δT⁵; (c) fitting of the difference specific heat Δc_p = c_el – γ_totT based upon the BSC theory; (d) upper critical field μ₀H_c2 of AlPd₁₅B₇vs. T derived from the midpoints of the superconducting transitions in c_p(T, H).

The electronic contribution c_el(T, H) below T_c can be analyzed by subtracting the lattice terms βT³ + δT⁵. Fig. 5c shows Δc_p = c_el – γ_totT which is well described by the BCS theory (for weak electron–phonon coupling) in the whole temperature range. The resulting parameters are the jump Δc_p/T_c = 37.5 mJ mol⁻¹ K⁻², the transition midpoint T^cal_c = 2.796 K, and the width of the transition of 0.026 T_c. The ratio Δc_p/(γ_totT_c) of 1.32 is somewhat lower than the value 1.43 from the BCS theory. At the lowest temperatures (in the range 0.35–0.70 K) c_el(T) is well fitted by (as shown in Fig S5a in the ESI†). Such exponential behavior is expected for an s-wave superconductor without nodes of the gap, as in the BCS theory. The resulting parameters for zero field are γ₀ = 2.17 mJ mol⁻¹ K⁻² and the energy gap ratio Δ/k_BT_c = 1.08. The non-zero γ₀ is probably due to the presence of a non-superconducting metallic impurity phase. We may thus correct the normal state electronic specific heat coefficient by γ_n = γ_tot − γ₀. The corrected value for the jump Δc_p/(γ_nT_c) = 1.44 reproduces even better the weak-coupling BCS value 1.43. However, the energy gap ratio Δ/k_BT_c observed at the lowest temperatures is much smaller than expected from BCS theory (Δ/k_BT_c = 1.76). It is therefore possible that AlPd₁₅B₇ needs to be described within a two-gap model. The resolution of the present specific heat data, due to the small available mass for the study, is insufficient for a more sophisticated analysis.

The DFT calculations reveal a DOS at the Fermi level N(E_F) = 7.9 states eV⁻¹ f.u.⁻¹ (see below), converting to a “bare” Sommerfeld coefficient of the electronic specific heat γ_bare = 18.6 mJ mol⁻¹ K⁻². The electron–phonon coupling parameter λ in the relation γ_N = (1 + λ) γ_bare is calculated to be 0.40. λ can also be estimated from the McMillan formula ln(1.45T_c/Θ_D) = −1.04 (1 + λ)/[λ − μ*(1 + 0.62λ)]. Assuming the common value μ* = 0.15, λ results as 0.58, which is somewhat larger than the above value.

The fitted Sommerfeld parameters γ(H) − γ₀, extrapolated to T = 0, were plotted against the fields (Fig. S5b in the ESI†), showing a linear relationship with the magnetic fields. This also indicates a typical s-wave gap for AlPd₁₅B₇. The upper critical field values were estimated from the midpoints of superconducting transition in c_p(T, μ₀H), as shown in Fig. 5d. It is obvious that T_c(μ₀H) varies almost linearly with μ₀H. This most simple extrapolation results in μ₀H_c2(0) ≈ 500(100) mT.

Electronic structure

The total and partial (atomic and orbital resolved) density of states (DOS) for AlPd₁₅B₇ are shown in Fig. 6(a–c). Similar to the electronic structures of the M₃Pt₄Ge₁₃ compounds,^12,13 the Fermi level E_F for AlPd₁₅B₇ is located close to a dip in the DOS. Thus, the system is a metal with 7.9 states eV⁻¹ f.u.⁻¹ at E_F. This DOS is mostly due to the contributions of the Pd 4d (∼71%) and the B 2p (∼25%) states. The broad valence band (∼7 eV) in the electronic structure of AlPd₁₅B₇ is dominated by Pd 4d states (Fig. 6b) with sizeable B 2p contributions (Fig. 6c) at lower energies (between −7 eV and −3.5 eV). Furthermore, the lowest lying separate band (between −11 eV and −7.5 eV) is mainly formed by B 2s and Pd 4d states. All this is related to the covalent bonding in the Pd–B framework. Al contributions to the valence band are negligibly small. Interestingly, a narrow separate band (∼0.3 eV) centered at −7.1 eV is mostly due to 4d states of Pd2 and Pd3 as well as Al 3s. Obviously, it reflects covalent interaction of Al and Pd atoms within the [Al@Pd₁₂] icosahedra (Fig. 2). The electronic band structure of AlPd₁₅B₇ is reminiscent of the electronic structures of such Pd-rich borides as Pd₃B and SrPd₄B.²⁵ They also possess a broad valence band dominated by Pd 4d and B 2p states followed by a separate low energy band due to the mixing of B 2s and Pd 4d states. The differences are that for AlPd₁₅B₇ a larger DOS at E_F as well as an additional narrow band at −7.1 eV are observed.

Fig. 6 (a) Total and atom resolved electronic density of states (DOS) for AlPd₁₅B₇. Orbital resolved DOS for (b) palladium and (c) boron atoms.

Conclusions

We gratefully acknowledge Prof. Yu. Grin's interest and steady support. A new ternary boride AlPd₁₅B₇, with a filled anti-Yb₃Rh₄Sn₁₃-type structure, has been synthesized by arc-melting mixtures of elements, and its crystal structure was determined from the single-crystal X-ray diffraction data. In this structure, the Al atoms reside in the [Pd₁₂] icosahedra, and each icosahedron interconnects with 14 neighboring [Pd₁₂] icosahedra, forming 8 corner-sharing trigonal prisms and 6 octahedra, which are all filled by the B atoms. In comparison, the corresponding octahedra are empty in the Yb₃Rh₄Sn₁₃-type structure.

Magnetic susceptibility, electrical resistivity, and specific heat measurements show a superconducting transition of AlPd₁₅B₇ at a T_c of about 2.9 K. The specific heat measurements reveal AlPd₁₅B₇ to be a conventional s-wave superconductor with weak electron–phonon coupling according to the BCS theory. Electronic structure calculations by DFT reveal that the DOS at E_F is dominated by d states.

AlPd₁₅B₇ is the first boride with a crystal structure comprising the framework of the Remeika Yb₃Rh₄Sn₁₃ prototype but being decorated by completely different types of elements. The occurrence of this new type of structure suggests that the constituting elements in the Remeika structure framework could be extended to a variety of elements in future investigations.

Acknowledgements

We thank Mr S. Hückmann and Dr H. Borrmann for performing powder X-ray diffraction measurements, Ms. P. Scheppan, Ms. M. Eckert and Ms. S. Kostmann for the metallographic analysis, and Mr R. Koban for physical property measurements.

References

1. J. L. Hodeau, J. Chenavas, M. Marezio and J. P. Remeika, Solid State Commun., 1980, 36, 839.
2. P. Villars, Pearson's Handbook, Crystallographic Data for Intermetallic Phases, Materials Park, OH, 1997.
3. J. M. Vandenberg, Mater. Res. Bull., 1980, 15, 835.
4. S. Miraglia, J. L. Hodeau, M. Marezio, C. Laviron, M. Ghedira and G. P. Espinosa, J. Solid State Chem., 1986, 63, 358.
5. G. K. Shenoy, B. D. Dunlap and F. Y. Fradin, Ternary Superconductors, Elsevier, North-Holland, Amsterdam, 1981.
6. J. P. Remeika, G. P. Espinosa, A. S. Cooper, H. Barz, J. M. Rowell, D. B. McWhan, J. M. Vandenberg, D. E. Moncton, Z. Fisk, L. D. Woolf, H. C. Hamaker, M. B. Maple, G. Shirane and W. Thomlinson, Solid State Commun., 1980, 34, 923.
7. Y. Mudryk, A. Grytsiv, P. Rogl, C. Dusek, A. Galatanu, E. Idl, H. Michor, E. Bauer, C. Godart, D. Kaczorowski, L. Romaka and O. Bodak, J. Phys.: Condens. Matter, 2001, 13, 7391.
8. N. Kase, H. Hayamizu and J. Akimitsu, Phys. Rev. B: Condens. Matter, 2011, 83, 184509.
9. B. K. Rai, I. W. H. Oswald, J. K. Wang, G. T. McCandless, J. Y. Chan and E. Morosan, Chem. Mater., 2015, 27, 2488.
10. W. Jeitschko and D. Braun, Acta Crystallogr., 1977, 33, 3401.
11. R. Gumeniuk, H. Borrmann, A. Ormeci, H. Rosner, W. Schnelle, M. Nicklas, Yu. Grin and A. Leithe-Jasper, Z. Kristallogr., 2010, 225, 531.
12. R. Gumeniuk, L. Akselrud, K. O. Kvashnina, W. Schnelle, A. A. Tsirlin, C. Curfs, H. Rosner, M. Schöneich, U. Burkhardt, U. Schwarz, Yu. Grin and A. Leithe-Jasper, Dalton Trans., 2012, 41, 6299.
13. R. Gumeniuk, M. Schöneich, K. O. Kvashnina, L. Akselrud, A. A. Tsirlin, M. Nicklas, W. Schnelle, O. Janson, Q. Zheng, C. Curfs, U. Burkhardt, U. Schwarz and A. Leithe-Jasper, Dalton Trans., 2015, 44, 5638.
14. R. Gumeniuk, M. Nicklas, L. Akselrud, W. Schnelle, U. Schwarz, A. A. Tsirlin, A. Leithe-Jasper and Yu. Grin, Phys. Rev. B, 2013, 87, 224502.
15. WinXPow, STOE and Cie GmbH, Darmstadt, 2003.
16. L. Akselrud and Yu. Grin, J. Appl. Crystallogr., 2014, 47, 803.
17. K. Koepernik and H. Eschrig, Phys. Rev. B, 1999, 59, 1743.
18. J. P. Perdew and Y. Wang, Phys. Rev. B, 1992, 45, 13244.
19. Q. Zheng, F. R. Wagner, A. Ormeci, Yu. Prots, U. Burkhardt, M. Schmidt, W. Schnelle, Yu. Grin and A. Leithe-Jasper, Chem. – Eur. J., 2015, 21, 16532.
20. Yu. B. Kuz'ma, Crystallochemistry of Borides, Lviv University Publishers, Lviv, 1983.
21. P. Rogl, in Inorganic Reactions and Methods, ed. A. P. Hagen, Wiley, 1991.
22. E. Stenberg, Acta Chem. Scand., 1961, 15, 861.
23. L.-E. Tergenius and T. Lundström, J. Solid State Chem., 1980, 31, 361.
24. J. Emsley, The Elements, Clarendon Press, Oxford, 1998.
25. R. Gumeniuk, M. Schmitt, W. Schnelle, U. Burkhardt, H. Rosner and A. Leithe-Jasper, Z. Anorg. Allg. Chem., 2010, 636, 954.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1440657. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt04751j

---