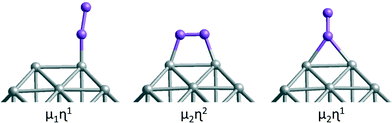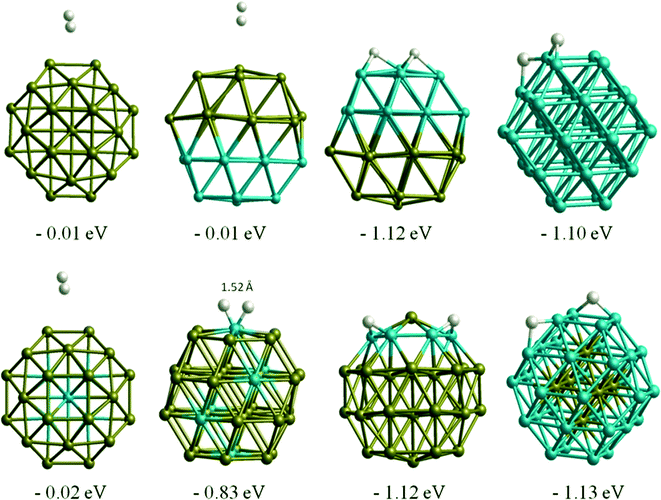Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A DFT study of molecular adsorption on Au–Rh nanoalloys
Ilker
Demiroglu
a,
Z. Y.
Li
b,
Laurent
Piccolo
c and
Roy L.
Johnston
*a
aSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK. E-mail: r.l.johnston@bham.ac.uk
bNanoscale Physics Research Laboratory, School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
cInstitut de recherches sur la catalyse et l'environnement de Lyon (IRCELYON) and UMR 5256 CNRS & Université Claude Bernard Lyon 1, 2 avenue Albert Einstein, F-69626 Villeurbanne, France
First published on 30th June 2016
Abstract
Density functional theory calculations are performed to investigate both mixing and adsorption properties of 38-atom and 79-atom Au–Rh nanoalloys at the nanoscale. The RhcoreAushell and RhballAucup isomers are found to be energetically favourable with respect to other isomers. The adsorption strengths of reactive species such as H2, O2 and CO are found to be greater on the Rh part than on the Au part of the nanoalloys and therefore a core–shell inversion is found to be feasible under a molecular environment. It is also found that underlying Rh atoms decrease the adsorption strength on the Au part whereas underlying Au atoms increase it on the Rh part of the nanoalloys. The strain, alloying and relaxation effects on adsorption strength are characterized using a sequential approach and their competing nature is demonstrated for the Au–Rh bimetallic system.
Introduction
At the nanoscale, catalytic as well as other properties of materials are often different from those of their bulk counterparts due to quantum size effects and geometric effects. In addition, since heterogeneous catalytic reactions take place on surfaces, nanoparticles are ideal catalysts due to their high surface/volume ratio. Moreover, they also possess a higher proportion of less-coordinated active sites. One example is gold, which in the bulk phase is catalytically inert for most heterogeneous reactions,1 but which has been found to show exceptional catalytic properties toward CO oxidation and a number of other reactions for ultra-fine particles.2Alloying different metals opens a way to achieve even greater potential for nanoparticles as catalysts, since additional structural motifs may enhance chemical and physical properties due to synergistic effects and properties can be tuned by varying composition and chemical ordering.3 Another advantage of multimetallic nanoalloys is the possibility of reducing the cost by mixing an efficient, but expensive catalyst—e.g. rhodium (Rh)—with another, cheaper metal without decreasing, or sometimes even improving catalytic performance.
The catalytic performance of multimetallic nanoalloys depends also on the chemical ordering in addition to the geometry and size of the particles. In the literature it has been shown both theoretically and experimentally that binding ligands can change the chemical ordering or the structure of nanoparticles, thin films, and bulk surfaces.4–11 For example, Andersson et al. have shown that CO adsorption on a Cu–Pt near-surface alloy drives the less reactive Cu to the surface, although CO does not bind directly to the surface Cu.4 Tao et al. have shown that reversible core–shell inversion takes place for Pd–Rh nanoparticles depending on which molecules are chemisorbed and suggested that this behaviour can lead to the design of “smart catalysts” that may catalyse different reactions depending on the reaction environment.5,6 Theoretically, West et al. have studied the segregation patterns of several bimetallic couples such as Au–Pd, Pd–Pt, Cu–Pt, and Pd–Rh and presented a model for relating the changes in the chemical ordering of nanoalloys in reactive environments with metal–ligand interaction strengths.7,8
Understanding metal–adsorbate interactions is important not only for determining the possible chemical ordering changes but also because adsorption is a key step in catalytic reactions. If reactive species are adsorbed too weakly, they may not be activated to undergo reaction, whereas if they are adsorbed too strongly, the desorption rate decreases and poisoning may occur (Sabatier's principle). Metal–ligand interactions have been extensively studied for metal surfaces both experimentally and theoretically and the d-band model1,12,13 has been shown to be particularly useful in understanding bond formation and trends in reactivity. According to this model, the d-band centre of the metal surface or particle is used as a descriptor to anticipate metal–adsorbate interaction strength. It is known from the literature that upon alloying metals both strain14,15 and ligand16,17 effects can broaden or narrow the surface d-band and in turn change the position of the d-band centre, although it is difficult to separate these effects for extended surfaces.18 However, there are known exceptions to the d-band model, when the ligand has an almost completely filled valence shell and the metal surface has a nearly full d-band.19 One should be careful, both for nanoparticles and extended surfaces, since there also exist relaxation20,21 and/or reconstruction effects,22–24 which may be induced by adsorbates. Moreover, for nanoparticles, low-coordinated sites (corners and edges) also complicate the picture relative to the extended surfaces.25
Rhodium is an important catalyst due to its efficiency in diverse reactions including hydrogenation, carbonylation, hydroformylation, and oxidation.26 However it is scarce and expensive, therefore mixing with another metal which is more abundant and/or less expensive is desirable. Rhodium and gold are immiscible in the bulk,27 however, alloying at nanoscale is possible but has been less extensively studied.28–34 Konuspayeva et al. synthesized ca. 3 nm sized Au–Rh bimetallic particles on well-defined rutile-titania nanorods by colloidal methods.29 The authors reported that pre-calcination of Au–Rh nanoparticles mostly lead to separated Au and Rh nanoparticles, whereas pre-reduction generates a well-defined segregated structure with Rh located at the interface between Au and titania. With respect to Rh/TiO2, the bimetallic catalyst exhibited improved resistance to air oxidation and to sulfidation during tetralin hydrogenation in the presence of H2S. Moreover, AuRh/TiO2 shows catalytic synergy for the hydrodeoxygenation of guaiacol.35
In this work, we have investigated theoretically bimetallic Au–Rh clusters and the effect of adsorption of reactive species such as H2, O2 and CO. In the first section, we focus on mixing patterns of bare Au–Rh clusters. In the following three sections, we present our results on (i) H and H2 adsorption, (ii) O and O2 adsorption, and (iii) CO adsorption. In the fifth section, we compare adsorption results for different species and discuss the strain, alloying and relaxation effects on adsorption strength. In the last section, we move on to adsorption of multiple molecules and investigate the segregation patterns under different molecular environments.
Methodology
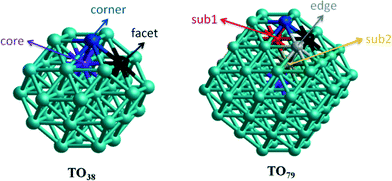
Though experimental catalysis studies have been performed on nanometre scale Au–Rh particles, DFT calculations are limited to clusters with a few tens or perhaps hundreds of atoms. In this study we have chosen to study 38-atom and 79-atom truncated octahedra (TO) clusters as models for bimetallic Au–Rh nanoparticles due to the high symmetry of the parent TO structure (Oh), and their fcc packing (as in the larger experimentally studied nanoparticles). While TO38 is in the non-scalable region (i.e. where properties do not scale simply with cluster size), comparison with TO79 (and in some cases with clusters with up to 260 atoms, see below) enable us to draw trends which we believe are applicable in the scalable region, thereby bridging the size gap to the experimental nanoparticles.Initially, single-atom substitutions of Au in Rh and Rh in Au were investigated for 38- and 79-atom TO clusters for all the symmetrical positions shown in Fig. 1. Following the single atom substitutions, we have constructed several nanoalloy models covering different compositions and morphologies, such as core–shell and Janus particles (Fig. 2 shows examples for TO38). Ordered alloy particles are generated by alternating layers of Au and Rh in the [100] or [111] directions and by occupying different fcc crystal positions with Au or Rh. To allow a comparison between bimetallic TO38 clusters which have the same composition, surface-decorated configurations of Au32Rh6 (hex and centroid) as in the study of West et al.8 are also included in the set, together with the RhcoreAushell structure. The hex structure (h-Au32Rh6) has 6 Rh atoms forming a hexagonal ring surrounding one of the (111) facets of TO38 (C3v symmetry), while the centroid structure (c-Au32Rh6) has 6 Rh atoms occupying the centres of 6 of the (111) facets, with overall D3d symmetry (see Fig. 2). Because of the impossibility of a perfect half and half Janus particle for the 79-atom TO, both Au- and Rh-rich Janus particles are studied together with “ball and cup” structures, in which one type of atom is embedded in the other but is not completely covered.36 These general structural types are then expanded to larger (116-, 140-, 201-, and 260-atom) TO clusters to gain insight into clusters with sizes approaching those of real nanocatalysts.
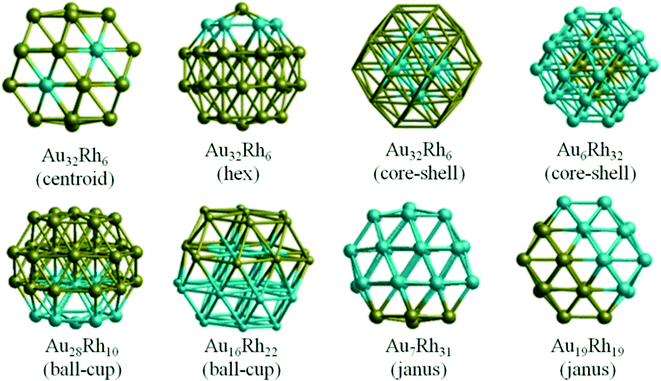 | ||
| Fig. 2 38-atom TO Au–Rh nanoalloy models showing several compositions and chemical orderings. Blue spheres represent Rh atoms and yellow spheres represent Au atoms. | ||
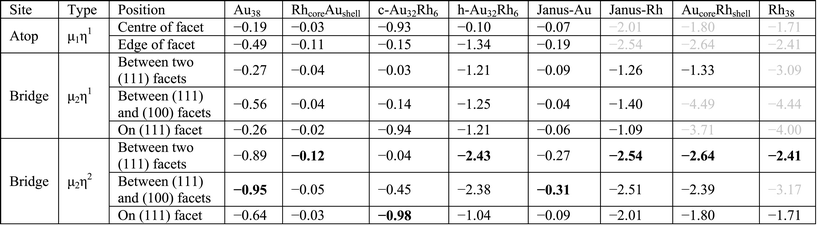
Both atomic and molecular adsorptions of hydrogen, oxygen and CO molecules are studied on selected 38-atom TO structures. In single-atom adsorption studies, adsorbates are initially placed on all possible surface sites. According to these results, several adsorption configurations are studied for molecular adsorbates, including both atoms of the adsorbate bonding to the cluster via two metal atoms for O2 adsorption, giving an M–O–O–M bridge, which is denoted μ2η2 type bonding. μ1η1 denotes one atom of the adsorbate connected to a metal atom on an atop position and μ2η1 denotes adsorption of the adsorbate through one atom bridging two metal atoms (see Fig. 3). For multiple adsorbate studies of O2 and CO molecules on TO38 clusters, simpler atop positions on (111) facets are chosen to investigate trends for these higher symmetry systems. When a comparison is made for clusters of the same composition for adsorption of 6 molecules, the best adsorption positions observed from single adsorbate considerations are also included and compared.
Calculations are performed using density functional theory (DFT) as implemented in the VASP37 code. The generalized gradient approximation (GGA) was employed within the Perdew–Burke–Ernzerhof (PBE)38 parameterization for the exchange-correlation energy functional. All the calculations are spin-polarized, with valence electrons treated explicitly (Rh: s1d8, Au: s1d10, C: s2p2, O: s2p4, and H: s1), while the ionic cores are represented by the projected augmented wave (PAW)39,40 method. To avoid spurious periodic interactions, unsupported clusters are placed into a sufficiently large supercell that ensures ∼10 Å separation by vacuum. The Γ point is used to sample the Brillouin zone. For all of the bare clusters and clusters with adsorbed molecules, local geometry optimizations were performed, at the DFT level, where all atoms are relaxed until the forces on the atoms are lower than 0.01 eV Å−1 and the electronic ground states are determined by requiring a total energy convergence of 10−6 eV. However, in section 5, to isolate the different effects contributing to the adsorption strength trends, partly or fully frozen geometry calculations were also performed for comparison. Dissociation energy barriers for H2 and O2 molecules on nanoparticles were calculated using the nudged elastic band (NEB) method.41,42
For the comparison of the energetics of different composition nanoalloys, a mixing energy term (Δ)43 was calculated, which is expressed as:
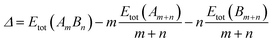 | (1) |
Adsorption energy (Eads) values are calculated as the differences in the total energies of the combined and separated systems:
| Eads = − (Etot(combined) − Etot(cluster) − Etot(adsorbate)) | (2) |
The d-band centre is calculated as:
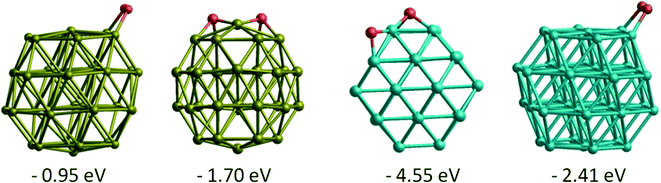
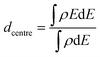 | (3) |
Results
1. Bare clusters
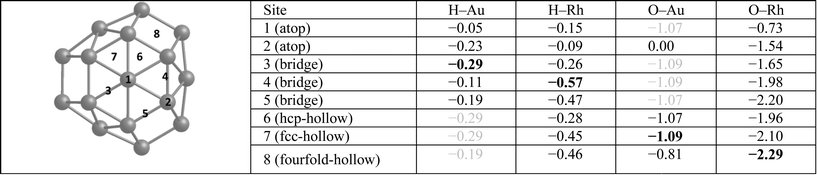
For TO38, a Rh dopant preferentially occupies a core position, while facet and corner positions also have negative (favourable) mixing energies (see Fig. 1 and Table 1). Conversely the preference for a single Au dopant is corner > facet > core, all having positive (unfavourable) mixing energies. These findings are consistent with the higher cohesive energy of Rh compared to Au.31 Similarly, for the larger TO79 cluster, a Rh dopant is favoured in the core position followed by subsurface positions, while surface Rh gives a positive mixing energy. In contrast, for a single Au dopant in TO79, the stability order is corner > edge > facet > subsurface > core, with only the corner position giving a negative mixing energy. Table 2 summarises the mixing energy results for the addition of a second dopant, both connected to (adjacent) and far from the first dopant in TO38. For both Au and Rh dopants, site preferences remain the same as for the first dopant, whether it is connected to the first dopant or not. However, while the Au dopants prefer to be connected to each other, Rh dopants prefer to be separate. This is because Rh dopants try to maximise the number of Au–Rh bonds as the strength of Rh–Au is greater than that of Au–Au bonds. As the strength of Rh–Au is lower than that of Rh–Rh bonds, Au dopants behave in the opposite fashion, to minimise disruption of Rh–Rh bonds by occupying adjacent positions.| Site | Au1Rh37 | Rh1Au37 | Au1Rh78 | Rh1Au78 |
|---|---|---|---|---|
| Core | 1.88 | −1.13 | 2.14 | −0.47 |
| Facet | 0.53 | −0.64 | 0.24 | 0.38 |
| Corner | 0.10 | −0.29 | −0.21 | 0.76 |
| Edge (79) | — | — | 0.16 | 0.40 |
| Sub1 (79) | — | — | 1.65 | −0.20 |
| Sub2 (79) | — | — | 1.69 | 0.03 |
| First dopant | Core (adjacent) | Core (far) | Facet (adjacent) | Facet (far) | Corner (adjacent) | Corner (far) |
|---|---|---|---|---|---|---|
| Au2Rh36 | ||||||
| Core | 3.58 | 3.80 | 2.24 | 2.41 | 1.72 | 1.91 |
| Facet | 2.24 | 2.41 | — | 1.04 | 0.57 | 0.53 |
| Corner | 1.72 | 1.91 | 0.57 | 0.53 | 0.02 | 0.16 |
| Rh2Au36 | ||||||
| Core | −2.09 | −2.21 | −1.61 | −1.60 | −1.28 | −1.33 |
| Facet | −1.61 | −1.60 | — | −0.87 | −0.65 | −0.73 |
| Corner | −1.28 | −1.33 | −0.65 | −0.73 | −0.37 | −0.47 |
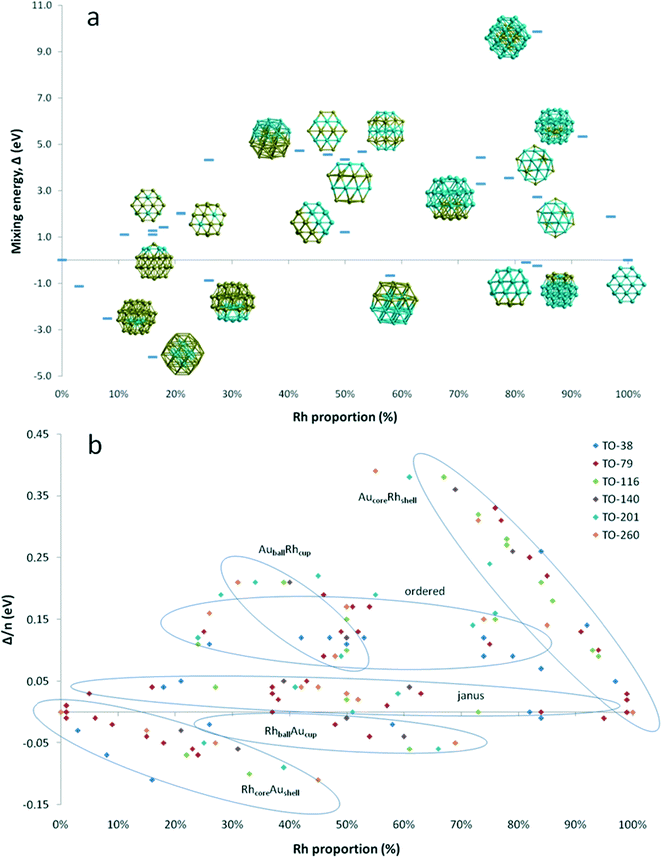
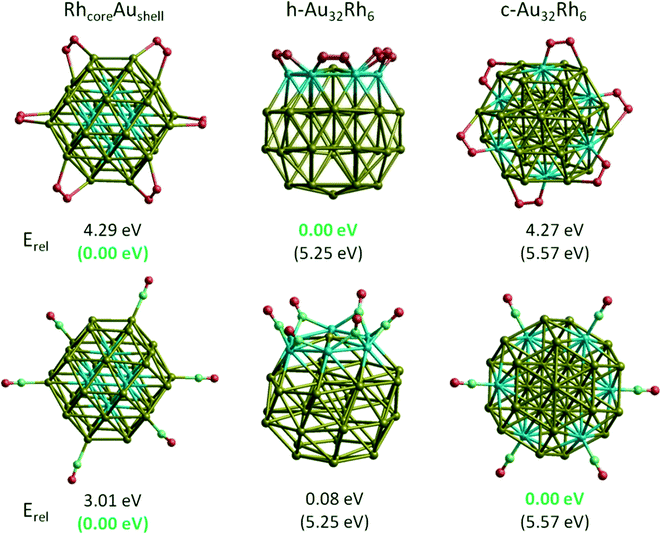
Fig. 4a shows the variation of mixing energy (Δ) with composition and type of Au–Rh segregation for 38-atom TO clusters. As expected from single-atom substitution results, as shown in Table 1, the RhcoreAushell isomer is the most stable configuration for all considered TO sizes, while the inverse AucoreRhshell isomer is the least stable configuration. One can see from Fig. 4a that the mixing energies of the intermediate structures between core–shell and the corresponding pure metal particles lie on a straight line for both RhcoreAushell and AucoreRhshell, where the core is partially filled with one atom type. When we swap one core Rh atom with a surface Au atom, the increase in energy is found to be 0.96 eV for facet positions, while it is 1.17–1.49 eV for corner positions. When we add another Rh atom on the surface of RhcoreAushell, it prefers facet over corner sites and the mixing energy values increase (the clusters are destabilised) by 0.32 eV and 0.58 eV, respectively.
For clusters with surface Rh and having the same composition (Au32Rh6) as RhcoreAushell, we have observed that corner sites (h-Au32Rh6: Δ = 1.10 eV) are preferred over facet sites (c-Au32Rh6: Δ = 1.28 eV) for Rh atoms, in contrast to single atom calculations and addition of a surface Rh atom on RhcoreAushell, where the additional Rh atom is more likely to occupy a facet site than a corner site. This is because the neighbouring Rh atoms stabilise each other due to the stronger Rh–Rh bonds, while the facet sites have isolated Rh atoms. Replacing the Au atom in the centre of the Rh6 ring in the h-Au6Rh32 isomer leads to an Au-rich Janus-type structure (Au31Rh7) with a mixing energy of 1.41 eV while the regular Janus particle is found to have Δ = 1.20 eV. At the Rh-rich side, the h-Au6Rh32 isomer (Δ = −0.25 eV) is found to be more stable than c-Au6Rh32 and AucoreRhshell. Similarly the Rh-rich Janus structure is found to also have negative mixing energy (−0.09 eV) and is therefore more stable than the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 Janus particle, whereas the Au-rich Janus particle is less stable. RhballAucup configuration is the second best structure type after RhcoreAushell particles, with mixing energies of −0.87 eV for Au28Rh10 and −0.67 eV for Au16Rh22. However the inverse of these particles (AuballRhcup) is found to be less stable than the Janus particles, with mixing energies of 3.29 eV for Au10Rh28 and 4.73 eV for Au22Rh16. Similarly, ordered alloy clusters are found instable. For the ordered L12 phase, mixing energies are 3.54 eV for Au8Rh30, 4.43 eV for Au10Rh28, 4.33 eV for Au28Rh10, and 2.01 eV for Au30Rh8. For alternating layers in the [100] direction (L11 phase), mixing energies are 4.67 eV for Au18Rh20 and 4.56 eV for Au20Rh18, while it is 4.35 eV for alternating layers in the [111] direction (L10 phase) for Au19Rh19.
50 Janus particle, whereas the Au-rich Janus particle is less stable. RhballAucup configuration is the second best structure type after RhcoreAushell particles, with mixing energies of −0.87 eV for Au28Rh10 and −0.67 eV for Au16Rh22. However the inverse of these particles (AuballRhcup) is found to be less stable than the Janus particles, with mixing energies of 3.29 eV for Au10Rh28 and 4.73 eV for Au22Rh16. Similarly, ordered alloy clusters are found instable. For the ordered L12 phase, mixing energies are 3.54 eV for Au8Rh30, 4.43 eV for Au10Rh28, 4.33 eV for Au28Rh10, and 2.01 eV for Au30Rh8. For alternating layers in the [100] direction (L11 phase), mixing energies are 4.67 eV for Au18Rh20 and 4.56 eV for Au20Rh18, while it is 4.35 eV for alternating layers in the [111] direction (L10 phase) for Au19Rh19.
To test that the isomer preferences observed for TO38 are applicable to larger clusters, we have compared the mixing energy per atom (Δ/n) as a function of composition and segregation type for TO clusters with 38, 79, 116, 140, 201 and 260 atoms. As shown in Fig. 4b, the stability order found for TO38 is maintained for TO79, TO116, TO140, TO201, and TO260, with the configurations grouped in the ellipses. The general stability order is RhcoreAushell > RhballAucup > Janus > AuRhordered ≈ AuballRhcup > AucoreRhshell, while only RhcoreAushell and RhballAucup structures have negative mixing energies.
2. H and H2 adsorption
Table 3 lists single H atom adsorption energies for all surface positions on both Au38 and Rh38 clusters. On Au38 the preferred position for adsorption of atomic H (i.e. the site with the most negative Eads) is the bridge position on the (111) facet, followed by the atop position on a corner atom of the (111) facet. On extended Au surfaces it has been reported that the preferred positions are the hollow sites (hcp and fcc sites are found to be degenerate) for Au(111) and the bridge site for Au(100), while the latter has a higher adsorption energy.44 Unlike on the Au(111) surface, all H placements on hollow and four-fold positions on the Au38 cluster converged to neighbouring bridge positions, probably because the corner atom of the (111) facet is no longer a true (111)-type surface atom, having a lower coordination number and therefore being more reactive, while the preference for the bridge site is in agreement with the extended Au(100) surface. On the Rh38 cluster the bridge positions at the edges are the favoured positions, followed by hollow positions in general. This is in agreement with extended surface studies, where the hollow sites are found to be preferred for Rh(111) and bridge and four-fold sites for the Rh(100) surface.6 On the Rh38 cluster, unlike Au38, atop positions are found to be the least favourable for binding atomic hydrogen. The H atom adsorption energy on Rh38 is higher than on Au38 (by 0.28 eV when comparing the most preferable adsorption sites).When we compare H atom results with H2 molecule adsorption, Au atoms tend to have almost no interaction with H2 molecules, while Rh readily dissociates H2. This is in agreement with previous theoretical study on Au1345 cluster, in which the authors also reported no adsorption of H2 molecules, whereas spontaneous H2 dissociation was reported on Au14 and Au29.46 On Rh38 the dissociative adsorption energies of H2 are consistent with the single H atom adsorptions. For example, for the lowest energy case, the H atoms migrate to two neighbouring bridge positions, with a total adsorption energy of −1.10 eV, which is only 0.04 eV lower than the sum of adsorption energies of two H atoms adsorbed on the corresponding sites (−0.57 and −0.47 eV). For the Au–Rh nanoalloys, the core–shell and Janus clusters are found to behave in the same way as the pure Au or Rh clusters, i.e. while there is almost no interaction on the Au part, spontaneous H2 dissociation takes place on the Rh part of the corresponding clusters (see Fig. 5). H2 dissociation is also observed for h-Au32Rh6 where there are neighbouring surface Rh atoms. The only case where the H2 adsorption strength is found to be smaller than for pure Rh38 is for c-Au32Rh6, in which there are isolated Rh atoms on the cluster surface and the H2 dissociates with the two H atoms remaining on the same Rh atom (H–H distance: 1.52 Å). There is a 0.5 eV energy barrier to migration onto another Rh atom via bonding to the Au atoms, however fully dissociated hydrogen (with the two H atoms on different Rh atoms) is less stable by 0.2 eV.
3. O and O2 adsorption
Single O atom adsorption energies for all surface sites on Au38 and Rh38 clusters are given in Table 3. Unlike the single H atom, on the Au38 cluster hollow positions are found to be the preferred sites for O adsorption while bridge and atop positions are not favourable and converge to hollow sites. This is in agreement with the higher adsorption energies reported on Au(111), Au(211) and Au13 for hollow sites, while the bridge positions except for Au(211) diffused to other positions.47 Similarly the fourfold hollow position was also found to be preferred on Rh38, followed by bridge positions. This disagrees with a previous study, which reported the fourfold sites are the least stable on Rh(211) and Rh13.47 In the same study, it is reported that the fcc-hollow site is preferred on Rh(111), followed by the hcp-hollow, which correlates well with the higher adsorption energies for fcc- and hcp-hollow sites on Rh38. Also in that study it was reported that bridge position is preferred on Rh(211), which correlates with the higher adsorption energies of bridge positions between lower-coordinated Rh atoms. Lastly, for Rh13 the threefold site is reported to be preferred, which we believe is because in Rh13 all three Rh atoms have low coordination, unlike in Rh38, while the fourfold site is composed of low coordination Rh atoms. Consistent with the previous study,47 in our work the atop positions have the lowest adsorption energies. For Rh38, the atomic O adsorption energy is higher on Rh than on Au, with a 1.20 eV energy difference between the best adsorption sites considered.Moving on to O2 adsorption, again the Rh cluster tends to adsorb O2 more strongly than the Au cluster (adsorption energies for best configurations: −2.41 eV (Rh) vs. −0.95 eV (Au)). This is in line with experimental studies which reported no adsorption for oxygen on clean Au(111) and Au(110) surfaces48 whereas O2 readily dissociates at low coverages on low index Rh surfaces.49 However, adsorption of molecular O2 has been shown to be possible on stretched Au(111),50 Au(211)50 and small Au nanoparticles,51 albeit with very weak binding energies.
The adsorption energy is lowest (least negative Eads) for the atop position on a (111) facet of Au38 (only – 0.19 eV), while for the atop position on an edge atom it is −0.49 eV. This difference is attributed to the edge atoms being more reactive due to having lower coordination numbers. The adsorption strength for the bridge positions on the (111) facet and the edge between two (111) facets of μ2η1 type are found to be relatively weak (Eads values are −0.26 and −0.27 eV, respectively) while for the bridge site between (111) and (100) facets it is found to be stronger (−0.56 eV) and is accompanied by a distortion, with the Au edge atoms moving apart from each other. The energetically best positions on the Au38 cluster are found for the μ2η2 type bonding on the bridge positions. On the bridge site on (111) facet the adsorption energy is −0.64 eV, while (111)–(111) and (111)–(100) bridge sites have adsorption energies of −0.89 eV and −0.95 eV, respectively.
For Rh38 no local minima could be found for the atop positions since Rh interacts more strongly than Au with the O2 molecule and therefore the second O atom spontaneously bonds to a neighbouring Rh atom to make a Rh–O–O–Rh bridge (μ2η2 type). The adsorption energy for the μ2η2 type bonding on the (111) facet is −1.71 eV while on the (111)–(111) bridge it is −2.41 eV. Similar to the atop positions, starting from μ2η1 type bonding on the bridge sites no local minima were located, with the O2 molecules dissociating spontaneously.
To determine the effect of alloying on O2 adsorption, we compared several adsorption geometries corresponding to those on the pure Au and Rh clusters (see Table 4). For all clusters μ2η2 type binding is found the most favourable, mainly on the bridge site between two (111) facets. For pure Au and on the Au side of Janus particles (Janus-Au), O2 adsorption on the bridge site between (111) and (100) facets is slightly lower in energy than between two (111) facets due to adsorbate-induced relaxation. The Au–Au distance of the (111)–(111) bridge site increases by 0.26 Å upon O2 adsorption while the Au–Au distance for the (111)–(100) bridge increases by 0.48 Å. Similarly, the Au–Au elongations are 0.22 Å for the (111)–(111) bridge versus 0.62 Å for the (111)–(100) bridge for Janus-Au. However, for the RhcoreAushell particle, the Rh core limits this Au–Au bond elongation and the bridge bond elongation values are lowered to 0.18 Å for (111)–(111) versus 0.14 Å for (111)–(100). Therefore adsorption energies are increased and O2 adsorption on the (111)–(111) bridge is favoured over the (111)–(100) bridge.
For c-Au32Rh6, the preference for μ2η2 binding is less pronounced since the O2 molecule prefers to bind to Rh atoms rather than Au and there is no possibility for μ2η2 binding through two Rh atoms. Hence, μ2η2 bridging between Rh and Au on the (111) facet (Eads: −0.98 eV) is significantly more favourable than other μ2η2 positions (Eads: −0.45 eV and −0.05 eV). Very similar energies are found for μ2η1 bridging between Rh and Au on (111) facets (Eads: −0.94 eV) and the μ1η1 atop site on Rh (Eads: −0.93 eV). When the O2 molecule binds only to Au atoms on c-Au32Rh6, adsorption energies are significantly reduced (less negative): the adsorption energy is only −0.15 eV for the μ1η1 atop binding on an edge Au atom, −0.14 eV for the μ2η1 bridge between two Au atoms and −0.45 eV for the μ2η2 bridge between two Au atoms. Adsorption on these sites is 0.34 eV, 0.42 eV and 0.50 eV less favourable, respectively, than for the same sites on the pure Au38 cluster.
For h-Au32Rh6, when the O2 molecule is bound to the (111) Au atom at the centre of the Rh6 hexagon, the adsorption energy (−0.10 eV) is lower than atop adsorption on the (111) facet of the pure Au38 cluster (−0.19 eV). Similarly, when O2 is bound across a Rh–Au bond in a μ2η2 bridge, the adsorption strength is reduced relative to that on pure Rh38 (−1.04 eV vs. −1.71 eV, respectively). However if the O2 molecule is bound to two Rh atoms, in the same position as on the pure Rh cluster, the adsorption energy increases slightly, by 0.02 eV.
For O2 adsorption on RhcoreAushell, we observe a very weak Au–O2 interaction, with a highest adsorption energy of −0.12 eV for the μ2η2 bridge between two (111) facets. For all positions the adsorption energies are significantly lower than on pure Au. In the reverse case, for the AucoreRhshell, atop positions spontaneously relax to μ2η2 bridge sites via O binding to a neighbouring Rh atom, as for the pure Rh case. Conversely, the adsorption energies for O2 on AucoreRhshell are −1.80 eV for the μ2η2 bridge on the (111) facet and −2.64 eV for the (111)–(111) bridge site, which are 0.09 and 0.23 eV higher than for pure Rh38. Similarly, adsorption energies on the Rh side of the Janus particle (Janus-Rh) are also greater than for pure Rh38. However, in this case the adsorption strength enhancement is greater for the μ2η2 bridge site on the (111) facet than for the (111)–(111) bridge site, with increases of 0.30 and 0.13 eV, respectively.
Comparing molecular O2 adsorptions with the separate adsorptions of two O atoms on the best adsorption sites, for both Au and Rh dissociated O2 is thermodynamically more favourable than molecularly adsorbed O2 (see Fig. 6). For a comparison between Au, Rh, Janus and core–shell structures, we have calculated the energy barriers for O2 dissociation on the same site (bridge μ2η2 site between two (111) facets) on clusters. The barrier is calculated to be 0.12 eV on Rh38 and 1.53 eV on Au38. When we compare the energy barriers for Au38 with the RhcoreAushell and Janus-Au ones, it increases to 2.04 eV and 1.82 eV, respectively. On the contrary, the energy barriers for AucoreRhshell and Janus-Rh decrease relative to the Rh38, to become almost zero (0.02 eV). These very low energy barriers on the Rh part also explain why O2 dissociates spontaneously on the μ2η1 bridge sites for most Rh and AucoreRhshell particles, since for O2 μ2η1 binding is less favourable than μ2η2.
 | ||
| Fig. 6 Adsorption energies and structures of both molecular and dissociated O2 on Au38 and Rh38 clusters. | ||
In order to determine to what extent the results obtained for the 38-atom clusters can be extended to larger clusters, we have performed calculations for O2 adsorption on the larger 79-atom TO clusters. We found the same adsorption sites to be the most favourable ones on TO79 as on TO38. For the Au79 cluster, μ2η2 type binding on the (111)–(100) bridge site has the highest adsorption energy (−0.37 eV), which is considerably weaker than on the Au38 cluster (Eads = −0.95 eV). This is consistent with the fact that molecular adsorption on large Au nanoparticles and extended Au surfaces is weaker than on small Au clusters.50,52 For Rh79, μ2η2 type binding to the (111)–(111) bridge site has the highest adsorption energy (−2.40 eV), which is same as for the Rh38 cluster. For Rh38, some starting positions for the O2 molecule on Rh79 resulted in O2 dissociation. For the alloyed particles, we see the same adsorption energy trends as in 38-atom TO clusters. For the RhcoreAushell cluster (Au19Rh60), the CO adsorption energy increases relative to pure Rh79 by 0.28 eV due to the underlying Au core atoms. On the other hand, the adsorption energy of CO on the AucoreRhshell cluster (Au60Rh19) decreases slightly relative to the pure Au79 case by 0.09 eV because of the underlying Rh core atoms.
4. CO adsorption
Similar to the O2 adsorption case, CO adsorbs more strongly on Rh38 than Au38, with adsorption energies of −2.15 eV and −1.12 eV, respectively for the best adsorption sites. On the Au nanocluster, CO atop adsorption and μ2η1 type binding on the (111) facet induce a spontaneous step formation on the (111) facet where the adsorbate binds, as shown in Fig. 7. This behaviour is consistent with experimentally observed CO-induced step-edge roughening on Au(111) surfaces.53,54 For Au38, the adsorption is stronger if the CO molecule binds in an atop position on the edge of a (111) facet instead of the centre of the (111) facet and the bridge positions (μ2η1 binding). In contrast to the Au cluster, μ2η1 binding on the (111)–(111) bridge site is preferred for Rh38.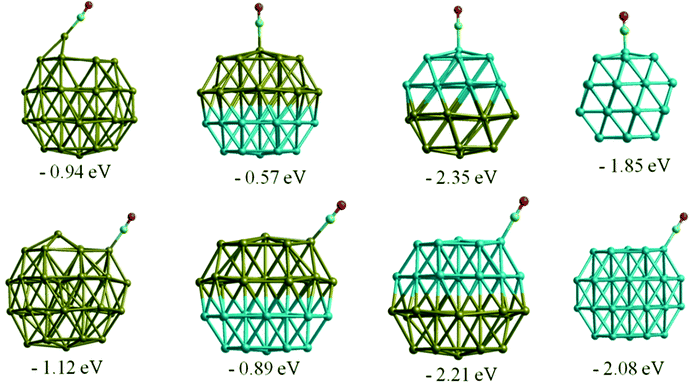 | ||
| Fig. 7 CO adsorption in atop positions on Au, Rh, and Janus clusters. Adsorption energies are given in eV. | ||
In a previous study, CO adsorption energies for atop and bridge sites on the Au(111) surface were reported as – 0.02 and 0.06 eV, respectively, while the adsorption energies were found to be increased on the step on the Au(211) surface, with the atop site still being slightly preferable over bridge positions (Eads: −0.32 and −0.31 eV, respectively).47 The site preferences are in agreement with our results, while the adsorption energies differ by ∼0.7 eV because of the extra reactivity of Au nanoparticles reported in the same study. The adsorption energy of CO on Au13 was also reported as −0.88 eV, which is similar to our values. For CO adsorption on Rh surfaces, while the atop site was preferred on Rh(111), the bridge site was favoured on the Rh(211) step (Eads: −1.55 and −1.67 eV, respectively).47 This is also in agreement with our results since the atop site on the edge of the (111) facet is preferred over the atop site on the (111) facet itself, due to the lower-coordinated edge atoms. Similarly, adsorption on the bridge site on the (111) facet is less favourable, while the bridge sites between facets are preferred since they represent the more reactive step edge. Although on Rh13 the threefold hollow site is reported to be preferred over bridge sites,47 we believe that this is again because all the Rh atoms in the threefold hollow site have low-coordination numbers, unlike Rh38. When we placed CO on a threefold site of Rh38, it migrated to the bridge site between two low coordinated Rh atoms.
Moving to the Au–Rh nanoalloys, similar trends are observed as for O2 adsorption, where the underlying Au or Rh layers affect the adsorption strength in opposite ways. As can be seen in Fig. 7, the adsorption strength is lower on Janus-Au than on Au38, due to the underlying Rh atoms, while CO-induced step formation is also hindered, possibly due to the strain induced by the lattice mismatch between Rh and Au. In the reverse scenario, where the CO adsorbs on Janus-Rh, generally the adsorption strength increases relative to the pure Rh case (see Table 5). While the μ2η1 bridge site is preferred on pure Rh, the atop position on the (111) facet becomes the favoured adsorption site on Janus-Rh.
Unlike O2 adsorption, where the O2 molecule tends to bridge two surface atoms, the CO molecule prefers to bind to the surface through only the carbon atom (μ1η1 or μ2η1). Thus, c-Au32Rh6, which has isolated Rh atoms on the cluster surface also shows stronger CO adsorption than the pure Rh cluster for the same atop configuration, while exhibiting weaker adsorption on the Au sides of the clusters for the atop and μ2η1 type bridge positions, even weaker than on pure Au. When the CO molecule is placed in a bridging site between Au and Rh atoms it spontaneously converges to an atop Rh site for both c-Au32Rh6 and h-Au32Rh6. For h-Au32Rh6, the most favoured adsorption position is the μ2η1 (111)–(100) Rh–Rh bridge position followed by the atop position on an edge Rh atom and the μ2η1 (111)–(111) bridge site, respectively.
Similar to the Janus cluster, the adsorption strength of CO on the RhcoreAushell particle is lowered relative to the pure Au cluster, and the best adsorption site is found to be the atop position as in the pure Au cluster (see Table 4). The reduction of the adsorption strength is generally higher for the RhcoreAushell cluster than for the Janus-Au cluster. In the reverse case, for the AucoreRhshell cluster, the adsorption is again stronger than pure Rh while the same position is found to be the most favourable adsorption site. In contrast to CO binding on Au in the presence of Rh, the enhancement in the adsorption strength relative to pure Rh38 for AucoreRhshell and the Janus-Rh structures varies for different positions, e.g. the adsorption strength for Janus-Rh is higher than AucoreRhshell for the atop position at the centre of the facet, while it is lower for the μ2η1 (111)–(111) bridge position.
When we compare CO adsorption on the 38-atom TO clusters with adsorption on the larger 79-atom TO clusters, we observe similar trends between adsorption sites. For Au79, the μ1η1 atop site has the highest adsorption energy (−0.93 eV), which is close to the value of −1.12 eV for Au38. μ2η1 CO adsorption on the (111)–(100) bridge site and on the (111) facet has adsorption energies of −0.78 eV and −0.73 eV, respectively. For Rh79, μ1η1 binding on the atop site and μ2η1 binding on the (111) facet have very similar adsorption energies of −2.23 eV and −2.22 eV, respectively. These values are slightly larger than the values for Rh38 (−2.08 eV and −2.15 eV, respectively). For the alloyed particles, we see the same adsorption energy trends as for 38-atom TO clusters. For the RhcoreAushell cluster (Au19Rh60), the CO adsorption energy increases relative to pure Rh79 by 0.25 eV due to the underlying Au core atoms. On the other hand, the adsorption energy of CO on AucoreRhshell (Au60Rh19) decreases slightly relative to pure Au79 by 0.09 eV because of the underlying Rh core atoms.
5. Alloying effect on adsorption strength
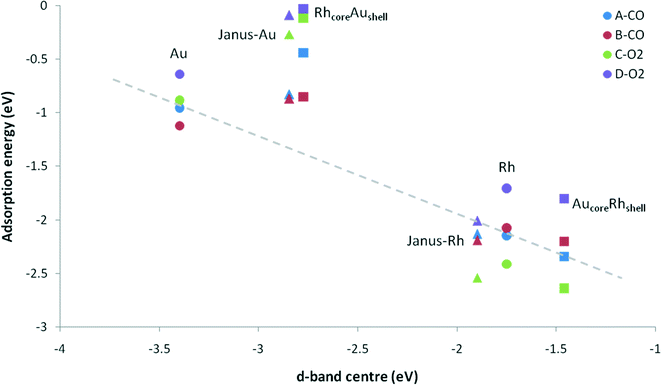
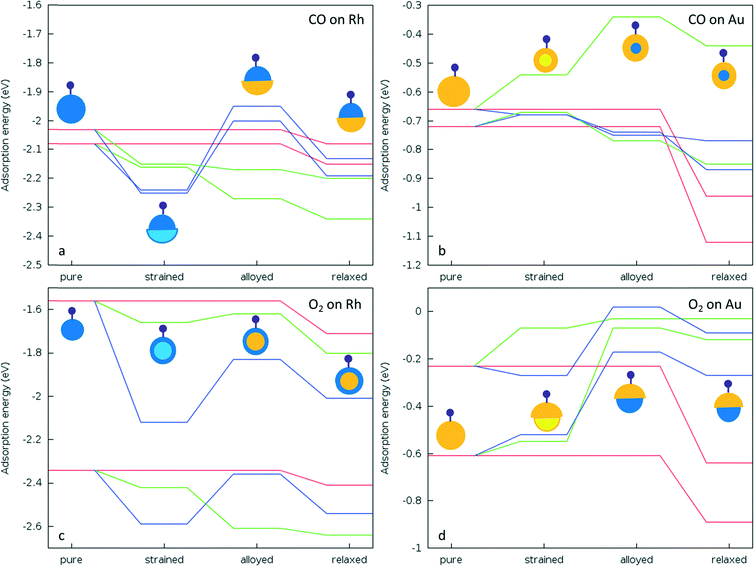
When we consider the molecular adsorption studies discussed above, one striking effect is that the adsorption strength on one particular metal (Au or Rh) is affected by the presence of the other metal, whether it is in direct contact with the adsorbing metal atom or not. For both CO and O2 adsorptions on the Au part of the clusters, in general the adsorption strength decreases relative to the pure Au case when there are underlying Rh atoms, as in the Janus-Au and Rh@Au core–shell cases, even though for Janus-Au the underlying Rh atoms are not in direct contact with the surface Au atoms to which the molecules are adsorbed. For the reverse situation, where there are Au atoms underneath the Rh surface atoms, the strength of molecular adsorption increases relative to the pure Rh case. Fig. 8 shows the relationship between the CO and O2 adsorption energies and the d-band centres of the clusters. According to the d-band model, an upshift in the d-band centre should correlate with higher adsorption strength. However, when we compare the d-band centres of Janus-Au and RhcoreAushell clusters with pure Au, we observe a significant upshift for both, although the adsorption strength decreases. When we compare the d-band centres of Janus-Rh and AucoreRhshell clusters with pure Rh, there is an upshift for AucoreRhshell while there is a downshift for Janus-Rh, although the adsorption strength increases for both. According to the graph, it is clear that only Au, Rh and AucoreRhshell clusters follow the relation, while there is deviation for adsorption on Janus-Rh. It is also interesting that for adsorption on the Au side of Janus and RhcoreAushell clusters we see the opposite relation between the adsorption strength and the d-band-centre position, i.e. the adsorption strength decreases while there is an upshift in the d-band centre.To understand whether these deviations are due to the mechanical effect of structural relaxation or to electronic effects caused by alloying, adsorption calculations were performed for the same sites for fixed (frozen) clusters in a sequential approach. Firstly, to isolate the strain effect caused by alloying, we relax the bare alloy clusters and calculate adsorption energies on these clusters as if they were pure parent (Au or Rh) clusters by fixing their coordinates. Secondly, to isolate the electronic effect we calculate the corresponding adsorption energies for fixed alloy clusters. Lastly, we also optimise the cluster coordinates to obtain final adsorbate-induced relaxations on alloy and pure clusters, as shown in Fig. 9.
For CO adsorption on both Janus-Rh and AucoreRhshell, the adsorption strength increases relative to pure Rh. However there is a downshift of the d-band centre in Janus-Rh whereas there is an upshift for AucoreRhshell. For Janus-Rh, when the competing effects are separated (see Fig. 9a), the alloying effect was found to lower the adsorption strength as expected, while the strain and relaxation effects strengthen the adsorption. As the strain and alloying effects are both due to the Au–Rh interface, the main reason for the higher adsorption energy as compared to pure Rh is the relaxation effect for CO adsorption on Janus-Rh. For CO adsorption on AucoreRhshell the strain and alloying effects reinforce each other, strengthening the adsorption while the strain effect is stronger for μ2η1 (111)–(111) and the alloying effect is stronger for μ1η1 type binding. This is because in μ2η1 binding two Rh atoms are involved and the change of their bond length becomes dominant, whereas in μ1η1 bonding the electronic effect on a single Rh atom is more important.
For O2 adsorption on Janus-Rh (see Fig. 9c), as for CO adsorption, strain and alloying effects act in opposing directions and the strain effect for μ2η2 (111)–(111) is less than for μ2η2 (111) since in the latter case the central atom in the (111) facet is affected more by the strain (0.05 Å bond elongation) than the bridge position between two facets (0.02 Å bond elongation). The possible reason why the strain and alloying effects act in opposite senses is that the Au atoms are not connected directly to the adsorbing Rh atoms, hence they enhance the adsorption strength mainly because the Rh is stretched (strained) due to the Au–Rh size mismatch. For O2 adsorption on AucoreRhshell, surprisingly the alloying effect also weakens the adsorption strength for μ2η2 (111) binding although there is an upshift in the d-band centre, whereas adsorption is strengthened, as expected, for μ2η2 (111)–(111). This is because the strain is responsible for the upshift in d-band centre (which increases from −1.748 eV to −1.406 eV), while upon alloying there is a slight downshift (decreased from −1.406 to −1.461 eV). Strain and alloying effects together strengthen O2 adsorption for both positions on AucoreRhshell.
On the Au side of the particles, the picture becomes more complicated. For CO μ1η1 binding to a corner atom, the strain effect slightly weakens the adsorption while the alloying effect slightly strengthens it for both Janus-Au and RhcoreAushell, and the main reason for the stronger adsorption on pure Au seems to be the relaxation effect. For CO μ2η1 (111)–(111) binding, however, the adsorption strength decreases both via the strain and alloying effects on RhcoreAushell, whereas they both strengthen the adsorption on Janus-Au. For O2 adsorption on both RhcoreAushell and Janus-Au, the alloying effect always weakens the adsorption, unlike for CO adsorption. This behaviour is in agreement with the exception to the d-band model previously suggested for Pt and Pd, where the authors claimed that there is a repulsion between metal d-band and the molecule when alloying nearly fully occupied d9 or d10 metals with more electropositive metals, leading to opposite behaviour when the adsorbate has a completely filled valence shell.19 The weakening of the adsorption for both Janus-Au and RhcoreAushell is also accompanied by a reduced charge transfer to the molecule, similar to the μ2η1 (111)–(111) CO adsorption case on RhcoreAushell (see Table 6). The charge transfer to the O2 molecule is −0.63 for μ2η2 (111) and −0.61 for μ2η2 (111)–(111) on pure Au. However, charge transfer decreases to −0.43 and −0.37 for μ2η2 (111) and −0.38 and −0.07 for μ2η2 (111)–(111) on Janus-Au and RhcoreAushell, respectively. For the μ2η1 (111)–(111) CO adsorption case, charge transfer decrease to the CO is 0.06 on RhcoreAushell than on pure Au, which explains the out of order behaviour of μ2η1 (111)–(111) on RhcoreAushell with respect to Janus-Au and μ2η1 (111) RhcoreAushell (see Fig. 9b).
| Cluster | d-centre | Layer charge | Charge transfer | d C–O | d M–C | E ads |
|---|---|---|---|---|---|---|
| A-CO | ||||||
| Pure-Au | −3.399 | −0.130 | −0.180 | 1.178 | 2.121 | 0.960 |
| RhcoreAushell | −2.772 | −0.360 | −0.120 | 1.169 | 2.133 | 0.440 |
| Janus-Au | −2.844 | −0.350 | −0.160 | 1.174 | 2.107 | 0.830 |
| Janus-Rh | −1.897 | 0.010 | −0.410 | 1.188 | 2.007 | 2.130 |
| AucoreRhshell | −1.461 | −0.020 | −0.420 | 1.191 | 1.988 | 2.340 |
| Pure-Rh | −1.748 | −0.260 | −0.430 | 1.192 | 1.992 | 2.150 |
| B-CO | ||||||
| Pure-Au | −3.399 | −0.130 | −0.020 | 1.152 | 1.947 | 1.120 |
| RhcoreAushell | −2.772 | −0.360 | −0.030 | 1.153 | 1.966 | 0.850 |
| Janus-Au | −2.844 | −0.350 | −0.030 | 1.153 | 1.951 | 0.870 |
| Janus-Rh | −1.897 | 0.010 | −0.300 | 1.170 | 1.828 | 2.190 |
| AucoreRhshell | −1.461 | −0.020 | −0.360 | 1.172 | 1.812 | 2.200 |
| Pure-Rh | −1.748 | −0.260 | −0.330 | 1.171 | 1.836 | 2.080 |
| Cluster | d-centre | Layer charge | Charge transfer | d O–O | d M–O | E ads |
|---|---|---|---|---|---|---|
| C-O2 | ||||||
| Pure-Au | −3.399 | −0.130 | −0.610 | 1.361 | 2.126 | 0.890 |
| RhcoreAushell | −2.772 | −0.360 | −0.370 | 1.296 | 2.315 | 0.120 |
| Janus-Au | −2.844 | −0.350 | −0.430 | 1.316 | 2.247 | 0.270 |
| Janus-Rh | −1.897 | 0.010 | −0.780 | 1.421 | 1.897 | 2.540 |
| AucoreRhshell | −1.461 | −0.020 | −0.970 | 1.633 | 1.815 | 2.640 |
| Pure-Rh | −1.748 | −0.260 | −0.770 | 1.403 | 1.910 | 2.410 |
| D-O2 | ||||||
| Pure-Au | −3.399 | −0.130 | −0.630 | 1.360 | 2.120–2.133 | 0.640 |
| RhcoreAushell | −2.772 | −0.360 | −0.070 | 1.237 | 3.378–3.980 | 0.030 |
| Janus-Au | −2.844 | −0.350 | −0.380 | 1.297 | 2.331–2.387 | 0.090 |
| Janus-Rh | −1.897 | 0.010 | −0.760 | 1.403 | 1.934–1.957 | 2.010 |
| AucoreRhshell | −1.461 | −0.020 | −0.790 | 1.416 | 1.922–1.934 | 1.800 |
| Pure-Rh | −1.748 | −0.260 | −0.780 | 1.407 | 1.931–1.987 | 1.710 |
Charge effects also play a role in the increase or decrease of adsorption strength on alloy clusters relative to their pure metal counterparts. For example, for both Janus-Rh and AucoreRhshell clusters the Rh layer charges become less negative (or even positive) than for pure Rh when alloyed with more electronegative Au atoms (see Table 6), which enhances the σ-donation from the adsorbate to the cluster. For Janus-Au and RhcoreAushell clusters, Au layer charges becomes more negative when alloyed with Rh, which reduces the σ-donation from the adsorbate to the cluster. However, charge effects alone cannot explain the extent of the change in the adsorption strength on alloying.
6. Multiple CO and O2 adsorption
As mentioned above, for bare clusters RhcoreAushell is the energetically most favourable isomer. However, in adsorption studies, this isomer has the lowest adsorption strength towards all adsorbates, even with respect to pure Au. Considering also that both CO and O2 adsorption strengths on Rh are much higher than on Au, adsorption of multiple CO or O2 molecules can potentially change the stability ordering of nanoalloy clusters,9i.e. can stabilise surface Rh atoms.Table 7 summarises the adsorption energy per O2 molecule (Eads/O2) for the 38-atom TO nanoalloy clusters. The general adsorption trend is unchanged on increasing the number of adsorbates for most of the structures in terms of adsorption energy per number of adsorbates. An exception is the inverse core–shell structure (AucoreRhshell), for which we observe significant distortions such as Au migration to the surface and spontaneous O2 dissociation during the initial computation stage. However, it should be noted that the AucoreRhshell structure was already the least stable structure among all of the considered nanoalloy morphologies, with a high mixing energy of ∼10 eV and therefore prone to reconstruction. The Eads/O2 values also start to decrease for h-Au32Rh6, Janus and c-Au32Rh6 configurations after adsorption of 3, 4, and 8 molecules, respectively. This is because beyond these numbers the additional O2 molecules have to bind to Au atoms rather than Rh atoms, due to the distribution of the Rh atoms.
| # O2 | Au38 | RhcoreAushell | c-Au32Rh6 | h-Au32Rh6 | Janus | AucoreRhshell | Rh38 |
|---|---|---|---|---|---|---|---|
| 1 | −0.19 | −0.02 | −0.37 | −0.93 | −2.03 | −1.70 | −1.71 |
| 2 | −0.12 | −0.00 | — | −1.01 | — | −2.41 | −1.80 |
| 3 | −0.09 | −0.00 | −0.14 | — | −1.95 | −1.87 | −1.77 |
| 4 | −0.10 | −0.00 | −0.12 | −0.99 | −1.47 | −3.22 | −1.86 |
| 6 | −0.08 | −0.01 | −0.08 | −0.98 | — | −3.67 | −1.77 |
| 8 | −0.16 | −0.00 | −0.07 | −0.72 | −0.98 | −3.06 | −1.87 |
When we compare the clusters of the same composition (Au32Rh6), where the RhcoreAushell structure was the most favoured structure for the bare clusters, we find that adsorption of 6 O2 molecules changes the stability orderings, with h-Au32Rh6 becoming the most stable (see Fig. 10). The c-Au32Rh6 isomer also slightly surpasses RhcoreAushell, however it is still 4.27 eV higher in energy than h-Au32Rh6.
As in the O2 adsorption case, we also systematically compared multiple CO adsorption for all the nanoalloy structures (see Table 8). Following the step formation on the pure Au cluster, we observed that multiple CO adsorption distorts the Au cluster drastically after adsorption of 2 CO molecules. For the RhcoreAushell cluster, since the Rh core holds the Au shell more rigidly, distortions only start after 6–8 CO molecules, while for h-Au32Rh6, where all the Rh atoms lie around a single (111) facet, distortions are already seen for fewer CO adsorbates. Most of the distortions show the characteristic step formation as in the case of 1 CO molecule on the pure Au cluster.
| # CO | Au38 | RhcoreAushell | c-Au32Rh6 | h-Au32Rh6 | Janus | AucoreRhshell | Rh38 |
|---|---|---|---|---|---|---|---|
| 1 | −0.94 | −0.14 | −0.86 | −2.32 | −2.35 | −1.94 | −1.85 |
| 2 | −1.20 | −0.09 | — | −2.29 | — | −2.03 | −1.89 |
| 3 | −1.30 | −0.23 | −0.99 | — | −2.30 | −2.03 | −2.04 |
| 4 | −1.16 | −0.25 | −0.88 | −2.28 | −1.80 | −2.05 | −2.09 |
| 6 | −0.98 | −0.78 | −0.89 | −2.27 | — | −2.09 | −2.05 |
| 8 | −1.00 | −0.81 | −1.07 | −1.81 | −1.41 | −2.09 | −2.08 |
Similar to the O2 adsorption case, we have also observed that multiple CO adsorption changes the stability ordering of the Au32Rh6 clusters. While RhcoreAushell is the lowest energy structure for bare clusters, the surface Rh-containing c-Au32Rh6 and h-Au32Rh6 structures become lower in energy than the core-shell particle upon adsorption of 6 CO molecules (see Fig. 10). In contrast to the O2 case, the c-Au32Rh6 structure becomes slightly more favoured due to each CO molecule binding to one metal atom on the surface in a μ1η1 fashion. However, the RhcoreAushell isomer still lies 3 eV higher in energy.
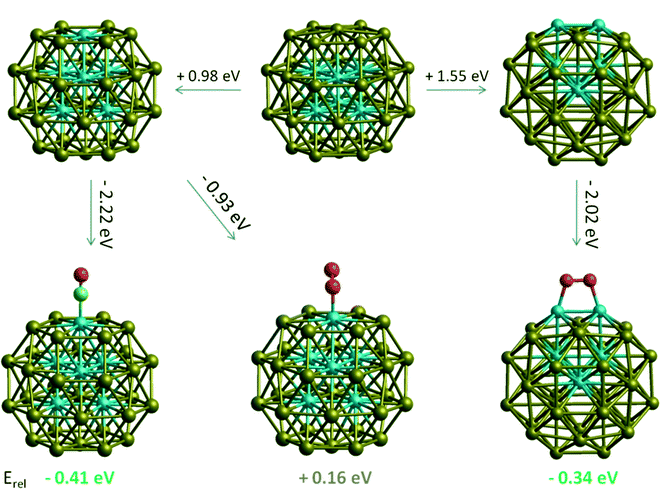
Considering that surface Rh-containing c-Au32Rh6 and h-Au32Rh6 structures become more stable than RhcoreAushell upon multiple molecular adsorption, we have also studied if one adsorbate can favour diffusion of Rh to the surface of the particle. To swap one core Rh atom to a surface position costs approximately 1 eV. However, when we adsorb one CO or O2 molecule on that site, we end up with an isomer which is 0.41 eV lower in energy for CO adsorption and 0.11 higher in energy for O2 adsorption. For O2 adsorption this is expected, as O2 prefers to bind to the surface through two surface Rh atoms. Displacing another Rh atom to the surface of the cluster is 0.34 eV lower in energy than for RhcoreAushell (see Fig. 11). Together these suggest that total core–shell inversion is possible, though the segregation patterns are different for CO and O2. For O2 adsorption, Rh atoms first prefer to occupy neighbouring corner sites which enable a stronger interaction with O2 molecules, while for CO adsorption higher coordinated centroid sites are favoured for Rh atoms.
Conclusions
Nanoscale mixing properties of Au–Rh, preferred adsorption sites of small molecules and the effect of adsorption on Au–Rh segregation have been investigated using first-principles DFT calculations. In agreement with the higher cohesive and surface energies of Rh with respect to Au,55 RhcoreAushell clusters are found to be the most stable isomers. Whatever the cluster size (38–260 atoms), the stability order for bare clusters is RhcoreAushell > RhballAucup > Janus > AuRhordered ≈ AuballRhcup > AucoreRhshell. Rh adsorbs reactive species such as H2, O2 and CO more strongly than Au and therefore the availability of surface Rh changes the chemisorption properties of Au–Rh nanoalloys. On pure Rh clusters and nanoalloys with neighbouring surface Rh atoms H2 spontaneously dissociates into H atoms, while the H2 molecule is elongated (but not broken) for nanoalloys with isolated surface Rh atoms. Similarly, on the Rh part of Au–Rh nanoalloys the dissociation barrier for O2 almost vanishes. It is also found that the molecular adsorption strength increases on the Rh part of the nanoalloys with respect to pure clusters, although it is not always caused by an upshift of the d-band. The opposite behaviour (to that predicted by the d-band model) has been observed for adsorption on the Au side of the nanoalloys and the competing nature of strain, alloying and relaxation effects in metal–adsorbate interactions has been demonstrated. It has also been shown that single or multiple Rh atoms bonded to CO or O2 molecules are thermodynamically more favourable than bare RhcoreAushell, and that core–shell inversion may therefore be induced by the molecular environment. Our segregation results are in agreement with the experimental results of Kiss et al., who observed CO-induced surface segregation of Rh at 300 K for Au–Rh particles grown on TiO2 surfaces.56It should be noted that the trends described here are based on changes in potential energy rather than in free energy, ignoring entropic effects. The trends in potential energy should give most insight into the behaviour of the considered nanoclusters, though the inclusion of entropy (e.g. configurational and vibrational entropy) could be investigated via DFT-molecular dynamics. Concerning kinetic effects, determination of the energy barriers and the mechanism of adsorbate-induced Rh segregation will be investigated via nudged elastic band calculations in future work.
Acknowledgements
This research was funded by the Engineering and Physical Sciences Research Council, UK (EPSRC) under Critical Mass Grant EP/J010804/1 “TOUCAN: Towards an Understanding of Catalysis on Nanoalloys”. Calculations were performed on the following HPC facilities: The University of Birmingham BlueBEAR facility (see http://www.bear.bham.ac.uk/bluebear for more details) and the UK's national HPC facility, ARCHER, both via membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), and via the TOUCAN grant.References
- B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240 CrossRef CAS.
- M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16, 405–408 CrossRef.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2006, 103, 845–910 Search PubMed.
- K. J. Andersson, F. Calle-Vallejo, J. Rossmeisl and I. Chorkendorff, J. Am. Chem. Soc., 2009, 131, 2404–2407 CrossRef CAS PubMed.
- F. Tao, M. E. Grass, Y. Zhang, D. R. Butcher, J. R. Renzas, Z. Liu, J. Y. Chung, B. S. Mun, M. Salmeron and G. A. Somorjai, Science, 2008, 322, 932–934 CrossRef CAS PubMed.
- F. Tao, M. E. Grass, Y. Zhang, D. R. Butcher, F. Aksoy, S. Aloni, V. Altoe, S. Alayoglu, J. R. Renzas, C. Tsung, Z. Zhu, Z. Liu, M. Salmeron and G. A. Somorjai, J. Am. Chem. Soc., 2010, 132, 8697–8703 CrossRef CAS PubMed.
- P. S. West, R. L. Johnston, G. Barcaro and A. Fortunelli, J. Phys. Chem. C, 2010, 114, 19678–19686 CAS.
- P. S. West, R. L. Johnston, G. Barcaro and A. Fortunelli, Eur. Phys. J. D, 2013, 67, 165 CrossRef.
- L. O. Paz-Borbon, R. L. Johnston, G. Barcaro and A. Fortunelli, Eur. Phys. J. D, 2009, 52, 131–134 CrossRef CAS.
- J. Knudsen, A. U. Nilekar, R. T. Vang, J. Schnadt, E. L. Kunkes, J. A. Dumesic, M. Mavrikakis and F. Besenbacher, J. Am. Chem. Soc., 2007, 129, 6485–6490 CrossRef CAS PubMed.
- O. M. Lovvik and S. M. Opalka, Surf. Sci., 2008, 602, 2840–2844 CrossRef CAS.
- S. Holloway, B. I. Lundqvist and J. K. Norskov, Proceedings of the Eighth Conference on Catalysis, Berlin, 1984, vol. IV, p. 85 Search PubMed.
- B. Hammer and J. K. Norskov, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- A. Ruban, B. Hammer, P. Stoltze, H. Skriver and J. Norskov, J. Mol. Catal. A: Chem., 1997, 115, 421–429 CrossRef CAS.
- M. Mavrikakis, B. Hammer and J. K. Norskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef.
- P. Liu and J. K. Norskov, Phys. Chem. Chem. Phys., 2001, 3, 3814–3818 RSC.
- Y. Gauthier, M. Schmid, S. Padovani, E. Lundgren, V. Bus, G. Kresse, J. Redinger and P. Varga, Phys. Rev. Lett., 2001, 87, 036103 CrossRef CAS PubMed.
- J. R. Kitchin, J. K. Norskov, M. A. Barteau and J. G. Chen, J. Chem. Phys., 2004, 120, 10240 CrossRef CAS PubMed.
- H. Xin and S. Linic, J. Chem. Phys., 2010, 132, 221101 CrossRef PubMed.
- Y. Lei, H. Zhao, R. D. Rivas, S. Lee, B. Liu, J. Lu, E. Stach, R. E. Winans, K. W. Chapman, J. P. Greeley, J. T. Miller, P. J. Chupas and J. W. Elam, J. Am. Chem. Soc., 2014, 136, 9320–9326 CrossRef CAS PubMed.
- P. C. Jennings, H. A. Aleksandrov, K. M. Neyman and R. L. Johnston, Nanoscale, 2014, 6, 1153–1165 RSC.
- K. P. McKenna and A. L. Schluger, J. Phys. Chem. C, 2007, 111, 18848–18852 CAS.
- L. O. Paz-Borbon, R. L. Johnston, G. Barcaro and A. Fortunelli, Eur. Phys. J. D, 2009, 52, 131–134 CrossRef CAS.
- N. Austin, J. K. Johnston and G. Mpourmpakis, J. Phys. Chem. C, 2015, 119, 18196–18202 CAS.
- G. Mpourmpakis, A. N. Andriotis and D. G. Vlachos, Nano Lett., 2010, 10, 1041–1045 CrossRef CAS PubMed.
- Y. Yuan, N. Yan and P. J. Dyson, ACS Catal., 2012, 2, 1057–1069 CrossRef CAS.
- R. H. Davies, A. T. Dinsdale, J. A. Gisby, J. A. J. Robinson and S. M. Martin, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2002, 26, 229–271 CrossRef CAS.
- S. Garcia, L. Zhang, G. W. Piburn, G. Henkelman and S. M. Humprey, ACS Nano, 2014, 8, 11512–11521 CrossRef CAS PubMed.
- Z. Konuspayeva, P. Afanasiev, T. S. Nguyen, L. D. Felice, F. Morfin, N. T. Nguyen, J. Nelayah, C. Ricolleau, Z. Y. Li, J. Yuan, G. Berhault and L. Piccolo, Phys. Chem. Chem. Phys., 2015, 17, 28112–28120 RSC.
- R. L. Chantry, W. Siriwatcharapiboon, S. L. Horswell, A. J. Longsdail, R. L. Johnston and Z. Y. Li, J. Phys. Chem. C, 2012, 116, 10312–10317 CAS.
- R. L. Chantry, I. Atanasov, W. Siriwatcharapiboon, B. P. Khanal, E. R. Zubarev, S. L. Horswell, R. L. Johnston and Z. Y. Li, Nanoscale, 2013, 5, 7452–7457 RSC.
- R. L. Chantry, I. Atanasov, S. L. Horswell, Z. Y. Li and R. L. Johnston, in Gold clusters, Colloids, and Nanoparticles II, ed. D. M. P. Mingos, Structure and Bonding, Springer International Publishing, 2014, vol. 162, pp. 67–90 Search PubMed.
- L. Ovari, A. Berko, R. Gubo, A. Racz and Z. Konya, J. Phys. Chem. C, 2014, 118, 12340–12352 CAS.
- E. R. Essinger-Hileman, D. DeCicco, J. F. Bondi and R. E. Schaak, J. Mater. Chem., 2011, 21, 11599–11604 RSC.
- T. S. Nguyen, D. Laurenti, Z. Konuspayeva, P. Afanasiev and L. Piccolo, in preparation.
- L. O. Paz-Borbon, A. Gupta and R. L. Johnston, J. Mater. Chem., 2008, 18, 4154–4164 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558–561 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775 CrossRef CAS.
- G. Mills, H. Jonsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- H. Jonsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, Singapore, 1998, p. 385 Search PubMed.
- R. Ferrando, A. Fortunelli and G. Rossi, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085449 CrossRef.
- P. Ferrin, S. Kandoi, A. U. Nilekar and M. Mavrikakis, Surf. Sci., 2012, 606, 679–689 CrossRef CAS.
- M. Okumura, Y. Kitagawa, M. Haruta and K. Yamaguchi, Appl. Catal., A, 2005, 291, 37–44 CrossRef CAS.
- L. Barrio, P. Liu, J. A. Rodriguez, J. M. Campos-Martin and J. L. G. Fierro, J. Chem. Phys., 2006, 125, 164715 CrossRef CAS PubMed.
- A. A. Peterson, L. C. Grabow, T. P. Brennan, B. Shong, C. Ooi, D. M. Wu, C. W. Li, A. Kushwaha, A. J. Medford, F. Mbuga, L. Li and J. K. Norskov, Top. Catal., 2012, 55, 1276–1282 CrossRef CAS.
- J. J. Pireaux, M. Chtaib, J. P. Delrue, P. A. Thiry, M. Liehr and R. Caudano, Surf. Sci., 1984, 141, 211–220 CrossRef CAS.
- C. Comelli, V. R. Dhanak, M. Kiskinova, K. C. Price and P. Rose, Surf. Sci. Rep., 1998, 32, 165–231 CrossRef.
- Y. Xu and M. Mavrikakis, J. Phys. Chem. B, 2003, 107, 9298–9307 CrossRef CAS.
- B. E. Salisbury, W. T. Wallace and P. L. Whetten, Chem. Phys., 2000, 262, 131–141 CrossRef CAS.
- A. Roldan, J. M. Ricard and F. Illas, Theor. Chem. Acc., 2011, 128, 675–681 CrossRef CAS.
- L. Piccolo, D. Loffreda, F. J. Cadete Santos Aires, C. Deranlot, Y. Jugnet, P. Sautet and J. C. Bertolini, Surf. Sci., 2004, 566–568, 995–1000 CrossRef CAS.
- J. Wang, M. McEntee, W. Tang, M. Neurock, A. P. Baddorf, P. Maksymovych and J. T. Yates, J. Am. Chem. Soc., 2016, 138, 1518–1526 CrossRef CAS PubMed.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollar, Surf. Sci., 1998, 411, 186–202 CrossRef CAS.
- J. Kiss, L. Ovari, A. Oszko, G. Potari, M. Toth, K. Baan and A. Erdohelyi, Catal. Today, 2012, 181, 163–170 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |