Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydration and self-aggregation of a neutral cosolute from dielectric relaxation spectroscopy and MD simulations: the case of 1,3-dimethylurea†
Vira
Agieienko
 ab,
Dominik
Horinek
*c and
Richard
Buchner
ab,
Dominik
Horinek
*c and
Richard
Buchner
 *c
*c
aDepartment of Physical Chemistry, Kazan Federal University, 420008 Kazan, Russia
bDepartment of Inorganic Chemistry, Chemical Faculty, V. N. Karazin Kharkiv National University, 4 Svobody sq., 61022 Kharkiv, Ukraine
cInstitut für Physikalische und Theoretische Chemie, Universität Regensburg, D-93040 Regensburg, Germany. E-mail: Dominik.Horinek@ur.de; Richard.Buchner@ur.de
First published on 30th November 2016
Abstract
The influence of the amphiphile 1,3-dimethylurea (1,3-DMU) on the dynamic properties of water was studied using dielectric relaxation spectroscopy. The experiment provided evidence for substantial retardation of water reorientation in the hydration shell of 1,3-DMU, leading to a separate slow-water relaxation in addition to contributions from bulk-like and fast water as well as from the solute. From the amplitudes of the resolved water modes effective hydration numbers were calculated, showing that each 1,3-DMU molecule effectively freezes the reorientation of 1–2 water molecules. Additionally, a significant amount of solvent molecules, decreasing from ∼39 at infinite dilution to ∼3 close to the solubility limit, is retarded by a factor of ∼1.4 to 2.3, depending on concentration. The marked increase of the solute amplitude indicates pronounced parallel dipole alignment between 1,3-DMU and its strongly bound H2O molecules. Molecular dynamics (MD) simulations of selected solutions revealed a notable slowdown of water rotation for those solvent molecules surrounding the methyl groups of 1,3-DMU and strong binding of ∼2H2O by the hydrophilic carbonyl group, corroborating thus the experimental results. Additionally, the simulations revealed 1,3-DMU self-aggregates of substantial lifetime.
Introduction
Various aspects of hydration in aqueous solutions of urea and its derivatives are of great interest, particularly when related to their denaturing properties. The denaturation of proteins by urea itself has been controversial for a long time, and despite decades of research1 agreement on a direct mechanism, driven by preferential binding of urea, has emerged only in recent years.2–6 Alkyl and aryl substituted ureas did not receive this attention despite their applications in biochemistry as even stronger denaturants than urea,2,7,8 and while an indirect effect – i.e. via modulation of the water structure – has been ruled out in the case of the parent compound, its possible contribution to the denaturation power of N-substituted urea derivatives has not been studied.Similar to urea, 1,3-dimethylurea (1,3-DMU) is used for the denaturation of proteins and the investigation of their structure.9–11 Like its parent, this compound has carbonyl and amino groups which can directly hydrogen bond to hydrophilic parts of proteins.2 Furthermore, urea can also directly bind to nonpolar groups by van der Waals interactions,12 and the presence of alkyl groups will render this interaction even more favourable.
Indirect cosolvent effects on protein stability are intricately linked to the thermodynamic properties of the cosolvent–water mixture and thus originate from the underlying molecular-level structure. For urea, indirect effects have been excluded, because the molecule fits nicely into the hydrogen bond network of water.13,14 This is unlikely for 1,3-DMU molecules because of the presence of two methyl groups which are expected to significantly affect the static and dynamic properties of the solvent. Indeed, a significant slowdown of water dynamics around the methyl groups of various osmolytes, such as tetramethylurea (TMU),15–17 trimethylamine-N-oxide (TMAO),16,18 proline,16 and N-methylacetamide,16 was observed. Accordingly, some authors7,19–21 claimed indirect contributions to be important in protein denaturation by substituted ureas.
Recently Sagle et al.22 investigated the conformational changes of the thermo-responsive polymer poly(N-isopropylacrylamide) (PNIPAM) in the presence of urea and its methyl substituted derivatives. No evidence for direct binding of 1,3-DMU to the amide moieties of the polymer was found. This contrasts the behavior of urea which directly interacts with the polymer by cross-linking the amide groups via hydrogen bonding. Molecular dynamics (MD) simulations23 of aqueous PNIPAM solutions, both in the presence and the absence of urea or 1,3-DMU, evidenced notable 1,3-DMU self-aggregation which apparently favours the unfolded state of PNIPAM and increases the lower critical solution temperature (LCST) of the mixture. On the other hand, urea binding to the folded state of PNIPAM decreased the LCST.
In view of the above findings, it is of interest to understand how 1,3-DMU behaves in aqueous solution. In a few experimental studies it was shown that this solute has a distinct effect on the dynamics of water molecules in its hydration shell. In particular, NMR experiments24 revealed a downfield shift of the water proton signal in the presence of 1,3-DMU, indicating an enhancement of the structure of the hydrating water molecules. Dielectric relaxation spectroscopy (DRS)25 indicated retarded rotational dynamics of hydration water due to the presence of hydrophobic methyl groups. The idea of a strengthened water structure around 1,3-DMU is also supported by data for heat capacities,24,26 molar volumes,26,27 and molar expansion coefficients.27 Nevertheless, these findings give no information on the magnitude and the molecular origin of the retarded hydration-shell dynamics.
As mentioned above, a comprehensive picture of their hydration pattern in aqueous solutions is a prerequisite for understanding the denaturation properties of substituted ureas. Among the experimental techniques capable of probing the hydration of polar molecular solutes, dielectric relaxation spectroscopy yields an excitingly wide scope of information both on structure and dynamics.28 Recently, this technique was applied to study aqueous solutions of urea29 and cosolutes such as TMU,15 TMAO,18,30 and ectoine.31 While urea strongly binds ∼2H2O molecules (where the term “strong binding” refers to the retardation of solvent molecules to such an extent that their contribution coincides with the solute) but otherwise has only small effects on water dynamics, it was possible for the other compounds to distinguish and quantify two fractions of bound water with significantly different dynamics. The disadvantage of DRS here is that no direct, i.e. molecular-level, information on the solute interaction sites of these two water fractions can be obtained. In this regard, molecular dynamics (MD) simulations provide valuable complementary insights in addition to a broad range of other important data. Accordingly, this contribution summarizes the results of a joint DRS and MD study on aqueous solutions of 1,3-DMU at 25 °C, covering solute molalities up to m = 8.0 mol kg−1. For the simulations an especially derived force-field model for the solute was used.
Method section
Experimental
Dielectric relaxation spectroscopy probes the macroscopic polarization of the sample in a time-dependent electric field.32 In the case of solutions of non-electrolytes, polarization originates from the reorientation of permanent dipoles (both solvent and solute molecules) and from intramolecular polarizability. As a function of frequency, ν, the response can be expressed in terms of the complex permittivity![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ν) = ε′(ν) − iε′′(ν), (ν) = ε′(ν) − iε′′(ν), | (1) |
The present dielectric spectra were recorded at (25.00 ± 0.05) °C in the frequency range of 0.2 ≤ ν/GHz ≤ 89. At ν ≤ 50 GHz a frequency-domain reflectometer, based on Agilent 85070E-20 and 85070E-50 dielectric probes connected to an Agilent E8364B vector network analyzer (VNA) and an electronic calibration module (Agilent N4693B), was used.33 A range of 60–89 GHz was covered using a waveguide interferometer.34 For selected samples the reliability of the reflection measurements was additionally crosschecked with a 27–40 GHz variable-pathlength waveguide transmission cell hooked to the VNA. Examples of the spectra are shown in Fig. 1 and 2.
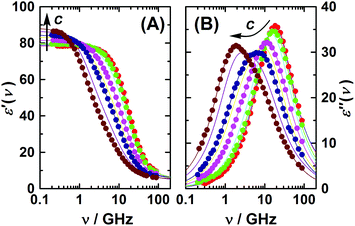 | ||
| Fig. 1 (A) Relative permittivity, ε′, and (B) dielectric loss, ε′′, spectra of aqueous 1,3-DMU solutions at 25 °C and c/M = 0.1157; 0.2519; 0.4794; 0.9156; 1.7079; 2.4521; 2.9910; 4.1322; 4.9118. Symbols show experimental data (omitted for some samples for clarity); lines show the fit using eqn (2); arrows indicate the trend of increasing solute concentration. | ||
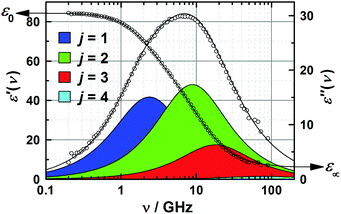 | ||
| Fig. 2 Relative permittivity, ε′(ν), and dielectric loss, ε′′(ν), spectrum of 3.0 M aqueous 1,3-DMU at 25 °C. The symbols indicate experimental values; lines show the results of the fit with eqn (2), with shaded areas indicating the loss of contributions of the resolved modes. | ||
Aqueous solutions of 1,3-DMU were prepared by weight without buoyancy correction from degassed Millipore Milli-Q water and 1,3-DMU (Sigma-Aldrich, >99%) vacuum-dried at 50 °C to constant mass. Densities, d, necessary for calculating molar solute concentrations, c [in M ≡ mol L−1], were determined using an Anton Paar DMA 5000 M vibrating tube densimeter yielding d with a nominal uncertainty of ±5 × 10−6 g cm−3 at (25.000 ± 0.005) °C. Solution viscosity, η, was measured at (25.00 ± 0.01) °C with an Anton Paar AMVn rolling ball viscometer using a 1.6 mm capillary calibrated with degassed Millipore Milli-Q water. The densities and viscosities of the solutions are given in Table S1 of the ESI.†
The dielectric spectra were evaluated by simultaneously fitting ε′(ν) and ε′′(ν) to conceivable relaxation models based on sums of n, n = 1…5, Havriliak–Negami equations or their simplified variants and the resulting fits and their parameters were scrutinized as described in detail elsewhere.35,36 It was found that all solution spectra were best fitted by the sum of four Debye equations (the 4D model), i.e.
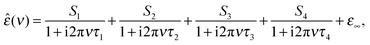 | (2) |
Molecular dynamics simulations
The equilibrium geometry of an isolated 1,3-DMU molecule was determined from quantum-chemical calculations utilizing the Gaussian 03 program.37 Calculations were performed at the density functional theory (DFT) level using the B3LYP exchange–correlation functional38 combined with the cc-PVTZ basis set.39 Implicit solvent-medium effects on the ground state geometry were taken into account by the self-consistent reaction field method (SCRF) via the self-consistent isodensity polarizable continuum model (PCM)40 implemented in the software. Default parameter values were used. The atomic charge distribution was obtained using the RESP-fit method.41,42 The obtained partial charges and structural characteristics of 1,3-DMU, together with the corresponding force-field parameters of all atoms of the molecule, namely carbonyl carbon, C, oxygen, O, nitrogen, N, hydrogen, HN, methyl-group carbon, CH, and methyl-group hydrogen, HC, are given in the ESI.†The equilibrium values for the bond lengths, angles and torsions used in the simulations were taken from the above DFT calculations, whereas the used force constants are those of the GROMOS 53 A6 force field version.43 Non-bonding van der Waals interactions were calculated using the Lennard-Jones 12-6 potential. The homoatomic pair parameters of the KBFF urea model44,45 were employed, whereas heteroatomic pair parameters were calculated by the geometric combination rule. Lacking Lennard-Jones parameters for the methyl carbons, CH, were calculated using the procedure given in ref. 45 based on a correlation between the atomic size and the atomic hybrid components of molecular polarizabilities.46 Required values for the atomic hybrid components and ionization potentials were taken from ref. 46 and 47, respectively. For the methyl hydrogen atoms, HC, the Lennard-Jones parameters were obtained by fitting the experimental values of the density and the diffusion coefficient of a 3.0 M solution. The obtained density and self-diffusivity values given in Table 1 show good agreement with experiment.48–50
| N 1 | N 2 | m | c | d | D 1 | ||
|---|---|---|---|---|---|---|---|
| Calc. | Exp.b | Calc. | Exp. | ||||
| a Obtained using the density values, dcalc, found using the present MD simulations. b Data of ref. 48 interpolated with a third-order polynomial. c Data of ref. 49 interpolated with polynomials. d Data of ref. 50 interpolated with polynomials. | |||||||
| 26 | 2921 | 0.4941 | 0.4755 | 1.0043 | 1.0012 | 1.3 ± 0.5 | 0.9144c; 0.8630d |
| 51 | 2814 | 1.0060 | 0.9327 | 1.0093 | 1.0053 | 1.0 ± 0.1 | 0.8028c; 0.7757d |
| 95 | 2625 | 2.0089 | 1.7373 | 1.0179 | 1.0130 | 0.89 ± 0.08 | 0.6750c; 0.6631d |
| 167 | 2320 | 3.9957 | 3.0463 | 1.0308 | 1.0261 | 0.56 ± 0.02 | 0.5828c; 0.5342d |
| 225 | 2085 | 5.9902 | 4.0780 | 1.0401 | 1.0367 | 0.5 ± 0.1 | 0.5352c; 0.4706d |
| 274 | 1899 | 8.0092 | 4.9172 | 1.0472 | 1.0447 | 0.42 ± 0.01 | 0.4629c; 0.4493d |
MD simulations were performed by means of the GROMACS software package (version 4.5.6).51 An isothermal–isobaric (NPT) ensemble with periodic boundary conditions and an integration time step of 1 fs was used. The temperature was set to 25 °C and controlled using a stochastic v-rescaling thermostat52 using a time constant of 0.1 ps for heat bath coupling. The pressure was controlled using an isotropic Parrinello–Rahman barostat53,54 at 1 bar using a time constant of 1 ps for pressure relaxation. The van der Waals interactions were computed with a cutoff of 1.0 nm with a smooth decay of the forces starting at 0.9 nm. Electrostatic interactions were computed by means of the particle-mesh Ewald technique55,56 with maximum space grid points being 0.12 nm.
Cubic boxes with lengths of 4.5 nm were created with water and solute molecules evenly distributed in the starting configuration and systems were then equilibrated for 5 ns. Depending on the desired properties, two different runs were performed: (i) structural properties were calculated from the configurations generated during the subsequent 45 ns, with coordinates being saved every 5000 steps; (ii) to calculate contact and H-bond dynamics, a 2 ns run was used where the coordinates were saved every 200 steps. Analysis was conducted using the GROMACS and TRAVIS57 programs. A summary of the performed simulations is given in Table 1.
Results and discussion
Dielectric relaxation spectroscopy
The two higher-frequency modes, (S3, τ3) and (S4, τ4), are readily assigned to the solvent as they also appear for pure water58 and – shown in Fig. 3 – their parameters smoothly evolve from the values at c = 0, obtained in our laboratory from fitting ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ν) in the 0.1–2000 GHz range (S3(0) = 72.42, τ3(0) = 8.35 ps, S4(0) = 2.43, τ4(0) = 0.278 ps, ε∞(0) = 3.52).59 The first peak, centred at ∼18 GHz, is due to the cooperative relaxation of the hydrogen-bond network of bulk-like water (i.e. more or less unperturbed H2O molecules behaving similar to the neat solvent). The underlying mechanism can be envisaged along the lines of the Laage–Hynes model of water dynamics60 as a wait, jump and settle sequence for the water dipole and its surroundings. According to this picture τ3 is essentially determined by the waiting time for the water molecule between two fast large-angle jumps, with this waiting time strongly influenced by the time required by the environment to equilibrate with the new dipole orientation. The fast dipole jump of this mechanism, leading to a change of H-bond allegations, gives rise to small-amplitude second (fast) water relaxation, at ∼500 GHz. The lowest-frequency mode (S1, τ1), shifting from ∼4 to ∼1.5 GHz with increasing concentration, can be attributed to the solute, whereas the relaxation at ∼10 GHz, the “slow-water” mode (S2, τ2), is typical for retarded H2O molecules in contact with hydrophobic moieties18,61 but appears also with solutes forming H-bonds somewhat stronger than those among water molecules.59,62 While S1 exhibits a linear increase with increasing solute molarity, S2 passes through a maximum at c ≈ 1.7 M (Fig. 3). The retardation factor for this slow water fraction increases from r = τ2/τ3 = 1.4 at the lowest solute concentration to 2.3 at c = 4.9 M.
(ν) in the 0.1–2000 GHz range (S3(0) = 72.42, τ3(0) = 8.35 ps, S4(0) = 2.43, τ4(0) = 0.278 ps, ε∞(0) = 3.52).59 The first peak, centred at ∼18 GHz, is due to the cooperative relaxation of the hydrogen-bond network of bulk-like water (i.e. more or less unperturbed H2O molecules behaving similar to the neat solvent). The underlying mechanism can be envisaged along the lines of the Laage–Hynes model of water dynamics60 as a wait, jump and settle sequence for the water dipole and its surroundings. According to this picture τ3 is essentially determined by the waiting time for the water molecule between two fast large-angle jumps, with this waiting time strongly influenced by the time required by the environment to equilibrate with the new dipole orientation. The fast dipole jump of this mechanism, leading to a change of H-bond allegations, gives rise to small-amplitude second (fast) water relaxation, at ∼500 GHz. The lowest-frequency mode (S1, τ1), shifting from ∼4 to ∼1.5 GHz with increasing concentration, can be attributed to the solute, whereas the relaxation at ∼10 GHz, the “slow-water” mode (S2, τ2), is typical for retarded H2O molecules in contact with hydrophobic moieties18,61 but appears also with solutes forming H-bonds somewhat stronger than those among water molecules.59,62 While S1 exhibits a linear increase with increasing solute molarity, S2 passes through a maximum at c ≈ 1.7 M (Fig. 3). The retardation factor for this slow water fraction increases from r = τ2/τ3 = 1.4 at the lowest solute concentration to 2.3 at c = 4.9 M.
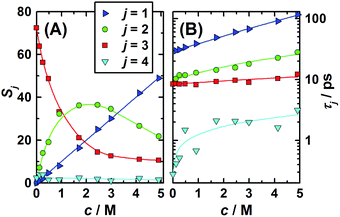 | ||
| Fig. 3 (A) Amplitudes, Sj, and (B) relaxation times, τj, of the 1,3-DMU (j = 1), slow (j = 2), bulk (j = 3), and fast water (j = 4) modes obtained from a fit of the spectra with the 4D model. Symbols indicate the values of Table S2 (ESI†); lines are low-order polynomial fits. | ||
A remarkable feature of the present spectra, irrespective of the chosen formal description and in line with previous findings,25 is the monotonic increase of ε′ at ν < 0.5 GHz with increasing solute concentration (Fig. 1A). Thus, also the static permittivity, 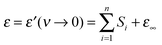 (Table S2 of the ESI†), increases. This observation is surprising because, based on the respective analytical concentrations, a decrease of ε from the pure-water value of 78.4 to 61.1 at c = 4.9 M would be expected from the effective dipole moments, μeff, of 1,3-DMU (5.5 D; from quantum-chemical calculations) and water (3.84 D63). This indicates that the dielectric relaxation of 1,3-DMU–water mixtures does not simply arise from independent reorientations of solute and solvent dipoles. The reasons for that will be explored in the following sections.
(Table S2 of the ESI†), increases. This observation is surprising because, based on the respective analytical concentrations, a decrease of ε from the pure-water value of 78.4 to 61.1 at c = 4.9 M would be expected from the effective dipole moments, μeff, of 1,3-DMU (5.5 D; from quantum-chemical calculations) and water (3.84 D63). This indicates that the dielectric relaxation of 1,3-DMU–water mixtures does not simply arise from independent reorientations of solute and solvent dipoles. The reasons for that will be explored in the following sections.
The starting point for the evaluation of the obtained relaxation amplitudes, Sj, and also of the above estimation of ε is the equation59,64
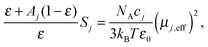 | (3) |
According to the Laage–Hynes model of water dynamics,60 and in line with previous observations,61 the bulk-like mode S3 and fast mode S4 do not represent different water species with distinct dynamics but merely highlight the two dominating steps in the time evolution of water reorientation. For this reason both amplitudes were combined with the amplitude of “unperturbed” (not bound to solute) water
| Sun(c) = S3(c) + S4(c) + ε∞(c) − ε∞(0) | (4) |
With the help of eqn (3), normalized to pure water,61 the concentrations of water not bound to solute, cun, and slow water, cs, were then calculated from Sun(c) and S2(c), respectively. In conjunction with the analytical water concentration, cw, the obtained results then yielded the effective hydration numbers
| Zt = (cw − cun)/c, | (5) |
| Zs = cs/c | (6) |
| Zib = Zt − Zs, | (7) |
As generally found for hydrophobic solutes,18,31,61,65 the present slow-water hydration number, Zs, strongly decreases with increasing solute concentration, dropping from ∼39 at c → 0 to ∼3 at 4.9 M. This is almost certainly due to the hydration-shell overlap, because at the highest solute concentration the solute![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent molar ratio has dropped to 1
solvent molar ratio has dropped to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
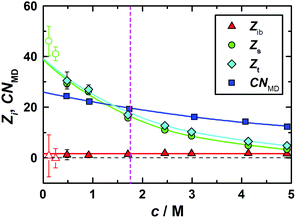
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7. Interestingly the dilute-solution values of Zs for 1,3-DMU are significantly larger than those for TMU15 (∼12), TMAO18 (∼9) and ectoine31 (∼12). On the other hand, the amount of strongly bound water, Zib ≈ 1.6, is independent of solute concentration (Fig. 4) and significantly smaller than the number of H2O molecules in the first hydration shell determined by MD which drops from ∼25.9 to 12.566 (Fig. 4).
7. Interestingly the dilute-solution values of Zs for 1,3-DMU are significantly larger than those for TMU15 (∼12), TMAO18 (∼9) and ectoine31 (∼12). On the other hand, the amount of strongly bound water, Zib ≈ 1.6, is independent of solute concentration (Fig. 4) and significantly smaller than the number of H2O molecules in the first hydration shell determined by MD which drops from ∼25.9 to 12.566 (Fig. 4).
One argument comes from the length of its relaxation time, τ1, which increases from 37 ps at c = 0.12 M to 115 ps at the highest concentration of this study, 4.9 M. The corresponding single-molecule rotational correlation times, τrot,1, calculated from τ1 using the Powles–Glarum equation67,68
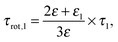 | (8) |
More quantitative information was obtained from the relaxation strength of 1,3-DMU, S1, which increased linearly when plotted against the molar concentration, c, of the solute (Fig. 3). This allowed for rearranging eqn (3) to yield
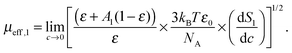 | (9) |
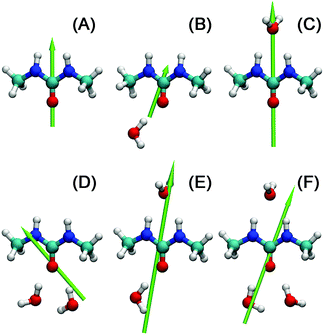
| Species | Species (Fig. 5) | μ | |
|---|---|---|---|
| Vacuum | Water | ||
| 1,3-DMU | A | 3.8 | 5.5 |
| 1,3-DMU·1H2O | B | 4.9 | 7.2 |
| C | 7.0 | 9.0 | |
| 1,3-DMU·2H2O | D | 6.2 | 10.6 |
| E | 8.1 | 10.5 | |
| 1,3-DMU·3H2O | F | 8.9 | 13.9 |
An argument against the formation of stable solute aggregates is that over the entire concentration range the solute mode is well described by a Debye equation and the rotational correlation times calculated from τ1 are linear in η over the entire concentration range (Fig. S2 of the ESI†). Thus, the existence of separate modes for monomeric and aggregated 1,3-DMU, a prerequisite for an aggregation equilibrium between two dipolar species, is unlikely. On the other hand, evaluation of the solvent relaxations indicated an equivalent of ∼1.6 water dipoles per solute molecule to be strongly bound in a hydrate. Additionally, ab initio quantum chemical calculations of 1,3-DMU·H2O, 1,3-DMU·2H2O and 1,3-DMU·3H2O complexes at the B3LYP/6-311++G(d,p) level of theory, either in a vacuum or embedded in water, suggested that some of them have large dipole moments (Fig. 5, Table 2). As discussed in detail below, also the MD simulations support the formation of hydrates with coupled dynamics of 1,3-DMU and strongly interacting water molecules but there are also indications from MD for g1 > 1 through moderately strong 1,3-DMU–1,3-DMU hydrogen bonds. As discussed in detail below, combining the results of the present quantum chemical calculations with the analysis of contact and H-bond lifetimes times from MD allows us to suggest that 2H2O molecules H-bonded to the solute's carbonyl oxygen are most likely responsible for the strongly bound water fraction observed in DRS. Indeed, the dipole moment of the corresponding hydrate (structure D of Fig. 5) is in good agreement with the experimental value of μeff,1 = (11.3 ± 0.6) D.
Molecular dynamics simulations
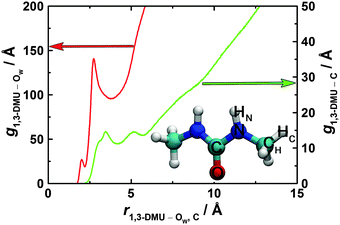
The pRDFs for the 1,3-DMU–OW and 1,3-DMU–C pairs are plotted in Fig. 6 (see the inset for the atom labeling on 1,3-DMU). Note that these pRDFs are not normalized by 4πr2. As the solute concentration does not greatly affect the positions of the maxima and the minima of these functions, but only their height or depth, only the pRDFs obtained at c = 3.0 M are shown (see Table S5 of the ESI† for more information). As can be seen, there are two peaks at ∼2.0 and ∼2.7 Å on the 1,3-DMU–OW pRDF. The first small peak is due to the interactions of the HN and HC atoms of 1,3-DMU with the oxygen atom of water; accordingly, the corresponding minimum at 2.2 Å does not correspond to the solute's first hydration shell (FHS). The second maximum indicates the interactions of water with the heavy solute atoms (N, O, C, CH). The corresponding minimum observed at 3.8 Å defines the complete first hydration shell of the solute comprising 25.9H2O molecules at infinite dilution. With increasing concentration CNMD(H2O) continuously drops, reaching a value of 12.5 at c = 4.9 M (Fig. 4).
Comparison of CNMD(H2O) with the total effective hydration number from DRS (Fig. 4) yields Zt > CNMD(H2O) for c < 1.5 M. This may indicate that at low solute concentrations also H2O molecules beyond the first hydration shell of 1,3-DMU are retarded in their dynamics. Currently, this cannot be confirmed by other methods. However, the present MD simulations clearly show (see below) that only a small fraction of the solvent molecules residing in the first hydration shell, equivalent to Zib ≈ 1.6 frozen H2O dipoles, is impeded so strongly in its rotational dynamics that these molecules are neither detectable as bulk-like nor as slow water by DRS.
Note that CNMD(H2O) > Zt at c > 2.0 M (Fig. 4) and eventually exceeding the solvent-to-solute ratio is a consequence of the strong solvation shell overlap, which is not taken into account in the calculation of CNMD(H2O). Instead, all H2O molecules surrounding a given 1,3-DMU molecule are counted irrespective if they are just in contact with this reference or are shared with neighbouring solute molecules.
Direct comparison of the present values from MD and DRS for 1,3-DMU with effective hydration numbers from compressibility studies, namely 4.773 and 4.374 at c → 0, is not straightforward but obviously also this technique monitors only a part of the first hydration shell. On the other hand the NMR study of Costantino et al.50 yielded a constant number, 19.79 ± 0.27, over the concentration range 0.061 ≤ c/M ≤ 1.76. According to the authors this number encompasses water molecules solvating both hydrophilic and hydrophobic moieties of 1,3-DMU and thus should correspond to Zt= Zib + Zs from DRS.75 However, since the NMR values are comparable to the first-shell coordination numbers, CNMD(H2O), but smaller than Zt for c < 1.7 M this indicates a “view range” of NMR restricted to the first hydration shell.
The 1,3-DMU–C pRDF describing solute–solute contacts exhibits a well-defined structure (Fig. 6). Two peaks at 3.5 and 5.1 Å are observed for the 3.0 M solution. Here each 1,3-DMU molecule is in contact with, on average, 1.7 other 1,3-DMU molecules within the radius of 4.1 Å defined by the first minimum. This number increases with increasing concentration from CNMD(DMU) = 0.3 at 0.48 M to CNMD(DMU) = 2.5 at 4.9 M. Inclusion of the second peak, i.e. integrating the pRDF up to 5.7 Å, gives 3.8 neighboring 1,3-DMU molecules at 0.48 M while at the highest studied concentration each 1,3-DMU is surrounded by 5.9 solute molecules within this distance. Similar to the 1,3-DMU–OW pRDF, the pronounced shoulder on the 1,3-DMU–C pRDF's at ∼3.0 Å is caused by HN and HC atoms interacting with the C atom of the reference molecule.
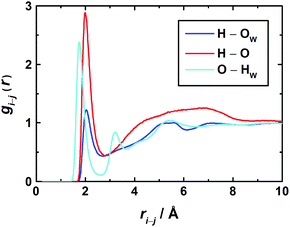
Further details on solute–solvent and solute–solute interactions can be extracted from the RDFs for individual atom pairs on solvent and solute. As the latter has two possible centers able to form hydrogen bonds, namely the carbonyl oxygen atom as an acceptor and the amino hydrogen atoms as donors, the most interesting RDFs are O–HW, HN–OW, and HN–O correlations. For the 3.0 M solution these are shown in Fig. 7.
In the O–HW RDF, the first peak corresponds to the direct coordination of the carbonyl oxygen to the hydrogen atoms of water. The second peak represents water molecules with an HW atom not directly bound to the O atom of 1,3-DMU. The third broad peak at about 5.2 Å corresponds to H2O molecules coordinated to the remaining part of the solute and to H2O molecules belonging to the second hydration shell.
With regard to the amino groups, the first peak in the HN–OW RDF is located at 2.0 Å. At about 5.2 Å, a second – rather broad – peak corresponds to H2O molecules located either in the second hydration shell or close to the carbonyl O. Interestingly, for the HN–OW and HN–O RDFs the positions of their first maxima practically coincide. This suggests that – at least at high concentrations – not only H-bonded hydrates are formed but also head-to-tail aggregates of 1,3-DMU molecules via amino groups interacting with carbonyl oxygen.
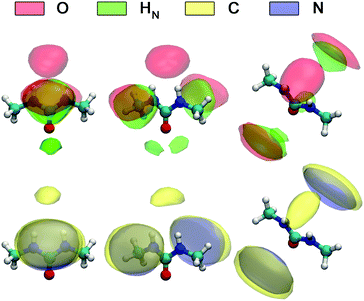
A detailed picture of the arrangement of the water molecules hydrogen bonded to 1,3-DMU is given by the spatial distribution function of the three closest water molecules, shown in Fig. 8. There are indeed two water molecules interacting with the carbonyl oxygen atom acting as the H-bond donor. Additionally, a further H2O molecule interacts simultaneously with both NH acceptor groups. The two water molecules bound to the CO group show up as bent toroidal clouds, the water molecule that is hydrogen bonded to the NH moieties forms a nearly ellipsoidal cloud located directly above the mid-point between these groups. The analysis of combined distribution functions linking the distance between the C atom of 1,3-DMU and water oxygen, OW, and relative orientations of water molecules hydrating the solute provided in the ESI† reveals that the orientations found for the closest three water molecules are consistent with the picture that they form hydrogen bonds to 1,3-DMU and to a certain extent align their dipole vectors with that of the solute. This picture agrees qualitatively with the minimum-energy structures of 1,3-DMU–H2O complexes shown in Fig. 5 and explains the experimental result of Zib ≈ 1.6 “frozen” water dipoles per solute molecule and the large effective dipole moment of μeff,1 = (11.3 ± 0.6) D of 1,3-DMU.
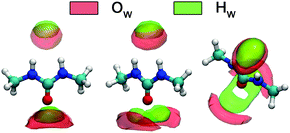 | ||
| Fig. 8 Spatial distribution functions of the atoms of the nearest three H2O molecules around 1,3-DMU in the 0.48 M solution. | ||
Fig. 9 shows the spatial distribution functions of the atoms of neighbouring 1,3-DMU molecules around the solute. Clearly, the bent oblate ellipsoid zones formed by the O, HN, C and N atoms above and below the CNN plane of the reference 1,3-DMU molecule indicate the tendency of solute molecules to form stacked structures. Simultaneously, the spherical distribution of O atoms just on top of the amino hydrogens of the reference, as well as the regions of H atoms in the vicinity of the carbonyl oxygen, suggests the formation of head-to-tail associates stabilized by H-bonding. At c = 3.0 M the solute dipole vectors are aligned roughly parallel with respect to each other in ∼36% of these structures, whereas in ∼23% they are anti-parallel. A more detailed analysis of the arrangement of nearest 1,3-DMU molecules around the reference solute, performed by means of a 2D analysis combining radial and angular distribution functions, is given in the ESI.†
| Cu,l(t) = 〈Pl[u(t) × u(0)]〉, | (10) |
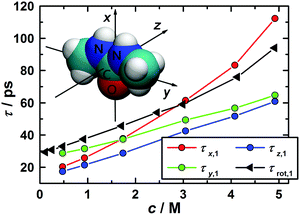
The correlation times for the reorientation of the three vectors depicted in the inset of Fig. 10 were derived from the MD simulations. The first vector, x, points along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and coincides with the dipole vector of 1,3-DMU. The second vector, y, which points along the N–N axis, lies in the molecular plane and is perpendicular to the first. The third vector, z, is perpendicular to both of them and thus normal to the molecular plane. To calculate their correlation times the corresponding Cu,l(t) functions were fitted to exponential decays and integrated analytically. The obtained values for τu,l are listed in Table 3.
O bond and coincides with the dipole vector of 1,3-DMU. The second vector, y, which points along the N–N axis, lies in the molecular plane and is perpendicular to the first. The third vector, z, is perpendicular to both of them and thus normal to the molecular plane. To calculate their correlation times the corresponding Cu,l(t) functions were fitted to exponential decays and integrated analytically. The obtained values for τu,l are listed in Table 3.
| c/M | x | y | z | ||||||
|---|---|---|---|---|---|---|---|---|---|
| τ 1 | τ 2 | τ 3 | τ 1 | τ 2 | τ 3 | τ 1 | τ 2 | τ 3 | |
| 0.4755 | 18.3 | 6.5 | 1.7 | 26.6 | 8.7 | 2.3 | 14.1 | 4.4 | 0.9 |
| 0.9327 | 21.0 | 8.1 | 1.9 | 31.5 | 9.9 | 2.6 | 16.1 | 5.1 | 1.0 |
| 1.7373 | 30.8 | 11.0 | 2.5 | 33.8 | 11.1 | 2.9 | 21.7 | 6.8 | 1.2 |
| 3.0463 | 46.3 | 16.3 | 3.6 | 43.5 | 15.3 | 3.8 | 30.3 | 9.9 | 1.6 |
| 4.0780 | 64.5 | 21.7 | 4.8 | 49.1 | 17.4 | 4.5 | 38.8 | 12.3 | 1.9 |
| 4.9172 | 94.0 | 30.7 | 6.4 | 59.9 | 22.5 | 5.4 | 47.1 | 15.4 | 2.4 |
In the case of molecular reorientation through rotational diffusion the ratio τu,1/τu,2 should be equal to 3. Inspection of the τu,1 and τu,2 data from MD summarized in Table 3 reveals 2.7 ≤ τu,1/τu,2 ≤ 3.1, depending on the chosen vector and solute concentration. This would suggest 1,3-DMU reorientation through rotational diffusion. However, as shown by Laage et al.,77 comparison of first- and second-order reorientation times may not be sufficient to identify the relaxation mechanism and additionally the ratio τu,1/τu,3 has to be considered. For rotational diffusion theory predicts τu,1/τu,3 = 6. In the present case the simulations yielded for the 3.0 M solution the ratios of 12.9, 11.4 and 18.8 for the vectors x, y and z, suggesting that the reorientation of 1,3-DMU molecules cannot be classified as rotational diffusion.
Due to missing far-infrared/terahertz data and the decomposition of the spectra into individual modes according to eqn (2) DRS does not yield the time integral of the collective dipole correlation function. Instead, the dielectric relaxation time of 1,3-DMU, τ1 (Table S2 of the ESI†), is given by the slope of this function at long times. The corresponding rotational correlation time, τrot,1, of a 1,3-DMU molecule, obtained from τ1 with the Powles–Glarum equation,67,68 is compared in Fig. 10 with the long-time slope, τu,1′, of the rotational correlation function, Cu,1(t), from the MD simulations (see Table S8 of the ESI† for details).
The very good general agreement between the experimental data and the rotational correlation times from MD immediately confirms our assignment of the lowest frequency mode (amplitude S1, relaxation time τ1) resolved in the dielectric spectra to the reorientation of 1,3-DMU dipoles. At the same token, this good agreement between experiment and simulation validates the force field used in this MD study. The combination of the SPC/E model for water and a customized KBFF model for 1,3-DMU is clearly able to reproduce the dynamic properties of 1,3-DMU–water mixtures.
Up to c ≈ 2.0 M the values for τx,1′, τy,1′, and τz,1′ remain rather similar. However, at higher concentrations the reorientation of the vector parallel to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is considerably slowed down, i.e. τx,1′ increases significantly. This suggests that, similar to urea,29,78–80 the reorientation of 1,3-DMU dipoles is becoming more and more anisotropic and possibly indicates increasing 1,3-DMU aggregation in line with the structural information from MD (Fig. 9) and the inference of Rodríguez-Ropero et al.23
O bond is considerably slowed down, i.e. τx,1′ increases significantly. This suggests that, similar to urea,29,78–80 the reorientation of 1,3-DMU dipoles is becoming more and more anisotropic and possibly indicates increasing 1,3-DMU aggregation in line with the structural information from MD (Fig. 9) and the inference of Rodríguez-Ropero et al.23
| C(t) = 〈aij(0)aij(t)〉/〈aij(0)2〉, | (11) |
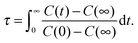 | (12) |
| c/M | τ C/ps | τ H/ps | |||||||
|---|---|---|---|---|---|---|---|---|---|
| OW–OW | O–OW | HN–OW | CH–OW | C–C | OW–OW | O–OW | HN–OW | HN–O | |
| r c = 3.3 Å | r c = 3.3 Å | r c = 2.7 Å | r c = 5.1 Å | r c = 5.0 Å | r c = 3.3 Å, θc = 30° | r c = 3.3 Å, θc = 30° | r c = 3.3 Å, θc = 40° | r c = 3.4 Å, θc = 40° | |
| 0.0000 | 7.9 | 7.1 | |||||||
| 0.4755 | 8.6 | 11.2 | 5.1 | 20.6 | 55.1 | 7.8 | 10.7 | 4.1 | 9.2 |
| 0.9327 | 9.3 | 12.6 | 5.8 | 22.1 | 51.0 | 8.5 | 12.1 | 4.7 | 12.5 |
| 1.7373 | 10.7 | 16.0 | 7.4 | 24.9 | 49.1 | 9.8 | 15.4 | 6.0 | 21.9 |
| 3.0463 | 13.7 | 22.1 | 10.6 | 30.4 | 57.6 | 12.5 | 21.3 | 8.9 | 34.0 |
| 4.0780 | 17.0 | 28.1 | 14.0 | 35.8 | 64.7 | 15.5 | 27.1 | 11.9 | 45.7 |
| 4.9172 | 19.8 | 36.5 | 19.1 | 42.2 | 73.8 | 18.2 | 35.4 | 16.5 | 60.3 |
As seen from Table 4, the contact times of H2O molecules in the vicinity of the various 1,3-DMU moieties, respectively, and H2O itself, decrease in the sequence CH > O > H2O > HN for all 1,3-DMU–H2O mixtures studied. Compared to water surrounded by water, the exchange of H2O near the O atom of the solute is retarded by a factor of 1.6, whereas H2O molecules near the amino groups exchange 1.3 times faster for the 3.0 M solution. This result is in line with an earlier MD investigation of urea–water mixtures by Kokubo et al.85 using the KBFF model for urea and TIP3P water. The authors showed that the HN atoms of urea are less effective hydrogen-bond donors than water itself due to the pronounced nucleophilicity of the carbonyl group. In the case of 1,3-DMU, methylation of the nitrogen atoms leads to an additional increase in the electron density of the oxygen lone pair orbitals and a decrease in the partial electron density of the nitrogen lone pair orbitals.86 This manifests in a less negative partial charge for nitrogen in 1,3-DMU (qN = −0.553) compared to urea (qN = −0.69345). Thus, methyl substitution reduces solvent interaction with the nitrogen atom and promotes it at the oxygen atom.
Comparison of τC and τH revealed that, similar to water surrounded by water, the contact times for H2O around the carbonyl and amino groups of the solute are mainly determined by H-bonding. For example, at 3.0 M the values of τC = 22.1 ps and τH = 21.3 ps were found for O–H2O interactions (Table 4). The corresponding data for H2O–H2O are τC = 13.7 ps and τH = 12.5 ps. Thus, O–H2O dynamics is slowed down by a factor of ∼1.6 compared that of H2O surrounded by H2O. Surprisingly, however, the dynamics of the HN–H2O interactions is notably faster with τC = 10.6 ps and τH = 8.9 ps. On the other hand, as predicted by the excluded volume mechanism in the study of Laage et al.,60,87 the contact time of H2O molecules with the methyl groups of 1,3-DMU, τC = 30.4 ps, is significantly (2.2 fold) increased.
When comparing these contact times with experimental dielectric relaxation times it has to be considered that the simulation data do not directly reflect the reorientation of the water-dipole vector. On the other hand, water reorientation is not diffusive but, due to H-bonding, occurs through sub-picosecond large-angle jumps separated by waiting times of several picoseconds.60,87 Whilst the sub-picosecond jumps can be associated with the present fast water mode (S4, τ4),58 the environment-dependent waiting time between these jumps determines the dielectric relaxation times τ2 and τ3. Although numerical equivalence cannot be expected, it is reasonable to assume that τ3 should be comparable to τC of H2O surrounded by H2O. Similarly, τ2, which is characteristic of hydration water impeded in its dynamics, should have an equivalent in the contact times of hydration water with appropriate solute moieties.
The experimental retardation factor (τ2/τ3 = 2.0 at 3.0 M) is indeed comparable to the relative increase of H2O contact times around the carbonyl (τC(O–OW)/τC(OW–OW) = 1.6) and the methyl groups (τC(CH–OW)/τC(OW–OW) = 2.2) of 1,3-DMU. At least for c ≥ 1.5 M where Zs ≤ CNMD and solute hydration shells start to overlap (Fig. 4), we may therefore assign the DRS-detected slow water fraction to H2O molecules in contact with these two groups of 1,3-DMU.
Note that from τC(HN–OW)/τC(OW–OW) < 1 a decrease of the dielectric relaxation time τ3 could be expected or even the emergence of a separate mode for water hydrating the amino groups. However, according to the present simulations only a single H2O molecule (the 3rd-next neighbor) shared by both amino groups is involved here (Fig. 8; also see the discussion in the ESI†). The contribution of this molecule is certainly too small to give rise to a detectable DRS mode. However, due to a likely band overlap it might be a possible reason for the rather strong increase of the fast-water relaxation time, τ4, with concentration (Table S2, ESI†).
The present MD simulations revealed that the dipole moment vectors of the three H2O molecules closest to the solute molecule, with neighbors 1 & 2 hydrogen bonding to the carbonyl group and the third shared by the amino groups essentially, wobble in a 30° cone around the dipole direction (x-vector) of 1,3-DMU (Fig. 10; also see Fig. 8 and the discussion in the ESI;† note that this structure is rather similar to hydrate cluster F in Fig. 5). Thus, their components normal to x will either contribute to Zs (neighbors 1 & 2) or to the bulk-water relaxation (neighbor 3) whereas the “frozen” parallel components give rise to Zib ≈ 1.6 and the large effective dipole moment, μeff,1 = (11.3 ± 0.6) D. Despite its short contact time also neighbor 3 may be involved here as the HN–OW RDF exhibits a well-defined maximum (Fig. S8, ESI†) clearly associated with hydrogen bonding (Fig. S9, ESI†).
It is noteworthy that the contact and H-bond lifetimes of direct 1,3-DMU–1,3-DMU interactions summarized in Table 4 are significantly longer than those for H2O molecules both near H2O and the solute but comparable to the rotational correlation time of the solute found with DRS (Fig. 10). According to the MD simulations solute–solute aggregates (Fig. 9 and Fig. S6, ESI†) live up to 57.6 ps and can remain H-bonded for about 34 ps at 3.0 M (Table 4), whereas the correlation time for the reorientation of the CNN plane of a 1,3-DMU molecule is τy,1′ = 59.0 ps (Table S8, ESI†). These values are similar to the experimental dielectric relaxation time, τ1 = 67 ps (Table S2, ESI†), of the solute at this concentration and suggest that the formation of such aggregates is a likely reason for the considerable increase of τ1 (and possibly also of viscosity) with solute concentration. The analysis of the number, nH, of H-bonds formed between solute molecules (Fig. S11, ESI†) showed indeed that the fraction of fully hydrated 1,3-DMU molecules (nH = 0) decreases from (98.5 ± 1.5)% at 0.48 M to (67.6 ± 5.2)% at 4.9 M. Therefore, in the most concentrated solution studied ∼30% of the solute molecules form head-to-tail associates via one (8.0 ± 0.6)% or even two (22.3 ± 4.3)% hydrogen bonds. Simultaneously, the tendency of anti-parallel stacking increases, see the detailed discussion in the ESI.† As a consequence, solute hydration shells increasingly overlap, leading to the pronounced decrease of the effective hydration number, Zs, associated with “slow” water from ∼39 at c → 0 to 3.3 at c = 4.9 M. Since the number of H2O molecules hydrogen bonded to the carbonyl groups of 1,3-DMU decreases only slightly (Fig. S11, ESI†) the number of “frozen” water dipoles remains practically constant at Zib ≈ 1.6. The opposing effects on the effective dipole moment of 1,3-DMU arising from the simultaneous formation of parallel head-to-tail aggregates and anti-parallel stacks apparently compensate, so that μeff,1 = (11.3 ± 0.6) D does not change with solute concentration.
Conclusions
In this contribution we studied 1,3-DMU–water mixtures combining dielectric relaxation spectroscopy (DRS) and molecular dynamics (MD) simulations. We found that the static permittivity increases considerably in solutions of 1,3-DMU relative to pure water due to the large effective dipole moment of the solute. The latter arises from the pronounced parallel alignment of the dipole moments of 1,3-DMU and its three closest H2O molecules, of which two form long-lived hydrogen bonds to the carbonyl oxygen atom of the solute, whereas the third forms surprisingly short-lived H-bonds to both amino groups. This configuration leads to Zib ≈ 1.6 “frozen” water dipoles independent of concentration. With increasing concentration solute aggregation via anti-parallel stacking and head-to-tail H-bonding becomes relevant. The associated overlap of hydration shells is reflected by a strong decrease of the number of “slow” (retarded) water molecules, Zs, hydrating 1,3-DMU. Interestingly, due to compensation effects this aggregate formation does neither affect Zib nor μeff,1.Acknowledgements
V. A. acknowledges support from the Russian Government Program for Competitive Growth of Kazan Federal University and thanks the Deutscher Akademischer Austauschdienst (DAAD) for a grant enabling her experiments in Regensburg.Notes and references
- E. Freire, A. Schön, B. M. Hutchins and R. K. Brown, Drug Discovery Today, 2013, 18, 1007–1013 CrossRef CAS PubMed.
- R. Kumaran and P. Ramamurthy, J. Fluoresc., 2011, 21, 1499–1508 CrossRef CAS PubMed.
- D. R. Canchi and A. E. García, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- D. Horinek and R. R. Netz, J. Phys. Chem. A, 2011, 115, 6125–6136 CrossRef CAS PubMed.
- B. Moeser and D. Horinek, J. Phys. Chem. B, 2014, 118, 107–114 CrossRef CAS PubMed.
- W. Zheng, A. Borgia, K. Buholzer, A. Grishaev, B. Schuler and R. B. Best, J. Am. Chem. Soc., 2016, 138, 11702–11713 CrossRef CAS PubMed.
- T. T. Herskovits, H. Jaillet and B. Gadegbeku, J. Biol. Chem., 1970, 245, 4544–4550 CAS.
- A. Shimizu, K. Fumino, K. Yukiyasu and Y. Taniguchi, J. Mol. Liq., 2000, 85, 269–278 CrossRef CAS.
- K. Hamaguchi and H. Sakai, J. Biochem., 1965, 57, 721–732 CAS.
- J. Quijada, G. López, R. Versace, L. Ramírez and M. L. Tasayco, Biophys. Chem., 2007, 129, 242–250 CrossRef CAS PubMed.
- V. M. Tischenko, Biophysics, 2011, 56, 602–605 CrossRef.
- R. Zangi, R. Zhou and B. J. Berne, J. Am. Chem. Soc., 2009, 131, 1535–1541 CrossRef CAS PubMed.
- D. R. Canchi, D. Paschek and A. E. García, J. Am. Chem. Soc., 2010, 132, 2338–2344 CrossRef CAS PubMed.
- S. Funkner, M. Havenith and G. Schwaab, J. Phys. Chem. B, 2012, 116, 13374–13380 CrossRef CAS PubMed.
- K.-J. Tielrooij, J. Hunger, R. Buchner, M. Bonn and H. J. Bakker, J. Am. Chem. Soc., 2010, 132, 15671–15678 CrossRef CAS PubMed.
- Y. L. A. Rezus and H. J. Bakker, Phys. Rev. Lett., 2007, 99, 148301 CrossRef CAS PubMed.
- Y. L. A. Rezus and H. J. Bakker, J. Phys. Chem. A, 2008, 112, 2355–2361 CrossRef CAS PubMed.
- J. Hunger, K.-J. Tielrooij, R. Buchner, M. Bonn and H. J. Bakker, J. Phys. Chem. B, 2012, 116, 4783–4795 CrossRef CAS PubMed.
- N. Poklar, G. Vesnaver and S. Lapanje, Biophys. Chem., 1993, 47, 143–151 CrossRef CAS.
- N. Poklar, G. Vesnaver and S. Lapanje, J. Protein Chem., 1995, 14, 709–719 CrossRef CAS PubMed.
- N. Poklar, G. Vesnaver and S. Lapanje, Biophys. Chem., 1996, 57, 279–289 CrossRef CAS PubMed.
- L. B. Sagle, Y. Zhang, V. A. Litosh, X. Chen, Y. Cho and P. S. Cremer, J. Am. Chem. Soc., 2009, 131, 9304–9310 CrossRef CAS PubMed.
- F. Rodríguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2014, 118, 7327–7334 CrossRef PubMed.
- S. Subramanian, T. S. Sarma, D. Balasubramanian and J. C. Ahluwalia, J. Phys. Chem., 1971, 75, 815–820 CrossRef CAS PubMed.
- U. Kaatze, H. Gerke and R. Pottel, J. Phys. Chem., 1986, 90, 5464–5469 CrossRef CAS.
- P. R. Philip, G. Perron and J. E. Desnoyers, Can. J. Chem., 1974, 52, 1709–1713 CrossRef CAS.
- E. V. Ivanov and V. K. Abrosimov, J. Chem. Eng. Data, 2013, 58, 1103–1111 CrossRef CAS.
- R. Buchner and G. Hefter, Phys. Chem. Chem. Phys., 2009, 11, 8984–8999 RSC.
- V. Agieienko and R. Buchner, Phys. Chem. Chem. Phys., 2016, 18, 2597–2607 RSC.
- T. Shikata and S. Itatani, J. Solution Chem., 2002, 31, 823–844 CrossRef CAS.
- A. Eiberweiser, A. Nazet, S. E. Kruchinin, M. V. Fedotova and R. Buchner, J. Phys. Chem. B, 2015, 119, 15203–15211 CrossRef CAS PubMed.
- A. Schönhals and F. Kremer, in Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer Berlin Heidelberg, 2003, ch. 1, pp. 1–33 Search PubMed.
- T. Sonnleitner, D. A. Turton, S. Waselikowski, J. Hunger, A. Stoppa, M. Walther, K. Wynne and R. Buchner, J. Mol. Liq., 2014, 192, 19–25 CrossRef CAS.
- J. Barthel, R. Buchner, P. N. Eberspächer, M. Münsterer, J. Stauber and B. Wurm, J. Mol. Liq., 1998, 78, 83–109 CrossRef CAS.
- R. Buchner, T. Chen and G. Hefter, J. Phys. Chem. B, 2004, 108, 2365–2375 CrossRef CAS.
- A. Stoppa, A. Nazet, R. Buchner, A. Thoman and M. Walther, J. Mol. Liq., 2015, 212, 963–968 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- J. B. Foresman, T. A. Keith, K. B. Wiberg, J. Snoonian and M. J. Frisch, J. Phys. Chem., 1996, 100, 16098–16104 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- S. Weerasinghe and P. E. Smith, J. Chem. Phys., 2003, 118, 5901–5910 CrossRef CAS.
- S. Weerasinghe and P. E. Smith, J. Phys. Chem. B, 2003, 107, 3891–3898 CrossRef CAS.
- K. J. Miller and J. Savchik, J. Am. Chem. Soc., 1979, 101, 7206–7213 CrossRef CAS.
- J. Hinze and H. H. Jaffe, J. Am. Chem. Soc., 1962, 84, 540–546 CrossRef CAS.
- M. G. Bravo-Sánchez, A. Estrada-Baltazar, G. A. Iglesias-Silva and M. Ramos-Estrada, J. Chem. Eng. Data, 2009, 55, 989–991 CrossRef.
- R. Sartorio, P. Padulano, L. Costantino and V. Vitagliano, J. Solution Chem., 1981, 10, 111–119 CrossRef CAS.
- L. Costantino, G. D'Errico, O. Ortona and V. Vitagliano, J. Mol. Liq., 2000, 84, 179–191 CrossRef CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nosé and M. L. Klein, Mol. Phys., 1983, 50, 1055–1076 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- T. Fukasawa, T. Sato, J. Watanabe, Y. Hama, W. Kunz and R. Buchner, Phys. Rev. Lett., 2005, 95, 197802 CrossRef PubMed.
- A. Eiberweiser, A. Nazet, G. Hefter and R. Buchner, J. Phys. Chem. B, 2015, 119, 5270–5281 CrossRef CAS PubMed.
- D. Laage, G. Stirnemann, F. Sterpone, R. Rey and J. T. Hynes, Annu. Rev. Phys. Chem., 2011, 62, 395–416 CrossRef CAS PubMed.
- R. Buchner, C. Holzl, J. Stauber and J. Barthel, Phys. Chem. Chem. Phys., 2002, 4, 2169–2179 RSC.
- H. M. A. Rahman, G. Hefter and R. Buchner, J. Phys. Chem. B, 2012, 116, 314–323 CrossRef CAS PubMed.
- R. Buchner, J. Barthel and J. Stauber, Chem. Phys. Lett., 1999, 306, 57–63 CrossRef CAS.
- J. Barthel, H. Hetzenauer and R. Buchner, Ber. Bunseng. Phys. Chem., 1992, 96, 1424–1432 CrossRef CAS.
- H. M. A. Rahman, G. Hefter and R. Buchner, J. Phys. Chem. B, 2013, 117, 2142–2152 CrossRef CAS PubMed.
- Note that the present CN numbers are calculated without taking into accout possible solvation shell overlap and associated sharing of H2O molecules.
- J. G. Powles, J. Chem. Phys., 1953, 21, 633–637 CrossRef CAS.
- S. H. Glarum, J. Chem. Phys., 1960, 33, 639–643 CrossRef CAS.
- J. L. Dote and D. Kivelson, J. Phys. Chem., 1983, 87, 3889–3893 CrossRef CAS.
- M. Obrzud, M. Rospenk and A. Koll, J. Phys. Chem. B, 2010, 114, 15905–15912 CrossRef CAS PubMed.
- P. K. Mehrotra and D. L. Beveridge, J. Am. Chem. Soc., 1980, 102, 4287–4294 CrossRef CAS.
- B. Lin and B. M. Pettitt, J. Chem. Phys., 2011, 134, 106101 CrossRef PubMed.
- A. Burakowski and J. Gliński, Chem. Phys. Lett., 2015, 641, 40–43 CrossRef CAS.
- J. Krakowiak, J. Wawer and A. Panuszko, J. Chem. Thermodyn., 2013, 58, 211–220 CrossRef CAS.
- Costantino et al.50 assume viscosity to be independent of the solute concentration. Correction of their diffusion data with the present η values (Table S1, ESI†) yields an even higher NMR hydration number of 22 ± 1.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier Science, 2006 Search PubMed.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832–835 CrossRef CAS PubMed.
- A. Idrissi, F. Sokolić and A. Perera, J. Chem. Phys., 2000, 112, 9479–9488 CrossRef CAS.
- A. Idrissi, P. Bartolini, M. Ricci and R. Righini, Phys. Chem. Chem. Phys., 2003, 5, 4666–4671 RSC.
- P. O. Åstrand, A. Wallqvist, G. Karlström and P. Linse, J. Chem. Phys., 1991, 95, 8419–8429 CrossRef.
- R. Adams, H. H. M. Balyuzi and R. E. Burge, J. Appl. Crystallogr., 1977, 10, 256–261 CrossRef.
- J. Jadżyn, L. Bouteiller, J.-L. Déjardinc and G. Czechowskia, Acta Phys. Pol., A, 2006, 110, 495–505 CrossRef.
- M. Obrzud, M. Rospenk and A. Koll, J. Mol. Struct., 2012, 1018, 54–63 CrossRef CAS.
- J. Świergiel, L. Bouteiller and J. Jadżyn, J. Phys. Chem. B, 2015, 119, 12947–12953 CrossRef PubMed.
- H. Kokubo and B. M. Pettitt, J. Phys. Chem. B, 2007, 111, 5233–5242 CrossRef CAS PubMed.
- E. I. Harnagea and P. W. Jagodzinski, Vib. Spectrosc., 1996, 10, 169–175 CrossRef CAS.
- D. Laage, G. Stirnemann and J. T. Hynes, J. Phys. Chem. B, 2009, 113, 2428–2435 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables with data for density, viscosity and with relaxation parameters describing the dielectric spectra; tables with bonded and non-bonded parameters for the solute force field; auxiliary tables and figures. See DOI: 10.1039/c6cp07407c |
| This journal is © the Owner Societies 2017 |