Study of entropic characteristics of strongly correlated systems using VO₂ as a model case

Abstract

To explain the huge caloric effects often observed in the first-order electronic phase transition in the strongly correlated oxides, the entropic characteristics are investigated in VO₂. By evaluating the spin and charge fluctuations based on the local moment model and the Sommerfeld coefficient in the high-temperature rutile phase, it is found that these fluctuations of the high-temperature phase are the main source of the entropic change during the transition. This mode of entropic change is realized by the quenching of these fluctuations owing to the formation of a singlet bonding state in the low-temperature monoclinic phase. By introducing oxygen deficiency, a vagueness in the gap at the Fermi level is confirmed by the transport data, the X-ray photoelectron spectra and also the electronic structure calculated by the first-principles calculations. In this case, the entropic feature at the transition is weakened. Consequently, the large caloric phenomena of the strongly correlated oxides are a result of the conversion of the internal energy gain owing to the orbital selection at the ground state into the free energy gain owing to the spin and charge fluctuations at finite temperature.

---

Introduction

Recently, concepts of the electronic phase and its transition have been widely accepted not only in research on solid-state physics but also in the development of novel functional devices.^1,2 Among their functions, the entropic behaviour is one of the unique abilities that can help in solving the energy problems.¹ The latent heat of the first-order electronic phase transition in some oxide compounds is enhanced to relatively high; e.g. 722 J cc⁻¹ for LiVO₂, 240 J cc⁻¹ for VO₂ and 42 J cc⁻¹ for MgTi₂O₄.^3–5 These latent heat values for the solid–solid transition are comparable to those for the solid–liquid transition such as the melting of H₂O ice (333 J cc⁻¹) or Paraffin (200–250 J cc⁻¹). The use of these oxides in cooling/heating packs is one of the passive applications of their latent heat release/absorption properties,¹ and some trials on the active control of the caloric effect using external fields, like magnetic or electric field, have also been carried out.^6,7 In the case of electric field control, a relatively large electrocaloric effect has been observed under low voltages for VO₂,⁷ in contrast to the high-voltage electrocaloric effect in ferroelectric materials.⁸

From the thermodynamic relation, the free energy of a low-temperature state F_l equals to that of a high-temperature state F_h at the first-order transition temperature T_C. The following relationship is straightforwardly obtained between the entropy S and the internal energy E^int; E^int_h − E^int_l = (S_h − S_l)T_C. Namely, a large caloric effect is observed when the internal energy difference ΔH = E^int_h − E^int_l between these two states is large and the entropy difference ΔS = S_h − S_l is also large. When only one of the two conditions is met, large but low-temperature phenomena or high-temperature but small phenomena would appear. For strongly correlated substances, a large internal energy difference originates mainly from electron correlation. In the case of VO₂, valence electrons form a covalent bond by putting two electrons into the bonding orbital with the formation of a singlet spin–spin pair in the insulating ground state.^9,10 The low-temperature state obtains an internal energy gain (or enthalpy gain under ambient pressure) owing to the removal of electron correlation U; in the ideal model, no spin and charge fluctuations appear in this state. General discussions in the solid-state physics have focused largely on the ground state; modifications such as filling or bandwidth control are all concerned with this Mott-insulator state.^11,12 Meanwhile, a large entropy difference generally emerges from the large entropy of the high-temperature state. In the high-temperature metallic state of VO₂, V 3d electrons form bands across the Fermi energy E_f and spin polarization forms the local moment,⁴ and this state obtains a free energy gain owing to the entropy term. In other words, strong electron correlations are evaded by the orbital freedom at the low temperature state, while the spin and charge freedoms do at the high temperature state. Unfortunately, the latter viewpoint regarding various fluctuations has not been investigated systematically, although multiple degrees of freedom would characterize the entropic behaviour of the strongly correlated electronic phase transitions. Certainly, the precise estimation of elementary excitations in each phase is very important in analyses of the driving force of the MIT transition. However, to solve these issues, an exact method to treat a quasi-stable state as the excited state is necessary, and instead, in the present study, we focus on the enthalpy–entropy compensation phenomenon as a source of the colossal caloric effect universally observed in the strongly correlated oxides.

Materials and methods

Commercially obtained VO₂ powder (Kojundo Chemical Lab. Co., Ltd) was used as the starting material for forming pellets by sintering. The spark plasma sintering (SPS) method was used for sintering. Before the sintering process, the average size of the powder was reduced to sub-μm by using ball milling. The VO₂ powder in the cemented carbide die/punch was heated to 773 K at a rate of 50 K min⁻¹ in an evacuated chamber, and this temperature was held for 5 min. During the heating process, a pressure of 1 GPa was applied to increase the pellet density. In addition, a carbon sheet was placed between the punch and the powder in order to improve the current conductivity. The annealed specimen was obtained by firing in ambient air at 773 K for 1 h by using a conventional tube furnace. Different types of annealing processes were also carried out for pellets encapsulated in an evacuated quartz tube under the same conditions.

Differential scanning calorimetry (DSC) measurement was carried out under ambient air using a SEIKO DSC6000. The magnetic properties were studied by using a superconducting interference device (SQUID) magnetometer. The electrical resistivity was measured by a 4-terminal method using Quantum Design PPMS. X-ray photoelectron spectroscopy (XPS) was performed using a PHI5000 VersaProve II (ULVAC-PHI Inc., Japan) with a monochromatic AlKα (1486.6 eV) X-ray source. The base pressure of the system was below 1 × 10⁻⁷ Pa. Photoelectron spectra of the valence band (V 3d) were recorded with a pass energy of 5.85 eV and an energy step of 0.05 eV, while for those of the V 2p core level a pass energy of 11.75 eV and a step of 0.10 eV were used.

First principles calculations using the coherent potential approximation (CPA) approach implemented in the Korringa Kohn Rostoker (KKR) method¹³ were performed by using the cpa2002v009c code in order to evaluate the magnetic moment in the disordered paramagnetic state. A mesh with 56 k points within the irreducible wedge of the Brillouin zone (BZ) was used for electronic structure calculations. In this CPA code, a void sphere is specified by selecting the atomic number Z = 0, and a certain magnitude of the deficiency can be introduced by treating one site as the mixture of the original element and void. In addition, another type of calculation was performed to check the influence of electron–electron correlation. For this purpose, the full-potential linearized augmented plane wave (FP-LAPW) code (Elk ver 3.0.8) was used for calculations, along with local density approximation plus on-site coulomb interaction (LDA+U). A 5 × 5 × 4 mesh containing 33 k irreducible points of the BZ was used for the unit cell proposed by R. M. Wentzcovitch et al. for both rutile and monoclinic phases of VO₂.¹⁴ For calculation of the density of states (DOSs), the number of k points was increased to 252.

Results and discussion

Fig. 1(a) shows the temperature dependence of magnetization for various VO₂ specimens obtained through different routes. The data can be roughly grouped into specimens showing a broad transition and those showing a sharp transition. The former type of transition is observed in an as-sintered specimen and in a specimen heated in an evacuated quartz tube at 473 K for 1 h. Meanwhile, the specimen annealed in air exhibits a sharp transition. A similar behaviour is observed in the specimen used in the caloric measurements (mentioned later) in the thermal cycle between room temperature and 453 K in air. Since a sharp transition is similar to the change reported in a previous study,⁴ this type of transition, which appears only when the oxidization is promoted, is an intrinsic behaviour. In other words, the broadening of transition in the as-sintered specimen is attributed to oxygen deficiency, which is induced by the reducing environment of SPS with a carbon sheet. Fig. 1(b) shows the thermal profiles obtained by DSC. The data were converted into heat change against temperature (dQ/dT) by dividing the heat flow (dQ/dt) with the temperature variation speed (dT/dt). The first scan was carried out with the as-sintered specimen up to 353 K, and the second scan was carried out up to 453 K under air. In the first cycle, broad negative and positive peaks for absorption and desorption of the latent heat appeared upon heating and cooling, respectively. After heating up to 353 K, which is a moderate temperature, no change was observed upon heating in the second run. Meanwhile, a sharp peak is observed in the dQ/dT curve upon cooling from 453 K. Upon further measurements, all curves trace the same peak pattern for both desorption and absorption of the latent heat. It should be noticed that the maximum positions for the negative and positive peaks for the broad DSC profiles almost correspond to the inflection points, respectively, in the heating and cooling branch of the thermomagnetization (M–T) curves of the as-sintered specimen in Fig. 1(a). In addition, the peak shifts after the high-temperature cycle under air are consistent with the shift of the inflection points of the M–T curves after annealing of the as-prepared specimen in air. These changes indicate that the transition temperature is slightly lowered by the oxygen deficiency.

Fig. 1 (a) Temperature dependence of magnetization for various VO₂ specimens obtained through different routes (inset; thermal variation of resistivity), and (b) thermal profiles obtained by DSC. The data were converted into heat change against temperature (dQ/dT).

As confirmed by the magnetization measurements shown in Fig. 1(a), the change in a DSC profile is related to the filling of oxygen deficiencies because of firing under air. From these data, the as-sintered (reductive) specimen exhibits a latent heat ΔH of 34 kJ kg⁻¹ at a transition temperature of about 333 K, which corresponds to a transition entropy change ΔS of 105 J kg⁻¹ K⁻¹. On the other hand, ΔH of the annealed (oxygen refilled) specimen is 43 kJ kg⁻¹ at 336 K, and ΔS is 128 J kg⁻¹ K⁻¹. In comparison with the reported ΔH value of about 50 kJ kg⁻¹,⁴ the value of ΔH for the annealed specimen is slightly smaller but is similar, while that for the as-sintered specimen is noticeably smaller. In order to confirm the feature of the Mott-type metal–insulator transition, a dc resistivity ρ was measured against temperature for both as-prepared and annealed specimens, as shown in the inset of Fig. 1. The change in ρ at the transition is about four orders of magnitude in the annealed specimen, while it is only two orders of magnitude in the as-sintered specimen. Upon decreasing the temperature, a large increase in ρ of a few orders of magnitude appears for the annealed specimen, whereas the variation is within the same order of magnitude for the as-sintered specimen.

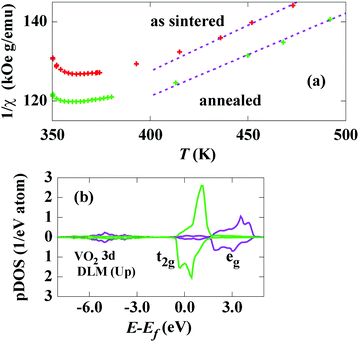
To reveal the entropic contribution during phase transition, we focused on spin and charge fluctuations in the high-temperature metallic phase. In the insulator phase with a monoclinic lattice, a single d electron per V atom occupies a bonding orbital formed by one of the lower-energy combinations of the d_‖ bands split by dimerization of the V–V pair.^10,15 A two-spin pair at this bonding state forms a singlet state and the total spin momentum is therefore zero. In other words, electrons increase energy gain by selecting an orbital degree of freedom with quenching of the spin and charge degrees of freedom. On the other hand, a metallic band across the Fermi energy E_f is formed, and d electrons possess an itinerant character above the transition temperature T_t.^10,15 Consequently, spin and charge fluctuations suddenly appear at this state. Recently, the emergence of the fluctuating local spin moment (disordered local moment: DLM) in the itinerant electron paramagnetic state has been discussed in relation to the electronic structure.^13,16 In view of the well-defined local moment, a conventional probe of its amplitude is the evaluation of the effective paramagnetic moment p_eff based on the Curie–Weiss law of the paramagnetic susceptibility χ. Fig. 2 shows the variation of the inverse paramagnetic susceptibility, 1/χ, with temperature for the as-sintered and annealed specimens. Just above T_t, a concave upward curvature is observed for both the specimens, and fairly linear variation is observed above 420 K. The least-square fit gives the Curie constants of 37.9 and 42.2 K emu g⁻¹ (@0.3 T), which correspond to p_eff = 1.67 and 1.58 μ_B, respectively. The reported value obtained from the experiment is 1.53 μ_B¹⁵ and the value from dynamical mean field calculation is 1.54 μ_B.¹⁷ By considering the non-linear part of the inverse susceptibility, the present value of p_eff for the annealed specimen is consistent with the reported values. The difference between the values of p_eff is therefore intrinsic rather than experimental error, viz., the oxygen deficiency induces an increase in the amplitude of the local moment. The DLM can be calculated using the coherent potential approximation (CPA) implemented in the density functional calculation code. Fig. 2(b) shows the partial density of state (pDOS) for V 3d in the DLM state. Note that the pDOS for only the up-direction DLM is displayed in this figure. A strong crystalline field effect owing to the O-octahedron surrounding the V site results in clear splitting into t_2g and e_g states, even in the DLM DOS. The amplitude of the DLM (p_DLM) is 0.60 μ_B, which corresponds to p_eff = 1.25 μ_B, for the stoichiometric state, and p_DLM becomes 0.66 μ_B by simulating 1% O-vacancy using the CPA method. Accordingly, the increase of p_eff owing to the oxygen deficiency is reproduced, although the value of p_DLM is underestimated by this method. The difference in the value of p_DLM could be attributed to the electron-correlation effect remaining in the high-temperature state,¹⁷ which is not accounted for in this calculation. However, a Rhodes–Wohlfarth (RW)-type enhancement of p_eff is another possible mechanism for this discrepancy.^18,19 According to this mechanism, the strong itinerancy of the d electron leads to larger p_eff compared to the value evaluated from the localized moment model because of the mode–mode coupling of spin fluctuations.¹⁹ To clarify this issue, further experimental observation such as using neutron scattering is necessary.

Fig. 2 (a) Temperature dependence of the inverse magnetic susceptibility above the transition temperature for the as-sintered and annealed specimens. (b) Partial density of state for 3d bands in the disordered local moment state.

When the paramagnetic state above T_t is regarded as the one in the high-temperature limit, the entropy of local moment fluctuations S_LM can be evaluated by using the general relation S_LM = R ln(2J + 1), where R is the gas constant and J is the total (spin) moment. By substituting 2J = p_DLM, S_LM becomes 62 and 66 J kg⁻¹ K⁻¹ for the as-sintered and annealed specimens, respectively. In addition, when the entropy of charge fluctuation S_cf mainly comes from the thermal smearing of the Fermi level, the Sommerfeld coefficient γ gives S_cf = γT_t at the transition. The value of S_cf is estimated to be 59 J kg⁻¹ K⁻¹ by applying a free-electron model to the DLM DOS at E_f. This value is not far from γT_t = 58 J kg⁻¹ K⁻¹ obtained by specific heat measurement.⁴ Since S_LM = S_cf = 0 at the ideal state of a spin-singlet Mott insulator, the entropy difference owing to the spin and charge fluctuations can be directly assigned as the sum of S_LM and S_cf for the metallic phase. For the annealed specimen, the experimentally obtained value, ΔS = 128 J kg⁻¹ K⁻¹, is quite close to the sum, S_LM + S_cf = 121 J kg⁻¹ K⁻¹. Meanwhile, the experimental value, ΔS = 105 J kg⁻¹ K⁻¹, is noticeably smaller than S_LM + S_cf = 125 J kg⁻¹ K⁻¹, for the as-prepared specimen. As explained in relation to Fig. 2(a), since p_eff of the as-prepared specimen is larger than that of the annealed one, S_LM is also expected to be large. For the estimation of S_cf, the assumption S_cf = 0 is valid only when a clear gap opens at E_f. However, the thermal dependence of ρ for the as-sintered specimen implies an imperfect gap state. The activation energy E_a defined by exp(−E_a/k_BT)-type variation¹⁴ becomes about 0.3 eV for the annealed specimen and 0.04 eV for the as-sintered specimen for temperatures between 200 K and T_t. The band gap at the ground state for VO₂ is reported to be about 0.5–0.7 eV.²⁰ Therefore, narrowing of the band gap or appearance of an in-gap state is brought about by the oxygen deficiency in the as-sintered specimen.

In order to verify the electronic structure around E_f, the X-ray photoelectron spectroscopy (XPS) was carried out. Fig. 3(a) shows the XPS spectra around a binding energy of 0 eV for the as-prepared and annealed specimens. The absolute energy scale was calibrated by matching the position and distance of the peaks of V 2p_3/2–3d⁰ and -3d¹ to standard values. For the annealed specimen, the spectrum intensity of the 3d valence state (around 0.5–2.5 eV) depends on the sampling position, which is randomly selected from the fractured surface after crushing an annealed pellet. Since the over-oxidized condition results in the V 3d⁰ state, the corresponding part gives no intensity at the 3d¹ position. Considering that the spectrum weight depends on the ratio between portions with 3d¹ and 3d⁰, each spectrum was arbitrarily enlarged so that the peak values coincided with each other. The spectra at the higher energy side around 1.5–2.5 eV were fairly overlapped, while those at the lower energy side exhibited a shoulder-like structure. On the whole, the larger the population of the over-oxidized (3d⁰) portion, the smaller the intensity of the shoulder. The shoulder position seems to be consistent with the 3d¹ spectra of the as-sintered specimen, which scarcely depends on the sampling position, as shown in Fig. 3(a). Since the spectra of the as-sintered specimen correspond to the electronic structure of a state with oxygen deficiency, the appearance of a shoulder in these spectra indicated that a small amount remains unreacted during annealing in air. From the spectra for the annealed specimen around binding energy E_B = 0, a gap width of about 0.3–0.4 eV is confirmed, being comparable to the activation energy for the thermal variation of ρ. Meanwhile, the gap is vague and a certain amount of intensity just above E_B = 0 suggests the imperfect gap state, as detected by the thermal variation of ρ for the as-sintered specimen.

Fig. 3 (a) XPS spectra around a binding energy of 0 eV for the as-prepared and annealed specimens, (b) total DOS around E_f for the monoclinic VO₂ and VO_2−δ (δ = 0.005) in the non-magnetic state, and (c) variation of the energy difference (ΔH), the gap width (W), and the density of state at the Fermi energy (D(E_f)) against the value of δ.

It is a useful manner to compare the experimental XPS spectra and the DOS obtained by the first-principles calculations. For the KKR-CPA method used to obtain data in Fig. 2(b), it is difficult to apply the on-site coulomb interaction by selecting a certain orbital such as V 3d, and as a result, the Mott gap cannot be realized. In addition, the energy scale of each state strongly depends on the muffin-tin radius of the elements. Accordingly, a calculation in the framework of local density approximation plus the on-site coulomb interaction (LDA+U) has additionally been carried out by using the full-potential linearized augmented-plane wave (FP-LAPW) code (Elk ver. 3.0.18). By referring to the reported results,^21,22 the value of U of 5 eV together with the Hund exchange interaction J of 0.12U are included in the calculation. The spin polarization was omitted so that a non-magnetic (NM) state was intentionally calculated. Furthermore, to simulate the oxygen deficiency, the virtual crystal approximation (VCA) is adopted, and the oxygen site was treated as if it possesses a non-integer atomic number, like Z = 7.98. In this treatment, it is impossible to count a structural vacancy of oxygen, while the influence of the valence doping effect because of the oxygen deficiency can be distinguished from the structural changes such as the local strain induced by the oxygen vacancy. Strictly speaking, the VCA would modify the electron correlation in some substances, resulting in a certain amount of artefact. In the present case, the on-site electron correlation mainly works on the V 3d orbital, and as a result, the singlet d_‖ bonding state is solely formed without a heavy hybridization with the O 2p orbital.⁹ In this regard, the oxygen deficiency largely brings about the crystalline field change (or the atomic potential change), as well as the charge doping. In such situations, the VCA is not considered as a conflicting method against the LDA+U,²³ or the dynamical mean-field theory (DMFT).²⁴Fig. 3(b) shows the total DOS around E_f for the monoclinic VO₂ and VO_2−δ (δ = 0.005) in the non-magnetic state. For stoichiometric VO₂ (upper panel), the gap around E_f appears and its width is about 0.54 eV, which is close to the experimental results for the optical gap.²⁰ The oxygen deficiency pushes up the lower Hubbard band, making it very close to E_f, and this resembles the change in the experimental spectra, as shown in the lower panel. In the qualitative comparison on the energy scale, a discrepancy of about 0.5 eV is not so small. Such a discrepancy, however, may not be attributed to the limitation of the VCA, but to the dynamic effect of the quasi-particles.²⁵ It is noteworthy that the position of the d_‖ band peak, obtained by the DMFT^25,26 or by the Coulomb-hole and screened-exchange approximation,²⁷ is similar to the present results, (∼0.5 eV), which is apparently lower than the experimental XPS peak of the 3d¹ valence spectrum. In order to evaluate the value of ΔH at the ground state, calculations for the tetragonal (rutile) structure were carried out using the same values of U and J, and the energy difference was obtained by changing the δ value within the VCA. Fig. 3(c) shows the variation of the energy difference (ΔH), the gap width (w), and the density of state at the Fermi energy (D(E_f)) against the value of δ. The calculated ΔH is 57 meV f.u.⁻¹ (66 kJ kg⁻¹) at δ = 0, which is slightly overestimated but with a similar magnitude to the experimental value of 43 kJ kg⁻¹ for the annealed specimen. The energy gain of the DLM state compared to the NM state for the same rutile structure is evaluated to be less than 5 J kg⁻¹ K⁻¹ in the KKR-CPA results. It should be noted that, although the various calculation methods yield various discrepancies with experimental facts, the total energy difference tends to fall into a relatively reliable scale even from the LDA+U method.²⁶ The value of ΔH is significantly reduced by increasing δ, especially for small δ values. Although the gap remains open regardless of the shrinkage of w against an increase in δ, at δ = 0.02, its position goes above E_f and a non-zero value of D(E_f) appears; the value increases with δ. These tendencies well explain the decrease in ΔH and ΔS_cf, as well as the drastic suppression in the activation energy of the ρ–T curve, because of the oxygen deficiency. From conventional θ–2θ scans of X-ray powder diffraction, no distinct difference was detected between the as-sintered and annealed specimens. Although more precise measurement could lead to the detection of the structural differences caused by the oxygen deficiency, their impact on the transition, or at least on the caloric properties of the transition, is not very large. On the basis of the thermodynamic framework, the relation (ΔH = ΔST_t) includes all the degrees of freedom that are not limited to electrons. For example, a change in volume affects both the E^int and S terms through the elastic energy and the phonon population, respectively. Actually, the phonon dispersion anomaly has been observed at the MIT transition in the previous study.²⁸ In the present study, we did not intentionally neglect other degrees of freedom like phonons. However, the electron degree of freedom is detected to be the major contribution to the entropic behaviour, and conversion between the internal energy gain by the selection of the orbital state and the free energy gain owing to the charge and spin fluctuations is enhanced by the electron correlation in strongly correlated materials.

Conclusions

In summary, we have evaluated the impact of the electron correlation on the entropic behaviour at the electronic phase transition in VO₂, which was considered a model case for the strongly correlated oxides. Under the assumption that quenching of spin and charge fluctuations in the ground state is due to the formation of a singlet d_‖ bonding state, the entropy difference at the transition was evaluated by the spin and charge fluctuations in the high-temperature rutile phase. From the disordered moment (DLM) first-principles calculations, the stability of local moment polarization is proved, although the calculated amplitude contains uncertainty to some extent because the DLM calculation performed in this work does not account for the electron correlation. The experimentally obtained value of the effective paramagnetic moment of VO₂ is 1.58 μ_B and it increases to 1.67 μ_B for a reductively treated specimen. The entropy values are obtained from the high-temperature limit of the localized moment model, these values correspond to the entropy change due to local-moment fluctuations, S_LM = 62 and 66 J kg⁻¹ K⁻¹. Furthermore, the estimated value of charge fluctuation contribution S_cf from the free-electron model using the calculated density of state (DOS) for the DLM state becomes 58 J kg⁻¹ K⁻¹. For the stoichiometric VO₂ specimen, the sum of these contributions (121 J kg⁻¹ K⁻¹) is fairly close to the value obtained by the caloric measurement, viz. 125 J kg⁻¹ K⁻¹. In contrast, the value for the reductively treated specimen is quite low of 105 J kg⁻¹ K⁻¹. From the electrical transport measurement, the activation energy in the monoclinic phase is drastically suppressed by the reductive treatment. In addition, the profile of the X-ray photoelectron spectroscopy indicates that the oxygen deficiency makes the gap structure unclear in the VO₂ monoclinic phase. These tendencies were well reproduced by the DOS profile calculated using the LDA+U procedure implemented in the full-potential linearized augmented-plane wave method. Oxidation deficiency is also explained by the same method with the virtual crystal approximation. The calculated difference in the internal energy between the monoclinic and rutile phases at the ground state is in relatively close magnitude with the latent heat evaluated from the calorimetric measurements.

Consequently, the entropic feature in VO₂ comes from the conversion of the internal energy gain owing to the orbital freedom into free energy gain owing to the spin and charge freedom of electrons. Realization of such a mechanism is brought about by the strong electron correlation; therefore, the caloric feature is enhanced in the strongly correlated oxide compounds.

References

1. H. Takagi and H. Y. Hwang, Science, 2010, 327, 1601–1602.
2. E. Dagotto, Science, 2005, 309, 257–262.
3. W. Tian, M. F. Chisholm, P. G. Khalifah, R. Jin, B. C. Sales, S. E. Nagler and D. Mandrus, Mater. Res. Bull., 2004, 39, 1319–1328.
4. C. N. Berglund and H. J. Guggenheim, Phys. Rev., 1969, 185, 1022–1033.
5. Y. Zhu, R. Wang, L. Wang, Y. Liu, R. Xiong and J. Shi, Mod. Phys. Lett. B, 2014, 28, 1450232.
6. C. Z. Wu, X. D. Zhang, J. Dai, J. L. Yang, Z. Wu, S. Q Wei and Y. Xie, J. Mater. Chem., 2011, 21, 4509–4517.
7. D. Matsunami and A. Fujita, Appl. Phys. Lett., 2015, 106, 042901.
8. X. Moya, S. Kar-Narayan and N. D. Mathur, Nature, 2014, 13, 439–450.
9. V. Eyert, Ann. Phys., 2002, 11, 650–702.
10. S. Belozerov, M. A. Korotin, V. I. Anisimov and A. I. Poteryaev, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045109.
11. A. Fujimori, I. Hase, Y. Tokura, M. Abbate, F. M. F. de Groot, J. C. Fuggle, H. Eisaki and S. Uchida, Phys. B, 1993, 186–188, 981–985.
12. M. Imada, A. Fujimori and Y. Tokura, Rev. Mod. Phys., 1998, 70, 1039–1247.
13. H. Akai and P. H. Dederichs, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 8739–8747.
14. R. M. Wentzcovitch, W. W. Schulz and P. B. Allen, Phys. Rev. Lett., 1994, 72, 3389–3392.
15. A. Zylbersztejn and N. F. Mott, Phys. Rev. B: Solid State, 1975, 11, 4383–4395.
16. J. Stauton, B. L. Gyorffy, A. J. Pindor, G. M. Stocks and H. Winter, J. Magn. Magn. Mater., 1984, 45, 15–22.
17. S. Belozerov, A. I. Poteryaev and V. I. Anisimov, JETP Lett., 2011, 93, 70–74.
18. P. Rhodes and E. P. Wohlfarth, Proc. – R. Soc. Edinburgh, Sect. A: Math. Phys. Sci., 1963, 273, 247–258.
19. Y. Takahashi, Spin Fluctuation Theory of Itinerant Electron Magnetism, 2013, Springer, p. 58.
20. S. Shin, S. Suga, M. Taniguchi, M. Fujisawa, H. Kanzaki, A. Fujimori, H. Daimon, Y. Ueda and K. Kosuge, and S. Kachi, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 4993–5009.
21. X. Yuan, Y. Zhang, T. A. Abtew and P. Zhang, W Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235103.
22. S. Chen, J. Liu, H. Luo and Y. Gao, J. Phys. Chem. Lett., 2015, 6, 3650–3656.
23. K.-W. Lee, J. Kuneš and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045204.
24. K. Haule, J. H. Shim and G. Kotliar, Phys. Rev. Lett., 2008, 100, 226402.
25. S. Biermann, A. Poteryaev, A. I. Lichtenstein and A. Georges, Phys. Rev. Lett., 2005, 94, 026404.
26. T. C. Koethe, Z. Hu, M. W. Haverkort, C. Schüßler-Langeheine, F. Venturini, N. B. Brookes, O. Tjernberg, W. Reichelt, H. H. Hsieh, H.-J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. Lett., 2006, 97, 116402.
27. M. Gatti, F. Bruneval, V. Olevano and L. Reining, Phys. Rev. Lett., 2007, 99, 266402.
28. J. D. Budai, J. Hong, M. E. Manley, E. D. Specht, C. W. Li, J. Z. Tischler, D. L. Abernathy, A. H. Said, B. M. Leu, L. A. Boatner, R. J. McQueeney and O. Delaire, Nature, 2014, 515, 535–539.

---