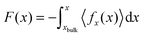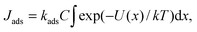Effects of carbon surface topography on the electrode/electrolyte interface structure and relevance to Li–air batteries

Abstract

This work is focused on the effect of the electrode/electrolyte interface restructuring under the variation of carbon surface topography, as one of the possible factors determining the electrochemical activity of different carbon materials in Li–air batteries. Molecular dynamics simulation was used to investigate an acetonitrile-based electrolyte in contact with the following carbon surfaces: graphene plane, single-layer graphene edge, and multi-layer graphene edge. It was shown that the surface topography strongly influences the electrolyte structure at the interface. Acetonitrile has a layered structure at the plane and the edge of graphene nanoribbons and a qualitatively different chessboard structure at the multi-layer graphene edge. It was found from the potentials of mean force that the variation of the surface topography induces the redistribution of the reactants Li⁺ and O₂ near the surface and influences their adsorption rate. This should affect the kinetics of the oxygen reduction reaction and may explain massive deposition of discharge products on graphene edges in Li–air batteries.

---

1 Introduction

Li–air batteries are among the most promising electrochemical power sources because of a very high practical energy density of about 1000 W h kg^−11,2 that significantly exceeds the energy density of state-of-the-art Li-ion batteries (150 W h kg⁻¹).³ However, such performance has not yet been achieved. To solve this problem new air cathodes are particularly developed based on carbon powders, nanotubes and fibers, and graphenes.⁴

The crucial role of the morphology and the microstructure of the air electrode has been well recognized. Optimization of these properties provides high electrode conductivity, fast transport of the reactants O₂ and Li⁺,⁵ and efficient deposition and storage of the insulating discharge products (Li₂O₂, Li₂O).^5,6 Experiments on materials with controlled porosity revealed that pores of 10–100 nm in diameter mainly contribute to discharge capacity.^6–9 The importance of establishing a 3-phase electrochemical interface was also demonstrated.^9,10

Another important issue concerns the electrochemical activity of carbon nanomaterials. It was shown that nitrogen-doped porous carbon, nanotubes, and graphenes catalyze the oxygen reduction reaction (ORR).^11–14 In addition, it was found that surface defects and singularities possess electrocatalytic activity. For example, the rate of electron transfer at the basal plane of graphite is negligibly small in comparison with that at edge-plane sites.^15–18 This fact possibly explains a large amount of Li₂O₂ at graphene edges after the discharge process,¹⁰ and selective electrodeposition of MoO₂ at step edges of graphite.¹⁹ In Patel's work the slow rate of the electron transfer at the basal plane was not confirmed.²⁰ However, recent delicate experiments on a single-layer graphene sheet removed the doubts concerning the unique electrochemical properties of graphene edges.^21,22 The accelerated electron transfer at open ends of carbon nanotubes was also reported.^15,17,23,24 Sidewalls of nanotubes also show electrocatalytic activity, which depends on electrochemical species dissolved in an electrolyte solution.^25,26

Interpretation of these experimental results is hindered by the lack of understanding of interfacial processes at the molecular level. Atomistic simulations are widely used to solve this problem. For instance, using quantum-chemical calculations, some features of oxygen reduction on the electrode surface,²⁷ the catalytic mechanism of nitrogen-doped graphenes,^28–30 as well as the mechanism and thermodynamics for the disproportionation of LiO₂ to Li₂O₂ were clarified.^31,32

The electrocatalytic properties of different carbon nanomaterials are typically attributed to the electronic structure of the surface and reactants.^16,33 This agrees with the DFT calculations predicting fast electron transfer at graphene edges due to the decreased energy difference between the Fermi level and the peak position of the density of states in the unoccupied O-2p orbital of the adsorbed O₂ molecule.²⁸ However, the electrode/electrolyte interface structure leaves out of account. In our previous works, it was shown by molecular dynamics (MD) simulation that an electrolyte is ordered at the interface,^34–39 and this ordering influences the kinetics of heterogeneous processes.^36,37 On the other hand, computer simulation and experimental results show the dependence of the interface structure on the surface type.^40–44 Thus, it can be supposed that the variation of the surface topography results in restructuring of the electrode/electrolyte interface and, in turn, affects the kinetics of the ORR.

The goal of this work is to determine and investigate the topography effect of the carbon surface on the interface structure, and analyze the results in the context of the ORR kinetics. The MD simulation was used for the investigation of the aprotic solvent acetonitrile (ACN) in contact with the following carbon surfaces: graphene plane, and single- and multi-layer graphene edges. ACN was chosen because it is quite stable toward superoxide and commonly used in investigations.⁴⁵ Potentials of mean force were calculated for the reactants Li⁺ and O₂ with the aim of estimating the influence of the surface topography on the concentration distributions and rates of adsorption of the reactants.

2. Computational details

We used an orthorhombic simulation box, which contained all the surfaces under the investigation simultaneously (Fig. 1). The solvent slab of 12 nm in width was confined on both sides by crystal surfaces 7.4 × 4.7 nm² in area. The left surface is the parallel-oriented four-layer graphene. The right surface is the perpendicularly oriented graphite with armchair edges. It imitates a multi-layer graphene edge. An armchair graphene nanoribbon of 3.7 nm in width is located in the central part of the box. Hydrogen atoms were attached to edges of all graphenes. The intersurface separations were chosen in such a way to avoid interference between nearby interfaces. 3D periodic boundary conditions were employed. Periodicity in the x direction was 25 nm.

Fig. 1 Snapshot of the simulation box.

The all-atom model developed by Nikitin et al. was used for ACN molecules.⁴⁶ The Lennard-Jones parameters for C and H surface atoms were taken from the AMBER force field. Carbon surface atoms were fixed during the simulation, while hydrogen atoms attached to the graphene edges were not fixed. The bond stretching parameters of the C–H bond and associated atom charges were equal to those of the benzene molecule.⁴⁷ The O–O bond length of the oxygen molecule was set to 1.21 Å;^48,49 the stretching force constant (k_r = 1694 kcal mol⁻¹ Å⁻²) was derived by fitting to the experimental vibrational frequency.⁵⁰ The Lennard-Jones parameters for O and Li were taken from the AMBER force field.

The MD simulation was performed in the NVT ensemble at temperature T = 300 K kept constant using a Nose–Hoover thermostat. The system contained 4573 ACN molecules to ensure 1 bar pressure in the liquid phase. The Ewald method with a real space cutoff value of 1 nm was used to investigate the electrostatic interaction. The equations of motion were solved using the Verlet leapfrog integration algorithm with a time step of 1 fs. The cutoff radius of the van der Waals interaction was 1 nm. The system was equilibrated for 0.2 ns before collecting data. The simulation length used for statistical averaging was 5 ns.

To compute the potential of mean force (PMF) we employed one of the variants of restrained MD simulation and thermodynamic integration.^51–53 The PMF for Li⁺ and O₂ in ACN as a function of the distance to a particular surface was calculated by integrating the average force in the direction perpendicular to the surface 〈f_x(x)〉, acting on the whole solute (Li⁺ or O₂):

where x_bulk is any position in the solvent bulk.

To estimate the average force, we ran a series of MD simulations where the solute is restrained at different distances from the surface with the step of 0.5 Å. The distance of the solute from the surface was fixed with the harmonic potentials U(x) = k(x − x_i)²(k = 500 kJ mol⁻¹ Å⁻²), acting on the Li⁺ ion or the oxygen molecule.

On average, the net force 〈f_x(x)〉, acting on the solute due to the solvent and the surface, is balanced by the harmonic restraint force 〈f^res_x(x)〉, i.e. 〈f_x(x)〉 + 〈f^res_x(x)〉 = 0. So, we can obtain 〈f_x(x)〉 indirectly using the equation 〈f_x(x)〉 = −〈f^res_x(x)〉. At each distance from the surface the force 〈f^res_z(z)〉 was averaged over 0.5 ns.

We used the DL_POLY classic package to perform MD simulations.⁵⁴ The calculations were run on the supercomputers MVS-100K and MVS-10P of the Joint Supercomputer Center of the Russian Academy of Sciences.

3. Results and discussion

3.1 Solvent structure at the interface

Fig. 2a–c show contour maps of the mass density of acetonitrile near the studied surfaces. It can be seen that the solvent has an ordered structure, which essentially depends on the surface topography. Solvent has a layered structure near the plane of the multi-layer graphene (Fig. 2a). The width of the layers is approximately 4 Å that corresponds to the size of ACN molecules. As one moves from the surface to the bulk, the structure of the solvent becomes less ordered as a result of the thermal motion of the solvent molecules. The ordering length is about 13 Å. This value characterizes spatial correlation in acetonitrile, i.e. the size of the short-range order in liquid. One can also note that the solvent structures near the planes of the single- and multi-layer graphene are nearly identical (Fig. 2a and b). This indicates that only the top graphene layer influences the interface structure.

Fig. 2 Maps of mass density (a–c), charge density (d–f), order parameter P₁ (g–i), and order parameter P₂ (j–l) near the studied surfaces.

This observation reflects the typical behavior of liquid at a crystal surface. A similar layered structure has been previously predicted in our works on MD simulation of various surface/liquid interfaces^34–39,55 and has been confirmed experimentally.^44,56–58

The layered structure is also observed near the edge of the single-layer graphene (Fig. 2b); in this case the solvent monolayers of ACN have some curvature because of the curved pattern of the surface. A qualitatively different structure is observed near the edge of the multi-layer graphene (Fig. 2c). In this case the graphene sheets are alternately shifted with respect to each other creating the lateral inhomogeneity of the surface. Due to this feature, the continuity of the solvent layers is broken. Peaks and valleys of local density form a “chessboard” structure.

For detailed quantitative analysis of the influence of a carbon surface topography on the electrode/solvent interface structure, we show in Fig. 3 the mass density profiles along the characteristic directions depicted in Fig. 2a–c. It can be noted that the oscillation amplitude along the direction D is smaller than that along the direction B, i.e. the layered structure at the single-layer graphene edge is less pronounced than that near the plane. The decrease of the closest to surface density maximum from 3.6 to 1.6 g cm⁻³ is especially noticeable. Oscillations of local density with an increased period of about 6 Å are obtained along the direction C near the graphene edges pushed out from the surface; the first density maximum amounts to 1.8 g cm⁻³. Density oscillations are largest near the deeper edges (direction A), and closest to the surface density maximum reach 4.4 g cm⁻³ while the bulk density of ACN equals to 0.79 g cm⁻³.

Fig. 3 Mass density profiles along the characteristic directions A, B, C, and D depicted in Fig. 2a–c.

In Fig. 2d–f we show maps of charge density. Due to the polarity of the ACN molecules, the ordering near the cathode surfaces leads to an inhomogeneous charge distribution. Such a distribution should result in the corresponding inhomogeneity of the electric field near the electrode surface and affect the behavior of charged and polar species at the interface. In general, the maps of charge density and mass density qualitatively duplicate each other.

To analyze the orientational order of acetonitrile molecules we calculated the order parameters P₁ = 〈cos θ〉 (Fig. 2g–i) and P₂ = 〈3/2 cos² θ − 1/2〉 (Fig. 2j–l), where θ is the angle between the vector directed along the ACN molecule (from C to N atoms) and the normal to the cathode surface. Near the graphene plane the parameters P₁ and P₂ behave in a qualitatively similar manner. In the region near x = −6 Å, which corresponds to the acetonitrile molecules adsorbed on the surface, we find that P₁ = 0.15 and P₂ = −0.45 (Fig. 2g and j). These values indicate nearly parallel orientation of the ACN molecules to the surface. The order parameter P₂ in Fig. 2k shows the orientational order near the plane as well as at the edge of the graphene. In contrast, the parameter P₁ in Fig. 2h depicts the orientational order produced by the graphene edge only, and does not reflect the ordering near the plane. Polar bonds C–H at the graphene edge orient dipole moments of the ACN molecules around it, thus forming the structure, which consists of concentric circles. This indicates that the electrode/electrolyte interface structure can be affected not only by the geometry of the cathode surface, but also by the polarity of functional groups attached to the edge. It is interesting to note that at the edge of the multi-layer graphene the length of the order characterized by the parameter P₁ in Fig. 2i is considerably larger than the one characterized by the parameter P₂ in Fig. 2l.

3.2 Potentials of mean force for Li⁺ and O₂

In order to determine the distributions of the main reactants of the ORR, we calculated the potential of mean force (PMF) for the lithium ion and the oxygen molecule. Distributions near the plane and the edge of the graphene (along the directions B and D in Fig. 2a and b, respectively) were compared.

The PMF (Fig. 4b for Li⁺ and Fig. 4c for O₂) exhibits qualitatively similar oscillating behavior in all cases. In Fig. 4a we show once again the mass density profiles of the solvent to facilitate the comparison with the potentials of mean force. One can see the correlation between the local density of the solvent and the potentials of mean force for the solutes. Energy barriers coincide with the mass density minima. This effect is associated with the energy consumption to move a solute from one solvent layer to another. The PMF minimum closest to the cathode surface corresponds to the adsorbed reactants. Thus, the adsorption of Li⁺ and O₂ is an activation process.

Fig. 4 Mass density profiles of acetonitrile (a), potentials of mean force for Li⁺ (b) and O₂ (c), and the concentration distributions of Li⁺ ions (d) and O₂ molecules (e) near the plane and the edge of the graphene along the directions B and D in Fig. 2a and b, respectively.

It is noticeable that for both reactants the height of the barriers is smaller near the edge than near the plane of graphene. It can be explained by the fact that the solvent layers near the edge are less pronounced and have smaller density. The most profound effect is observed for oxygen, for which the value of the highest energy barrier becomes smaller than kT. In this case the adsorption mechanism changes from activation to diffusion control. Consequently, the rate of Li⁺ and O₂ adsorption is higher on the edge of graphene. It may lead to acceleration of the ORR if the rate of adsorption is comparable to or slower than that of the rate-limiting step of the ORR.

Because of the complexity of the oxygen reduction reaction and the dependence of the rates of elementary steps on the solvent,^59,60 such a comparison requires a separate study. For a crude estimate we compare rates of adsorption and the heterogeneous electron transfer from the surface to an oxygen molecule with the formation of a superoxide ion O₂⁻ (the first elementary step of the ORR). The experimentally measured standard rate constant of the electron transfer in acetonitrile k⁰_et is approximately equal to 10⁻⁴ cm c⁻¹.^61,62 Thus, the electron transfer rate (electron flow per unit area) can be estimated using the Tafel equation J_et = k⁰_etC exp(αFη/RT), where C is the oxygen concentration in an electrolyte, η is the overpotential, α is the charge transfer coefficient, and F is the Faraday constant. Adsorption of the electrolyte components may become quite slow due to the solvent structure near the surface. The characteristic time of adsorption can be as large as 10 ns.^42,63 This value corresponds to the adsorption constant k_ads ∼ 10⁸ c⁻¹. Therefore, the rate of adsorption (the process when the oxygen molecule transfer from the second minimum near x = 7 Å in Fig. 4c to the minimum closest to the surface at x = 3.5 Å) can be calculated from the following equation:

where integral is taken over the second minimum of the PMF (5 Å < x < 8.5 Å), and U(x) is the PMF of the oxygen molecule. From the equation J_ads = J_et one can find the overpotential η ∼ 0.5 V, which corresponds to the equal rates of the electron transfer and adsorption. Therefore, the transport of the reactants to the surface (slowed down due to the interface ordering) may influence the kinetics of ORR under experimentally attainable electrode overpotentials.

If the adsorption rate is significantly larger than the rate of electrochemical processes, one can calculate the equilibrium concentration distributions of reactants near the surface using the Boltzmann equation: C(x) = C₀ exp(−U(x)/kT). Distributions of Li⁺ ions and O₂ molecules normalized to the bulk concentration C₀ are shown in Fig. 4d and e, respectively. It can be seen that the reactants are mostly located in solvent monolayers. The distribution of reactants is more homogeneous (the oscillation amplitude is smaller) near the graphene edge. For this reason, the integral of the oxygen concentration from 0 to 8 Å is higher near the edge than the plane of graphene. Because the electronic transmission coefficient in this region is close to 1 (adiabatic electron transfer),^37,64,65 this increase in the oxygen total amount at the interface should lead to the acceleration of the heterogeneous electron transfer, which is in agreement with the experimental results.^{15–18,21,22}

4. Conclusions

We used MD simulation to investigate the behavior of the acetonitrile-based electrolyte at the graphene plane, and single- and multi-layer graphene edge.

(1) It was shown that the electrolyte structure at the interface largely depends on the surface topography. In particular, the layered structure was observed at the graphene plane, while the chessboard structure at the multi-layer graphene edge.

(2) The free energy profiles were determined for the main reactants (Li⁺, O₂) of the oxygen reduction reaction, from which appears the correlation between the solvent structure and the concentration distributions of the reactants.

(3) We observed that the variation of the surface topography allows altering the adsorption rates and distributions of Li⁺ and O₂ at the interface, and thus may influence the kinetics of the oxygen reduction reaction.

(4) The results point to the high electrocatalytic activity of graphene edges that agrees with the experimentally observed fast electron transfer and massive deposition of discharge products at graphene edges.

Acknowledgements

This work was supported by the Russian Science Foundation (project no. 14-50-00124).

Notes and references

1. J. Christensen, P. Albertus, R. S. Sanchez-Carrera, T. Lohmann, B. Kozinsky, R. Liedtke, J. Ahmed and A. Kojic, J. Electrochem. Soc., 2011, 159, R1–R30.
2. J. P. Zheng, R. Y. Liang, M. Hendrickson and E. J. Plichta, J. Electrochem. Soc., 2008, 155, A432–A437.
3. N.-S. Choi, Z. Chen, S. A. Freunberger, X. Ji, Y.-K. Sun, K. Amine, G. Yushin, L. F. Nazar, J. Cho and P. G. Bruce, Angew. Chem., Int. Ed., 2012, 51, 9994–10024.
4. M. A. Rahman, X. Wang and C. Wen, J. Appl. Electrochem., 2014, 44, 5–22.
5. S. S. Sandhu, J. P. Fellner and G. W. Brutchen, J. Power Sources, 2007, 164, 365–371.
6. X.-h. Yang, P. He and Y.-y. Xia, Electrochem. Commun., 2009, 11, 1127–1130.
7. M. Mirzaeian and P. J. Hall, Electrochim. Acta, 2009, 54, 7444–7451.
8. M. Mirzaeian and P. J. Hall, J. Power Sources, 2010, 195, 6817–6824.
9. C. Tran, X.-Q. Yang and D. Qu, J. Power Sources, 2010, 195, 2057–2063.
10. Y. Li, J. Wang, X. Li, D. Geng, R. Li and X. Sun, Chem. Commun., 2011, 47, 9438–9440.
11. P. Kichambare, J. Kumar, S. Rodrigues and B. Kumar, J. Power Sources, 2011, 196, 3310–3316.
12. P. Kichambare, S. Rodrigues and J. Kumar, ACS Appl. Mater. Interfaces, 2012, 4, 49–52.
13. Y. Li, J. Wang, X. Li, D. Geng, M. N. Banis, R. Li and X. Sun, Electrochem. Commun., 2012, 18, 12–15.
14. Y. Li, J. Wang, X. Li, J. Liu, D. Geng, J. Yang, R. Li and X. Sun, Electrochem. Commun., 2011, 13, 668–672.
15. C. E. Banks, T. J. Davies, G. G. Wildgoose and R. G. Compton, Chem. Commun., 2005, 829–841.
16. T. J. Davies, M. E. Hyde and R. G. Compton, Angew. Chem., 2005, 117, 5251–5256.
17. C. E. Banks and R. G. Compton, Analyst, 2006, 131, 15–21.
18. A. Ambrosi, A. Bonanni and M. Pumera, Nanoscale, 2011, 3, 2256–2260.
19. M. P. Zach, K. H. Ng and R. M. Penner, Science, 2000, 290, 2120–2123.
20. A. N. Patel, M. G. Collignon, M. A. O'Connell, W. O. Y. Hung, K. McKelvey, J. V. Macpherson and P. R. Unwin, J. Am. Chem. Soc., 2012, 134, 20117–20130.
21. W. Yuan, Y. Zhou, Y. Li, C. Li, H. Peng, J. Zhang, Z. Liu, L. Dai and G. Shi, Sci. Rep., 2013, 3, 2248.
22. S. Banerjee, J. Shim, J. Rivera, X. Jin, D. Estrada, V. Solovyeva, X. You, J. Pak, E. Pop, N. Aluru and R. Bashir, ACS Nano, 2013, 7, 834–843.
23. C. E. Banks and R. G. Compton, Analyst, 2005, 130, 1232–1239.
24. A. Chou, T. Bocking, N. K. Singh and J. J. Gooding, Chem. Commun., 2005, 842–844,  10.1039/B415051A.
25. T. S. Miller, N. Ebejer, A. G. Guell, J. V. Macpherson and P. R. Unwin, Chem. Commun., 2012, 48, 7435–7437.
26. K. Gong, S. Chakrabarti and L. Dai, Angew. Chem., Int. Ed., 2008, 47, 5446–5450.
27. Z. Shi, J. Zhang, Z.-S. Liu, H. Wang and D. P. Wilkinson, Electrochim. Acta, 2006, 51, 1905–1916.
28. H. Kim, K. Lee, S. I. Woo and Y. Jung, Phys. Chem. Chem. Phys., 2011, 13, 17505–17510.
29. H. Tominaga, W. Ikeda and M. Nagai, Phys. Chem. Chem. Phys., 2011, 13, 2659–2662.
30. T. Ikeda, M. Boero, S.-F. Huang, K. Terakura, M. Oshima and J.-i. Ozaki, J. Phys. Chem. C, 2008, 112, 14706–14709.
31. V. S. Bryantsev, M. Blanco and F. Faglioni, J. Phys. Chem. A, 2010, 114, 8165–8169.
32. U. Das, K. C. Lau, P. C. Redfern and L. A. Curtiss, J. Phys. Chem. Lett., 2014, 5, 813–819.
33. K. K. Cline, M. T. McDermott and R. L. McCreery, J. Phys. Chem., 1994, 98, 5314–5319.
34. S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590.
35. S. A. Kislenko, R. H. Amirov and I. S. Samoylov, Phys. Chem. Chem. Phys., 2010, 12, 11245–11250.
36. S. A. Kislenko, R. H. Amirov and I. S. Samoylov, J. Phys. Chem. C, 2013, 117, 10589–10596.
37. V. A. Nikitina, S. A. Kislenko, R. R. Nazmutdinov, M. D. Bronshtein and G. A. Tsirlina, J. Phys. Chem. C, 2014, 118, 6151–6164.
38. S. A. Kislenko, V. A. Nikitina and R. R. Nazmutdinov, High Energy Chem., 2015, 49, 341–346.
39. S. A. Kislenko, V. A. Nikitina and R. R. Nazmutdinov, Phys. Chem. Chem. Phys., 2015, 17, 31947–31955.
40. J. Vatamanu, L. Cao, O. Borodin, D. Bedrov and G. D. Smith, J. Phys. Chem. Lett., 2011, 2, 2267–2272.
41. C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, B. Daffos, P. L. Taberna, P. Simon and M. Salanne, Nat. Commun., 2013, 4, 2701.
42. S. Kerisit, D. J. Cooke, D. Spagnoli and S. C. Parker, J. Mater. Chem., 2005, 15, 1454–1462.
43. N. Sieffert and G. Wipff, J. Phys. Chem. C, 2008, 112, 19590–19603.
44. R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162–5168.
45. V. S. Bryantsev, V. Giordani, W. Walker, M. Blanco, S. Zecevic, K. Sasaki, J. Uddin, D. Addison and G. V. Chase, J. Phys. Chem. A, 2011, 115, 12399–12409.
46. A. M. Nikitin and A. P. Lyubartsev, J. Comput. Chem., 2007, 28, 2020–2026.
47. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
48. K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979.
49. C. Hartnig and M. T. M. Koper, J. Electroanal. Chem., 2002, 532, 165–170.
50. K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397.
51. J. Van Eerden, W. J. Briels, S. Harkema and D. Feil, Chem. Phys. Lett., 1989, 164, 370–376.
52. V. Vivcharuk, B. Tomberli, I. S. Tolokh and C. G. Gray, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031913.
53. I. S. Tolokh, V. Vivcharuk, B. Tomberli and C. G. Gray, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031911.
54. I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918.
55. S. A. Kislenko, V. A. Kislenko and V. F. Razumov, Colloid J., 2015, 77, 727–732.
56. S. H. Oh, Y. Kauffmann, C. Scheu, W. D. Kaplan and M. Rühle, Science, 2005, 310, 661–663.
57. R. G. Horn and J. N. Israelachvili, J. Chem. Phys., 1981, 75, 1400–1411.
58. H. K. Christenson, J. Chem. Phys., 1983, 78, 6906–6913.
59. K. M. Abraham, J. Electrochem. Soc., 2015, 162, A3021–A3031.
60. L. Johnson, C. Li, Z. Liu, Y. Chen, S. A. Freunberger, P. C. Ashok, B. B. Praveen, K. Dholakia, J.-M. Tarascon and P. G. Bruce, Nat. Chem., 2014, 6, 1091–1099.
61. C. O. Laoire, S. Mukerjee, K. M. Abraham, E. J. Plichta and M. A. Hendrickson, J. Phys. Chem. C, 2009, 113, 20127–20134.
62. C. O. Laoire, S. Mukerjee, K. M. Abraham, E. J. Plichta and M. A. Hendrickson, J. Phys. Chem. C, 2010, 114, 9178–9186.
63. S. Kerisit and S. C. Parker, J. Am. Chem. Soc., 2004, 126, 10152–10161.
64. V. A. Nikitina, A. V. Rudnev, G. A. Tsirlina and T. Wandlowski, J. Phys. Chem. C, 2014, 118, 15970–15977.
65. D. E. Khoshtariya, T. D. Dolidze, M. Shushanyan, K. L. Davis, D. H. Waldeck and R. van Eldik, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2757–2762.

---