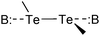Open Access Article
Open Access Article125Te NMR provides evidence of autoassociation of organo-ditellurides in solution†
P. J. W.
Elder
and
I.
Vargas-Baca
 *
*
Department of Chemistry and Chemical Biology, McMaster University, 1280 Main St. West, Hamilton, Ontario L8S 4M1, Canada. E-mail: vargas@chemistry.mcmaster.ca
First published on 13th October 2016
Abstract
The frequency of the resonance of 125Te of two organo-ditellurides, R–Te–Te–R (R = 4-CH3C6H4 and 2-(CH3)2NCH2C6H4), in solution undergoes a low-field shift as the concentration of the sample increases. In sharp contrast, the resonance of a sterically hindered ditelluride (R = (C6H5(CH3)2Si)3C) and telluric acid display the opposite effect. While the negative concentration coefficients can be explained by the change in magnetic susceptibility, the positive coefficients are consistent with autoassociation of the molecules through tellurium-centred supramolecular interactions. Although the corresponding equilibrium constants are small, the process is shown to be exothermic. However, the influence of autoassociation is much smaller than the effects of solvent polarity and the conformation of the ditelluride bond.
Introduction
Supramolecular association is a recurrent feature in the structural chemistry of organic derivatives of heavy p-block elements. The success of halogen bonding1–4 in areas as diverse as crystal engineering,5–16 photonic materials17,18 organocatalysis19 and biomimetic chemistry20 – to name a few – has stimulated the resurgence of interest in the study of analogous interactions centred on other heavy main-group elements, including the chalcogens (S, Se, Te).21–23While tellurium-centred supramolecular interactions (alternatively termed secondary bonding or chalcogen bonding interactions) are primarily characterized in the solid state through X-ray diffraction structural determination, non-crystalline systems must be studied by means of spectroscopic methods.
UV photoelectron spectroscopy (UVPES) has been unable to provide evidence of aggregation through these interactions in the gas phase. Even in the case of benzo-2,1,3-telluradiazole, which is strongly associated in the solid state, the UVPES spectrum corresponds to individual molecules only.24 Electrospray mass spectrometry of 1,2,5-telluradiazoles has detected protonated dimers25 and the adduct of a neutral molecule with Cl−.26 However, the interpretation of such experiments is complicated by the charge of the ions and side reactions within the instrument. As organo-tellurium compounds are often coloured, UV-vis absorption spectroscopy is an appealing option in solution; this technique has been used to measure association constants for the adducts of benzotelluradiazoles with Lewis bases26 and monitor the association of anions with tellurophenes.27 However, photolysis can be a concern with many systems.
Arguably the most practical spectroscopic method for the characterization of tellurium-centred supramolecular interactions in solution is NMR. Indeed 1H and 19F resonances have been used to monitor the association of 1,2,5-telluradiazoles with Lewis bases26 and, very recently, 1H NMR was used to demonstrate the persistence in solution of the macrocyclic aggregates of iso-tellurazole N-oxides.28 However, such measurements rely on effects secondary to the interactions of the chalcogen atom. Fortunately, tellurium can be directly observed because it has two NMR-active isotopes with spin 1/2 and no quadrupole moment: 123Te and 125Te. Observation of the latter is most convenient as it has relatively high receptivity (DC = 13.1) in spite of its low natural abundance (7.12%).29 Its chemical shift range is wider than 4000 ppm:30 from −1214 ppm for (Me3Sn)2Te31 to 3102 ppm for the Se2Te22+ dication in 30% oleum.32 The frequency of resonance of 125Te is therefore very sensitive, so much that the effect of supramolecular association could possibly be masked by the influence of small structural changes or the dielectric and diamagnetic properties of the medium.
Based on these considerations, we have conducted a detailed 125Te NMR investigation of a selected set of tellurium compounds intended to probe the presence of tellurium-centred supramolecular interactions in solution, quantify their impact on the measured chemical shifts and compare this effect with the influence of other environmental factors. The molecules selected for this study are simple compounds that differ from each other in their relative ability to undergo autoassociation in solution though tellurium-centred supramolecular interactions.
Results and discussion
System of choice
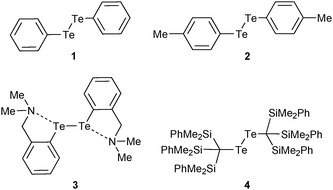
The compounds used for this study (Chart 1) are organo-ditellurides. The Te–Te bond in these heavy congeners of peroxides is analogous to the I–I linkage in molecular iodine in that the bond between the heavy atoms generates a pair of distal σ holes and a low-lying σ*Te–Te antibonding orbital. Fig. 1 portrays those features on the molecule of diphenyl ditelluride (1); being the prototypical organo-ditelluride, this compound was selected as a model for supporting DFT calculations. The combined electrostatic and covalent effects enable attractive interactions of the chalcogen atoms with Lewis bases (Scheme 1);33–35 however, Symmetry-Adapted Perturbational Theory calculations strongly indicate that dispersion is an important component of such interactions.36 Only a handful of ditelluride structures deposited in the Cambridge structural database exhibit no short contacts with the tellurium atoms, such cases are the result of steric hindrance or peculiar packing effects. | ||
| Fig. 1 Selected computational results of Ph2Te2 (1). The (a) HOMO; (b) LUMO; and (c) electrostatic potential mapped onto the SCF electron density. All isosurfaces are plotted at 0.03 a.u. | ||
Intramolecular interactions are common when substituents bearing atoms with lone pairs are present in the molecular structure. Intermolecular interactions in ditellurides are most commonly observed in the solid state with either Te atoms,37–40 or aryl rings,41,42 or through interactions with electron-donor functional groups on adjacent molecules.43
The crystal structures of organo-ditellurides which display short contacts with the chalcogen can be classified by the type of intermolecular interactions into two major groups: those displaying Aryl⋯Te interactions and those with Te⋯Te interactions. Within the first group, there are cases in which the aryl group is opposite to the Te–Te bond (Scheme 2 (i)) or a Te–C bond (Scheme 2 (ii)). Similarly, in the second group a Te atom is opposite to the Te–Te bond (Scheme 2 (iii)) or a Te–C bond (Scheme 2 (iv)), in a third category the lattice features linear (Te2)∞ chains (Scheme 2 (v)).
For our experimental investigations we compared the behavior of ditellurides 2–4, in which the organic substituents were selected in order to influence the intermolecular interactions centred on tellurium. Table 1 presents a comparison of key properties of their molecules. Bis-4-methyl-phenyl ditelluride (2) displays a gauche conformation in the solid state.44 Its tellurium atoms are readily accessible for interaction with other molecules. Because of the potential for photolysis and other degradation mechanisms, the para-methyl groups were used as a spectroscopic handle to readily monitor the integrity of the samples throughout all experiments; the effect of these substituents on autoassociation is assumed to be negligible. Bis(ortho-(dimethylamino-methyl)phenyl)-ditelluride (3) features two pendant dialkylamino groups that in the crystal engage in Te⋯N intramolecular interactions with an average distance of 2.876(3) Å. Its Te–Te bond is somewhat longer than in 2, the C–Te–Te–C dihedral angle45 is wider and the compound is photosensitive. Should the Te⋯N interactions in 3 persist in solution, they would compete with autoassociation and binding to solvent molecules. The bulky substituents of bis(tris-dimethylphenylsilyl)methyl ditelluride (4) prevent any intermolecular contacts with tellurium. The steric demands of the substituents force the C–Te–Te–C dihedral angle to 180° and elongate the Te–Te bond distance; the compound is stable in the solid state but decomposes slowly in solution, even in the dark.46
Effect of concentration on the 125Te chemical shift
If ditelluride A underwent autoassociation equilibrium in solution, dimerization in the simplest case (eqn (1)), the proportion of associated molecules (α, eqn (2)) would increase with an increase of the total concentration:| A + A ⇌ A2 | (1) |
 | (2) |
 | (3) |
| δ = δA + (δA2 − δA)α = δA + Δδα. | (4) |
The values of δ125Te of ditellurides 2–4 were measured in solution as a function of concentration and temperature. Because of their different solubilities, 3 had to be studied in hexane and toluene only, while 4 could only be dissolved in CH2Cl2; 2 was soluble in all three solvents. The results are graphically presented in Fig. 2. In all cases there is an apparent linear dependence of the 125Te NMR chemical shift on concentration. Given the significant effect of concentration, comparable in magnitude to the effect of temperature in most instances, the chemical shift values were extrapolated to zero concentration for each temperature. Such chemical shifts at infinite dilution are hereafter denoted as δ0. In each case, δ0 exhibits a linear dependence on temperature.
Concentration coefficients measured at selected temperatures are presented in Table 2. Notably, while δ125Te of ditellurides 2 and 3 increases with concentration, irrespective of the solvent, data from the sterically encumbered ditelluride 4 displays the opposite behaviour. Positive slopes (concentration coefficients) for 2 and 3 would be the result of supramolecular interactions if δA2 > δA. Although less data are available for 125Te NMR, supramolecular interactions usually cause downfield shifts of 77Se resonances. In fact, the δ77Se value of dialkyl-2-oxazolinyl-diaryldiselenides correlates with the crystallographic Se⋯N distance.9
| Ditelluride | Solvent | T (K) | Coefficient (ppm L mol−1) |
|---|---|---|---|
| 2 | Hexane | 296.6 | 11.8 ± 0.1 |
| 2 | Toluene | 296.3 | 7.6 ± 0.1 |
| 2 | CH2Cl2 | 295.6 | 5.04 ± 0.04 |
| 3 | Hexane | 296.2 | 9.3 ± 0.2 |
| 3 | Toluene | 297.6 | 3.5 ± 0.2 |
| 4 | CH2Cl2 | 296.0 | −7.2 ± 0.9 |
In contrast, the behaviour of the 125Te resonance of 4 parallels observations made for telluric acid. Fig. 3 summarizes the dependency on concentration and temperature of the 125Te chemical shift of Te(OH)6 in D2O. The octahedral arrangement of oxygen atoms in the molecule of telluric acid shields the chalcogen from interactions with other atoms. Although intermolecular hydrogen-bonding between hydroxyl groups is possible, in dilute aqueous solutions the interaction with the solvent is dominant. Here the negative concentration coefficients should result from the increase of magnitude of the diamagnetic (negative) susceptibility of the solution. In dilute solutions the concentration coefficient should be constant (eqn (5), where χv are the volume magnetic susceptibilities, FWsample and ρsample, respectively, are the formula weight and density of the pure solute). The concentration coefficient estimated in this way from literature47,48 data for water and telluric acid is −0.5 ppm L mol−1 at 293 K, which compares well to the −0.4 ± 0.1 ppm L mol−1 experimentally measured at 296.2 K.
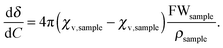 | (5) |
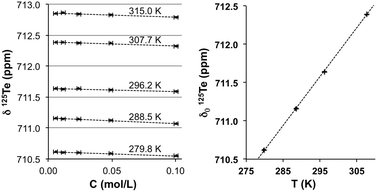 | ||
| Fig. 3 Effects of concentration (left) and temperature (right) on δ175Te NMR (ppm) of Te(OH)6 in water. Standard errors in δ125Te (<0.005 pm) and T (<0.05 K) are not discernible at this scale. | ||
If the preceding arguments hold in the case of sterically encumbered 4, the steeper negative slope would reflect the much larger formula weight and smaller density than those of telluric acid. From the crystallographic density, the volume susceptibility of 4 is estimated as χv = −1.5 × 10−6 esu at 296.0 K.
The augmentation of the diamagnetic response upon an increase of concentration must occur as well in solutions of 2 and 3, but the effect is clearly overshadowed by the high-field shift of the 125Te resonance. Beyond qualitative arguments, the positive concentration coefficients should be examined in terms of the equilibrium of autoassociation. While the fraction of associated molecules α does not depend linearly on concentration (eqn (6)), simulations (Fig. 4) show that at low concentrations and small equilibrium constants, the α(C) curves approach linear behaviour. Indeed it can be shown that the slope (eqn (7)) at low concentrations is nearly constant for K ≪ 1 and approaches 2 K (eqn (8)), thus the concentration coefficient is ≈2 ΔδK,
 | (6) |
 | (7) |
 | (8) |
 | ||
| Fig. 4 Calculated fraction of associated molecules (α) and the corresponding curve slopes as a function of total concentration (C) and magnitude of the dimerization equilibrium constant (K). | ||
Measurements performed for 2 in donor solvents like DMSO and pyridine also yielded positive concentration coefficients (Fig. 5), 18.8 ± 1.4 and 7.9 ± 0.2 ppm L mol−1, respectively, at 303.0 K; the corresponding δ0 values are 403.9 and 422.1 ppm. This observation suggests that autoassociation is still present in these media. However, these experiments were complicated by a chemical reaction. Changes are noticeable in the 1H NMR spectrum and a white solid is separated from the solutions over time. This process could be slowed by shielding samples from light and storing them in sealed containers to exclude oxygen. Although similar observations have been reported,49,50 the products are not conclusively identified. The proposed products include a variety of oxygen-containing species (R2Te2O, R2Te2O2, and R2Te2O3) based on infrared spectroscopy and elemental analysis, but it is likely that these are species related to 551 (Chart 2).
Effect of temperature
Temperature coefficients for δ0125Te of ditellurides 2–4 in the non-donor solvents and telluric acid in water are compiled in Table 3. The sensitivity of δ0125Te to temperature correlates with the size of the molecule; compound 4 displays the largest coefficient as expected from the number of vibrational degrees of freedom and molecular weight.| Compound | Solvent | Coefficient × 102 (ppm K−1) | δ 0 at 298.0 K (ppm) |
|---|---|---|---|
| 2 | Hexane | 22.7 ± 0.2 | 419.3 |
| 2 | Toluene | 25.5 ± 0.3 | 419.8 |
| 2 | CH2Cl2 | 17.9 ± 0.3 | 420.8 |
| 3 | Hexane | 11.2 ± 0.1 | 344.1 |
| 3 | Toluene | 12.3 ± 0.2 | 347.4 |
| 4 | CH2Cl2 | 44 ± 1 | 418.8 |
| Te(OH)6 | Water | 6.38 ± 0.04 | 711.8 |
Although in the absence of values of the differences in chemical shift of the individual molecules and their dimers (Δδ) in each solvent it is not possible to extract the actual equilibrium constants, a van't Hoff plot based on the observed concentration coefficients would provide an estimate of ΔH. The fitted value for 3 in hexane solution (Fig. 6) of −4.1 ± 0.2 J mol−1 is small and is likely biased by solvation and the lack of a diamagnetic correction. The relative errors for the ΔH values fitted from the other measurement sets are too large for a comparison but it is clear that the association of the molecules of 2 is exothermic in all three solvents.
 | ||
| Fig. 6 van't Hoff plot for the proposed equilibrium of autoassociation of 3 in hexane. The standard error in T (<0.05 K) is not discernible at this scale. | ||
Aggregation vs. other effects
Compared to the range of possible values of 125Te NMR chemical shift, the influence of concentration on δ is small and should be compared with other effects that originate in the local environment of the molecule.The first is the structure of the molecule itself. Table 1 illustrates the wide range of values the C–Te–Te–C dihedral angle can adopt. This internal coordinate is especially important because of its effect on the energy (ΔE) of the first electronic excitation, LUMO ← HOMO, which in turn impacts the shielding (σ) according to Ramsey's equation (eqn (9)). The HOMO is particularly sensitive to the torsion angle because it consists of a combination of the lone-pair orbitals on the tellurium atoms (Fig. 1). TD-DFT/DFT-GIAO calculations for compound 1 estimate ΔE values from 2.9 to 1.7 eV with concomitant changes in δ125Te within the range 350–750 ppm for C–Te–Te–C torsion angles of 0–180°. The same conformational variation would result in molecular dipole moments ranging from 0 to 3.0 D,
 | (9) |
Experimental section
Materials and methods
The manipulation of air-sensitive materials was carried out in a glove box or using standard Schlenk techniques under an atmosphere of nitrogen. Solvents were purified by using an Innovative Technologies purification system or by distillation over appropriate dehydrating agents. Elemental tellurium (Cerac) and deuterated solvents (Aldrich) were used as received without further purification. Telluric acid (Aldrich) was purified by recrystallization. The laboratory sample of dimethyl telluride was handled within a sealed quartz NMR tube at all times.Ditellurides 2,523,33 and 446 were prepared by methods adapted from the literature. In general, elemental tellurium was treated with organolithium or Grignard reagents to give a tellurolate which was oxidized by I2 or O2. The final products were extracted in an aqueous work up and rigorously purified by recrystallization, sublimation or chromatography.
NMR spectra were acquired on a Bruker Avance 500 (500 MHz). A Bruker 5 mm broad band inverse probe was used to acquire 1H spectra and a 5 mm broad band probe was used to acquire 13C{1H} and 125Te spectra. Chemical shifts are reported in δ units and are referenced to the residual resonances of the solvent in the cases of 1H and 13C. To ensure the highest accuracy possible, δ0125Te is referenced to the absolute frequency of resonance interpolated to 298.0 K from measurements of a sample of pure Me2Te between 270.0 and 305.0 K; within this range the resonance depends linearly (1.03 ± 0.01 × 10−1 ppm K−1) on temperature, in agreement with the literature.53 Corrections for the diamagnetic susceptibility of each solvent were performed using eqn (10). The volume susceptibility of dimethyl telluride (χv,reference) was approximated using literature methods,54
 | (10) |
Ultraviolet-visible spectroscopy
Absorption spectra were measured in quartz cuvettes on a Varian Cary 300 spectrometer with a temperature-controlled stage in dual beam mode from 200 to 800 nm with a scan rate of 10 nm s−1. The solvent background was subtracted using external blank samples.Computational details
All calculations were carried out using the Amsterdam Density Functional Package.56 For computational expediency all calculations were carried out within the general gradient approximation using the PW9157 functional, while relativistic effects were approached using the Zeroth Order Regular Approximation.58–62 In preliminary geometry optimizations it was established that while most optimized bond distances, bond angles and torsion angles satisfactorily reproduced the experimental values the C–Te–Te–C torsion angle required a basis set of quadruple-ζ quality with four polarization sets (QZ4P) to be calculated within 0.5 degrees of the experimental value. Solvent properties were modeled using the Conductor like Screening Model63–65 (COSMO). Time dependent calculations were used to evaluate the first 100 excitations in the electronic spectrum using the Davidson diagonalization method and the statistical average of model potentials66 (SAOP). GIAO NMR shielding constants were calculated using the NMR ADF module.67–69Conclusions
The solution 125Te NMR chemical shift of all the compounds included in this study is dependent on concentration. While negative concentration coefficients are explicable by changes in the diamagnetism of the sample solutions, positive coefficients are consistent with independent observations of the effect of chalcogen-centred supramolecular interactions. Such intermolecular interactions could only be prevented when the tellurium atom is inaccessible because of steric protection. The influence of concentration on the measured δ125Te, however, is dwarfed by the effects of conformational changes or the dielectric properties of the medium. This observation has important implications for spectroscopic studies of supramolecular interactions of tellurium compounds. For example, studying the association of Lewis bases with these or other tellurium-containing molecules in solution would likely require a significant excess of base that could easily alter the dielectric constant of the medium and mask the effect of association on δ125Te.Albeit small, the effect of concentration is enough to cause variations that can complicate the comparison and interpretation of 125Te NMR data, reporting precise chemical shifts requires specifying the concentration in addition to temperature or stating the value at infinite dilution. The current IUPAC standard for 125Te NMR is “a solution of less than 10% benzene-d6in dimethyl telluride”.70 Aside from its high toxicity, (CH3)2Te (1) poses a fundamental challenge: its molecules are very likely to undergo autoassociation equilibria because of the two σ holes on tellurium,71 the orientation of the σ*Te–C orbitals72 and the high polarizability of the chalcogen.36 Although the use of an absolute scale, in which the resonances are referenced to the frequency of TMS protons, has been suggested,73 a simpler alternative would be to specify a precise composition and temperature for the standard.
Acknowledgements
Funding from the Natural Sciences and Engineering Research Council (NSERC) of Canada is gratefully acknowledged. We thank Professor G. J. Schrobilgen (McMaster) for the loan of the laboratory sample of Me2Te. Portions of this work were made possible by the facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET: http://www.sharcnet.ca) and Compute/Calcul Canada.Notes and references
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CrossRef CAS.
- A. Priimagi, G. Cavallo, P. Metrangolo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686–2695 CrossRef CAS PubMed.
- P. Metrangolo and G. Resnati, Cryst. Growth Des., 2012, 12, 5835–5838 CAS.
- V. R. Pedireddi, D. S. Reddy, B. S. Goud, D. C. Craig, A. D. Rae and G. R. Desiraju, J. Chem. Soc., Perkin Trans. 2, 1994, 2353–2360 RSC.
- Halogen Bonding, ed. P. Metrangolo and G. Resnati, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, vol. 126 Search PubMed.
- K. Rissanen, CrystEngComm, 2008, 10, 1107–1113 RSC.
- P. Metrangolo and G. Resnati, Chem. – Eur. J., 2001, 7, 2511–2519 CrossRef CAS.
- P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395 CrossRef CAS PubMed.
- M. Fourmigué, Curr. Opin. Solid State Mater. Sci., 2009, 13, 36–45 CrossRef.
- P. Metrangolo, G. Resnati, T. Pilati, R. Liantonio and F. Meyer, J. Polym. Sci., Part A: Polym. Chem., 2006, 45, 1–15 CrossRef.
- M. Erdelyi, Chem. Soc. Rev., 2012, 41, 3547–3557 RSC.
- P. Metrangolo, Curr. Opin. Colloid Interface Sci., 2003, 8, 215–222 CrossRef CAS.
- P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127 CrossRef CAS PubMed.
- R. Bertani, P. Sgarbossa, A. Venzo, F. Lelj, M. Amati, G. Resnati, T. Pilati, P. Metrangolo and G. Terraneo, Coord. Chem. Rev., 2010, 254, 677–695 CrossRef CAS.
- P. Metrangolo and G. Resnati, Science, 2008, 321, 918–919 CrossRef CAS PubMed.
- K. Raatikainen and K. Rissanen, Chem. Sci., 2012, 3, 1235–1239 RSC.
- O. Bolton, K. Lee, H.-J. Kim, K. Y. Lin and J. Kim, Nat. Chem., 2011, 3, 205–210 CrossRef CAS PubMed.
- M. Virkki, O. Tuominen, A. Forni, M. Saccone, P. Metrangolo, G. Resnati, M. Kauranen and A. Priimagi, J. Mater. Chem. C, 2015, 3, 3003–3006 RSC.
- F. Kniep, S. H. Jungbauer, Q. Zhang, S. M. Walter, S. Schindler, I. Schnapperelle, E. Herdtweck and S. M. Huber, Angew. Chem., Int. Ed., 2013, 52, 7028–7032 CrossRef CAS PubMed.
- D. Manna and G. Mugesh, J. Am. Chem. Soc., 2012, 134, 4269–4279 CrossRef CAS PubMed.
- T. Chivers and R. S. Laitinen, Chem. Soc. Rev., 2015, 44, 1725–1739 RSC.
- P. Politzer, J. Murray, G. Janjić and S. Zarić, Crystals, 2014, 4, 12–31 CrossRef.
- E. R. T. Tiekink and J. Zukerman-Schpector, Coord. Chem. Rev., 2010, 254, 46–76 CrossRef CAS.
- A. F. Cozzolino, N. E. Gruhn, D. L. Lichtenberger and I. Vargas-Baca, Inorg. Chem., 2008, 47, 6220–6226 CrossRef CAS PubMed.
- A. F. Cozzolino, G. Dimopoulos-Italiano, L. M. Lee and I. Vargas-Baca, Eur. J. Inorg. Chem., 2013, 2751–2756 CrossRef CAS.
- G. E. Garrett, G. L. Gibson, R. N. Straus, D. S. Seferos and M. S. Taylor, J. Am. Chem. Soc., 2015, 137, 4126–4133 CrossRef CAS PubMed.
- G. E. Garrett, E. I. Carrera, D. S. Seferos and M. S. Taylor, Chem. Commun., 2016, 52, 9881–9884 RSC.
- P. C. Ho, P. Szydlowski, J. Sinclair, P. J. W. Elder, J. Kübel, C. Gendy, L. M. Lee, H. Jenkins, J. F. Britten, D. R. Morim and I. Vargas-Baca, Nat. Commun., 2016, 7, 11299 CrossRef CAS PubMed.
- P. Enghag, Encyclopedia of the Elements, Wiley, Weinheim, 2008 Search PubMed.
- P. E. Lazlo, NMR of newly accessible nuclei, Academic Press, New York, 1983 Search PubMed.
- H. C. E. McFarlane and W. McFarlane, J. Chem. Soc., Dalton Trans., 1973, 2416–2418 RSC.
- G. J. Schrobilgen, R. C. Burns and P. Granger, J. Chem. Soc., Chem. Commun., 1978, 957–960 RSC.
- G. Mugesh, A. Panda, S. Kumar, S. D. Apte, H. B. Singh and R. J. Butcher, Organometallics, 2002, 21, 884–892 CrossRef CAS.
- F. H. Kruse, R. E. Marsh and J. D. McCullough, Acta Crystallogr., 1957, 10, 201–209 CrossRef CAS.
- K. Kandasamy, S. Kumar, H. B. Singh and G. Wolmershäuser, Organometallics, 2003, 22, 5069–5078 CrossRef CAS.
- C. Bleiholder, D. B. Werz, H. Köppel and R. Gleiter, J. Am. Chem. Soc., 2006, 128, 2666–2674 CrossRef CAS PubMed.
- S. Ludlow and A. E. McCarthy, J. Organomet. Chem., 1981, 219, 169–176 CrossRef CAS.
- S. K. Kumar, H. B. Singh, K. Das and U. C. Sinha, J. Organomet. Chem., 1990, 397, 161–167 CrossRef CAS.
- Y. Aso, K. Yui, T. Miyoshi, T. Otsubo, F. Ogura and J. Tanaka, Bull. Chem. Soc. Jpn., 1988, 61, 2013–2018 CrossRef CAS.
- K. K. Bhasin, V. Arora, T. M. Klapötke and M. J. Crawford, Eur. J. Inorg. Chem., 2004, 4781–4788 CrossRef CAS.
- A. Edelmann, S. Brooker, N. Bertel, M. Noltemeyer, H. W. Roesky, G. M. Sheldrick and F. T. Edelmann, Z. Naturforsch., B: Chem. Sci., 1992, 47, 305–309 CrossRef CAS.
- S. K. Tripathi, U. Patel, D. Roy, R. B. Sunoj, H. B. Singh, G. Wolmershäuser and R. J. Butcher, J. Org. Chem., 2005, 70, 9237–9247 CrossRef CAS PubMed.
- R. A. Zingaro, C. Herrera and E. A. Meyers, J. Organomet. Chem., 1986, 306, C36–C40 CrossRef CAS.
- W.-W. du Mont, A. Martens-von Salzen, F. Ruthe, E. Seppälä, G. Mugesh, F. A. Devillanova, V. Lippolis and N. Kuhn, J. Organomet. Chem., 2001, 623, 14–28 CrossRef CAS.
- R. Kaur, H. B. Singh and R. J. Butcher, Organometallics, 1995, 14, 4755–4763 CrossRef CAS.
- T. M. Klapötke, B. Krumm, H. Nöth, J. C. Gálvez-Ruiz, K. Polborn, I. Schwab and M. Suter, Inorg. Chem., 2005, 44, 5254–5265 CrossRef PubMed.
- E. W. Washburn, International Critical Tables of Numerical Data, Physics, Chemistry and Technology, Knovel, 1st electronic edn, 2003, http://app.knovel.com Search PubMed.
- O. Lindqvist, Acta Chem. Scand., 1970, 24, 3178–3188 CrossRef CAS.
- M. Sharma, K. K. Bhasin, S. K. Mehta, N. Singh and S. Kumar, Radiat. Phys. Chem., 2006, 75, 2029–2038 CrossRef CAS.
- R. T. Mehdi, D. Miller and T. A. Tahir, Inorg. Chim. Acta, 1984, 90, 85–89 CrossRef CAS.
- K. Srivastava, S. Sharma, H. B. Singh, U. P. Singh and R. J. Butcher, Chem. Commun., 2010, 46, 1130–1132 RSC.
- G. Llabres, O. Dideberg and L. Dupont, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 2438–2444 CrossRef CAS.
- P. Granger and S. Chapelle, J. Magn. Reson., 1980, 39, 329–334 CAS.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- C. Ammann, P. Meier and A. Merbach, J. Magn. Reson., 1982, 46, 319–321 CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. Van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- E. Van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281–293 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981 CrossRef CAS.
- O. V. Gritsenko, P. R. T. Schipper and E. J. Baerends, Chem. Phys. Lett., 1999, 302, 199–207 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1995, 99, 606–611 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, Int. J. Quantum Chem., 1996, 60, 753–766 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, Int. J. Quantum Chem., 1997, 61, 899–918 CrossRef CAS.
- R. K. Harris, E. D. Becker, S. M. C. De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Magn. Reson. Chem., 2008, 46, 582–598 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189 RSC.
- A. F. Cozzolino, P. J. W. Elder and I. Vargas-Baca, Coord. Chem. Rev., 2011, 255, 1426–1438 CrossRef CAS.
- R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795–1818 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Derivations of selected equations and detailed tables and plots of experimental and computational results. See DOI: 10.1039/c6cp05892b |
| This journal is © the Owner Societies 2016 |