 Open Access Article
Open Access ArticleHigh-mobility two-dimensional electron gas in SrGeO3- and BaSnO3-based perovskite oxide heterostructures: an ab initio study†
Yaqin
Wang
ab,
Wu
Tang
a,
Jianli
Cheng
b,
Safdar
Nazir
b and
Kesong
Yang
 *b
*b
aState Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu 610054, P. R. China
bDepartment of NanoEngineering, University of California, San Diego, La Jolla, CA 92093-0448, USA. E-mail: kesong@ucsd.edu; Fax: +1-858-534-9553; Tel: +1-858-534-2514
First published on 27th October 2016
Abstract
We explored the possibility of producing a high-mobility two-dimensional electron gas (2DEG) in the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 heterostructures using first-principles electronic structure calculations. Our results show that the 2DEG occurs at n-type LaAlO3/SrGeO3 and LaGaO3/BaSnO3 interfaces. Compared to the prototype LaAlO3/SrTiO3, LaAlO3/SrGeO3 and LaGaO3/BaSnO3 systems yield comparable total interfacial charge carrier density but much lower electron effective mass (nearly half the value of LaAlO3/SrTiO3), thus resulting in about twice larger electron mobility and enhanced interfacial conductivity. This work demonstrates that SrGeO3 and BaSnO3 can be potential substrate materials to achieve a high-mobility 2DEG in the perovskite-oxide heterostructures.
1 Introduction
The recent development of epitaxial technology has made it possible to achieve high-quality oxide heterostructures (HS) with novel interfacial material properties that are absent in the bulk materials.1–3 A prominent example is a LaAlO3/SrTiO3 HS system that consists of two wide band gap insulators LaAlO3 and SrTiO3.1 This HS system has displayed some unique interfacial properties such as two-dimensional electron gases (2DEGs),1 superconductivity,2 and ferromagnetism.3 These interesting interfacial properties have attracted great attention not only because of its fundamental physics but also because of its promising applications in next-generation nanoelectronics.1–3Although the 2DEG at the LaAlO3/SrTiO3 interface shows an extremely high charge carrier density,4,5 its relatively low mobility is still a critical problem and very sensitive to the growth conditions.6,7 To maximize the function of a perovskite-oxide-based 2DEG for high-performance nanoelectronics, it is necessary to further improve its conductivity with higher charge density and electron mobility. To do this, some approaches such as defect engineering,8,9 strain engineering,10–14 and doping engineering15–18 have been proposed to optimize the interfacial conductive property of perovskite-oxide HS systems. In addition, some experimental efforts have also been made to prepare novel perovskite-oxide-based HS systems such as NdAlO3/SrTiO319 and LaTiO3/SrTiO3,20 and to explore their interfacial conductive properties. However, all these perovskite-oxide-based HS systems still use SrTiO3 as the substrate, and the interfacial conductivity is caused by the partially occupied Ti 3d orbitals. It is known that the localized Ti 3d orbital has an intrinsic low-dispersion character, which yields a large electron effective mass and relatively low charge carrier mobility. As a result, even though the charge carrier density could be effectively tuned in the SrTiO3-based HS systems via various approaches mentioned above, the charge carrier mobility might not be significantly tuned.
To improve the 2DEG mobility in the perovskite-oxide-based HS systems, one approach is to replace the SrTiO3 with other nonpolar perovskite oxides whose bottom conduction bands are comprised of s or p orbitals. This is because s and p orbitals are less localized than the d orbital, which can potentially lead to larger band dispersion and lower electron effective mass.21 In terms of this hypothesis, BaSnO3 and SrGeO3 are two potential substrate materials for growing perovskite-oxide HS systems because of their s/p hybridization characters at the bottom of conduction bands.22,23 Interestingly, several recent experimental studies have provided a solid support for this hypothesis.24–28 The bulk single crystal of La-doped BaSnO3 has a high room-temperature mobility of 320 cm2 V−1 s−1, though the epitaxial films have relatively lower values in the range from 10 to 150 cm2 V−1 s−1 in either doped BaSnO3 films or BaSnO3-based HS.29 Very recently, Bharat Jalan et al. have studied the band alignment in epitaxial BaSnO3/SrTiO3 (001) and BaSnO3/LaAlO3 (001) HSs using ex situ X-ray photoelectron spectroscopy (XPS) and spectroscopic ellipsometry (SE).29 Correspondingly, a recent computational study revealed that there exists a conduction-band offset of 1.14 eV at the BaSnO3/SrTiO3 interface.30 These experimental and computational studies both suggest that BaSnO3 is an appropriate electron acceptor for LaAlO3 and SrTiO3. Nevertheless, the extremely large lattice mismatch between BaSnO3 and LaAlO3 (about 8%) is pernicious to minimize the defects at the interfacial region or to improve the electron mobility.25,31 Hence, it is quite necessary to find an alternative perovskite oxide material to match with the BaSnO3 substrate or to find an alternative substrate material with equivalent or higher electron mobility as compared with that of BaSnO3.
In this work, by using first-principles electronic structure calculations, we have modeled LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems in which SrGeO3 and BaSnO3 are used as substrate materials, and explored the possibility of producing a high-mobility 2DEG in these two HS systems, respectively. Our results show that these two perovskite-oxide HS systems are able to produce the interfacial metallic states due to the polar catastrophe mechanism, and they keep the comparable total charge carrier density with that of the LaAlO3/SrTiO3 system. Moreover, by calculating and analyzing electron effective masses, we show that the electron mobility of these two substrate materials is about two times larger than that of LaAlO3/SrTiO3. These results indicate that, with respect to the model LaAlO3/SrTiO3 system, an enhanced interfacial electron conductivity is expected in the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems.
2 Computational and structural details
The density functional theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP).35 The electron–ion interaction was treated by the projector augmented wave (PAW) potential,36 and the electron exchange–correlation interaction was described by the generalized-gradient approximation (GGA) parameterized by Perdew–Burke–Ernzerhof (PBE).37 A cutoff energy of 450 eV for the planewave basis set and a Monkhorst–Pack k-point mesh of 4 × 4 × 1 were employed. To simulate the epitaxial film growth process in the experiments, the lattice parameters along the ab-plane were fixed while those along the c-axis and all the ions' positions were fully relaxed until the force tolerance on each atom was smaller than 0.03 eV Å−1. All the structural relaxations were carried out using the standard DFT calculations within the GGA-PBE framework. To reproduce the accurate experimental band gap of the parent materials (BaSnO3 and SrGeO3), the Heyd–Scuseria–Ernzerhof (HSE06)38 hybrid functional was employed in the single-point total energy calculations. The electronic energy convergence was set to 10−4 eV, and a Gaussian smearing of 0.08 eV was employed for density of states (DOS) calculations. Although not shown here, the calculated band gaps with varied percent HF exchange contributions show that a 33% HF exchange contribution can yield well the experimental band gaps of 2.7 eV for SrGeO3 and 3.1 eV for BaSnO3, which is exactly the same as the case of SnO2.39 Thus, the same HF exchange was used for the following heterostructure calculations.A superlattice approach was used to model LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems that contain symmetrical n-type (LaO)+/(SnO2)0 and (LaO)+/(GeO2)0 interfaces. To model the HS, 7.5 unit cells of SrGeO3 (BaSnO3) were used as the substrate and 4.5 unit cells of LaAlO3 (LaGaO3) were stacked on the substrate. It is worth mentioning that the superlattice model could exhibit different materials properties from the HS-based slab model in which both the film and the substrate have a surface.40,41 The difference is mainly caused by the surface effects in the HS-based slab mode in which the film and the substrate both have a surface. For instance, for the well-known LaAlO3/SrTiO3 system, prior computational studies indicate that only a HS-based slab model can well depict the polarization behavior in the LaAlO3 film though both models can reproduce the interfacial electron reconstruction phenomenon.40–42
At room temperature, BaSnO3 crystallizes in a cubic phase,25 and LaAlO3 and LaGaO3 crystallize in an orthorhombic phase.43 For SrGeO3, under appropriate conditions such as high pressure and temperature, it can exhibit a cubic phase. For example, Mizoguchi et al. prepared the cubic SrGeO3 with a typical perovskite structure upon high-pressure treatment at 1100 °C.22 Herein, by following the widely used approach,40,42,44 we built the HS models (1 × 1 in the ab-plane) by treating these non-cubic perovskite oxides as pseudo-cubic structures. In fact, to investigate the possible structural rotation in LaAlO3/SrGeO3, we also carried out test calculations for a larger HS model by using a  supercell in the ab-plane. Our calculated energy function versus the rotation angle indicates that the structural rotation of the GeO6 cage is not energetically favorable in this model, see the ESI.†Table 1 lists the experimental and calculated structural parameters and band gaps of LaAlO3, SrGeO3, and LaGaO3 and BaSnO3 in their pseudo-cubic (cubic) phase. The lattice mismatch f, defined as f = (af − as)/as, for the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS models is also listed. The negative values of f indicate that the film materials experience a tensile strain from the substrate.
supercell in the ab-plane. Our calculated energy function versus the rotation angle indicates that the structural rotation of the GeO6 cage is not energetically favorable in this model, see the ESI.†Table 1 lists the experimental and calculated structural parameters and band gaps of LaAlO3, SrGeO3, and LaGaO3 and BaSnO3 in their pseudo-cubic (cubic) phase. The lattice mismatch f, defined as f = (af − as)/as, for the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS models is also listed. The negative values of f indicate that the film materials experience a tensile strain from the substrate.
3 Results and discussion
3.1 Cleavage energy
To evaluate the strength of interfacial cohesion for the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems, we calculated their cleavage energies utilizing the following formula:15,45| Ecleav = (E1slab + E2slab − EHS)/2A | (1) |
The cleavage energy is the energy needed to separate the HS system. That is, a larger cleavage energy indicates a stronger cohesion between the two materials at the interface. The calculated cleavage energies within standard DFT calculations are 0.230 eV Å−2 for LaAlO3/SrGeO3 and 0.241 eV Å−2 for LaGaO3/BaSnO3, respectively, slightly larger than that of the LaAlO3/SrTiO3 HS system (0.19 eV Å−2, ref. 45). This indicates that the n-type (LaO)+/(GeO2)0 and (LaO)+/(SnO2)0 interfaces are more cohesive than (LaO)+/(TiO2)0, and thus the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 interfaces are thermodynamically more favorable than the LaAlO3/SrTiO3 interface.
3.2 Density of states
The calculated total DOS plots of LaAlO3/SrGeO3 and LaGaO3/BaSnO3 are shown in Fig. 1. It shows that the Fermi level is pinned to the bottom of conduction bands, indicating typical n-type conductivity. To understand the origin of the metallic electronic states in these two HS systems, we calculated the layer-resolved partial DOSs for LaGaO3/BaSnO3 and LaAlO3/SrGeO3 models and are shown in Fig. 2 and 3, respectively. For convenience, here we defined three consecutive SnO2 (GeO2) layers, i.e., the 1st, 3rd, and 5th BaSnO3 (SrGeO3) layers as IF-I, IF-III, and IF-V layers, respectively. Our calculations show that the O 2p states in the layers of the substrate materials shift toward high energy with layers moving from the interfacial layer to the deeper layer. The interfacial metallic states are mainly contributed by IF-I, IF-III, and IF-V SnO2 (GeO2) layers, and these metallic states are mostly composed of Sn 5s (Ge 4s) and O 2p orbitals, displaying a large energy dispersion within the band gap. The formation of the interfacial metallic states indicates that there exists a polar-catastrophe-driven charge transfer from LaGaO3 to BaSnO3 for the LaGaO3/BaSnO3 (see Fig. 2) system and from LaAlO3 to SrGeO3 for the LaAlO3/SrGeO3 (see Fig. 3) system, similar to the case of the LaAlO3/SrTiO3 system. Interestingly, the largest charge densities for LaGaO3/BaSnO3 (LaAlO3/SrGeO3) HS systems occur in the IF-III SnO2 (GeO2) layer. This is mainly because the SnO6 (GeO6) octahedra in the IF-I layer have a larger structural distortion than that in the IF-III layer. The structural distortion produces a dipole moment towards the deep layers, leading to more charge transfer to the IF-III layer. This fact is different from the case of the LaAlO3/SrTiO3 HS system, in which the 2DEG mainly resides in the IF-I TiO2 layer.11 In addition, in the LaGaO3/BaSnO3 system (see Fig. 2 and 4b), few electrons released from the interfacial (LaO)+ layer are also transferred to La 5d orbitals in its adjacent (LaO)+ layer, forming partially occupied La 5d states. As discussed below, the partially occupied La 5d states also increase the electron effective mass of the LaGaO3/BaSnO3 system. In contrast, interestingly, the LaAlO3/SrGeO3 system (see Fig. 3 and 4a) does not show a similar phenomenon. This implies that La 5d orbitals have much weaker ability to capture electrons compared to Ge 4s orbitals and Sn 5s orbitals either, but to a lesser extent for the later.21 Therefore, La 5d orbitals are partially occupied in the LaGaO3/BaSnO3 system. | ||
| Fig. 1 Calculated total DOSs for (a) LaGaO3/BaSnO3 and (b) LaAlO3/SrGeO3 HS systems, respectively. The Fermi level is represented by the vertical dashed line at 0 eV. | ||
3.3 Band structures and effective masses
Next, we calculated the electronic band structures for the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems along the path M–Γ–X of the interfacial Brillouin zone, along with that of the prototype LaAlO3/SrTiO3 HS system for a direct comparison (see Fig. 4c). As shown in the band structures, some electronic states reside below the Fermi level in all the three HS systems, indicating an n-type conductivity in the systems. For the LaAlO3/SrTiO3 HS system (non-spin-polarized calculation), the light band dxy around Γ is parabolic and the heavy band extends along the Γ–X direction. In contrast, in the case of LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems (see Fig. 4a and b), the hybridization between Ge 4s (Sn 5s) states and O 2p states leads to more delocalized conduction bands near the Fermi level than that of the LaAlO3/SrTiO3 system, and thus a smaller electron effective mass is expected.To quantitatively verify this inference, we then calculated the electron effective mass, m*/me, for the minimum conduction bands along the Γ–X and Γ–M directions, in which me is the free electron rest mass. The effective mass m* was calculated using the parabolic approximation using the formula:46
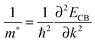 | (2) |
| Systems | m*/me | |
|---|---|---|
| Γ–X | Γ–M | |
| LaAlO3/SrGeO3 | 0.20 | 0.22 |
| LaGaO3/BaSnO3 | 0.24 | 0.25 |
| LaAlO3/SrTiO3 | 0.49 | 0.51 |
3.4 Charge carrier density, mobility and conductivity
Besides the charge carrier mobility, the interfacial charge carrier density is also an important factor in determining the interfacial conductivity of the 2DEG. To have a quantitative comparison of the interfacial charge carrier density among the LaAlO3/SrGeO3, LaGaO3/BaSnO3, and LaAlO3/SrTiO3 HS systems, we calculated the total and layer charge carrier densities by integrating their total and layer-resolved partial DOSs for the conducting gap states below the Fermi level, see Fig. 5a. Our calculations show that these three HS systems nearly show a comparable total charge density of about 3.0–3.5 × 1014 cm−2, which corresponds to a charge transfer of 0.5e− from the polar LaAlO3 (LaGaO3) to the nonpolar SrTiO3 (SrGeO3 and BaSnO3) substrate. This indicates that the polar catastrophe at the (AO)+/(BO2)0 interface can drive about 0.5e− charge transfer, which is independent of the choice of the substrate. It is worth mentioning that the present calculations are based on the superlattice model, which leads to a higher charge carrier density than that of the HS-based slab model.41To have a direct comparison of the interfacial conductivity among these three HS systems, we calculated the normalized charge carrier mobility (μ/μ0) and conductivity (σ/σ0) with respect to those of the LaAlO3/SrTiO3 system, see Fig. 5b. μ0 and σ0 refer to the charge carrier mobility and conductivity of the LaAlO3/SrTiO3 HS system, respectively. The following two equations were used:51μ = e〈τ〉/m* and σ = neμ, in which e, 〈τ〉, m*, n, μ, and σ are the elementary charge, average scattering time (also called “relaxation time”),51,52 electron effective mass, charge carrier density, electron mobility, and electrical conductivity, respectively. The scattering time τ is determined by all the scattering events such as impurity scattering, electron–phonon scattering, and electron–electron scattering, and the inverse of τ can be expressed as the sum of rates associated with different scattering mechanisms according to Matthiessen's rule.53 It has been extremely challenging to calculate the scattering time τ due to the complicated scattering mechanism. One common and simplified approach is to treat τ as a constant under the constant scattering (relaxation) time approximation,54,55 which has been validated in prior studies.46,56,57 In this work, by assuming that 〈τ〉 is a constant, our calculations show that the electron mobility and the electrical conductivity of LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems are nearly 2.5 and 2.0 times larger than those of the LaAlO3/SrTiO3 HS system, respectively. This indicates that using BaSnO3 and SrGeO3 as the host substrates one can effectively improve the charge carrier mobility and conductivity of the 2DEG.
4 Conclusions
In conclusion, first-principles electronic structure calculations are employed to explore the possibility of producing a high-quality 2DEG in the LaAlO3/SrGeO3 and LaGaO3/BaSnO3 HS systems. Our results reveal that these two HS systems can form interfacial metallic states consisting of less localized Ge 4s and Sn 5s orbitals, respectively, which leads to smaller electron effective mass and higher charge carrier mobility compared to the well-known LaAlO3/SrTiO3 HS model. This work shows a feasible route to enhance the 2DEG mobility and interfacial conductivity using novel substrate materials such as SrGeO3 and BaSnO3.Acknowledgements
This work was supported by the National Science Foundation under the award number ACI-1550404 and a Department of Defense National Security Science and Engineering Faculty Fellowship (under the ONR contract number N000141510030). This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by a National Science Foundation grant number OCI-1053575. Y. W. is grateful for the visiting graduate student fellowship from the University of Electronic Science and Technology of China.References
- A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423–426 CrossRef CAS PubMed.
- N. Reyren, S. Thiel, A. D. Caviglia, L. F. Kourkoutis, G. Hammer, C. Richter, C. W. Schneider, T. Kopp, A. S. Rüetschi, D. Jaccard, M. Gabay, D. A. Muller, J. M. Triscone and J. Mannhart, Science, 2007, 317, 1196–1199 CrossRef CAS PubMed.
- A. Brinkman, M. Huijben, M. van Zalk, J. Huijben, U. Zeitler, J. C. Maan, W. G. van der Wiel, G. Rijnders, D. H. A. Blank and H. Hilgenkamp, Nat. Mater., 2007, 6, 493–496 CrossRef CAS PubMed.
- S. Thiel, G. Hammerl, A. Schmehl, C. W. Schneider and J. Mannhart, Science, 2006, 313, 1942–1945 CrossRef CAS PubMed.
- W. Siemons, G. Koster, H. Yamamoto, W. A. Harrison, G. Lucovsky, T. H. Geballe, D. H. A. Blank and M. R. Beasley, Phys. Rev. Lett., 2007, 98, 196802 CrossRef PubMed.
- T. Fix, F. Schoofs, J. L. MacManus-Driscoll and M. G. Blamire, Phys. Rev. Lett., 2009, 103, 166802 CrossRef CAS PubMed.
- T. Hernandez, C. W. Bark, D. A. Felker, C. B. Eom and M. S. Rzchowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 161407 CrossRef.
- Z. Liu, C. Li, W. Lü, X. Huang, Z. Huang, S. Zeng, X. Qiu, L. Huang, A. Annadi, J. Chen, J. Coey, T. Venkatesan and Ariando, Phys. Rev. X, 2013, 3, 021010 Search PubMed.
- L. Weston, X. Cui, S. Ringer and C. Stampfl, Phys. Rev. Lett., 2014, 113, 186401 CrossRef CAS PubMed.
- B. Kalisky, E. M. Spanton, H. Noad, J. R. Kirtley, K. C. Nowack, C. Bell, H. K. Sato, M. Hosoda, Y. Xie, Y. Hikita, C. Woltmann, G. Pfanzelt, R. Jany, C. Richter, H. Y. Hwang, J. Mannhart and K. A. Moler, Nat. Mater., 2013, 12, 1091–1095 CrossRef CAS PubMed.
- S. Nazir, M. Behtash and K. Yang, Appl. Phys. Lett., 2014, 105, 141602 CrossRef.
- S. Nazir and K. Yang, ACS Appl. Mater. Interfaces, 2014, 6, 22351–22358 CAS.
- S. Nazir, M. Behtash and K. Yang, RSC Adv., 2015, 5, 15682–15689 RSC.
- Z. Huang, Z. Q. Liu, M. Yang, S. W. Zeng, A. Annadi, W. M. Lü, X. L. Tan, P. F. Chen, L. Sun, X. Renshaw Wang, Y. L. Zhao, C. J. Li, J. Zhou, K. Han, W. B. Wu, Y. P. Feng, J. M. D. Coey, T. Venkatesan and Ariando, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125156 CrossRef.
- S. Nazir, J. Cheng, M. Behtash, J. Luo and K. Yang, ACS Appl. Mater. Interfaces, 2015, 7, 14294–14302 CAS.
- S. Nazir, M. Behtash, J. Cheng, J. Luo and K. Yang, Phys. Chem. Chem. Phys., 2016, 18, 2379–2388 RSC.
- T. Yajima, Y. Hikita, M. Minohara, C. Bell, J. A. Mundy, L. F. Kourkoutis, D. A. Muller, H. Kumigashira, M. Oshima and H. Y. Hwang, Nat. Commun., 2015, 6, 6759 CrossRef PubMed.
- S. Nazir, C. Berna and K. Yang, ACS Appl. Mater. Interfaces, 2015, 7, 5305–5311 CAS.
- X. Xiang, L. Qiao, H. Xiao, F. Gao, X. Zu, S. Li and W. Zhou, Sci. Rep., 2014, 4, 5477 CAS.
- J. Biscaras, S. Hurand, C. Feuillet-Palma, A. Rastogi, R. Budhani, N. Reyren, E. Lesne, J. Lesueur and N. Bergeal, Sci. Rep., 2014, 4, 6788 CrossRef CAS PubMed.
- L. Bjaalie, B. Himmetoglu, L. Weston, A. Janotti and C. G. V. de Walle, New J. Phys., 2014, 16, 025005 CrossRef.
- H. Mizoguchi, T. Kamiya, S. Matsuishi and H. Hosono, Nat. Commun., 2011, 2, 470 CrossRef PubMed.
- S. Ismail-Beigi, F. J. Walker, S.-W. Cheong, K. M. Rabe and C. H. Ahn, APL Mater., 2015, 3, 062510 CrossRef.
- H. J. Kim, T. H. Kim, W.-J. Lee, Y. Chai, J. W. Kim, Y. J. Jwa, S. Chung, S. J. Kim, E. Sohn and S. M. Lee, et al. , Thermochim. Acta, 2014, 585, 16–20 CrossRef CAS.
- P. V. Wadekar, J. Alaria, M. OSullivan, N. L. O. Flack, T. D. Manning, L. J. Phillips, K. Durose, O. Lozano, S. Lucas, J. B. Claridge and M. J. Rosseinsky, Appl. Phys. Lett., 2014, 105, 052104 CrossRef.
- K. Ganguly, P. Ambwani, P. Xu, J. S. Jeong, K. A. Mkhoyan, C. Leighton and B. Jalan, Appl. Mater., 2015, 3, 062509 CrossRef.
- Z. Lebens-Higgins, D. Scanlon, H. Paik, S. Sallis, Y. Nie, M. Uchida, N. Quackenbush, M. Wahila, G. Sterbinsky and D. A. Arena, et al. , Phys. Rev. Lett., 2016, 116, 027602 CrossRef CAS PubMed.
- S. Raghavan, T. Schumann, H. Kim, J. Y. Zhang, T. A. Cain and S. Stemmer, Appl. Mater., 2016, 4, 016106 CrossRef.
- S. A. Chambers, T. C. Kaspar, A. Prakash, G. Haugstad and B. Jalan, Appl. Phys. Lett., 2016, 108, 152104 CrossRef.
- K. Krishnaswamy, L. Bjaalie, B. Himmetoglu, A. Janotti, L. Gordon and C. G. Van de Walle, Appl. Phys. Lett., 2016, 108, 083501 CrossRef.
- H. Mun, U. Kim, H. Min Kim, C. Park, T. Hoon Kim, H. Joon Kim, K. Hoon Kim and K. Char, Appl. Phys. Lett., 2013, 102, 252105 CrossRef.
- P. Perna, D. Maccariello, M. Radovic, U. Scotti di Uccio, I. Pallecchi, M. Codda, D. Marré, C. Cantoni, J. Gazquez, M. Varela, S. J. Pennycook and F. M. Granozio, Appl. Phys. Lett., 2010, 97, 152111 CrossRef.
- K. Ogisu, A. Ishikawa, Y. Shimodaira, T. Takata, H. Kobayashi and K. Domen, J. Phys. Chem. C, 2008, 112, 11978–11984 CAS.
- W. Zhang, J. Tang and J. Ye, J. Mater. Res., 2007, 22, 1859–1871 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- M. Behtash, P. H. Joo, S. Nazir and K. Yang, J. Appl. Phys., 2015, 117, 175101 CrossRef.
- W.-J. Son, E. Cho, B. Lee, J. Lee and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245411 CrossRef.
- M. Behtash, S. Nazir, Y. Wang and K. Yang, Phys. Chem. Chem. Phys., 2016, 18, 6831–6838 RSC.
- R. Pentcheva and W. E. Pickett, Phys. Rev. Lett., 2009, 102, 107602 CrossRef PubMed.
- D. Lybye, F. W. Poulsen and M. Mogensen, Solid State Ionics, 2000, 128, 91–103 CrossRef CAS.
- Z. Zhong, P. X. Xu and P. J. Kelly, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165127 CrossRef.
- S. Nazir, M. Behtash and K. Yang, J. Appl. Phys., 2015, 117, 115305 CrossRef.
- G. Hautier, A. Miglio, D. Waroquiers, G.-M. Rignanese and X. Gonze, Chem. Mater., 2014, 26, 5447–5458 CrossRef CAS.
- N. Bristowe, E. Artacho and P. Littlewood, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045425 CrossRef.
- A. Janotti, D. Steiauf and C. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 201304 CrossRef.
- H.-R. Liu, J.-H. Yang, H. Xiang, X. Gong and S.-H. Wei, Appl. Phys. Lett., 2013, 102, 112109 CrossRef.
- S. Dabaghmanesh, R. Saniz, M. Amini, D. Lamoen and B. Partoens, J. Phys.: Condens. Matter, 2013, 25, 415503 CrossRef CAS PubMed.
- Y. Peter and M. Cardona, Fundamentals of semiconductors: physics and materials properties, Springer Science & Business Media, 2010 Search PubMed.
- P. B. Allen, W. E. Pickett and H. Krakauer, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 7482–7490 CrossRef CAS.
- M. C. Karamargin, C. A. Reynolds, F. P. Lipschultz and P. G. Klemens, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 3624–3633 CrossRef CAS.
- T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210 CrossRef.
- J. Yang, L. Xi, W. Qiu, L. Wu, X. Shi, L. Chen, J. Yang, W. Zhang, C. Uher and D. J. Singh, npj Comput. Mater., 2016, 2, 15015 CrossRef.
- G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12140–12146 CrossRef CAS PubMed.
- W. Chen, J.-H. Pohls, G. Hautier, D. Broberg, S. Bajaj, U. Aydemir, Z. M. Gibbs, H. Zhu, M. Asta, G. J. Snyder, B. Meredig, M. A. White, K. Persson and A. Jain, J. Mater. Chem. C, 2016, 4, 4414–4426 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp05572a |
| This journal is © the Owner Societies 2016 |




