Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The first example of ab initio calculations of f–f transitions for the case of [Eu(DOTP)]5− complex—experiment versus theory†
Rafał
Janicki
*a,
Andrzej
Kędziorski
*b and
Anna
Mondry
a
aUniversity of Wrocław, Faculty of Chemistry, Address F. Joliot-Curie 14, 50-383 Wrocław, Poland. E-mail: rafal.janicki@chem.uni.wroc.pl
bNicolaus Copernicus University, Faculty of Physics, Astronomy and Informatics, Address Toruń, Institute of Physics, Poland. E-mail: andrzej.kedziorski@fizyka.umk.pl
First published on 12th September 2016
Abstract
Crystal structures and photophysical properties (IR and UV-vis-NIR) of two compounds, [C(NH2)3]5[Eu(DOTP)]·12.5H2O and K5[Eu(DOTP)]·11H2O (DOTP = 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetrakis (methylenephosphonic acid)), were determined. The DOTP ligand is bonded to Eu3+via four O and four N atoms, filling thus eight coordination sites of Eu3+. The experimental structures of two [K4Eu(DOTP)]− clusters were used as a starting point for theoretical ab initio calculations based on a multireference wavefunction approach. Positions of the energy levels of the 4f6 configuration of the Eu3+ ion have been calculated and compared with those derived from the experimental spectra. This enabled us to tentatively assign energy levels of the Eu3+ ion. The relationship between calculated energies of excited states and Eu–N and Eu–O bond lengths was discussed with respect to the nephelauxetic effect.
1. Introduction
Lanthanide complexes with polydendate amino acids, which are based on the cyclen backbone (1,4,7,10-tetraazacyclododecane), are of considerable interest at present, since Gd–DOTA (DOTA = 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacete ligand) and Tm–DOTP complexes were found to be useful in medical and biological diagnostics.1 The Gd–DOTA complex serves as a MRI contrast agent while Tm–DOTP has been used as a NMR effective shift reagent and extracellular space marker.2 Ligand modifications consisting of carboxylic or phosphonic arms substitution by an aromatic group may expand the applications of such complexes as potential multifunctional luminescence bioprobes3 and single molecular magnets.4 In this context the Ln–DOTA and Ln–DOTP systems may be considered as model compounds. From this point of view, the physicochemical properties in relation to theoretical study are of utmost importance in designing compounds in new applications. It is worthwhile noting that the diversity of potential applications for this class of compounds is related to the presence of incompletely filled 4f orbitals, which are only slightly disturbed by the ligand field. This is a reason why ab initio calculations of lanthanide systems are not straightforward—they have to include electron correlation and relativistic effects simultaneously.4b Addressing the theoretical ab initio study to such group of compounds is of particular interest. For example, the ab initio calculations of the lowest energy levels of Dy–DOTA complex have already been performed in the context of its magnetic properties.4b,c Comparison of the results for such calculations with the experimental ones may verify the quality of the former. On the other hand, theoretical results may provide additional information about a particular system that cannot be extracted from the experiment. However, it should be pointed out that many theoretical studies devoted to structural properties of lanthanide molecular complexes have already been completed using density functional theory (DFT).5 In such an approach it is very common to represent the open 4f shell of the lanthanide ion by effective core pseudopotential due to computational savings and the inability of DFT methods to describe properly the highly localized and correlated f-electrons. Furthermore, the semi-empirical analysis of energy levels based on crystal-field theory needs a priori assumptions about the assignment of energy levels, which in low-symmetry systems is ambiguous and also suffers from the large number of adjustable parameters.6This paper focuses on the experimental and ab initio theoretical study of the [Eu(DOTP)]5− complex in single crystals of the following formulas: [C(NH2)3]5[Eu(DOTP)]·12.5H2O and K5[Eu(DOTP)]·11H2O. Only two crystal structures of monomeric Ln–DOTP complex (Ln = Gd, Tm) have been reported7,8 and neither spectroscopic properties of monocrystals nor theoretical ab initio calculations have been described thus far. Theoretical calculations are performed for the two clusters {K4[Eu(DOTP)]}− representing two different Eu sites for the K5[Eu(DOTP)]·11H2O crystal. Energies of the excited states for the 4f6 configuration were obtained within the quantum chemistry ab initio methods based on the multireference wave-function approach, which allows accounting for static and dynamic electron correlation as well as relativistic effects.
2. Results and discussion
2.1 Crystal structures
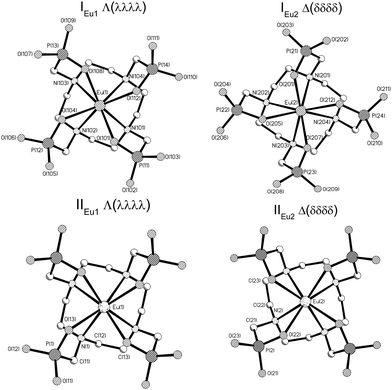
The [Eu(DOTP)]5− complex crystallizes in the form of compounds of the following formulas: [C(NH2)3]5[Eu(DOTP)]·12.5H2O (hereinafter I) and K5[Eu(DOTP)]·11H2O (hereinafter II). The crystals of I are monoclinic and belong to the P2/n space group while those of II crystallize in the tetragonal system (P4cc space group). The crystals of I comprise [Eu(DOTP)]5− complexes, guanidinium cations and water molecules, while II consist of [Eu(DOTP)]5− complexes, potassium cations and lattice water molecules. In both compounds the [Eu(DOTP)]5− complex anions are deprotonated and their negative charge is compensated by [C(NH2)3]+ (in I) or K+ (in II) cations. The [DOTP]8− ligand is bonded to the Eu3+ cation by four oxygen and four nitrogen atoms, filling thus eight coordination places of the Eu3+ cation. Both structures contain two symmetry-independent [Eu(DOTP)]5− anions that differ in the conformation of the DOTP ligand, giving rise to two enantiomers Λ(λλλλ) (hereinafter IEu1, IIEu1) and Δ(δδδδ) (hereinafter IEu2, IIEu2). The molecular structures of [Eu(DOTP)]5− anions are presented in (Fig. 1).Selected Eu–O and Eu–N bond lengths are presented in Table 1. The average Ln–O and Ln–N distances in the case of Gd–DOTP and Tm–DOTP complexes are also presented in the table for comparison purposes.7,8
| IEu1 | Eu1–O108 | 2.321(3) | Eu1–N102 | 2.679(3) |
| Eu1–O104 | 2.339(3) | Eu1–N101 | 2.677(3) | |
| Eu1–O112 | 2.331(3) | Eu1–N104 | 2.710(3) | |
| Eu1–O101 | 2.338(3) | Eu1–N103 | 2.706(3) | |
| IEu2 | Eu2–O201 | 2.294(3) | Eu2–N201 | 2.646(3) |
| Eu2–O207 | 2.328(3) | Eu2–N203 | 2.696(3) | |
| Eu2–O205 | 2.343(3) | Eu2–N202 | 2.698(3) | |
| Eu2–O212 | 2.342(3) | Eu2–N204 | 2.721(3) | |
| IIEu1 | Eu1–O13 | 2.325(4) | Eu1–N1 | 2.732(5) |
| IIEu2 | Eu2–O22 | 2.346(4) | Eu2–N2 | 2.705(5) |
| I | Eu–O av | 2.330(16) | Eu–N av | 2.691(24) |
| II | Eu–O av | 2.336(15) | Eu–N av | 2.719(19) |
| Gd–O av | 2.314(1) | Gd–N av | 2.660(10) | |
| Tm–O av | 2.26(1) | Tm–N av | 2.63(1) | |
Respective Eu–O and Eu–N distances for both isomers in I are similar. However, there are two exceptions—namely, Eu2–O201 and Eu2–N201 bond lengths in I are significantly shorter. For this reason the structure of the IEu2 enantiomer is more distorted than the IEu1 one.
Average Eu–O and Eu–N distances are longer compared to those determined for [Gd(DOTP)]5− and [Tm(DOTP)]5− complexes.7,8 This is brought about by the lanthanide contraction.
The coordination polyhedra in I and II may be described as twisted square antiprism (TSAP), in which the corners are occupied by four O atoms (OIV – plane) and four N atoms (NIV – plane). In I the OIV and NIV planes are almost parallel to each other, with the dihedral angle between them equal to 0.6° and 0.9° in enantiomers IEu1 and IEu2, respectively. In II both OIV and NIV planes are perfectly parallel owing to the fact that the Eu3+ ion is located in fourfold axes. The twist angles of rectangles formed by four OIV atoms as well as by four NIV atoms in I and II are schematically presented in Fig. 2a.
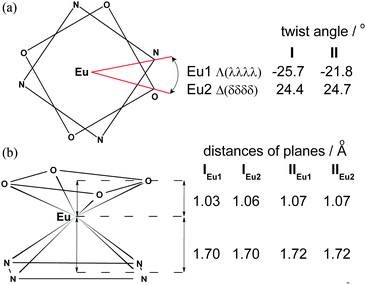 | ||
| Fig. 2 (a) Twist angle and (b) schematic coordination polyhedron and distances of Eu3+ from OIV and NIV planes. | ||
The small twist angle values between the OIV and NIV planes and the absence of a water molecule in the first coordination sphere of Eu3+, indicate that the crystals contain a minuscule type of the m′ isomer as a racemic mixture of two Λ(λλλλ) and Δ(δδδδ) enantiomers. The average distances between OIV and NIV planes are similar in both crystals and range from 2.73 Å to 2.79 Å. The Eu3+ cation is located inside the square antiprism at a distance of 1.03–1.07 Å to OIV and 1.70–1.72 Å to NIV planes (Fig. 2b).
All phosphonic groups are deprotonated; thus the P–O bond lengths are similar and range from 1.508(4) Å to 1.550(5) Å. The average P–O bond length is equal to ∼1.527(8) Å, and is very close to those found in other lanthanide aminophosphonates such as Ln–EDTMP and Ln–CDTMP.9,10
There are no water molecules coordinated to Eu3+ in the [EuDOTP]5− complexes in I and II, while in its carboxylic analogue, [Eu(DOTA)(H2O)]−, one water molecule is directly bonded to the Eu3+ ion.11 The absence of the water molecule in the closest neighbourhood of [Eu(DOTP)]5− is likely caused by the spherical hindrance connected with an accumulation of highly negative phosphonic oxygen atoms, which strongly repels water molecules and prevents their coordination to Eu3+. The water molecules were found in the second coordination sphere of [Eu(DOTP)]5− complex. The nearest H2O molecule is about 4 Å from the Eu3+ cation as shown in Table 2.
| I | II | ||
|---|---|---|---|
| Eu1–OW1 | 4.388 | Eu1–OW4 | 4.181 |
| Eu2–OW2 | 4.360 | Eu2–OW1 | 4.029 |
Similar interaction of water molecules from the second sphere was observed in the case of the Ho–DOTMA complex (where DOTMA is 1R,4R,7R,10R-α,α′,α′′,α′′′-tetramethyl-1,4,7,10-tetraazacyclo-dodecane-1,4,7,10-tetraacetic acid).12 Weak interaction of outer-sphere water molecules with [Ln(DOTP)]5− anions is probably a reason of high relaxivity of the [Gd(DOTP)]5− system.13
Distortion of the [Eu(DOTP)]5− complex in I brings about its symmetry that is approximately C4, while in II the complex's symmetry is exact (C4) because it is imposed by crystallographic fourfold axes.
Taking into account the structural variations of the [Eu(DOTP)]5− complex in I and II, the question that arises is how they are reflected in the IR and UV-vis spectra of both crystals.
2.2 IR spectroscopy
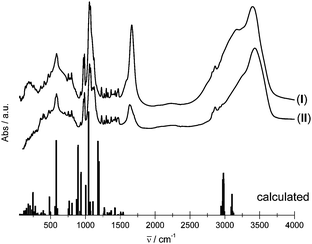
The IR spectra of both compounds were measured and the theoretical IR spectra of {K4[Eu(DOTP)]}− clusters representing IIEu1 and IIEu2 sites were obtained within the DFT approach for the B3LYP exchange–correlation functional. Because the theoretical DFT calculations were performed for isolated the {K4[Eu(DOTP)]}− anion (C1 symmetry) in the simulated spectra, there are no bands attributed to internal vibrations of water molecules and guanidinium cations. The complex anion {K4[Eu(DOTP)]}− contains 61 atoms giving rise to 177 fundamental vibrations that may be decomposed into 45A + 44B + 44E, where A, B and E denote irreducible representations of the C4 point group. Owing to the selection rules, all A → B fundamental excitations are forbidden in the IR spectra. The spectra of crystals under study are presented in Fig. 3. As seen here the spectral features of both crystals are similar. Theoretical study results enabled us to assign the bands observed in the experimental spectrum (see Table S1, ESI†).The main differences between the experimental spectra of both compounds are observed for bands located between 1490 cm−1 and 4000 cm−1. In this spectral range, the broad bands centered at ∼1630 cm−1 and ∼3425 cm−1 are attributed to the δOH2 and νOH vibrations, respectively, from the lattice water molecules. The δOH2 band in the I spectrum is partly covered by the intense δNH2 band from the guanidine cations. Certain differences appear in the spectral pattern of bands centered at ∼1070 cm−1. These bands are ascribed to νPOsym and νPOasym. In general, splitting and shape changes of the νPO bands reflect various geometrical changes of phosphonic groups as shown previously.9 The bands attributed to the Eu–O and Eu–N vibrations are located below 450 cm−1.
Observed similarities of the spectral features of I and II strongly suggest that the geometry of [Eu(DOTP)]5− complexes is substantially the same. Therefore, it seems to be justified to consider the local symmetry of both complex anions as C4 in spite of the fact that there is some certain deformation of [Eu(DOTP)]5− complex in I.
2.3 UV-vis electronic spectroscopy
The UV-vis absorption 7F0 → 5DJ (J = 0, 1, 2, 3, 4),5L6 and luminescence 5D0 → 7FJ (J = 0, 1, 2, 3, 4, 5, 6) spectra of crystals, recorded at RT in the spectral region 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–28
000–28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are shown in Fig. 4 and 5, respectively.
000 cm−1 are shown in Fig. 4 and 5, respectively.
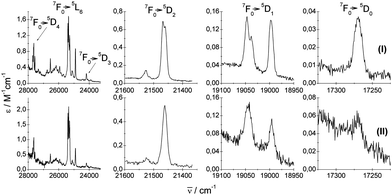 | ||
| Fig. 4 Experimental (I and II) UV-vis absorption 7F0 → 5DJ=0,1,2,3,4,5L6 spectra of crystals under study. | ||
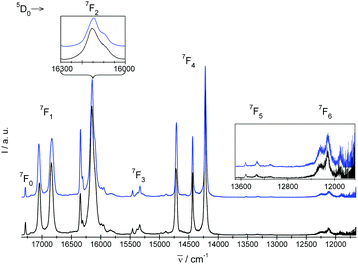 | ||
| Fig. 5 Experimental emission 5D0 → 7FJ=0,1,2,3,4,5,6 spectra of crystals under study. I = blue and II = black. | ||
Experimental absorption spectra consist of narrow bands attributed to transitions from the ground 7F0 state to the excited levels of the 4f6 configuration. The experimental emission spectra comprise bands corresponding to transitions from the excited 5D0 state to lower-lying 7FJ levels (where J = 0, 1, 2, 3, 4, 5, 6). Mechanisms of the electric-dipole f–f transitions, where J = 0–J′ = 2, 4, 6, observed in Eu3+ materials can be described via standard Judd–Ofelt theory,14,15 whereas the electric-dipole J = 0–J′ = 0, 3, 5 demands extended theory.16,177F0–5D1 and 5D0–7F1 transitions are of magnetic dipole character. The ΔS = 0 selection rule for both electric- and magnetic-dipole transitions is relaxed via the spin–orbit interaction within the lanthanide ion. Now, consider the selection rules from the point of view of the local symmetry of the europium crystallographic site.
In the case of the Eu3+ cation, both ground (7F0) and emission excited (5D0) states are fully symmetric. According to group theory, the A ↔ A,E electronic-dipole and magnetic-dipole transitions between the crystal field (CF) states are allowed in the C4 symmetry; at the same time, the A ↔ B transitions are forbidden. The numbers of spectral lines expected for Eu3+ ion in the site of C4 symmetry are collected in Table 3 along with the total numbers of experimentally observed lines in the absorption and emission spectra of I and II.
| J | C 4 symmetry | Absorption spectra | Luminescence spectra | |||
|---|---|---|---|---|---|---|
| 7F0 → 2S+1LJ | 5D0 → 7FJ | |||||
| I | II | I | II | |||
a
C
4 symmetry of I is not exact, thereby allowing larger number of spectral lines than expected for C4 symmetry.
b Line at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 in Fig. 5 finally interpreted as of cooperative vibronic origin was taken into account here. 400 cm−1 in Fig. 5 finally interpreted as of cooperative vibronic origin was taken into account here.
|
||||||
| 0 | A | 1 | 1 | 1 | 1 | 1 |
| 1 | A + E | 2 | 2 | 2 | 2 | 2 |
| 2 | A + 2·B + E | 2 | 3a | 2 | 3b | 3b |
| 3 | A + 2·B + 2·E | 3 | 3 | 3 | 3 | 3 |
| 4 | 3·A + 2·B + 2·E | 5 | 4 | 3 | 4 | 4 |
| 5 | 3·A + 2·B + 3·E | 6 | 4 | 4 | ||
| 6 | 3·A + 4·B + 3·E | 6 | 3 | 3 | ||
In most cases, the experimental number of observed spectral lines is smaller compared to the theoretical prediction. We were unable to separate CF levels of individual Eu sites. To unequivocally assign the bands observed in the spectra of I and II, the analysis was extended into theoretical calculations.
2.4 Theoretical energy levels
The ab initio calculations of energies of the IIEu1 and IIEu2 complexes were performed in the following steps:• complete active space self-consistent field method (CASSCF)18
• complete active space perturbation theory of second-order (CASPT2)19,20
• restricted active space state interaction (RASSI)21
CASSCF and CASPT2 methods account for non-dynamic (static) and dynamic correlation effects, respectively, whereas the RASSI one includes the spin–orbit (SO) interaction. This sequence of calculations, denoted here by CASSCF/CASPT2/RASSI-SO, was performed for the active space that corresponds to the 4f6 configuration of the Eu3+ ion. In this way the energies of 7F and 5D, 5F, 5G, 5H, 5I, 5K and 5L states were calculated within the ab initio approach (for details see Section 3.4). Selected experimental and theoretical energy levels are collected in Table 4. A complete list of calculated energy levels is presented in Table S2 in ESI.†
| 2S+1LJ | Experimental | Symmetry | IIEu1 (theory) | IIEu2 (theory) | |||
|---|---|---|---|---|---|---|---|
| I | II | Irrep | Energy/cm−1 | Irrep | Energy/cm−1 | ||
| 7F0 | 0 | 0 | 1A | 1A | 0 | 1A | 0 |
| 7F1 | 230 | 237 | 2A | 2A | 192 | 2A | 206 |
| 452 | 442 | 1E | 1E | 520 | 1E | 507 | |
| 7F2 | 939 | 934 | ? | 2E | 1091 | 2E | 1079 |
| 1139 | 1129 | 2E | 1B | 1111 | 3A | 1107 | |
| 1180 | 1179 | 3A | 3A | 1116 | 1B | 1111 | |
| 2B | 1362 | 2B | 1333 | ||||
| 7F3 | 1826 | 1826 | 3E | 3E | 2015 | 3E | 2006 |
| 1915 | 1905 | 4A | 4A | 2043 | 4A | 2033 | |
| 3B | 2084 | 3B | 2069 | ||||
| 1956 | 1951 | 4E | 4E | 2110 | 4E | 2093 | |
| 4B | 2138 | 4B | 2128 | ||||
| 7F4 | 2571 | 2563 | 5A | 5A | 2869 | 5A | 2864 |
| 6A | 3058 | 6A | 3048 | ||||
| 2848 | 2847 | 6A | 5E | 3064 | 5E | 3050 | |
| 5E | |||||||
| 3064 | 3058 | 6E | 6E | 3152 | 6E | 3134 | |
| 5B | 3216 | 7A | 3196 | ||||
| 3095 | 3085 | 7A | 7A | 3218 | 5B | 3200 | |
| 6B | 3353 | 6B | 3338 | ||||
| 7F5 | 3760 | 3768 | 7E | 7E | 3993 | 7E | 3995 |
| 3959 | 3949 | 8E | 8E | 4169 | 8E | 4158 | |
| 7B | 4199 | 7B | 4180 | ||||
| 4181 | 4160 | 8A | 8A | 4259 | 8A | 4257 | |
| 9A | 4291 | 9A | 4282 | ||||
| 8B | 4409 | 8B | 4371 | ||||
| 4202 | 4198 | 9E | 9E | 4486 | 9E | 4454 | |
| 10A | 4537 | 10A | 4503 | ||||
| 7F6 | 9B | 5037 | 9B | 5066 | |||
| 10B | 5038 | 10B | 5067 | ||||
| 5019 | 5015 | 10E | 10E | 5232 | 10E | 5218 | |
| 5149 | 5154 | 11A | 11A | 5473 | 11A | 5447 | |
| 5374 | 5366 | 12A | 12A | 5504 | 12A | 5472 | |
| 11E | 11E | 5589 | 11E | 5560 | |||
| 13A | 11B | 5611 | 11B | 5583 | |||
| 12E | 13A | 5719 | 13A | 5681 | |||
| 12E | 5732 | 12E | 5691 | ||||
| 12B | 5743 | 12B | 5702 | ||||
| 5D0 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 269 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 269 |
14A | 14A | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169 169 |
14A | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 156 |
| 5D1 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 998 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 996 |
15A | 15A | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896 896 |
15A | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 885 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 038 038 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 045 |
13E | 13E | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
13E | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 948 948 |
|
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047 047 |
|||||||
| 5D2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459 459 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 462 462 |
16A | 16A | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 529 529 |
16A | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 512 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 468 468 |
|||||||
| 13B | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535 535 |
13B | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 525 |
||||
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 526 526 |
14E | 14E | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 581 |
14E | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571 571 |
|
| 14B | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
14B | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587 587 |
||||
| 5D3 | 15B | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
15B | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144 |
|||
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307 307 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 313 313 |
15E | 15E | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 163 163 |
15E | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 157 |
|
| 16B | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
16B | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 181 181 |
||||
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 387 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
16E | 16E | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 210 |
16E | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 197 |
|
| 17A | 17A | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214 214 |
17A | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 205 205 |
|||
| 5D4 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 563 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 563 563 |
18A | 18A | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 903 903 |
18A | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 894 894 |
| 19A | 19A | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 912 |
19A | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904 904 |
|||
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 632 632 |
17E | 17E | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917 917 |
17E | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909 909 |
||
| 17B | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951 951 |
17B | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939 939 |
||||
| 18B | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965 965 |
18B | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 953 |
||||
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 654 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 632 632 |
18E | 18E | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 011 011 |
18E | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 995 995 |
|
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 693 693 |
20A | 20A | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043 043 |
20A | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 026 |
|
| 5L6 | 27B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 584 |
27B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 537 537 |
|||
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 094 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
27E | 27E | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598 598 |
27E | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 555 555 |
|
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 125 125 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 093 093 |
29A | 29A | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610 |
29A | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 565 |
|
| 28B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 678 |
28B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608 |
||||
| 29B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682 682 |
29B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618 618 |
||||
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 284 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 285 285 |
28E | 28E | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777 777 |
28E | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 747 |
|
| 30B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 802 802 |
30B | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761 761 |
||||
| 30A | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 827 827 |
30A | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 806 806 |
||||
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 361 361 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 351 351 |
30A | 29E | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 847 847 |
29E | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 808 |
|
| 29E | |||||||
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 401 |
31A | 31A | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911 911 |
31A | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 876 876 |
|
Absolute differences of the ab initio energies of respective levels (vis-a-vis7F0 ground level) between IIEu1 and IIEu2 do not exceed 82 cm−1, and these differences are much lower in most pairs of states. Almost all theoretically determined energy levels with respect to 7F0 ground level in IIEu1 are larger than in IIEu2. Such a relationship does not seem to be accidental if the Eu–N and Eu–O bond lengths are considered. As shown in Section 2.1, the Eu1–N1 bond length in isomer IIEu1 is about 0.039 Å longer than the Eu2–N2 in IIEu2. In the case of Eu–O bond lengths, the opposite situation is observed—the Eu1–O13 bond length is 0.026 Å shorter in IIEu1 than the corresponding Eu2–O22 in IIEu2. The obtained lowering of the energy levels of 4f6 of IIEu2 with respect to the 7F0 level is theoretical evidence that weak donor atoms (such as N) brings about a bathochromic shift of f–f transitions. At the same time, in the case of hard, highly negatively charged O donor atoms, the reverse effect is expected such that the result reinforces the considered energy shift.
2.5 Assignment of experimental energy levels
Comparison of theoretical and experimental energy levels of II allowed us to tentatively assign the irreducible representations of C4 point group to experimental energy levels of II (Table 4).The ordering number preceding the symbol of the irreducible representation is added in order to uniquely identify the states of the same symmetry. It is seen in Table 4 that the ordering of theoretical energy levels is almost the same in the case of IIEu1 and IIEu2, with the exception of two pairs—1B and 3A, energy levels of 7F2 multiplet and 5B and 7A ones of 7F4—where the ordering of levels is interchanged.
As seen from the theoretical results, differences between corresponding CF levels of individual 2S+1LJ multiplets in both isomers are usually only of a few cm−1. For this reason it was not possible to separate CF levels of the individual Eu sites in the experimental spectra of I and II.
In the emission spectrum of II there are two relatively strong spectral lines originating from 5D0 level centered at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 cm−1 and 16
335 cm−1 and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 cm−1 (energy separation 195 cm−1). A closer look at the line at 16
140 cm−1 (energy separation 195 cm−1). A closer look at the line at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 cm−1 (inset in Fig. 5) shows that in fact it consists of two lines separated by 50 cm−1. A similar spectral pattern is observed in the case of 5D0 → 7F2 of I. At the same time, only two distinct lines separated by only 25 cm−1 and 28 cm−1 for IIEu1 and IIEu2, respectively, that originate from 5D0 → 7F2(2E) and 5D0 → 7F2(3A) transitions can be derived from the ab initio calculations. Therefore the symmetry of the CF components of the 7F2 multiplet at 1129 cm−1 and 1179 cm−1 derived from the luminescence spectrum of II were ascribed as 2E and 3A, respectively. Despite of its relatively high intensity, the position of the line centered at 16
140 cm−1 (inset in Fig. 5) shows that in fact it consists of two lines separated by 50 cm−1. A similar spectral pattern is observed in the case of 5D0 → 7F2 of I. At the same time, only two distinct lines separated by only 25 cm−1 and 28 cm−1 for IIEu1 and IIEu2, respectively, that originate from 5D0 → 7F2(2E) and 5D0 → 7F2(3A) transitions can be derived from the ab initio calculations. Therefore the symmetry of the CF components of the 7F2 multiplet at 1129 cm−1 and 1179 cm−1 derived from the luminescence spectrum of II were ascribed as 2E and 3A, respectively. Despite of its relatively high intensity, the position of the line centered at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 cm−1 matches relatively well the energy of the cooperative vibronic transition that couples the electronic 7F0 state with one of the νP–O stretching vibrations of the energy ranging between 900 cm−1 and 1000 cm−1. In this way the number of CF levels is in accordance with that predicted by the theory. Similar vibronic lines were observed in emission spectra of other Eu3+ complexes containing phosphonic groups,9,22 but authors of those papers interpreted the lines as of pure electronic origin.
335 cm−1 matches relatively well the energy of the cooperative vibronic transition that couples the electronic 7F0 state with one of the νP–O stretching vibrations of the energy ranging between 900 cm−1 and 1000 cm−1. In this way the number of CF levels is in accordance with that predicted by the theory. Similar vibronic lines were observed in emission spectra of other Eu3+ complexes containing phosphonic groups,9,22 but authors of those papers interpreted the lines as of pure electronic origin.
2.6 Experimental versus theoretical energies
There are two energy scales that govern the energy level schemes of ground 4fn configurations of Ln3+ ions, namely the energy separations between barycentres of 2S+1LJ multiplets (103–104 cm−1) and the crystal field splittings (101–102 cm−1) of these multiplets.The centres of gravity of experimental (for I and II) and theoretical energy levels 2S+1LJ are listed and compared in Table 5. The table shows that calculated energies of states are overestimated in the case of majority 7FJ levels with the one exception of the 7F2 energy level, for which the experimental energy is larger than the theoretical counterpart. The absolute differences between experimental and theoretical energies of 7FJ states (hereinafter referred to as Δ) do not exceed 280 cm−1.
| Experimental | Calculations | Δ I -calc | Δ II -calc | ||
|---|---|---|---|---|---|
| I | II | I and IIa | |||
| a Theoretical values are averaged over the SA-CASSCF/MS-CASPT2/RASSI-SO energies obtained for both sites IIEu1 and IIEu2. | |||||
| 7F1 | 378 | 374 | 409 | 31 | 35 |
| 7F2 | 1153 | 1146 | 1094 | –59 | –52 |
| 7F3 | 1826 | 1826 | 2102 | 276 | 276 |
| 7F4 | 2956 | 2910 | 3085 | 129 | 175 |
| 7F5 | 4004 | 3999 | 4216 | 212 | 217 |
| 7F6 | — | — | 5464 | — | — |
| 5D0 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 269 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 269 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 163 163 |
894 | 894 |
| 5D1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028 028 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 029 029 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933 933 |
–95 | –96 |
| 5D2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 505 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 505 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 558 |
–947 | –947 |
| 5D3 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 372 372 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 210 |
–1150 | –1162 |
| 5D4 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 953 |
–686 | –648 |
| 5L6 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195 195 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214 214 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 737 737 |
3542 | 3523 |
Direct comparison of theoretical energies for the excited states with respect to the 7F0 ground level with experimental counterparts shows that they may differ even by thousands of cm−1, reaching 3500 cm−1 for the 5L6 level. Such discrepancies are expected in the case of many-electron systems in which electron correlation and relativistic effects are important. Theoretical studies for the CaF2:Pr3+ case have shown that discrepancies in energy calculations of free lanthanide ions are transferred to more complex systems containing lanthanide ions.23 To illustrate this problem we have performed similar CASSCF/CASPT2/RASSI-SO calculations for the Eu3+ free ion that were compared with energy levels of the experimental Eu3+ aqua ion24 as presented in Table 6. Energy levels of Eu3+ free ion calculated within the Dirac–Fock multiconfiguration interaction approach (MCDF-CI)25 are presented in Table 6. More recently the ab initio calculations within fully relativistic Kramers pairs configuration interaction method for free Eu3+ ions as well as for aqua ions were reported.26
| 2S+1LJ | Energy/cm−1 | ||||
|---|---|---|---|---|---|
| Experimental24 | MCDF-CI25 | ΔE | This work | ΔE | |
| 7F1 | 360 | 347 | −13 | 395 | 35 |
| 7F2 | 1020 | 965 | −55 | 1115 | 95 |
| 7F3 | 1887 | 1775 | −112 | 2049 | 162 |
| 7F4 | 2865 | 2712 | −153 | 3095 | 230 |
| 7F5 | 3908 | 3735 | −173 | 4203 | 295 |
| 7F6 | 4980 | 4810 | −170 | 5387 | 407 |
| 5D0 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 277 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 857 |
1580 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 733 |
456 |
| 5D1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028 028 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
1476 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 499 499 |
−529 |
| 5D2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 519 519 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896 896 |
1377 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119 119 |
−1400 |
| 5D3 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 408 408 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728 728 |
1320 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 744 744 |
−1664 |
| 5L6 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 178 |
2778 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405 405 |
3005 |
| 5D4 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 632 632 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
1503 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545 545 |
−1087 |
The experimental energy levels of the Eu3+ free ion are not known to the authors. At the same time the aqua ion seems to be the system reasonably “similar” to the free ion; for example, it is interesting to note that the experimentally observed Eu3+ aqua ion energy levels24 are very close to those interpolated to approach the Eu3+ free ion ones.27 Comparison of the performance of the present theoretical approach with the benchmark MCDF-CI calculations presented in Table 6 shows that the discrepancies with respect to the experiment of the order of thousands of cm−1 is what one can expect from ab initio calculations performed for the Eu3+ ion. Furthermore, similarities of the energy differences between the CASSCF/CASPT2/RASSI-SO calculations and experimental counterparts presented in Tables 5 and 6 support the conclusion that the main deficiencies in the proper theoretical description of f-electron systems are due to insufficient accounting for correlation effects within the lanthanide ion. For example, detailed analysis of radial correlation effects in free lanthanide ions based on ab initio calculations was performed by Barandiaran and Seijo.28 Their study indicated that the most probable improvement of the description of energies for excited states of heavy lanthanide ions—for example, of Eu3+—was obtained by inclusion of 5f orbitals into the active space. However, such enlargement of the active space in the case of considered (large) Eu–DOTP complexes is not tractable with the authors' available computational resources.
The other energy scale is associated with splitting of the 2S+1LJ energy levels in the crystal field potential. Absolute values of differences between the theoretical and experimental crystal field splittings—that is, splittings of 2S+1LJ levels—do not exceed the value of 220 cm−1; this maximum discrepancy is observed within 5L6 multiplets and can be derived from Table 4. However, it should not be interpreted as the crystal field splittings being much better described within CASSCF/CASPT2/RASSI-SO approach than positions of levels with respect to the energy of the ground state 7F0. Rather, it is attributed to the fact that differences between theoretical and experimental energies follow the scale of considered energies. Namely, upon considering relative energy differences, then it would turn out that the relative differences are larger in the case of crystal field splittings.
2.7 5D0 → 7F0 transition energy
Among the f–f transitions observed in the electronic spectra of Eu3+, the 7F0 ↔ 5D0 transition is the most suitable for a study of Eu–ligand interaction. The ground 7F0 and the excited 5D0 states are non-degenerated and do not split in the crystal field of any symmetry. Therefore, the number of components observed in the spectrum of this transition indicates the minimal number of chemically distinct environments of the Eu3+ ion.The energy of the 7F0 → 5D0 transition is also used to study the nephelauxetic effect of europium compounds. This effect is probably connected with the covalent contribution to the bonding between the Eu3+ ion and the ligands, metal–ligand distances, coordination numbers and the total charge and acid base properties of ligands bonded with Eu3+.29 However, there is no simple correlation between the energy of the 7F0 → 5D0 transition and these physical quantities.30 Bathochromic shifts of the 7F0 → 5D0 band are very often explained as resulting from the change in the interelectronic repulsion Slater Fk parameters of Eu3+ ion in the ligand field with respect to those for the free ion  .31 In general in the case of the rare earth complexes for which the semi-empirical values of the Fk parameters of the free ions are not known, the nephelauxetic ratio is approximated as
.31 In general in the case of the rare earth complexes for which the semi-empirical values of the Fk parameters of the free ions are not known, the nephelauxetic ratio is approximated as 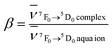 , where
, where 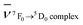 and
and 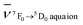 are the wavenumbers of the 7F0 → 5D0 bands for the complex and the aqua ion, respectively.
are the wavenumbers of the 7F0 → 5D0 bands for the complex and the aqua ion, respectively.
Present work allows for the direct calculation of the nephelauxetic ratios. All the nephelauxetic ratios β calculated using the formula with Fk radial integrals (obtained within the ab initio approach) are equal to about 0.99. Radial 4f functions used for calculating Slater radial integrals were extracted from the molecular orbitals of IIEu and Eu3+ free ions obtained within the CASSCF method. Details of calculations for radial integrals based on molecular orbitals will be presented elsewhere.32 The result that the values of β are close to unity supports the ionic character of Eu–L interaction. Furthermore, the nephelauxetic ratios β are smaller than unity, which is expected from the point of view of the nature of the nephelauxetic effect.
It is worth stressing that the energy of the 7F0 → 5D0 transition of [Eu(DOTP)]5− (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 cm−1) and Eu3+ aqua ion (17
269 cm−1) and Eu3+ aqua ion (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 cm−1)24 differs by 6 cm−1 only. Usually, for eight-coordinated Eu3+ complexes, the shift of the 7F0 → 5D0 band to the lower energies in relation to the aqua ion is much larger. The opposite relation is obtained in the CASSCF/CASPT2/RASSI-SO approach, where the energy of the 5D0 level with respect to 7F0 ground state of free Eu3+, 17
277 cm−1)24 differs by 6 cm−1 only. Usually, for eight-coordinated Eu3+ complexes, the shift of the 7F0 → 5D0 band to the lower energies in relation to the aqua ion is much larger. The opposite relation is obtained in the CASSCF/CASPT2/RASSI-SO approach, where the energy of the 5D0 level with respect to 7F0 ground state of free Eu3+, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 cm−1, is smaller than the 7F0 → 5D0 transition energies obtained for IIEu1 and IIEu2, 18
733 cm−1, is smaller than the 7F0 → 5D0 transition energies obtained for IIEu1 and IIEu2, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169 cm−1 and 18
169 cm−1 and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 cm−1, respectively. At first glance it may be considered as being in contradiction to the result of the ab initio calculations that β < 1. However, the fact that the theoretical free ion 7F0 → 5D0 transition energy is smaller than that of the Eu–DOTP complex probably can be ascribed to the effect of the crystal-field upon the lowest 7FJ levels.33 Unfortunately, the preliminary analysis within the crystal field approach has not succeeded in clarifying this problem.
156 cm−1, respectively. At first glance it may be considered as being in contradiction to the result of the ab initio calculations that β < 1. However, the fact that the theoretical free ion 7F0 → 5D0 transition energy is smaller than that of the Eu–DOTP complex probably can be ascribed to the effect of the crystal-field upon the lowest 7FJ levels.33 Unfortunately, the preliminary analysis within the crystal field approach has not succeeded in clarifying this problem.
2.8 Conclusions
Structural, spectroscopic and theoretical studies of two monocrystals, namely [C(NH2)3]5[Eu(DOTP)]·12.5H2O and K5[Eu(DOTP)]·11H2O, were performed. Both compounds contain [Eu(DOTP)]5− complex in the form of minor m′ (Λ(λλλλ) and Δ(δδδδ)) isomers. The [DOTP]8− ligand is bonded to the Eu3+ cation via four oxygen and four nitrogen atoms, thereby filling eight coordination places of Eu3+ cations. Symmetry of the [Eu(DOTP)]5− complexes in the II crystal are of C4, whereas their structures are slightly disrupted in the case of I crystal resulting in C1 symmetry. It is found that the closest outer sphere water molecule is 4.374(20) Å and 4.105(107) Å away from the Eu3+ in I and II, respectively. This weak interaction of outer-sphere water molecules with [Ln(DOTP)]5− anions, is probably one of the reasons for high relaxivity of the [Gd(DOTP)]5− system in MRI.Using available spectroscopic techniques, it was not possible to distinguish the spectral lines coming from two Eu sites existing in both crystals. Therefore, results of ab initio calculations allowed us to assign the spectral lines tentatively to particular crystal field components of the energy levels for the 4f6 configuration of the Eu3+ ion.
Differences between theoretical and experimental values of the energies of Eu–DOTP complexes can reach about 3500 cm−1, as observed in the case of 5L6 energy levels. At the same time the structure of Eu–DOTP energy levels is retained strictly up to 5D3 energy levels. Such calculations are of general interest because it is possible to conclude that the correlation between structure and spectroscopic features is by its very nature discrete for the case of lanthanide systems.
The correlation between Eu–ligand bond lengths and energies of excited energy levels is obtained. It was shown that weak donor atoms (such as N) bring about the bathochromic shift of f–f transitions and reverse hard, highly negatively charged O donor atoms reinforcing the energy shift.
Discrepancies between theoretical and experimental values of energies of states for the 4f6 configuration of Eu3+ ion can be mainly attributed to treatment of correlation effects in the Eu–DOTP complex in the present ab initio approach. Considering the details of CASSCF/CASPT2/RASSI-SO calculations and results of other ab initio calculations,24 it may be concluded that theoretical energies are expected to be improved via inclusion of the “double f-shell” into the CASSCF/CASPT2/RASSI-SO approach, which means that the radial correlation between 4f and 5f shells is treated in a non-perturbative way. In the present work this correlation effect was taken into account perturbatively within the CASPT2 method.
To summarize, the experimental and theoretical properties of Eu–DOTP complex were studied and discussed in detail. Although there are some discrepancies between experimental and theoretical results, the presented results enabled us to calculate the energies of 4f6 configuration of Eu3+ in molecular [EuDOTP]5− complex, for the first time. It is worth noting that the energies of the lower lying 7FJ states are relatively well described.
The energies of the 7FJ states are particularly important from the application point of view of Eu3+ compounds as luminescent materials, since the emission spectra of Eu3+ usually consist of 5D0 → 7FJ lines. Another important aspect of the [EuDOTP]5− spectra is connected with the f–f transition intensities, therefore our future study will be focused on this problem.34
3. Experimental section
3.1 Preparation of crystals
Two samples each of which contained a suspension of Eu2O3 (0.250 g, Stanford Materials) and H8DOTP (0.75 g, Macrocyclics) in 25 ml of H2O were heated at ca. 80 °C. Next, a small portion of [C(NH2)3]2CO3 was added to the first one and KOH to the other until the precipitate was dissolved. The final pH of solutions was 7.5. Solutions were filtrated and left for crystallization. Colourless crystals of [C(NH2)3]5[Eu(DOTP)]·13H2O and K5[Eu(DOTP)]·11H2O were formed during very slow evaporation of water after s few months.3.2 X-ray crystal analysis
An appropriate crystal was cut from a larger one and mounted on a Kuma KM4 diffractometer equipped with a CCD counter. The collected data were corrected for polarization, Lorentz and absorption, the latter calculated from the crystal habits captured from photo scans. The positions of Eu were found from Patterson maps and the remainder of non-H atoms from difference Fourier maps. Positions of the C- and N-bonded hydrogen atoms were calculated geometrically. It was found that three water molecules and two guanidinium cations in I, and 1.5 H2O molecules in II were disordered. The final refinements were anisotropic for all ordered non-H atoms, whereas the disordered C, N and O atoms were treated isotropically. The refinement was full matrix with all non-H atoms anisotropic. All computations were performed using SHELXS97 and SHELXL97 programs.35,36 Molecular graphics were prepared with XP–Interactive Molecular Graphics.37[C(NH2)3]5[Eu(DOTP)]·12.5H2O (I) – C17H79EuN19O24.50P4, M = 1184.52, monoclinic, space group P2/n, Z = 8, a = 26.576(2), b = 14.451(2), c = 27.285(2) Å, β = 111.21(4)°, V = 9768.2(8) Å3, μ = 1.51 mm−1, Dc = 1.656 g cm−3, F(000) = 5064, crystal size = 0.43 × 0.23 × 0.21 mm, θ = 3–29°, index ranges: −35 ≤ h ≤ 33, −19 ≤ k ≤ 19, −30 ≤ l ≤ 36, reflections collected/unique = 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186/23
186/23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 (Rint = 0.0400). Final R indices [I > 2σ(I)] R(F) = 0.0518, Rw(F2) = 0.1507 and R(F) = 0.0628, Rw(F2) = 0.1627 (all data). Data completeness to 2θ = 28.78°, 99.06%. Largest differential peak and hole 4.337 and −2.405 e Å−3. CCDC 1484638.
210 (Rint = 0.0400). Final R indices [I > 2σ(I)] R(F) = 0.0518, Rw(F2) = 0.1507 and R(F) = 0.0628, Rw(F2) = 0.1627 (all data). Data completeness to 2θ = 28.78°, 99.06%. Largest differential peak and hole 4.337 and −2.405 e Å−3. CCDC 1484638.
K5[Eu(DOTP)]·11H2O (II) – C12H46EuK5N4O23P4, M = 1063.67, tetragonal, space group P4cc, Z = 4, a = 12.5231(10), b = 12.5231(10), c = 24.8781(4) Å, V = 3901.58(8) Å3, μ = 2.39 mm−1, Dc = 1.849 g cm−3, F(000) = 2192, crystal size = 0.24 × 0.13 × 0.09 mm, θ = 3–29° index ranges: −15 ≤ h ≤ 16, −15 ≤ k ≤ 16, −33 ≤ l ≤ 33, reflections collected/unique = 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178/4869 (Rint = 0.0368). Final R indices [I > 2σ(I)] R(F) = 0.0447, Rw(F2) = 0.1340 and R(F) = 0.0532, Rw(F2) = 0.1399 (all data). Data completeness to 2θ = 28.74°, 97.5%. Largest differential peak and hole 1.960 and −0.855 e Å−3. CCDC 1484639.
178/4869 (Rint = 0.0368). Final R indices [I > 2σ(I)] R(F) = 0.0447, Rw(F2) = 0.1340 and R(F) = 0.0532, Rw(F2) = 0.1399 (all data). Data completeness to 2θ = 28.74°, 97.5%. Largest differential peak and hole 1.960 and −0.855 e Å−3. CCDC 1484639.
3.3 Spectroscopic analysis
IR spectra were recorded with a Bruker IF S66 spectrometer. The spectra of crystalline complexes in KBr pellets and nujol suspension were recorded in the range of 50–4000 cm−1. Electronic absorption spectra were recorded with a Cary 500 UV/Vis/NIR spectrophotometer. The corrected emission spectra were recorded with an Edinburgh Instruments FLS 920 spectrofluorometer.3.4 Theoretical calculations
Vibrational frequencies of {K4[Eu(DOTP)]}− clusters representing IIEu1 and IIEu2 sites were obtained via the DFT approach for the B3LYP exchange–correlation functional. The Eu ion was represented by the quasi-relativistic effective core potential (ECP) created by Dolg et al.,38 along with the valence basis set [5s4p3d]-GTO. Remaining atoms, C, N, O, P, K, H, were represented by the 6-31G* basis set. Both structures of the {K4[Eu(DOTP)]}− cluster were optimized (in vacuum) and harmonic vibrational frequencies were calculated for their optimized structures. Cartesian coordinates of the optimized geometries of {K4[Eu(DOTP)]}− cluster are listed in Table S3 of the ESI.†Energy levels were obtained via ab initio calculations based on the multireference wave function approach. These single-point calculations were performed for the two clusters {K4[Eu(DOTP)]}− representing two different Eu sites of K5[Eu(DOTP)]·11H2O crystal. Ab initio model potentials (AIMP) were used to represent the [Kr]-core of Eu ion closed shells along with the valence basis set of Gaussian-type orbitals (14s10p10d8f3g) contracted to obtain the [6s5p6d4f3g] basis set.39 For the remaining atoms of the considered system, C, N, O, P, K, the AIMP effective core potentials along with valence Gaussian-type basis sets follow:40
• O: [He]-core, (5s6p1d)/[2s4p1d] basis set
• N: [He]-core, (5s5p1d)/[2s3p1d] basis set
• P: [Ne]-core, (7s6p1d)/[2s3p1d] basis set
• C: [He]-core, (5s5p1d)/[2s3p1d] basis set
• K: [Mg]-core, (9s7p)/[2s3p] basis set
In the case of H atoms, the 6-31G* basis set was used.41 All effective core potentials account for mass-velocity and Darwin relativistic corrections by means of Cowan–Griffin approach.42 The calculations were performed within C2 symmetry with the MOLCAS package.43
The open-shell character of the Eu3+ ion ([Xe]4f6 configuration) causes strong non-dynamic correlations effects. In this work the non-dynamic effects of electron correlation were taken into account within complete active space self-consistent field method (CASSCF),18 where the active space was set by distributing six electrons onto one molecular orbital (MO) of a symmetry, two MOs of b symmetry and four MOs of e symmetry; all seven MOs defining the active space were predominantly of the Eu3+ ion 4f character. The molecular orbitals were optimized within separate state average (SA) CASSCF calculations minimizing the average energy of the following sets of spin-free states: one 7A and two 7B states; four 7E; 19 5A and 20 5B states; and 38 5E states. In this way the following states of 4f6 for the Eu3+ ion were taken into account: 7F, 5D, 5L, 5G, 5H, 5F, 5I and 5K. The effects of dynamical electron correlation were taken into account via second-order correction to the energy obtained within complete active space perturbation theory CASPT2.19,20 In this work the multistate (MS) CASPT219,20 approach was used for the same sets of states as in the case of SA-CASSCF calculations. IPEA shift was set to zero.44 In order to avoid the effect of so-called weak intruder states, the imaginary shift of 0.1 a.u. value was applied. Since the main interest of the present work is focused on low-lying states of the 4f6 configuration of the Eu3+ ion, accounting for dynamical effects is limited to the central ion by means of the AFREeze option in the MOLCAS “caspt2” program, where inactive molecular orbitals with density on the Eu ion smaller than 0.1 were kept frozen during the MS-CASPT2 calculations. As a result, only three occupied orbitals localized on oxygens non-bonded to the Eu ion were correlated explicitly by means of the CASPT2 method. Cholesky decomposition45 was performed for the matrix of the electron repulsion integrals with the threshold 10−8 Hartree, and consequently used thoroughout each step of calculations. In fact, just-mentioned approximations made these calculations tractable considering the particular choice of active space and accessible computational resources. Spin–orbit interaction was taken into account via the RASSI-SO approach,21 where the matrix of the Hamiltonian including spin–orbit operator (coming from Douglas–Kroll Hamiltonian) over all considered above, MS-CASPT2 spin-free mixed states were constructed and diagonalized.
Acknowledgements
This work was supported by Wrocław University (grant 2178/W/WCH/09). A. K. acknowledges financial support from the Polish Ministry of Science and Higher Education (research project N N202 187636). A. K. also thanks Prof. Marek Krośnicki from the Institute of Theoretical Physics and Astrophysics, Gdańsk University, Poland, and Prof. Zoila Barandiaran and Prof. Luis Seijo from the Departamento de Química, Universidad Autónoma de Madrid, Spain, for discussions concerning calculations performed within the wave function-based multireference methods of quantum chemistry. Finally, computational time at the computing center of Institute of Theoretical Physics and Astrophysics, Gdańsk University, Poland, is acknowledged.References
-
A. Merbach, L. Helm and E. Toth, The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, John Wiley & Sons, Ltd, 2013 Search PubMed
.
-
(a) A. D. Sherry, J. Ren, J. Huskens, E. Brücher, É. Tóth, C. F. C. G. Geraldes, M. M. C. A. Castro and W. P. Cacheris, Inorg. Chem., 1996, 35, 4604–4612 CrossRef CAS
; (b) P. M. Winter and N. Bansal, Magn. Reson. Med., 2001, 45, 436–442 CrossRef CAS PubMed
.
-
(a) E. J. New, D. Parker, D. G. Smith and J. W. Walton, Curr. Opin. Chem. Biol., 2010, 14, 238–246 CrossRef CAS PubMed
; (b) J. C. G. Bünzli and S. V. Eliseeva, Chem. Sci., 2013, 4, 1939–1949 RSC
; (c) S. J. Butler, M. Delbianco, L. Lamarque, B. K. McMahon, E. R. Neil, R. Pal, D. Parker, J. W. Walton and J. M. Zwier, Dalton Trans., 2015, 4791–4803 RSC
; (d) J. C. Bünzli, J. Lumin., 2016, 170, 866–878 CrossRef
.
-
(a) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC
; (b) J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556–13567 RSC
; (c) G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed
.
-
(a) L. Smentek, B. A. Hess, Jr., J. P. Cross, H. C. Manning and D. J. Bornhop, J. Chem. Phys., 2005, 123, 244302 CrossRef PubMed
; (b) B. A. Hess, Jr, A. Kędziorski, L. Smentek and D. J. Bornhop, J. Phys. Chem. A, 2008, 112, 2397–2407 CrossRef PubMed
; (c) M. Purgel, Z. Baranyai, A. de Blas, T. Rodríguez-Blas, I. Bányai, C. Platas-Iglesias and I. Tóth, Inorg. Chem., 2010, 49, 4370–4382 CrossRef CAS PubMed
; (d) L. Smentek, J. Phys.: Condens. Matter, 2011, 23, 143202 CrossRef PubMed
; (e) C. Platas-Iglesias, A. Roca-Sabio, M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas and T. Rodríguez-Blas, Curr. Inorg. Chem., 2011, 1, 91–116 CrossRef CAS
; (f) A. Roca-Sabio, M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas and C. Platas-Iglesias, Comp. Theor. Chem., 2012, 999, 93–104 CrossRef CAS
; (g) C. Platas-Iglesias, Eur. J. Inorg. Chem., 2012, 2023–2033 CrossRef CAS
; (h) M. Regueiro-Figueroa, D. Esteban-Gomez, A. de Blas, T. Rodri guez-Blas and C. Platas-Iglesias, Chem. – Eur. J., 2014, 20, 3974–3981 CrossRef CAS PubMed
.
-
C. Görller-Walrand and K. Binnemans, in Handbook of the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, Jr. and L. Eyring, Elsevier, Amsterdam, 1996, vol. 23 Search PubMed
.
- F. Avecilla, J. A. Peters and C. F. G. C. Geraldes, Eur. J. Inorg. Chem., 2003, 4179–4186 CrossRef CAS
.
-
E. F. Paulus, P. Juretschke and J. Lang, Jahrestag der Deutschen Gesellschaft für Kristallographie, Darmstadt, 1995 Search PubMed
.
-
(a) A. Mondry and R. Janicki, Dalton Trans., 2006, 4702–4710 RSC
; (b) R. Janicki and A. Mondry, Polyhedron, 2008, 27, 1942–1946 CrossRef CAS
; (c) R. Janicki and A. Mondry, Eur. J. Inorg. Chem., 2013, 3429–3438 CrossRef CAS
; (d) R. Janicki, M. Monteil, M. Lecouvey and A. Mondry, Opt. Mater., 2013, 36, 259–264 CrossRef CAS
.
- J. Gałęzowska, R. Janicki, A. Mondry, R. Burgada, T. Bailly, M. Lecouvey and H. Kozłowski, Dalton Trans., 2006, 4384–4394 RSC
.
-
(a) M. R. Spirlet, J. Rebizant, J. F. Desreux and M. F. Loncin, Inorg. Chem., 1984, 23, 359–363 CrossRef CAS
; (b) F. Benetollo, G. Bombieri, S. Aime and M. Botta, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 353–356 Search PubMed
.
- K. M. Payne, E. J. Valente, S. Aime, M. Botta and M. Woods, Chem. Commun., 2013, 49, 2320–2322 RSC
.
-
(a) S. Aime, M. Botta, E. Terreno, P. L. Anelli and F. Uggeri, Magn. Reson. Med., 1993, 30, 583–591 CrossRef CAS PubMed
; (b) R. A. Carvalhoa, J. A. Petersc and C. F. G. C. Geraldesa, Inorg. Chim. Acta, 1997, 262, 167–176 CrossRef
; (c) Z. Kotková, G. A. Pereira, K. Djanashvili, J. Kotek, J. Rudovský, P. Hermann, L. Vander Elst, R. N. Muller, C. F. G. C. Geraldes, I. Lukes and J. A. Peters, Eur. J. Inorg. Chem., 2009, 119–136 CrossRef
; (d) G. A. Pereira, L. Ball, A. D. Sherry, J. A. Peters and C. F. G. C. Geraldes, Helv. Chim. Acta, 2009, 92, 2532–2551 CrossRef CAS
.
- B. R. Judd, Phys. Rev., 1962, 127, 750–761 CrossRef CAS
.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511–519 CrossRef CAS
.
- P. A. Tanner, Chem. Soc. Rev., 2013, 42, 5090–5101 RSC
.
- A. Kędziorski and L. Smentek, J. Lumin., 2007, 127, 552–560 CrossRef
.
-
(a) B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS
; (b) P. E. M. Siegbahn, A. Heiberg, B. O. Roos and B. Levy, Phys. Scr., 1980, 21, 323–327 CrossRef CAS
; (c) P. E. M. Siegbahn, A. Heiberg, J. Almlöf and B. O. Roos, J. Chem. Phys., 1981, 74, 2384–2396 CrossRef
.
-
(a) K. Andersson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS
; (b) K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS
.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS
.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS
.
-
(a) F. Serpaggi, G. FeHrey and E. Antic-Fidancev, J. Solid State Chem., 1999, 148, 347–352 CrossRef CAS
; (b) J.-G. Mao, Coord. Chem. Rev., 2007, 251, 1493–1520 CrossRef CAS
.
- M. Krośnicki, A. Kędziorski, L. Seijo and Z. Barandiarán, J. Phys. Chem. A, 2014, 118, 358–368 CrossRef PubMed
.
- W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4450–4455 CrossRef CAS
.
- M. Seth, K. G. Dyall, R. Shepard and A. Wagner, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 2383–2406 CrossRef CAS
.
- C. Holzer, A. M. Wernbacher, J. M. Senekowitsch, K. Gatterer and A. M. Kelterer, J. Phys. Chem. A, 2014, 118, 1149–11511 CrossRef PubMed
.
- A. Kramida, Yu. Ralchenko, J. Reader and NIST ASD Team (2015). NIST Atomic Spectra Database (ver. 5.3), [Online]. Available: http://physics.nist.gov/asd [2016, April 28]. National Institute of Standards and Technology, Gaithersburg, MD.
- Z. Barandiarán and L. Seijo, J. Chem. Phys., 2013, 138, 074102 CrossRef PubMed
.
-
(a) M. Albin and W. D. Horrocks Jr., Inorg. Chem., 1985, 24, 895–900 CrossRef CAS
; (b) S. T. Frey and W. D. Horrocks Jr., Inorg. Chim. Acta, 1995, 229, 383–390 CrossRef CAS
; (c) G. R. Choppin and Z. M. Wang, Inorg. Chem., 1997, 36, 249–252 CrossRef CAS
.
-
(a) H. D. Amberger, H. Reddmann and C. Hagen, Inorg. Chim. Acta, 2005, 358, 3745–3752 CrossRef CAS
; (b) P. A. Tanner, Y. Y. Yeung and L. Ning, J. Phys. Chem., 2013, 117, 2771–2781 CrossRef CAS PubMed
.
- S. P. Sinha and H.-H. Schmidtke, Mol. Phys., 1965, 10, 7–11 CrossRef CAS
.
- A. Kędziorski, in preparation.
- P. A. Tanner, Y. Y. Yeung and L. Ning, J. Phys. Chem. A, 2013, 117, 2771–2781 CrossRef CAS PubMed
.
- R. Janicki, A. Kędziorski and A. Mondry, in preparation.
-
G. M. Sheldrick, SHELXS-97, program for structure solution, University of Göttingen, 1997 Search PubMed
.
-
G. M. Sheldrick, SHELXL-97, program for structure refinement, University of Göttingen, 1997 Search PubMed
.
- 40 XP-Interactive Molecular Graphics, v. 5.1–Bruker Analytical X-ray Systems 1998.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173 CrossRef CAS
.
- L. Seijo, Z. Barandiarán and B. Ordejon, Mol. Phys., 2003, 101, 73 CrossRef CAS
.
- Z. Barandiarán and L. Seijo, Can. J. Chem., 1992, 70, 409 CrossRef
.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef CAS
.
- R. D. Cowan and D. C. Griffin, J. Opt. Soc. Am., 1976, 66, 1010 CrossRef CAS
.
-
(a) F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.-Å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224 CrossRef CAS PubMed
; (b) V. Veryazov, P.-O. Widmark, L. Serrano-Andres, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626 CrossRef CAS
; (c) G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrády and L. Seijo, Comput. Mater. Sci., 2003, 28, 222 CrossRef
.
- G. Ghigo, B. O. Roos and P. Å. Malmqvist., Chem. Phys. Lett., 2004, 396, 142 CrossRef CAS
.
-
F. Aquilante, L. Boman, J. Boström, H. Koch, R. Lindh, A. S. de Merás and T. B. Pedersen in Challenges and Advances in Computational Chemistry and Physics, ed. R. Zalesny, M. G. Papadopoulos, Mezey, G. Paul and J. Leszczynski, Springer Science + Business Media B.V., 2011, vol. 13, pp. 301–343 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1. The assignments of the selected vibrations in IR spectra of I and II, Table S2. Theoretical energies (in cm−1) 2S+1LJ states of IIEu1 and IIEu2 obtained within CASSCF/CASPT2/RASSI calculations. Table S3. Cartesian coordinates (in Å) of the DFT optimized geometry of {K4[Eu(DOTP)]}− cluster representing IEu1 and IIEu1 sites. CCDC 1484638 and 1484639. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cp05284c |
| This journal is © the Owner Societies 2016 |