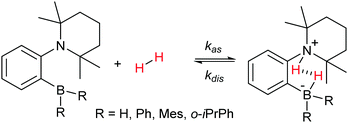Open Access Article
Open Access ArticleNuclear spin hyperpolarization with ansa-aminoboranes: a metal-free perspective for parahydrogen-induced polarization†
Vladimir V.
Zhivonitko
*ab,
Kristina
Sorochkina
c,
Konstantin
Chernichenko
c,
Bianka
Kótai
d,
Tamás
Földes
d,
Imre
Pápai
d,
Ville-Veikko
Telkki
e,
Timo
Repo
c and
Igor
Koptyug
ab
aLaboratory of Magnetic Resonance Microimaging, International Tomography Center SB RAS, Institutskaya St. 3A, 630090 Novosibirsk, Russia. E-mail: v_zhivonitko@tomo.nsc.ru
bDepartment of Natural Sciences, Novosibirsk State University, Pirogova St. 2, 630090 Novosibirsk, Russia
cDepartment of Chemistry, University of Helsinki, A. I. Virtasen Aukio 1, 00014 Helsinki, Finland
dResearch Centre for Natural Sciences, Hungarian Academy of Sciences, Magyar Tudósok Körútja 2, H-1117 Budapest, Hungary
eNMR Research Unit, University of Oulu, P.O. Box 3000, 90014 Oulu, Finland
First published on 6th September 2016
Abstract
The parahydrogen-induced polarization (PHIP) phenomenon, observed when parahydrogen is used in H2 addition processes, provides a means for substantial NMR signal enhancements and mechanistic studies of chemical reactions. Commonly, noble metal complexes are used for parahydrogen activation, whereas metal-free activation is rare. Herein, we report a series of unimolecular metal-free frustrated Lewis pairs based on an ansa-aminoborane (AAB) moiety in the context of PHIP. These molecules, which have a “molecular tweezers” structure, differ in their substituents at the boryl site (–H, –Ph, –o-iPr-Ph, and –Mes). PHIP effects were observed for all the AABs after exposing their solutions to parahydrogen in a wide temperature range, and experimental measurements of their kinetic and thermodynamic parameters were performed. A theoretical analysis of their nuclear spin polarization effects is presented, and the roles of chemical exchange, chemical equilibrium and spin dynamics are discussed in terms of the key dimensionless parameters. The analysis allowed us to formulate the prerequisites for achieving strong polarization effects with AAB molecules, which can be applied for further design of efficient metal-free tweezers-like molecules for PHIP. Mechanistic (chemical and physical) aspects of the observed effects are discussed in detail. In addition, we performed quantum chemical calculations, which confirmed that the J-coupling between the parahydrogen-originated protons in AAB–H2 molecules is mediated through dihydrogen bonding.
1. Introduction
The high reactivity of frustrated Lewis pairs (FLPs) was discovered only recently,1,2 inspiring numerous brilliant studies in this field over the last few years.3–12 Many small molecules have been shown to be activated by FLPs,6,12 including dihydrogen (H2). In addition to the apparent applications in catalysis,13–24 addition of H2 to FLPs may be useful for hyperpolarizing nuclear spins when parahydrogen, one of the nuclear spin isomers of H2, is used as a reagent. Due to the symmetry of the H2 molecule, the correlation of its nuclear spins survives for a long time and can be transformed into observable nuclear spin hyperpolarization upon a chemical transformation of H2 molecules if this transformation causes the two hydrogens to be magnetically inequivalent. At the same time, the H2 activation mechanism must be pairwise, meaning that both hydrogens should follow each other throughout all elementary reaction steps and end up in the same product molecule. Because of this prerequisite, only certain catalytic systems are applicable in this hyperpolarization technique, which is referred to in the literature as PASADENA,25 ALTADENA,26 or, generally, parahydrogen-induced polarization (PHIP).27 To date, PHIP mediated by FLPs was demonstrated only in a few examples as a proof-of-principle.28,29 In particular, it has been shown that the reversibility of the H2 interaction with FLPs allows one to achieve reproducible nuclear spin hyperpolarization each time the parahydrogen flux is introduced to a QCAT ansa-aminoborane solution (Scheme 1), imitating a kind of nuclear spin polarization “pumping”.28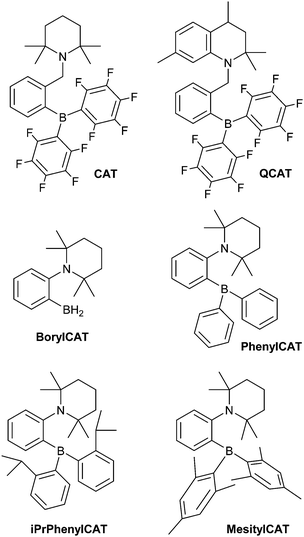 | ||
| Scheme 1 ansa-Aminoboranes which have been shown to enable PHIP observation in previous work28 (CAT and QCAT) and herein (BorylCAT, PhenylCAT, iPrPhenylCAT and MesitylCAT). | ||
In addition to the production of nuclear spin hyperpolarization for substantial signal enhancement in NMR and MRI, PHIP can shed light on the mechanistic features of molecular activation. Particularly, parahydrogen provides a unique type of labeling which is sensitive to the pairwise mechanism. At the same time, progress in understanding the involved mechanisms can provide a means for the development of new efficient FLP systems for PHIP. In particular, determination and optimization of the kinetic parameters of the activation are also crucial for maximizing PHIP. Unlike the spin correlation in parahydrogen, the lifetime of nuclear spin polarization in FLP–H2 adducts is relatively short, which strongly diminishes the achievable polarization levels if the kinetics of the hydrogen addition is slow. This actually means that high addition rates compared to the spin relaxation rates are favorable for the observation of high polarization levels.
Recently, we reported that ansa-aminoboranes (AABs), N–B based FLPs, demonstrate PHIP effects, indicating that these compounds possess the required properties.28 The chelating arrangement of the N and B reactive centers in AABs favors rapid H2 addition dynamics. Importantly, the intrinsic feature of AABs is the presence of a dihydrogen NH⋯HB bond in the AAB–H2 adducts. This bond is evident from X-ray and neutron diffraction studies30 and from computational results. Thus, AABs are referred to in the literature as “molecular tweezers” that stretch, but do not completely split, H2 molecules. As shown below, the dihydrogen bond enables the observation of PHIP. Apparently, with further development, AABs may have great prospects in PHIP production. Namely, an appropriate molecular design could allow one to use close-to-ambient temperatures and, as an ultimate goal, to design moisture-tolerant AABs for in vivo MRI applications. Fundamentally, molecular activation with these compounds is of exceptional interest for metal-free catalysis as a new area with major potential for significant future advances.
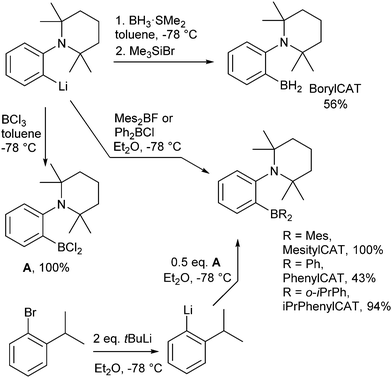
Switching from the originally developed AABs, which were based on the 2-boryl-benzylamine core, to 2-aminophenylboranes provided more favorable thermodynamics of H2 addition.31 Due to its unique properties, which enable unprecedented catalytic hydrogenations11 and C–H borylations,32,33 the 2-aminophenylboryl core allowed us to design novel AABs with substituents other than C6F5 at the boryl site. Particularly, we have recently reported that BorylCAT, the AAB with the smallest boryl site (–BH2), also demonstrates a reversible dihydrogen addition at ambient temperatures.34 In the present work, we prepared several analogues of BorylCAT which contain various aryl substituents (phenyl, mesityl, 2-(isopropyl)phenyl) at the boryl site (Scheme 1). These di(aryl)boryl-substituted AABs, together with BorylCAT, constitute a series of isostructural compounds with varied electronic and, especially, steric properties of their Lewis acidic sites. We found that all these AABs add hydrogen with nearly neutral thermodynamics at close to ambient conditions. Moreover, we show that PHIP effects can be observed for these compounds under similar conditions. The influences of reaction kinetics, relaxation and scalar spin coupling parameters on the intensity of the PHIP signal is discussed in detail. Based on computational analysis of the BorylCAT–H2 adduct, it is shown that the scalar spin coupling between the two protons originating from H2 is the result of dihydrogen bonding and that borate (–BH3) fragment rotation (libration) occurs.
2. Experimental
2.1 PHIP experiments
PHIP NMR experiments were performed on a Bruker AV 300 SB NMR spectrometer operating at 300 MHz 1H resonance frequency and equipped with a broad-band 10 mm RF probe. The standard temperature control unit of the NMR spectrometer was used to maintain the desired temperature of the sample. The sample temperature was controlled by programmatically adjusted heating of a cold N2 flow from a liquid nitrogen tank.Commercially available high-purity H2 gas was used for producing parahydrogen-enriched H2, referred to below as “para-H2”. In this enrichment, H2 from a gas cylinder was supplied through a spiral-shaped copper tube immersed in liquid N2 at 77 K. The ortho–para conversion catalyst (FeO(OH)) was packed at the end of the spiral. As cooled H2 flowed through the cold catalyst, parahydrogen-enriched H2 with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ortho
1 ortho![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) para ratio was produced for further use in the experiments.
para ratio was produced for further use in the experiments.
In a typical workflow, a 5 mm sample tube (Wilmad) containing a ∼0.05 M solution of AAB in degassed dry methylene chloride-d2 was placed inside the NMR magnet, and para-H2, obtained as described above, was bubbled through the solution for 10 s. Then, the parahydrogen flow was abruptly terminated and the NMR experiment was started. 14N decoupling (WALTZ16) was used for the acquisitions.
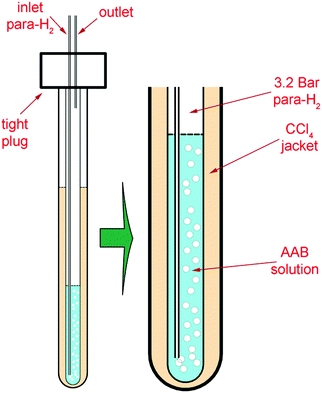
The 5 mm tube was fixed in a heavy-wall 10 mm tube including a CCl4 jacket, stabilizing the temperature in the solution (Fig. 1). para-H2 was supplied to the bottom of the sample tube through 1/32′′ PTFE tubing under a pressure of 3.2 bar. The bubbling at elevated pressure resulted in a higher para-H2 concentration (ca. 10−2 M) in the solution.
2.2 Measurements of kinetic and thermodynamic parameters
The measurements of kinetic constants were performed using the spin saturation transfer method35–37 on a Bruker Avance III 600 MHz spectrometer. A heavy-wall 5 mm NMR tube equipped with a tight plug was used in the experiments. The samples were prepared by charging the tube with AAB solutions (∼0.05 M) and 5 bar of normal (thermal) H2. 14N decoupling (WALTZ16) was used for all acquisitions. The thermally polarized NH group proton signals were used to determine the rate constants for the dissociation of AAB–H2 adducts into AAB and H2 (kdis, see eqn (1) in Section 4.2.1). The constants were calculated from the ratios of the signals in the normal spectra and in the spectra acquired with presaturation of the ortho-H2 resonance at ca. 4.6 ppm. In the latter case, the resonance of ortho-H2 was irradiated (saturated) in a continuous wave mode for 30 s at the beginning of the pulse sequence. To determine kdis, the following expression was used: kdis = (Sn/Ss − 1)/TNH1, in which Sn is the signal intensity in the normal spectrum, Ss is the signal intensity in the spectrum with saturation, and TNH1 is the relaxation time of the proton in the NH group. As the T1 relaxation times of the NH and H2 protons were significantly different, the standard inversion-recovery experiment was inappropriate for determining the correct value of TNH1 because the chemical exchange couples the relaxation of the exchanging nuclei. To overcome this obstacle, the inversion-recovery experiment was replaced with the saturation-recovery protocol with irradiation of H2 resonance during the recovery delays.The AAB + H2 equilibrium constants Kc (see eqn (4)) were determined from the ratios of the AAB, AAB–H2 adduct and H2 signals in the thermally polarized 1H NMR spectra measured from the samples under 5 bar pressure of H2. Concentration scaling was required for the conversion from signal amplitude units to concentrations; this was performed using the signal integrals and the known initial concentrations of the AABs. The association rate constant was derived as kas = Kckdis.
Energetic parameters (ΔS# and ΔH#) for the AAB–H2 dissociation step were determined from the corresponding Eyring38 plots using linear regression. The corresponding Eyring plots for the AAB compounds under study are shown in the ESI† (Fig. S5–S8).
2.3 Quantum chemical calculations
Density functional theory was applied to calculate the JHH coupling constants between the NH and BH protons of BorylCAT–H2 and ascertain the role of dihydrogen bonding. Coupling constants were calculated for several structures derived via the rotation of the BH3 group in BorylCAT–H2. Geometry optimizations and potential energy surface scan calculations were carried out at the ωB97X-D/6-311G** level of theory. ωB97X-D refers to the dispersion-corrected, range-separated hybrid exchange–correlation functional developed by Chai and Head-Gordon.39–41 For numerical integrations, the ultra-fine integration grid was employed. The rotation of the BH3 moiety was studied via potential energy surface scan calculations with respect to a dihedral angle involving the B–N bond; this was followed by transition state identification. JHH coupling constants were computed for several conformers of BorylCAT–H2 at the ωB97X-D/6-311G** level of theory using the Gauge-Independent Atomic Orbital (GIAO) method as implemented in Gaussian 09 software.42To illustrate the presence of dihydrogen bonding, reduced density gradient (RDG) isosurface plots were generated using the NCIPLOT program for the optimized structure of BorylCAT–H2 as well as for the rotational transition state.43,44 The NCI (Non-Covalent Interactions) index enables real-space visualization of both attractive and repulsive interactions based on properties of the electron density.
2.4 Synthesis of ansa-aminoboranes
BorylCAT was synthesized as described previously.34 Diaryl-substituted ansa-aminoboranes were prepared as shown in Scheme 2. According to a modified procedure,31 treatment of (2-(2,2,6,6-tetramethylpiperidin-1-yl)phenyl)lithium with dimesitylfluoroborane or diphenylchloroborane in diethyl ether gave MesitylCAT and PhenylCAT in 100% and 43% yields, respectively. Addition of boron trichloride to the lithium compound afforded dichloroaminoborane A, which gave iPrPhenylCAT in 94% yield upon reacting with two equivalents of ortho-isopropylphenyllithium that were generated in situ by a Br–Li exchange of ortho-isopropylbromobenzene.3. Results
Dihydrogen addition to AABs with different structures, which was investigated in this work using para-H2, is represented by Scheme 3.The scheme does not include nuclear spin dynamics and nuclear spin relaxation in AAB–H2 because there is no obvious way to include these processes in chemical equations. Instead, they will be considered in subsequent discussions when it is required.
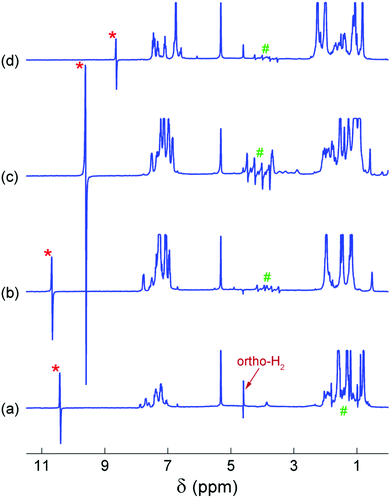
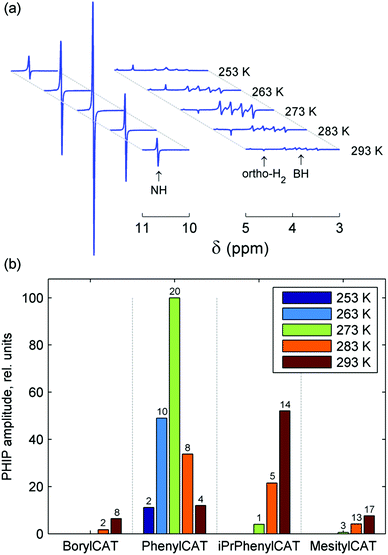
The 14N-decoupled 1H NMR spectra acquired at 20 °C after bubbling para-H2 through the AAB solutions are shown in Fig. 2. In all cases, characteristic antiphase (PASADENA-type) signals were observed for the NH and BH hydrogens in the NMR spectra (signal regions marked with “*” and “#”, respectively). For an AX spin system of spin-1/2 nuclei, a single antiphase doublet would be expected in its spectrum. The shape of the NH signals is close to this conventional shape because the internal multiplet structure introduced by the spin-1 14N nucleus is collapsed due to the self-decoupling caused by a rapid spin relaxation of the 14N nucleus. The amplitudes of the emissive (e) and absorptive (a) components of the antiphase doublet are not equal. This may be the result of the cross-relaxation occurring during the para-H2 bubbling (for e > a)28 or low hyperpolarization at low temperatures (for e < a); see Fig. S1–S4 (ESI†). In contrast, the polarized 1H NMR signals of the BH group appear as a set of four antiphase doublets instead of a single doublet because of the splitting induced by the spin-3/2 11B nucleus.
In contrast to our previous study,28 elevated temperature was not required here to observe polarization effects, meaning that PHIP can be produced at ambient temperatures with the AABs under study. Moreover, these effects were observed even at subzero temperatures (see below, and also Fig. S1–S4 in the ESI†). Comparison of the polarized signal intensities at room temperature reveals that the polarized signal intensity varied in the following order: MesitylCAT < BorylCAT ≈ PhenylCAT < iPrPhenylCAT. Taking into account the steric hindrance introduced by the substituents at the boryl site, one could draw the conclusion that iPrPhenylCAT has optimal properties to produce polarization at room temperature, as the corresponding substituent is located between the highly hindered mesityl group and the moderately hindered phenyl group. However, due to the significant dependence of molecular processes on temperature, the H2 addition process and, consequently, the polarization levels should exhibit a pronounced temperature dependence. To examine this, we performed experiments in which the temperature was varied in the range from −20 °C to 20 °C (see ESI,† Fig. S1 to S4). It was found that the intensity of the 1H PHIP effect of the N–H⋯H–B hydrogen pair decreased gradually with decreasing temperature for BorylCAT, iPrPhenylCAT and MesitylCAT, whereas a clear maximum of PHIP was observed for PhenylCAT at ca. 0 °C (Fig. 3).
The existence of the maximum can be explained as the result of an interplay between the nuclear spin relaxation and reaction kinetics, as discussed in detail in Section 4.2.3. Briefly, for low H2 addition rates (slow equilibrium establishment), nuclear polarization is destroyed by the relaxation, whereas at high addition rates, the relaxation is not significant, but the line broadening induced by the exchange diminishes the amplitude of the overlapping antiphase signals. Finally, at very high addition rates (very fast equilibrium establishment), nuclear spin correlation cannot efficiently evolve into observable polarization during the lifetime of the bound state of H2. However, as discussed in Section 4.2.3, this simple explanation cannot exactly explain the position of the maximum if the experimentally measured relaxation times are taken into account.
The reaction kinetic parameters and the relaxation times were measured using the spin saturation transfer (SST)35–37 method. The data are shown in Table 1. The details of the determination of the parameters are explained in Section 2.2.
| AAB,a ΔH# (kcal mol−1), ΔS# (cal mol−1) | T (K) | k dis × 102 (s−1) | K c × 10−3 (M−1) | NH T 1 (s) | BH T 1 (s) | J HH (Hz) | Δνe (Hz) |
|---|---|---|---|---|---|---|---|
| a ΔS# and ΔH# values corresponding to the dissociation rate constant kdis. b The rate constant was predicted using the energetic parameters in the first column. c Equilibrium constants were calculated by extrapolating experimental data. d T 1 measurement was impossible to perform because the BH signal overlapped with other signals or it was very weak. e The full line width at half maximum determined for the NH proton signal. | |||||||
| BorylCAT, 24.2 ± 2.9, 16.3 ± 9.1 | 273 | 0.1b | 0.11c | 0.73 | —d | 2.9 | 4.8 |
| 283 | 0.4b | 0.05c | 0.88 | —d | 2.9 | 4.7 | |
| 293 | 1.1 | 0.03 | 1.07 | —d | 2.9 | 4.9 | |
| 303 | 7.6 | 0.01 | 1.21 | —d | — | — | |
| PhenylCAT, 21.3 ± 0.6, 15.0 ± 2.0 | 273 | 5.1 | 7.1 | 0.24 | 0.16 | 5.3 | 6.2 |
| 283 | 38.2 | 2.1 | 0.28 | 0.2 | 5.3 | 5.9 | |
| 293 | 160.0 | 0.9 | 0.32 | 0.25 | 5.6 | 6.2 | |
| 303 | 540.2 | 0.3 | 0.38 | 0.29 | — | — | |
| iPrPhenylCAT, 22.9 ± 0.9, 13.4 ± 2.8 | 273 | 0.2b | 3.2c | 0.23 | 0.15 | 4.8 | 7.6 |
| 283 | 1.0b | 1.2c | 0.30 | 0.16 | 4.8 | 6.5 | |
| 293 | 3.8 | 0.5 | 0.35 | 0.18 | 5.0 | 6.5 | |
| 303 | 17.9 | 0.2 | 0.42 | 0.23 | — | — | |
| MesitylCAT, 23.2 ± 7.7, 16.0 ± 25.7 | 273 | 0.5b | 0.014c | 0.34 | 0.16 | 4.3 | 6.2 |
| 283 | 2.2b | 0.005 | 0.38 | 0.17 | 4.2 | 4.9 | |
| 293 | 10.4 | 0.002 | 0.42 | 0.20 | 4.2 | 4.9 | |
| 303 | 32.2 | 0.001 | 0.49 | —d | — | — | |
4. Discussion
4.1 Dihydrogen-bond-mediated J-coupling in AABs as a prerequisite for PHIP
In this study, we used the so-called PASADENA experimental scheme,25,45i.e., the reaction with para-H2 was performed in a relatively high magnetic field (7 T). Under these conditions, the weak-coupling regime is fulfilled for all AAB–H2 adducts of para-H2, with the resonance frequency differences between the –NH and –BH protons (>1.2 kHz) in the adducts largely exceeding the J-coupling scalar constants (<6 Hz). The initial nuclear spin correlation of parahydrogen protons, also called the scalar spin order (∼INH·IBH), transforms upon adduct formation into the longitudinal two-spin order (∼INHz·IBHz)45 because the transverse spin angular momentum components vanish due to decoherence induced by the resonance frequency differences. The INHz·IBHz two-spin order can be transformed into the two-spin single quantum coherence orders (INHz·IBHx, INHx·IBHz, INHz·IBHy, INHy·IBHz) by a strong radio-frequency pulse of arbitrary phase, and a maximal amplitude is achieved if the pulse flip angle is equal to 45°. The latter orders cannot be observed in NMR directly, as NMR detection is only sensitive to single-quantum single-spin orders (IBHx, INHx, IBHy, INHy). Only these spin orders can contribute to the formation of transverse magnetization detected in practice. However, under the action of J-coupling interactions, the two-spin orders can evolve into observable magnetization.It is clear from the above brief consideration that a nonzero spin–spin scalar constant between the –NH and –BH hydrogens is required to observe PHIP effects,45 and the observation of these effects (Fig. 2) serves as evidence of a nonzero coupling constant.28 However, the nature of this scalar coupling constant has been an open question. The J-coupling can be induced indirectly through the –N–C–C–B– molecular chain of the AABs. However, the typical values expected for a long-range 5J constant are on the order of 1 Hz, which is much smaller than that observed experimentally (2.9 to 5.6 Hz, see Table 1). Previously,28 we proposed that J-coupling in the H2 adducts of AABs is likely direct in nature and may be induced by dihydrogen bonding between the –NH and –BH hydrogens.
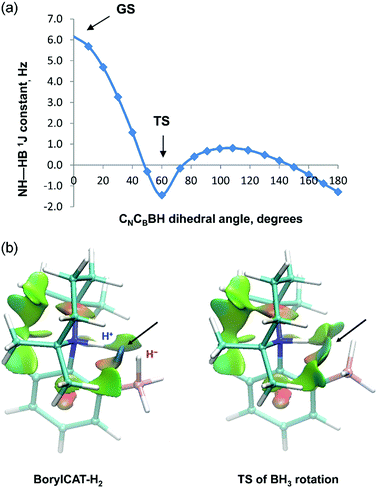
DFT calculations carried out for the BorylCAT–H2 adduct species provided further information on the origin of the J-coupling. The optimized structure of the BorylCAT–H2 molecule features a short distance between the NH and BH hydrogens (1.44 Å), and the JHH coupling constant is computed to be 6.2 Hz at this geometry.
Computations also reveal that the BH3 group of the adduct can easily rotate (or undergo a librational motion) around the B–C bond, as the rotational barrier is predicted to be only 3.8 kcal mol−1 on the potential energy surface. We have therefore calculated the coupling constants along the rotational pathway, i.e. as a function of the CN–CB–B–H dihedral angle (see Fig. 4a). The results show a large variation of the JHH values along the rotation. The coupling constant decreases rapidly as the H⋯H distance increases (it is 2.00 Å in the TS structure), suggesting that the J-coupling is induced by direct H⋯H interaction rather than via the covalent –N–C–C–B– linkage. The statistical averaging of the computed values gives 2.1 Hz for the coupling constant, which is in reasonable agreement with the experimentally observed value (2.9 Hz, see Table 1). Note that for other AABs, this rotation has much higher energy barriers and thus does not occur at ambient temperature.
To assess the nature of H⋯H interaction in the BorylCAT–H2 adduct, we carried out NCI (non-covalent interactions) analysis by generating reduced electron density gradient isosurface plots for the ground state as well as for the rotational transition state (see Fig. 4b). In both structures, the blue regions between the NH and BH hydrogens reveal favorable (attractive) interactions, thus pointing to the presence of dihydrogen bonds. These results underline that dihydrogen bonding interactions play an important role in the observation of PHIP effects with AABs.
4.2 Reaction kinetics, nuclear spin relaxation and PHIP with AABs
In terms of the time scales involved, successful observation of PHIP effects (PASADENA in this work) requires a certain balance between reaction kinetics, nuclear spin relaxation and coherent spin dynamics to convert unobservable nuclear spin orders into observable ones. Any imbalance (e.g., slow or very fast kinetics, slow spin dynamics or fast relaxation) will significantly decrease the observable polarization. The role of coherent spin dynamics requiring a nonzero J-coupling constant was discussed in Section 4.1. There is, however, another requirement: the value of the J-coupling constant must not be much smaller than the linewidth of the multiplet components, or the antiphase components will cancel each other out. The linewidth and the amplitude of the longitudinal two-spin order, in turn, are determined by the kinetic and relaxation parameters. To discuss this complex picture, it is convenient to consider the processes before and after the RF excitation pulse separately. | (1) |
As was discussed in Section 4.1, the nuclear spin correlation originating from para-H2 transforms into the two-spin order (INHz·IBHz) in the adducts of AABs with para-H2. It should be noted that in general, the efficiency of the transformation from the scalar spin order (INH·IBH) to only INHz·IBHz depends on the difference between the resonance frequencies of the –NH and –BH protons, their mutual J-coupling constant, and the reaction rate constant (kdis or kas; they are interdependent under chemical equilibrium conditions). The frequency difference for all AABs in this study (>1.2 kHz) is much larger than the J-coupling constant and the rate constant, leading to the production of the INHz·IBHz order with an efficiency close to 100% (see ESI†). Thus, continuous para-H2 bubbling accompanied by intermolecular exchange leads to pumping of the INHz·IBHz order with time, and the nuclear spin order amplitude reaches a stationary state at some point. In turn, the nuclear spin relaxation destroys the order. Therefore, the amplitude and the kinetics of the pumping process will depend on both the reaction rate constants and the nuclear spin relaxation parameters.
For simplicity, we assume that the para-H2 flux into the solution is a fast process and that all free H2 molecules in the solution are present in the form of para-H2 under the stationary conditions of para-H2 bubbling. Moreover, we assume that the para-H2/AAB/AAB–H2 system is in chemical and magnetic equilibrium before the bubbling and that the Boltzmann polarization can be ignored due to its low amplitude. Then, if we mark the adduct molecules carrying non-equilibrium nuclear spin orders (e.g. INHz·IBHz) with “*”, the kinetic equation determining the pumping process will be
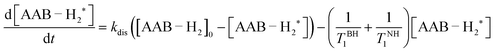 | (2) |
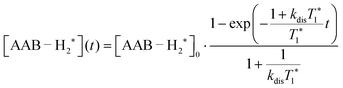 | (3) |
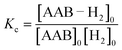 | (4) |
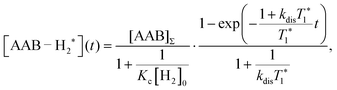 | (5) |
It should be noted that eqn (5) assumes that the para-H2 singlet order is transformed to INHz·IBHz with 100% efficiency in AAB–H2 molecules; however, in general, this does not hold. Heuristically, eqn (5) can be equipped with the INHz·IBHz amplitude factor (fzz) derived in the ESI† for chemically exchanging para-H2 under stationary conditions for a two-spin system. Finally, the following formula for the maximum amplitude of INHz·IBHz nuclear spin order acquired in the para-H2 bubbling process is obtained:
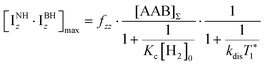 | (6) |
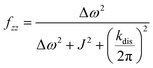 | (7) |
Let us first consider the line broadening, and assume for simplicity that we have an AX spin system. The evolution of the magnetization that resulted from the INHz·IBHz nuclear spin order is detected as an antiphase Lorentzian doublet of the following shape:
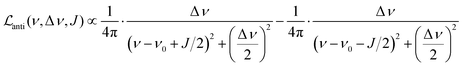 | (8) |
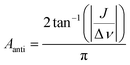 | (9) |
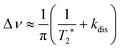 | (10) |
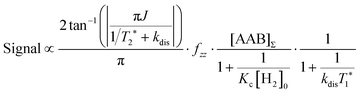 | (11) |
| AAB | T (K) | πJ/(1/T2* + kdis) | K c[H2]0 | k dis T 1* × 104 | Enh. factora |
|---|---|---|---|---|---|
| a Experimentally measured enhancement factors, i.e., ratios of hyperpolarized (after para-H2 bubbling) and thermally polarized (after relaxation) signals. | |||||
| BorylCAT | 273 | 0.6 | 1.1 | 4.4 | 1 |
| 283 | 0.6 | 0.5 | 18.5 | 2 | |
| 293 | 0.6 | 0.3 | 58.8 | 8.4 | |
| 303 | — | 0.1 | 459.8 | — | |
| PhenylCAT | 273 | 0.8 | 71 | 49.0 | 20 |
| 283 | 0.9 | 21 | 445.7 | 8 | |
| 293 | 0.9 | 9 | 2245.6 | 4 | |
| 303 | — | 3 | 8885.1 | — | |
| iPrPhenylCAT | 273 | 0.6 | 32 | 2.0 | 1.2 |
| 283 | 0.7 | 12 | 10.6 | 5 | |
| 293 | 0.8 | 5 | 45.2 | 14 | |
| 303 | — | 2 | 266.0 | — | |
| MesitylCAT | 273 | 0.7 | 0.14 | 5.7 | 3 |
| 283 | 0.9 | 0.05 | 26.1 | 13 | |
| 293 | 0.9 | 0.02 | 140.9 | 17 | |
| 303 | — | 0.01 | 457.3 | — | |
The first parameter, πJ/(1/T2* + kdis), determines the strength of the signal self-cancellation due to the line broadening of the overlapping antiphase components. Low values of J or a large sum of 1/T2* + kdis will significantly diminish the observable antiphase PHIP signal. For the given AABs, the parameter did not exceed 0.9, meaning that at least 53% (see eqn (11) and Table S1 in the ESI†) of the polarized signal amplitude was lost due to the line broadening effect. The variation of this parameter from one AAB to another is not very significant, and we can conclude that the signal attenuation effect due to the line broadening was on the same order for all AABs. It should be noted that FWHM (Δν) values presented in Table 1 for the –NH proton resonances are on the order of 8 Hz, meaning that the sum of 1/T2* + kdis is ca. 25 Hz (see eqn (10)). This relatively large number implies that the line broadening is primarily determined by T2* nuclear spin relaxation in the AAB molecules because kdis does not exceed 1 Hz for the considered temperatures.
The second parameter, (Kc[H2]0), determines the number of available AAB–H2 molecules. This parameter controls the amplitude of the signal through the chemical equilibrium determined by thermodynamics. Larger Kc values or larger para-H2 concentrations increase the overall signal. The former can be adjusted somewhat by varying the temperature, while the latter can be increased by performing experiments at high para-H2 pressures to increase the concentration. Note that under the given experimental conditions, the parameter Kc[H2]0 varied in the following sequence: PhenylCAT > iPrPhenylCAT > BorylCAT > MesitylCAT (Table 2), meaning that thermodynamically, PhenylCAT is the best candidate for PHIP.
The third parameter (kdisT1*) is an intensive property which characterizes the strength of nuclear spin relaxation with respect to the rate of chemical exchange. A low value of this parameter indicates that either the nuclear spin relaxation is very fast or the reaction activity is weak, which leads to significant diminishing of the possible polarization levels. For every AAB in this study, this parameter was not high; however, it was more favorable in the case of PhenylCAT (Table 2).
The above discussion of the experimental data shows that the dimensionless parameters presented in Table 2 conveniently characterize the observed PHIP effects. They also can provide a good strategy basis for maximizing the polarization effects by using eqn (11) if the corresponding kinetic, thermodynamic and NMR parameters are known. Namely, the best results would be expected when πJ/(1/T2* + kdis) > 4, as the arctan function varies weakly once the argument value exceeds 4. Also, other parameters should be Kc[H2]0 ≫ 1 and kdisT1* ≫ 1 to minimize the respective denominators in eqn (11). These prerequisites, however, are not easy to fulfill in practice. The analysis has shown that the parameters for the considered AABs are far from optimal (see Table 2).
Moreover, the mechanistic features of H2 activation may not be simple to describe. In particular, eqn (11) predicts that the maxima of antiphase PHIP signals should be observed at a certain temperature because kdisT1* decreases significantly at low temperatures, whereas πJ/(1/T2* + kdis) (and possibly Kc[H2]0) decrease significantly at high temperatures. This happens as a result of the exponential dependence of kdis on temperature and qualitatively could explain the distinctive PHIP signal dependence obtained for PhenylCAT (Fig. 3). The position of the PHIP signal maximum, however, cannot be explained quantitatively using eqn (11). Fig. 5 compares the experimentally observed temperature of the PHIP signal amplitude maximum and the theoretically predicted temperature dependence of the PHIP signal amplitude for PhenylCAT. The fact that the positions of the two maxima do not match implies that some hidden dynamics occurs which displaces the experimental maximum to lower temperatures compared to the expected position. The nature of this effect is not clear; however, it may be related to the increase of thermodynamic variance at higher temperatures, defrosting a non-pairwise H2 activation path. The latter process can occur in parallel to the pairwise path; however, in contrast, it does not lead to PHIP effects. Thus, the activation of a non-pairwise path could shift the temperature of the PHIP maximum toward lower temperatures. Another reason for the signal maximum shift may be the temperature sensitivity of the dihydrogen bond in AAB–H2 molecules. The weakening of the dihydrogen bond at higher temperatures can cause the J-coupling between the NH and BH protons to vanish, leading to the disappearance of the PHIP effect (see Section 4.1). Additionally, in the derivation of eqn (11), we assumed that para-H2 dissolution during the bubbling process is very fast, which may not be a good approximation and may cause some deviations.
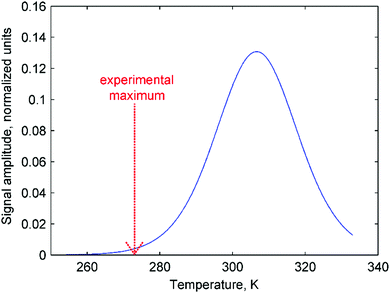 | ||
| Fig. 5 Theoretically predicted antiphase PHIP signal amplitude as a function of temperature (eqn (11)) calculated using parameters for PhenylCAT from Table 2 (blue trace). [AAB]∑ parameter was set to unity in the calculation. Additionally, the position of the experimentally observed maximum of the PHIP signal amplitude is shown in the graph with a red dashed arrow. | ||
Temperature dependence with a PHIP amplitude maximum was observed only for PhenylCAT; for the other AABs, the amplitude of the polarized signals gradually increased with increasing temperature (see Fig. 2 and Fig. S1–S4 in ESI†). This observation is in agreement with the theoretical expectations based on the parameters for BorylCAT, MesitylCAT and iPrPhenylCAT (Table 2). Higher temperatures are required to observe maxima for the latter compounds. BorylCAT, however, is somewhat different from the other AABs. In contrast to the others, at low temperatures, it demonstrated antiphase signals for two unknown polarized species in addition to those for BorylCAT–H2 (see Fig. S1 in ESI†). The attempts to elucidate the structures of these species were not successful because of their very low concentrations. These species could be intermediates, side-products or impurities capable of activating H2 in a pairwise manner, with N and B serving as active FLP centers.
Another peculiar finding for BorylCAT is the observation of a dispersive ortho-H2 signal at elevated temperatures of 283 to 293 K (see Fig. 1a and Fig. S1a–c in the ESI†). This signal looks very similar to a signal with an antiphase shape; however, this shape is impossible for species where two protons have identical resonance frequencies, as in ortho-H2.27 Instead, the observed effect likely arises from a complex phase accumulation induced by a chemical exchange.48 The exchange takes place between the protons captured in BorylCAT–H2 and free H2 molecules. After bubbling para-H2 through BorylCAT solution followed by an RF pulse, free H2 will still be present in the form of NMR-silent para-H2, as it is insensitive to RF pulses. On the other hand, the proton pair in BorylCAT–H2 will be polarized, and the polarization is transferred to free H2 molecules after some time by the chemical exchange. The delayed appearance of ortho-H2 molecules is equivalent to the accumulation of a complex phase for a particular NMR signal, which was observed experimentally in this study. This picture could explain our observations, but only qualitatively.
It was found using numerical spin dynamics simulations that the amplitude of the dispersive signal is very sensitive to the frequency differences between the H2, –NH and –BH resonances (see Fig. S9 in the ESI†), and the large differences present for BorylCAT significantly decrease the amplitude of the dispersive ortho-H2 signal. It is likely that a cross-correlated relaxation in BorylCAT–H2 accompanied by chemical exchange may also have an influence on the dispersive ortho-H2 signal by alternating the signal phase. This was indirectly confirmed by the observation of emissive ortho-H2 signals (signals with negative amplitudes) at almost all temperatures in the experiments with BorylCAT; it can be explained in terms of the cross-correlated relaxation. Evidence that relaxation can convert an originally antiphase polarization to an in-phase (net) polarization is reported in the literature.49,50 Moreover, similar emissive ortho-H2 signals were observed in experiments with other AABs in this work (PhenylCAT), in our previous studies28 on metal-free H2 activation, and also in experiments with diamagnetic Ru complexes.50 As can be seen from the above discussion, a clear understanding of the peculiar subtle effects for ortho-H2 signals requires separate exploration to be considered in full; this will be addressed in future works.
5. Conclusions
In conclusion, we have shown that all AABs studied in this work demonstrate the ability to provide PHIP. Moreover, the required reaction temperatures are close to ambient temperature; thus, the young field of FLP chemistry may bring the efficient production of nuclear spin polarization closer to realization. The experiments are not demanding, and, due to reversibility of H2 addition to the AABs, the polarization can be observed after each cycle of parahydrogen bubbling. The experimentally measured kinetic, thermodynamic and NMR parameters allowed us to analyze the results with the aim of understanding current drawbacks. In particular, it was shown that nuclear spin relaxation accompanied by slow reaction kinetics significantly diminishes the nuclear spin polarization values. Moreover, the rapid nuclear spin relaxation increases the cancellation effect in the antiphase PHIP multiplets. One plausible solution for diminishing the influence of the nuclear spin relaxation would be the replacement of 14N nuclei with 15N. Eliminating the quadrupolar nucleus should increase T1 as well as T2 of the nuclear spins. The reaction kinetics issue can be improved by careful molecular design of the N–B FLP activation centers. The results obtained in this work clarify that variation of the substituents solely at the B-center significantly changes the reaction rates. However, as was found for PhenylCAT, increasing the reaction rates by increasing the temperature may not lead to the expected increase in signal enhancements because the activation of a non-pairwise reaction path or weakening of dihydrogen bonding may occur. Molecular “tuning” at the N-center would provide further flexibility in creating efficient AABs. Thermodynamically, PhenylCAT and iPrPhenylCAT have suitable characteristics, allowing close to quantitative conversion of the AAB molecules to the AAB–H2 adducts, implying high concentrations of the hyperpolarized form of AAB–H2. We believe that further rational investigation of the interactions between para-H2 and AABs can lead to an efficient metal-free para-H2 transfer to various substances and to high NMR signal enhancements. Meanwhile, the mechanistic information provided by PHIP shows that this class of molecules primarily activate H2 molecules in a pairwise manner; demonstrations are already available for six different compounds, including the four studied in this work and two more in a study published earlier.28 We are interested in both generating high levels of hyperpolarization and studying the AABs themselves, as they are unique. The observed hyperpolarization levels are not superior; however, we believe that the relevant improvements described above can provide efficient production of hyperpolarization with AABs. The theoretical analysis presented in the manuscript gives us and other researchers a direction and platform for further development. This analysis shows that for the systems studied here, the relevant kinetic and NMR parameters are suboptimal for observation of high hyperpolarization; however, this situation can be improved by further design of the AABs.Acknowledgements
The financial support by the grant from RFBR (14-03-93183-MCX-a) is acknowledged. VVZ and IVK thank RSF (grant #14-13-00445) for the support of the experiments with AAB compounds and parahydrogen. VVT acknowledges the Academy of Finland for financial support (grant numbers 289649 and 294027). This work was also partially supported by a Hungarian NKFI grant (K-115660).Notes and references
- G. C. Welch, R. R. S. Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124–1126 CrossRef CAS PubMed.
- G. C. Welch and D. W. Stephan, J. Am. Chem. Soc., 2007, 129, 1880–1881 CrossRef CAS PubMed.
- D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2015, 54, 6400–6441 CrossRef CAS PubMed.
- D. W. Stephan, J. Am. Chem. Soc., 2015, 137, 10018–10032 CrossRef CAS PubMed.
- D. W. Stephan, Acc. Chem. Res., 2015, 48, 306–316 CrossRef CAS PubMed.
- D. W. Stephan, Dalton Trans., 2009, 3129–3136, 10.1039/b819621d.
- Frustrated Lewis Pairs I: Uncovering and Understanding, ed. G. Erker and D. W. Stephan, Springer Berlin Heidelberg, 2013 Search PubMed.
- Frustrated Lewis Pairs II: Expanding the Scope, ed. G. Erker and D. W. Stephan, Springer Berlin Heidelberg, 2013 Search PubMed.
- V. Sumerin, K. Chernichenko, M. Nieger, M. Leskelä, B. Rieger and T. Repo, Adv. Synth. Catal., 2011, 353, 2093–2110 CrossRef CAS.
- S. Grimme, H. Kruse, L. Goerigk and G. Erker, Angew. Chem., Int. Ed., 2010, 49, 1402–1405 CrossRef CAS PubMed.
- K. Chernichenko, Á. Madarász, I. Pápai, M. Nieger, M. Leskelä and T. Repo, Nat. Chem., 2013, 5, 718–723 CrossRef CAS PubMed.
- B. Waerder, M. Pieper, L. A. Körte, T. A. Kinder, A. Mix, B. Neumann, H.-G. Stammler and N. W. Mitzel, Angew. Chem., Int. Ed., 2015, 54, 13416–13419 CrossRef CAS PubMed.
- D. W. Stephan, S. Greenberg, T. W. Graham, P. Chase, J. J. Hastie, S. J. Geier, J. M. Farrell, C. C. Brown, Z. M. Heiden, G. C. Welch and M. Ullrich, Inorg. Chem., 2011, 50, 12338–12348 CrossRef CAS PubMed.
- D. W. Stephan, Org. Biomol. Chem., 2012, 10, 5740–5746 CAS.
- J. Paradies, Angew. Chem., Int. Ed., 2014, 53, 3552–3557 CrossRef CAS PubMed.
- D. J. Scott, M. J. Fuchter and A. E. Ashley, Angew. Chem., Int. Ed., 2014, 53, 10218–10222 CrossRef CAS PubMed.
- S. Tussing, L. Greb, S. Tamke, B. Schirmer, C. Muhle-Goll, B. Luy and J. Paradies, Chem. – Eur. J., 2015, 21, 8056–8059 CrossRef CAS PubMed.
- M. Lindqvist, K. Borre, K. Axenov, B. Kótai, M. Nieger, M. Leskelä, I. Pápai and T. Repo, J. Am. Chem. Soc., 2015, 137, 4038–4041 CrossRef CAS PubMed.
- P. Eisenberger, B. P. Bestvater, E. C. Keske and C. M. Crudden, Angew. Chem., Int. Ed., 2015, 54, 2467–2471 CrossRef CAS PubMed.
- I. Chatterjee and M. Oestreich, Angew. Chem., Int. Ed., 2015, 54, 1965–1968 CrossRef CAS PubMed.
- Z. Zhang and H. Du, Angew. Chem., Int. Ed., 2015, 54, 623–626 CAS.
- Á. Gyömöre, M. Bakos, T. Földes, I. Pápai, A. Domján and T. Soós, ACS Catal., 2015, 5, 5366–5372 CrossRef.
- D. J. Scott, T. R. Simmons, E. J. Lawrence, G. G. Wildgoose, M. J. Fuchter and A. E. Ashley, ACS Catal., 2015, 5, 5540–5544 CrossRef CAS PubMed.
- Z. Zhang and H. Du, Org. Lett., 2015, 17, 6266–6269 CrossRef CAS PubMed.
- C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542 CrossRef CAS.
- M. G. Pravica and D. P. Weitekamp, Chem. Phys. Lett., 1988, 145, 255–258 CrossRef CAS.
- J. Natterer and J. Bargon, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 293–315 CrossRef.
- V. V. Zhivonitko, V.-V. Telkki, K. Chernichenko, T. Repo, M. Leskelä, V. Sumerin and I. V. Koptyug, J. Am. Chem. Soc., 2014, 136, 598–601 CrossRef CAS PubMed.
- L. E. Longobardi, C. A. Russell, M. Green, N. S. Townsend, K. Wang, A. J. Holmes, S. B. Duckett, J. E. McGrady and D. W. Stephan, J. Am. Chem. Soc., 2014, 136, 13453–13457 CrossRef CAS PubMed.
- F. Schulz, V. Sumerin, S. Heikkinen, B. Pedersen, C. Wang, M. Atsumi, M. Leskela, T. Repo, P. Pyykko, W. Petry and B. Rieger, J. Am. Chem. Soc., 2011, 133, 20245–20257 CrossRef CAS PubMed.
- K. Chernichenko, M. Nieger, M. Leskelä and T. Repo, Dalton Trans., 2012, 41, 9029–9032 RSC.
- K. Chernichenko, M. Lindqvist, B. Kótai, M. Nieger, K. Sorochkina, I. Pápai and T. Repo, J. Am. Chem. Soc., 2016, 138, 4860–4868 CrossRef CAS PubMed.
- M.-A. Légaré, M.-A. Courtemanche, E. Rochette and F.-G. Fontaine, Science, 2015, 349, 513–516 CrossRef PubMed.
- K. Chernichenko, B. Kótai, I. Pápai, V. Zhivonitko, M. Nieger, M. Leskelä and T. Repo, Angew. Chem., Int. Ed., 2015, 54, 1749–1753 CrossRef CAS PubMed.
- R. L. Jarek, R. J. Flesher and S. K. Shin, J. Chem. Educ., 1997, 74, 978 CrossRef CAS.
- M. Montag, J. Zhang and D. Milstein, J. Am. Chem. Soc., 2012, 134, 10325–10328 CrossRef CAS PubMed.
- W. G. Wang, T. B. Rauchfuss, L. Y. Zhu and G. Zampella, J. Am. Chem. Soc., 2014, 136, 5773–5782 CrossRef CAS PubMed.
- P. W. Atkins and J. De Paula, Physical chemistry, W.H. Freeman, Oxford: Oxford University Press, New York, 9th edn, 2010 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- C. R. Bowers, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, Wiley, Chichester, 2002, vol. 9, pp. 750–769 Search PubMed.
- M. H. Levitt, Spin dynamics: basics of nuclear magnetic resonance, John Wiley & Sons, Chichester, England, Hoboken, NJ, 2nd edn, 2008 Search PubMed.
- A. D. Bain, Prog. Nucl. Magn. Reson. Spectrosc., 2003, 43, 63–103 CrossRef CAS.
- R. O. Kühne, T. Schaffhauser, A. Wokaun and R. R. Ernst, J. Magn. Reson., 1979, 35, 39–67 Search PubMed.
- S. Aime, R. Gobetto and D. Canet, J. Am. Chem. Soc., 1998, 120, 6770–6773 CrossRef CAS.
- S. Aime, W. Dastru, R. Gobetto, A. Russo, A. Viale and D. Canet, J. Phys. Chem. A, 1999, 103, 9702–9705 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Full sets of 1H NMR spectra measured with AABs at variable temperatures after para-H2 bubbling; Eyring plots used for extraction of energetic parameters from kdis at variable temperatures; evaluation of analytical expression for INHz·IBHz spin order strength accumulated during para-H2 bubbling by AAB–H2 compounds; preparation procedures and characterization spectra; details of quantum chemical computations; table of calculated PHIP signal attenuation factors for the AABs under study. See DOI: 10.1039/c6cp05211h |
| This journal is © the Owner Societies 2016 |