Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Radiative cooling of H3O+ and its deuterated isotopologues†
Vladlen V.
Melnikov
a,
Sergei N.
Yurchenko
*b,
Jonathan
Tennyson
b and
Per
Jensen
c
aSiberian Institute of Physics & Technology, Tomsk State University, Tomsk, 634050, Russia
bDepartment of Physics & Astronomy, University College London, London WC1E 6BT, UK. E-mail: s.yurchenko@ucl.ac.uk
cPhysikalische und Theoretische Chemie, Fakultät für Mathematik und Naturwissenschaften, Bergische Universität Wuppertal, 42097 Wuppertal, Germany
First published on 1st September 2016
Abstract
In conjunction with ab initio potential energy and dipole moment surfaces for the electronic ground state, we have made a theoretical study of the radiative lifetimes for the hydronium ion H3O+ and its deuterated isotopologues. We compute the ro-vibrational energy levels and their associated wavefunctions together with Einstein coefficients for electric dipole transitions. A detailed analysis of the stability of the ro-vibrational states has been carried out and the longest-living states of the hydronium ions have been identified. We report estimated radiative lifetimes and cooling functions for temperatures <200 K. A number of long-living meta-stable states are identified, capable of population trapping.
1 Introduction
In the Universe, molecules are found in a wide variety of environments: from diffuse interstellar clouds at very low temperatures to the atmospheres of planets, brown dwarfs and cool stars which are significantly hotter. In order to describe the evolution of the diverse, complex environments, it is essential to have realistic predictions of the radiative and cooling properties of the constituent molecules. Such predictions, in turn, require reasonable models for the energetics of each molecular species present.Although interstellar molecular clouds are usually characterised as cold, they are mostly not fully thermalized. Whether a species attains thermal equilibrium with the environment depends on the radiative lifetimes of its states and the rate of collisional excitations to the states: this is normally characterised by the critical density. In non-thermalized regions, radiative lifetimes are also important for modelling the maser activity observed for many species. The long lifetimes associated with certain excited states can lead to population trapping and non-thermal, inverted distributions. Such unexpected state distributions have been observed for the H3+ molecule both in space1,2 and in the laboratory.3,4
Dissociative recombination of hydronium H3O+ has been extensively studied in ion storage rings.5–9 The lifetimes calculated in the present work suggest that H3O+ and its isotopologues will exhibit population trapping in a manner similar to that observed for H3+ in storage rings. Dissociative recombination of hydronium has been postulated as a possible cause of emissions from super-excited water in cometary comae10 and as the mechanism for a spontaneous infrared water laser.11
Hydronium and its isotopologues play an important role in planetary and interstellar chemistry.7,12 These molecular ions are found to exist abundantly in both diffuse and dense molecular clouds as well as in comae. Moreover, H3O+ is a water indicator and can be used to estimate water abundances when direct detection is unfeasible.13 Consequently, the ions have been the subject of numerous theoretical and experimental studies (see, for example, ref. 7, 8, 12–46 and references therein) mainly devoted to the spectroscopy and chemistry of the species.
Whereas the cooling function of the H3+ ion has been extensively studied by Miller et al.,47–49 no information about the radiative and cooling properties of H3O+ and its deuterated isotopologues has been available thus far. In the present work, we remedy this situation by determining theoretically the ro-vibrational states of the ions H3O+, H2DO+, HD2O+, and D3O+. We use ab initio potential energy (PES) and dipole moment surfaces (DMS) for the ground electronic states of H3O+ from ref. 50 to compute for each of the four ions considered here, ro-vibrational energy levels, the accompanying wavefunctions, and Einstein coefficients for the relevant ro-vibrational (electric dipole) transitions by means of the nuclear-motion program TROVE.51 Lifetimes of individual ro-vibrational states are calculated and analyzed together with the overall cooling rates. Recently, the same methodology was used to estimate the sensitivities of hydronium-ion transition frequencies to a possible time variation of the proton-to-electron mass ratio.50
We present a detailed analysis of the stability of the ro-vibrational states of the hydronium ions and identify the states with the longest lifetimes. This study is based on the methodology52 developed very recently as part of the ExoMol project.53 The ExoMol project aims at a comprehensive description of the spectroscopic properties of molecules important for atmospheres of exoplanets and cool stars. The molecular lifetimes and cooling functions determined for H3O+ and its deuterated isotopologues in the present work are available in the new ExoMol data format.54
2 Theory and computation
The ro-vibrational energy levels and wavefunctions of the ions under study were calculated variationally using the TROVE program51,55 in a manner similar to the successful calculations previously carried out for several other XY3 pyramidal molecules56–61 including ammonia NH3 (see ref. 62 and 63), which exhibits the same large-amplitude, ‘umbrella-flipping’ inversion motion as H3O+. The inversion barrier of H3O+ is 650.9 cm−1,64 which is lower than 1791 cm−1 found for NH3.39 As a result, H3O+ inversion splitting of the ro-vibrational ground state, 55.35 cm−1 (ref. 65), is significantly larger than 0.793 cm−1 (ref. 39) of NH3.We have used ab initio PES and DMS of H3O+ (ref. 50), computed at the MRCI/aug-cc-pwCV5Z(5Z) and MRCI/aug-cc-pwCVQZ(QZ) levels of theory, respectively. Complete basis set (CBS) extrapolation was used to obtain the Born–Oppenheimer PES (see ref. 50 for details).
The basis set used in the variational computations of the ro-vibrational states is defined in ref. 51. In all calculations of the present work, the orders of kinetic and potential energy expansions were set to 6 and 8, respectively. We used Morse-type basis functions for the stretching modes and numerical basis functions (numerical solutions of the corresponding 1D problem obtained within the framework of the Numerov–Cooley scheme66) for the bending vibrations. The ab initio equilibrium structure of H3O+ is characterized by an O–H bond length of 0.9758 Å and a H–O–H angle of 111.95°. The vibrational basis set is controlled by the polyad number defined by
| P = 2(v1 + v2 + v3) + v4 + v5 + v6/2, | (1) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3h(M) molecular symmetry group,67 while the calculations for the asymmetric isotopologues H2DO+ and HD2O+ were done under the
3h(M) molecular symmetry group,67 while the calculations for the asymmetric isotopologues H2DO+ and HD2O+ were done under the ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) symmetry. The computational details of the basis set construction can be found in ref. 62 as well as the details of the calculations of the Einstein coefficients Aif. The latter were computed for all possible initial, i, and final, f, states lying less than 600 cm−1 above the zero point energy with J ≤ 7. According to our estimations, this should be sufficient to describe the populations of the ro-vibrational states at thermodynamic temperatures up to 200 K. In this work we concentrate on the low energy applications. Higher temperatures would require higher rotational excitations J and therefore more involved calculations.
2v(M) symmetry. The computational details of the basis set construction can be found in ref. 62 as well as the details of the calculations of the Einstein coefficients Aif. The latter were computed for all possible initial, i, and final, f, states lying less than 600 cm−1 above the zero point energy with J ≤ 7. According to our estimations, this should be sufficient to describe the populations of the ro-vibrational states at thermodynamic temperatures up to 200 K. In this work we concentrate on the low energy applications. Higher temperatures would require higher rotational excitations J and therefore more involved calculations.
The lifetimes of the states were computed as52
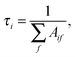 | (2) |
 | (3) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) if (cm−1) is the wavenumber of the line, (hc
if (cm−1) is the wavenumber of the line, (hc![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) if = Ef − Ei), Jf is the rotational quantum number for the final state, Ψi and Ψf represent the ro-vibrational eigenfunctions of the final and initial states, respectively, mi and mf are the corresponding projections of the total angular momentum on the Z axis, and
if = Ef − Ei), Jf is the rotational quantum number for the final state, Ψi and Ψf represent the ro-vibrational eigenfunctions of the final and initial states, respectively, mi and mf are the corresponding projections of the total angular momentum on the Z axis, and ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) A is the electronically averaged component of the dipole moment (Debye) along the space-fixed axis A = X, Y, Z (see also ref. 69).
A is the electronically averaged component of the dipole moment (Debye) along the space-fixed axis A = X, Y, Z (see also ref. 69).
The cooling function W(T) is the total power per unit solid angle emitted by a molecule at temperature T; it is given by the following expression:52
 | (4) |
 | (5) |
The same PES and DMS were used for each isotopologue, which means that no allowance was made for the breakdown of the Born–Oppenheimer approximation. The energies of H3O+ and the three deuterated isotopologues are very different not only due to the mass changes, but also due to the different symmetries these species belong to and the ensuing nuclear spin statistics. We use the molecular symmetry group67 ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3h(M) to classify the ro-vibrational states of the highest-symmetry species H3O+ and D3O+, and
3h(M) to classify the ro-vibrational states of the highest-symmetry species H3O+ and D3O+, and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) for the lower-symmetry isotopologues H2DO+ and HD2O+. The differences in the Einstein coefficients are also quite substantial, especially between the
2v(M) for the lower-symmetry isotopologues H2DO+ and HD2O+. The differences in the Einstein coefficients are also quite substantial, especially between the ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3h(M) and the
3h(M) and the ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) isotopologues. In general, isotope substitution in ions often leads to large changes in ro-vibrational intensities. This is because these intensities depend on the components of the electric dipole moment in the molecule-fixed axis system which, by definition, has its origin in the nuclear center-of-mass. Upon isotopic substitution, the center-of-mass, and thus the origin of the molecule-fixed axis system, are displaced. For a neutral molecule (i.e., a molecule with no net charge) this does not change the dipole moment components but, for an ion, they do (see, for example, ref. 70). Owing to intensities and Einstein coefficients changing much upon isotopic substitution, the lifetimes of the ro-vibrational states are expected to vary strongly with isotopologue for H3O+. Selection rules for J are
2v(M) isotopologues. In general, isotope substitution in ions often leads to large changes in ro-vibrational intensities. This is because these intensities depend on the components of the electric dipole moment in the molecule-fixed axis system which, by definition, has its origin in the nuclear center-of-mass. Upon isotopic substitution, the center-of-mass, and thus the origin of the molecule-fixed axis system, are displaced. For a neutral molecule (i.e., a molecule with no net charge) this does not change the dipole moment components but, for an ion, they do (see, for example, ref. 70). Owing to intensities and Einstein coefficients changing much upon isotopic substitution, the lifetimes of the ro-vibrational states are expected to vary strongly with isotopologue for H3O+. Selection rules for J are
| J′ − J′′ = 0, ±1 and J′ + J′′ > 0. | (6) |
| A1′ ↔ A1′′, A2′ ↔ A2′′, E′ ↔ E′′ | (7) |
| A1 ↔ A2, B1 ↔ B2. | (8) |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) isotopologues H2DO+ and HD2O+ have ortho and para states: for H2DO+, B1 and B2 states are ortho with gns = 9, and A1 and A2 states are para with gns = 3. For HD2O+, the ortho–para states are interchanged relative to H2DO+: A1 and A2 states are now ortho with gns = 12 whereas B1 and B2 states are para with gns = 6.
2v(M) isotopologues H2DO+ and HD2O+ have ortho and para states: for H2DO+, B1 and B2 states are ortho with gns = 9, and A1 and A2 states are para with gns = 3. For HD2O+, the ortho–para states are interchanged relative to H2DO+: A1 and A2 states are now ortho with gns = 12 whereas B1 and B2 states are para with gns = 6.
3 Results and discussion
In order to validate our description of the energetics of H3O+ and its deuterated isotopologues, we compare in Table 1 calculated vibrational energies for these molecules with the available, experimentally derived values. In view of the fact that the calculations are based on a purely ab initio PES, the agreement between theory and experiment is excellent. The results suggest that the ab initio data used in the present work, in conjunction with the variational TROVE solution of the ro-vibrational Schrödinger equation, are more than adequate for obtaining accurate lifetimes of the molecules studied.| State | Sym. | Exp. | Ref. | Calc. | Exp.–Calc. |
|---|---|---|---|---|---|
| H3O+ | |||||
| ν 2 + | A 1 | 581.17 | 26 | 579.07 | 2.10 |
| 2ν2+ | A 1 | 1475.84 | 25 | 1470.67 | 5.17 |
| ν 1 + | A 1 | 3445.01 | 65 | 3442.61 | 2.40 |
| ν 3 + | E | 3536.04 | 65 | 3532.58 | 3.46 |
| ν 4 + | E | 1625.95 | 27 | 1623.02 | 2.93 |
| 0− | A 1 | 55.35 | 65 | 55.03 | 0.32 |
| ν 2 − | A 1 | 954.40 | 26 | 950.94 | 3.46 |
| ν 1 − | A 1 | 3491.17 | 65 | 3488.32 | 2.85 |
| ν 3 − | E | 3574.29 | 65 | 3571.04 | 3.25 |
| ν 4 − | E | 1693.87 | 27 | 1690.65 | 3.22 |
| D3O+ | |||||
| ν 2 + | A 1 | 453.74 | 31 | 451.58 | 2.16 |
| ν 3 + | E | 2629.65 | 31 | 2627.14 | 2.51 |
| 0− | A 1 | 15.36 | 71 | 15.38 | −0.02 |
| ν 2 − | A 1 | 645.13 | 31 | 642.79 | 2.34 |
| ν 3 − | E | 2639.59 | 31 | 2637.10 | 2.49 |
| H2DO+ | |||||
| 0− | B 1 | 40.56 | 43 | 40.39 | 0.17 |
| ν 1 + | A 1 | 3475.97 | 42 | 3473.27 | 2.70 |
| ν 1 − | B 1 | 3508.63 | 42 | 3505.51 | 3.12 |
| ν 3 + | B 2 | 3531.50 | 42 | 3528.07 | 3.43 |
| ν 3 − | A 2 | 3556.94 | 42 | 3553.63 | 3.31 |
| HD2O+ | |||||
| 0− | B 1 | 26.98 | 43 | 26.92 | 0.06 |
In Fig. 1, we plot the lifetimes calculated for the ro-vibrational states of H3O+ and its deuterated isotopologues against the associated term values Ẽ (J ≤ 7, Ẽ < 600 cm−1). In general, the lifetimes exhibit the expected gradual decrease with increasing term value. The complete list of lifetimes for all four isotopologues is given as ESI† to this paper.
 | ||
| Fig. 1 Calculated lifetimes τ of the ro-vibrational states (J ≤ 7) of H3O+ and its deuterated isotopologues. The lifetime values are plotted logarithmically. | ||
Lifetimes τ of the longest-lived states of the ions are compiled in Table 2. The lowest-lying state of each of the nuclear spin species ortho and para (and meta for D3O+) has an infinitely long lifetime; it has no state to decay to.
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3h(M) and
3h(M) and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) isotopologues, respectively, with Γ as the symmetry of the state in the respective group
2v(M) isotopologues, respectively, with Γ as the symmetry of the state in the respective group
| State | Term value, cm−1 | τ |
|---|---|---|
| H3O+ | (Years) | |
| (1,0,A2′) | 22.47 | ∞ |
| (1,1,E′′) | 17.38 | ∞ |
| (3,3,A2′′) | 88.96 | ∞ |
| (5,5,E′′) | 209.58 | 140.1 |
| (2,1,E′′) | 62.29 | 26.2 |
| (2,2,E′) | 47.03 | 23.9 |
| (4,4,E′) | 143.15 | 17.7 |
| D3O+ | (Years) | |
| (0,0,A1′) | 0.00 | ∞ |
| (1,0,A2′) | 11.33 | ∞ |
| (1,1,E′′) | 8.78 | ∞ |
| (3,3,A2′′) | 45.02 | ∞ |
| (5,5,E′′) | 106.15 | 3816.0 |
| (2,2,E′) | 23.79 | 857.1 |
| (4,4,E′) | 72.48 | 594.4 |
| (3,3,A1′′) | 45.02 | 190.4 |
| H2DO+ | (Days) | |
| (00,0,A1) | 0.00 | ∞ |
| (11,1,B1) | 15.70 | ∞ |
| (11,0,B2) | 18.07 | 265.4 |
| (22,1,A2) | 55.82 | 89.1 |
| (22,0,A1) | 56.60 | 4.8 |
| (10,1,A2) | 11.69 | 3 |
| HD2O+ | (Days) | |
| (00,0,A1) | 0.00 | ∞ |
| (11,1,B1) | 9.53 | ∞ |
| (11,0,B2) | 14.24 | 21.6 |
| (22,1,A2) | 35.35 | 8.9 |
| (10,1,A2) | 12.19 | 1.8 |
| (22,0,A1) | 27.77 | 1.4 |
Low-lying, purely rotational states with low J values have the longest lifetimes; they have the smallest numbers of decay channels and/or the lowest probability for spontaneous emission transitions. The higher-symmetry species H3O+ and D3O+ (with ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3h(M) symmetry) have more restrictive selection rules than the
3h(M) symmetry) have more restrictive selection rules than the ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) species HD2O+ and H2DO+, and so H3O+ and D3O+ states live significantly longer (typically tens to hundreds of years) compared to the day-long lifetimes of HD2O+ and H2DO+. Thus, D3O+ has three meta-stable states with lifetimes longer than 100 years. The longest-lived of these, with τ = 3816 years, is the rotational state (J = 5, K = 5, E′′) of the vibrational ground state. In comparison, the longest-lived meta-stable state of H2DO+ the rotational state (JKa,Kc,Γ) = (11,0,B2) has a lifetime of 265 days.
2v(M) species HD2O+ and H2DO+, and so H3O+ and D3O+ states live significantly longer (typically tens to hundreds of years) compared to the day-long lifetimes of HD2O+ and H2DO+. Thus, D3O+ has three meta-stable states with lifetimes longer than 100 years. The longest-lived of these, with τ = 3816 years, is the rotational state (J = 5, K = 5, E′′) of the vibrational ground state. In comparison, the longest-lived meta-stable state of H2DO+ the rotational state (JKa,Kc,Γ) = (11,0,B2) has a lifetime of 265 days.
As mentioned above, the symmetry lowering from ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3h(M) to
3h(M) to ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) gives rise to another important effect illustrated in Fig. 2. For H3O+ and D3O+ both the nuclear center-of-mass and the nuclear center-of-charge lie on the C3 symmetry axis for nuclear geometries with
2v(M) gives rise to another important effect illustrated in Fig. 2. For H3O+ and D3O+ both the nuclear center-of-mass and the nuclear center-of-charge lie on the C3 symmetry axis for nuclear geometries with ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 3v geometrical symmetry.67 We take the C3 axis to be the z axis of the molecule-fixed axis system whose origin, by definition, is at the nuclear center-of-mass. Consequently, at
3v geometrical symmetry.67 We take the C3 axis to be the z axis of the molecule-fixed axis system whose origin, by definition, is at the nuclear center-of-mass. Consequently, at ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 3v-symmetry geometries the dipole moment lies along the z axis and its x- and y-components vanish. The non-zero z-component is responsible for the parallel bands in the spectra of these species, including the rotation-inversion band44 (the pure rotation band is forbidden by symmetry). Botschwina et al.18 estimated the corresponding transition dipole for the inversion 0− ↔ 0+ band to be 1.47 D. Our ab initio value is slightly higher, 1.80 D. For H2DO+ and HD2O+, the center-of-charge obviously is unchanged relative to H3O+ and D3O+ but the center-of-mass is shifted, and this produces a non-vanishing perpendicular dipole moment at
3v-symmetry geometries the dipole moment lies along the z axis and its x- and y-components vanish. The non-zero z-component is responsible for the parallel bands in the spectra of these species, including the rotation-inversion band44 (the pure rotation band is forbidden by symmetry). Botschwina et al.18 estimated the corresponding transition dipole for the inversion 0− ↔ 0+ band to be 1.47 D. Our ab initio value is slightly higher, 1.80 D. For H2DO+ and HD2O+, the center-of-charge obviously is unchanged relative to H3O+ and D3O+ but the center-of-mass is shifted, and this produces a non-vanishing perpendicular dipole moment at ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 3v-symmetry geometries. If we take the x axis to be in the plane defined by the C3 symmetry axis67 and the O–H bond for HD2O+, and in the plane defined by the C3 symmetry axis and the O–D bond for H2DO+, then HD2O+ and H2DO+ acquire non-vanishing x dipole moment components. Therefore the perpendicular transitions (ΔKc = ±1) of H2DO+ and HD2O+ in the vibrational ground state are much stronger than the ΔK = ±1 transitions of H3O+ and D3O+ which are caused by intensity stealing from the vibrational spectrum.67 Besides, this x component is larger for HD2O+ than for H2DO+ owing to the greater displacement of the nuclear center-of-mass. This is probably why the HD2O+ lifetimes are shorter on the average than those of H2DO+. The z dipole moment component also changes with isotopic substitutions, see Fig. 2.
3v-symmetry geometries. If we take the x axis to be in the plane defined by the C3 symmetry axis67 and the O–H bond for HD2O+, and in the plane defined by the C3 symmetry axis and the O–D bond for H2DO+, then HD2O+ and H2DO+ acquire non-vanishing x dipole moment components. Therefore the perpendicular transitions (ΔKc = ±1) of H2DO+ and HD2O+ in the vibrational ground state are much stronger than the ΔK = ±1 transitions of H3O+ and D3O+ which are caused by intensity stealing from the vibrational spectrum.67 Besides, this x component is larger for HD2O+ than for H2DO+ owing to the greater displacement of the nuclear center-of-mass. This is probably why the HD2O+ lifetimes are shorter on the average than those of H2DO+. The z dipole moment component also changes with isotopic substitutions, see Fig. 2.
 | ||
| Fig. 2 Displacements of the center-of-mass (green crosses) upon deuteration of H3O+. Arrows indicate the dipole moment components. | ||
The longest-living states of D3O+ (Table 2) have lifetimes about 27 times longer than those of H3O+. Presumably, this is mainly caused by the fact that D3O+ has lower ro-vibrational term values than H3O+. Thus, D3O+ has lower values of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) if in eqn (3) and this, in turn, causes lower Einstein-A coefficients and higher values of τ [eqn (2) and (3)].
if in eqn (3) and this, in turn, causes lower Einstein-A coefficients and higher values of τ [eqn (2) and (3)].
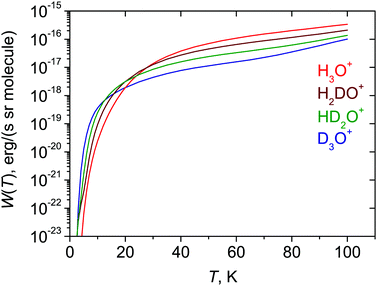
The calculated radiative cooling functions W(T) [eqn (4)] for H3O+ and its deuterated isotopologues are shown in Fig. 3. At temperatures above 30 K the cooling decreases with increasing numbers of deuterium atoms in the molecule. This can be easily understood from eqn (3) and (4): W(T) is proportional to ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) if4, and
if4, and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) if is approximately inversely proportional to the mass of hydrogen for the rotational states populated at the temperatures considered. Therefore, at moderate and high temperatures the lighter isotopologues are better coolers. However, Fig. 3 shows that at lower temperatures their roles change and the deuterated species become the better coolers. This is because the term values of the lowest, infinite-lifetime (and therefore coldest) states vary as 47.03 cm−1 (2,2,E′,0+), 23.79 cm−1 (2,2,E′,0+), 12.19 cm−1 (10,1+,A2), and 11.69 cm−1 (10,1+,A2) for H3O+, D3O+, HD2O+, and H2DO+, respectively. At very low temperatures, the molecules will tend to collect in the lowest accessible state, and the higher the term value of this state, the more difficult it is to cool the isotopologue in question. Because of this, for example, it is more difficult to cool H3O+ than D3O+ at temperatures below 30 K.
if is approximately inversely proportional to the mass of hydrogen for the rotational states populated at the temperatures considered. Therefore, at moderate and high temperatures the lighter isotopologues are better coolers. However, Fig. 3 shows that at lower temperatures their roles change and the deuterated species become the better coolers. This is because the term values of the lowest, infinite-lifetime (and therefore coldest) states vary as 47.03 cm−1 (2,2,E′,0+), 23.79 cm−1 (2,2,E′,0+), 12.19 cm−1 (10,1+,A2), and 11.69 cm−1 (10,1+,A2) for H3O+, D3O+, HD2O+, and H2DO+, respectively. At very low temperatures, the molecules will tend to collect in the lowest accessible state, and the higher the term value of this state, the more difficult it is to cool the isotopologue in question. Because of this, for example, it is more difficult to cool H3O+ than D3O+ at temperatures below 30 K.
4 Conclusions
We have carried out a theoretical study of the ro-vibrational states of the hydronium ion H3O+ and its deuterated isotopologues. Ab initio potential energy and electric dipole moment surfaces were used to calculate ro-vibrational energy levels, corresponding wavefunctions and Einstein coefficients for the low-lying ro-vibrational transitions of these ions. We have analyzed the stability of the ro-vibrational states and computed the radiative lifetimes and cooling functions for temperatures below 200 K.Taking into account only spontaneous emission as a cause of decay of ro-vibrational states (and neglecting collisions and stimulated emission) we find the longest-lived hydronium state for D3O+: the population in the rotational state with (J,K,Γ) = (5,5,E′′) is trapped for 3816.0 years, which is relatively ‘hot’ (152 K), at least in the context of molecular cooling, for example in storage rings. In this work we have identified a number of relatively hot (E/k > 100 K) meta-stable states with a lifetime longer than 10 s (typical timescales of ion storage experiments). Such meta-stable states which will be populated and hamper the cooling of hydronium ions to a temperature of a few Kelvin. The molecule with the shortest-lived meta-stable states is HD2O+ with lifetimes of a few days. The timescale of interstellar collisions in diffuse clouds is longer (about a month), and thus some of these states undergo spontaneous emission.
Our calculations show that deuteration influences significantly the hydronium lifetimes. This effect is mostly caused by the symmetry lowering from ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 3h(M) to
3h(M) to ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) 2v(M) and the ensuing perpendicular dipole moment component. A number of long-living meta-stable states are identified, capable of population trapping. Compared to the deuterated species, the cooling of the lightest isotopologue H3O+ is most efficient at higher temperatures (T > 30 K). However, this changes at very low temperatures where the H3O+ ions are trapped at relatively high energy.
2v(M) and the ensuing perpendicular dipole moment component. A number of long-living meta-stable states are identified, capable of population trapping. Compared to the deuterated species, the cooling of the lightest isotopologue H3O+ is most efficient at higher temperatures (T > 30 K). However, this changes at very low temperatures where the H3O+ ions are trapped at relatively high energy.
The results obtained can be used to assess the cooling properties of the hydronium ion in ion storage rings and elsewhere.
Acknowledgements
This work was supported in part by “The Tomsk State University Academic D. I. Mendeleev Fund Program” grant no. 8.1.51.2015, and in part by the ERC under the Advanced Investigator Project 267219. SNY, JT, and PJ are grateful to the COST action MOLIM (CM1405) for support. We thank Andreas Wolf for suggesting this work.References
- M. Goto, B. J. McCall, T. R. Geballe, T. Usuda, N. Kobayashi, H. Terada and T. Oka, Publ. Astron. Soc. Jpn., 2002, 54, 951–961 CrossRef CAS.
- T. Oka, T. R. Geballe, M. Goto, T. Usuda and B. J. McCall, Astrophys. J., 2005, 632, 882–893 CrossRef CAS.
- H. Kreckel, S. Krohn, L. Lammich, M. Lange, J. Levin, M. Scheffel, D. Schwalm, J. Tennyson, Z. Vager, R. Wester, A. Wolf and D. Zajfman, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 052509 CrossRef.
- H. Kreckel, D. Schwalm, J. Tennyson, A. Wolf and D. Zajfman, New J. Phys., 2004, 6, 151 CrossRef.
- L. H. Andersen, O. Heber, D. Kella, H. B. Pedersen, L. Vejby-Christensen and D. Zajfman, Phys. Rev. Lett., 1996, 77, 4891–4894 CrossRef PubMed.
- A. Neau, A. Al Khalili, S. Rosén, A. Le Padellec, A. M. Derkatch, W. Shi, L. Vikor, M. Larsson, J. Semaniak, R. Thomas, M. B. Någård, K. Andersson, H. Danared and M. af Ugglas, J. Chem. Phys., 2000, 113, 1762–1770 CrossRef CAS.
- M. J. Jensen, R. C. Bilodeau, C. P. Safvan, K. Seiersen, L. H. Andersen, H. B. Pedersen and O. Heber, Astrophys. J., 2000, 543, 764–774 CrossRef CAS.
- H. Buhr, J. Stuetzel, M. B. Mendes, O. Novotny, D. Schwalm, M. H. Berg, D. Bing, M. Grieser, O. Heber, C. Krantz, S. Menk, S. Novotny, D. A. Orlov, A. Petrignani, M. L. Rappaport, R. Repnow, D. Zajfman and A. Wolf, Phys. Rev. Lett., 2010, 105, 103202 CrossRef CAS PubMed.
- O. Novotny, H. Buhr, J. Stuetzel, M. B. Mendes, M. H. Berg, D. Bing, M. Froese, M. Grieser, O. Heber, B. Jordon-Thaden, C. Krantz, M. Lange, M. Lestinsky, S. Novotny, S. Menk, D. A. Orlov, A. Petrignani, M. L. Rappaport, A. Shornikov, D. Schwalm, D. Zajfman and A. Wolf, J. Phys. Chem. A, 2010, 114, 4870–4874 CrossRef CAS PubMed.
- R. J. Barber, S. Miller, N. Dello Russo, M. J. Mumma, J. Tennyson and P. Guio, Mon. Not. R. Astron. Soc., 2012, 425, 21–33 CrossRef.
- E. A. Michael, C. J. Keoshian, D. R. Wagner, S. K. Anderson and R. J. Saykally, Chem. Phys. Lett., 2001, 338, 277–284 CrossRef CAS.
- J. R. Goicoechea and J. Cernicharo, Astrophys. J., 2001, 554, L213–L216 CrossRef CAS.
- T. G. Phillips, E. F. van Dishoeck and J. Keene, Astrophys. J., 1992, 399, 533–550 CrossRef CAS.
- H. Lischka and V. Dyczmons, Chem. Phys. Lett., 1973, 23, 167–177 CrossRef CAS.
- W. I. Ferguson and N. C. Handy, Chem. Phys. Lett., 1980, 71, 95–100 CrossRef CAS.
- V. Špirko and P. R. Bunker, J. Mol. Spectrosc., 1982, 95, 226–235 CrossRef.
- M. H. Begemann, C. S. Gudeman, J. Pfaff and R. J. Saykally, Phys. Rev. Lett., 1983, 51, 554–557 CrossRef CAS.
- P. Botschwina, P. Rosmus and E.-A. Reinsch, Chem. Phys. Lett., 1983, 102, 299–306 CrossRef CAS.
- M. Bogey, C. Demuynck, M. Denis and J. L. Destombes, Astron. Astrophys., 1985, 148, L11–L13 CAS.
- P. B. Davies, P. A. Hamilton and S. A. Johnson, Astron. Astrophys., 1984, 141, L9–L10 CAS.
- P. R. Bunker, T. Amano and V. Špirko, J. Mol. Spectrosc., 1984, 107, 208–211 CrossRef CAS.
- M. H. Begemann and R. J. Saykally, J. Chem. Phys., 1985, 82, 3570–3579 CrossRef CAS.
- D. J. Liu and T. Oka, Phys. Rev. Lett., 1985, 54, 1787–1789 CrossRef CAS PubMed.
- G. M. Plummer, E. Herbst and F. C. De Lucia, J. Chem. Phys., 1985, 83, 1428–1429 CrossRef CAS.
- P. B. Davies, S. A. Johnson, P. A. Hamilton and T. J. Sears, Chem. Phys., 1986, 108, 335–341 CrossRef CAS.
- D. J. Liu, T. Oka and T. J. Sears, J. Chem. Phys., 1986, 84, 1312–1316 CrossRef CAS.
- M. Gruebele, M. Polak and R. J. Saykally, J. Chem. Phys., 1987, 87, 3347–3351 CrossRef CAS.
- N. N. Haese, D. J. Liu and T. Oka, J. Mol. Spectrosc., 1988, 130, 262–263 CrossRef CAS.
- P. Verhoeve, J. J. Termeulen, W. L. Meerts and A. Dymanus, Chem. Phys. Lett., 1988, 143, 501–504 CrossRef CAS.
- M. Okumura, L. I. Yeh, J. D. Myers and Y. T. Lee, J. Chem. Phys., 1990, 94, 3416–3427 CrossRef CAS.
- H. Petek, D. J. Nesbitt, J. C. Owrutsky, C. S. Gudeman, X. Yang, D. O. Harris, C. B. Moore and R. J. Saykally, J. Chem. Phys., 1990, 92, 3257–3260 CrossRef CAS.
- W. C. Ho, C. J. Pursell and T. Oka, J. Mol. Spectrosc., 1991, 149, 530–541 CrossRef CAS.
- D. Uy, E. T. White and T. Oka, J. Mol. Spectrosc., 1997, 183, 240–244 CrossRef CAS PubMed.
- M. Araki, H. Ozeki and S. Saito, Mol. Phys., 1999, 97, 177–183 CrossRef CAS.
- G. M. Chaban, J. O. Jung and R. B. Gerber, J. Phys. Chem. A, 2000, 104, 2772–2779 CrossRef CAS.
- Y. Aikawa, N. Ohashi, S. Inutsuka, E. Herbst and S. Takakuwa, Astrophys. J., 2001, 552, 639–653 CrossRef CAS.
- V. A. Ermoshin, A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 2002, 356, 556–562 CrossRef CAS.
- P. Caselli, C. M. Walmsley, A. Zucconi, M. Tafalla, L. Dore and P. C. Myers, Astrophys. J., 2002, 565, 344–358 CrossRef CAS.
- T. Rajamäki, A. Miani and L. Halonen, J. Chem. Phys., 2003, 118, 6358–6369 CrossRef.
- X. C. Huang, S. Carter and J. Bowman, J. Chem. Phys., 2003, 118, 5431–5441 CrossRef CAS.
- S. N. Yurchenko, P. R. Bunker and P. Jensen, J. Mol. Struct.: THEOCHEM, 2005, 742, 43–48 CrossRef CAS.
- F. Dong and D. J. Nesbitt, J. Chem. Phys., 2006, 125, 144311 CrossRef PubMed.
- T. Furuya and S. Saito, J. Chem. Phys., 2008, 128, 034311 CrossRef PubMed.
- S. Yu, B. J. Drouin, J. C. Pearson and H. M. Pickett, Astrophys. J. Suppl. Ser., 2009, 180, 119–124 CrossRef CAS.
- H. S. P. Müller, F. Dong, D. J. Nesbitt, T. Furuya and S. Saito, Phys. Chem. Chem. Phys., 2010, 12, 8362–8372 RSC.
- A. S. Petit, B. A. Wellen and A. B. McCoy, J. Chem. Phys., 2012, 136, 074101 CrossRef PubMed.
- L. Neale, S. Miller and J. Tennyson, Astrophys. J., 1996, 464, 516–520 CrossRef CAS.
- S. Miller, T. Stallard, H. Melin and J. Tennyson, Faraday Discuss., 2010, 147, 283–291 RSC.
- S. Miller, T. Stallard, J. Tennyson and H. Melin, J. Phys. Chem. A, 2013, 117, 9770–9777 CrossRef CAS PubMed.
- A. Owens, S. N. Yurchenko, O. L. Polyansky, R. I. Ovsyannikov, W. Thiel and V. Špirko, Mon. Not. R. Astron. Soc., 2015, 454, 2292–2298 CrossRef.
- S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2007, 245, 126–140 CrossRef CAS.
- J. Tennyson, K. Hulme, O. K. Naim and S. N. Yurchenko, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 044002 CrossRef.
- J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2012, 425, 21–33 CrossRef CAS.
- J. Tennyson, S. N. Yurchenko, A. F. Al-Refaie, E. J. Barton, K. L. Chubb, P. A. Coles, S. Diamantopoulou, M. N. Gorman, C. Hill, A. Z. Lam, L. Lodi, L. K. McKemmish, Y. Na, A. Owens, O. L. Polyansky, T. Rivlin, C. Sousa-Silva, D. S. Underwood, A. Yachmenev and E. Zak, J. Mol. Spectrosc., 2016, 327, 73–94 CrossRef CAS.
- S. N. Yurchenko, W. Thiel and P. Jensen, J. Mol. Spectrosc., 2007, 245, 126–140 CrossRef CAS.
- S. N. Yurchenko, M. Carvajal, A. Yachmenev, W. Thiel and P. Jensen, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 2279–2290 CrossRef CAS.
- C. Sousa-Silva, S. N. Yurchenko and J. Tennyson, J. Mol. Spectrosc., 2013, 288, 28–37 CrossRef CAS.
- D. S. Underwood, J. Tennyson and S. N. Yurchenko, Phys. Chem. Chem. Phys., 2013, 15, 10118–10125 RSC.
- D. S. Underwood, S. N. Yurchenko, J. Tennyson and P. Jensen, J. Chem. Phys., 2014, 140, 244316 Search PubMed.
- C. Sousa-Silva, A. F. Al-Refaie, J. Tennyson and S. N. Yurchenko, Mon. Not. R. Astron. Soc., 2015, 446, 2337–2347 CrossRef.
- A. Y. Adam, A. Yachmenev, S. N. Yurchenko and P. Jensen, J. Chem. Phys, 2015, 143, 244306 CrossRef PubMed.
- S. N. Yurchenko, R. J. Barber, A. Yachmenev, W. Thiel, P. Jensen and J. Tennyson, J. Phys. Chem. A, 2009, 113, 11845–11855 CrossRef CAS PubMed.
- S. N. Yurchenko, R. J. Barber and J. Tennyson, Mon. Not. R. Astron. Soc., 2011, 413, 1828–1834 CrossRef CAS.
- T. Rajamäki, J. Noga, P. Valiron and L. Halonen, Mol. Phys., 2004, 102, 2259–2268 CrossRef.
- J. Tang and T. Oka, J. Mol. Spectrosc., 1999, 196, 120–130 CrossRef CAS PubMed.
- J. W. Cooley, Math. Comput., 1961, 15, 363 Search PubMed.
- P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, 2nd edn, 1998 Search PubMed.
- R. R. Gamache and L. S. Rothman, J. Quant. Spectrosc. Radiat. Transfer, 1992, 48, 519–525 CrossRef CAS.
- S. N. Yurchenko, W. Thiel, M. Carvajal, H. Lin and P. Jensen, Adv. Quantum Chem., 2005, 48, 209–238 CrossRef.
- P. Jensen, J. Mol. Spectrosc., 1988, 132, 429–457 CrossRef CAS.
- M. Araki, H. Ozeki and S. Saito, J. Chem. Phys., 1998, 109, 5707–5709 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04661d |
| This journal is © the Owner Societies 2016 |