Tuning thermal transport in Si nanowires by isotope engineering

Abstract

We study thermal transport in isotopically disordered Si nanowires, discussing the feasibility of phonon engineering for thermoelectric applications within these systems. To this purpose, we carry out atomistic molecular dynamics and nonequilibrium Green's function calculations to characterize the dependence of the thermal conductance as a function of the isotope concentration, isotope radial distribution and temperature. We show that a reduction of the conductivity of up to 20% can be achieved with suitable isotope blends at room temperature and approximately 50% at low temperature. Interestingly, precise control of the isotope composition or radial distribution is not needed. An isotope disordered nanowire roughly behaves like a low-pass filter, as isotope impurities are transparent for long wave-length acoustic phonons, while only mid- and high-frequency optical phonons undergo significant scattering.

---

In the quest for renewable energy sources, thermoelectricity is one of the most appealing alternatives and has long been sought for.^1–5 Heat is the most pervasive form that energy takes in our world, but regretfully is also the one that we are less able to govern. As a matter of fact, despite its ubiquitous nature, heat is normally related to the concept of dissipation and is regarded as a source of loss. The conversion of heat into electricity is possibly the ideal paradigm of a clean energy source: heat is freely available and is often the product of other energy conversion processes, such as the friction within the bearings of a mechanical engine or Joule heating in an electric circuit.

The thermoelectric efficiency of a semiconductor is given by the dimensionless figure of merit:

where S is the Seebeck coefficient, T is the temperature, and σ and κ are electrical and thermal conductivity. Hence, an efficient thermoelectric device simultaneously requires a high σ and a low κ. Unfortunately, however, the electrical and the thermal conductivities are magnitudes that normally exhibit a high degree of correlation and any attempt at increasing σ leads to an increase in κ and vice versa. Semiconducting nanowires^6,7 have been proved to be a promising platform for such kinds of applications, because phonons can be scattered off the surface, while electrons are mostly confined to one-dimensional motion along the conductor axis.⁸ It follows that, as the conductor size shrinks down, surface scattering becomes increasingly important for phonon mobility, pushing it down, while electrical conductivity will be mostly preserved, thus partially decoupling σ and κ. Indeed, a ZT value around 1 was reported for Si nanowires (an approximately 100-fold improvement over bulk Si).^9,10

A textbook approach to further increase ZT of a semiconductor involves isotope blends, either disordered or in the form of ordered superlattices. Isotopes have different masses, but the same electron shell configuration. Therefore, the electrical conductivity, σ, is preserved, while – as by adding different isotopes one is adding scattering centers for the incoming phonons – κ will decrease, leading to the corresponding increase of ZT. However, controlling the isotopic composition of a material is challenging and this strategy is normally implemented with SiGe alloys: Ge has an atomic mass that is roughly 2.5 times larger than Si and the same valence electron shell. Yet, as demonstrated in a recent study, the effect of Ge impurities on the electrical conductivity cannot be completely neglected.¹¹ To date, there have been only a few theoretical studies on the effect of the isotopic composition of nanowires and they are restricted to idealized structures, namely relying on very small computational cells where realistic disorder cannot be described¹² or to ordered superlattices whose practical realization is very challenging.¹³

Isotope engineering can be a powerful paradigm to manipulate some of the important physical properties of semiconducting nanowires and exploit them in innovative device structures.^14–17 Recently, Mukherjee and coworkers¹⁸ reported an unprecedented control of isotope concentration and distribution in Si nanowires. Raman nanothermometry measurements yield thermal conductivities considerably lower than in isotope purified nanowires of similar diameter. In this article we carry out atomistic molecular dynamics and nonequilibrium Green's function calculations of Si nanowires with isotopic disorder and study the dependence of their thermal conductivity on the isotope concentration, isotope radial distribution and temperature. We show that reductions of the thermal conductivity in the 20–50% range can be achieved, depending on the operation temperature.

Computational methods

We perform approach-to-equilibrium molecular dynamics (AEMD) calculations.¹⁹ This method, extensively described in the ESI† and by Melis and coworkers,²⁰ consists in driving the system to a suitable nonequilibrium condition and then studying the transient that takes it to equilibrium. In this work we use a velocity rescaling algorithm to equilibrate half of the system to a temperature T₀ + ΔT/2 and half of the system to T₀ − ΔT/2. After a long enough equilibration, all temperature constraints are released and the system is left free to evolve microcanonically and reach equilibrium at T₀. The time dependence of the temperature difference between the two halves can be fitted to the analytical solution of the heat equation. One of the fitting parameters is the thermal diffusivity, [small kappa, Greek, macron] which in turn gives the thermal conductivity as κ = ρC_v[small kappa, Greek, macron], where ρ is the atomic density and C_v is the specific heat capacity; the latter is renormalized to include quantum corrections. The energy and the forces are calculated within the environment-dependent interatomic potential (EDIP).²¹ The full simulation protocol plus additional details of the AEMD calculations can be found in the ESI.†

We also perform nonequilibrium Green's function (NEGF) calculations in the harmonic approximation. There the NW is partitioned into a scattering region (channel) and two reservoirs (contacts) that are held at a constant temperature. We compute the key magnitude in the NEGF approach, the phonon transmission function, Ξ(ω), from which we estimate the thermal conductance of the system in the limit of small temperature difference with the Landauer formula,

where the last quotient of exponential functions stems from the temperature derivative of the Bose–Einstein phonon distribution function.

In order to obtain Ξ(ω), we need to calculate first the Green's function of the semi-infinite contacts, which we do by means of an efficient iterative method.²² Then, the effect of the contacts is incorporated into the channel Green's function as a self-energy correction. As for the AEMD calculations, we use the EDIP potential to obtain the force-constant matrix elements necessary for the NEGF calculations. The formulas employed to calculate Green's functions and the phonon transmission are standard and can be found elsewhere,^23,24 a detailed description of the methodology employed here is presented in the ESI† for the sake of completeness.

Dependence of κ on the composition

The first goal of this work was characterizing the dependence of the thermal conductivity on the degree of isotope purity. We studied ²⁸Si_x³⁰Si_1−x NWs with x varying from 0 to 1 (which correspond to ³⁰Si and ²⁸Si isotope purified NWs, respectively). This is the same isotope blend used in recent experiments.¹⁸

Similar to other molecular dynamics techniques,²⁵ a converged estimate of the thermal conductivity by means of the approach-to-equilibrium methodology employed here requires very large simulation cells, which are often beyond current computational capabilities. Not only these cells must be large enough to fit all the long wavelength phonons whose contribution to thermal transport is not negligible; they must also account properly for the anharmonic phonon–phonon scattering, i.e. they must be larger than the phonon mean free path. An effective workaround consists in performing a series of calculations in increasingly long nanowires and studying 1/κ as a function of 1/L_z. If the simulation cells considered are sufficiently large, the dependence is linear²⁵ and it is easy to extrapolate the value of κ for an infinitely long nanowire (1/L_z → 0). We followed this procedure for each of the blends considered, studying 90, 180, 450, and 900 nm long NWs with a diameter of 10 nm (see Fig. 1a for the κ⁻¹(L_z⁻¹) dependence of a subset of the values of x considered). For this set of calculations T₀ and ΔT are fixed at 300 K and 200 K, respectively.

Fig. 1 (a) Dependence of κ on L_z in ²⁸Si_x³⁰Si_1−x NWs for a subset of the concentrations x investigated. Extrapolating κ⁻¹(L_z⁻¹) for L_z⁻¹ → 0 gives an estimate of κ for an infinitely large computational cell. (b) κ of a ²⁸Si_x³⁰Si_1−x NW as a function of the composition. (c) Thermal conductivity accumulation function for the values of x selected in panel (a). The inset shows a zoom of the curves in the indicated region.

Because of the intrinsically random nature of the isotope distribution, for the 90 nm and the 180 nm ²⁸Si_0.4³⁰Si_0.6 NW we generated four independent samples and calculated the thermal conductivity for each of them to assess to what extent κ depended on the specific realization of a given blend. We obtained variations in the thermal conductivity of at most 1.5% (standard deviations of 0.05 and 0.02 for the 90 and 180 nm NW, respectively) and thus concluded that the sample-to-sample fluctuations of κ can be neglected. Notice that these fluctuations will further decrease in the longer NWs. Therefore, unless where noted, our calculations of the thermal conductivity refer to an individual, randomly generated structure for each isotope blend and NW length.

The results of the dependence of κ on the isotope composition are summarized in Fig. 1b. This figure conveys a couple of interesting indications. The first is quantitative: suitable isotope blends result in a decrease of ∼20% of the thermal conductivity with respect to the isotope purified NWs. The second is that such a decrease does not depend on the exact ratio of Si²⁸ and Si³⁰ isotopes: as long as x falls in the 0.3–0.6 range, the thermal conductivity has approximately the same value. A similar dependence has been previously reported for Si_1−xGe_x alloys.^26–28 This is an important result, because it means that to achieve the maximum decrease of κ a precise control of the isotope composition is not needed.

The thermal conductivity accumulation function (TCAF), defined as the ratio between κ(L_z) and its extrapolated value for L_z → ∞, is plotted in Fig. 1c for some of the blends considered and for the isotope purified NWs. The TCAF provides valuable information about the phonon mean free path (MFP) contribution to the thermal conductivity. By looking at the value of L_z for which the TCAF is, say, 0.5, we know that half of the thermal conductivity is built up by phonons with MFP up to L_z, because they can be described by computational cells of that length. We compared the TCAF for all the isotope blends studied and the isotope purified NWs. It is easy to see that, in general, the same amount of thermal conductivity is accounted for by phonons with shorter MFP in NWs with isotope blends (see the inset of Fig. 1c for this analysis at TCAF = 0.9). Notice that the differences tend to vanish for x = 0.4−0.6, in agreement with the trend of κ(x), which is minimum in the same concentration range.

Next, we performed a series of calculations where we varied the equilibrium temperature. The two halves of the system are still equilibrated at T₀ + ΔT/2 and T₀ − ΔT/2, with ΔT = 200 K like previously described, but T₀ now goes from 150 to 500. In these calculations we restricted to ²⁸Si_0.5³⁰Si_0.5 and an isotope purified ²⁸Si NW of length 180 nm. The results, plotted in Fig. 2, show the expected increase of κ with temperature due to the increment in phonon population, followed by its decrease, as a result of increased phonon–phonon scattering, for both wires. However, this decrease is more pronounced for the ²⁸Si NW (the inset of Fig. 2), so that anharmonic scattering, more efficient at higher temperatures, attenuates the reduction of κ by isotope scattering.

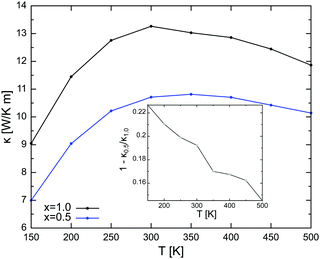Fig. 2 Dependence of κ on temperature in a ²⁸Si_x³⁰Si_1−x NW for x = 0.5 and x = 1. Inset: Reduction of κ by isotope engineering as a function of temperature.

We expect these results to be qualitatively valid at larger diameters as well. Even going beyond a pure Matthiessen's rule picture of thermal transport, where the different scattering mechanisms operate in parallel, the possible coupling between the lifetime of boundary scattering (the one that changes when the diameter increases) and the lifetime of scattering with impurities (isotopes, in our case) should yield very minor corrections.

Harmonic scattering by NEGF

The molecular dynamics calculations discussed thus far have the advantage that all orders of anharmonicity of phonon–phonon scattering are naturally included. Their accuracy is only limited by the reliability of the potential and by the fact that the dynamics is classic, thus at low temperatures quantum effects cannot be neglected. Yet, we partially account for the latter effect by renormalizing the specific heat capacity (see the ESI†).

NEGF provides a complementary description valid in the low temperature regime: the phonon population is described by a Bose–Einstein distribution, the proper quantum statistics, and anharmonic effects, which are not accounted for, can be neglected. Most importantly, within this approach it is straightforward to track the behavior of phonons in a given frequency range and see where the reduction of thermal conductivity originates from.

Due to huge computational effort required to calculate the force-constant matrix and then the transmission function in NWs of the same size of those considered in the molecular dynamics study, we have carried out these calculations in a thinner NW. Our case study is a 3 nm thick NW with ²⁸Si contacts and a central ²⁸Si_x³⁰Si_1−x scattering region with x = 1 (homogeneous ²⁸Si NW, no scattering), 0.6 and 0.3. See the ESI† for a sketch of the computational setup.

In the absence of scattering centers, i.e. within a perfect, homogeneous medium, the vibrational eigenstates of the ²⁸Si NW transmit with probability equal to one and the conductance only depends on the number of phonon bands at that energy (black line in Fig. 3a). The addition of impurities, a random distribution of substitutional ³⁰Si atoms in our case, results in a degradation of the phonon transmission, which in turn depends on the elastic scattering that each phonon of the ²⁸Si NW suffers (blue and red lines in Fig. 3a).

Fig. 3 (a) Phonon transmission of a ²⁸Si_x³⁰Si_1−x NW for x = 0.3 and x = 0.6 compared to the case of a homogeneous ²⁸Si NW. (b) Frequency transfer function of the isotope blends of panel (a) showing that ³⁰Si isotopes are transparent (F(ω) = 1) for the low-frequency phonons of a ²⁸Si NW. (c) Thermal conductance as a function of temperature calculated plugging the transmission function of panel (a) into eqn (2).

Because of their higher group velocity, acoustic phonons carry most of the heat, and the contribution of optical phonons is even disregarded within the crudest models of heat transport. When a sizable reduction of the thermal conductivity is observed, it is then natural to assume that acoustic phonons undergo a strong scattering. Isotope scattering does not work in this way: acoustic phonons are almost unaffected and it is the scattering suffered by optical phonons with ω > 20 THz that is almost entirely responsible for the reduction of thermal conductance (see, e.g., the frequency transfer function in Fig. 3b). A substitutional isotope defect does not distort the host lattice, thus scattering mostly comes from short wavelength phonons. These results are in qualitative agreement with previous reports of isotope scattering in BN nanotubes, which also highlighted the role of optical phonon scattering,¹⁵ and suggest that isotope engineering can be used to implement a phonon low-pass filter that mostly suppresses midrange and high phonon frequencies. This effect is expected to be more important as one increases the length of the scattering region and approaches a diffusive regime.¹⁴

The computed conductance as a function of temperature is shown in Fig. 3c. In the harmonic approximation the reduction is even larger than in our AEMD results and is about 50%. We have already shown that increasing the temperature, i.e. the anharmonic effects, results in a lower decrease of κ upon the introduction of isotope disorder. Accordingly, a full suppression of anharmonicity yields the largest reduction of the thermal conductance. Notice that also within a NEGF description the dependence on the composition is almost negligible (Fig. 3c).

Dependence of κ on the radial distribution

In the last part of our study we address explicitly the effect that a nonuniform radial profile of the isotope distribution has on the thermal conductivity. This radial distribution, with accumulation of light isotopes at the surface and heavy isotopes at the core, was observed by Mukherjee and coworkers¹⁸ in their experiments and was attributed to specific features of the Au catalyzed vapor–liquid–solid growth of the nanowires. Preliminary analysis carried out in the same group indicates that the isotopes are uniformly distributed in Al-catalyzed Si NWs,²⁹ thus suggesting that the radial distribution of the isotopes can be controlled, at least to some extent, by selecting the catalytic nanoparticle.

We generate samples of ²⁸Si_x³⁰Si_1−x NWs, with an overall content of ²⁸Si x = 0.4, but with the following isotope distribution: for r < 1.5 nm, x = 0.25; for 1.5 nm < r < 3.75 nm, x grows linearly from 0.25 to 0.55; for 3.75 nm < r < R, x = 0.55, where r is the radial coordinate and R is the NW radius. We compare these results with wires with the same overall isotopic composition, x = 0.4, but with a uniform radial distribution (see Fig. 4). The isotope purified NW used as a reference by Mukherjee and coworkers was a ²⁹Si NW, and we calculated its thermal conductivity as well. The estimate of κ follows the same procedure described above and relies on the linear extrapolation of four calculated values of κ(L_z), with L_z varying from 90 to 900 nm (see Fig. 5). κ(L_z) of the shorter wires (L_z = 90 and 180 nm), where, as discussed above, the variability is a more important effect, was averaged over four independently generated samples. We obtain values of κ of both radial distributions, 14.6 and 14.9 W m⁻¹ s⁻¹, within the uncertainties of the calculation, a reduction of ∼22% with respect to the isotope purified ²⁹Si NW.¹⁸ The nonuniform mixing of ²⁸Si and ³⁰Si during the growth was suggested to be responsible for the excess broadening of the Raman spectra of the ²⁸Si_x³⁰Si_1−x NWs. Nevertheless, our calculations suggest that such a nonuniform mixing does not translate into a sizable variation of the thermal conductivity.

Fig. 4 Radial profiles of a ²⁸Si_0.4³⁰Si_0.6 NW similar to those of ref. 18. (a) Uniform distribution and (b) accumulation of heavy isotopes in the wire core.

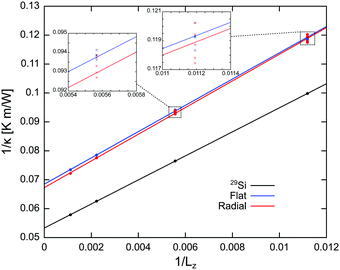Fig. 5 κ as a function of L_z for the radial distributions of Fig. 4. The insets show the dispersion for the shorter wires where we calculated κ in four independently generated samples. The thermal conductivity of an isotope purified ²⁹Si NW, like the one used for comparison in ref. 18, is also shown.

The nanowires used in the experiments of ref. 18 have a larger diameter than those considered here, thus we cannot rule that measurable differences in κ for different radial isotope distributions emerge for thicker wires. However, this does not seem likely. Nanowires with a radial concentration profile like that of Fig. 4b can be seen as coaxial structures with a ²⁸Si_0.25³⁰Si_0.75 core and a ²⁸Si_0.55³⁰Si_0.45 shell (and a transition region of 1.5 nm between the two). We have shown that ²⁸Si_x³⁰Si_1−x NWs with x = 0.25 and x = 0.55 have roughly the same thermal conductivity (see Fig. 1b), thus it is not unexpected that radial distributions of the kind of Fig. 4b result in values of κ that are similar to the case of a radially uniform profile with the same overall composition. This behavior is thus not expected to exhibit a sizable dependence on the nanowire diameter.

In summary, we have studied thermal transport in isotopically disordered Si NWs. We have shown that the thermal conductivity in ²⁸Si_x³⁰Si_1−x NWs decreases of ∼20% with respect to isotope purified ²⁸Si or ³⁰Si wires as long as 0.3 < x < 0.6; the reduction of the thermal conductivity tends to become less efficient as the temperature is increased. At low temperature, on the other hand, where anharmonic effects can be neglected, the decrease of the thermal conductivity can be as large as 50%. The radial distribution of the isotope content, reported in recent experiments, does not yield a measurable difference in the thermal conductivity, which only depends on the overall concentration and on the temperature. Low-frequency acoustic phonons are transparent to isotope disorder and scattering affects exclusively mid- and high-frequency optical phonons. We expect that these results, together with the unprecedented control of isotope composition of Si nanowires recently achieved,¹⁸ will stimulate a thorough experimental verification of these predictions and will possibly pave the way to the engineering of novel thermoelectric devices.

Acknowledgements

We thank Luciano Colombo for useful discussions. We acknowledge financial support from the Ministerio de Economía y Competitividad (MINECO) under grant FEDER-MAT2013-40581-P and the Severo Ochoa Centres of Excellence Program under Grant SEV-2015-0496 and from the Generalitat de Catalunya under grants no. 2014 SGR 301 and through the Beatriu de Pinós fellowship program (2014 BP_B 00101). The calculations were performed at the Barcelona Supercomputing Center (BSC-CNS) within the project “Thermal transport in isotopically disordered Si nanowires (FI-2016-1-0022)”.

References

1. S. Riffat and X. Ma, Appl. Therm. Eng., 2003, 23, 913–935.
2. M. S. Dresselhaus, G. Chen, M. Y. Tang, R. G. Yang, H. Lee, D. Z. Wang, Z. F. Ren, J.-P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043–1053.
3. A. Shakouri, Annu. Rev. Mater. Res., 2011, 41, 399–431.
4. M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2012, 5, 5147–5162.
5. N. Li, J. Ren, L. Wang, G. Zhang, P. Hänggi and B. Li, Rev. Mod. Phys., 2012, 84, 1045–1066.
6. W. Lu and C. M. Lieber, J. Phys. D: Appl. Phys., 2006, 39, R387–R406.
7. R. Rurali, Rev. Mod. Phys., 2010, 82, 427–449.
8. L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16631–16634.
9. A. I. Hochbaum, R. Chen, R. D. Delgado, W. Liang, E. C. Garnett, M. Najarian, A. Majumdar and P. Yang, Nature, 2008, 451, 163–167.
10. A. I. Boukai, Y. Bunimovich, J. Tahir-Kheli, J.-K. Yu, W. A. Goddard III and J. R. Heath, Nature, 2008, 451, 168–171.
11. M. Amato, S. Ossicini and R. Rurali, Nano Lett., 2012, 12, 2717–2721.
12. J. Hattori and S. Uno, Jpn. J. Appl. Phys., 2013, 52, 04CN04.
13. N. Yang, G. Zhang and B. Li, Nano Lett., 2008, 8, 276–280.
14. I. Savić, N. Mingo and D. A. Stewart, Phys. Rev. Lett., 2008, 101, 165502.
15. D. A. Stewart, I. Savić and N. Mingo, Nano Lett., 2009, 9, 81–84.
16. L. Lindsay, D. A. Broido and T. L. Reinecke, Phys. Rev. Lett., 2012, 109, 095901.
17. Z. Yang, R. Feng, F. Su, D. Hu and X. Ma, Phys. E, 2014, 64, 204–210.
18. S. Mukherjee, U. Givan, S. Senz, A. Bergeron, S. Francoeur, M. de la Mata, J. Arbiol, T. Sekiguchi, K. M. Itoh, D. Isheim, D. N. Seidman and O. Moutanabbir, Nano Lett., 2015, 15, 3885–3893.
19. E. Lampin, P. L. Palla, P.-A. Francioso and F. Cleri, J. Appl. Phys., 2013, 114, 033525.
20. C. Melis, R. Dettori, S. Vandermeulen and L. Colombo, Eur. Phys. J. B, 2014, 87, 96.
21. M. Z. Bazant, E. Kaxiras and J. F. Justo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8542–8552.
22. M. L. Sancho, J. L. Sancho and J. Rubio, J. Phys. F: Met. Phys., 1984, 14, 1205.
23. M. Pourfath, The Non-Equilibrium Green's Function Method for Nanoscale Device Simulation, Springer, 2014.
24. S. Sadasivam, Y. Che, Z. Huang, L. Chen, S. Kumar and T. S. Fisher, Annu. Rev. Heat Transfer, 2014, 17, 89–145.
25. P. K. Schelling, S. R. Phillpot and P. Keblinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144306.
26. J. Garg, N. Bonini, B. Kozinsky and N. Marzari, Phys. Rev. Lett., 2011, 106, 045901.
27. C. Melis and L. Colombo, Phys. Rev. Lett., 2014, 112, 065901.
28. M. Amato, M. Palummo, R. Rurali and S. Ossicini, Chem. Rev., 2014, 114, 1371–1412.
29. O. Moutanabbir, private communication.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04581b

---