Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gd(III) and Mn(II) complexes for dynamic nuclear polarization: small molecular chelate polarizing agents and applications with site-directed spin labeling of proteins†
Monu
Kaushik
ab,
Thorsten
Bahrenberg‡
ab,
Thach V.
Can
c,
Marc A.
Caporini§
d,
Robert
Silvers
bce,
Jörg
Heiliger
ab,
Albert A.
Smith¶
c,
Harald
Schwalbe
be,
Robert G.
Griffin
c and
Björn
Corzilius
*abc
aInstitute of Physical and Theoretical Chemistry and Institute of Biophysical Chemistry, Goethe University Frankfurt, Max-von-Laue-Str. 7-9, 60438 Frankfurt am Main, Germany. E-mail: corzilius@em.uni-frankfurt.de
bCenter for Biomolecular Magnetic Resonance (BMRZ), Goethe University Frankfurt, Max-von-Laue-Str. 9, 60438 Frankfurt am Main, Germany
cFrancis Bitter Magnet Laboratory and Department of Chemistry, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA
dBruker Biospin Ltd., Billerica, Massachusetts 01821, USA
eInstitute of Organic Chemistry and Chemical Biology, Goethe University Frankfurt, Max-von-Laue-Str. 7, 60438 Frankfurt am Main, Germany
First published on 12th August 2016
Abstract
We investigate complexes of two paramagnetic metal ions Gd3+ and Mn2+ to serve as polarizing agents for solid-state dynamic nuclear polarization (DNP) of 1H, 13C, and 15N at magnetic fields of 5, 9.4, and 14.1 T. Both ions are half-integer high-spin systems with a zero-field splitting and therefore exhibit a broadening of the mS = −1/2 ↔ +1/2 central transition which scales inversely with the external field strength. We investigate experimentally the influence of the chelator molecule, strong hyperfine coupling to the metal nucleus, and deuteration of the bulk matrix on DNP properties. At small Gd-DOTA concentrations the narrow central transition allows us to polarize nuclei with small gyromagnetic ratio such as 13C and even 15N via the solid effect. We demonstrate that enhancements observed are limited by the available microwave power and that large enhancement factors of >100 (for 1H) and on the order of 1000 (for 13C) can be achieved in the saturation limit even at 80 K. At larger Gd(III) concentrations (≥10 mM) where dipolar couplings between two neighboring Gd3+ complexes become substantial a transition towards cross effect as dominating DNP mechanism is observed. Furthermore, the slow spin-diffusion between 13C and 15N, respectively, allows for temporally resolved observation of enhanced polarization spreading from nuclei close to the paramagnetic ion towards nuclei further removed. Subsequently, we present preliminary DNP experiments on ubiquitin by site-directed spin-labeling with Gd3+ chelator tags. The results hold promise towards applications of such paramagnetically labeled proteins for DNP applications in biophysical chemistry and/or structural biology.
Introduction
Dynamic nuclear polarization
Over the last two decades high field dynamic nuclear polarization (DNP) has emerged as a prominent field of research and has impacted approaches to solution NMR, solid-state or magic-angle spinning (MAS) NMR, electron paramagnetic resonance (EPR), and magnetic resonance imaging (MRI). Furthermore, DNP has spawned fundamental investigations and new applications in each of these areas. For example, the development of the instrumentation for MAS DNP at high magnetic fields1–4 has catalyzed fundamental studies of quantum mechanical properties of spin-systems,5–14 applications in materials science15–20 and structural biology.21–30DNP polarizing agents and field profiles
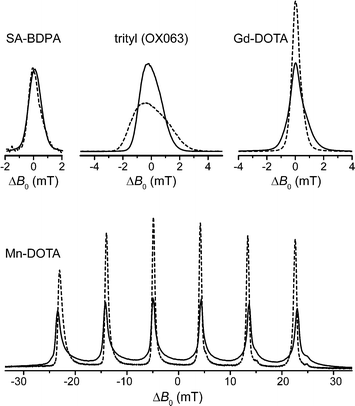
Paramagnetic species act as polarizing agents by transferring the large electron spin polarization to nuclear spins upon irradiation with microwaves (μw) of an appropriate frequency. Microwave radiation is generated by either a solid-state source or—in the case of MAS DNP—by a gyrotron maser source due to the high power requirement in the absence of a μw resonance structure.31 Since gyrotrons typically emit a fixed, narrow-band frequency the NMR magnetic field has to be adjusted if polarizing agents with varying EPR resonance fields are to be used or investigated.In Fig. 1 we give an overview of several polarizing agents representing different classes of paramagnetic substances. TOTAPOL32 is one of the most prominent examples of bis-nitroxide biradicals38,39 which allow for efficient cross effect (CE) DNP of 1H and 13C.33 Trityl OX06340 and SA-BDPA34 are water-soluble, persistent organic (carbon-based) radicals with rather narrow EPR resonances. At 5 T the linewidth of trityl (∼50 MHz) only allows for the solid effect (SE) of 1H with 212 MHz Larmor frequency,35,41 while the smaller frequency of 13C (53 MHz) leads to efficient CE.7,36 For SA-BDPA with 28 MHz linewidth both nuclei can only be polarized via the SE.34,36 Paramagnetic metal complexes of Gd3+ and Mn2+ have been demonstrated as polarizing agents for 1H DNP earlier;37 recently we have shown that Mn2+ naturally bound to RNA can be used to hyperpolarize 13C within a nucleic acid complex.42 Even though the enhancement factors cannot compete quantitatively with the highly efficient bis-nitroxides, the natural occurrence in metalloproteins—in the case of Mn2+—or the possibility to replace diamagnetic metal ions such as Mg2+ or Ca2+ make these high-spin metal ions interesting targets for further research.
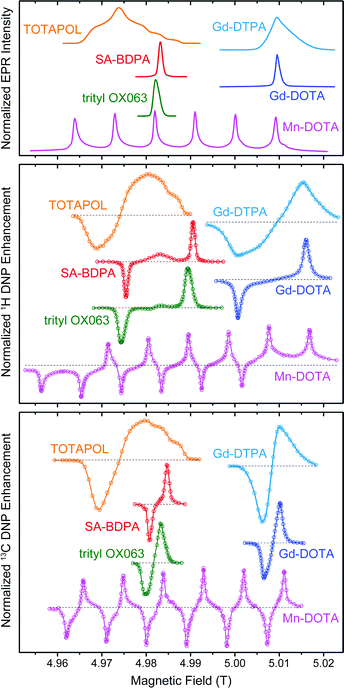 | ||
| Fig. 1 EPR spectra (top) as well as field-dependent 1H (middle) and 13C (bottom) DNP profiles of various polarizing agents at 140 GHz μw frequency. TOTAPOL DNP data taken from ref. 32 (1H) and 33 (13C). SA-BDPA and trityl OX063 data from ref. 34 and 35, respectively, except 13C DNP profiles which were taken from ref. 36. Gd(III) and Mn(II) EPR spectra taken from ref. 37; DNP data from this work. | ||
DNP with intrinsic polarizing agents
One aspect that has become of particular interest is the incorporation of polarizing agent with respect to the analyte. In “conventional” studies the polarizing agent—consisting of a paramagnetic molecule and providing the large electron polarization to be transferred to the nuclear spins—is dissolved in a cryoprotecting matrix. The matrix is highly deuterated with reduced proton abundance of ∼10% in order to optimize signal enhancement factors and transfer of enhanced polarization to the analyte via spin-diffusion.43 This method has been successfully applied to several biological sample systems, including membrane proteins in native phospholipid environments as well as liposomes,22,26,44,45 and dispersed micro-/nano-crystalline proteins and peptides or amyloid fibrils.25,46–48 A similar approach is used for microcrystalline materials49 or by impregnation wetting of insoluble materials with polarizing agent solutions for surface-enhanced NMR spectroscopy.17Immobilized paramagnetic species being covalently or non-covalently bound to or near the biomolecule to be investigated have recently attracted interest. In a first and elegant demonstration an endogenous flavin in its reduced semiquinone radical form has been used to polarize 1H within the protein.50 Besides circumventing the addition of a solvent matrix and potential phase separation,51–54 this approach is also aimed towards more efficient utilization of enhanced nuclear polarization near the site of interest at high magnetic field and fast MAS where spin-diffusion efficiency is limited,55 and towards further structural insights by analysis of site- or state-specific DNP enhancement.56,57 Furthermore, we have shown that endogenously bound, diamagnetic metal ions can be substituted with paramagnetic analogs in order to allow for DNP of ribonucleic acids.42
Paramagnetic metal chelates in magnetic resonance
Gd(III) and Mn(II) chelate complexes are currently in the focus of several magnetic resonance techniques, including their use as efficient contrast agents in magnetic resonance imaging (MRI).58–61 Spin labels based on Gd(III) have been demonstrated for distance measurements by dipolar EPR spectroscopy.62–69 Additionally, both Mn2+ and Gd3+ have been used to study metal binding to biomolecules by paramagnetic relaxation enhancement of nuclear spins in solution NMR.70,71 Similarly both ions have been artificially attached to proteins by site-directed spin labeling with chelators for determination of structural constraints;72,73 such applications have been demonstrated for magic-angle spinning (MAS) NMR as well.74,75 Additionally, covalent labeling with Mn(II) or Gd(III) chelates allows for distance measurements by dipolar EPR spectroscopy.62,63,65,68,69 Due to their chemical stability under redox-active conditions these complexes have proven extremely interesting for the investigation of in-cell EPR spectroscopy,67 where nitroxide radicals suffer from chemical inactivation76,77 and in-cell applications demand additional precautions.78,79 Given these prospects in combination with the ubiquitous use of lanthanide chelate tags in NMR and the large availability of respective labeling techniques80 we have earlier investigated the use of Mn(II) and Gd(III) chelate model compounds as polarizing agents for sensitivity-enhanced MAS NMR using dynamic nuclear polarization (DNP) of 1H at a field of 5 T.37 Here, we want to extend this investigation to fields of 9.4 T and up to 14.1 T. Furthermore, we focus on direct DNP of low-γ nuclei 13C and 15N for which slower spin-diffusion might enable a site-selective DNP enhancement of resonances in biomolecules which contain a specifically-bound metal polarizing agent. Preliminary experiments obtained with chelator-labeled and uniformly isotope labeled ubiquitin yield promising results.Theory
DNP mechanisms
Under the conditions relevant here DNP can occur via two different mechanisms: solid effect (SE) and cross effect (CE). SE enhancements are driven directly by μw excitation of nominally forbidden zero quantum (ZQ) and double quantum (DQ) electron–nuclear coherences.81 Anisotropic hyperfine interaction (HFI) leads to partial state mixing of the nuclear substates; the respective ZQ and DQ SE matching conditions occur at the sum or difference combinations of the electron and nuclear Larmor frequencies. Due to the ZQ and DQ transitions leading to opposite nuclear enhancement and cancellation of the SE when excited equally, the polarizing agent has to feature a narrow EPR spectrum with an effective overall breadth smaller than the nuclear Larmor frequency.The CE occurs when two electron spins are dipolar coupled. Upon μw saturation of one of the spins their polarization difference can be transferred to a coupled nuclear spin if the Larmor frequencies of the electron spins differ by the nuclear Larmor frequency: Δω0S = ω0I.82 In this case an energy-conserving three-spin flip–flop–flip process can occur. This process has been shown to be highly efficient for bis-nitroxide polarizing agents under MAS, where the variation in electron Larmor frequencies is achieved by significant g anisotropy, and the spin eigenstates undergo several level crossings during one sample rotational period.12,13
In the preceding article we have described the theoretical background in detail and have developed a model for CE with high-spin electrons with isotropic electron Zeeman interaction and significant ZFS such as Gd(III) and Mn(II).83 We strongly encourage the reader to refer to this work for theoretical background as basis of discussion of the experiments described here.
Magnetic properties of Gd(III) and Mn(II)
The high-spin states of Gd(III) and Mn(II) lead to several peculiar properties which can be either advantageous or detrimental for applications in magnetic resonance. We have described these properties in detail in the preceding article;83 nevertheless we want to briefly summarize these here. Even though the electron Zeeman interaction is isotropic with a g value close to that of the free electron the S = 7/2 and S = 5/2 states of Gd(III) and Mn(II), respectively, are subject to zero-field splitting (ZFS) most commonly caused by non-cubic ligand environment. In typical complexes this leads to an anisotropic broadening of the satellite transitions (ST)—where mS changes its absolute value—by up to several GHz in total breadth. Due to the half-integer spin state a narrow central transition (CT)—where |mS| is conserved—is observed which is not affected by ZFS in first-order; however, a second-order broadening occurs if the ZFS parameters are of significant magnitude with respect to the Zeeman splitting. Furthermore, Mn(II) underlies strong isotropic hyperfine interaction (HFI) to its core 55Mn nucleus (I = 5/2) with typical coupling constants ∼250 MHz, leading to a characteristic sextet pattern in EPR spectra. For Gd(III) small HFI to the minority magnetic nuclei 157Gd and 159Gd (both I = 3/2 and 15% abundance each) can be neglected in most cases.Experimental
EPR
Pulsed EPR spectra at 140 GHz and 275 GHz have been recorded using custom-built EPR spectrometers at a temperature of 80 K. Spectra were acquired by recording the field-swept intensity of a Hahn-echo of frozen solutions of each polarizing agent in 1 mM concentration in D8-glycerol/D2O (60/40 vol%) mixture. Detailed descriptions of the instruments can be found elsewhere.84–86Continuous-wave EPR spectra of Gd(III)-labeled protein (see below) have been recorded using a Bruker EleXsys E780 spectrometer operating at 263 GHz and utilizing a sweepable Bruker Ascent DNP magnet (89 mm) centered at 9.40 T and contained a superconducting sweep coil with a nominal range of ±75 mT. The Bruker magnet power supply is remotely controlled by the Bruker Xepr software used for data acquisition. The spin-labeled proteins were dissolved at concentrations between 2 and 4 mM in a D8-glycerol/D2O/H2O (60/30/10 vol%) mixture, packed into 0.2 mm (i.d.) clear fused quartz capillaries and frozen inside a custom-built TE011 resonator. Experiments were performed at a temperature of 100 K inside an Oxford instruments flow cryostat using liquid Helium as cryogen. For detailed set of parameters see ESI.†
DNP at 5 T (140 GHz)
DNP experiments at 5 T were performed on samples containing 10 mM Gd-DOTA (Macrocyclics, Dallas, TX), Gd-DTPA (gracious gift of E. Ravera and C. Luchinat, Florence), or GdCl3 (Sigma-Aldrich, St. Louis, MO) in a 13C3-glycerol/H2O (60/40 vol%) or a [D8, 13C3]-glycerol/D2O/H2O (60/30/10 vol%) mixture. 13C-labeled glycerol was purchased from Cambridge Isotope Laboratories (Tewksbury, MA). All compounds were used as received without further purification. The custom-built spectrometer operating at 213 MHz 1H frequency is courtesy of D. Ruben. A custom-built MAS NMR probe was utilized which features a triple resonance rf circuit (1H, 13C, 15N) and efficient microwave coupling to the sample using overmoded corrugated waveguides (similar to a design published by Barnes et al.87). The probe was also equipped with a cryogenic sample exchange system. Microwaves were generated using a custom-built gyrotron oscillator operating at 139.65 GHz with a maximum output power of ∼13 W.2,31,88 Sample temperature was measured via a fiber optical sensor (Neoptix, Québec City, Canada) outside the MAS stator and was maintained at about 84 K. Experiments were performed using a MAS frequency of ωr/2π = 5 kHz. A detailed description of experiments is given in the ESI.†DNP at 9.4 T (263 GHz) and above
The comparison of 1H DNP at 9.4 T and 14.1 T was performed at Bruker BioSpin (Billerica, MA) on two different DNP/NMR spectrometers operating at 400 MHz/263 GHz and 600 MHz/395 GHz, respectively. The sample contained 10 mM Gd-DOTA and 100 mM [13C, 15N]-proline dissolved in D8-glycerol/D2O/H2O (60/30/10 vol%). The spectrometers are equipped with 3.2 mm H–X probes of which the X channels are tuned to 13C. The 13C NMR signals of proline were measured by CP pulse sequence with a pre-saturation period. The temperature of the sample was ∼90 K without microwave and ∼100 K with ∼15 W of microwave. The sample was spun at ωr/2π = 12.5 kHz.All other DNP experiments at 9.4 T were performed using a commercially available Bruker AVANCE III DNP spectrometer operating at 401.7 MHz 1H frequency. 2 M [13C, 15N2]-urea (CortecNet) was dissolved in a glass forming solvent of [D8, 12C3]-glycerol/H2O (60/40 vol%). The glycerol depleted in 13C (99.95% 12C) was purchased from Euriso-Top. Gd-DOTA-NH3 (gracious gift of J. Plackmeyer, Frankfurt) was used as polarizing agent in concentrations of 2 mM, 10 mM and 20 mM. All compounds were used as purchased without further purification. A Bruker gyrotron yielding 263.4 GHz microwaves, operating at the maximum beam current of 115 mA was used. 1H enhancement was recorded using cross-polarization to 13C. Direct 13C and 15N enhancements were measured using Bloch decay. Microwave on and off experiments were performed at 114 K and 105 K respectively; this temperature was measured outside the stator. Sample heating due to μw irradiation was not quantified or controlled for. MAS of 8 kHz was employed. For further information see ESI.†
Protein expression and labeling
A detailed description of protein expression, purification, and labeling is given in the ESI.† 4-Mercaptomethyl dipicolinic acid (4MMDPA) has been synthesized following the procedure published by Potapov et al.;63 1,4,7,10-tetraazacyclododecane-1,4,7-tris-acetic acid-10-maleimidoethylacetamide (DOTA-M) was purchased from Macrocyclics, Inc. (Plano, TX). After recombinant expression, purification, labeling, and concentration, the uniformly [13C, 15N]-labeled protein was transferred to an NH4OAc buffer (pH = 7.0) for DNP with a final concentration of ∼1 mM ubiquitin in 60% (v/v) [D8, 12C3]-glycerol, 36% D2O, and 4% H2O. The labeling efficiency was quantified using cw spin-counting at X-band frequency at 80 K and was determined as ∼90% in the case of 4MMDPA and ∼100% for DOTA-M.Results and discussion
EPR linewidth of the CT at different fields
With the introduction of several custom-built or commercially available DNP spectrometers operating at fields between 9.4 and 18.8 T considerable focus should be laid on the efficiency of polarizing agents with increasing fields. One important aspect in this context is the broadening of the EPR line and resulting excitation efficiency with a monochromatic microwave source.In Fig. 2 we demonstrate the effect of increasing external magnetic field strength on the line shape of several polarizing agents with narrow EPR lines which have been utilized for SE at high field. While SA-BDPA shows no significant variation in linewidth between 140 GHz (5 T) and 275 GHz (9.8 T) due to negligible g-anisotropy and inhomogeneous broadening dominated by unresolved hyperfine couplings to 1H, the axially symmetric g-anisotropy of trityl leads to an increase of spectral breadth proportional to the external field. The high-spin complexes of Gd3+ and Mn2+, on the other hand, show an effective reduction in linewidth of the EPR CT with higher field which seems counterintuitive at first, but is explained by the occurrence of a second-order effect due to ZFS which scales inversely proportional with respect to the Zeeman strength. In the preceding article we have described in detail the unique properties of these high-spin metal ions regarding DNP;83 here we will demonstrate these properties in DNP experiments performed on 1H and 13C at a field of 5 T. Further experiments conducted at high fields of 9.4 T and 14.1 T demonstrate the unique line-narrowing properties of Gd-DOTA and underline the potential of this class of polarizing agents under these high-field conditions, especially when compared to the efficiency of the SE with radical polarizing agents at these high field strengths.8
Effect of different complex ligands on DNP
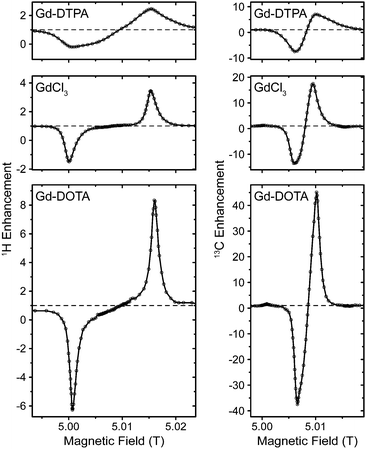
In Fig. 3 we compared several different chelate complexes of Gd3+ as polarizing agents for 1H and 13C DNP at 140 GHz, recorded at a μw power level of 6 W (at probe input). There is a clear correlation between EPR line width of each complex and induced DNP enhancement (given as relative difference in relation to thermal polarization, i.e., ε − 1) for 1H and 13C, see Table 1. While for Gd-DOTA and GdCl3 (the latter exists as an aquo complex in aqueous solution)89 the positive and negative 1H SE legs are separated by a plateau area, they overlap for 13C even for the complex with the smallest linewidth due to mutual overlap of the ZQ and DQ electron–nuclear transitions. Interestingly, for GdCl3 two components with starkly different ZFS parameters have been reported from EPR experiments.90 We do not observe such a biphasic behavior; however, our observations only seem to show a contribution from the component with smaller D value. This might indicate that the complex species with large ZFS might not be effective as polarizing agent for DNP, or that its contribution to DNP is unproportionally small compared to the EPR contribution, as can also be seen by the ∼3-fold reduction in enhancement w.r.t. Gd-DOTA while the apparent linewidth only increases by ∼50%.| Complex | ZFS parametersb | EPR linewidth (MHz) | ε H − 1a | ε C − 1a | |
|---|---|---|---|---|---|
| D (MHz) | ΔD (MHz) | ||||
| a Measured at ∼6 W μw power; values given at the field of max. positive enhancement, values in parentheses at field of max. magnitude of negative enhancement. b From ref. 90. c At 5 T, simulated from given ZFS parameters. d Two components contributing to the spectrum with relative weight given in parentheses. | |||||
| Gd-DOTA | 672 | 336 | 30c | 7.3 (−7.3) | 44.0 (−38.5) |
| GdCl3d | 784/2184 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8) 2.8) |
448/952 | 50c | 2.5 (−2.5) | 16.5 (−14.5) |
| Gd-DTPA | 1568 | 728 | 170c | 1.5 (−1.2) | 6.0 (−8.5) |
13C enhancements are significant, with ∼6–7 times larger values than for 1H. For Gd-DTPA this ratio is somewhat smaller, however, in this case the magnitude of the negative enhancement is larger than that of the positive leg, most probably due to complicated overlap of SE transitions and other mechanisms leading to opposing DNP effects. We did not detect any sign of solid-state Overhauser effect (OE) as has been reported on BDPA radicals.8,34 Factors contributing to the OE in BDPA are the presence of significantly hyperfine-coupled 1H and slow spin–lattice relaxation of the electron spin, both of which are less favorable in Gd3+ complexes.
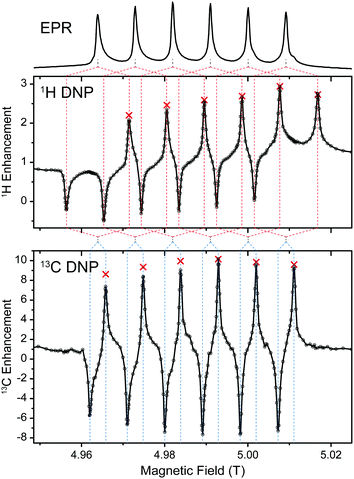
Experiments using Mn-DOTA reveal a very similar situation; the main difference being the splitting of the rather narrow CT into an almost equally spaced sextet caused by hyperfine coupling to 55Mn with a coupling constant of 254 MHz.37 This leads to a complicated system of six individual SE features evoked by each EPR line as is shown in Fig. 4. For 1H these SE pairs are intricately intertwined due the 1H nuclear Zeeman frequency being larger than half the 55Mn HFI constant. For 13C we encounter the opposite situation and each EPR line's SE pair is individually resolved. Furthermore, the small EPR linewidth now allows for almost complete separation of positive and negative enhancement legs with little-to-none mutual cancellation. NMR intensity comparisons between μw-irradiation and non-irradiation allowed us to measure the enhancement factor for each EPR line (see red symbols in Fig. 4). Towards lower field slight deviations between the DNP-enhanced signal intensity and enhancement (obtained by on/off-comparison) occur which are due to lower efficiency of the spectrometer components (i.e., preamplifiers, filters, etc.). Nevertheless, for 13C a symmetric variation of enhancement factors is observed which closely resembles the peak amplitude pattern of the EPR spectrum; for 1H slight overlap of SE conditions lead to an asymmetric variation with larger enhancements obtainable for the second-to-outermost lines. Destructive interference occurs when 2ω0I = nA(55Mn), where ω0I is the Larmor frequency of the nucleus to be enhanced, A(55Mn) is the isotropic hyperfine coupling constant to the metal nucleus and n is any integer between 1 and 5. In such a case a positive enhancement peak is canceled by a negative peak of another HFI peak; however, the n outermost (positive or negative) SE peaks are never canceled in such a way. Since peaks of equal sign cannot overlap, constructive interference of SE peaks is not possible. Nevertheless, when ω0I = nA(55Mn), a ZQ/DQ peak can be on resonance with a SQ transition of a another dipolar coupled Mn2+. This situation might lead to efficient CE matching, for example at a magnetic field of 11.7 T (500 MHz), where ω0I(1H) ≈ 2A(55Mn), and will be subject to further research.
Influence of bulk protonation level
For Gd-DOTA we investigated the effect of solvent deuteration level on 13C DNP. Earlier studies have shown that slightly larger enhancement factors and faster polarization build-up can be achieved without matrix deuteration, in stark contrast to radical polarizing agents.35 Here, we record a ∼13% larger enhancement of 13C for full protonation—with a maximum positive enhancement of 70—compared to 62 for typically utilized 12% protonation within “DNP juice” (i.e., 60/30/10 vol% mixture of D8-glycerol/D2O/H2O) even though a slight broadening of the peaks within the field profile is visible (Fig. 5). This might be caused due to improved proton-driven spin diffusion and/or longer build-up and longitudinal relaxation time constants. A complete overview of 1H and 13C enhancements at various protonation levels can be found in the ESI† in Table S2.An interesting effect occurs at the fields of most efficient (positive or negative) 1H enhancement. Here, we see a small, but significant 13C DNP enhancement of inverse sign with respect to 1H. The effect is observed with a fully protonated sample and does not occur with low 1H levels (see below and Fig. 5). Possible multi-spin flips, where 1H and 13C are excited at the same time are theoretically and experimentally expected, but would occur at offsets of nuclear combination frequencies with respect to the SQ (EPR) frequency.91,92 We do not observe any splitting or shift of these features with respect to the 1H SE peaks. Therefore, we attribute this effect to heteronuclear cross relaxation. 1H populations—driven away from thermal equilibrium by SE DNP—may enhance 13C in a similar way to the classical nuclear Overhauser effect (NOE). Due to relaxation from a hyperpolarized state instead of simple saturation this would result in opposite sign of 13C enhancement with respect to that of 1H. Similar effects have been reported in samples after dissolution where molecular tumbling provides the required dynamics for relaxation.93 In our case it is unclear which dynamical process enables this relaxation process in the solid. The reader should note that the effect is rather weak (∼2% of maximum cross-relaxation enhancement); therefore even absolutely small variation of spectral density at the required sum and difference of nuclear Larmor frequencies might suffice for the observed effect to occur.
Power dependence of DNP enhancement
The power dependence of DNP enhancements is perfectly linear in most cases, as seen in Table 2 and shown in Fig. S1 (ESI†). Interestingly, the DNP efficiency which is given by polarization increase of the nucleus relative to the theoretical maximum is almost identical for 1H and 13C; consequently enhancement factors scale inversely with the nuclear gyromagnetic factor. 13C DNP power dependence with Gd-DOTA shows a slight reduction of slope with larger power compared to the Mn2+ complex. The ‘relayed’ DNP enhancement of 13C caused by μw excitation at the field of 1H SE seems to indicate a more significant ‘saturation’ effect at larger powers, the reason for this is still unclear.| Solvent D8-glyc./H8-glyc. + D2O/H2O (vol%) | 1H conc. (mol L−1) | 1H ratio (%) | ε (H) 5/9/14 W | T (H)1 (s) no μw | T (H)B (s) 5/9/14 W | ε (C) 5/9/14 W | T (C)1 (s) no μw | T (H)B (s) 5/9/14 W |
|---|---|---|---|---|---|---|---|---|
| Multiple values separated by slashes given for different μw power levels of 5, 9, and 14 W (measured at probe entrance).a Estimated from solvent composition.b Not measured. | ||||||||
| 0/60 + 0/40 | 111.9a | 100 | 8/13/19 | 3.2 | 3.1/3.0/2.8 | 45/71/103 | 86 | 85/83/80 |
| 0/60 + 40/0 | 66.3a | 59 | —/—/—b | —b | —/—/—b | 40/61/89 | 82 | 82/81/78 |
| 60/0 + 0/40 | 47.2a | 42 | —/—/—b | —b | —/—/—b | 39/59/90 | 56 | 57/55/55 |
| 60/0 + 30/10 | 13.0a | 12 | 8/13/18 | 5.2 | 5.1/5.1/5.0 | 41/61/91 | 55 | 52/50/48 |
| 60/0 + 40/0 | ∼1.6a | ∼1.4 | 5/8/12 | 12 | 12/14/13 | 41/64/93 | 51 | 50/49/48 |
Also, a slight reduction of polarization time constant with increasing μw power is noticed (see Table 2). This trend is expected for SE,41 and has been already observed for trityl on the same instrument where we have also experimentally excluded sample heating as the major cause.35
Furthermore, in order to assess the achievable DNP enhancement in the excess of μw field strength we have investigated a static sample inside a μw cavity resonator driven by low-power solid-state source. With this instrument a typical Q factors on the order of ∼1000 leads to an effective nutation frequency of ∼16 MHz for the CT of the S = 7/2 spin; this allows for significant 1H DNP enhancement of >100 as we have reported earlier.84 Direct DNP of 13C under irradiation of the 13C SE transition leads to large absolute intensity of the enhanced NMR signal of 13C3-glycerol, see Fig. S2 (ESI†). Due to the large μw field strength available we reach a near-saturation condition already at ∼60% μw power; nevertheless a further reduction in polarization build-up time constant provides further sensitivity gains. A similar situation occurs for 1H DNP at lower temperature.84 Unfortunately, we have been unable to measure the 13C enhancement factor because no signal could be observed without μw irradiation; analysis of the noise level allows us to provide a lower bound of ε of 400. For comparison we performed 13C CP experiment with 1H DNP enhancement (by irradiation at the 1H SE condition). We observe a 2.8-fold larger intensity of the direct polarization (DP) spectrum, indicating that the large, direct 13C SE enhancement easily overcompensates the up to 4-fold signal increase which can be achieved by 1H DNP and subsequent CP transfer to 13C. Reduced CP efficiency due to the inhomogeneously broadened resonances and the presence of the paramagnetic polarizing agent cannot completely be neglected. Nevertheless, considering the larger signal intensity of the non-DNP-enhanced CP spectrum with respect to the DP spectrum, it is clear that CP efficiency >1. We therefore conclude that for 13C, ε ≥ 400, with estimated factors of 800–1000 being much more likely. Enhancement factors of >700 have been observed for 30 mM trityl solution by Banerjee et al. at 3.4 T but otherwise similar conditions.7 Our observations indicate that very large enhancement factors can be observed with sufficient μw field strength which makes Gd-DOTA a promising target for further investigations under these conditions.
Reduction of temperature has been shown to be more favorable, leading to larger enhancement factors already with smaller μw power.84 However, below a certain temperature (14 K at 5 T and increasing with larger fields) the depopulation of excited magnetic spin states of the S = 7/2 system leads to reduced absolute population difference of the CT, rendering high-spin systems inactive as polarizing agents at low temperatures where kBT < γB0. This situation could be alleviated by the employment of sophisticated adiabatic sweep or pulse schemes which are able to transfer population from the highly polarized ground state transition into the DNP-enabling CT.10,94
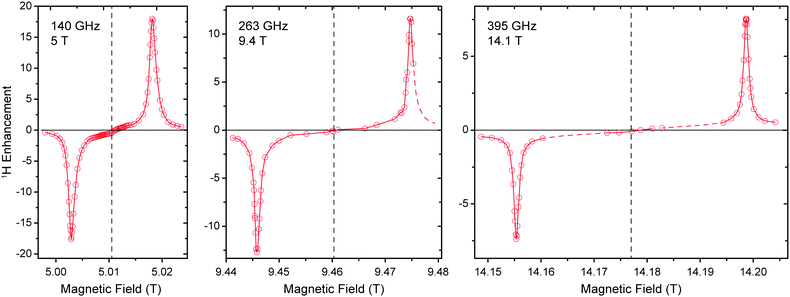
Field dependence of 1H DNP
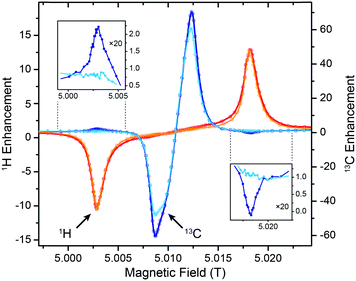
5 T is an ideal testbed for DNP experiments due to its instrumental robustness in terms of magnet sweep capability and μw power availability in combination with rather straightforward scalability of results to higher fields. Nevertheless, experiments at the commercially accessible fields of 9.4 and 14.1 T are important to confirm predictions based on lower field experiments and might also yield unexpected observations. Therefore we conducted 1H DNP experiments using Gd-DOTA at these fields (Fig. 6). As expected, the matching field offset for positive and negative SE enhancement scale with the nuclear Larmor frequency and become more separated at higher field. Additionally, slight reduction in linewidth of the DNP peaks is observed with larger external field. This narrowing manifests when comparing the field dependence with that reported for BDPA,8 where at 9.4 T a slightly larger ε was observed than for Gd-DOTA, however, at 14.1 T this ratio is inverse. Therefore we expect, that Gd-DOTA would significantly outperform BDPA at 18.8 T (reaching only vanishing ε ≈ 2).The narrowing is less pronounced than would be expected from the B0−1 dependence of the second-order ZFS. In fact a considerable amount of dipolar broadening of the Gd(III) EPR spectrum occurs within the 10 mM Gd-DOTA solution; when comparing DNP peak widths we found a reduction from 34.0 (30.8) MHz to 22.6 (22.0) MHz at 9.4 (14.1) T by lowering the Gd-DOTA concentration from 10 to 1 mM; we discuss this broadening in detail below. Nevertheless, we want to emphasize that a linewidth of 22 MHz at 395 GHz Larmor frequency corresponds to only 56 ppm, which is exceptionally small for a metal complex. For comparison, typical low-spin complex ions such as Cu2+ feature g anisotropy of ∼20%.
Power dependence and build-up dynamics at 9.4 and 14.1 T are both similar to what we observed at 5 T. With larger μw power the 1H enhancement shows a nearly linear increase at all fields; build-up times become slightly longer at higher field (∼3 s at 5 T, ∼4 s at 9.4 T, ∼5 s at 14.1 T).
Effect of inter-complex couplings on direct DNP of 13C and 15N
Stimulated by the observed broadening of the DNP field profiles above, we have performed a detailed analysis of DNP enhancements of 1H, 13C, and 15N in comparison with EPR spectra for Gd-DOTA concentrations between 2 and 20 mM at a μw frequency of 263 GHz and a field of 9.4 T (Fig. 7). Due to technical reasons the DNP magnet used could only be swept slightly past the EPR resonance field of the CT, therefore we were only able to record the negative enhancement of all nuclei except 15N. Note the reduced EPR linewidth compared to 5 T (15 MHz vs. 25 MHz) due to the less pronounced second-order ZFS acting on the CT. This narrowing in combination with larger separation of the electron–nuclear ZQ and DQ transitions leads to positive and negative 13C SE legs being now fully separated. A similar central plateau region occurs as seen for 1H at 5 T because of similar ratios between nuclear Zeeman frequency and inhomogeneous linewidth. Even for 15N we observe the occurrence of a distinctive reduction of slope around the inflection point between the positive and negative legs, indicative of nearly complete separation of opposing enhancement regions. This is—to our knowledge—the first example of a well-resolved SE profile for such a low-γ nucleus reported in literature.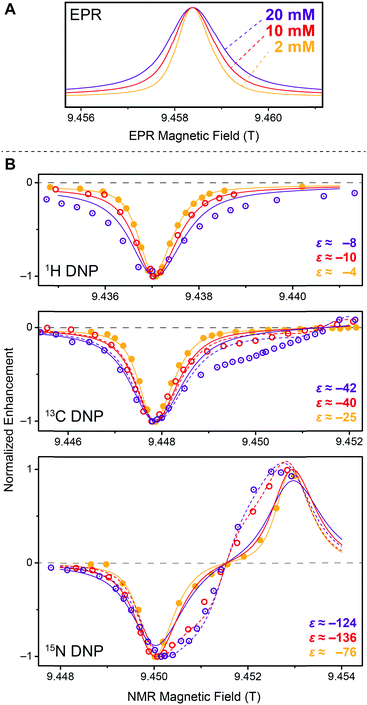 | ||
| Fig. 7 (A) EPR spectra of 2 mM (orange), 10 mM (red), and 20 mM (purple) Gd-DOTA at 263 GHz. Curves were obtained by simulating experimental cw (field-modulated) EPR spectra using Easyspin95 in order to avoid artifacts by integration. (B) Normalized DNP enhancement of 1H, 13C, and 15N at 263 GHz at 2 mM (filled circles), 10 mM (open circles), and 20 mM (dotted open circles). Solid lines represent SE simulations according to eqn (1); dashed lines CE simulations according to eqn (2). Enhancement factors given are taken at field of maximum magnitude enhancement. | ||
The SE field profile can relatively simply be approximated by an approach based on the EPR spectral shape. Superposition of modeled ZQ and DQ peaks (i.e., by shifting the EPR spectral function by the field corresponding to the nuclear Zeeman frequency) of opposite sign allows for generation of a simulated SE DNP profile:11
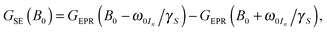 | (1) |
For 13C we observe an additional shoulder emerging in the DNP profile on the inner side of the negative SE peak, decreasing in magnitude with a constant slope towards the central inflection point. In the case of 15N the effect is even more pronounced; leading to a shift of the field of max. DNP enhancement towards the CT. Interestingly, we have succeeded in fitting the latter feature (see dashed lines in Fig. 7B) using a different approach based on a CE-type matching probability analysis:11
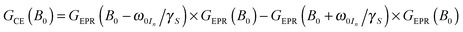 | (2) |
Observation of enhanced polarization spreading by spin-diffusion
When directly polarizing 13C or 15N of isotope-labeled urea using 20 mM Gd-DOTA through the glycerol/water matrix depleted in 13C we observe an interesting behavior: while for very short polarization times the NMR signal shows significant homogeneous broadening, this broadening is reduced when more time is available for enhanced polarization to build up as can be seen in Fig. S3 (ESI†). We explain this with a non-uniform spatial distribution of nuclear polarization where large enhancement is quickly generated for nuclei in close proximity to the paramagnetic ion. For polarization to spread further out towards less paramagnetically influenced nuclei spins, spin-diffusion has to occur through the bulk. Due to the small concentration of 13C and 15N with an average nearest-neighbor distance of ∼0.5 nm, spin diffusion constants are small and we observe overall build-up time constants on the order of ∼400 s and ∼1000 s for bridging the distance of ∼2.4 nm between polarizing agent centers. A complete set of build-up time constants for 13C and 15N at various Gd-DOTA concentrations is given in Table 3. Our experiments here also confirm an earlier observations, where we had measured through-bulk build-up time constants in excess of 5000 s even for 13C when both the urea and polarizing agent concentration were considerably smaller.42| c Gd-DOTA (mol L−1) | ε (H) | T B (H) (s) | ε (C) | T (C)B,f (s) | T (C)B,s (s) | φ (C) | ε (N) | T (N)B,f (s) | T (N)B,s (s) | φ (N) |
|---|---|---|---|---|---|---|---|---|---|---|
| a Fast component of bi-exponential build-up. b Slow component of bi-exponential build-up. c Ratio between contribution of fast and slow component to overall signal as described by Wenk et al.42 d Not measured. | ||||||||||
| 2 | −4 | 17 | −25 | 1213 | 3471 | 0.314 | −76 | 296 | 2990 | 0.198 |
| 10 | −10 | 4.6 | −40 | —d | —d | —d | −136 | —d | —d | —d |
| 20 | −8 | 2.2 | −42 | 113 | 396 | 0.351 | −124 | 114 | 1003 | 0.721 |
DNP with Gd(III) chelate tags attached to protein
In a series of preliminary experiments we attached Gd3+-binding chelator tags to ubiquitin using site-directed spin labeling. Ubiquitin is an excellent model system due to typically large overexpression efficiency, and biochemical robustness under different environmental conditions. Furthermore, spin-labeled ubiquitin could potentially be utilized as a protein tag targeting other proteins in larger complexes via ubiquitylation for site-selective DNP applications, a route we plan to investigate in the near future.We carried out experiments using three different single-site mutations of ubiquitin where in each case one cysteine residue was introduced by mutagenesis. We selected phenylalanine F4, alanine A28, as well as glycine G75 as favorable targets for mutation because these sites possess large surface accessibility and are situated in differing secondary structure elements (i.e., beta sheet, alpha helix, and terminal loop, respectively). Furthermore, the varying flexibility of the sites (e.g., G75 being situated in the flexible C-terminal tail region) might lead to different conformational inhomogeneity during freezing. 4MMDPA and DOTA-M were chosen as promising chelator tags as described by Goldfarb and co-workers.63,67
In Fig. 8 we show the direct DNP-enhancement of 13C within uniformly [13C, 15N]-labeled A28C ubiquitin mutant with each attached Gd(III) tag, a comparison with the direct polarization 13C MAS NMR spectrum of unlabeled A28C, the chemical structures of the tags and a model of the protein showing the single point mutation sites investigated. Within these preliminary experiments we have observed a rather small 13C DNP enhancement by Gd3+ SE on the order between approximately −1 to −3 when [D8, 12C3]-glycerol/D2O mixture was used as solvent. We have not been able to observe significant differences between the different mutation sites so far. We assume that intra-molecular spin diffusion is sufficiently fast within the uniformly 13C-labeled protein, so that any variation in DNP efficiency is averaged after a few seconds of longitudinal magnetization build-up. Depletion of 13C in the matrix below natural abundance strongly attenuates intermolecular spin-diffusion so that enhanced polarization is mostly maintained within the protein also carrying the Gd(III) polarization source as we have demonstrated with endogenously bound Mn2+.42
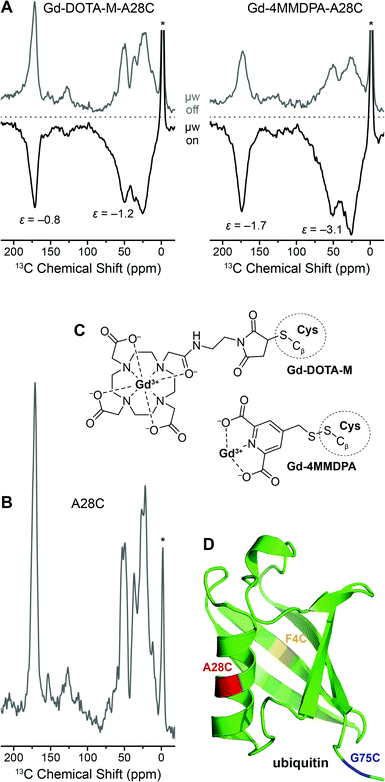 | ||
| Fig. 8 (A) Direct 13C DNP enhancement of uniformly [13C, 15N]-labeled ubiquitin mutant A28C using site-directed spin labeling with Gd-DOTA-M and Gd-4MMDPA tags at 9.4 T. The field was optimized for Gd3+ 13C SE resulting in negative signal enhancement. Read-out was performed via Bloch decay with 6 and 2.3 s polarization delay, respectively. (B) 13C MAS spectrum of A28C ubiquitin (without attached spin label), read-out via Bloch decay and 16 s polarization delay. Asterisks mark signals from silicone plugs. (C) Chemical structures of Gd-4MMDPA and Gd-DOTA-M spin labels connected to cysteine residues. (D) Ribbon structure of ubiquitin (PDB ID 1UBQ) with F4C, A28C, and G75C single-site mutations marked in yellow, red, and blue, respectively. | ||
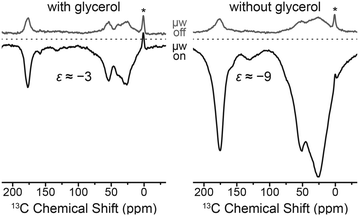
DNP enhancements are larger and build-up times are faster for Gd-4MMDPA labeled protein. EPR spectra of the Gd-labeled proteins at the same frequency (263 GHz) show a ∼2 times larger linewidth of the CT in 4MMDPA as in DOTA-M caused by the lower symmetry and larger ZFS in the former complex (Fig. S4, ESI†). Therefore we would also expect lower efficiency of DNP according to Fig. 3 in this case. The opposite finding is likely explained by the shorter tether between chelator moiety and protein. We observe significant broadening of 13C resonances especially with Gd-4MMDPA due to similar reasons. Also, upon μw irradiation and hence DNP enhancement (μw on), additional broadening occurs as compared to the spectra acquired using thermal polarization (μw off). All these observations indicate more favorable DNP enhancement of 13C nuclei in close distance to the paramagnetic ion.
We have determined labeling efficiencies between 90% (for 4MMDPA) and 100% (for DOTA-M) by cw EPR spin counting; both values can be interpreted as quantitative within the experimental error. Therefore we assume that a significant contribution of unlabeled protein—which could lead to similar observations—is rather unlikely. Due to the rather short spin–lattice relaxation of 13C in the fully protonated (diamagnetic) protein with T1n of about 10 s we expect the enhancement to drastically improve upon deuteration (fully or selectively of methyl-carrying amino acids); such experiments are currently pursued.
An unexpected phenomenon was observed when the cryoprotectant was absent from the aqueous buffer solution. Since the paramagnetic label is covalently attached to the biomolecule, separation of the polarizing agent and protein in different phases—which reportedly inhibits DNP51—cannot occur. DNP enhancement factors improved three-fold to about −9 while at the same time strong line broadening occurs. This is shown in Fig. 9 on the F4C mutant labeled with Gd-DOTA-M; we have observed very similar effects with other point mutation/chelate tag combinations as well. We explain this by agglomeration of paramagnetically labeled ubiquitins and hence a local increase in Gd(III) concentration. This is supported by shorter build-up time constants in the cryoprotectant-free samples.
Of course, the increase in linewidth in the small globular protein due to the presence of Gd3+ complicates the extraction of structural information in the typical way. However, such approaches might be fruitful with respect to specifically labeled proteins or ligands where spectral resolution is less important, or for problems in larger biomolecular systems where, for example, contacts between subunits are of interest. In fact, the occurrence of additional polarization pathways—including CE enabled by direct dipolar contact between Gd3+ of different proteins—bears an interesting prospect for future studies including multiply-labeled proteins and singly-labeled subunits within protein complexes, enabling efficient CE only upon direct contact of their constituents. Similar concepts have been demonstrated with nitroxides.56 This could allow for filtering towards a minority of bound species in co-existence next to the majority of unbound components; a situation which poses a significant problem in biophysical chemistry or structural biology.
Conclusion
While the indirect enhancement of 13C NMR spectra via1H DNP using complexes of Gd3+ and Mn2+ has already been demonstrated in principle,37 we have now extended the investigation especially for direct 13C DNP. 1H DNP enhancements of up to 20 have been measured which are yet unable to compete with those factors obtained by more efficient bis-nitroxide polarizing agents on model systems. However, paramagnetic metal ions still offer various other interesting properties especially in the context of biomolecular DNP. We have shown that deuteration of the matrix—which is rather difficult in cellular milieu—is not required because it does not lead to larger enhancement factors in model systems. Furthermore, many biomolecules are routinely investigated with paramagnetic NMR using lanthanide probes where paramagnetic relaxation enhancements (PREs) and pseudocontact shifts (PCSs) are analyzed for structural constraints in solution.80,97 MAS DNP could be able to contribute additional information without further modification of the sample. This is especially interesting in regards to highly efficient direct DNP of 13C or 15N with enhancement factors of ∼100 and larger. While at low polarizing agent concentrations SE is the dominating DNP mechanism for these nuclei, at large concentrations we observed a significant contribution of the CE which is achieved by electron spin frequency offsets caused by ZFS.Direct DNP of low-γ nuclei allows for a better control of spreading of enhanced polarization due to small spin-diffusion rates in environments with small isotope concentration. Furthermore, we have demonstrated in preliminary experiments that proteins labeled with Gd3+-binding chelator tags could themselves be used as polarizing agents. This approach could in the future be extended in order to investigate protein–protein interactions, allowing enhanced polarization to spread from one domain to another only when a close contact is maintained.
Acknowledgements
P. Gast (Leiden University) has kindly acquired the 275 GHz EPR spectra. Access to the 9.4 and 14.1 T DNP spectrometers has been generously provided by Bruker Biospin (Billerica, MA) for acquisition of data presented in Fig. 6. All other data at 9.4 T has been measured at Technical University Darmstadt with access provided by G. Buntkowsky and technical support from T. Gutmann. V. Denysenkov (Frankfurt) has helped with the acquisition of 263 GHz EPR spectra. We acknowledge help from F. Sochor (Frankfurt) regarding protein expression and J. Knauer (Frankfurt) for synthesis of 4MMDPA, for which A. Heckel (Frankfurt) has kindly provided laboratory space. We thank M. Reese (formerly MIT) for helpful discussions. RGG acknowledges funding by the National Institutes of Health (NIH) projects EB-002026 and EB-002804. BC has been funded by the Deutsche Forschungsgemeinschaft (DFG) through Emmy Noether grant CO802/2-1. RS is funded by a DFG research fellowship (SI2105/1-1). BC and HS acknowledge financial and technical support as well as spectrometer access from the Center for Biomolecular Magnetic Resonance (BMRZ).References
- D. A. Hall, D. C. Maus, G. J. Gerfen, S. J. Inati, L. R. Becerra, F. W. Dahlquist and R. G. Griffin, Science, 1997, 276, 930–932 CrossRef CAS PubMed.
- L. R. Becerra, G. J. Gerfen, R. J. Temkin, D. J. Singel and R. G. Griffin, Phys. Rev. Lett., 1993, 71, 3561–3564 CrossRef CAS PubMed.
- G. J. Gerfen, L. R. Becerra, D. A. Hall, R. G. Griffin, R. J. Temkin and D. J. Singel, J. Chem. Phys., 1995, 102, 9494–9497 CrossRef CAS.
- V. S. Bajaj, M. K. Hornstein, K. E. Kreischer, J. R. Sirigiri, P. P. Woskov, M. L. Mak-Jurkauskas, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Magn. Reson., 2007, 189, 251–279 CrossRef CAS PubMed.
- K. N. Hu, G. T. Debelouchina, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2011, 134, 19 Search PubMed.
- E. A. Chekhovich, M. N. Makhonin, A. I. Tartakovskii, A. Yacoby, H. Bluhm, K. C. Nowack and L. M. K. Vandersypen, Nat. Mater., 2013, 12, 494–504 CrossRef CAS PubMed.
- D. Banerjee, D. Shimon, A. Feintuch, S. Vega and D. Goldfarb, J. Magn. Reson., 2013, 230, 212–219 CrossRef CAS PubMed.
- T. V. Can, M. A. Caporini, F. Mentink-Vigier, B. Corzilius, J. J. Walish, M. Rosay, W. E. Maas, M. Baldus, S. Vega, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2014, 141, 064202 CrossRef CAS PubMed.
- Y. Hovav, A. Feintuch and S. Vega, J. Magn. Reson., 2010, 207, 176–189 CrossRef CAS PubMed.
- I. Kaminker, A. Potapov, A. Feintuch, S. Vega and D. Goldfarb, Phys. Chem. Chem. Phys., 2009, 11, 6799–6806 RSC.
- D. Shimon, Y. Hovav, A. Feintuch, D. Goldfarb and S. Vega, Phys. Chem. Chem. Phys., 2012, 14, 5729–5743 RSC.
- K. R. Thurber and R. Tycko, J. Chem. Phys., 2012, 137, 084508 CrossRef PubMed.
- F. Mentink-Vigier, Ü. Akbey, Y. Hovav, S. Vega, H. Oschkinat and A. Feintuch, J. Magn. Reson., 2012, 224, 13–21 CrossRef CAS PubMed.
- D. Mance, P. Gast, M. Huber, M. Baldus and K. L. Ivanov, J. Chem. Phys., 2015, 142, 234201 CrossRef PubMed.
- A. S. Lilly Thankamony, C. Lion, F. Pourpoint, B. Singh, A. J. Perez Linde, D. Carnevale, G. Bodenhausen, H. Vezin, O. Lafon and V. Polshettiwar, Angew. Chem., Int. Ed., 2015, 54, 2190–2193 CrossRef PubMed.
- D. Lee, G. Monin, N. T. Duong, I. Z. Lopez, M. Bardet, V. Mareau, L. Gonon and G. De Paëpe, J. Am. Chem. Soc., 2014, 136, 13781–13788 CrossRef CAS PubMed.
- A. Lesage, M. Lelli, D. Gajan, M. A. Caporini, V. Vitzthum, P. Miéville, J. Alauzun, A. Roussey, C. Thieuleux, A. Mehdi, G. Bodenhausen, C. Copéret and L. Emsley, J. Am. Chem. Soc., 2010, 132, 15459–15461 CrossRef CAS PubMed.
- P. Wolf, M. Valla, A. J. Rossini, A. Comas-Vives, F. Núñez-Zarur, B. Malaman, A. Lesage, L. Emsley, C. Copéret and I. Hermans, Angew. Chem., Int. Ed., 2014, 53, 10179–10183 CrossRef CAS PubMed.
- L. Zhao, W. Li, A. Plog, Y. Xu, G. Buntkowsky, T. Gutmann and K. Zhang, Phys. Chem. Chem. Phys., 2014, 16, 26322–26329 RSC.
- T. Gutmann, J. Liu, N. Rothermel, Y. Xu, E. Jaumann, M. Werner, H. Breitzke, S. T. Sigurdsson and G. Buntkowsky, Chem. – Eur. J., 2015, 21, 3798–3805 CrossRef CAS PubMed.
- M. Rosay, J. C. Lansing, K. C. Haddad, W. W. Bachovchin, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Am. Chem. Soc., 2003, 125, 13626–13627 CrossRef CAS PubMed.
- M. L. Mak-Jurkauskas, V. S. Bajaj, M. K. Hornstein, M. Belenky, R. G. Griffin and J. Herzfeld, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 883–888 CrossRef CAS PubMed.
- V. S. Bajaj, M. L. Mak-Jurkauskas, M. Belenky, J. Herzfeld and R. G. Griffin, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 9244–9249 CrossRef CAS PubMed.
- A. B. Barnes, B. Corzilius, M. L. Mak-Jurkauskas, L. B. Andreas, V. S. Bajaj, Y. Matsuki, M. L. Belenky, J. Lugtenburg, J. R. Sirigiri, R. J. Temkin, J. Herzfeld and R. G. Griffin, Phys. Chem. Chem. Phys., 2010, 12, 5861–5867 RSC.
- G. T. Debelouchina, M. J. Bayro, A. W. Fitzpatrick, V. Ladizhansky, M. T. Colvin, M. A. Caporini, C. P. Jaroniec, V. S. Bajaj, M. Rosay, C. E. MacPhee, M. Vendruscolo, W. E. Maas, C. M. Dobson and R. G. Griffin, J. Am. Chem. Soc., 2013, 135, 19237–19247 CrossRef CAS PubMed.
- L. B. Andreas, A. B. Barnes, B. Corzilius, J. J. Chou, E. A. Miller, M. Caporini, M. Rosay and R. G. Griffin, Biochemistry, 2013, 52, 2774–2782 CrossRef CAS PubMed.
- I. Gelis, V. Vitzthum, N. Dhimole, M. Caporini, A. Schedlbauer, D. Carnevale, S. Connell, P. Fucini and G. Bodenhausen, J. Biomol. NMR, 2013, 56, 85–93 CrossRef CAS PubMed.
- E. J. Koers, E. A. W. van der Cruijsen, M. Rosay, M. Weingarth, A. Prokofyev, C. Sauvée, O. Ouari, J. van der Zwan, O. Pongs, P. Tordo, W. E. Maas and M. Baldus, J. Biomol. NMR, 2014, 60, 157–168 CrossRef CAS PubMed.
- Y. Su, L. Andreas and R. G. Griffin, Annu. Rev. Biochem., 2015, 84, 465–497 CrossRef CAS PubMed.
- A. Potapov, W.-M. Yau, R. Ghirlando, K. R. Thurber and R. Tycko, J. Am. Chem. Soc., 2015, 137, 8294–8307 CrossRef CAS PubMed.
- L. R. Becerra, G. J. Gerfen, B. F. Bellew, J. A. Bryant, D. A. Hall, S. J. Inati, R. T. Weber, S. Un, T. F. Prisner, A. E. McDermott, K. W. Fishbein, K. E. Kreischer, R. J. Temkin, D. J. Singel and R. G. Griffin, J. Magn. Reson., Ser. A, 1995, 117, 28–40 CrossRef CAS.
- C. Song, K.-N. Hu, C.-G. Joo, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 11385–11390 CrossRef CAS PubMed.
- T. Maly, A. F. Miller and R. G. Griffin, ChemPhysChem, 2010, 11, 999–1001 CrossRef CAS PubMed.
- O. Haze, B. Corzilius, A. A. Smith, R. G. Griffin and T. M. Swager, J. Am. Chem. Soc., 2012, 134, 14287–14290 CrossRef CAS PubMed.
- B. Corzilius, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2012, 137, 054201 CrossRef PubMed.
- V. K. Michaelis, A. A. Smith, B. Corzilius, O. Haze, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2013, 135, 2935–2938 CrossRef CAS PubMed.
- B. Corzilius, A. A. Smith, A. B. Barnes, C. Luchinat, I. Bertini and R. G. Griffin, J. Am. Chem. Soc., 2011, 133, 5648–5651 CrossRef CAS PubMed.
- K. N. Hu, H. H. Yu, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2004, 126, 10844–10845 CrossRef CAS PubMed.
- C. Sauvée, M. Rosay, G. Casano, F. Aussenac, R. T. Weber, O. Ouari and P. Tordo, Angew. Chem., Int. Ed., 2013, 52, 10858–10861 CrossRef PubMed.
- J. H. Ardenkjær-Larsen, I. Laursen, I. Leunbach, G. Ehnholm, L. G. Wistrand, J. S. Petersson and K. Golman, J. Magn. Reson., 1998, 133, 1–12 CrossRef PubMed.
- A. A. Smith, B. Corzilius, A. B. Barnes, T. Maly and R. G. Griffin, J. Chem. Phys., 2012, 136, 015101 CrossRef PubMed.
- P. Wenk, M. Kaushik, D. Richter, M. Vogel, B. Suess and B. Corzilius, J. Biomol. NMR, 2015, 63, 97–109 CrossRef CAS PubMed.
- M. Rosay, V. Weis, K. E. Kreischer, R. J. Temkin and R. G. Griffin, J. Am. Chem. Soc., 2002, 124, 3214–3215 CrossRef CAS PubMed.
- T. Jacso, W. T. Franks, H. Rose, U. Fink, J. Broecker, S. Keller, H. Oschkinat and B. Reif, Angew. Chem., Int. Ed., 2012, 51, 432–435 CrossRef CAS PubMed.
- J. Becker-Baldus, C. Bamann, K. Saxena, H. Gustmann, L. J. Brown, R. C. D. Brown, C. Reiter, E. Bamberg, J. Wachtveitl, H. Schwalbe and C. Glaubitz, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9896–9901 CrossRef CAS PubMed.
- P. C. A. van der Wel, K. N. Hu, J. Lewandowski and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 10840–10846 CrossRef CAS PubMed.
- G. T. Debelouchina, M. J. Bayro, P. C. A. van der Wel, M. A. Caporini, A. B. Barnes, M. Rosay, W. E. Maas and R. G. Griffin, Phys. Chem. Chem. Phys., 2010, 12, 5911–5919 RSC.
- M. J. Bayro, G. T. Debelouchina, M. T. Eddy, N. R. Birkett, C. E. MacPhee, M. Rosay, W. E. Maas, C. M. Dobson and R. G. Griffin, J. Am. Chem. Soc., 2011, 133, 13967–13974 CrossRef CAS PubMed.
- A. J. Rossini, A. Zagdoun, F. Hegner, M. Schwarzwälder, D. Gajan, C. Copéret, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2012, 134, 16899–16908 CrossRef CAS PubMed.
- T. Maly, D. Cui, R. G. Griffin and A.-F. Miller, J. Phys. Chem. B, 2012, 116, 7055–7065 CrossRef CAS PubMed.
- T.-C. Ong, M. L. Mak-Jurkauskas, J. J. Walish, V. K. Michaelis, B. Corzilius, A. A. Smith, A. M. Clausen, J. C. Cheetham, T. M. Swager and R. G. Griffin, J. Phys. Chem. B, 2013, 117, 3040–3046 CrossRef CAS PubMed.
- C. Fernández-de-Alba, H. Takahashi, A. Richard, Y. Chenavier, L. Dubois, V. Maurel, D. Lee, S. Hediger and G. De Paëpe, Chem. – Eur. J., 2015, 21, 4512–4517 CrossRef PubMed.
- M. A. Voinov, D. B. Good, M. E. Ward, S. Milikisiyants, A. Marek, M. A. Caporini, M. Rosay, R. A. Munro, M. Ljumovic, L. S. Brown, V. Ladizhansky and A. I. Smirnov, J. Phys. Chem. B, 2015, 119, 10180–10190 CrossRef CAS PubMed.
- H. Takahashi, S. Hediger and G. De Paepe, Chem. Commun., 2013, 49, 9479–9481 RSC.
- A. N. Smith, M. A. Caporini, G. E. Fanucci and J. R. Long, Angew. Chem., Int. Ed., 2015, 54, 1542–1546 CrossRef CAS PubMed.
- B. J. Wylie, B. G. Dzikovski, S. Pawsey, M. Caporini, M. Rosay, J. H. Freed and A. E. McDermott, J. Biomol. NMR, 2015, 61, 361–367 CrossRef CAS PubMed.
- E. A. W. van der Cruijsen, E. J. Koers, C. Sauvée, R. E. Hulse, M. Weingarth, O. Ouari, E. Perozo, P. Tordo and M. Baldus, Chem. – Eur. J., 2015, 21, 12971–12977 CrossRef CAS PubMed.
- V. M. Runge, R. G. Stewart, J. A. Clanton, M. M. Jones, C. M. Lukehart, C. L. Partain and A. E. James, Radiology, 1983, 147, 789–791 CrossRef CAS PubMed.
- J. A. Koutcher, C. T. Burt, R. B. Lauffer and T. J. Brady, J. Nucl. Med., 1984, 25, 506–513 CAS.
- R. H. Knop, J. A. Frank, A. J. Dwyer, M. E. Girton, M. Naegele, M. Schrader, J. Cobb, O. Gansow, M. Maegerstadt, M. Brechbiel, L. Baltzer and J. L. Doppman, J. Comput. Assist. Tomogr., 1987, 11, 35–42 CrossRef CAS PubMed.
- P. Hermann, J. Kotek, V. Kubicek and I. Lukes, Dalton Trans., 2008, 3027–3047 RSC.
- A. M. Raitsimring, C. Gunanathan, A. Potapov, I. Efremenko, J. M. L. Martin, D. Milstein and D. Goldfarb, J. Am. Chem. Soc., 2007, 129, 14138–14139 CrossRef CAS PubMed.
- A. Potapov, H. Yagi, T. Huber, S. Jergic, N. E. Dixon, G. Otting and D. Goldfarb, J. Am. Chem. Soc., 2010, 132, 9040–9048 CrossRef CAS PubMed.
- H. Yagi, D. Banerjee, B. Graham, T. Huber, D. Goldfarb and G. Otting, J. Am. Chem. Soc., 2011, 133, 10418–10421 CrossRef CAS PubMed.
- D. Banerjee, H. Yagi, T. Huber, G. Otting and D. Goldfarb, J. Phys. Chem. Lett., 2012, 3, 157–160 CrossRef CAS.
- D. T. Edwards, Z. Ma, T. J. Meade, D. Goldfarb, S. Han and M. S. Sherwin, Phys. Chem. Chem. Phys., 2013, 15, 11313–11326 RSC.
- A. Martorana, G. Bellapadrona, A. Feintuch, E. Di Gregorio, S. Aime and D. Goldfarb, J. Am. Chem. Soc., 2014, 136, 13458–13465 CrossRef CAS PubMed.
- P. Lueders, G. Jeschke and M. Yulikov, J. Phys. Chem. Lett., 2011, 2, 604–609 CrossRef CAS.
- D. Akhmetzyanov, J. Plackmeyer, B. Endeward, V. Denysenkov and T. F. Prisner, Phys. Chem. Chem. Phys., 2015, 17, 6760–6766 RSC.
- J. Eisinger, R. G. Shulman and W. E. Blumberg, Nature, 1961, 192, 963–964 CrossRef CAS PubMed.
- A. Cavé, M.-F. Daures, J. Parello, A. Saint-Yves and R. Sempere, Biochimie, 1979, 61, 755–765 CrossRef.
- A. Dvoretsky, V. Gaponenko and P. R. Rosevear, FEBS Lett., 2002, 528, 189–192 CrossRef CAS PubMed.
- M. D. Vlasie, C. Comuzzi, A. M. C. H. van den Nieuwendijk, M. Prudêncio, M. Overhand and M. Ubbink, Chem. – Eur. J., 2007, 13, 1715–1723 CrossRef CAS PubMed.
- P. S. Nadaud, J. J. Helmus, S. L. Kall and C. P. Jaroniec, J. Am. Chem. Soc., 2009, 131, 8108–8120 CrossRef CAS PubMed.
- I. Sengupta, P. S. Nadaud, J. J. Helmus, C. D. Schwieters and C. P. Jaroniec, Nat. Chem., 2012, 4, 410–417 CrossRef CAS PubMed.
- W. R. Couet, R. C. Brasch, G. Sosnovsky and T. N. Tozer, Magn. Reson. Imaging, 1985, 3, 83–88 CrossRef CAS PubMed.
- S. Belkin, R. J. Mehlhorn, K. Hideg, O. Hankovsky and L. Packer, Arch. Biochem. Biophys., 1987, 256, 232–243 CrossRef CAS PubMed.
- I. Krstić, R. Hänsel, O. Romainczyk, J. W. Engels, V. Dötsch and T. F. Prisner, Angew. Chem., Int. Ed., 2011, 50, 5070–5074 CrossRef PubMed.
- A. P. Jagtap, I. Krstic, N. C. Kunjir, R. Hänsel, T. F. Prisner and S. T. Sigurdsson, Free Radical Res., 2015, 49, 78–85 CrossRef CAS PubMed.
- G. Otting, Annu. Rev. Biophys., 2010, 39, 387–405 CrossRef CAS PubMed.
- C. D. Jeffries, Phys. Rev., 1960, 117, 1056–1069 CrossRef CAS.
- C. F. Hwang and D. A. Hill, Phys. Rev. Lett., 1967, 19, 1011–1014 CrossRef CAS.
- B. Corzilius, Phys. Chem. Chem. Phys., 2016 10.1039/c6cp04621e.
- A. A. Smith, B. Corzilius, J. A. Bryant, R. DeRocher, P. P. Woskov, R. J. Temkin and R. G. Griffin, J. Magn. Reson., 2012, 223, 170–179 CrossRef CAS PubMed.
- H. Blok, J. A. J. M. Disselhorst, S. B. Orlinskii and J. Schmidt, J. Magn. Reson., 2004, 166, 92–99 CrossRef CAS PubMed.
- G. Mathies, H. Blok, J. A. J. M. Disselhorst, P. Gast, H. van der Meer, D. M. Miedema, R. M. Almeida, J. J. G. Moura, W. R. Hagen and E. J. J. Groenen, J. Magn. Reson., 2011, 210, 126–132 CrossRef CAS PubMed.
- A. B. Barnes, M. L. Mak-Jurkauskas, Y. Matsuki, V. S. Bajaj, P. C. A. van der Wel, R. DeRocher, J. Bryant, J. R. Sirigiri, R. J. Temkin, J. Lugtenburg, J. Herzfeld and R. G. Griffin, J. Magn. Reson., 2009, 198, 261–270 CrossRef CAS PubMed.
- C. D. Joye, R. G. Griffin, M. K. Hornstein, H. Kan-Nian, K. E. Kreischer, M. Rosay, M. A. Shapiro, J. R. Sirigiri, R. J. Temkin and P. P. Woskov, IEEE Trans. Plasma Sci., 2006, 34, 518–523 CrossRef PubMed.
- C. Cossy, L. Helm, D. H. Powell and A. E. Merbach, New J. Chem., 1995, 19, 27–35 CAS.
- A. M. Raitsimring, A. V. Astashkin, O. G. Poluektov and P. Caravan, Appl. Magn. Reson., 2005, 28, 281–295 CrossRef CAS.
- A. A. Smith, B. Corzilius, O. Haze, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2013, 139, 214201 CrossRef PubMed.
- D. Shimon, Y. Hovav, I. Kaminker, A. Feintuch, D. Goldfarb and S. Vega, Phys. Chem. Chem. Phys., 2015, 17, 11868–11883 RSC.
- K. J. Donovan, A. Lupulescu and L. Frydman, ChemPhysChem, 2014, 15, 436–443 CrossRef CAS PubMed.
- A. Doll, S. Pribitzer, R. Tschaggelar and G. Jeschke, J. Magn. Reson., 2013, 230, 27–39 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- S. Chandrasekhar, Rev. Mod. Phys., 1943, 15, 1–89 CrossRef.
- K. Barthelmes, A. M. Reynolds, E. Peisach, H. R. A. Jonker, N. J. DeNunzio, K. N. Allen, B. Imperiali and H. Schwalbe, J. Am. Chem. Soc., 2011, 133, 808–819 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04623a |
| ‡ Present address: Department of Chemical Physics, Weizmann Institute of Science, 76100 Rehovot, Israel. |
| § Present address: Amgen, Inc., 360 Binney Street, Cambridge, Massachusetts 02142, USA. |
| ¶ Present address: Department of Chemistry and Applied Biosciences, Laboratory of Physical Chemistry, ETH-Zürich, CH-8093 Zürich, Switzerland. |
| This journal is © the Owner Societies 2016 |