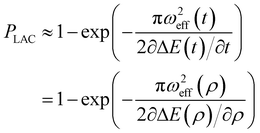Theory of solid effect and cross effect dynamic nuclear polarization with half-integer high-spin metal polarizing agents in rotating solids
Received
1st July 2016
, Accepted 12th August 2016
First published on 12th August 2016
Abstract
Dynamic nuclear polarization (DNP) is a powerful method to enhance sensitivity especially of solid-state magic-angle spinning (MAS) NMR by up to several orders of magnitude. The increased interest both from a practical as well as theoretical viewpoint has spawned several fields of active research such as the development of new polarizing agents with improved or unique properties and description of the underlying DNP mechanisms such as solid effect (SE) and cross effect (CE). Even though a novel class of unique polarizing agents based on high-spin metal ions such as Gd(III) and Mn(II) has already been utilized for MAS DNP a theoretical description of the involved DNP mechanism is still incomplete. Here, we review several aspects of DNP-relevant electron-paramagnetic resonance (EPR) properties of the general class of these half-integer high-spin metal ions with isotropic Zeeman interaction but significant zero-field splitting (ZFS). While the SE can be relatively easily described similar to that of a S = 1/2 system and is assumed to be effective only for polarizing agents featuring a narrow central EPR transitions (i.e., mS = −1/2 → +1/2) with respect to the nuclear Larmor frequency, the CE between two high-spin ions requires a more detailed theoretical investigation due to a multitude of possible transitions and matching conditions. This is especially interesting in light of recent understanding of CE being induced by MAS-driven level anti-crossings (LACs) between dipolar-coupled electron spins. We discuss the requirements of such CE-enabling LACs to occur due to anisotropy of ZFS, the expected adiabaticity, and the resulting possibilities of high-spin metal ion pairs to act as polarizing agents for DNP. This theoretical description serves as a framework for a detailed experimental study published directly following this work.
Introduction
Dynamic nuclear polarization mechanisms
Seven decades ago electron paramagnetic resonance (EPR)1–3 and nuclear magnetic resonance (NMR)4,5 emerged from a common theoretical and experimental basis. However, over time several experimental revolutions such as the emergence of Fourier-transform (FT) NMR6 in combination with the inherently different experimental time scales (relevant EPR frequencies and switching electronic have to be ∼three orders of magnitude faster than those in NMR) have created a gap between the NMR and EPR communities. This was further exacerbated by an everlasting push in NMR towards higher magnetic field while EPR applications have several advantages at low to medium field strengths. With the emergence of high-frequency microwave sources reaching the terahertz mark and sufficiently fast electronics, EPR applications at very high fields of 5 T and larger have become easily accessible and might lead to a closing of the gap between the two methods. This approach is currently practiced by the renaissance of a technique based on combination of NMR and EPR which has been known since the early days of magnetic resonance: dynamic nuclear polarization (DNP) is an outstanding technique for sensitivity enhancement of NMR by signal increase of up to several orders of magnitude.7,8 This is achieved by transfer of large electron spin polarization to surrounding nuclei by means of EPR excitation via one of several mechanisms. Most mechanisms have already been known and have been investigated at low and intermediate field strengths for many decades. Several years ago DNP for sensitivity enhancement of magic-angle spinning (MAS) NMR at high fields has been finally made available by the creativity and perseverance by Griffin and co-workers as well as the development of high-power/high-frequency gyrotrons for continuous-wave generation of microwaves by Temkin and co-workers.9–12 This has led to a renaissance of active research in this field and sparked renewed interest in elucidation of underlying theory.
The earliest mechanism investigated was the Overhauser effect (OE) where itinerant electrons are saturated by microwave irradiation and subsequent electron–nuclear (e–n) cross-relaxation—caused by time-dependent e–n (hyperfine) coupling—leads to nuclear spin hyperpolarization. This mechanism was first predicted by Overhauser and immediately thereafter observed experimentally by Carver and Slichter in metallic lithium.7,8 Later, OE was also observed in liquid solutions of solvated electrons13 and persistent radicals14 as well as in dielectric solids doped with radicals.15,16
A much more common mechanism occurring in insulating solids is the solid effect (SE).17–20 Here, e–n dipolar coupling in the rigid spin system leads to partial state mixing of the nuclear spin states which in turn allows for excitation of nominally forbidden e–n double quantum (DQ) and zero quantum (ZQ) transitions occurring at either the sum or difference of the electron and nuclear Larmor frequencies ωL and ω0I, respectively, with microwaves of frequency ωμw:
We explicitly define and utilize an effective electron Larmor frequency
ωL (
i.e., the spin precessional frequency influenced by all secular interactions including spin and quadrupolar interactions) instead of the often used electron Zeeman frequency
ω0S. For two high-spin electronic systems with isotropic Zeeman interaction additional sources of strong frequency shifts such as zero-field splitting (ZFS) have to be considered as we will describe below. A general situation is shown in
Fig. 1 (left). Selective excitation of such a forbidden transition then directly results in nuclear hyperpolarization with opposite sign of enhanced NMR signal for DQ and ZQ excitation. Therefore, simultaneous excitation of both DQ and ZQ transitions of different spin packets in an inhomogeneously broadened EPR line with overall breadth exceeding
ω0I leads to mutual cancellation of DNP enhancements and vanishing net hyperpolarization in the differential SE (see
Fig. 2).
21 Therefore, persistent carbon-based radicals such as trityl or BDPA derivatives with small g-anisotropy and consequently narrow EPR line even at high magnetic field are utilized.
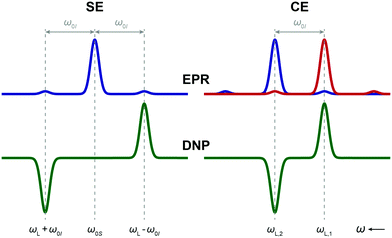 |
| | Fig. 1 Illustration of the relationship between EPR spectra (top) and DNP field profiles (bottom). For the SE (left) irradiation of the forbidden e–n DQ and ZQ transitions (intensity highly exaggerated in the EPR simulation) leads to negative and positive enhancement of NMR signal amplitude, respectively. For the ideal CE (right) in a static sample irradiation of one of two electron spins with Larmor frequencies differing by the nuclear Larmor frequency leads to DNP enhancement. | |
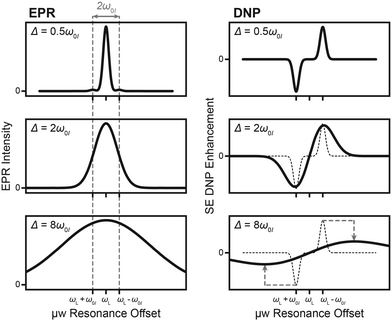 |
| | Fig. 2 Mutual cancellation of positive and negative enhancement in inhomogeneously broadened EPR spectra with breadth the nuclear Larmor frequency. The DNP field profile of the narrow case is shown with a dashed line for comparison. Overlap of ZQ and DQ transitions of different spin packets leads to a reduction of SE enhancement and an increase of separation between frequency of maximum positive and negative enhancement. | |
In samples where moderate electron dipole–dipole interactions between polarizing agents are present two additional mechanisms can occur: cross effect (CE) and thermal mixing (TM).22–24 The latter is only active at very low temperatures (typically ≤4 K) where the inhomogeneously broadened EPR line is characterized by strong exchange between spectral bins and behaves highly homogeneous under microwave hole-burning due to a strongly coupled spin system and slow relaxation.25 As MAS NMR is typically performed at temperatures around 100 K or above this mechanism does not play a significant role and we will not discuss it further.
CE on the other hand is currently the most efficient mechanism especially under MAS conditions.26 In a static sample (without MAS) the Larmor frequencies of the spin packets of two dipolar coupled electrons strictly have to be separated by the Larmor frequency of the nucleus to be polarized:27
In this case, two spin eigenstates connected by an electron–electron–nuclear (e–e–n) flip–flop–flip transition are degenerate which allows for efficient population transfer by DNP when one of the electrons is selectively irradiated by microwaves at its Larmor frequency (
Fig. 1, right).
Recently, it has become clear that the CE follows a much more complicated but robust mechanism in rotating solids as long as electron Larmor frequency separation is dominated by anisotropic interactions. Theoretical and practical studies have revealed a fundamental role of level anti-crossings (LACs) which dynamically occur under MAS.28,29 Strong anisotropic interactions lead to modulation of spin energy eigenstates during the rotation period; at certain rotor angles degeneracies are approached at which strong mixing occurs due to couplings between the involved states. Under optimal conditions adiabatic transitions can occur which lead to population transfer and finally accumulation of enhanced nuclear polarization. For a complete understanding of CE three different rotor events have to be considered: (i) microwave events, where the transition frequency of one electron single quantum (SQ) transition matches the irradiation frequency and the polarization of this transition is reduced; (ii) e–e dipolar flip–flop events, where the two electron spins exchange population while the nuclear spin state is conserved; and (iii) e–e–n three-spin flip–flop–flip events, where the CE transfer occurs and polarization is transferred to the nucleus. All three events are crucial for efficient CE.28 As long as spin–lattice relaxation during the rotor period does not lead to full thermalization of populations, the events can occur temporally separated as they are memorized by the system due to the inflicted polarization changes (Fig. 3). This makes the CE under MAS a rather robust mechanism where the above matching condition (2) does not have to be fulfilled at all times, especially not during the brief μw excitation event.
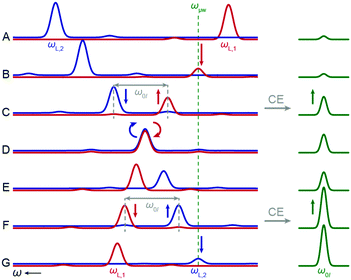 |
| | Fig. 3 Spectral representation of rotor events during MAS for CE: (A) two electron spins (red and blue, left) are arbitrarily separated in their Larmor frequencies. (B) μw rotating frame LAC: when the Larmor frequency of electron spin 1 (red) crosses the μw frequency partial saturation of the SQ transition occurs and a difference in polarization of the two electron spins is inflicted. (C) CE LAC: when the separation of the two electron Larmor frequencies matches the nuclear Larmor frequency energy conserving e–e–n flip–flop–flips lead to a partial transfer of electron spin polarization to the nucleus (green, right). (D) Dipolar LAC: when the two electron spin transitions are degenerate dipolar coupling leads to strong mixing of the electron spin states by ZQ flip–flops. (E) After the dipolar LAC the polarization difference has been swapped between the two electrons. This allows for additional increase in nuclear polarization during another CE LAC (F) even though the frequency difference between the electron spins is now inverted. (G) Finally, electron spin 2 is crossing μw resonance and the process can begin anew. Note that electronic spin–lattice relaxation has been omitted for simplicity. | |
High-spin polarizing agents
For DNP the large polarization to be transferred to nuclei is typically provided by paramagnetic species which act as polarizing agents. In the following we will discuss the influence of high-spin properties on DNP exemplarily for Gd(III) and Mn(II) as they have already been shown to act as polarizing agents for DNP.30 Furthermore these metal ions share rather similar magnetic properties which allows us to describe their behavior in a more general manner.
Being central-standing members of the respective rare earths or transition metal group they both feature half-filled electronic subshells (4f7 and 3d5, respectively), resulting in vanishing orbital momentum and concomitantly negligible spin–orbit coupling despite the relatively large atomic masses. The high-spin character (S = 7/2 for Gd(III) and S = 5/2 for Mn(II)) leads to the occurrence of ZFS in non-cubic environments. The ZFS constant can range from a few hundreds of MHz to several GHz.31–35 Nevertheless, due to the half-integer (Kramer's type) spin system, the EPR central transition (CT) between the mS = −1/2 and mS = +1/2 state is rather narrow because it is only influenced by ZFS in second-order and higher. Due to the large shielding of the deeply buried f-orbitals and negligible admixture of higher s-orbitals through configuration interaction the g tensor of Gd(III) is virtually isotropic with values around 1.99 and only a rather small hyperfine coupling of ∼15 MHz to the metal nuclear isotopes (157Gd and 159Gd isotopes with I = 3/2 and ∼15% natural abundance each) occurs.36 EPR of Mn(II) on the other hand shows significant isotropic hyperfine interaction (HFI) to the isotopically pure 55Mn nucleus (I = 5/2) on the order of ∼250 MHz; while the isotropic g factor is very close that of the free electron.32
Based on these properties we will first describe a general high-spin system consisting of a half-integer electron spin S together with the metal nuclear spin Im. After we have determined the EPR properties including those unique to high-spin systems—such as quadrupolar interactions and effective transition moments—we will extend the description by another nucleus In to be polarized. Here, we have chosen a typical In = 1/2 nucleus, for example 1H, 13C, 15N, for simplicity and due to their prevalence in NMR. This will allow us to discuss SE between an electronic high-spin system and a nucleus. Finally, we will investigate the additional interaction with another high-spin electronic system of similar type—representing the minimal system required for simulations of CE. We analyze potential CE within such a system where ZFS is the only source of strong shifts of the electron spin eigenenergies. The anisotropy of ZFS and its evolution under MAS is simulated and discussed in the context of current CE theory.
The EPR properties of high-spin metal ions
The EPR Hamiltonian of high-spin metal ions such as Gd(III) and Mn(II) in low concentration—such that dipolar interactions between metal ions are vanishing—can be sufficiently described by a system constituent of an electron spin with S > 1/2 and an Im > 1/2 nuclear spin of the core metal:| | 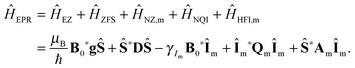 | (3) |
The Hamiltonian is given in units of angular frequency and consists of electron Zeeman (EZ), ZFS, nuclear Zeeman (NZ), nuclear quadrupole interaction (NQI), and HFI terms. The index ‘m’ denotes the high-spin metal nucleus; μB is the Bohr magneton, γIm is the (metal) nuclear gyromagnetic ratio, g, A, D, and Q are the EZ, HFI, ZFS, and NQI tensors, respectively. B0 is the external magnetic field vector constituent of static component B0 pointing in the z-direction as well as the oscillating μw field linearly polarized in the x-direction of the laboratory frame: B0* = (2B1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωμwt), 0, B0). Ŝ and Îm are the electron and (metal) nuclear spin operator vectors with elements Ŝx, Ŝy, Ŝz, and Îmx, Îmy, Îmz, respectively; asterisks denote the transpose.
cos(ωμwt), 0, B0). Ŝ and Îm are the electron and (metal) nuclear spin operator vectors with elements Ŝx, Ŝy, Ŝz, and Îmx, Îmy, Îmz, respectively; asterisks denote the transpose.
The ZFS Hamiltonian has the same general form as the NQI term. Therefore, high-spin electronic systems underlie the same effects as quadrupolar nuclei regarding resonance line shapes, state mixing, and transition probabilities. Nevertheless, due to differences in nomenclature and definitions of parameters we review these effects in detail. As the ZFS tensor often contains elements of similar magnitude to the EZ interaction, a simple reduction to secular components strictly cannot be performed. Individually, the ZFS Hamiltonian can be simply given in the tensor frame operator basis set (denoted by prime symbols),
| | | ĤZFS = D[Ŝ2′2 − ⅓S(S + 1)1] + E(Ŝ+′2 + Ŝ−′2), | (4) |
where
S is the electron spin quantum number,
1 is the unity matrix, and
D and
E represent the ZFS constants in their common form:
D = 3/2
D33;
E = 1/2(
D22 −
D11); 0 ≤
E ≤ 1/3
D. Step-operators are given by their usual definitions:
Ô± =
Ôx ±
iÔy. By transformation into the laboratory frame defined by the magnetic field (where
z is dictated by the static external field and
x is given by the microwave field direction) it becomes apparent that besides first-order shifts of the spin eigenstates (according to
Ŝz2 − 1/3
S(
S + 1)
1) EPR DQ (
Ŝ±2) and SQ coherences (
ŜzŜ± +
Ŝ±Ŝz) are introduced. The single quantum coherences lead to mixing of states with adjacent
mS; however, this does not occur between the central magnetic spin states (
i.e.,
mS = −1/2 ↔ +1/2) because the respective matrix elements are absent. The exact treatment would require full diagonalization of the Hamiltonian which is rather tedious analytically.
Spin energy eigenstates by perturbation treatment
In an attempt to simplify this problem we will focus on two features that are of significant importance for the further understanding and interpretation of line shape and other experimental observations: resonance frequencies and transition probabilities. Resonance frequencies can be deduced from a simple perturbation theoretical approach and analysis of resulting eigenenergies, while for the transition probabilities a quantum mechanical treatment can be performed on a highly truncated Hamiltonian.
NQI of the metal nucleus can be neglected since it does not lead to significant shifts of EPR/DNP-relevant transitions; for more sophisticated EPR techniques such as hyperfine spectroscopy this term might have to be considered in some cases. Furthermore we can assume that the EZ and the HFI are sufficiently described by the isotropic constants giso = 1/3tr(g) and aiso = 1/3tr(A), respectively, which is reasonable for many Mn(II) and Gd(III) complexes; for the latter the small hyperfine coupling to the minority magnetic metal nuclei could even be omitted. The resulting static Hamiltonian has the form
| | | ĤEPR ≈ ω0SŜz + ω0ImÎmz + aiso[ŜzÎmz + ½(Ŝ+Îm− + Ŝ−Îm+)] + Ŝ*DŜ | (5) |
where
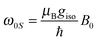
and
ω0Im =
γImB0 are the electron and nuclear Zeeman frequencies, respectively.
The eigenenergies of this system can be derived by perturbation theory:37
| | 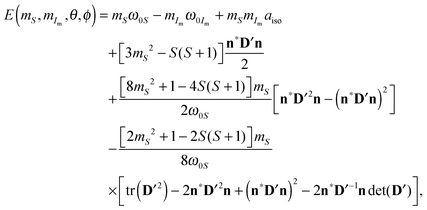 | (6) |
where
D′ is the ZFS tensor in its principal axes system;
n* = (sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ, sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ, cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ) is the orientation vector between the tensor frame and the laboratory frame in the unit sphere with longitudinal and azimuthal angles,
θ and
ϕ, respectively. Note that
eqn (6) includes up to second-order terms for ZFS but only first-order terms for all other interactions. All satellite transitions (ST)—where |
mS| is changing by one unit—can be sufficiently described by only considering first-order terms. This is especially true for line shape analysis of frozen solutions at high field where typically the distribution of ZFS parameters is much larger than second-order effects (see below). In this case the eigenenergies are given by
| | 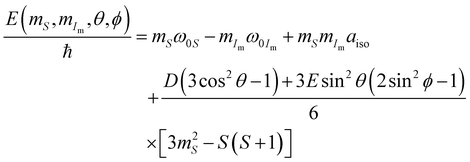 | (7) |
and the EPR frequencies for a transition |
mS,
mIm〉 ← |
mS − 1,
mIm〉 are:
| | 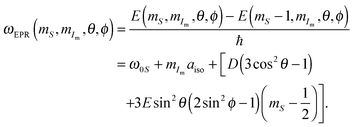 | (8) |
The resulting eigenstate and transition frequency shifts are depicted in
Fig. 4.
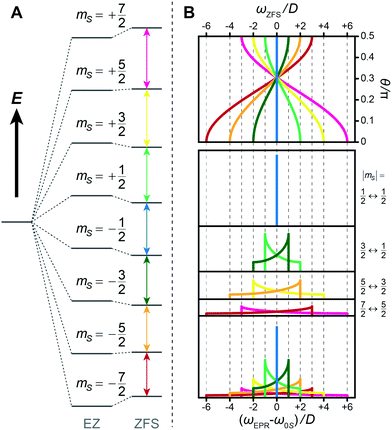 |
| | Fig. 4 (A) Spin energy splitting of an S = 7/2 system typical for Gd3+ with axially symmetric ZFS (E = 0). Note that EZ and ZFI interaction are not to scale; at high field relevant for MAS DNP EZ is ∼two orders of magnitude larger than ZFS. (B) Angular dependence of EPR transitions shifted by ZFS (first-order) and resulting shape of the EPR line as deduced from individual EPR transitions. | |
For the EPR central transition (CT), where |mS| = 1/2 is conserved, the first-order ZFS vanishes and the second-order term dominates the line shape. Therefore the transition frequency can be expressed as
| | 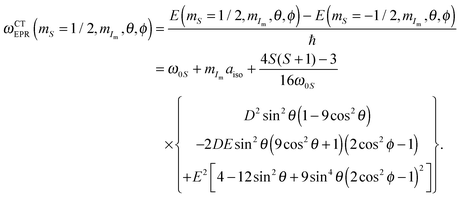 | (9) |
This second-order ZFS scales inversely with the Zeeman frequency—and thus the external magnetic field—and is therefore most important at small magnetic fields usually employed in EPR. Nevertheless, due to the oftentimes large ZFS constant in combination with the absence of other broadening mechanisms the CT lineshape is in most cases dominated by ZFS even at magnetic fields of 5 T and higher.
EPR transition probabilities
Probabilities of μw-induced transitions can generally be determined by transforming the μw Hamiltonian—which in the respective rotating Zeeman frame can be expressed aswith the Rabi frequency 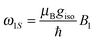 —into the eigenframe of the full (static) spin Hamiltonian. In the limit of small μw fields—and without state mixing introduced by ZFS—the nutation frequency for the transition |mS, mIm〉 ← |mS − 1, mIm〉 can be deduced from the matrix elements 〈mS, mIm|ω1SŜx|mS − 1, mIm〉 and can be calculated as:38
—into the eigenframe of the full (static) spin Hamiltonian. In the limit of small μw fields—and without state mixing introduced by ZFS—the nutation frequency for the transition |mS, mIm〉 ← |mS − 1, mIm〉 can be deduced from the matrix elements 〈mS, mIm|ω1SŜx|mS − 1, mIm〉 and can be calculated as:38| | | ωEPRN(mS) = [S(S + 1) − mS(mS − 1)]½ω1S. | (11) |
The respective transition probabilities scale as the square of these nutation frequencies. Without ZFS, transitions where mS changes by more than one unit are forbidden and their respective transition moments are vanishing. Moderate ZFS will influence the transition moments of allowed transitions while also introducing non-vanishing matrix elements for electronic ZQ and DQ transitions.31 In cases where ω0S ≫ D the effects of these perturbed transition moments can nevertheless be neglected for line shape and absorption intensity considerations.
The shape of EPR spectra
In order to demonstrate the line shape caused by ZFS and the robustness of the perturbation treatment under the conditions considered here we have performed numerical simulations comparing full diagonalization with the “hybrid” approximation where the CT is treated in second-order while all other transitions are truncated after first-order terms; transition probabilities are calculated according to eqn (11) and all forbidden transitions are neglected. In Fig. 5 the result is shown for a powder average of three different, typical cases with D = 1.2 GHz each and E = 0, 200 MHz, and 400 MHz, respectively, representing the axially symmetric, an intermediate as well as the full orthorhombic case accordingly. It should be noted that these line shapes only occur under ideal crystalline conditions; in amorphous frozen solution significant distribution of ZFS parameters leads to complete loss of visible structure of the STs due to rather free organization of ligands around the metal ion. This leads to a bimodal, near-Gaussian distribution of D symmetric to 0, with the width of each lobe being half of its average D value; The E/D ratio takes up a quadratic distribution with a maximum occurrence near 0.25 and vanishing probability towards E/D = 0.39 The resulting, typical shape of an EPR spectrum broadened by such a distributed ZFS can be seen in Fig. 6.
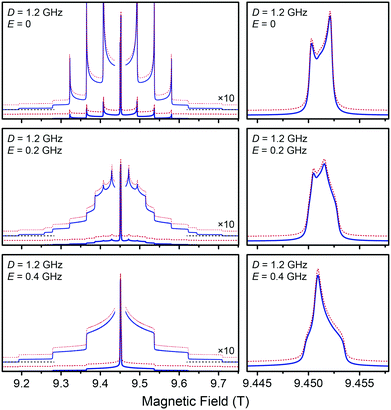 |
| | Fig. 5 Simulations of 263.47 GHz EPR line shape under high-temperature approximation of Gd3+ with three different ZFS parameter sets representing axial (top), intermediate orthorhombic (middle), and the ideal orthorhombic (bottom) case. Solid blue lines are calculated via full matrix diagonalization, red dashed lines via “hybrid” perturbation theory (see text). The slightly thinner sets of lines are the same spectra multiplied by a factor of 10; baseline is indicated by horizontal, dashed black lines at the edges of the spectrum. The red lines show almost perfect congruence with the blue spectra and have therefore been vertically offset for better visibility. Powder averages over 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 and 131 384 and 131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 328 molecular orientations were calculated for the axial and orthorhombic cases, respectively; Lorentzian line broadening of 10 MHz (FWHM) was applied to the stick spectra. The right column shows horizontal magnifications of the respective CTs in a narrow field range. 328 molecular orientations were calculated for the axial and orthorhombic cases, respectively; Lorentzian line broadening of 10 MHz (FWHM) was applied to the stick spectra. The right column shows horizontal magnifications of the respective CTs in a narrow field range. | |
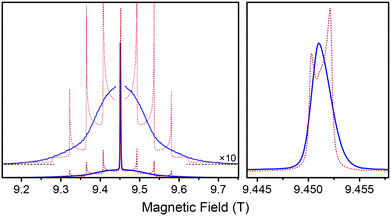 |
| | Fig. 6 Simulations of 263.47 GHz EPR line shape of Gd3+ with axial ZFS of D = 1.2 GHz (dashed red line) in comparison with a bimodal ZFS distribution with a maximum occurrence at D = 1.2 GHz (solid blue line), following the model of Raitsimring et al.39 Averages were calculated over 526 orientations and 4096 different combinations of D and E. Lorentzian line broadening of 10 MHz (FWHM) was applied to the stick spectra. The slightly thinner sets of lines are the same spectra multiplied by a factor of 10; baseline is indicated by horizontal dashed black lines. The right plot shows a horizontal magnification of the CT in a narrow field range. | |
Solid effect DNP with half-integer high-spin systems
The SE Hamiltonian of a high-spin metal ion
The solid effect is one of the major mechanisms for DNP-enhanced MAS NMR besides the cross effect. Generally it occurs between the unpaired electron(s) of the polarizing agent and hyperfine-coupled nuclear spins. In the simple case of a metal ion with S > 1/2, Im > 1/2 and another vicinal In = 1/2 nuclear spin to be polarized the static spin Hamiltonian can be expressed by the EZ and NZ interaction, HFI, as well as ZFS and NQI terms for the metal ion:| | 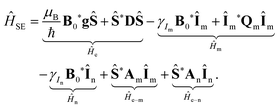 | (12) |
Note that the terms with index ‘n’ are now referring to the general nucleus to be polarized while index ‘m’ refers to the metal core nucleus; otherwise the symbol notation is equal to eqn (3). Analytical treatment for the simpler system with S = 1/2, In = 1/2 has been demonstrated earlier.21,40–42
All these treatments have been specifically solved by assuming a doublet electron spin so that nuclear spin quantization branching by non-secular HFI only has to be described between the α and β electron spin subspaces. For a high-spin system branching will vary within all possible subspaces so that the specific S = 1/2 case has to be generalized. First, we assume that interactions including the metal nucleus can be neglected. This is again valid for Gd3+ but does not account for shifts due to 55Mn HFI. Furthermore, ZFS shall be small compared to EZ so that shifts and mixing of electron spin states can be neglected; shifts of eigenstates due to ZFS and metal HFI could be easily reintroduced after the treatment. Therefore we can truncate the Hamiltonian to the following simplified form under pseudo-high-field approximation (i.e., ω0S ≫ An, Bn):
| | | ĤSE = ω0SŜz − ω0InÎnz + AnŜzÎnz + BnŜzÎnx | (13) |
Here,
An =
Azz and
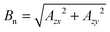
are the secular and pseudo-secular elements of the HFI tensor, respectively. Since this Hamiltonian is reminiscent of the
S = 1/2 case it can be analyzed using a similar, but more general description.
43 For this we have to derive the branching angles
ηmS which describe deviation of the effective nuclear spin quantization axis from the NZ axis under ideal high-field approximation. These effective fields acting on the nuclear spin are depicted in
Fig. 7 and are analytically obtained by simple geometric considerations including NZ as well as secular and pseudo-secular HFI:
| | 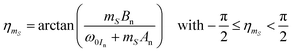 | (14) |
We will see that in the pseudo high-field approximation—where pseudo-secular HFI acting on the nuclear spin is considered but the relatively small effects on the electron spin are neglected—the eigenenergies of magnetic spin states are given by
| | 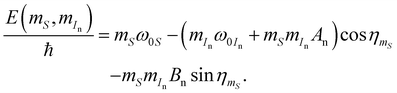 | (15) |
For paramagnetic NMR effective frequencies of nuclear SQ transition |
mS,
mIn = ±1/2〉 ← |
mS,
mIn = ∓1/2〉 within the respective
mS subspaces lead to a multiplet of 2
S + 1 lines split by HFI:
| | ωIn(mS) = (ω0In + mSAn)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηmS + mSBn ηmS + mSBn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηmS. ηmS. | (16) |
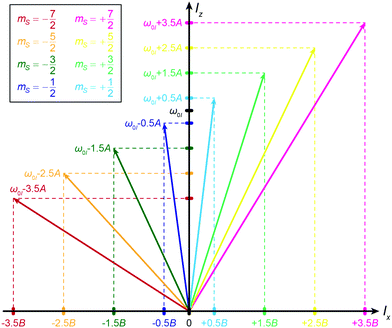 |
| | Fig. 7 Branching of effective nuclear spin fields in the different mS substates of an S = 7/2, In = 1/2 spin system. | |
Now we have to consider SE transitions between neighboring mS states. Analogous to the S = 1/2 case we find that the matching condition for a ZQ or DQ transition |mS, mIn = ∓1/2〉 ← |mS − 1, mIn = ±1/2〉, respectively, is given by
| | 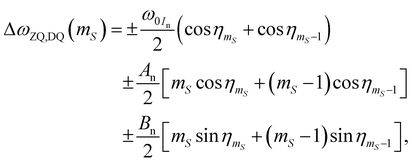 | (17) |
where Δ
ωZQ,DQ(
mS) is the offset to the pure EZ transition frequency required for ZQ or DQ excitation of the e–n system ending in the respective
mS state. Especially for large
mS absolute values, branching angle cosines might deviate considerably from unity so that their differences may not be neglected.
In most cases ω0In ≫ An, Bn so that ηi ≪ 1, Under these conditions the branching angle approaches
| | 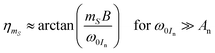 | (18) |
It should be noted that—except for the CT, see below—the secular HFI term does not vanish even when the branching angle cosine approaches unity and its sine vanishes. Then, the SE matching condition can be approximated as:
| | | ΔωZQ,DQ(mS) = ±ω0In ± (mS − ½)An | (19) |
This is in contrast to the
S = 1/2 case where—obviously due to the restriction to
mS = +1/2—the HFI completely cancels for the ZQ and DQ transitions.
For a ZQ or DQ transition within the EPR CT space, that is |mS = +1/2, mIn = ∓1/2〉 ← |mS − 1/2, mIn = ±1/2〉, we obtain a special case from eqn (17):
| | 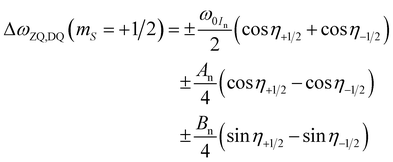 | (20) |
Then the branching angles for the two states connected by the CT are of equal magnitude but different sign, therefore we can simplify the matching condition even further:
| | 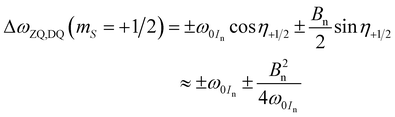 | (21) |
In any case under the conditions considered in MAS DNP we can often assume that ω0In ≫ An, Bn so that we can neglect any shifts in eigenstates. In this case we are left with the commonly stated SE matching condition
which describes the well-known offset requirement relative to the EZ frequency of the EPR spin packet in order to achieve DNP enhancement by excitation of e–n ZQ or DQ transitions. Nevertheless, if visible HFI to the nucleus to be polarized is observed in the EPR spectrum, the more general
eqn (19) has to be evoked. Furthermore, the above exact treatment has to be considered in cases where the high-field assumption is less appropriate. Such cases might be SE DNP at smaller fields which are often employed in Q- or X-band instruments or in general EPR applications including hyperfine spectroscopy where larger HFI might be faced. It should be noted, however, that this derivation is only valid for
In = 1/2 systems and would have to be extend for the general case of an arbitrary spin or particularly of a high-spin nucleus.
Effective SE transition moments
Besides shifts in eigenvalues we must investigate the effects of the high-spin character on the effective transition probabilities of the SE within the different mS substates. Analogous to the S = 1/2 case the transition moments for the ZQ and DQ transition can be deduced from the respective matrix elements and are influenced by the difference in nuclear branching angle between connected mS states:| | 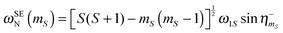 | (23) |
Here, 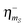 is the difference in branching angles between the initial state mS − 1 and the final state mS:
is the difference in branching angles between the initial state mS − 1 and the final state mS:| | 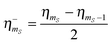 | (24) |
In Fig. 7 it becomes obvious that this difference may not be equal between different mS states, especially if the high-field approximation is significantly diverged. In detail, this leads to a variation of transition moments between transitions with different sign of mS and might lead to an imbalance in transition probabilities between SE from different STs. Close to the ideal high field limit (ω0In ≫ An) we find| | 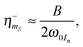 | (25) |
so that the high-spin system behaves similar to the S = 1/2 case albeit the larger transition moments due to the spin-operator elements following [S(S + 1) − mS(mS − 1)]1/2. This leads to up to 4 times larger transition moments and subsequently 16 times larger transition probability for the CT of S = 7/2 Gd(III) as compared to that of S = 1/2 while the outermost ST still experiences a 7-fold increase in probability.
The effective SE in presence of ZFS
In the S = 1/2 case the SE can be evoked by selective irradiation of the general e–n ZQ or DQ transitions |mS, mIn = ∓1/2〉 ← |mS − 1, mIn = ±1/2〉, whereby each of the two cases leads to opposite signs of nuclear polarization enhancement. In a simple but effective model the net enhancement can be deduced by the difference spectrum of these ZQ and DQ transitions.44
In high-spin systems the STs (ending in mS ≠ +1/2) underlie severe broadening due to first-order ZFS and distribution of ZFS parameters in amorphous frozen solutions. For D ≥ ω0In this would lead to strong overlap of ZQ and DQ transitions and mutual cancellation of positive and negative enhancements. Since these overlapping transitions stem from different spin states in the high-spin system, full cancellation of the ZQ and DQ transitions may not occur and residual net enhancement might be observed. However, due to the large spectral distribution of the STs these net effects can be neglected in most cases.
It should be noted that the above discussed description is valid under the condition that ZFS does not lead to significant mixing of the electron spin states; for typical ZFS parameters at high field this approximation is certainly reasonable. Since Bn is determined by the dipolar HFI—which can be described by the point-dipole approximation in most cases—variations in SE efficiency might furthermore be observed when the orientation of the ZFS tensor is correlated to the HFI tensor of the nucleus to be polarized. These effects would be restricted to nuclei within the polarizing agent complex and should be effectively averaged out within the disordered solvent matrix.
Therefore, we conclude that a sufficient description of SE DNP profile is obtained in most practical cases by a second-order perturbation approximation of the CT where the respective transition frequencies can be expressed as:
| | 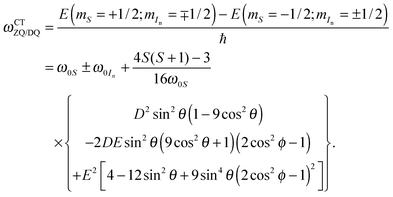 | (26) |
Comparing these SE-enabling transitions with the CT EPR frequency in
eqn (9) it becomes apparent that the second-order ZFS leads to the same frequency shift, but the transition is now offset by the Larmor frequency of the nucleus to be polarized. Hyperfine coupling to this nucleus does not affect the frequency of the DQ and ZQ frequencies. The reader should note that all other potential hyperfine couplings of nuclei not involved in the SE two-spin-flip process (including the metal nucleus) still lead to observable splittings or broadenings.
Under MAS the angular dependence of the second-order ZFS will lead to a modulation of the CT frequency during one rotor period. This will lead to the situation that individual spin packets transiently fulfill the SE resonance condition when μw irradiation at a suitable offset relative to the nuclear Larmor frequency occurs. During such a transient excitation enhanced nuclear polarization is generated and slowly accumulated over many rotor periods. The effective irradiation efficiency is reduced as compared to on-resonance irradiation of a spin-packet inside a static sample, however, many spin-packets not initially fulfilling the resonance condition will eventually undergo SE resonance under MAS. This will at least partially compensate for the reduced irradiation time and might even improve excitation if excessive μw power is available for significant saturation of SE. The situation is in principle comparable to other SE-enabling radicals where g anisotropy or dipolar HFI is dominating the EPR linewidth.
Cross effect DNP with high-spin metal ion pair
CE Hamiltonian of a metal high-spin system
A full treatment of CE DNP requires at least a three-spin system comprised of two dipolar coupled electron spins and one nuclear spin to be polarized which is in turn hyperfine coupled to one or both electron spins. We consider two electron spins with S > 1/2 (indexed with ‘1’ and ‘2’, respectively) and one metal nucleus of Im > 1/2 each, as well as another In = 1/2 nuclear spin to be polarized. In this case the static Hamiltonian contains EZ and NZ terms for each spin, as well as ZFS and NQI for the metal ions. Spin interactions are considered between electrons and nuclei, interactions between nuclei are neglected due to their small magnitude:| | | ĤCE = Ĥe + Ĥm + Ĥn + Ĥe–e + Ĥe–m + Ĥe–n | (27) |
The individual terms are:| | 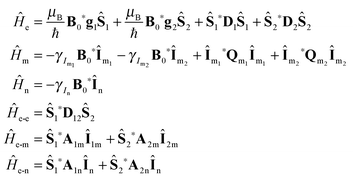 | (28) |
We can reduce the problem by neglecting the metal nuclei and due to the fact that g values of both electrons are isotropic and equal. Furthermore, the nucleus to be polarized shall be situated much closer to one electron spin than to the other so that the HFI to the latter can be neglected. The simplified Hamiltonian has the form:
| | 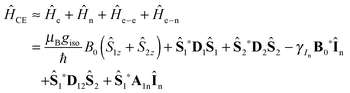 | (29) |
An approximate analytical treatment is considerably more complex compared to the SE. If ZFS was absent the problem could be further simplified by a rotating frame transformation applied to the electron spins; this is described in detail elsewhere.41,45 Due to the potentially large magnitude of ZFS and induced electron spin state mixing a numerical approach would be well suited. Full treatment of the S1 = 7/2, S2 = 7/2, In = 1/2 system including non-secular ZFS interactions would require a 128-dimensional Hilbert space under laboratory frame propagation which is generally not a problem even for desktop-type workstations. However, in a disordered matrix each anisotropic high-spin system has an arbitrary molecular frame of reference resulting in four independent rotational parameters; additionally five unique geometrical parameters (out of three longitudinal angles and three distances) have to be defined to describe the interconnectivity between the three spins with respect to the external magnetic field axis. In a numerical simulation all nine independent parameters have to be varied and an average response is obtained according to the distribution weights. Furthermore, recent studies have shown that MAS plays a fundamental role in CE DNP which requires propagation of the density matrix over at least one rotor period in order to find the initial rates of transfer; a self-consistent feedback over several periods would be required for the quasi-stationary solution. Such a long propagation in the Liouville-von Neumann formulism in the presence of ZFS on the order of ∼1 GHz is computationally extremely demanding and practically unfeasible.
Eigenstates and CE matching conditions by perturbation treatment of ZFS
In an attempt to simplify the problem and gain better general understanding we treat the problem in eqn (29) again using a perturbation approach. Similar to the single electron spin case above, we can derive the first-order eigenstates of the Hamiltonian (29) as:| | 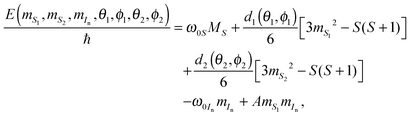 | (30) |
where MS = mS1 + mS2, and di(θi,ϕi) = Di(3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi − 1) + 3Ei
θi − 1) + 3Ei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi(2sin2
θi(2sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi − 1) is the instantaneous ZFS parameter for the i-th electron spin depending on the orientation of the tensor frame during MAS. Here, we have exemplarily truncated ZFS after first-order for analytical demonstration; an approximation up to second-order could be derived similar to eqn (6). Furthermore, we assume that dipolar coupling—even though crucial for CE—is small and does not lead to significant shifts. In Fig. 8A we have sketched the 64 eigenstates split by EZ interaction and ZFS; for the sake of simplicity we have neglected NZ, HFI, and e–e coupling in this figure. Under MAS the molecular frame of each Gd3+ is rotating (Fig. 8B) which results in periodically evolving eigenstates. In Fig. 8C we have performed numerical simulations as a function of the rotor angle; subfigure D shows the evolution of individual EPR transitions which have to be directly excited with μw irradiation for CE during MAS.
ϕi − 1) is the instantaneous ZFS parameter for the i-th electron spin depending on the orientation of the tensor frame during MAS. Here, we have exemplarily truncated ZFS after first-order for analytical demonstration; an approximation up to second-order could be derived similar to eqn (6). Furthermore, we assume that dipolar coupling—even though crucial for CE—is small and does not lead to significant shifts. In Fig. 8A we have sketched the 64 eigenstates split by EZ interaction and ZFS; for the sake of simplicity we have neglected NZ, HFI, and e–e coupling in this figure. Under MAS the molecular frame of each Gd3+ is rotating (Fig. 8B) which results in periodically evolving eigenstates. In Fig. 8C we have performed numerical simulations as a function of the rotor angle; subfigure D shows the evolution of individual EPR transitions which have to be directly excited with μw irradiation for CE during MAS.
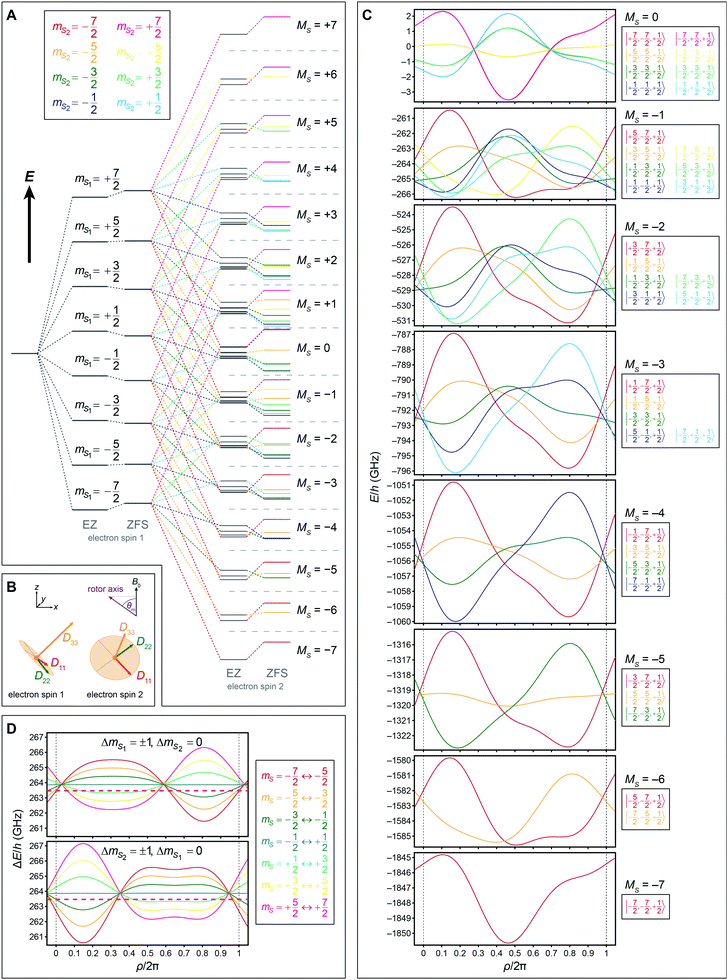 |
| | Fig. 8 (A) Level splitting scheme including EZ interaction and ZFS for a S1 = 7/2, S2 = 7/2, In = 1/2 system of two Gd3+ and one proton at a magnetic field of B0 = 9.4654 T. Shifts by NZ and HFI are not shown. (B) Orientation of ZFS tensors in laboratory frame used in subplot A and as initial setting (ρ = 0) in subplots (C) and (D). The ZFS parameter D/2π = 570 MHz (E = 0) and initial tensor orientations of θ1(ρ = 0) = 0.865, ϕ1(ρ = 0) = 0.628 and θ2(ρ = 0) = 0.716, ϕ2(ρ = 0) = −1.037 were used. (C) Evolution of eigenstates due to ZFS (up to second-order) under one period of MAS. Only the mIn = +1/2 subspace is shown. Subspaces with positive MS are not shown since they closely resemble their negative counterparts. (D) Evolution of resonance frequencies for allowed SQ EPR transitions for electron spin 1 (top) and electron spin 2 (bottom) due to ZFS (up to second-order). The red dashed line represents μw irradiation with a frequency of ωμw/2π = 263.47 GHz being offset by the nuclear Zeeman frequency of 1H (ω0In/2π = 403 MHz). | |
For a CE transition to occur we have to consider a three-spin flip–flop–flip where each of the magnetic spin quantum numbers changes by one unit and MS is conserved. Therefore we only have to consider transitions |mS1, mS2, mIn〉 ← |mS1 ± 1, mS2 ∓ 1, −mIn〉 for positive or negative nuclear enhancement depending on the sign of mIn. We can obtain the frequencies for these transitions according to:
| | 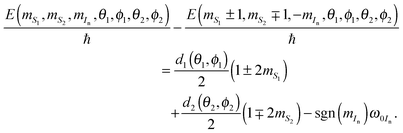 | (31) |
CE-enabling LACs occur, when the two states involved are degenerate; that is when the matching condition
| | 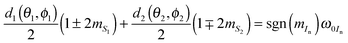 | (32) |
is satisfied. Here, again, we specifically neglect e–e dipolar coupling for the sake of simplicity. Secular e–e coupling elements will generally lead to shifts in eigenstate, while non-secular elements generate state mixing and cause additional separation of levels near the above degeneracies. Nevertheless, this simplified treatment allows us to identify these LACs and discuss the adiabaticity of the avoided crossings during MAS (see below).
Besides these CE-enabling LACs, purely electron–electron (e–e) flip–flop transitions, where the nuclear spin state is conserved, play an important role in MAS CE DNP. In Fig. 9(A–C) we have chosen a representative, exemplary evolution within the MS = −1 subspace; Fig. 9(D) shows one possible orientation where a degeneracy between two states connected by a CE-enabling transition is fulfilled (red dotted box). Several CE LACs (marked by red circles) can be identified which can transfer polarization from one nuclear spin state to the other during one rotor period. Dipolar LACs are marked with green circles.
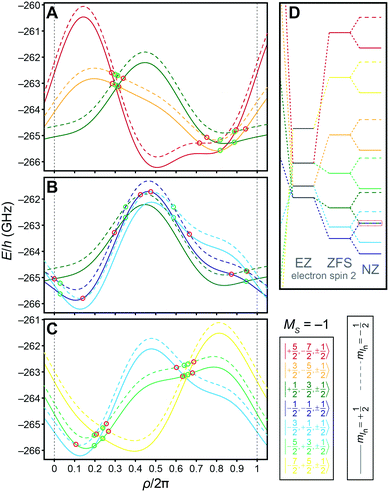 |
| | Fig. 9 (A–C) Evolution of eigenstates under one period of MAS due to ZFS (up to second-order) within the MS = −1 subspace. For better visibility the levels have been separated into three graphs in a way that all relevant LACs can be identified. Different mIn states are shown with solid and dashed lines, respectively. CE LACs (red circles) occur between lines of different type, purely e–e dipolar LACs (green circles) between lines of same type. (D) Level splitting scheme including EZ, ZFS, and NZ for a S1 = 7/2, S2 = 7/2, In = 1/2 system of two Gd3+ and one proton showing only the MS = −1 subspace including NZ splitting. CE-enabling degeneracy is fulfilled within the red dotted box. Simulation parameters are equal to those used in Fig. 8. | |
If only the CT is considered the simplified matching condition (32) cannot be applied since second-order ZFS is the only interaction responsible for shifts in electron Larmor frequency. Analytical derivation of a matching condition based on second-order shifts is unpractical, therefore we numerically simulated two situations where a nucleus with large gyromagnetic ratio (i.e., 1H) and with small gyromagnetic ratio (i.e., 15N) is to be polarized. In the former case—even with a D value of 1150 MHz—second-order ZFS is too small to allow for energy conserving CE matching (Fig. 10A, 1H case). Nuclear spin conserving dipolar LACs (marked by green circles) occur at two orientations. However, for highly concentrated samples or bis-complexes with rather short inter-metal distance, dipole coupling will effectively lead to permanent state mixing between |mS1 = ±1/2, mS2 = ∓1/2, mIn〉 and |mS1 = ∓1/2, mS2 = ±1/2, mIn〉 because the energy separation between these states never becomes larger than a few MHz. For 1H, direct irradiation of the CT is not expected to lead to a tangible CE because of the symmetry of the energy level system. Events leading to positive and negative enhancement would occur with (practically) equal probability thus net enhancement is expected to vanish. Nevertheless, microwave irradiation of the system with a frequency offset equaling ω0In below the EZ frequency might allow for partial saturation of the STs during μw resonant level transits (see Fig. 10B, left, where the red dashed line crosses the green levels). CE LACs which occur between these μw events could then transfer the polarization difference between electron spin transitions to the nucleus.
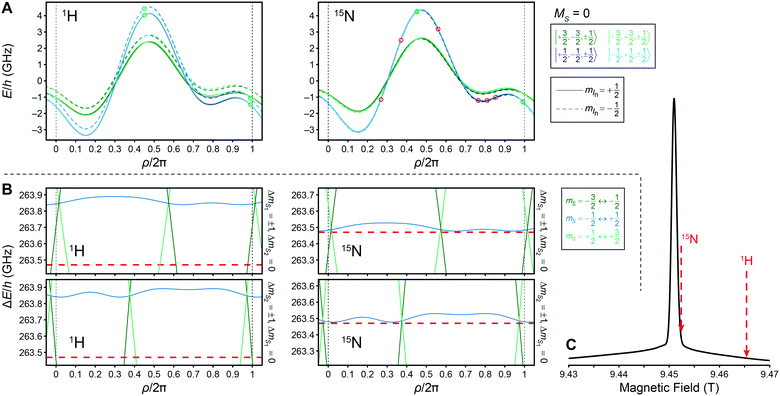 |
| | Fig. 10 (A) Evolution of eigenstates connected to the CT under one period of MAS due to ZFS (up to second-order) for a S1 = 7/2, S2 = 7/2, In = 1/2 system of two Gd3+ and one 1H (left) or one 15N (right), respectively, in the MS = 0 subspace. Different mIn states are shown with solid and dashed lines, respectively. CE LACs (red circles) occur between lines of different type, purely e–e dipolar LACs (green circles) between lines of same type. Note that the sign of γIn differs between the two cases. (B) Evolution of resonance frequencies for allowed SQ EPR transitions for electron spin 1 (top) and electron spin 2 (bottom) for the case of 1H (left) and 15N (right). The red dashed line represents μw irradiation with a frequency of ωμw/2π = 263.47 GHz being offset by the nuclear Zeeman frequency of either 1H (ω0In/2π = 403 MHz) or 15N (ω0In/2π = 40.8 MHz). In all simulations the field was set to either B0 = 9.4654 T (1H) or B0 = 9.4524 T (15N) as can be seen in subplot (C) for a simulated EPR spectrum. D/2π = 1150 MHz (E = 0) and θ1(ρ = 0) = 0.910, θ2(ρ = 0) = 0.836; all other parameters were used as described in Fig. 8. | |
The situation is starkly different when a nuclear spin with significantly smaller gyromagnetic ratio is considered. Also in Fig. 10 we show the same simulations as discussed before for 1H but now for 15N. In order to compensate for the smaller ω0In the magnetic field was adjusted and μw irradiation occurs now much closer to the CT. As can be seen in subplot A (right) CE-enabling LACs can now occur within the CT subspace; in fact, significant state mixing of the levels connected by the three-spin flip–flop–flip is expected for a large fraction of the rotor period given sufficient dipolar coupling between the electron spins. Due to the smaller resonance offset, μw-induced SQ excitation of the CT occurs directly at certain rotor angles. Given appropriate mutual orientation of the ZFS tensors the μw-irradiation of the two dipolar coupled electron spins occur at separate positions during the rotor period with CE and e–e dipolar LACs being situated in between the μw events (Fig. 10B, right). This potentially allows for an efficient CE due to the high adiabaticity (see below) of the involved LACs and slow transients through μw events resulting in larger electron spin saturation.
The adiabaticity of MAS-induced level anti-crossings due to ZFS
The occurrence of CE-enabling LACs alone is not an indication that CE can be utilized to generate net nuclear enhancement. Two additional factors have to be considered: adiabaticity of level crossings and longitudinal relaxation times.
Populations can only be exchanged between levels during an avoided crossing if the transition is sufficiently adiabatic. High adiabaticity is achieved when the rate with which the two energy eigenstates cross each other is slower than the off-diagonal coupling matrix element V connecting the two states. The probability of an adiabatic transition through LAC can be calculated via the Landau–Zener equation:
| | | PLAC = 1 − exp(−2πΓ). | (33) |
The adiabaticity parameter
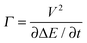
can be utilized to quantitatively determine the efficiency of population exchange during the LAC: for
Γ ≫ 1 the ideal LAC is fully adiabatic and populations are completely exchanged because the system always remains in an energy eigenstate; for
Γ ≈ 0 an ideal (non-avoided) level crossing occurs where populations are maintained for the same state before and after the crossing. Starting from thermal polarization, in the former case the lowest energy eigenstate always is most populated while in the latter case population inversions occur during crossings. This concept is applicable to all types of LACs encountered during MAS CE: for μw events the μw term connects two states separated by an EPR SQ transition; the e–e dipole coupling connects two states within a ZQ e–e flip–flop; finally the states involved in a CE-enabling three-spin flip–flop–flip are connected
via a combination of e–e dipole coupling and hyperfine coupling.
In our case ZFS is the main effect leading to variations in eigenenergies. Therefore we can express the Landau–Zener probability as
| | 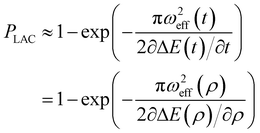 | (34) |
since the rotor angle
ρ is linearly varied with time:
ωeff is the respective off-diagonal term in the Hamiltonian introducing the state mixing. For the three cases mentioned above this is the effective μw nutation frequency, pseudo-secular e–e dipolar coupling, or effective e–e–n coupling elements driving the flip–flop–flip transition, respectively. Notice that the two latter terms are also time or angle dependent while
eqn (33) is strictly applicable for time independent
V; nevertheless, the Landau–Zener equation is valid if the effective coupling can be considered constant during strong mixing periods. Furthermore, quantitative analysis is tedious because of the large parameter space of orientations of ZFS tensors and dipolar vectors. Nevertheless we can draw qualitative conclusions based on
Fig. 8 and 9. Variations in eigenenergies vary strongly between different
mS states. For a semi-quantitative analysis we compare the rate with which the (unperturbed) eigenstates cross in our case with values derived by Thurber and Tycko for the CE between two nitroxide radicals. In their case typical rates of ∂(Δ
E/
h)/∂
t = 20 THz s
−1 and 30 THz s
−1 occur for μw and multi-spin flip events, respectively, at a MAS frequency of 7 kHz. In our case we irradiate a system of two Gd
3+ with rather small, axial ZFS of
D = 570 MHz (typical for Gd-DOTA) at 402 MHz offset with respect to the isotropic Zeeman frequency (corresponding to
ω0In of
1H). Somewhat surprisingly, for the innermost ST small μw event crossing rates of 1.6 THz s
−1 are observed. This rate can in fact become arbitrarily small for certain ZFS tensor orientations; at the same times it has to be noted that all crossing rates scale proportionally with larger
D. Furthermore, due to the larger spin operator elements in the high spin case an additional factor 15 can be gained in transition probability for this transition if compared with nitroxides. Even for transitions involving states with the largest absolute
mS value, level crossings with rates of ∼150 THz s
−1 occur. Here, the transition probability “advantage” of the high-spin system is a factor of 7 which makes the adiabaticity effectively equal to the typical μw events considered by Thurber and Tycko in the nitroxide case. Thus we conclude that μw-induced electron spin saturation during appropriate LACs is at least equally efficient as in the case of nitroxides at similar magnetic field and might even be significantly more efficient, especially at larger external fields. However, faster longitudinal relaxation in the high-spin case is expected to counteract efficient saturation of EPR SQ transitions. For the CT of Gd-DOTA,
T1S on the order of ∼25 times faster than that of nitroxide has been measured at 5 T and ∼80 K.
46
Electron–electron flip–flop LACs occur with rates between ∼30 THz s−1 and ∼250 THz s−1 while CE-enabling three spin flip LACs occur as slow as ∼18 THz s−1; this puts crossing rates for certain transitions involving states with small magnitude of mS in the same order of magnitude as for nitroxides (Fig. 9B specifically visualizes this situation). Again, due to the high-spin nature of Gd3+ effective transition moments are larger than for S = 1/2, resulting in 7- to 16-fold boost of effective transition probabilities between connected levels. That indicates that the adiabaticity of all dipolar and CE LACs is at least comparable to those observed for nitroxides given otherwise equal coupling constants.
Net enhancement of nuclear polarization by partial cancellation of positive and negative hyperpolarization transfer steps
Finally, one sign of nuclear hyperpolarization has to be favored over the opposite sign for achieving a tangible net enhancement. The sign of relative nuclear enhancement during one CE event is determined by the direction of the LAC (i.e., if the partially saturated state crosses the flip–flop–flip-connected state from smaller or larger energy). If an e–e dipolar event occurs in between two CE events with different directions, the relative electron spin populations are exchanged (under ideally adiabatic conditions) and both CE events lead to equal sign and subsequently net accumulation of nuclear hyperpolarization. If two or more CE events occur consecutively between the same set of states, LACs with opposite direction lead to (partial) cancellation of opposite signs of hyperpolarization, so that only one net transfer step remains for a typically odd number of crossings (see Fig. 10A in the case of 15N).
The position of μw events can be easily adjusted by the irradiation frequency—or from a practical viewpoint by adjusting the external magnetic field. Because in most cases it is unpractical or impossible to irradiate one electron spin transition selectively, excitation of several SQ electron spin transitions during one rotor cycle will lead to multiple CE events between several sets of states resulting in reduced net hyperpolarization. Intuitively, excitation at the global turning point of one of the extreme electron spin states (i.e., mS = ±7/2) would result in uni-directional transfer of polarization to the nucleus; in contrast, irradiation of the CT would lead to an equal number of positive and negative CE events for nuclei with large gyromagnetic ratio (so that the nuclear Larmor frequency exceeds the frequency variation of the CT due to second-order ZFS). Any irradiation offset in between these extreme cases would result in a situation where one direction would occur more often than the other and a net enhancement would be observed. In the absence of severe distribution of ZFS parameters (e.g., in a polycrystalline powder) irradiation at a turning point of a ST with respect to the rotor angle might be beneficial since a slower passage through the μw event can be achieved, favoring excitation of this specific transition over the other transitions which pass through the irradiation frequency with a much larger energetic slope. However, given the large distribution and featureless shape of the ST region in a typical amorphous solution one might expect that these effects will not manifest under experimental conditions.
When the overall breadth of the CT due to second-order ZFS is of equal magnitude or larger than the nuclear Larmor frequency, irradiation of one electron spin on one edge of the CT and thus on the turning point of the frequency dependence is expected to lead to significant nuclear hyperpolarization by matching to the CT of the other electron spin (see 15N case in Fig. 10B). Note, that after a certain fraction of the rotor period the two electrons effectively “swap places” so that the irradiation is now inverse; however, this change strictly has to be accompanied by an e–e dipolar event so that under ideally adiabatic conditions all irradiation events would act in favor of one sign of hyperpolarization, irrespective of which electron spin is irradiated.
Conclusion
Despite the rather complicated theory high-spin metal ions show intriguing properties as DNP polarizing agents. To date this potential has only been shown experimentally for a selective set of metal ions including Gd(III) and Mn(II), as well as Cr(III) under certain conditions.30,47 For efficient SE DNP high-spin metal ions are expected to feature a half-integer spin in combination with small to moderate ZFS, so that a narrow EPR CT is observed at high field. Irradiation of this CT with a frequency offset matching the nuclear Larmor frequency then leads to significant nuclear hyperpolarization. Due to their featureless nature we expect that net enhancement achieved by SE matching of the ST will be vanishing in most cases.
Due to the more complicated mechanism of the CE involving LACs during the evolution of ZFS under MAS the situation is starkly different. However, we expect that efficient μw irradiation of a significant fraction of polarizing agent molecules in a disordered sample is only possible at distinct turning points of the angular dependence of the transition frequencies, or practically at sharp features in the spectrum. Therefore we predict that efficient CE is only possible for nuclei with Larmor frequencies smaller than the effective breadth of the CT. Nevertheless, the multitude of different LACs observed in the evolution of the 64 eigenstates of the two electron spins during one rotor period might lead to interesting features—especially within a crystalline system not underlying strong distribution—and warrants further examination. In all cases the larger transition moments due the high-spin character—leading to up to ∼4 times larger coherences between states connected by dipolar coupling or μw irradiation in the S = 7/2 case—at least partially compensate for faster relaxation and less efficient excitation by larger spectral dispersion.
In the following article we present experimental data on Gd(III) and Mn(II) polarizing agents.48 The obtained results will be discussed in light of the theoretical framework which has been derived here. We will not only show that Gd(III) and Mn(II) complexes with narrow CT linewidth can be used for highly efficient polarization of 13C and 15N via the SE but also that significant CE can in fact be obtained for 15N with large concentrations of Gd-DOTA, where the CT breadth encompasses the nuclear Larmor frequency at a field of 9.4 T and sufficient intermolecular e–e dipolar coupling exists.
Acknowledgements
Helpful discussions with D. Akhmetzyanov and M. Kaushik (Frankfurt) as well as I. Kuprov (Southampton) are gratefully acknowledged. This work has been fully funded by the Deutsche Forschungsgemeinschaft (DFG) through Emmy Noether grant CO802/2-1. Additional support by the Center for Biomolecular Magnetic Resonance (BMRZ) is acknowledged.
References
- E. Zavoisky, J. Phys. (USSR), 1945, 9, 211 Search PubMed.
- E. Zavoisky, Zhurn Eksperiment. Teoret. Fiziki, 1946, 16, 603–606 Search PubMed.
- E. Zavoisky, J. Phys. (USSR), 1946, 10, 197 Search PubMed.
- F. Bloch, W. W. Hansen and M. Packard, Phys. Rev., 1946, 69, 680 Search PubMed.
- E. M. Purcell, H. C. Torrey and R. V. Pound, Phys. Rev., 1946, 69, 37–38 CrossRef CAS.
- R. R. Ernst and W. A. Anderson, Rev. Sci. Instrum., 1966, 37, 93–102 CrossRef CAS.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS.
- T. R. Carver and C. P. Slichter, Phys. Rev., 1953, 92, 212–213 CrossRef CAS.
- L. R. Becerra, G. J. Gerfen, B. F. Bellew, J. A. Bryant, D. A. Hall, S. J. Inati, R. T. Weber, S. Un, T. F. Prisner, A. E. McDermott, K. W. Fishbein, K. E. Kreischer, R. J. Temkin, D. J. Singel and R. G. Griffin, J. Magn. Reson., Ser. A, 1995, 117, 28–40 CrossRef CAS.
- G. J. Gerfen, L. R. Becerra, D. A. Hall, R. G. Griffin, R. J. Temkin and D. J. Singel, J. Chem. Phys., 1995, 102, 9494–9497 CrossRef CAS.
- D. A. Hall, D. C. Maus, G. J. Gerfen, S. J. Inati, L. R. Becerra, F. W. Dahlquist and R. G. Griffin, Science, 1997, 276, 930–932 CrossRef CAS PubMed.
- L. R. Becerra, G. J. Gerfen, R. J. Temkin, D. J. Singel and R. G. Griffin, Phys. Rev. Lett., 1993, 71, 3561–3564 CrossRef CAS PubMed.
- T. R. Carver and C. P. Slichter, Phys. Rev., 1956, 102, 975–980 CrossRef CAS.
- K. H. Hausser and D. Stehlik, Adv. Magn. Reson., 1968, 3, 79 CAS.
- O. Haze, B. Corzilius, A. A. Smith, R. G. Griffin and T. M. Swager, J. Am. Chem. Soc., 2012, 134, 14287–14290 CrossRef CAS PubMed.
- T. V. Can, M. A. Caporini, F. Mentink-Vigier, B. Corzilius, J. J. Walish, M. Rosay, W. E. Maas, M. Baldus, S. Vega, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2014, 141, 064202 CrossRef CAS PubMed.
- M. Abraham, R. W. Kedzie and C. D. Jeffries, Phys. Rev., 1957, 106, 165–166 CrossRef CAS.
- C. D. Jeffries, Phys. Rev., 1957, 106, 164–165 CrossRef CAS.
- E. Erb, J. L. Motchane and J. Uebersfeld, C. R. Hebd. Seances Acad. Sci., 1958, 246, 2121–2123 CAS.
- A. Abragam and W. G. Proctor, C. R. Hebd. Seances Acad. Sci., 1958, 246, 2253–2256 CAS.
- W. T. Wenckebach, Appl. Magn. Reson., 2008, 34, 227–235 CrossRef.
- A. V. Kessenikh, V. I. Lushchikov, A. A. Manenkov and Y. V. Taran, Sov. Phys.-Solid State, 1963, 5, 321–329 Search PubMed.
- C. F. Hwang and D. A. Hill, Phys. Rev. Lett., 1967, 18, 110–112 CrossRef CAS.
- C. F. Hwang and D. A. Hill, Phys. Rev. Lett., 1967, 19, 1011–1014 CrossRef CAS.
- M. Borghini, Phys. Rev. Lett., 1968, 20, 419–421 CrossRef CAS.
- Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941 CrossRef CAS PubMed.
- D. S. Wollan, Phys. Rev. B: Solid State, 1976, 13, 3671–3685 CrossRef CAS.
- K. R. Thurber and R. Tycko, J. Chem. Phys., 2012, 137, 084508 CrossRef PubMed.
- F. Mentink-Vigier, Ü. Akbey, Y. Hovav, S. Vega, H. Oschkinat and A. Feintuch, J. Magn. Reson., 2012, 224, 13–21 CrossRef CAS PubMed.
- B. Corzilius, A. A. Smith, A. B. Barnes, C. Luchinat, I. Bertini and R. G. Griffin, J. Am. Chem. Soc., 2011, 133, 5648–5651 CrossRef CAS PubMed.
- S. K. Misra, Appl. Magn. Reson., 1996, 10, 193–216 CrossRef CAS.
- S. Un, L. C. Tabares, N. Cortez, B. Y. Hiraoka and F. Yamakura, J. Am. Chem. Soc., 2004, 126, 2720–2726 CrossRef CAS PubMed.
- M. Benmelouka, J. Van Tol, A. Borel, M. Port, L. Helm, L. C. Brunel and A. E. Merbach, J. Am. Chem. Soc., 2006, 128, 7807–7816 CrossRef CAS PubMed.
- H. Käss, F. MacMillan, B. Ludwig and T. F. Prisner, J. Phys. Chem. B, 2000, 104, 5362–5371 CrossRef.
- L. C. Tabares, J. Gätjens and S. Un, Biochim. Biophys. Acta, 2010, 1804, 308–317 CrossRef CAS PubMed.
- W. Low, Phys. Rev., 1956, 103, 1309 CrossRef CAS.
-
A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, Oxford, 2001 Search PubMed.
- A. V. Astashkin and A. Schweiger, Chem. Phys. Lett., 1990, 174, 595–602 CrossRef CAS.
- A. M. Raitsimring, A. V. Astashkin, O. G. Poluektov and P. Caravan, Appl. Magn. Reson., 2005, 28, 281–295 CrossRef CAS.
- Y. Hovav, A. Feintuch and S. Vega, J. Magn. Reson., 2010, 207, 176–189 CrossRef CAS PubMed.
- K. N. Hu, G. T. Debelouchina, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2011, 134, 19 Search PubMed.
- B. Corzilius, A. A. Smith and R. G. Griffin, J. Chem. Phys., 2012, 137, 054201 CrossRef PubMed.
- J. A. Weil and J. H. Anderson, J. Chem. Phys., 1961, 35, 1410–1417 CrossRef CAS.
- D. Shimon, Y. Hovav, A. Feintuch, D. Goldfarb and S. Vega, Phys. Chem. Chem. Phys., 2012, 14, 5729–5743 RSC.
- Y. Hovav, A. Feintuch and S. Vega, J. Magn. Reson., 2012, 214, 29–41 CrossRef CAS PubMed.
- B. Corzilius, L. B. Andreas, A. A. Smith, Q. Z. Ni and R. G. Griffin, J. Magn. Reson., 2014, 240, 113–123 CrossRef CAS PubMed.
- B. Corzilius, V. K. Michaelis, S. A. Penzel, E. Ravera, A. A. Smith, C. Luchinat and R. G. Griffin, J. Am. Chem. Soc., 2014, 136, 11716–11727 CrossRef CAS PubMed.
- M. Kaushik, T. Bahrenberg, T. V. Can, M. A. Caporini, R. Silvers, J. Heiliger, A. A. Smith, H. Schwalbe, R. G. Griffin and B. Corzilius, Phys. Chem. Chem. Phys., 2016 10.1039/C6CP04623A.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article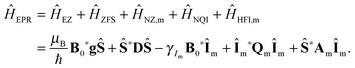
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωμwt), 0, B0). Ŝ and Îm are the electron and (metal) nuclear spin operator vectors with elements Ŝx, Ŝy, Ŝz, and Îmx, Îmy, Îmz, respectively; asterisks denote the transpose.
cos(ωμwt), 0, B0). Ŝ and Îm are the electron and (metal) nuclear spin operator vectors with elements Ŝx, Ŝy, Ŝz, and Îmx, Îmy, Îmz, respectively; asterisks denote the transpose.
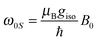 and ω0Im = γImB0 are the electron and nuclear Zeeman frequencies, respectively.
and ω0Im = γImB0 are the electron and nuclear Zeeman frequencies, respectively.
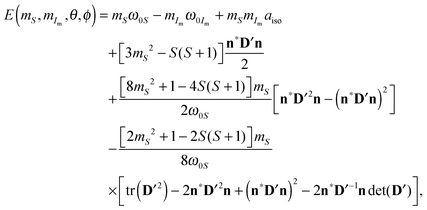
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, sin
ϕ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, cos
ϕ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is the orientation vector between the tensor frame and the laboratory frame in the unit sphere with longitudinal and azimuthal angles, θ and ϕ, respectively. Note that eqn (6) includes up to second-order terms for ZFS but only first-order terms for all other interactions. All satellite transitions (ST)—where |mS| is changing by one unit—can be sufficiently described by only considering first-order terms. This is especially true for line shape analysis of frozen solutions at high field where typically the distribution of ZFS parameters is much larger than second-order effects (see below). In this case the eigenenergies are given by
θ) is the orientation vector between the tensor frame and the laboratory frame in the unit sphere with longitudinal and azimuthal angles, θ and ϕ, respectively. Note that eqn (6) includes up to second-order terms for ZFS but only first-order terms for all other interactions. All satellite transitions (ST)—where |mS| is changing by one unit—can be sufficiently described by only considering first-order terms. This is especially true for line shape analysis of frozen solutions at high field where typically the distribution of ZFS parameters is much larger than second-order effects (see below). In this case the eigenenergies are given by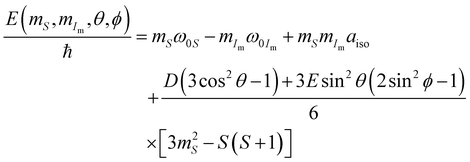
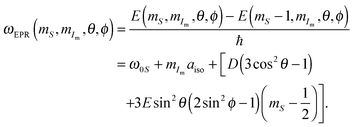
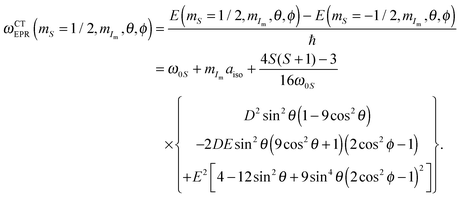
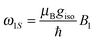 —into the eigenframe of the full (static) spin Hamiltonian. In the limit of small μw fields—and without state mixing introduced by ZFS—the nutation frequency for the transition |mS, mIm〉 ← |mS − 1, mIm〉 can be deduced from the matrix elements 〈mS, mIm|ω1SŜx|mS − 1, mIm〉 and can be calculated as:38
—into the eigenframe of the full (static) spin Hamiltonian. In the limit of small μw fields—and without state mixing introduced by ZFS—the nutation frequency for the transition |mS, mIm〉 ← |mS − 1, mIm〉 can be deduced from the matrix elements 〈mS, mIm|ω1SŜx|mS − 1, mIm〉 and can be calculated as:38
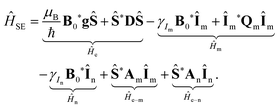
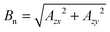 are the secular and pseudo-secular elements of the HFI tensor, respectively. Since this Hamiltonian is reminiscent of the S = 1/2 case it can be analyzed using a similar, but more general description.43 For this we have to derive the branching angles ηmS which describe deviation of the effective nuclear spin quantization axis from the NZ axis under ideal high-field approximation. These effective fields acting on the nuclear spin are depicted in Fig. 7 and are analytically obtained by simple geometric considerations including NZ as well as secular and pseudo-secular HFI:
are the secular and pseudo-secular elements of the HFI tensor, respectively. Since this Hamiltonian is reminiscent of the S = 1/2 case it can be analyzed using a similar, but more general description.43 For this we have to derive the branching angles ηmS which describe deviation of the effective nuclear spin quantization axis from the NZ axis under ideal high-field approximation. These effective fields acting on the nuclear spin are depicted in Fig. 7 and are analytically obtained by simple geometric considerations including NZ as well as secular and pseudo-secular HFI: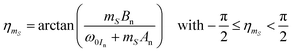
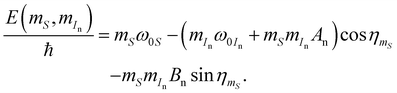
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηmS + mSBn
ηmS + mSBn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηmS.
ηmS.
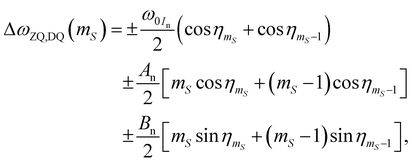
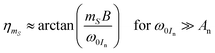
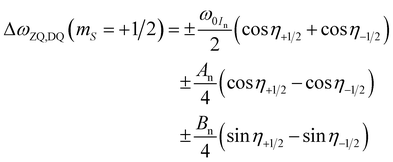
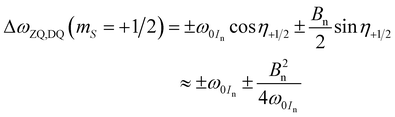
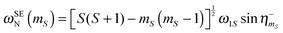
 is the difference in branching angles between the initial state mS − 1 and the final state mS:
is the difference in branching angles between the initial state mS − 1 and the final state mS: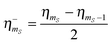
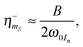
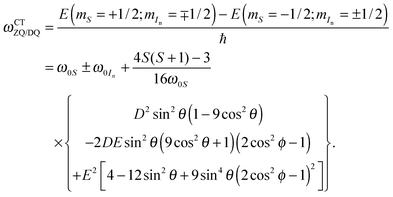
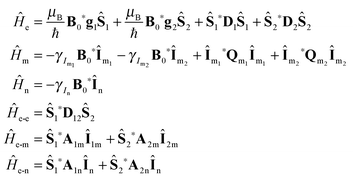
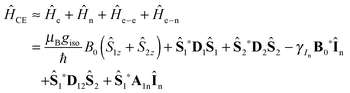
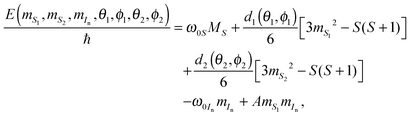
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi − 1) + 3Ei
θi − 1) + 3Ei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi(2sin2
θi(2sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi − 1) is the instantaneous ZFS parameter for the i-th electron spin depending on the orientation of the tensor frame during MAS. Here, we have exemplarily truncated ZFS after first-order for analytical demonstration; an approximation up to second-order could be derived similar to eqn (6). Furthermore, we assume that dipolar coupling—even though crucial for CE—is small and does not lead to significant shifts. In Fig. 8A we have sketched the 64 eigenstates split by EZ interaction and ZFS; for the sake of simplicity we have neglected NZ, HFI, and e–e coupling in this figure. Under MAS the molecular frame of each Gd3+ is rotating (Fig. 8B) which results in periodically evolving eigenstates. In Fig. 8C we have performed numerical simulations as a function of the rotor angle; subfigure D shows the evolution of individual EPR transitions which have to be directly excited with μw irradiation for CE during MAS.
ϕi − 1) is the instantaneous ZFS parameter for the i-th electron spin depending on the orientation of the tensor frame during MAS. Here, we have exemplarily truncated ZFS after first-order for analytical demonstration; an approximation up to second-order could be derived similar to eqn (6). Furthermore, we assume that dipolar coupling—even though crucial for CE—is small and does not lead to significant shifts. In Fig. 8A we have sketched the 64 eigenstates split by EZ interaction and ZFS; for the sake of simplicity we have neglected NZ, HFI, and e–e coupling in this figure. Under MAS the molecular frame of each Gd3+ is rotating (Fig. 8B) which results in periodically evolving eigenstates. In Fig. 8C we have performed numerical simulations as a function of the rotor angle; subfigure D shows the evolution of individual EPR transitions which have to be directly excited with μw irradiation for CE during MAS.
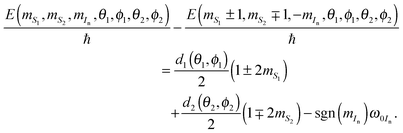
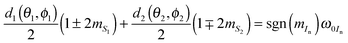


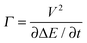 can be utilized to quantitatively determine the efficiency of population exchange during the LAC: for Γ ≫ 1 the ideal LAC is fully adiabatic and populations are completely exchanged because the system always remains in an energy eigenstate; for Γ ≈ 0 an ideal (non-avoided) level crossing occurs where populations are maintained for the same state before and after the crossing. Starting from thermal polarization, in the former case the lowest energy eigenstate always is most populated while in the latter case population inversions occur during crossings. This concept is applicable to all types of LACs encountered during MAS CE: for μw events the μw term connects two states separated by an EPR SQ transition; the e–e dipole coupling connects two states within a ZQ e–e flip–flop; finally the states involved in a CE-enabling three-spin flip–flop–flip are connected via a combination of e–e dipole coupling and hyperfine coupling.
can be utilized to quantitatively determine the efficiency of population exchange during the LAC: for Γ ≫ 1 the ideal LAC is fully adiabatic and populations are completely exchanged because the system always remains in an energy eigenstate; for Γ ≈ 0 an ideal (non-avoided) level crossing occurs where populations are maintained for the same state before and after the crossing. Starting from thermal polarization, in the former case the lowest energy eigenstate always is most populated while in the latter case population inversions occur during crossings. This concept is applicable to all types of LACs encountered during MAS CE: for μw events the μw term connects two states separated by an EPR SQ transition; the e–e dipole coupling connects two states within a ZQ e–e flip–flop; finally the states involved in a CE-enabling three-spin flip–flop–flip are connected via a combination of e–e dipole coupling and hyperfine coupling.