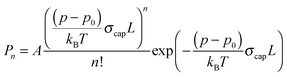Infrared spectroscopy of the ν₂ band of the water monomer and small water clusters (H₂O)_n=2,3,4 in helium droplets

Abstract

We have recorded infrared spectra in the frequency range of the ν₂ band of water monomer and water clusters in superfluid helium droplets. In order to be able to map the chemically important fingerprint range, we have used an IR quantum cascade laser as a radiation source. We were able to observe three ro-vibrational transitions of the water monomer between 1590 and 1670 cm⁻¹. The lines were assigned to the 1₁₀ ← 1₀₁, 1₁₁ ← 0₀₀ and 2₁₂ ← 1₀₁ transitions of the ν₂ vibration of H₂O. Based upon the linewidths, we could deduce relaxation times of 1.9 to 4.2 ps for the monomer. Additional absorption bands could be assigned to ν₂ vibrational bands of water clusters (H₂O)_n with n = 2, 3, 4. These experimental results are compared to theoretical calculations by Wang and Bowman which are reported in an accompanying paper [ref. 1, Y. Wang and J. M. Bowman, Phys. Chem. Chem. Phys., 2016, DOI: 10.1039/C6CP04329A]. We find a very good agreement of our results with both calculations and with previous results from gas phase cavity ringdown experiments.

---

Introduction

A molecular understanding of water–water interactions is a crucial endeavor for the advancement of modern science and has, therefore, been subject of numerous experimental and theoretical studies. For the water monomer, gas phase reference data of the H₂¹⁶O isotopomer cover a total of more than 12 000 ro-vibrational states² and more than 25 000 ro-vibrational transitions have been assigned.³ To describe the water–water interactions quantitatively, many detailed studies of small water clusters [(H₂O)_n with n = 2–10] have been published in recent articles and reviews.^4–7 Of particular relevance to the present study are the measurements including IR spectroscopic studies in helium nanodroplets^8–12 and gas phase cavity ringdown experiments in supersonic beams.^13–17 In addition, numerous spectroscopic studies of isolated water clusters in noble gas matrices^18–24 as well as many theoretical studies^25–30 have been carried out in the past few decades. The most recent investigations on the structure of water clusters (H₂O)_n with n = 6–10 were performed using broadband rotational spectroscopy⁶ and terahertz VRT spectroscopy.⁷

Helium droplets provide a unique soft matrix for spectroscopic measurements.^31–33 They offer the possibility to study single molecules or clusters under ultracold, well-defined conditions. The temperature of helium droplets has been found to be 0.37 K.³⁴ At this temperature only a small number of rotational states in the vibrational ground state of the embedded species are populated. It has been found that molecules can rotate freely in helium droplets.^31–33 For light molecules (e.g. water monomer) with rotational constants B_gas > 1 cm⁻¹, only weak coupling with the helium is expected while for heavy rotors with B_gas < 0.5 cm⁻¹ (e.g. SF₆³⁴) rotational constants are typically reduced by a factor of three compared to the gas phase.^32,33

Previously, the IR spectra of water in helium droplets have been reported for the ν₁ and ν₃ stretch vibrations.^10–12 Here, we report IR spectra of water clusters embedded in helium nanodroplets showing the ν₂ bending vibration. We have expanded the frequency range by integrating quantum cascade lasers (QCL) into our setup. IR OPO systems are restricted to frequencies above 2500 cm⁻¹, which excludes the chemically important fingerprint region. Nowadays, narrow band tunable quantum cascade lasers allow probing of the frequency range between 600 cm⁻¹ and 2500 cm⁻¹. The principle of quantum cascade lasers has first been described by Faist et al. in 1994.³⁵ The main advantage of quantum cascade lasers is that the wavelength can be tuned within the same semiconductor material over a wide spectral range. Using different semiconductor materials, a large part of the mid-infrared region^36–40 as well as parts of the THz region⁴¹ can be covered. Continuous wave (CW) operation of a QCL at room-temperature has been first described by Beck⁴² in 2002. Nowadays, widely tunable QCL systems are commercially available using an external cavity configuration.⁴³ First measurements employing a quantum cascade laser as a radiation source for spectroscopy in helium nanodroplets have been reported by the groups of Douberly and Momose at around the same time in 2011.^44,45 In this work, we report spectroscopic measurements with a tunable external cavity quantum cascade laser (EC-QCL) on our helium nanodroplet spectrometer in Bochum. The experimental results are compared to theoretical predictions by Bowman and co-workers in an accompanying paper.¹

Experimental

The experimental setup of the helium nanodroplet beam apparatus used in this study is explained in detail elsewhere.⁴⁶ Briefly, helium droplets are formed by the expansion of ultra-pure ⁴He 5.0 through a pre-cooled nozzle with a diameter of 5 μm into vacuum. Here, we used a stagnation pressure of 60 bar and a nozzle temperature of 16 K. A 0.5 mm skimmer collimates the evolving helium droplet beam. The helium droplets are doped with water molecules in a differentially pumped pickup chamber connected to the expansion chamber. Small amounts of water are added to the chamber via a dosing valve.

For the measurements in this work, a tunable EC-QCL (Daylight Solutions) was used which emits light between 1570 and 1720 cm⁻¹ with an output power of 50–230 mW. The laser beam is superposed with the molecular helium nanodroplet beam in an antiparallel configuration. The infrared radiation excites ro-vibrational transitions of the dopants inside the helium droplets. The ro-vibrationally excited molecules relax into the ground state by releasing energy to the helium droplets resulting in evaporation of helium atoms (about 5 cm⁻¹ per atom⁴⁷). The depleted helium droplets are ionized and detected by a mass spectrometer (Pfeiffer QMG 422). The mass spectrum shows characteristic fragment signals for the doped species and its aggregates. By observing the ion current of one of these fragments separately, mass-selective absorption spectra can be recorded. However, different aggregates can decompose into fragments with equal mass-to-charge ratios. In these cases, the recorded absorption spectrum is a superposition of the absorption spectra of the individual aggregates. A lock-in amplifier allows phase-sensitive detection at the frequency of the amplitude modulated laser beam.

Results

Observation of the ν₂ band of H₂O monomer

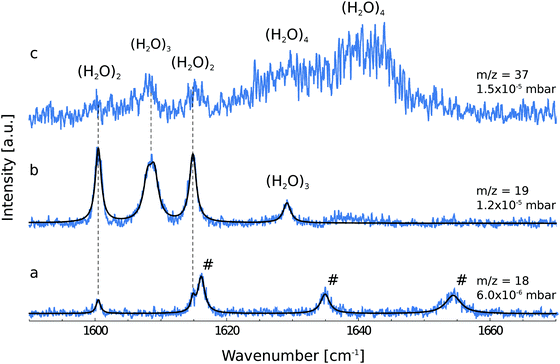
Fig. 1 shows the depletion spectra for ionic fragments observed in the mass spectrum at m/z = 18, 19 and 37. The ion current at m/z = 18 corresponds to the ionic fragment (H₂O)⁺, m/z = 19 to [H(H₂O)]⁺ and m/z = 37 to [H(H₂O)₂]⁺. The IR depletion spectrum detected at m/z = 18 shows a total of five peaks (Fig. 1a). By comparison with gas phase data,³ three lines are assigned to ro-vibrational transitions of the water monomer.

Fig. 1 Mass-selective depletion spectra for the ionic fragments at m/z = 18 (a), m/z = 19 (b) and m/z = 37 (c). The experimental data are fitted by Lorentzian functions. Transitions assigned to the water monomer are marked with a "#" (a). Dashed lines connect the same transitions at increasing pressure regimes for the different ionic fragments.

For light rotors all rotational constants are well above the temperature of the helium droplets, thus, only the lowest ro-vibrational state will be populated at 0.37 K. However, due to slow spin conversion in helium droplets,^{33,34,48–50} spin statistical weights are conserved during the internal cooling of the molecules embedded in helium nanodroplets. For the water monomer, there are two different nuclear spin species, para and ortho, for which the spin statistical weights are 1 : 3, respectively. The water monomer is an asymmetric rotor with ground-state rotational constants of C₀ = 9.2877 ± 0.0021 cm⁻¹, B₀ = 14.5074 ± 0.0090 cm⁻¹ and A₀ = 27.8761 ± 0.0034 cm⁻¹ in the gas phase.⁵¹ The Boltzmann distribution at 0.37 K allows only the energetically lowest ro-vibrational states of each nuclear spin species to be populated, namely 0₀₀ and 1₀₁. Therefore, the number of transitions that can be observed is restricted to transitions from these two populated levels. All allowed ro-vibrational transitions from these two states are shown in Fig. 2 (solid lines).

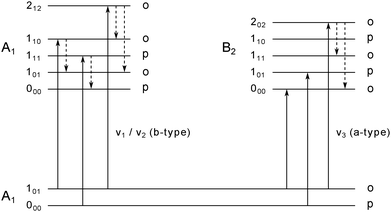Fig. 2 Energy level diagram for the water monomer. The labels of the rotational states are following the nomenclature for asymmetric rotors J_KaKc with their association to ortho and para spin states. In superfluid helium nanodroplets only the lowest lying rotational state for each spin state, i.e. 1₀₁ (ortho) and 0₀₀ (para), is populated. IR active b-type (left) and a-type (right) transitions from the lowest populated states are displayed as solid lines. Dashed arrows indicate possible pathways for rotational relaxation. Relaxation processes are restricted to relaxations within the same spin state. Adapted from ref. 11.

In previous publications, the symmetric and asymmetric stretch vibrations ν₁ and ν₃ of the water monomer in helium droplets have been observed.^10,11 Here, we focus on the ν₂ bending vibration. We report the observation of three ro-vibrational transitions at 1616.1, 1634.9 and 1654.4 cm⁻¹, which are assigned to the b-type 1₁₀ ← 1₀₁, 1₁₁ ← 0₀₀ and 2₁₂ ← 1₀₁ transitions of the ν₂ band, respectively. The line positions, the linewidths and the deduced lifetimes as determined by the fit to a Lorentzian line shape are shown in Table 1. The b-type ro-vibrational lines are separated by ≈2C each, yielding an estimate for the rotational constant. We obtain a rotational constant C_He = 9.56 ± 0.23 cm⁻¹ which is slightly higher than the experimentally observed gas phase rotational constant C₀ = 9.2877 ± 0.0021 cm⁻¹.⁵¹ A similar observation was made by the Vilesov group who have reported a rotational constant C_He = 9.5 cm⁻¹ for the ν₁ band of water.¹¹ Since the effect of the superfluid helium environment on the rotational constant C is very small, we assume the same for the rotational constants A and B. Using the gas phase rotational constants and the line position of the 1₁₁ ← 0₀₀ transition, the band origin is estimated to be [small nu, Greek, tilde]₀ = 1597.7 cm⁻¹. Compared to the gas phase, this value is blue-shifted by 2.8 cm⁻¹.

Table 1 Comparison of the line positions found in He droplets with gas phase data. Frequencies are given in cm⁻¹. In addition, lifetimes for all ro-vibrational transitions were deduced based upon the experimentally observed linewidths

Line	Gas phase^a	He		δν		τ [ps]
a From ref. 3. b From ref. 11. c From ref. 10.
ν 2
110 ← 101	1616.7	1616.1		1.3		4.2
111 ← 000	1635.0	1634.9		1.7		3.2
212 ← 101	1653.3	1654.4		2.8		1.9
ν 1
110 ← 101	3674.7	3674.3^b		2.4^b		2.2
111 ← 000	3693.3	3693.1^b		3.0^b		1.8
212 ← 101	3711.1	—		—		—
ν 3
000 ← 101	3732.1	3732.0^b	3731.9^c	0.34^b	0.30^c	15.6	17.7
101 ← 000	3779.5	3778.2^b	3778.3^c	0.34^b	0.26^c	15.6	20.6
202 ← 101	3801.4	3800.9^b	3800.7^c	2.3^b	1.9^c	2.3	2.8

---

We want to point out that the line position of the 1₁₁ ← 0₀₀ transition shows virtually no shift compared to the gas phase (1634.9 cm⁻¹versus 1635.0 cm⁻¹). The small increase of C is considered to be an artifact due to the restricted number of rotational lines.

The deduced lifetimes of the excited ro-vibrational states are in the range between 1.9 to 4.2 ps as summarized in Table 1. These values can be compared to previous observations for the ν₁ and ν₃ stretch bands.^10,11 While for the 2₀₂ ← 1₀₁ a-type transition a lifetime of 2.8 ps has been deduced, the 1₀₁ ← 0₀₀ and 0₀₀ ← 1₀₁ a-type transitions of the ν₃ band have lifetimes which exceed this value by one order of magnitude (see Table 1). This observation is explained by a lack of lower rotational states with the same symmetry in the excited vibrational state, thus, excluding population relaxation of the excited states 1₀₁ and 0₀₀.^10,11 All excited ro-vibrational states of the b-type transitions observed in this work as well as the excited state 2₀₂ of the a-type transition of the ν₃ band can relax rotationally to lower lying states (see Fig. 2, dashed lines). The energy gaps between the distinct rotational states are in the range ≈18–56 cm⁻¹ (see Table 2). We want to point out that the maximum energy of the elementary excitations of liquid ⁴He is of the order of ≈14 cm⁻¹.⁵² Therefore, these excited rotational states can couple efficiently to the rotons in the liquid. Roton-coupling in helium droplets has been observed for different molecular systems (e.g. methane,^50,53 CO⁴⁶ and the methyl radical⁵⁴).

Table 2 Rotational relaxation channels in the ν₂ excited vibrational level of the water monomer and their associated energy gaps ΔE. The energy gaps have been calculated from the gas phase rotational constants

Initial JKaKc	Final JKaKc	ΔE [cm^−1]
101	110	18.6
111	000	37.2
212	110	37.2
212	101	55.8

---

Observation of the ν₂ band of water clusters (H₂O)_n, n = 2, 3, 4

The depletion spectrum recorded at m/z = 19, which corresponds to the ionic fragment [H(H₂O)]⁺, shows four peaks at 1600.5, 1608.5, 1614.8 and 1629.1 cm⁻¹ (Fig. 1b). The peaks at 1600.5 and 1614.8 cm⁻¹ are also observed in the depletion spectrum recorded at m/z = 18 (Fig. 1a). In order to unambiguously assign these peaks to a specific cluster size we have recorded the pressure dependence.

The pickup probability of molecules by helium droplets can be described by a Poisson distribution.^31,32,55 The probability P_n to embed n molecules into a helium droplet with the capturing cross section σ_cap in a pickup-chamber of length L is described as:

with an amplitude A and a pressure offset p₀ that takes into account the residual water in the chamber. The pressure offset p₀ and the product of the capturing cross section σ_cap and the length L are adjusted to describe the pressure dependence of the dimer bands at 1600.5 and 1614.8 cm⁻¹ and kept constant for the fits of the other bands.

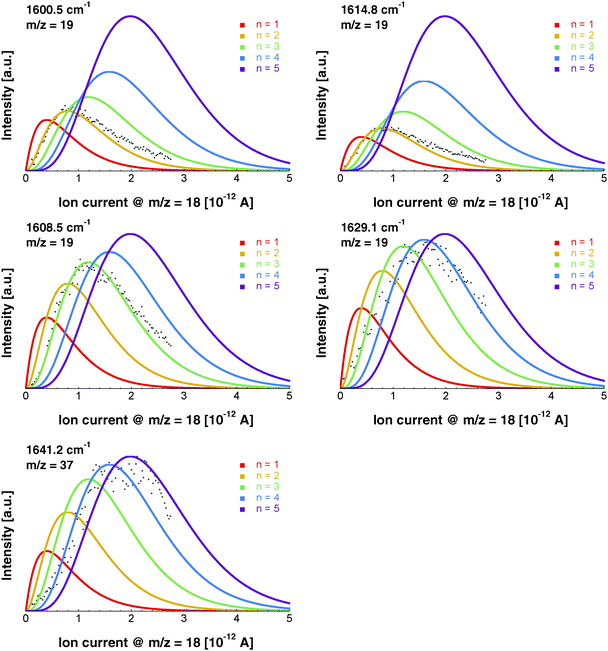
The pressure dependence of the signals of the two spectral features at 1600.5 and 1614.8 cm⁻¹ could be reproduced well by a Poisson distribution with n = 2 (see Fig. 3). The assignment to (H₂O)₂ is confirmed by the fact that these bands are observed at m/z = 18 and m/z = 19. The two bands at 1600.5 and 1614.8 cm⁻¹ are assigned to the water bending mode of the proton acceptor and the proton donor of the water dimer, respectively. In Table 3 we summarize the center frequencies obtained for the gas phase and in helium nanodroplets and compare these to the theoretical predictions. Compared to the gas phase, we observe a red-shift (≈5.2 cm⁻¹) of the bending mode for the proton donor, while virtually no shift for the proton acceptor is observed (≈0.1 cm⁻¹). The band contour can be attributed to an underlying rotational fine structure of the bands (see Fig. 4). The rotational constants of the water dimer were determined as 7.02, 0.22 and 0.22 cm⁻¹ by theoretical calculations on the B3LYP/cc-pVTZ level of theory. To simulate the experimental band contours, the rotational constants of 0.22 cm⁻¹ were reduced by a factor of three to account for the effect of the surrounding helium, whereas the rotational constant of 7.02 cm⁻¹ was assumed to be unaffected.

Fig. 3 Pressure dependence of the signal intensity for distinct IR bands assigned to (H₂O)_n with n = 2, 3, 4. All data were recorded at a given mass-to-charge ratio. The pressure dependence of the signal intensity was fitted assuming Poisson distributions for n = 1, 2, 3, 4, 5 (red, yellow, green, blue, purple).

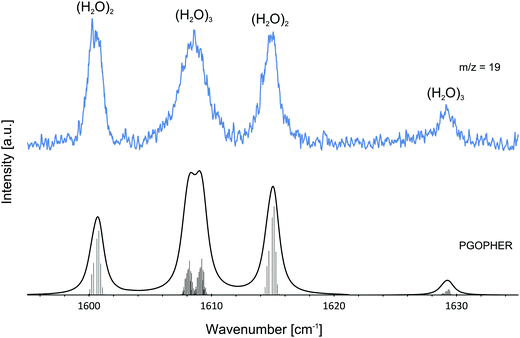Fig. 4 Experimentally observed bands of the water dimer (H₂O)₂ and water trimer (H₂O)₃ at m/z = 19. The observed bands are compared with the predictions assuming a Boltzmann distribution at 0.37 K. For the simulations of the water dimer (H₂O)₂ and water trimer (H₂O)₃ transitions, rotational constants of A = 7.02 cm⁻¹, B = C = 0.07 cm⁻¹ and A = B = 0.08 cm⁻¹, C = 0.04 cm⁻¹ were used, respectively. Lines were broadened assuming a Lorentzian line shape. The broad feature at about 1608.5 cm⁻¹ is explained by two overlapping bands in agreement with theoretical predictions.¹ The ro-vibrational fine structure was plotted using PGOPHER.⁵⁷

Based upon the pickup curves, the bands at 1608.5 and 1629.1 cm⁻¹ are assigned to the water trimer (Fig. 3). For the water trimer, the global minimum structure, labeled 3(a) (see Fig. 5), is cyclic. Each water molecule serves as a proton donor as well as a proton acceptor. Two of three free OH moieties are oriented up while the third is oriented down with respect to the ring. In Table 3 we compare the experimental and the predicted frequencies for the water trimer. The rotational constants of the water trimer were predicted to be 0.23, 0.23, 0.12 cm⁻¹ at the B3LYP/cc-pVTZ level of theory. For the predictions of the line contours, we assume a reduction of the rotational constants by a factor of three to account for the effect of the surrounding helium. The experimentally observed line broadening of the band at 1629.1 cm⁻¹ is in agreement with the predicted convolution of an underlying rotational fine structure as indicated in Fig. 4. However, the linewidth of the band centered at 1608.5 cm⁻¹ clearly exceeds the predicted rotational broadening. The experimentally observed line shape can be reproduced assuming two close-lying absorption bands separated by 1 cm⁻¹. The experimental result is in good agreement with the predictions of Wang and Bowman¹ who predict bands at 1617, 1619 and 1634 cm⁻¹ for the water trimer.

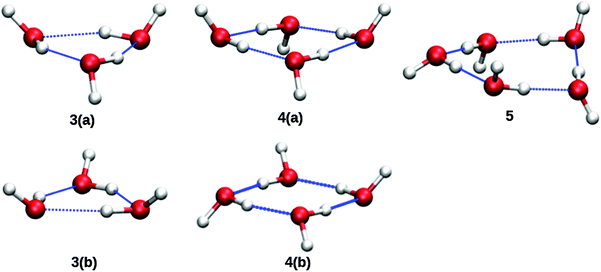Fig. 5 Molecular structures of cyclic (H₂O)_n=2,3,4 clusters. Structures labeled with a “b” are higher energy isomers. From ref. 1.

Table 3 Experimental and predicted frequencies of the ν₂ mode for different water clusters (H₂O)_n with n = 2, 3, 4. The predicted relative intensities are shown in parentheses. For comparison purposes, the band origin [small nu, Greek, tilde]₀ of the water monomer is shown. All frequencies are given in cm⁻¹

		Experiment		Theory
n		He	Gas phase	Bowman
a From ref. 2. b From ref. 14. c From ref. 26. d From ref. 1.
1	[small nu, Greek, tilde] 0	1597.5	1594.7^a
2	Acceptor	1600.5	1600.6^b	1584^c
2	Donor	1614.8	1620^b	1607^c
3	Cyclic	1608.0	1609^b	1617 (0.12)^d
		1609.0		1619 (0.09)^d
		1629.1	1638^b	1634 (0.03)^d
4	Cyclic	1629.0	1629^b	1629 (0.09)^d
		1641.2		1634 (0.06)^d
				1634 (0.06)^d
				1654 (0.0)^d

---

In order to search for absorption bands of larger clusters, we recorded an additional depletion spectrum at a higher pressure on mass m/z = 37, which corresponds to the ionic fragment [H(H₂O)₂]⁺ (Fig. 1c). Here, we expected to observe only water clusters (H₂O)_n with n ≥ 3. Surprisingly, we also observed bands attributed to the water dimer in this spectrum, however, with decreased intensity. Based upon mass spectrometric observations,⁵⁶ we propose that these are due to fragments of clusters of helium with H₂O with the general formula [H(He)_n]⁺. The dimer bands at 1600.5 and 1614.8 cm⁻¹ are detected at m/z = 37 which corresponds to the ionic fragment [H(He)₉]⁺. However, the intensity is considerably reduced compared to the intensity at m/z = 37, which corresponds to the ionic fragment [H(H₂O)₂]⁺.

In the accompanying paper, Wang and Bowman have carried out anharmonic, coupled-mode VSCF/VCI calculations in a subspace of modes.¹ They predict for the cyclic global minimum structure of the water tetramer, labeled 4(a) (see. Fig. 5), four bands in the ν₂ frequency range, one band at 1629 cm⁻¹, two bands at 1634 cm⁻¹, and one band at 1654 cm⁻¹ which is not IR active. Experimentally, a broad absorption feature is observed between 1620 and 1650 cm⁻¹ with two broad bands centered at 1629.0 and 1641.2 cm⁻¹. Based upon the pickup curves, we assign the absorption band at 1641.2 cm⁻¹ to the water tetramer. The broad band at 1629.0 cm⁻¹ overlaps with the band of the water trimer at 1629.1 cm⁻¹. However, the pickup curve recorded at 1629.1 cm⁻¹ shows, for higher pressures, a clear deviation from the Poisson distribution for n = 3 and resembles more a pressure dependence that would be expected for n = 4. In addition, the contour of the band at 1629.1 cm⁻¹ differs depending on whether we record the IR spectrum at m/z = 37 or m/z = 19. This supports the assignment of the broad feature to two overlapping bands.

Experimentally, the two water tetramer bands are found to be separated by about 12 cm⁻¹. This value can be compared to calculations in the accompanying paper of Wang and Bowman¹ who predicted a splitting of 5 cm⁻¹. However, in their paper they argue that this value might be an underestimation since high-level direct ab initio calculations show a splitting of 12 cm⁻¹ (compare to ref. 5c and 6 in Wang and Bowman¹), which is in good agreement with experiment.

The formation of the higher energy isomer, labeled 4(b) (see Fig. 5), can be excluded since the theoretical calculations for this isomer predict a band highly blue-shifted compared to the bands found experimentally. At higher pressures, the pickup curve at 1641.2 cm⁻¹ deviates from the n = 4 Poisson distribution and resembles more a distribution for n = 5. Therefore, we propose a spectral overlap of the bands of the water tetramer with the bands of the water pentamer.

Summary

We report the IR spectra of the ν₂ band of water clusters (H₂O)_n with n = 1, 2, 3, 4 embedded in helium nanodroplets. For the water monomer, we observed the ro-vibrational transitions 1₁₀ ← 1₀₁, 1₁₁ ← 0₀₀ and 2₁₂ ← 1₀₁ at 1616.1, 1634.9 and 1654.4 cm⁻¹, respectively. Based upon the linewidths, we deduced lifetimes of 1.9–4.2 ps. We speculate that these short lifetimes are caused by coupling to the rotons of the helium bath, similar to that seen for the ν₁ and ν₃ bands of water,^10,11 methane,^50,53 CO,⁴⁶ and the methyl radical.⁵⁴ A rotational constant C_He of 9.56 ± 0.23 cm⁻¹ was deduced, which is close to the constant in the gas phase C₀ = 9.2877 ± 0.0021 cm⁻¹.⁵⁰

Two bands at 1600.5 and 1614.8 cm⁻¹ were assigned to the water dimer (H₂O)₂ in good agreement with the bands at 1600.6 and 1620 cm⁻¹ observed in the gas phase.¹⁴ The broadening of the lines can be explained by the underlying ro-vibrational fine structure. Furthermore, we have assigned three bands at 1608.0, 1609.0 and 1629.1 cm⁻¹ to the water trimer (H₂O)₃. For higher water pressures, a broad absorption feature between 1620 and 1650 cm⁻¹ arises. Within this absorption, two broad bands centered at 1629.9 and 1641.2 cm⁻¹ could be assigned to the water tetramer (H₂O)₄. The experimental data are in good agreement with the theoretical predictions in the accompanying paper of Wang and Bowman.¹

Acknowledgements

We thank Y. Wang and J. Bowman for helpful discussions. We acknowledge financial support from the Cluster of Excellence RESOLV (EXC 1069) funded by the Deutsche Forschungsgemeinschaft.

References

1. Y. Wang and J. M. Bowman, Phys. Chem. Chem. Phys., 2016 10.1039/C6CP04329A.
2. J. Tennyson, N. F. Zobov, R. Williamson, O. L. Polyansky and P. F. Bernath, J. Phys. Chem. Ref. Data, 2001, 30, 735–831.
3. L. S. Rothman, R. R. Gamache, A. Goldman, L. R. Brown, R. A. Toth, H. M. Pickett, R. L. Poynter, J.-M. Flaud, C. Camy-Peyret, A. Barbe, N. Husson, C. P. Rinsland and M. A. H. Smith, Appl. Opt., 1987, 26, 4058.
4. F. N. Keutsch and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10533–10540.
5. A. Mukhopadhyay, W. T. S. Cole and R. J. Saykally, Chem. Phys. Lett., 2015, 633, 13–26.
6. J. O. Richardson, C. Pérez, S. Lobsiger, A. A. Reid, B. Temelso, G. C. Shields, Z. Kisiel, D. J. Wales, B. H. Pate and S. C. Althorpe, Science, 2016, 351, 1310–1313.
7. W. T. S. Cole, J. D. Farrell, D. J. Wales and R. J. Saykally, Science, 2016, 352, 1194–1197.
8. K. Nauta, Science, 2000, 287, 293–295.
9. C. J. Burnham, S. S. Xantheas, M. A. Miller, B. E. Applegate and R. E. Miller, J. Chem. Phys., 2002, 117, 1109.
10. C. M. Lindsay, G. E. Douberly and R. E. Miller, J. Mol. Struct., 2006, 786, 96–104.
11. K. E. Kuyanov, M. N. Slipchenko and A. F. Vilesov, Chem. Phys. Lett., 2006, 427, 5–9.
12. K. Kuyanov-Prozument, M. Y. Choi and A. F. Vilesov, J. Chem. Phys., 2010, 132, 014304.
13. J. B. Paul, C. P. Collier, R. J. Saykally, J. J. Scherer and A. O'Keefe, J. Phys. Chem. A, 1997, 101, 5211–5214.
14. J. B. Paul, R. A. Provencal, C. Chapo, K. Roth, R. Casaes and R. J. Saykally, J. Phys. Chem. A, 1999, 103, 2972–2974.
15. J. B. Paul, R. A. Provencal and R. J. Saykally, J. Phys. Chem. A, 1998, 102, 3279–3283.
16. N. Pugliano and R. Saykally, Science, 1992, 257, 1937–1940.
17. K. Liu, J. D. Cruzan and R. J. Saykally, Science, 1996, 271, 929–933.
18. A. Engdahl and B. Nelander, J. Mol. Struct., 1989, 193, 101–109.
19. A. J. Tursi, J. Chem. Phys., 1970, 52, 1521.
20. G. P. Ayers and A. D. E. Pullin, Spectrochim. Acta, Part A, 1976, 32, 1629–1639.
21. J. P. Perchard, Chem. Phys., 2001, 273, 217–233.
22. S. Coussan, P. Roubin and J. P. Perchard, Chem. Phys., 2006, 324, 527–540.
23. J. Ceponkus, G. Karlström and B. Nelander, J. Phys. Chem. A, 2005, 109, 7859–7864.
24. J. Ceponkus, A. Engdahl, P. Uvdal and B. Nelander, Chem. Phys. Lett., 2013, 581, 1–9.
25. Y. Wang, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 131, 054511.
26. A. Shank, Y. Wang, A. Kaledin, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 130, 144314.
27. Y. Bouteiller and J. P. Perchard, Chem. Phys., 2004, 305, 1–12.
28. S. S. Xantheas and T. H. Dunning, J. Chem. Phys., 1993, 99, 8774.
29. S. S. Xantheas, J. Chem. Phys., 1994, 100, 7523–7534.
30. S. S. Xantheas, J. Chem. Phys., 1995, 102, 4505.
31. J. P. Toennies and A. F. Vilesov, Annu. Rev. Phys. Chem., 1998, 49, 1–41.
32. J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648.
33. C. Callegari, K. K. Lehmann, R. Schmied and G. Scoles, J. Chem. Phys., 2001, 115, 10090–10110.
34. M. Hartmann, R. E. Miller, J. P. Toennies and A. Vilesov, Phys. Rev. Lett., 1995, 75, 1566–1569.
35. J. Faist, F. Capasso, D. L. Sivco, C. Sirtori, A. L. Hutchinson and A. Y. Cho, Science, 1994, 264, 553–556.
36. Y. Bai, S. Slivken, S. R. Darvish and M. Razeghi, Appl. Phys. Lett., 2008, 93, 1–4.
37. A. Lyakh, R. Maulini, A. Tsekoun, R. Go, C. Pflügl, L. Diehl, Q. J. Wang, F. Capasso and C. K. N. Patel, Appl. Phys. Lett., 2009, 95, 141113.
38. J. Faist, F. Capasso, D. L. Sivco, A. L. Hutchinson, S. N. G. Chu and A. Y. Cho, Appl. Phys. Lett., 1998, 72, 680–682.
39. J. Devenson, D. Barate, O. Cathabard, R. Teissier and A. N. Baranov, Appl. Phys. Lett., 2006, 89, 2004–2007.
40. O. Cathabard, R. Teissier, J. Devenson, J. C. Moreno and A. N. Baranov, Appl. Phys. Lett., 2010, 96, 12–15.
41. B. S. Williams, Nat. Photonics, 2007, 1, 517–525.
42. M. Beck, Science, 2002, 295, 301–305.
43. A. Hugi, R. Maulini and J. Faist, Semicond. Sci. Technol., 2010, 25, 083001.
44. T. Liang, S. D. Flynn, A. M. Morrison and G. E. Douberly, J. Phys. Chem. A, 2011, 115, 7437–7447.
45. A. Ravi, S. Kuma, C. Yearwood, B. Kahlon, M. Mustafa, W. Al-Basheer, K. Enomoto and T. Momose, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 020502.
46. K. von Haeften, S. Rudolph, I. Simanovski, M. Havenith, R. E. Zillich and K. B. Whaley, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–17.
47. D. M. Brink and S. Stringari, Zeitschrift für Phys. D Atoms, Mol. Clust., 1990, 15, 257–263.
48. C. Callegari, A. Conjusteau, I. Reinhard, K. K. Lehmann and G. Scoles, J. Chem. Phys., 2000, 113, 10535–10550.
49. M. Hartmann, N. Pörtner, B. Sartakov, J. P. Toennies and A. F. Vilesov, J. Chem. Phys., 1999, 110, 5109.
50. K. Nauta and R. E. Miller, Chem. Phys. Lett., 2001, 350, 225–232.
51. R. T. Hall and J. M. Dowling, J. Chem. Phys., 1967, 47, 2454.
52. E. Manousakis and V. R. Pandharipande, Phys. Rev. B, 1986, 33, 150–161.
53. S. Rudolph, G. Wollny, K. von Haeften and M. Havenith, J. Chem. Phys., 2007, 126, 124318.
54. A. M. Morrison, P. L. Raston and G. E. Douberly, J. Phys. Chem. A, 2013, 117, 11640–11647.
55. M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15–75.
56. R. Fröchtenicht, M. Kaloudis, M. Koch and F. Huisken, J. Chem. Phys., 1996, 105, 6128.
57. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2016, 108.

---