Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Atomistic insights into deep eutectic electrolytes: the influence of urea on the electrolyte salt LiTFSI in view of electrochemical applications†
Volker
Lesch
a,
Andreas
Heuer
ab,
Babak R.
Rad
a,
Martin
Winter
ac and
Jens
Smiatek
*d
aHelmholtz-Institute Muenster (IEK-12): Ionics in Energy Storage, Forschungszentrum Juelich, Corrensstrasse 46, 48153 Muenster, Germany
bInstitute of Physical Chemistry, University of Muenster, Corrensstrasse 28/30, 48149 Muenster, Germany
cMEET Battery Research Centre, Institute of Physical Chemistry, University of Muenster, Corrensstrasse 46, 48149 Muenster, Germany
dInstitute for Computational Physics, University of Stuttgart, Allmandring 3, 70569 Stuttgart, Germany. E-mail: smiatek@icp.uni-stuttgart.de; Fax: +49 711 685 63658; Tel: +49 711 63757
First published on 22nd September 2016
Abstract
The influence of urea on the conducting salt lithium bis-(trifluoromethanesulfonyl)-imide (LiTFSI) in terms of lithium ion coordination numbers and lithium ion transport properties is studied via atomistic molecular dynamics simulations. Our results indicate that the presence of urea favors the formation of a deep eutectic electrolyte with pronounced ion conductivities which can be explained by a competition between urea and TFSI in occupying the first coordination shell around lithium ions. All simulation findings verify that high urea concentrations lead to a significant increase of ionic diffusivities and an occurrence of relatively high lithium transference numbers in good agreement with experimental results. The outcomes of our study point at the possible application of deep eutectic electrolytes as ion conducting materials in lithium ion batteries.
Deep eutectic electrolytes (DEEs), also called deep eutectic solvents, are mixtures of salts with small polar organic molecules, which have a melting temperature lower than the melting temperatures of the constituting components. DEEs are nowadays used for synthesis purposes, separation techniques and also for electrochemical applications.1–3 Initially in 2003, Abbott et al. studied the prototype of a DEE by adding urea to choline chloride,4 which was later also investigated by molecular dynamics (MD) simulations.5 In contrast to most conventional organic solvents, choline based eutectic electrolytes are non-toxic, and have good biodegradability and low cost. Also, in terms of biochemical applications, the usage of DEEs might be a beneficial option to circumvent problems found for ordinary ILs.6,7 In addition, it was discussed that lithium based DEEs are potential candidates to replace IL/lithium salt mixtures in battery applications.8 In contrast to DEEs, ILs typically require a relatively large amount of dissolved lithium salt in order to be applicable for electrochemical devices with the drawback of high viscosities and low lithium ion conductivity.9–13 The main advantage of DEEs is the presence of a single cation species, for example Li+ in LiTFSI, such that relatively high Li+ transference numbers can be observed.8
A few years before the establishment of choline/urea DEEs, Liang et al.14 investigated the influence of urea on lithium bis-(trifluoromethanesulfonyl)-imide (LiTFSI) in terms of electrochemical stabilities and lithium ion diffusivities. For specific molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.6 between LiTFSI and urea, ionic conductivities of around 10−4 to 10−3 S cm−1 at temperatures in the range from 300 to 330 K were reported.14 Furthermore, the eutectic melting temperature was found to be 240 K whereas LiTFSI and urea have individual melting temperatures of 507 K and 405 K. First MD simulations revealed the presence of strong interactions between the oxygen atoms of urea and TFSI, which are mainly responsible for the observed effects.15 In addition, it was shown that mixtures of urea and LiTFSI are also applicable for polymer electrolyte systems16 and further results also revealed a similar behavior for LiTFSI/acetamide.17 Based on the experimental results, it can be concluded that the presence of urea weakens the interaction between the lithium and the TFSI ions but it yet has not been clarified in detail whether the lithium cation, the TFSI anion or both of them interact with urea and how the molecular composition arranges in contrast to the often studied interaction between urea and macromolecules.18–22 More recent technological applications of DEEs in the context of electrochemical devices include glycerol and choline iodide as electrolytes in solar cells23 and as solvents for the electrodeposition of zinc.24
3.6 between LiTFSI and urea, ionic conductivities of around 10−4 to 10−3 S cm−1 at temperatures in the range from 300 to 330 K were reported.14 Furthermore, the eutectic melting temperature was found to be 240 K whereas LiTFSI and urea have individual melting temperatures of 507 K and 405 K. First MD simulations revealed the presence of strong interactions between the oxygen atoms of urea and TFSI, which are mainly responsible for the observed effects.15 In addition, it was shown that mixtures of urea and LiTFSI are also applicable for polymer electrolyte systems16 and further results also revealed a similar behavior for LiTFSI/acetamide.17 Based on the experimental results, it can be concluded that the presence of urea weakens the interaction between the lithium and the TFSI ions but it yet has not been clarified in detail whether the lithium cation, the TFSI anion or both of them interact with urea and how the molecular composition arranges in contrast to the often studied interaction between urea and macromolecules.18–22 More recent technological applications of DEEs in the context of electrochemical devices include glycerol and choline iodide as electrolytes in solar cells23 and as solvents for the electrodeposition of zinc.24
Although the benefits of DEEs were often reported,2,3 atomistic insights into the underlying mechanisms that lead to the improvement of the mixtures with DEEs are sparse. A deeper understanding might stimulate the optimization of lithium transference numbers which is of prior importance for the application of DEEs in lithium based electrochemical devices. In order to study the interaction between urea and LiTFSI on the atomistic scale, we performed classical molecular dynamics simulations using the OPLS-AA25 force field. Our results indicate a subtle competing effect between urea and TFSI to occupy the coordination shell around lithium. The composition of the local environment strongly influences the dynamic properties of Li+ such that high urea concentrations facilitate the occurrence of relatively high lithium transference numbers.
All molecular dynamics (MD) simulations were performed with the simulation package GROMACS (version 4.6.7).26–28 The starting structures of LiTFSI/urea mixtures were produced by PACKMOL.29,30 The force field parameters for LiTFSI were extracted from the OPLS-AA25 force field which was verified to reproduce structural properties for systems containing lithium salts in good agreement with the experimental results.31 In fact, classical atomistic force fields like OPLS-AA usually disregard the electronic properties of atoms which influences the dynamic behavior.32 Hence, it has to be noted that the obtained diffusion coefficients as well as the mass densities might vary quantitatively from experimental results.31,33,34 For a more reliable description in terms of exact values, the usage of polarizable atomistic force fields was proposed.32 Due to the absence of consistent polarizable force fields for the combination of urea and LiTFSI, we chose to study the properties of the system qualitatively in order to elucidate the main mechanisms in good agreement with the approach presented in ref. 33 and 34. We simulated three different systems of LiTFSI and urea, namely mixtures of 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300
300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ions and molecules for urea
300 ions and molecules for urea![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li+
Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TFSI− denoted as U1
TFSI− denoted as U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 900
1, 900![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300
300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (U1
300 (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) and 1800
3) and 1800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300
300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 (U1
300 (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6). The integration of Newton's equation of motion was performed by a Leapfrog algorithm. The elementary integration time step was δt = 2 fs. The simulation time for all systems was 500 ns, whereby the first 150 ns were used for equilibration and the remaining 350 ns were used for the analysis. We performed an energy minimization using the conjugate gradient method (energy tolerance: 100 kJ mol−1 nm, step size: 10−4 nm). The simulations were performed in NPT ensemble using the velocity rescale thermostat35 (coupling time: 1.0 ps) with a temperature of T = 400 K in combination with the Berendsen barostat36 (coupling time: 1.0 ps, compressibility: 10−6 bar−1, reference pressure: 1 bar). All covalent bonds involving hydrogens were constrained by the LINCS algorithm.37 The electrostatic interactions were calculated using the smooth particle-mesh-Ewald method38,39 with a cutoff range of 1.4 nm and an accuracy of 10−6.
6). The integration of Newton's equation of motion was performed by a Leapfrog algorithm. The elementary integration time step was δt = 2 fs. The simulation time for all systems was 500 ns, whereby the first 150 ns were used for equilibration and the remaining 350 ns were used for the analysis. We performed an energy minimization using the conjugate gradient method (energy tolerance: 100 kJ mol−1 nm, step size: 10−4 nm). The simulations were performed in NPT ensemble using the velocity rescale thermostat35 (coupling time: 1.0 ps) with a temperature of T = 400 K in combination with the Berendsen barostat36 (coupling time: 1.0 ps, compressibility: 10−6 bar−1, reference pressure: 1 bar). All covalent bonds involving hydrogens were constrained by the LINCS algorithm.37 The electrostatic interactions were calculated using the smooth particle-mesh-Ewald method38,39 with a cutoff range of 1.4 nm and an accuracy of 10−6.
We start the discussion with the dynamic properties of the species. The mean square displacement (MSD) of a species 〈[![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) −
i(t) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t0)]2〉 is directly proportional to the diffusion coefficient Divia the Einstein relation40
i(t0)]2〉 is directly proportional to the diffusion coefficient Divia the Einstein relation40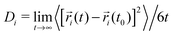 where
where ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i denotes a Cartesian coordinate at time t. Diffusive motion can be found for 〈[
i denotes a Cartesian coordinate at time t. Diffusive motion can be found for 〈[![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) −
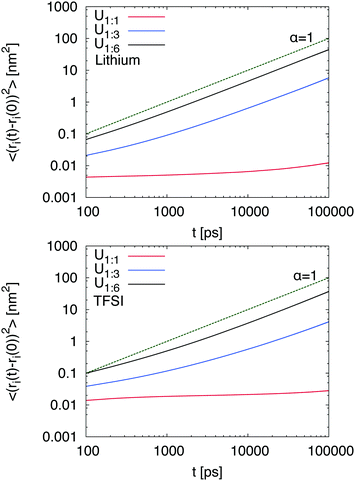
i(t) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t0)]2〉 ∼ tα with α = 1 whereas subdiffusive motion is evident for α < 1.33 The corresponding MSDs for lithium and TFSI in the presence of different urea concentrations are shown in Fig. 1. It can be clearly seen that low urea concentrations (U1
i(t0)]2〉 ∼ tα with α = 1 whereas subdiffusive motion is evident for α < 1.33 The corresponding MSDs for lithium and TFSI in the presence of different urea concentrations are shown in Fig. 1. It can be clearly seen that low urea concentrations (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) hardly affect the dynamic properties of lithium and TFSI ions. Hence, any motion is nearly absent and it can be concluded that the chosen urea concentration is too low to impose the formation of a DEE in agreement with experimental results.14 Thus, it can be assumed that a fully equilibrated structure even at an elevated temperature of 400 K is absent. Therefore, we will mainly focus on the results obtained for the systems U1
1) hardly affect the dynamic properties of lithium and TFSI ions. Hence, any motion is nearly absent and it can be concluded that the chosen urea concentration is too low to impose the formation of a DEE in agreement with experimental results.14 Thus, it can be assumed that a fully equilibrated structure even at an elevated temperature of 400 K is absent. Therefore, we will mainly focus on the results obtained for the systems U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and U1
3 and U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 whereas the results for low urea content serve as a reference for the illustration of the main mechanisms. In contrast, higher urea concentrations (U1
6 whereas the results for low urea content serve as a reference for the illustration of the main mechanisms. In contrast, higher urea concentrations (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and U1
3 and U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) induce a diffusive behavior of lithium and TFSI ions already after 10 ns. The corresponding transition times to the diffusive regime are comparable to alkylimidazolium based ionic liquids33,34 which points at the formation of a liquid DEE. The corresponding individual diffusion coefficients are presented in the ESI† where one can recognize the highest diffusivity for urea, followed by lithium and TFSI ions. The differences between lithium and TFSI are marginal with regard to the limited accuracy for dynamic properties obtained by non-polarizable force fields.41 Nevertheless, the small difference between lithium and TFSI diffusion coefficients stands in contrast to the behavior of LiTFSI in ionic liquids where the diffusion coefficient of TFSI is significantly higher.42 We will study this effect in more detail in the future.
6) induce a diffusive behavior of lithium and TFSI ions already after 10 ns. The corresponding transition times to the diffusive regime are comparable to alkylimidazolium based ionic liquids33,34 which points at the formation of a liquid DEE. The corresponding individual diffusion coefficients are presented in the ESI† where one can recognize the highest diffusivity for urea, followed by lithium and TFSI ions. The differences between lithium and TFSI are marginal with regard to the limited accuracy for dynamic properties obtained by non-polarizable force fields.41 Nevertheless, the small difference between lithium and TFSI diffusion coefficients stands in contrast to the behavior of LiTFSI in ionic liquids where the diffusion coefficient of TFSI is significantly higher.42 We will study this effect in more detail in the future.
After fitting the MSD to obtain the diffusion coefficients for all three species, we calculated the transference numbers for lithium ions. The lithium ion transference numbers give insights into the relative mobility of lithium ions in comparison to the other species in the system and are defined as 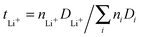 where ni denotes the number of ions or molecules of a species in the system. The resulting values are tLi+ = 0.09 (U1
where ni denotes the number of ions or molecules of a species in the system. The resulting values are tLi+ = 0.09 (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) and tLi+ = 0.07 (U1
3) and tLi+ = 0.07 (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6). In comparison with ILs, Lesch et al.42,43 found a transference number of tLi+ = 0.039 for 0.85 [emimTFSI]/0.15[LiTFSI] at 423 K. Moreover, Ye et al.9 reported a transference number of tLi+ = 0.034 at 293 K for a 1 M LiTFSI/P13TFSI/PVDF–HFP mixture. Thus, the slightly higher results for tLi+ in LiTFSI/urea mixtures indicate that the DEE seems to be a potential candidate for the usage as an ion conducting material in lithium based battery applications.
6). In comparison with ILs, Lesch et al.42,43 found a transference number of tLi+ = 0.039 for 0.85 [emimTFSI]/0.15[LiTFSI] at 423 K. Moreover, Ye et al.9 reported a transference number of tLi+ = 0.034 at 293 K for a 1 M LiTFSI/P13TFSI/PVDF–HFP mixture. Thus, the slightly higher results for tLi+ in LiTFSI/urea mixtures indicate that the DEE seems to be a potential candidate for the usage as an ion conducting material in lithium based battery applications.
In order to achieve a consistent framework for the molecular composition of the DEE, we analyzed the local environment around lithium and TFSI ions in terms of radial distribution functions (RDFs) gαβ(r) and coordination numbers CNβ(r). The coordination numbers for a species β around a molecule α can be obtained by 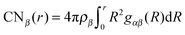 with the number density ρβ.
with the number density ρβ.
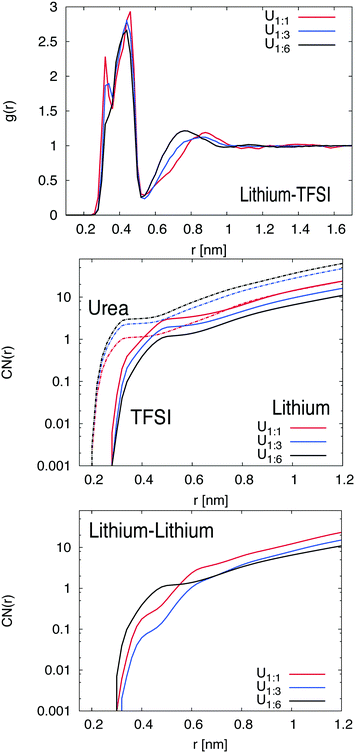
The center-of-mass RDFs between TFSI and lithium ions are shown in Fig. 2. More results for different components are depicted in the ESI.† Interestingly, one can see that the RDF between lithium and TFSI strongly depends on the amount of urea in the system. For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, a double peak structure in the first coordination shell between r = 0.28 nm and 0.52 nm can be observed which can be assigned to monodentate and bidentate coordinated TFSI ions (one or two oxygen atoms of one TFSI ion bound to a single lithium ion).43,44 The double peak structure is less pronounced for the 1
1 mixture, a double peak structure in the first coordination shell between r = 0.28 nm and 0.52 nm can be observed which can be assigned to monodentate and bidentate coordinated TFSI ions (one or two oxygen atoms of one TFSI ion bound to a single lithium ion).43,44 The double peak structure is less pronounced for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture and vanishes completely for the 1
3 mixture and vanishes completely for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 mixture. Hence, it can be concluded that TFSI significantly prefers the monodentate coordination at higher urea concentrations. Furthermore, a second coordination peak of TFSI at r ≈ 0.92 nm (U1
6 mixture. Hence, it can be concluded that TFSI significantly prefers the monodentate coordination at higher urea concentrations. Furthermore, a second coordination peak of TFSI at r ≈ 0.92 nm (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is shifted to shorter distances for increasing urea concentrations. With regard to these results, it becomes obvious that a higher urea concentration leads to a more compact coordination of TFSI around lithium ions.
1) is shifted to shorter distances for increasing urea concentrations. With regard to these results, it becomes obvious that a higher urea concentration leads to a more compact coordination of TFSI around lithium ions.
The corresponding findings for the coordination numbers of urea and TFSI molecules around lithium ions are shown in the middle of Fig. 2. It can be seen that urea molecules in comparison to TFSI accumulate at shorter distances around lithium ions, which can be attributed to the smaller size of urea. Moreover, the plateau region of the first urea shell around the lithium ion, which is located at r = 0.3–0.45 nm, is filled with an increasing number of urea molecules at higher urea concentration in order to replace TFSI ions. Hence, while the TFSI number in the first shell decreases, the number of urea molecules increases. These findings explain the occurrence of a monodentate TFSI coordination at higher urea concentration due to a larger number of urea molecules in the local vicinity around lithium ions. With regard to the RDFs for lithium ions (shown in the ESI†), one can calculate the potential of mean force in accordance with PMF(r) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(gβ(r)/gβ(∞)) with the molar gas constant R and the temperature T to estimate the individual binding strength. The resulting values with regard to the binding to lithium ions are PMF(r) ≈ −3 kJ mol−1 for TFSI and PMF(r) ≈ −4 kJ mol−1 for urea, valid for all mixtures in the first coordination shell at r = 0.27 nm. Moreover, the results for the RDF between TFSI and urea indicate only a very weak affinity between urea and TFSI which even decreases at higher urea concentrations. Therefore, we can safely assume that the presence of urea mostly affects the properties of lithium ions in contrast to the previously found strong interaction between urea and negatively charged spheres in aqueous solution.19 Based on these findings, we can relate the lithium preference of urea to the high dipole moment (μ = 4.56 D) of the molecule which favors the oxygen orientation of urea towards lithium ions in good agreement with experimental and numerical findings.14,15 It is noteworthy that comparable results for oxygen orientation towards cations were also found for the solvation of sodium ions in dimethyl sulfoxide.45 These conclusions are also supported by the results for the local/bulk partition coefficient as shown in the ESI† which reveals the accumulation behavior of different species around a central particle. Based on the corresponding results, it can be concluded that higher urea concentrations enforce a significant replacement of TFSI around lithium ions. The corresponding probabilities for specific coordination numbers of urea and TFSI around lithium ions in the first coordination shell can be also found in the ESI.† In fact, for the lowest urea concentration (U1
log(gβ(r)/gβ(∞)) with the molar gas constant R and the temperature T to estimate the individual binding strength. The resulting values with regard to the binding to lithium ions are PMF(r) ≈ −3 kJ mol−1 for TFSI and PMF(r) ≈ −4 kJ mol−1 for urea, valid for all mixtures in the first coordination shell at r = 0.27 nm. Moreover, the results for the RDF between TFSI and urea indicate only a very weak affinity between urea and TFSI which even decreases at higher urea concentrations. Therefore, we can safely assume that the presence of urea mostly affects the properties of lithium ions in contrast to the previously found strong interaction between urea and negatively charged spheres in aqueous solution.19 Based on these findings, we can relate the lithium preference of urea to the high dipole moment (μ = 4.56 D) of the molecule which favors the oxygen orientation of urea towards lithium ions in good agreement with experimental and numerical findings.14,15 It is noteworthy that comparable results for oxygen orientation towards cations were also found for the solvation of sodium ions in dimethyl sulfoxide.45 These conclusions are also supported by the results for the local/bulk partition coefficient as shown in the ESI† which reveals the accumulation behavior of different species around a central particle. Based on the corresponding results, it can be concluded that higher urea concentrations enforce a significant replacement of TFSI around lithium ions. The corresponding probabilities for specific coordination numbers of urea and TFSI around lithium ions in the first coordination shell can be also found in the ESI.† In fact, for the lowest urea concentration (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), we found maximum probabilities around 30% for two and three coordinating TFSI ions which decreases to the values between one and two TFSI ions (both with probabilities around 35%) for U1
1), we found maximum probabilities around 30% for two and three coordinating TFSI ions which decreases to the values between one and two TFSI ions (both with probabilities around 35%) for U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and finally one coordinating TFSI ion with an occurrence probability of roughly 60% for U1
3 and finally one coordinating TFSI ion with an occurrence probability of roughly 60% for U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. In contrast, the number of coordinating urea molecules increases with higher urea concentration from one molecule with a probability of 65% for U1
6. In contrast, the number of coordinating urea molecules increases with higher urea concentration from one molecule with a probability of 65% for U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 over two molecules (both with probabilities around 37%) for U1
1 over two molecules (both with probabilities around 37%) for U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to three urea molecules with a maximum probability of 40% for U1
3 to three urea molecules with a maximum probability of 40% for U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. Thus, we observe a competition between TFSI and urea in occupying the first coordination shell around lithium ions which is in agreement with the roughly comparable potentials of mean force for both species as discussed above. In summary, increasing urea concentrations impose a decreasing TFSI coordination number and favor a monodentate coordination. Moreover, one can assume that different TFSI coordination properties influence the resulting lithium ion transport behavior which was discussed above.
6. Thus, we observe a competition between TFSI and urea in occupying the first coordination shell around lithium ions which is in agreement with the roughly comparable potentials of mean force for both species as discussed above. In summary, increasing urea concentrations impose a decreasing TFSI coordination number and favor a monodentate coordination. Moreover, one can assume that different TFSI coordination properties influence the resulting lithium ion transport behavior which was discussed above.
Finally, the influence of urea on the lithium–lithium ion coordination number is shown at the bottom of Fig. 2. It can be clearly seen for distances r ≥ 0.6 nm, that the lithium coordination number for systems with higher urea concentration is significantly smaller. In contrast, for distances shorter than r = 0.6 nm, one can instead observe an increase of the lithium coordination number for higher urea concentrations. In fact, these results clearly illustrate that urea influences the short-range as well as the long-range order around lithium ions. These findings are also supported by the corresponding lithium–lithium radial distribution functions as presented in the ESI.†
In order to study the energetic contributions to the binding mechanism in more detail, we calculated the potential energies, namely electrostatic and Lennard-Jones interactions between the constituents of the DEE. The results are depicted in the ESI† and demonstrate that the systems are strongly dominated via electrostatic interactions. In contrast, the influence of Lennard-Jones interactions is negligible. At a low urea content, the system is dominated by strong interactions between lithium and TFSI ions. For increasing urea concentration, the amount of urea binding energy increases whereas the importance of the TFSI interaction with lithium ions decreases. In more detail for the U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture, one can observe that the electrostatic potential energy between lithium and TFSI ions is nearly comparable to lithium ions and urea. These findings point at a critical urea concentration, which is needed to foster the formation of a DEE.14 Thus, it can be concluded that the interaction between lithium ions and urea is mainly responsible for the depression of the melting temperature.
3 mixture, one can observe that the electrostatic potential energy between lithium and TFSI ions is nearly comparable to lithium ions and urea. These findings point at a critical urea concentration, which is needed to foster the formation of a DEE.14 Thus, it can be concluded that the interaction between lithium ions and urea is mainly responsible for the depression of the melting temperature.
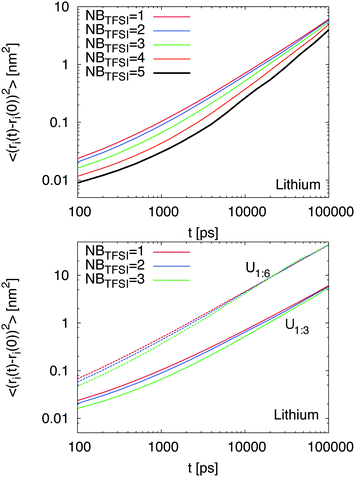
In order to understand the influence of the initial local environment, we studied the influence of coordinating TFSI ions on the dynamic behavior of Li+. Therefore, we determined the number of neighboring TFSI ions in the first shell around lithium for the systems U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and U1
3 and U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 at different points of the simulation and considered them as starting points for our analysis. The corresponding evolution in time provides the MSD for the central lithium ion and reveals the influence of the initial local environment configuration on the lithium dynamics. Our results evidence that the initial number of TFSI ions NBTFSI in the first coordination shell around Li+ strongly influences the dynamic behavior of lithium ions (Fig. 3). Based on our findings, it can be concluded that a larger number of coordinating TFSI ions NBTFSI ≥ 4 strongly decrease the lithium MSD at short times while the influence for NBTFSI ≤ 3 is less pronounced. In agreement with previous results (Fig. 1), we found a slightly higher MSD for lithium ions in the presence of higher urea concentrations (bottom part of Fig. 3). Moreover, it can be observed that the onset of the diffusive regime occurs at shorter times for a smaller number of initial coordinating TFSI ions. However, the relative slow down for a fixed number of coordinating TFSI ions NBTFSI between both mixtures is roughly comparable. At long times, one can clearly see that all results coincide with a single MSD, which indicates that the influence of an initial local environment becomes negligible on these time scales. With regard to these findings, we conclude that higher TFSI coordination numbers significantly decrease the lithium transference numbers at short times in agreement with some properties observed for ionic liquids.12,43 In addition, our results indicate that higher concentrations of urea impose a faster MSD for all species.
6 at different points of the simulation and considered them as starting points for our analysis. The corresponding evolution in time provides the MSD for the central lithium ion and reveals the influence of the initial local environment configuration on the lithium dynamics. Our results evidence that the initial number of TFSI ions NBTFSI in the first coordination shell around Li+ strongly influences the dynamic behavior of lithium ions (Fig. 3). Based on our findings, it can be concluded that a larger number of coordinating TFSI ions NBTFSI ≥ 4 strongly decrease the lithium MSD at short times while the influence for NBTFSI ≤ 3 is less pronounced. In agreement with previous results (Fig. 1), we found a slightly higher MSD for lithium ions in the presence of higher urea concentrations (bottom part of Fig. 3). Moreover, it can be observed that the onset of the diffusive regime occurs at shorter times for a smaller number of initial coordinating TFSI ions. However, the relative slow down for a fixed number of coordinating TFSI ions NBTFSI between both mixtures is roughly comparable. At long times, one can clearly see that all results coincide with a single MSD, which indicates that the influence of an initial local environment becomes negligible on these time scales. With regard to these findings, we conclude that higher TFSI coordination numbers significantly decrease the lithium transference numbers at short times in agreement with some properties observed for ionic liquids.12,43 In addition, our results indicate that higher concentrations of urea impose a faster MSD for all species.
In order to investigate the exchange of TFSI ions in the first coordination shell in more detail, we calculated the autocorrelation function for the number of TFSI ions around lithium ions 〈NBTFSI(t)NBTFSI(t0)〉/〈NBTFSI2(t0)〉 within r = 0.27 nm. The corresponding results for the autocorrelation function are shown in the ESI.† For a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, we found the slowest decay of the autocorrelation function with the largest residence time of τ ≈ 15 ns. Increasing the concentration of urea leads to a fast decrease of the residence times (τ ≈ 2.7 ns (U1
1 mixture, we found the slowest decay of the autocorrelation function with the largest residence time of τ ≈ 15 ns. Increasing the concentration of urea leads to a fast decrease of the residence times (τ ≈ 2.7 ns (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) and τ ≈ 0.6 ns (U1
3) and τ ≈ 0.6 ns (U1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6)) and thus a faster exchange rate of TFSI molecules. These results are in good agreement with the data presented in the bottom panel of Fig. 3, where it can be seen that the corresponding onset of diffusive behavior at τD follows the relation τD > τ, which reveals that the rearrangement of the local coordination shell is of significant importance for the dynamic behavior of Li+. Thus, a larger amount of urea favors the occurrence of higher TFSI exchange rates which can be brought into agreement with a transition from vehicular to structural transport of lithium ions.12
6)) and thus a faster exchange rate of TFSI molecules. These results are in good agreement with the data presented in the bottom panel of Fig. 3, where it can be seen that the corresponding onset of diffusive behavior at τD follows the relation τD > τ, which reveals that the rearrangement of the local coordination shell is of significant importance for the dynamic behavior of Li+. Thus, a larger amount of urea favors the occurrence of higher TFSI exchange rates which can be brought into agreement with a transition from vehicular to structural transport of lithium ions.12
In summary, the results of our atomistic molecular dynamics simulations reveal a strong influence of urea on the local environment around Li+. Previous experimental studies showed that LiTFSI/urea mixtures form deep eutectic electrolytes at specific molar ratios.14 We found pronounced effects of urea on the transport and the structural properties of LiTFSI. Based on our findings, we can conclude that urea systematically replaces TFSI ions in the first coordination shell around lithium ions which results in the formation of a DEE and furthermore induces a faster diffusional behavior. Hence, we assume that LiTFSI/urea mixtures are potential candidates to improve the ion transport in lithium metal and lithium ion batteries. In the future, we will study these systems by experiments and simulations in more detail to verify their applicability for electrochemical storage devices.
The authors thank Markus Blank-Burian and Oliver Rubner for technical help and the Deutsche Forschungsgemeinschaft (DFG) via the cluster of excellence ‘Simulation Technology’ (EXC 310) for financial support.
References
- Q. Zhang, K. D. O. Vigier, S. Royer and F. Jérôme, Chem. Soc. Rev., 2012, 41, 7108–7146 RSC.
- B. Tang and K. H. Row, Monatsh. Chem., 2013, 144, 1427–1454 CrossRef CAS.
- D. A. Alonso, A. Baeza, R. Chinchilla, G. Guillena, I. M. Pastor and D. J. Ramón, Eur. J. Org. Chem., 2016, 4, 612–632 CrossRef.
- A. P. Abbott, G. Capper, D. L. Davies, R. K. Rasheed and V. Tambyrajah, Chem. Commun., 2003, 70–71 RSC.
- H. Sun, Y. Li, X. Wu and G. Li, J. Mol. Model., 2013, 19, 2433–2441 CrossRef CAS PubMed.
- A. Romero, A. Santos, J. Tojo and A. Rodriguez, J. Hazard. Mater., 2008, 151, 268–273 CrossRef CAS PubMed.
- V. Lesch, A. Heuer, V. A. Tatsis, C. Holm and J. Smiatek, Phys. Chem. Chem. Phys., 2015, 17, 26049–26053 RSC.
- A. D. Pauric, I. C. Halalay and G. R. Goward, Phys. Chem. Chem. Phys., 2016, 18, 6657–6667 RSC.
- H. Ye, J. Huang, J. J. Xu, A. Khalfan and S. G. Greenbaum, J. Electrochem. Soc., 2007, 154, A1048–A1057 CrossRef CAS PubMed.
- M. Ishikawa, T. Sugimoto, M. Kikuta, E. Ishiko and M. Kono, J. Power Sources, 2006, 162, 658–662 CrossRef CAS.
- O. Borodin, G. D. Smith and W. Henderson, J. Phys. Chem. B, 2006, 110, 16879–16886 CrossRef CAS PubMed.
- Z. Li, G. D. Smith and D. Bedrov, J. Phys. Chem. B, 2012, 116, 12801–12809 CrossRef CAS PubMed.
- A. Matic and B. Scrosati, MRS Bull., 2013, 38, 533–537 CrossRef CAS.
- H. Liang, H. Li, Z. Wang, F. Wu, L. Chen and X. Huang, J. Phys. Chem. B, 2001, 105, 9966–9969 CrossRef CAS.
- S. Li, L. Liu, Z. Cao, J.-Q. Wang and T.-Y. Yan, Acta Phys. Chim. Sin., 2007, 23, 983–986 CAS.
- L. Sim, R. Yahya and A. Arof, Opt. Mater., 2016, 56, 140–144 CrossRef CAS.
- Y. Hu, Z. Wang, H. Li, X. Huang and L. Chen, Spectrochim. Acta, Part A, 2005, 61, 2009–2015 CrossRef PubMed.
- D. Horinek and R. R. Netz, J. Phys. Chem. A, 2011, 115, 6125–6136 CrossRef CAS PubMed.
- J. Smiatek, J. Phys. Chem. B, 2014, 118, 771–782 CrossRef CAS PubMed.
- A. Narayanan Krishnamoorthy, C. Holm and J. Smiatek, J. Phys. Chem. B, 2014, 118, 11613–11621 CrossRef CAS PubMed.
- F. Rodriguez-Ropero and N. F. A. van der Vegt, Phys. Chem. Chem. Phys., 2015, 17, 8491–8498 RSC.
- S. Micciulla, J. Michalowsky, M. A. Schroer, C. Holm, R. von Klitzing and J. Smiatek, Phys. Chem. Chem. Phys., 2016, 18, 5324–5335 RSC.
- H.-R. Jhong, D. S.-H. Wong, C.-C. Wan, Y.-Y. Wang and T.-C. Wei, Electrochem. Commun., 2009, 11, 209–211 CrossRef CAS.
- L. Vieira, A. Whitehead and B. Gollas, J. Electrochem. Soc., 2014, 161, D7–D13 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- J. M. Martinez and L. Martinez, J. Comput. Chem., 2003, 24, 819–825 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- T. Mendez-Morales, J. Carrete, S. Bouzon-Capelo, M. Perez-Rodriguez, O. Cabeza, L. J. Gallego and L. M. Varela, J. Phys. Chem. B, 2013, 117, 3207–3220 CrossRef CAS PubMed.
- F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, ChemPhysChem, 2012, 13, 1625–1637 CrossRef CAS PubMed.
- V. Lesch, A. Heuer, C. Holm and J. Smiatek, Phys. Chem. Chem. Phys., 2015, 17, 8480–8490 RSC.
- V. Lesch, A. Heuer, C. Holm and J. Smiatek, ChemPhysChem, 2016, 387–394 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. Berendsen, J. Postma, W. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- A. Einstein and M. von Smoluchowski, Untersuchungenüber die Theorie der Brownschen Bewegung, Deutsch, 1997 Search PubMed.
- F. Dommert, J. Schmidt, C. Krekeler, Y. Y. Zhao, R. Berger, L. Delle Site and C. Holm, J. Mol. Liq., 2010, 152, 2–8 CrossRef CAS.
- V. Lesch, S. Jeremias, A. Moretti, S. Passerini, A. Heuer and O. Borodin, J. Phys. Chem. B, 2014, 118, 7367–7375 CrossRef CAS PubMed.
- V. Lesch, Z. Li, D. Bedrov, O. Borodin and A. Heuer, Phys. Chem. Chem. Phys., 2016, 18, 382–392 RSC.
- J. Pitawala, A. Martinelli, P. Johansson, P. Jacobsson and A. Matic, J. Non-Cryst. Solids, 2015, 407, 318–323 CrossRef CAS.
- J. Smiatek, A. Wohlfarth and C. Holm, New J. Phys., 2014, 16, 025001 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04217a |
| This journal is © the Owner Societies 2016 |