 Open Access Article
Open Access ArticleInfluence of counterions on the conformation of conjugated polyelectrolytes: the case of poly(thiophen-3-ylacetic acid)†
Gregor
Hostnik
a,
Matjaž
Bončina
a,
Caterina
Dolce
b,
Guillaume
Mériguet
b,
Anne-Laure
Rollet
b and
Janez
Cerar
*a
aFaculty of Chemistry and Chemical Technology, University of Ljubljana, Večna pot 113, SI-1000 Ljubljana, Slovenia. E-mail: janez.cerar@fkkt.uni-lj.si
bSorbonne Universités, UPMC Univ Paris 06, CNRS, Laboratoire PHENIX, Paris, France
First published on 11th August 2016
Abstract
The addition of simple salt to a solution of conjugated polyelectrolyte can lead to substantial changes in its optical properties caused by the conformational change of the polymer chain. The effect of the addition of alkali metal and tetraalkylammonium chlorides to solutions of lithium salt of poly(thiophen-3-ylacetic acid) is investigated by NMR. The fractions of free alkali metal counterions are in agreement with predictions of the cylindrical Poisson–Boltzmann cell model. On the other hand, the fractions of free tetraalkylammonium counterions deviate from the prediction of this model and diminish with increasing size of these counterions. This trend is consistent with observed ultraviolet-visible absorption spectra and measured self-diffusion coefficients of the polyion in mixtures with tetraalkylammonium salts. A transition to more constricted conformation of the polyion chain becomes more pronounced with the lengthening of alkyl groups in the added tetraalkylammonium cation. Taking into account the obtained fractions of free counterions, existing thermodynamic data are reanalysed in order to determine thermodynamic parameters for binding of different counterions to the polyion. This analysis shows that standard enthalpies of binding of alkali metal counterions are distinctively different, which is most probably related to differences in hydration shells of counterions. On the other hand, such an analysis fails in the case of tetraalkylammonium chlorides where obviously more complex changes take place.
1 Introduction
Poly(thiophen-3-ylacetic acid) (PTAA) is a polymer (Fig. 1) from a class of conjugated polyelectrolytes (PEs). These polymers are, due to their favourable physical properties, the subject of intensive application studies in the field of optoelectronic devices1–9 and sensors.10–24 Although conjugated PEs are mostly used in the form of thin layers,1–9 their properties in solutions, from which those layers are made, are of crucial importance.25–27 One of the parameters that have a decisive effect on the properties of conjugated PEs in the solid state7,25 and in solution28 is the nature of the counterion.It is well known that the spectral properties of conjugated PE solutions depend on their conformation and the potential formation of aggregates.28–30 Both properties can be influenced by the degree of neutralisation and by the selection of counterion species. In this respect, polythiophenes are no exception. Kim et al.29 and Vallat et al.30 have shown that the position of the absorption maximum in the spectra of PTAA aqueous solutions depends on the level of neutralisation. In both cases a red shift was observed when the degree of neutralisation was increased. This effect was explained by the conformational change induced by the increased density of charged groups on the polyion.29,30
An existence of the ionochromic effect in polythiophene solutions was observed by McCullough et al.,28 who found a strong dependence of absorption spectra on the counterion nature. They showed that the decrease of the counterion size (from tetrabutylammonium to ammonium) leads to a red-shift in the absorption spectrum of aqueous solutions of salts of poly(thiophen-3-ylpropionic acid). This effect was ascribed to the ability of larger counterions (e.g. tetrabutylammonium) to hinder polyion main chains from getting into contact with one another, thus preventing the aggregation of polyions while this is not the case for smaller counterions (e.g. tetramethylammonium). The strong dependence of the absorption and emission spectra on the length of alkyl chains in cationic surfactants added to aqueous solution of fully ionised regio-irregular PTAA confirmed the pronounced sensitivity of conjugated polyanions to their environment.31 In this case, observed changes in spectra were explained by the formation of mixed aggregates between polyion and surfactant molecules.
The goal of the present study is to address quantitatively the influence of the nature of counterions on the properties of the PTAA in solution. For this purpose, we have previously determined the fraction of free counterions, f, in aqueous solutions of PTAA lithium, sodium, and caesium salts using the combination of conductivity and transference number measurements.32 It turned out that f does not depend on the nature of the alkali metal counterion, i.e. none of the mentioned alkali metal counterions seems to show specific interactions towards the poly(thiophen-3-ylacetate) polyion (PTA−). In contrast, heats of dilution and heats of mixing strongly depend on the nature of the alkali metal counterion.33 This dependence, however, is most probably not directly related to the properties of PTAA but rather to the different affinities of the alkali counterions towards water.34 As a part of our latest study,33 heats of dilution of tetraalkylammonium salts of PTAA and heats of mixing of lithium PTAA salt (PTALi) with tetraalkylammonium chlorides were also determined. Measured heats of mixing PTALi solution with solutions of alkali metal chlorides on one side and with solutions of tetraalkylammonium chlorides on the other side were fundamentally different and the differences were ascribed to the existence of hydrophobic interactions between the PTAA hydrophobic backbone and the alkyl chains of tetraalkylammonium counterions.33 Considering that heats of mixing alone cannot provide information about the preferential binding of tetraalkylammonium over alkali counterions to PTA−, the current study investigates this competition further by measuring self-diffusion coefficients of counterions and polyions as well as by carrying out a thermodynamic analysis using both these new data and existing calorimetric data.
When association processes in solutions are studied, various NMR techniques can be used for the investigation of such phenomena.35 For example, NMR quadrupole splitting has been used successfully for assessing the specific adsorption of lithium and sodium ions to dodecyl carboxylate and dodecyl sulphate bilayers36 as well as for studying the specificity of binding of rubidium and caesium ions to dodecyl carboxylate in a liquid crystalline phase.37 However, for the system under study, i.e. for solutions of polyelectrolytes, the order parameter averages to zero and the NMR quadrupole splitting method cannot be used. In order to assess the physical origin of measured enthalpies of mixing,33 the process of mixing the polyion and the counterions was investigated by using another NMR method, namely the pulsed field gradient spin-echo NMR method (PFG SE NMR). By the use of PFG SE NMR it is possible to determine self-diffusion coefficients of the polyion and counterions that are valuable tools for the evaluation of counterion–polyelectrolyte interactions.38,39 Pulsed field gradient spin-echo NMR experiments were then performed at 298.1 K and, due to the lower sensitivity of NMR experiments, at somewhat higher (four-fold) concentrations than those used in the calorimetric measurements. The obtained self-diffusion coefficients were used to evaluate f for every single counterion species involved in the mixing experiment. The experimental values were compared with f derived from the solution of the Poisson–Boltzmann equation within the cell model of cylindrical symmetry. Finally, using the results of NMR experiments, the calorimetric data from mixing experiments were evaluated through a model thermodynamic analysis which enabled us to determine standard thermodynamic quantities for alkali metal counterions involved in mixing.
2 Experimental part
2.1 Synthesis and sample preparation
Lithium salt solution of PTAA was prepared by dissolving the dry PTAA sample in 0.1 mol dm−3 LiOH solution and light water (H2O) was removed afterwards by freeze-drying to obtain dry PTALi salt. The degree of neutralisation of PTAA with LiOH in the solution prepared for freeze-drying was around 97%. This value was verified by the use of atomic absorption spectroscopy (concentration of Li+ ions) and potentiometric titration of remaining non-neutralised carboxylic groups. Taking that PTAA is a representative of weak polyacids its degree of ionisation can be equalled with its degree of ionisation. The pH value of aqueous (H2O) PTAA solutions having a degree of neutralisation of 97% slightly depends on concentration and is around 8. This holds true both for solutions without simple salt added and for solutions with low or moderate concentration of simple salt added.41 Complete neutralisation of PTAA was in our case avoided in order to prevent introducing surplus of Li+ ions. When NMR experiments with these samples in deuterated water (D2O) are considered, some small departures from pH values measured in non-deuterated water can be expected.42 These differences, however, are too small to influence notably experimental results under given experimental conditions. The dried sample of PTALi was then dissolved in the corresponding amount of D2O to obtain PE solution with a concentration of 0.02 monomol dm−3. In order to prepare solutions with selected molar ratios (rn) between the added counterion and the PE's monomeric units, a corresponding volume of 0.2 mol dm−3 simple salt solution was added to 0.02 monomol dm−3 solution of PTALi in D2O. Here the molar ratio rn is defined as
 | (1) |
The self-diffusion coefficients of Li+ and of PTA− polyions (stemming from PTALi) as well as of the added counterion (from the simple salt added) were measured in prepared mixtures according to the procedure described in the following subsection.
2.2 Measurements
For 7Li ions and 1H (TMA+, TEA+, TPA+, and TBA+ ions and PTA− polyions), a Bruker Avance DRX 500 NMR spectrometer operating at 499.76 MHz for 1H was used. Spectra were recorded using a 1H/X BBO broadband probe equipped with z-gradient coil producing 0.55 T m−1 at maximum. During these measurements the temperature was maintained at 298.1 K (±0.1 K).
For 23Na and 133Cs ions, higher gradients were required. Due to the fast relaxation of 23Na nuclei magnetisation (T1 ∼ 20 ms), short and intense gradient pulses had to be used. In the case of 133Cs, the high gradient field was needed to compensate the low gyromagnetic ratio of this nucleus and to obtain sufficient signal attenuation (see eqn (2) and (3)).43 All these special demands, required by the properties of 23Na and 133Cs nuclei, were met by using a Bruker Avance III narrow bore Spectrometer operating at a magnetic field of 7.05 T equipped with a Diff30 gradient probe (producing 12 T m−1 A−1 at maximum) with a single (i.e. z) shielded gradient coil connected to a GREAT30 current amplifier capable of generating current pulses of 30 A amplitude.
All NMR experiments were performed in D2O. A stimulated echo pulse sequence with longitudinal eddy current delay (BPP-LED,44Te = 5 ms) and bipolar gradient pulses of sine-shaped amplitude was used. During measurements the gradient of the magnetic field was increased in 16 increments (from 2% to 60% of maximal gradient strength for 133Cs and from 2% to 90% for 23Na). Gradient pulse lengths were δ = 2 × 1 ms for 133Cs, and δ = 2 × 0.5 ms for 23Na while the diffusion delay Δ was 100 ms for 133Cs and 15 ms for 23Na.
The self-diffusion coefficient of counterions D was calculated by fitting expression (2) to experimental points
| A(k) = A0·e−kD | (2) |
 | (3) |
In the above equation, δ stands for the duration of gradient pulses, g for the magnetic field gradient, γ for the nuclear gyromagnetic ratio of the nucleus under study, Δ for the separation time between a pair of gradient pulses, and τ for the separation time between the second gradient pulse in the pair and the next radiofrequency pulse.
Regarding polyion self-diffusion coefficient (Dp) determination, a correction for sample dispersity was taken into account by using the equation45
 | (4) |
| D(M) ≈ M−α | (5) |
Assuming a log-normal polymer molar mass distribution, 〈D2〉m and 〈D〉m can be computed using eqn (5) since all the moments of the distribution are known. Eqn (4) is then rewritten as (see the ESI† for derivation):
 | (6) |
The measured self-diffusion coefficient of the counterions was used to evaluate the fraction of free counterions, f, a quantity that has in the case of PE solution a similar value as the osmotic coefficient or the activity coefficient of counterions.47 In PE solutions, f can be obtained from the ratio between the measured self-diffusion coefficient of the counterion (D) and the self-diffusion coefficient of the given counterion in the limit of infinite dilution (D°). In order to eliminate the contribution of counterions bound to polyions to diffusion processes, in our case the self-diffusion of the polyion (Dp) was also taken into account:
 | (7) |
3 Theoretical part
3.1 Cylindrical cell model
In order to estimate f in the salt-free PE solution as well as in the PE solution with the simple salt added, the Poisson–Boltzmann equation in cylindrical symmetry47–49 was solved, and its solution was used in the theoretical prediction of f. This approach takes into account only electrostatic interactions and ignores possible specific interactions stemming from the hydrophobic effect. Taking that this theory is frequently used in the scientific literature, the calculation procedure is omitted here and is given in the ESI† instead.3.2 Thermodynamic analysis of cation–polyion association
Calorimetric data obtained in our previous study33 cannot provide per se a molecular insight into the processes occurring when PE solution is mixed with simple salt solution. In order to get such a picture from calorimetric data, a new model, based on our previous work,50,51 was developed. In this new model, besides calorimetric data, measured fractions of free counterions are used as relevant input parameters.It is assumed that each monomeric unit of the polymer can be represented as one independent binding site. This binding site can be either unoccupied (this is a model representation of the –COO− group where no counterion is present in its immediate vicinity) or occupied (a counterion is bound to the –COO− group thus screening its charge effectively). In the pure PE solution without added simple salt (in our case this corresponds to PTALi solution) there exists an equilibrium between unoccupied and with lithium counterions occupied binding sites. When simple salt is added, the added counterions compete with the already present lithium counterions for unoccupied binding sites. This new equilibrium in solution can be written down as:
 | (8) |
 | (9) |
![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) M(T) stands for the standard molar enthalpy of binding of counterion M and square brackets denote the equilibrium concentration of given species in solution. The latter concentrations can be calculated from the total concentration of added salt (cx), monomeric unit concentration (cp), and equilibrium constant for binding of the lithium ion (eqn (10)) and of the added counterion (eqn (11)), respectively.
M(T) stands for the standard molar enthalpy of binding of counterion M and square brackets denote the equilibrium concentration of given species in solution. The latter concentrations can be calculated from the total concentration of added salt (cx), monomeric unit concentration (cp), and equilibrium constant for binding of the lithium ion (eqn (10)) and of the added counterion (eqn (11)), respectively. | (10) |
 | (11) |
The temperature dependence of standard molar Gibbs energies, ΔbG![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T), and enthalpies of binding can be expressed by the Gibbs–Helmholtz relation (eqn (12)) and by the Kirchhoff law (eqn (13)).
i(T), and enthalpies of binding can be expressed by the Gibbs–Helmholtz relation (eqn (12)) and by the Kirchhoff law (eqn (13)).
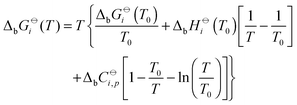 | (12) |
ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T) = ΔbH i(T) = ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T0) + ΔbC i(T0) + ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i,p(T − T0) i,p(T − T0) | (13) |
The use of the above written relations allows us to describe the binding of each type of counterion with a single set of adjustable parameters Ki, ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T0), and the difference in the molar heat capacities of products and reactants (ΔbC
i(T0), and the difference in the molar heat capacities of products and reactants (ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i,p), respectively (keep in mind that ΔbG
i,p), respectively (keep in mind that ΔbG![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T) = −RT
i(T) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ki) at arbitrary T). In order to minimize the number of adjustable parameters, the equilibrium constants Ki can be calculated from the measured fractions of free counterions using the approximation that the activity coefficient of counterions is equal to f and that activity coefficients of –COO− and –COO− M+ species are equal to 1. Although the first approximation is believed to hold rather well,47 the validity of the last two is more questionable. Therefore, Ki are not the true thermodynamic constants but the apparent ones.
ln(Ki) at arbitrary T). In order to minimize the number of adjustable parameters, the equilibrium constants Ki can be calculated from the measured fractions of free counterions using the approximation that the activity coefficient of counterions is equal to f and that activity coefficients of –COO− and –COO− M+ species are equal to 1. Although the first approximation is believed to hold rather well,47 the validity of the last two is more questionable. Therefore, Ki are not the true thermodynamic constants but the apparent ones.
Since previous32 and current experiments (see Fig. 2 in Section 4.1) show that the fractions of free lithium, sodium, and caesium counterions in salt-free PTAA solutions are equal within the experimental error, it is assumed that KLi = KNa = KCs. The binding constant KLi was estimated from the analytical concentration (cLi) and the fraction of free lithium counterions (fLi) at rn = 0 ([Li+] = [PTA−] = cLi·fLi and [PTALi] = cLi·(1 − fLi)). The values of remaining adjustable parameters (ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T0) and ΔbC
i(T0) and ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i,p) were finally determined by the global fitting of the model function to the experimental calorimetric isothermal titration curves, measured at various temperatures and for titrations with different alkali metal salts (LiCl, NaCl, CsCl).
i,p) were finally determined by the global fitting of the model function to the experimental calorimetric isothermal titration curves, measured at various temperatures and for titrations with different alkali metal salts (LiCl, NaCl, CsCl).
4 Results and discussion
4.1 Fractions of free counterions
In Fig. 2 and 3 fractions of free alkali metal (Fig. 2) and tetraalkylammonium (Fig. 3) counterions in PTALi solutions containing various amounts of simple salts added are shown. The presented experimental points were obtained during the mixing of 0.020 monomol dm−3 aqueous solution of PTALi with 0.2 mol dm−3 solutions of alkali metal chlorides (LiCl, NaCl, and CsCl), and tetraalkylammonium chlorides (TMACl, TEACl, TPACl, and TBACl), respectively. Measured values are shown as a function of rn, representing a ratio between the concentration of simple salt added and the monomolar concentration of PTA−. | ||
Fig. 3 The same as in Fig. 2 but for the addition of tetraalkylammonium chlorides (TMACl, TEACl, TPACl, and TBACl) to PTALi. Symbols: Li+ (■), TMA+ ( ), TEA+ ( ), TEA+ ( ), TPA+ ( ), TPA+ ( ), and TBA+( ), and TBA+( ). ). | ||
Therefore, fLi values in Fig. 2 and 3 are shown as an average of values obtained for the addition of all simple salts whereas error bars show the largest deviation of measured values from the average value of fLi.
As one can see, f increases in all cases with increasing rn. Such a trend is also predicted by electrostatic theories: as an example of such calculations the result of the cylindrical cell model (a = 0.4 nm, b = 0.38 nm) is depicted by continuous black lines in both figures. Since counterions are considered to be pointlike in these calculations, this line holds for all monovalent salts of PTAA. It is possible to mimic the effect of finite radii of counterions by increasing the radius a of the polyion in these calculations (a can also be regarded as a distance of the closest approach of the centre of counterions to the axis of the polyion). Such calculations would show that increasing the radius of counterions leads to slightly larger values of f. As can be seen in Fig. 2, theoretical and measured values agree very well for the case of lithium and caesium counterions whereas for sodium ones the agreement is apparently good only at large enough rn values. The reason for sodium deviation at rn = 0.25 and 0.5 is most probably an experimental error which can be attributed to the low signal-to-noise ratio stemming from the short relaxation time of the 23Na nucleus (see the ESI†).
Fig. 2 shows that sodium counterions bind to PTA− to a similar extent as other alkali ions for large values of rn and the values of f measured in solutions of alkali metal salts of PTAA suggest32 that this is also valid at low rn values.
In the absence of more accurate experimental results, it will be assumed that in the case of alkali metal ions no preferential binding of counterions to PTA− exists. The exchange of different alkali metal counterions bound to PTA− therefore seems to be of statistical nature. In addition, regarding the concordance of measured f of alkali metal counterions with the ones calculated from the theory it is possible to say that electrostatic interactions satisfactorily explain the binding of alkali metal counterions to the polyanion. Yet, the observation that all the studied alkali metal counterions are bound to the PTA− polyion approximately to the same extent tells nothing about details how34,54,55 these counterions are bound. The used PFG SE NMR method cannot give such a kind of information and other methods should be used for this purpose.
From f it is possible to calculate the fraction of charged groups on the polyion counterbalanced by bound counterions (also known as the degree of condensation or the fraction of occupied binding sites, depending on the model used), θ. This quantity is for some purposes a better indicator of processes occurring on the polyion than f. If one calculates θ from theoretically computed f as
| θ = (1 − f)·(1 + rn) | (14) |
The highest f is exhibited by the smallest counterion, i.e. the tetramethylammonium (TMA+) ion. Measured fTMA is almost identical to those predicted by electrostatics and measured for alkali metal counterions. The values of fTMA deviate considerably (beyond experimental error) from those observed for alkali metal counterions only at rn = 0.125 and rn = 0.25. However, this deviation is (at least partially) an artefact of measurements, as for 23Na, though for a different reason. For TMA+, it arises from the overlap of the 1H NMR signal of TMA+ and PTA− peaks (see the ESI†). For larger values of rn, the ratio of the intensity of PTA− to TMA+ peaks is much smaller and consequently the error diminishes. Taking this factor into account, it may be claimed that the values of fTMA do not deviate considerably from fractions of free alkali metal counterions. This observation is also in line with some earlier findings.56
In the case of tetraalkylammonium counterions with longer alkyl chains (TEA+, TPA+, and TBA+) there exist counterion peaks in the 1H NMR spectrum which are well separated from the polyion peaks and difficulties related to the peak overlap vanish. The effect of diminishing f with the increased length of alkyl chains is especially pronounced at low values of rn. To be more specific, at rn = 0.125 approximately 60% of TEA+, 70% of TPA+, and 80% of TBA+ counterions are bound to the polyion. Obviously, in the case of counterions with longer alkyl chains, the polyion–counterion association is driven by some additional attractive interactions. These interactions, provoked probably by the presence of hydrophobic thiophene rings, should at least partially contribute to the measured enthalpies of mixing and thus to the different trends in the dependence of enthalpies of mixing on hydration enthalpies of tetraalkylammonium counterions.33 With increasing rn differences in f diminish.
The plot of the total fraction of occupied sites, θtot, and the fraction of sites occupied by lithium counterions, θLi, versus rn (Fig. 4) shows an even more interesting picture. The values of θtot are here calculated from the experimentally determined fLi and fractions of free added tetraalkylammonium counterions, fTAA, as
| θtot = (1 − fLi) + (1 − fTAA)·rn | (15) |
Since the fraction of bound counterions (at rn = 2.5, θtot is about 50% greater for the addition of TBA+ than for TMA+) increases with the length of the alkyl chain in counterions, one might expect that the conformation of the PTA− polyion is dependent on the kind of counterion.
4.2 Conformation of the polyion
A transition of the conjugated polyion from an extended conformation to a more compact one may be evidenced, among others, from the change in the polyion self-diffusion coefficient (Dp) and from the position of the absorption maximum in its UV/vis spectrum.In the present case, the addition of any simple salt to PTALi solution leads to the increase of Dp as rn increases (Fig. 5). Regarding differences among results obtained for various simple salts one has to say that the relative error in measured self-diffusion coefficients can exceed 5% (the estimated uncertainty is shown in Fig. 5 by error bars) (see the ESI†). Despite the experimental uncertainty, it seems that two counterions (TPA+ and TBA+) have a more pronounced effect on Dp than the other ones. This holds true especially for TBA+ where distinctively larger values of Dp are observed at all rn values. For TPA+, noticeably different values are present only at high rn. Regarding the addition of salts, presented in Fig. 5, the smallest increase of Dp is observed for the addition of LiCl, while the remaining two studied simple salts (i.e. NaCl and CsCl; not shown in Fig. 5) give similar to or slightly smaller effects than the addition of LiCl.
 | ||
| Fig. 5 Dependence of the self-diffusion coefficient of the polyion (Dp) on ratio rn obtained during mixing 0.020 monomol dm−3 PTALi aqueous solution with 0.2 mol dm−3 LiCl, TMACl, TEACl, TPACl, and TBACl at 298.15 K, respectively. Legend as in Fig. 3. Lines are used to guide the eye. | ||
The observed general trend of increasing Dp with increasing rn can be ascribed to the screening of electrostatic forces in solution. In principle, electrostatic forces could stem either from inter- or intramolecular interactions. It is known that screening of intermolecular interactions is the most probable reason for the increase of ‘slow’ diffusion coefficient57 observed in dynamic light scattering (DLS) experiments during the addition of simple salt to PE solution. On the other hand, the ‘slow’ diffusion coefficient cannot be equated using the self-diffusion process58 and the increase of Dp therefore cannot be unambiguously ascribed to screening of intermolecular interactions. Consequently, the trend observed in Fig. 5 may be at least partially a result of the screening of intramolecular electrostatic forces by added simple salt, which provokes transition to more constricted conformation of the polyion. Using the Stokes–Einstein relation, one can estimate the hydrodynamic radius of the PTALi polyion (Dp = 9.1 × 10−11 m2 s−1; see Fig. 5) at rn = 2.5 to lie around 2.7 nm, which is a reasonable estimate for our sample.
The effect of screening of intramolecular electrostatic forces observed through the dependence of Dp on rn can be verified in Fig. 6, where λmax is the position of the absorption maximum in the UV/vis spectrum of 5 × 10−3 monomol dm−3 solution of PTALi, as a function of rn and the nature of added salt is reported. When solutions of alkali metal chlorides are added to PTALi solution, the position of the absorption maximum does not change notably (these data are omitted in Fig. 6). λmax does not change either upon TMACl addition, similar to what was observed for f. In contrast, upon addition of TEACl to PTALi, a blue shift of up to 5 nm is observed. With TPACl, the blue shift is slightly more pronounced (7 nm) while the largest shift is observed during titration with TBACl where λmax shifts for about 20 nm towards lower wavelengths. As for Dp, the main change in λmax takes place at low rn values (rn < 0.5).
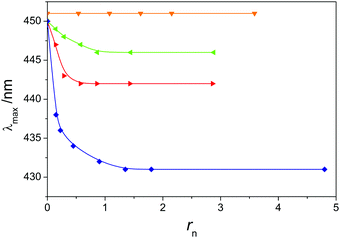 | ||
| Fig. 6 Position of the maximum of the UV/vis absorption spectra as a function of rn for the titration of 0.005 monomol dm−3 PTALi aqueous solution with different tetraalkylammonium chlorides. Legend as in Fig. 3. Lines are used to guide the eye. | ||
The blue shift in the spectra of conjugated PEs can be explained by two phenomena. The first one is a dissolution of π-aggregates28 and the second one is the collapse of the polymer chain that leads to a shorter effective conjugation length.59 In the classical study of McCullough et al. the blue shift observed during the addition of different counterions to aqueous solution of regio-regular poly(thiophen-3-ylpropionic acid) was explained by the decomposition of π-aggregates.28 On the other side, in our study regio-irregular PTAA was used and the blue shift can hardly be ascribed to the disaggregation of π-aggregates due to the following reasons: (i) blue shifts observed in the study of McCullough et al.28 are much more pronounced than those found here (in the case of TBACl 130 nm vs. 20 nm observed in this study); (ii) the formation of π-aggregates is far less likely to occur in the case of regio-irregular conjugated polymers than in the case of regio-regular ones;60 (iii) the disappearance of π-aggregates would very likely influence the shape of the absorption spectrum;60 (iv) it was shown by X-ray scattering that no reversible aggregates were formed in aqueous solutions of sodium salt of the regio-irregular PTAA sample having a similar molar mass as the sample used in our study.30 Considering also the above mentioned arguments, we ascribe the blue shift observed during the addition of tetraalkylammonium counterions with longer alkyl chains to the transition of the polyion to a more compact conformation.
The most pronounced blue shift, provoked by the addition of TBA+ counterions, can be explained by a stronger/more extensive counterion binding (higher θtot, see Fig. 4) which leads to a more effective screening of electrostatic forces on the polyion. The correlation between θtot and the blue shift holds quite well also for other tetraalkylammonium counterions: they both increase by increasing the length of alkyl chains in these counterions. On the other side, Dp increases irrespective of the kind of simple salt added while λmax remains unchanged only in the case of the addition of alkali metal salts and TMACl. This might be a consequence of the transition of the polyion to a more compact conformation which does not affect notably an effective conjugation length. Namely, certain theoretical studies61,62 have shown that the moderate loss of coplanarity does not change significantly the conjugation length in polythiophenes.
4.3 Thermodynamic analysis
Fractions of free counterions, obtained in the current study, are valuable information that supplements the enthalpies of mixing, ΔmixH, measured in our previous study.33 The study showed that ΔmixH measured during the mixing of PTALi with alkali and tetraalkylammonium chlorides has distinctly a different dependence on the enthalpy of hydration of the salt cation, ΔhydH. This different dependence was ascribed to the dissimilar nature of both groups of cations (i.e. hydrophilic and hydrophobic) and to leaving/entering of water molecules from/to solvent sheaths of solutes being dependent on the nature of counterions. Due to uncertainties related to possible preferential binding of certain kinds of counterions more detailed analysis of calorimetric data at that moment would be pure speculation and was therefore omitted. By having determined f for every kind of counterion under similar conditions at which ΔmixH was measured it is then possible to keep one step forward and to make use of thermodynamic analysis described in Section 3.2 of this paper. The reader should be aware that the calorimetric data, although being the same, are shown in ref. 33 as cumulative heats of mixing per mole of monomeric units (in order to compare the figures with theoretical calculations of Boyd et al.63) while in the present analysis differential heats of mixing, ΔdmixH, expressed per mole of added simple salt are used.In our thermodynamic analysis, the standard Gibbs energy of binding, ΔbG![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T), of a given counterion i to the PTA− polyion was directly calculated from the apparent equilibrium constant Ki for binding of counterion i. Following the results of one of our previous studies32 and the present NMR data (see Fig. 2), Ki values (and thus ΔbG
i(T), of a given counterion i to the PTA− polyion was directly calculated from the apparent equilibrium constant Ki for binding of counterion i. Following the results of one of our previous studies32 and the present NMR data (see Fig. 2), Ki values (and thus ΔbG![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T)) were set equal for all three added alkali counterions. A single optimization procedure was then used to determine ΔbH
i(T)) were set equal for all three added alkali counterions. A single optimization procedure was then used to determine ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T), ΔbS
i(T), ΔbS![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i(T), and ΔbC
i(T), and ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) i,p(T) from calorimetric titration curves at all given temperatures (278.15 K, 298.15 K, and 318.15 K) for all alkali counterions simultaneously. Due to the reliability of data, values of Ki were determined from KLi whereas the value of KLi was calculated from fLi at rn = 0. The agreement between experimental and model values of mixing of PTALi with NaCl (Fig. 7) and of mixing of PTALi with CsCl (Fig. 8) is reasonably good. The agreement could be even improved if the assumption of equal constants of binding for all counterions was not made or if the existence of more than one set of independent binding sites50,64 was assumed. Nevertheless, in order to get physically reasonable results which are consistent with our previous observations no such sidesteps from our understanding of the studied system were made.
i,p(T) from calorimetric titration curves at all given temperatures (278.15 K, 298.15 K, and 318.15 K) for all alkali counterions simultaneously. Due to the reliability of data, values of Ki were determined from KLi whereas the value of KLi was calculated from fLi at rn = 0. The agreement between experimental and model values of mixing of PTALi with NaCl (Fig. 7) and of mixing of PTALi with CsCl (Fig. 8) is reasonably good. The agreement could be even improved if the assumption of equal constants of binding for all counterions was not made or if the existence of more than one set of independent binding sites50,64 was assumed. Nevertheless, in order to get physically reasonable results which are consistent with our previous observations no such sidesteps from our understanding of the studied system were made.
 | ||
Fig. 7 Comparison of experimental33 (symbols) differential enthalpies of mixing, ΔdmixH, and results of global fitting (lines) for the titration of 0.005 monomol dm−3 PTALi with 0.15 mol dm−3 NaCl (278.15 K –  , 298.15 K – ■, and 318.15 K – , 298.15 K – ■, and 318.15 K –  ) and for reverse titration (0.005 monomol dm−3 PTANa with 0.15 mol dm−3 LiCl) at 298.15 K (◆). ) and for reverse titration (0.005 monomol dm−3 PTANa with 0.15 mol dm−3 LiCl) at 298.15 K (◆). | ||
 | ||
| Fig. 8 Comparison of experimental33 (symbols) differential enthalpies of mixing, ΔdmixH, and results of global fitting (lines) for the titration of 0.005 monomol dm−3 PTALi with 0.15 mol dm−3 CsCl at 278.15 K, 298.15 K, and 318.15 K (legend as in the previous figure) and for reverse titration (0.005 monomol dm−3 PTACs with 0.15 mol dm−3 LiCl) at 298.15 K (◆). | ||
As a part of the fitting procedure, the fractions of free counterions fi for every ionic species i were calculated from the calorimetric model at each rn. These fractions are shown in Fig. 9 together with the experimentally determined values. It can be seen that experimentally determined and model values of f coincide at rn = 0, which is a direct consequence of the fact that Ki of alkali metal counterions was estimated from fLi in PTALi solution at rn = 0. At higher values of rn, the concordance between measured and modelled f is poorer although it is still reasonably good. As a consequence, the use of Ki at larger rn values underestimates f which consequently leads to the overestimation of θ.
On the other hand, the existence of different kinds of binding sites64 cannot be completely discarded although no such evidence exists. It is quite possible that some counterions are non-specifically bound in the electrostatic atmosphere while the other ones may be bound by site-binding.65 In such a case it cannot be expected that the model which takes into account only one binding mode would successfully describe the observed mixing process.
The thermodynamic parameters, obtained during global fitting of the model function to the experimental data shown in Fig. 7 and 8, are graphically represented in Fig. 10 for T = 298.15 K.
Taking into account coulombic interactions only, the addition of simple salt to PE salt solution should be an endothermic process.63 For the system under study, where the strongly hydrated lithium counterion was present both in the PE and in the added salt solutions, it was observed that the exchanged heat qualitatively agrees with the theoretical prediction assuming only Coulombic interactions.33 The mixing was notably more endothermic than expected when the PE salt included the weakly hydrated caesium counterion and LiCl was added whereas the process was strongly exothermic when lithium PE salt was mixed with CsCl. It is therefore not surprising that thermodynamic analysis gave (at 298.15 K) a slightly positive value for ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) Li while ΔbH
Li while ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) Na and ΔbH
Na and ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) Cs were negative: the latter more than the former. The extent of hydration of alkali ions decreases with increasing crystallographic radius of the ion and accordingly, hydration is becoming less and less exothermic from lithium to caesium.66 Although ΔbH
Cs were negative: the latter more than the former. The extent of hydration of alkali ions decreases with increasing crystallographic radius of the ion and accordingly, hydration is becoming less and less exothermic from lithium to caesium.66 Although ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) is small (in absolute sense) in comparison with ΔbG
is small (in absolute sense) in comparison with ΔbG![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) , values of standard molar enthalpies are measured rather accurately (see error bars in Fig. 10) so that the dependence of ΔbH
, values of standard molar enthalpies are measured rather accurately (see error bars in Fig. 10) so that the dependence of ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) on the kind of counterion can be firmly determined. If we recall Fig. S3 in the ESI,† where the total fraction of occupied binding sites on PTA− (i.e. the total fraction of polyion charge neutralised by bound counterions) is plotted, the mixing seems to be reduced to a process where upon mixing the bound counterion is just replaced by a counterion of the other kind.
on the kind of counterion can be firmly determined. If we recall Fig. S3 in the ESI,† where the total fraction of occupied binding sites on PTA− (i.e. the total fraction of polyion charge neutralised by bound counterions) is plotted, the mixing seems to be reduced to a process where upon mixing the bound counterion is just replaced by a counterion of the other kind.
During the binding of a counterion to a polyion some water molecules are released from the solvation shell of the counterion67,68 (and usually also from the solvation shell of the polyion) to the bulk. The release of water molecules is energetically less favourable for counterions having more negative standard enthalpies of hydration – in our case this would apply to lithium counterions. This is reflected in ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) calculated, where the highest ΔbH
calculated, where the highest ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) was obtained for lithium and the lowest one for caesium.
was obtained for lithium and the lowest one for caesium.
By fixing ΔbG![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) to be equal for all alkali counterions, the dependence of ΔbH
to be equal for all alkali counterions, the dependence of ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) on the kind of counterion also determines such a dependence of ΔbS
on the kind of counterion also determines such a dependence of ΔbS![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) . The increase of ΔbS
. The increase of ΔbS![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) is the highest for strongly hydrated lithium counterions, whereas it is the smallest for caesium counterions. The entropy increase can be explained by the release of water molecules. Namely, one can expect that the ion having more water molecules in its solvation shell will lose more water molecules upon binding than the ion that is poorly hydrated. The release of more water molecules from the solvation shell to bulk water is accompanied by a higher increase of entropy. When values of ΔbH
is the highest for strongly hydrated lithium counterions, whereas it is the smallest for caesium counterions. The entropy increase can be explained by the release of water molecules. Namely, one can expect that the ion having more water molecules in its solvation shell will lose more water molecules upon binding than the ion that is poorly hydrated. The release of more water molecules from the solvation shell to bulk water is accompanied by a higher increase of entropy. When values of ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) and −T·ΔbS
and −T·ΔbS![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) are compared, it is evident that the contribution to ΔbG
are compared, it is evident that the contribution to ΔbG![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) stems almost entirely from the product −T·ΔbS
stems almost entirely from the product −T·ΔbS![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) . Obviously, the increase of entropy is a driving force of the studied process which is an observation, which was in similar cases often quoted also in the literature.50,68,69
. Obviously, the increase of entropy is a driving force of the studied process which is an observation, which was in similar cases often quoted also in the literature.50,68,69
The assumption that the binding of counterions to the polyion is accompanied by the partial dehydration of counterions is also corroborated by changes in ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) p. Fig. 10 shows that changes of ΔbC
p. Fig. 10 shows that changes of ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) p do not show any obvious dependence on the counterion size. However, the changes in ΔbC
p do not show any obvious dependence on the counterion size. However, the changes in ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) p upon counterion binding are positive for all the counterions studied. The increase of ΔbC
p upon counterion binding are positive for all the counterions studied. The increase of ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) p may be in our case explained by the increased fluctuations of the enthalpy of the system.70 Namely, the gap between different energy levels accessible to water molecules being part of the ionic hydration shell is large and thus the fluctuations in enthalpy are relatively small. When a water molecule is released into the bulk phase, the differences between enthalpic levels accessible to the water molecule become smaller. Consequently, the fluctuations in enthalpy are increased, which leads to an increased value of ΔbC
p may be in our case explained by the increased fluctuations of the enthalpy of the system.70 Namely, the gap between different energy levels accessible to water molecules being part of the ionic hydration shell is large and thus the fluctuations in enthalpy are relatively small. When a water molecule is released into the bulk phase, the differences between enthalpic levels accessible to the water molecule become smaller. Consequently, the fluctuations in enthalpy are increased, which leads to an increased value of ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) p.
p.
The positive values of ΔbC![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) p therefore confirm our premise that some water molecules are released upon counterion binding. These results are in good agreement with similar treatment of calorimetric data for some other polyelectrolytes.50,51
p therefore confirm our premise that some water molecules are released upon counterion binding. These results are in good agreement with similar treatment of calorimetric data for some other polyelectrolytes.50,51
A similar analysis of titration curves as performed for mixing PTALi with alkali chlorides was tried to be carried out also for mixing PTALi with tetraalkylammonium chlorides. Considering the different nature of tetraalkylammonium ions, in addition to a fit with one set of binding sites we also tried a fit with two sets of binding sites but in both cases analysis failed to give any reasonable result. This was yet another indication that in the case of tetraalkylammonium counterions besides electrostatics other interactions are at play and that a more elaborate model should be used for obtaining standard thermodynamic parameters.
5 Conclusions
The binding of counterions to the conjugated polyion, observed during the mixing aqueous solution of lithium salt of poly(thiophen-3-ylacetic acid) (PTALi) with alkali metal chlorides at 25 °C, can be satisfactorily described by electrostatic theories. While none of the alkali metal counterions seems to bind preferentially, the mixing of tetraalkylammonium (TAA+) chlorides with PTALi showed that TAA+ cations with longer alkyl chains bind to the polyion more extensively than predicted by electrostatics. The fraction of bound counterions increases in the order from the tetramethylammonium to tetrabutylammonium counterion and is in the case of tetrapropylammonium and tetrabutylammonium ions accompanied by the blue shift in the UV/vis absorption spectrum. The increase of the diffusion coefficient Dp of the polyion was observed in all cases when alkali metal or tetraalkylammonium chlorides were added to PTALi but the increase of Dp was again more pronounced when tetrapropylammonium and tetrabutylammonium chloride solutions were added, suggesting that the addition of these counterions promotes further transition of PTA− polyions to more compact conformation.Thermodynamic analysis of calorimetric data obtained upon mixing PTALi solution with solutions of alkali metal chlorides confirmed our assumption that observed differences in heats of mixing are a consequence of different strengths and extents of hydration of these cations. The calculated standard enthalpies of binding of alkali metal counterions clearly indicate that dehydration of these counterions (release of water molecules from the counterion hydration shell into the bulk water) takes place upon binding. Namely, while ΔbH![[circle, cut, short horiz bar]](https://www.rsc.org/images/entities/char_e0eb.gif) is positive for Li+, the same quantity is increasingly negative from Na+ to Cs+ which is in concordance with the finding that the hydrogen bond in the first hydration shell of Li+ is stronger than the one in the bulk water and, vice versa, hydrogen bonds in hydration shells of Na+ and (especially) Cs+ are weaker than those in the bulk water.71,72 On the other side, the thermodynamic model, despite including an additional kind of binding site, completely failed in describing mixing of PTALi with tetraalkylammonium chloride solutions. This is yet another evidence that the nature of binding of tetraalkylammonium counterions to the PTA− polyion is different from the one observed for alkali counterions and that it may include additional interactions, which are most probably of hydrophobic nature. Further theoretical studies based on molecular dynamics and experiments exploiting the nuclear Overhauser effect between the ions and the polyelectrolyte might be of help in resolving different modes of binding of both kinds of counterions to PTA−.
is positive for Li+, the same quantity is increasingly negative from Na+ to Cs+ which is in concordance with the finding that the hydrogen bond in the first hydration shell of Li+ is stronger than the one in the bulk water and, vice versa, hydrogen bonds in hydration shells of Na+ and (especially) Cs+ are weaker than those in the bulk water.71,72 On the other side, the thermodynamic model, despite including an additional kind of binding site, completely failed in describing mixing of PTALi with tetraalkylammonium chloride solutions. This is yet another evidence that the nature of binding of tetraalkylammonium counterions to the PTA− polyion is different from the one observed for alkali counterions and that it may include additional interactions, which are most probably of hydrophobic nature. Further theoretical studies based on molecular dynamics and experiments exploiting the nuclear Overhauser effect between the ions and the polyelectrolyte might be of help in resolving different modes of binding of both kinds of counterions to PTA−.
Acknowledgements
This study was supported by the Slovenian Research Agency fund (ARRS) through the Program 0103-0201. The use of instruments at the NMR Spectroscopy Unit of the Research Infrastructure Centre UL FCCT while performing preliminary measurements is acknowledged. G. H. was supported by the National Grant for young researchers and by Slovene human resources development and scholarship fund. Prof. Dr Vojko Vlachy (University of Ljubljana) is acknowledged for valuable discussion through this work. The authors also thank Isabelle Correia (Laboratoire des Biomolécules) and Francois Ribot (Laboratoire de la Chimie de la Matière Condensée de Paris) for the access to the 500 MHz and the 300 MHz NMR spectrometers and fruitful discussions.References
- Y.-J. Cheng, S.-H. Yang and C.-S. Hsu, Chem. Rev., 2009, 109, 5868–5923 CrossRef CAS.
- Z. He, C. Zhong, X. Huang, W.-Y. Wong, H. Wu, L. Chen, S. Su and Y. Cao, Adv. Mater., 2011, 23, 4636–4643 CrossRef CAS.
- Y.-M. Chang, R. Zhu, E. Richard, C.-C. Chen, G. Li and Y. Yang, Adv. Funct. Mater., 2012, 22, 3284–3289 CrossRef CAS.
- H.-J. Wang, C.-P. Chen and R.-J. Jeng, Materials, 2014, 7, 2411–2439 CrossRef CAS.
- J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. Mackay, R. H. Friend, P. L. Burn and A. B. Holmes, Nature, 1990, 347, 539–541 CrossRef CAS.
- V. Cimrová, W. Schmidt, R. Rulkens, M. Schulze, W. Meyer and D. Neher, Adv. Mater., 1996, 8, 585–588 CrossRef.
- A. F. Thünemann and D. Ruppelt, Langmuir, 2001, 17, 5098–5102 CrossRef.
- F. Huang, H. Wu, D. Wang, W. Yang and Y. Cao, Chem. Mater., 2004, 16, 708–716 CrossRef CAS.
- Z. Gu, Y.-J. Bao, Y. Zhang, M. Wang and Q.-D. Shen, Macromolecules, 2006, 39, 3125–3131 CrossRef CAS.
- P. Bäuerle and S. Scheib, Adv. Mater., 1993, 5, 848–853 CrossRef.
- I. Levesque and M. Leclerc, Chem. Commun., 1995, 2293–2294 RSC.
- R. D. McCullough and S. P. Williams, Chem. Mater., 1995, 7, 2001–2003 CrossRef CAS.
- M. J. Marsella and T. M. Swager, J. Am. Chem. Soc., 1993, 115, 12214–12215 CrossRef CAS.
- A. Boldea, I. Levesque and M. Leclerc, J. Mater. Chem., 1999, 9, 2133–2138 RSC.
- S. Bernier, S. Garreau, M. Béra-Abérem, C. Gravel and M. Leclerc, J. Am. Chem. Soc., 2002, 124, 12463–12468 CrossRef CAS PubMed.
- I.-B. Kim, A. Dunkhorst, J. Gilbert and U. H. F. Bunz, Macromolecules, 2005, 38, 4560–4562 CrossRef CAS.
- Z. Zhang, Q. Fan, P. Sun, L. Liu, X. Lu, B. Li, Y. Quan and W. Huang, Macromol. Rapid Commun., 2010, 31, 2160–2165 CrossRef CAS PubMed.
- L. Chen, D. W. McBranch, H.-L. Wang, R. Helgeson, F. Wudl and D. G. Whitten, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 12287–12292 CrossRef CAS.
- A. Satrijo and T. M. Swager, J. Am. Chem. Soc., 2007, 129, 16020–16028 CrossRef CAS PubMed.
- F. Chu, G. Tsiminis, N. A. Spooner and T. M. Monro, Sens. Actuators, B, 2014, 199, 22–26 CrossRef CAS.
- H.-A. Ho, M. Béra-Abérem and M. Leclerc, Chem. – Eur. J., 2005, 11, 1718–1724 CrossRef CAS PubMed.
- A. V. Ambade, B. S. Sandanaraj, A. Klaikherd and S. Thayumanavan, Polym. Int., 2007, 56, 474–481 CrossRef CAS.
- M. Béra-Abérem, H.-A. Ho and M. Leclerc, Tetrahedron, 2004, 60, 11169–11173 CrossRef.
- X. Liu, Q. Fan and W. Huang, Biosens. Bioelectron., 2011, 26, 2154–2164 CrossRef CAS PubMed.
- R. Yang, H. Wu, Y. Cao and G. C. Bazan, J. Am. Chem. Soc., 2006, 128, 14422–14423 CrossRef CAS PubMed.
- D. K. Kim, S. W. Han, C. H. Kim, J. D. Hong and K. Kim, Thin Solid Films, 1999, 350, 153–160 CrossRef CAS.
- O. Mermut, J. Lefebvre, D. G. Gray and C. J. Barrett, Macromolecules, 2003, 36, 8819–8824 CrossRef CAS.
- R. D. McCullough, P. C. Ewbank and R. S. Loewe, J. Am. Chem. Soc., 1997, 119, 633–634 CrossRef CAS.
- B.-S. Kim, L. Chen, J. P. Gong and Y. Osada, Macromolecules, 1999, 32, 3964–3969 CrossRef CAS.
- P. Vallat, J.-M. Catala, M. Rawiso and F. Schosseler, Macromolecules, 2007, 40, 3779–3783 CrossRef CAS.
- I. E. Franco, P. Lorchat, J.-P. Lamps, M. Schmutz, A. Schröder, J.-M. Catala, J. Combet and F. Schosseler, Langmuir, 2012, 28, 4815–4828 CrossRef CAS.
- G. Hostnik, D. Bondarev, J. Vohlídal, S. Čebašek, E. Žagar, V. Vlachy and J. Cerar, J. Mol. Liq., 2014, 198, 173–180 CrossRef CAS.
- G. Hostnik, V. Vlachy, D. Bondarev, J. Vohlídal and J. Cerar, Phys. Chem. Chem. Phys., 2015, 17, 2475–2483 RSC.
- K. Collins, Biophys. J., 1997, 72, 65–76 CrossRef CAS.
- I. Furó, J. Mol. Liq., 2005, 117, 111–137 CrossRef.
- S. Dengler, A. Klaus, G. J. T. Tiddy and W. Kunz, Faraday Discuss., 2013, 160, 121–133 RSC.
- S. Dengler, G. J. T. Tiddy, L. Zahnweh and W. Kunz, Colloids Surf., A, 2014, 457, 414–418 CrossRef CAS.
- P. Stilbs and B. Lindman, J. Magn. Reson., 1982, 48, 132–137 CAS.
- R. Rymdén and P. Stilbs, J. Phys. Chem., 1985, 89, 2425–2428 CrossRef.
- G. Hostnik, V. Vlachy, D. Bondarev, J. Vohlídal and J. Cerar, Acta Chim. Slov., 2012, 59, 571–581 CAS.
- G. Hostnik, V. Vlachy, D. Bondarev, J. Vohlídal and J. Cerar, Acta Chim. Slov., 2012, 59, 582–589 CAS.
- A. Krȩżel and W. Bal, J. Inorg. Biochem., 2004, 98, 161–166 CrossRef.
- C. S. Johnson, Jr., Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 203–256 CrossRef.
- D. Wu, A. Chen and C. Johnson, J. Magn. Reson., 1995, 115, 260–264 CrossRef CAS.
- P. T. Callaghan and D. N. Pinder, Macromolecules, 1983, 16, 968–973 CrossRef CAS.
- P. T. Callaghan and J. Lelievre, Biopolymers, 1985, 24, 441–460 CrossRef CAS.
- A. Katchalsky, Pure Appl. Chem., 1971, 26, 327–374 CrossRef CAS.
- D. Dolar, in Polyelectrolytes, ed. E. Sélégny, M. Mandel, U. P. Strauss and D. Reidel, Dordrecht, Netherlands, 1st edn, 1974, vol. 1, pp. 97–113 Search PubMed.
- J. Piñero, L. B. Bhuiyan, J. Reščič and V. Vlachy, Acta Chim. Slov., 2008, 55, 521–527 Search PubMed.
- M. Bončina, J. Lah, J. Reščič and V. Vlachy, J. Phys. Chem. B, 2010, 114, 4313–4319 CrossRef.
- M. Bončina, M. Lukšič, M. Seručnik and V. Vlachy, Mol. Phys., 2014, 112, 1222–1229 CrossRef.
- J. Lah, N. M. Maier, W. Lindner and G. Vesnaver, J. Phys. Chem. B, 2001, 105, 1670–1678 CrossRef CAS.
- J. Lah, I. Drobnak, M. Dolinar and G. Vesnaver, Nucleic Acids Res., 2008, 36, 897–904 CrossRef CAS.
- K. D. Collins, Methods, 2004, 34, 300–311 CrossRef CAS.
- N. Vlachy, B. Jagoda-Cwiklik, R. Vácha, D. Touraud, P. Jungwirth and W. Kunz, Adv. Colloid Interface Sci., 2009, 146, 42–47 CrossRef CAS.
- F. J. M. Schipper, K. Kassapidou and J. C. Leyte, J. Phys.: Condens. Matter, 1996, 8, 9301 CrossRef CAS.
- S. Förster, M. Schmidt and M. Antonietti, Polymer, 1990, 31, 781–792 CrossRef.
- L. Wang, M. M. Garner and H. Yu, Macromolecules, 1991, 24, 2368–2376 CrossRef CAS.
- P. Vallat, J. M. Catala, M. Rawiso and F. Schosseler, Europhys. Lett., 2008, 82, 28009 CrossRef.
- K. Faïd, M. Frechette, M. Ranger, L. Mazerolle, I. Levesque, M. Leclerc, T.-A. Chen and R. D. Rieke, Chem. Mater., 1995, 7, 1390–1396 CrossRef.
- J. L. Brédas, G. B. Street, B. Thémans and J. M. André, J. Chem. Phys., 1985, 83, 1323–1329 CrossRef.
- M. Bernardi, M. Giulianini and J. C. Grossman, ACS Nano, 2010, 4, 6599–6606 CrossRef CAS.
- G. E. Boyd, D. P. Wilson and G. S. Manning, J. Phys. Chem., 1976, 80, 808–810 CrossRef CAS.
- G. Scatchard, J. S. Coleman and A. L. Shen, J. Am. Chem. Soc., 1957, 79, 12–20 CrossRef CAS.
- I. Rouzina and V. A. Bloomfield, Biophys. Chem., 1997, 64, 139–155 CrossRef CAS.
- Y. Marcus, J. Chem. Soc., Faraday Trans., 1987, 83, 339–349 RSC.
- M. Satoh and J. Komiyama, Polymeric Materials Encyclopedia, CRC Press, Inc., Boca Raton, Florida, 1st edn, 1996, vol. 8, pp. 5807–5816 Search PubMed.
- C. G. Sinn, R. Dimova and M. Antonietti, Macromolecules, 2004, 37, 3444–3450 CrossRef CAS.
- I. Pochard, A. Foissy and P. Couchot, Colloid Polym. Sci., 1999, 277, 818–826 CAS.
- K. A. Sharp and B. Madan, J. Phys. Chem. B, 1997, 101, 4343–4348 CrossRef CAS.
- J. Stangret and T. Gampe, J. Phys. Chem. A, 2002, 106, 5393–5402 CrossRef CAS.
- J. Mähler and I. Persson, Inorg. Chem., 2012, 51, 425–438 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04193k |
| This journal is © the Owner Societies 2016 |



















