Theoretical and experimental investigation on structural, electronic and magnetic properties of layered Mn₅O₈

Abstract

We have investigated the crystal, electronic, and magnetic structures of Mn₅O₈ by means of state-of-the-art density functional theory calculations and neutron powder diffraction (NPD) measurements. This compound stabilizes in the monoclinic structure with space group C2/m where the Mn ions are in the distorted octahedral and trigonal prismatic coordinations with oxygen atoms. The calculated structural parameters based on total energy calculations are found to be in excellent agreement with low temperature NPD measurements when we accounted for the correct magnetic structure and Coulomb correlation effect in the computation. Using fully relativistic generalized-gradient approximation with Hubbard U (GGA+U) we found that the magnetic ordering in Mn₅O₈ is A-type antiferromagnetic and the direction of the easy axis is [1 0 0] in agreement with susceptibility and NPD measurements. However, the calculation without the inclusion of Hubbard U leads to ferrimagnetic half metal as a ground state contradictory to experimental findings, indicating the presence of a strong Coulomb correlation effect in this material. The GGA calculation without the Coulomb correction effect itself is sufficient to reproduce the experimentally observed magnetic moments in various Mn sites. We found that Mn in this material exhibits mixed valence behavior with 2+ and 4+ oxidation states reflecting different magnetic moments in the Mn sites. We explored the electronic band characteristics using total, site-, and orbital-projected density of states which emphasized the mixed-valent nature of Mn. A dominant Mn 3d character of the density of states at Fermi energy is the origin for the metallic behavior of Mn₅O₈. The bond strength analysis based on the crystal orbital Hamiltonian population between constituents indicates strong anisotropy in the bonding behavior which results from the layered nature of its crystal structure. Our bonding analysis shows that there is a noticeable covalent bond between Mn 3d–O 2p states which stabilizes the observed low symmetric structure. Our experimental findings and theoretical predictions suggest that Mn₅O₈ can be classified as a strongly correlated mixed valent antiferromagnetic metal.

---

1 Introduction

Manganese (Mn) oxides can be considered as an interesting class of materials among various transition metal oxides because they crystallize in different structures with many oxidation states (2+, 3+, and 4+ etc.)^1–4 that exhibit exotic magnetic behaviors. Among them, Mn²⁺ has basically no preference on coordination due to the 3d⁵ electronic configuration and it occupies almost indifferently crystallographic sites with coordination numbers of 4, 6, and/or 8, depending on other structural constraints. On the other hand, Mn³⁺ and Mn⁴⁺ are commonly found in octahedral sites in complex oxides. Also, the Mn³⁺ (t_2g³e_g¹) ion in LaMnO₃⁵ makes it a typical Jahn–Teller system which results in a distortion of the MnO₆ octahedron with four shorter equatorial bonds and two longer axial bonds. In terms of ionic radius, the difference in the ionic radii between Mn²⁺ and Mn³⁺ [0.185 Å (=0.83–0.645 Å)] is larger than that between Mn³⁺ and Mn⁴⁺ [0.115 Å (=0.645–0.53 Å, based on r(O²⁻) = 1.40 Å)].⁶ Namely, the divalent Mn ion has somehow a unique feature in the oxide form, and this has important consequences on the crystal chemistry and physical properties. Binary manganese oxides such as MnO, Mn₃O₄, Mn₂O₃, MnO₂, and Mn₅O₈ possess a wide variety of technological applications due to their unique structural and physical properties. Owing to the presence of mixed valences of Mn atoms, this family of compounds is a quite attractive and potential candidate for catalysis, electrode materials for batteries and soft magnetic materials for transformer cores.^7,8 Due to the complex interplay between orbital, spin, and lattice degrees of freedom, Mn oxides exhibit intriguing properties such as colossal magnetoresistance, metal–insulator transitions, charge as well as orbital ordering,^9,10 and complex magnetic behavior.^4,11–14 For example, MnO is a type-II antiferromagnetic (AFM-II) insulator below the Néel temperature of T_N = 118 K,¹⁵ Mn₃O₄ shows a ferrimagnetic (FiM) behavior at T_C = 42 K, upon further cooling it exhibits a spiral spin structure at 39 K and then it transforms into a canted spin array at 33 K.^16–18 α-Mn₂O₃ exhibits a complex noncollinear AFM ordering and β-MnO₂ has a screw-type magnetic structure with ordered helical moments.^19,20 Among the stable binary Mn oxides, Mn₅O₈ has been reported in the literature as a metastable phase.^21–23

It is reported that the crystal structure of Mn₅O₈ is also isostructural with Ca₂Mn₃O₈²⁴ and Cu₂Mn₃O₈.²⁵ Yamamoto et al.²⁶ reported that Mn₅O₈ orders antiferromagnetically at Néel temperature T_N ≃ 136 K, which was the highest among most of the known manganese oxides. Mn₅O₈ has higher magnetic transition temperature than its isomorphous compounds such as Cd₂Mn₃O₈ (T_N ≃ 10 K) and Ca₂Mn₃O₈ (T_N ≃ 60 K) due to the fact that both the interlayer and intralayer distances between magnetic ions in Cd₂Mn₃O₈ and Ca₂Mn₃O₈ are larger than those in Mn₅O₈ and this will reduce the corresponding exchange integrals in Cd₂Mn₃O₈ and Ca₂Mn₃O₈, resulting in lower values of Θ and magnetic ordering temperature. In other words, the substitution of nonmagnetic Cd²⁺ and Ca²⁺ ions for the magnetic Mn²⁺ ions weakens the magnetic exchange interactions, which leads to a decrease in the magnetic ordering temperature.

Several other experimental studies also reported that Mn₅O₈ is an antiferromagnet with Néel temperature T_N ≃ 128 K,²⁷T_N ≃ 133 K,²⁸T_N ≃ 131 K,²⁹ and T_N ≃ 126 K.³⁰ A noticeable difference in the reported Néel temperature is due to the finite-size effect on the antiferromagnetic transition temperature T_N.^31,32 In addition to the characteristic antiferromagnetic ordering peak of Mn₅O₈, a sharp peak is observed at around 40 K^27,28 by magnetization measurements which is believed to be associated with T_C of ferrimagnetic Mn₃O₄ because Mn₅O₈ is synthesized by the oxidation of Mn₃O₄. However, our low temperature Neutron Powder Diffraction (NPD) measurements were unable to detect any secondary phases and the details will be discussed below.

X-ray photoemission spectroscopy (XPS) measurements on Mn₅O₈ have been made and the analysis^28,30 confirms the two possible types of Mn with oxidation states 4+ and 2+. It may be noted that it is difficult to distinguish between Mn²⁺ and Mn⁴⁺ due to the small binding energy shift (less than ca. 1.0 eV) and it will be even more complicated if the Mn is present in mixed valence states.³³ Jeong et al.³⁴ reported that the Mn³⁺ ions are involved in the oxygen evolution reaction process of Mn₅O₈ nanoparticles, which is contradictory to the XPS analysis mentioned above. Therefore, apart from calculating the Bond Valence Sum (BVS), we have used various theoretical tools to analyze the oxidation of manganese ions in Mn₅O₈ as we have reported earlier.³⁵

The details of magnetic ordering, the direction of easy axis, and anisotropy in the magnetic and transport properties for Mn₅O₈ are not yet identified though nanorods of Mn₅O₈ have been reported recently.²⁸ To our knowledge, no theoretical study on Mn₅O₈ has been reported in the literature. In the present study, we attempt to identify the ground state magnetic structure, electronic structure, and the mixed valent behavior of manganese ions in Mn₅O₈ using experimental measurements and computational studies.

2 Methods

2.1 Experimental details

A polycrystalline sample of Mn₅O₈ was synthesized by a wet chemical reaction route.³⁶ Prior to NPD measurements, the synthesized sample was characterized by X-ray diffraction and found not to contain detectable impurities. NPD data at 298 K, 70 K, and 9 K were collected with the PUS two-axis diffractometer at the JEEP II reactor, Kjeller, Norway.³⁷ The powder sample was kept in cylindrical sample holders. Monochromatized neutrons of wavelength 1.5556 Å were obtained by reflection from Ge(311). NPD data were measured in the 10.00° ≤ 2θ ≤ 129.95° range with a scan-step of 0.05°. The simulation and Rietveld methods³⁸ were performed with the Fullprof code.³⁹ NPD data and reflections from the Displex cryostat at 46.00° ≤ 2θ ≤ 46.90°, 76.90° ≤ 2θ ≤ 77.60°, and 115.90° ≤ 2θ ≤ 117.20° in all collected NPD data were excluded prior to the refinements. Scale factor, zero point, pseudo-Voigt profile parameters, unit-cell dimensions, positional parameters, together with four isotropic displacement factors, and the magnetic moments of manganese, were entered into the final least-squares refinement.

2.2 Computational details for the full-potential linear augmented plane-wave (FP-LAPW) calculations

Calculations were performed using the standard full-potential linear augmented plane-wave method based on density functional theory (DFT) as implemented in the Wien2k code.⁴⁰ We have used the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof for the exchange–correlation functional.⁴¹ The muffin tin sphere radii (R_MT) values for Mn and O atom were taken to be 1.87 and 1.61 a.u, respectively. The plane wave cut-off parameters were decided by R^min_MTK_max = 7 (the product of the smallest of the atomic sphere radii R_MT and the plane wave cut-off parameter K_max) and 400 k-points were used over the irreducible part of the first Brillouin zone (IBZ). We have also included both Mott–Hubbard parameter U, and spin–orbit coupling (SO) in the calculations to account for the correlation effect (GGA+U) and the relativistic effect (GGA+SO) respectively. The value of U_eff = U − J (U and J are on-site Coulomb and exchange interaction, respectively) chosen for this calculation is 5 eV which is normally used for manganese oxides to account for Coulomb correlation effects. There are many different implementations to calculate the U value precisely.^42–46 Though U is a computational parameter, the calculated magnetic moments, magnetic ground state, etc., for the chosen U value are in good agreement with the experimental results indicating that the value of the currently used U parameter is justified.

2.3 Computational details for Vienna ab initio simulation package (VASP) calculations

Structural optimizations were done using VASP code⁴⁷ within the projector augmented wave (PAW) method. The generalized gradient approximation proposed by Perdew, Burke and Ernzrhof (GGA-PBE)⁴¹ was used for the exchange and correlation functional. As we have found earlier that a sufficiently large basis set with a reasonable number of k-points is needed to predict reliable structural parameters for transition metal oxides,⁴⁸ we have used the energy cut off of 875 eV and the k-points value is 2 × 4 × 4 for the irreducible part of the first Brillouin zone of base centered monoclinic lattice. The force minimization steps were continued until the maximum Hellmann–Feynman forces acting on each atom was less than 0.01 eV Å⁻¹. Also, the pressure in the unit cell was kept below 1 kbar.

3 Results and discussion

3.1 Crystal structure

Mn₅O₈ possess a layered Birnessite-type structure.⁴⁹ The crystal structure reported by Oswald et al.⁵⁰ for Mn₅O₈ having the compositional formula Mn₂²⁺Mn₃⁴⁺O₈ is isotypic with base-centered monoclinic Cd₂Mn₃O₈ with space group C2/m. This structure can be considered as a layered structure with two formula units per unit cell as indicated in Fig. 1. The overall crystal structure of Mn₅O₈ can be described as infinite sheets of [Mn₃⁴⁺O₈]⁴⁻ where the Mn⁴⁺ ions are held together by Mn²⁺ ions. This structure consists of distorted MnO₆ (Mn1O^o₆ and Mn2O^o₆) edge shared octahedral layers with Mn⁴⁺ ions in the bc plane separated by Mn²⁺ ions as shown in Fig. 1. One fourth of the cationic sites in the main octahedra sheets are vacancies which result in charge imbalance and consequently its composition becomes [Mn₃⁴⁺O₈]⁴⁻. This charge imbalance was neutralized by the Mn²⁺ ions situated above and below the empty Mn⁴⁺ sites completing the composition Mn₂²⁺Mn₃⁴⁺O₈.

Fig. 1 (a) Polyhedral representation of Mn₅O₈ crystal structure, (b) octahedral coordination of Mn⁴⁺ atoms, and (c) trigonal prismatic coordination of Mn²⁺ atoms. The atom labels are given in (a).

Also, the oxygen ions are located in three different sites in Mn₅O₈. One of the Mn⁴⁺(Mn1^o) ions is in the 2c site (C_2h symmetry) coordinated octahedrally to four equatorial O atoms at 1.921 Å and two apical O atoms at 1.937 Å where the average Mn–O distance is 1.926 Å. The O–Mn–O angles within this Mn1O^o₆ octahedron vary between 85° and 95° when O atoms are cis-arranged and 180° when O atoms are trans-arranged. Two Mn⁴⁺ (Mn2^o) atoms are in 4g sites (C₂ symmetry) coordinated by highly distorted octahedra of O atoms with two Mn–O distances at 1.867 Å and two at 1.913 Å and two at 1.971 Å with an average Mn–O distance of 1.917 Å. The O–Mn–O angles within this Mn2O^o₆ distorted octahedron vary between 81.9° and 96.4° when the O atoms are cis-arranged and between 168.7° and 177.6° when the O atoms are trans-arranged. Mn²⁺ ions (Mn3^t) form a trigonal-prismatic coordination with six oxygen atoms, out of which three are from one octahedral layer and three are from the next octahedral layer. As shown in Fig. 1, O(1) is coordinated by two Mn⁴⁺ and two Mn²⁺ ions, O(2) is coordinated by three Mn⁴⁺ and one Mn²⁺ ions, and O(3) is coordinated by two Mn⁴⁺ and one Mn²⁺ ion. Due to this difference in coordination of Mn with O atoms, different magnetic moments in various manganese sites arise.

3.2 Magnetic structure

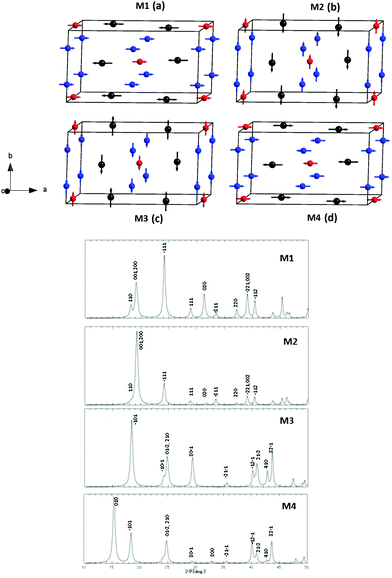
Before discussing the magnetic structure of Mn₅O₈, the NPD data at 298 K based on the result of Rietveld analysis as shown in Fig. 2 is described. Careful indexing of all observed peaks in the collected data confirms the previously proposed systematic extinction scheme,⁵¹ corresponding to the space group of C2/m (No. 12) (a = 10.372 Å, b = 5.733 Å, c = 4.860 Å, and β = 109.4°). The present NPD pattern at 9 K shows extra intensity compared to that at 298 K, which can be expected from the magnetic reflection arising from magnetic ordering occurring around T_N = 136 K as shown in Fig. 3. In order to get more clarity on the magnetic reflections, in Fig. 3 we have also plotted the differential intensity between 298 K and 9 K [I(9 K)–I(298 K)]. We have assumed four possible AFM models in the 1 × 1 × 1 crystal structural dimension, which are shown in Fig. 4 together with the corresponding simulated scattering patterns. It may be noted that we have used the ratio of the magnetic moments for octahedral Mn⁴⁺ and trigonal prismatic Mn²⁺ of 2 : 1 for the present NPD pattern simulation. For these simulations we have also used the peak profile function yielded by Rietveld analysis at 298 K.

Fig. 2 Experimental, calculated, and difference NPD patterns of Mn₅O₈ at 298 K. Bars denote Bragg positions; space group C2/m, λ = 1.5556 Å.

Fig. 3 Experimental NPD data at 298 K and 9 K, and the corresponding differential curve.

Fig. 4 The proposed magnetic structures M1, M2, M3, and M4 based on experimental measurements are shown as (a), (b), (c), and (d), respectively. The manganese ions with different spin moments are denoted as Mn1(red), Mn2(blue), and Mn3(grey) in these figures. The corresponding simulated Neutron Powder Diffraction patterns for Mn₅O₈ in these four magnetic models are given in the lower panel.

As seen in Fig. 3, there is a magnetic contribution outside of the Bragg positions, e.g. (0 1 0) and (−1 0 1) arising from the chemical unit cell with the space group C2/m in the NPD pattern taken at 9 K. It is worth noting that there are no magnetic super reflections at (hkl) with non-integer value of h, k, and/or l, and hence one can rule out the possibility of forming complicated modulated magnetic ordering in Mn₅O₈. We have found that the magnetic model associated with M4 alone is compatible with the measured low temperature diffraction data with observed magnetic reflections. In this model, the magnetic moments at the Mn1, Mn2, and Mn3 (and symmetry related positions) sites exist only in the ac plane, and hence no magnetic component was found along the b-axis. The components of magnetic moment along a- and c-axes, i.e. m_x and m_z, were refined using Rietveld refinement for Fig. 5 and those for Mn1, Mn2, and Mn3 sites are found to be 2.4 μ_B, 2.4 μ_B, and 3.8 μ_B, respectively. The refined magnetic moment data are tabulated in Table 1 for the 9 K NPD pattern.

Table 1 The refined unit cell dimensions, atomic coordinates, and magnetic moments at various Mn sites for Mn₅O₈, derived from Rietveld refinement of NPD data 9 K well below the magnetic transition temperature are listed in this table. The crystal structure is found to be base centered monoclinic with space group C2/m. The calculated standard deviations are given in parentheses. a = 10.325(2) Å, b = 5.7181(7) Å, c = 4.8594(6) Å, β = 109.63(2)° R_wp = 4.86%, R_P = 3.67%, χ² = 2.08

Atom							Moment^a
	Wyckoff position	x	y	z	Occupancy	B iso (Å^2)	M x (μB)	M y (μB)	M z (μB)	M tot (μB)
a Magnetic moments were constrained at same values for Mn1 and Mn2. b Isotropic atomic displacement parameters were constrained at same values for respectively, Mn and O.
Mn1	2c (0 0 1/2)	0	0	1/2	1	0.2(2)	2.3(2)	0	1.8(2)	2.4(2)
Mn2	4g (0 y 0)	0	0.247(4)	0	1	0.2(2)	2.3(2)	0	1.8(2)	2.4(2)
Mn3	4i (x 0 z)	0.729(2)	0	0.665(5)	1	0.2(2)	4.02(9)	0	1.7(3)	3.8(2)
O1	8j (x y z)	0.114(2)	0.222(2)	0.395(2)	1	1.7(2)
O2	4i (x 0 z)	0.114(2)	0	0.922(5)	1	1.7(2)
O3	4i (x 0 z)	0.591(2)	0	0.872(4)	1	1.7(2)

---

Fig. 5 Experimental, calculated, and difference NPD patterns of Mn₅O₈ at 9 K. Upper and lower bars denote Bragg positions of nuclei and magnetic reflections, respectively. Space group C2/m, λ = 1.5556 Å.

Based on our experimental results we have proposed four different magnetic structure models for Mn₅O₈ namely M1, M2, M3, and M4 (see Fig. 4). So, in order to identify the ground state among these proposed four magnetic structures we have done ab initio total energy calculation for all these four models by including spin–orbit coupling as well as Coulomb correlation effects. Obviously, models M1 and M2 are similar in that Mn1 and Mn2 atoms are arranged FM in the layer, but coupled AFM to the moments in the Mn3 layer, with moments aligned either perpendicular (M1) or parallel (M2) to the layers. These models give the overall ferrimagnetic structure. Models M3 and M4 are similar in the alignment of moments to models M2 and M1, respectively, but the orientation of the moments alternates as one goes from one Mn1/Mn2 layer to the next, and the moments in the Mn3 layer are coupled AFM, thus giving the overall AFM structure.

3.3 Electronic and magnetic properties

The input structural parameters used for the present calculations are taken from our NPD results obtained at 9 K (see Table 1). In order to identify the equilibrium structural parameters, we have performed the total energy calculation for Mn₅O₈ as a function of volume for the fully relaxed M4 structure as shown in Fig. 6. As the convergence is very slow due to the large number of atoms involved with spin polarization, spin orbit coupling, and Coulomb correlation effects included in the calculations, we have not done structural optimization for all the magnetic configurations discussed here, except for the ground state magnetic structure M4. Using a force minimization method in the Wien2k code, the atom positions are optimized. Moreover, in order to find the ground state with global minima we have adopted force as well as stress minimization methods implemented in VASP code for the ground state magnetic configuration and the optimized structural parameters are compared with our NPD measurements. The calculated equilibrium structural parameters for Mn₅O₈ using VASP and Wien2k codes are compared with our low temperature NPD data in Table 3. The equilibrium volume obtained from Fig. 6 using the Birch–Murnaghan equation of states (EOS) is overestimated by only 1.1% compared with the experimental values and hence the calculated lattice parameters are in good agreement with the corresponding experimental values. From the EOS fit we have calculated the bulk modulus and its pressure derivative for Mn₅O₈, which are given in Table 3. Haines et al.⁵² reported that the bulk modulus and its pressure derivative for β-MnO₂ are 3.28 Mbar and 4, respectively. The experimentally measured bulk modulus and its pressure derivative for MnO are 1.70 MBar and 4.8, respectively.⁵³ Using a linear muffin-tin orbital atomic sphere approximation (LMTO-ASA) approach, Cohen et al.⁵⁴ calculated the bulk modulus and its pressure derivative of MnO as 1.96 Mbar and 3.9, respectively. Our calculated bulk modulus for Mn₅O₈ is smaller than MnO and β-MnO₂. Hence, experimental high pressure studies are needed to confirm our predictions.

Fig. 6 Calculated total energy versus cell volume for Mn₅O₈ in the ground state M4 configuration.

Table 2 Calculated orbital magnetic moment (μ_B) at various Mn sites for Mn₅O₈ without (SO) and with orbital-polarization corrections (SO + OP)

	Orbital moment (Mn1/Mn2/Mn3)
M4 (SO)	−0.018/−0.023/0.006
M4 (SO + OP)	−0.022/−0.030/0.007

---

Table 3 Optimized structural parameters (a, b, c in Å, β in deg, equilibrium volume V₀ in ų), and bulk modulus (B₀ in Mbar) and its pressure derivative (B₀′) for Mn₅O₈ in ground state M4 configuration from VASP and Wien2k^a calculations. Values given in parenthesis refer to the low temperature NPD measurements. The space group is C2/m and Z = 2

Unit cell	Atom	Site	x	y	z	B 0	B 0′
a Optimised atom positions (x, y, z) calculated using the Wien2k code.
a = 10.3228(10.3250)	Mn1	2c	0.0000(0.0000)	0.0000(0.0000)	0.5000(0.5000)	1.26	5.10
b = 5.7436(5.7181)			0.0000	0.0000	0.5000^a
c = 4.8887(4.8594)	Mn2	4g	0.0000(0.0000)	0.2600(0.2470)	0.0000(0.0000)
β = 109.43(109.63)			0.0000	0.2603	0.0000^a
V 0 = 273.36(270.24)	Mn3	4i	0.7163(0.7290)	0.0000(0.0000)	0.6576(0.6550)
			0.7173	0.0000	0.6595^a
	O1	8j	0.1137(0.1140)	0.2272(0.2220)	0.3984(0.3950)
			0.1134	0.2274	0.3995^a
	O2	4i	0.1054(0.1140)	0.0000(0.0000)	0.9118(0.9220)
			0.1049	0.0000	0.9119^a
	O3	4i	0.6064(0.5910)	0.0000(0.0000)	0.9247(0.8720)
			0.6062	0.0000	0.9252^a

---

The calculated total density of states (DOS) for the proposed magnetic structures M1, M2, M3, and M4 are shown in Fig. 7. It may be noted that our GGA+SO calculations predict M1 magnetic configuration as ground state with ferrimagnetic half metallic behavior. A finite DOS is present in the minority-spin channel at E_F indicating metallic behavior. However, in the majority spin channel, a band gap of 1.283 eV opens up resulting in the half metallicity of the system. It may be noted that our GGA+SO calculations predict M1 magnetic configuration as the ground state with ferrimagnetic half metallic behavior. The calculated magnetic moments are listed in Table 4, which are in good agreement with the experimental neutron diffraction study. We found that the total DOS distribution and the spin moment are almost the same for M1 and M2; and also M3 and M4 which is consistent with our experimental observation. Even though our theoretical calculations predict the ferrimagnetic ground state, the experimentally observed magnetic structure corresponds to the antiferromagnetic state. So we concluded that GGA+SO calculations are unable to predict the correct magnetic ground state in Mn₅O₈.

Fig. 7 The calculated total DOS for Mn₅O₈ in four different M1, M2, M3, and M4 magnetic configurations (described in the text). The DOS calculated using GGA+SO and GGA+SO+U are given in left and right panel, respectively. The Fermi level is set to zero.

It is well known that, the transition metal oxides usually have a strong Coulomb correlation which was not accounted for in the GGA+SO calculations. Hence, we have made total energy calculations by accounting Coulomb correlation effects through GGA+SO+U. Interestingly when we include the Coulomb correlation effect in our calculation, the total DOS obtained for M1 configuration having narrow d band states is moved towards lower energy bringing metallic states instead of half metallic behavior. Furthermore, in a major spin channel we have found a sharp peak in the DOS curve indicating instability in the system. As a result, the M1 configuration becomes energetically unfavorable compared with the M4 configuration. In the case of M4 configuration, the magnetic moments are exactly canceled between various Mn sublattices bringing perfect antiferromagnetic ordering with metallic behavior, which is consistent with experimental observations. So, we can classify Mn₅O₈ as a strongly correlated antiferromagnetic metal. As the orbital moments obtained from relativistic spin-polarized calculations are usually smaller than the corresponding experimental value,⁵⁵ we have calculated the orbital moments (see Table 2) using orbital polarization correction proposed by Brooks and Eriksson et al.^56,57 We found that the calculated orbital moments obtained from SO calculation and SO + OP calculations are not changed much 0.0072 μ_B and also the estimated orbital moments are small 0.030 μ_B, as expected in transition metal compounds where spin–orbital coupling is generally weak.

The orbital-projected DOS for Mn 3d electrons in the ground state M4 magnetic configuration within GGA+SO+U is shown in Fig. 8. It is well known that the Mn d orbitals in octahedral coordination split into t_2g triplet (d_xy, d_xz, d_yz) and e_g doublet (d_x²−y², d_z²) by the cubic crystal field. As both Mn1 and Mn2 are in octahedral coordination with oxygen, their magnetic moments in these two sites can be analyzed easily using the orbital projected DOS. For Mn⁴⁺ oxidation state, there will be totally three d electrons which occupy the majority spin t_2g states and the e_g states will be empty in the high spin configuration. So one can expect 3 μ_B per Mn sites in a pure ionic picture. In conformity with the above view, our calculated DOS shows that the e_g states are almost empty in the valence band. Moreover, the t_2g states in the minority spin channel are negligibly small confirming the high-spin (HS) state of Mn⁴⁺ ions. However, the calculated magnetic moment (2.69 μ_B) in the Mn2 site is lower than 3 μ_B, indicating that there is a substantial covalent bond between Mn2–O. Usually, the electrons in solids may participate either in bonding or magnetism. Hence due to the covalency effect, the average bond length between Mn2–O(1.917 Å) is smaller than that between Mn1–O(1.926 Å). Owing to the short Mn2–O distance, there is a substantial induced moment of 0.027 μ_B per atom present in the oxygen sites around Mn2. However, the magnetic moment in oxygen sites around Mn1 is comparatively small 0.006 μ_B per atom. The calculated exchange splitting energy for Mn1 and Mn2 are 2.01 eV and 1.9 eV, respectively, correlating linearly with the corresponding magnetic moment. So, the larger exchange splitting at the Mn1 site could explain why Mn1 site has larger moments compared to the Mn2 site. Due to the Coulomb correlation effect d states get localized and hence the magnetic moment is increased in GGA+SO+U calculation as indicated in Table 4. As the pseudocubic crystal field operates in the MnO₆ octahedra, the electronic states at the Fermi level display both Mn(e_g) and Mn(t_2g) bands. The calculated energy difference between M3 and M4 models is less than 30 μeV only in the GGA+SO calculation and that is increased slightly to 40 μeV when we account correlation effect into the calculation. As mentioned above the GGA+SO+U calculation correctly predicted experimentally observed antiferromagnetic ground state with magnetic configuration of M4 suggesting the presence of a strong Coulomb correlation effect in this material.

Fig. 8 The calculated orbital decomposed DOS for Mn1 and Mn2 sites of Mn₅O₈ in the ground state antiferromagnetic configuration obtained from GGA+SO+U. The Fermi level is set to zero.

Table 4 The total magnetic moment, site projected magnetic moment at various Mn sites, and the relative total energy (ΔE) of various magnetic configurations with respect to the ground state are listed in this table

	Magnetic model	Total mom. (μB per f.u.)	Mn mom. Mn1/Mn2/Mn3 (μB per atom)	Total energy (meV per atom)
GGA+SO	M1	−0.99	2.26/2.30/−3.84	0
	M2	−0.99	2.26/2.30/−3.84	78.21
	M3	0	2.72/2.41/−3.83	52.32
	M4	0	2.72/2.41/−3.83	52.29
GGA+SO+U	M1	−1	2.51/2.59/−4.21	84.29
	M2	−1	2.51/2.59/−4.21	84.44
	M3	0	3.05/2.69/−4.18	0.04
	M4	0	3.05/2.69/−4.18	0
Exp.		0	2.4/2.4/−3.8

---

The Mn d levels in a trigonal prismatic coordination split into non-degenerate 1a (d_z²), doubly degenerate 1e (d_xy,d_x²−y²), and doubly degenerate 2e (d_xz,d_yz) levels. As there are five d electrons present in the Mn²⁺ ion residing in the Mn3 site, one would expect that these five electrons occupy the above mentioned levels. For the pure ionic case, the spin moment at the Mn3^t site in low-spin(LS; 1a²1e³2e⁰), intermediate-spin (IS; 1a²1e²2e¹), and high-spin (HS; 1a¹1e²2e²) configurations will then be 1, 3, and 5 μ_B, respectively. The experimentally measured magnetic moment at the Mn3^t site is 3.8 μ_B, whereas our calculated magnetic moment gave a somewhat higher spin moment of 4.18 μ_B. The site-projected DOS for Mn and O atoms of Mn₅O₈ in the ground state M4 configuration are shown in Fig. 9. The bands originating from oxygen are lying in the energy range −8 and −2 eV which are almost completely filled. The DOS at E_F is mainly contributed by the Mn 3d states. From this figure, it is clear that the observed metallic behavior in Mn₅O₈ is mainly originating from Mn atoms with ∼18% contribution from oxygen. The minority spin electrons at the E_F for Mn3 are almost negligible indicating that the majority spin electrons alone participate in the electrical conductivity, as evident from the Fig. 9. We have observed a noticeable hybridization between the metal Mnd and the ligand Op states in the whole valence band indicating significant covalency in this system. As a result, the calculated magnetic moments in the Mn sites are smaller than those expected from a pure ionic picture. Owing to the covalency effect, the oxygen atoms close to Mn have non-negligible magnetic moments.

Fig. 9 Calculated orbital-projected DOS for Mn and O sites of Mn₅O₈ in the ground-state M4 configuration obtained from GGA+SO+U. The Fermi level is set to zero. Note that s and p states of Mn and s states of O are magnified.

In order to understand the spin and valence states of Mn1^o, Mn2^o, and Mn3^t ions in Mn₅O₈ we have displayed the orbital-projected d-electron DOS of these Mn ions in Fig. 10. For d³ system, Hund's rule predicts that the electrons will not pair and occupy the t_2g orbitals alone by leaving the e_g orbitals completely empty. As a result, Fig. 10 shows almost equal occupation of electrons in all the five d orbitals for Mn1^o and Mn2^o. The electron occupation in the e_g orbitals of Mn1^o and Mn2^o bring strong covalent interaction between Mn⁴⁺ ions and oxygen in the whole valence band region. This figure reveals that Mn3^t is in HS state as it is evident from the occupation of majority spin channel of all the five d orbitals. It is also clear that higher lying DOS of Mn3 (d_yz and d_xz) and O1 play an important role to bring metallic behavior in this compound.

Fig. 10 Orbital (d) decomposed DOS for Mn1^o, Mn2^o and Mn3^t in Mn₅O₈ for the ground-state M4 configuration. The Fermi level is set to zero.

It may be recalled that there are two types of exchange interactions one can expect between the magnetic cations in ionic crystals: cation–cation and cation–anion–cation (or even cation–anion–anion–cation) interactions. For the case of 90° cation–anion–cation interaction, Goodenough⁵⁸ has pointed out that if the octahedral interstices of two neighboring cations share a common edge then there is a direct overlap of the d_xy or d_yz or d_xz orbitals of these two cations. As a result, the anion plays a less obvious role in the delocalization–superexchange process. In Mn₅O₈ also the Mn ions Mn1^o, Mn2^o form edge-shared octahedra and hence the interaction between the two neighboring Mn ions can be referred to as cation–cation interactions. When the cation–cation separation is short and the t_2g orbitals are half filled, then cation–cation interactions tend to dominate the 90° superexchange. In the present case also the interatomic distance between Mn1 and Mn2 is small (2.81 Å) and comparable to other magnetic oxides such as NaCrO₂ (2.96 Å) and NaFeO₂ (3.02 Å).⁵⁹ It is expected that in the octahedral crystal field the Mn⁴⁺ ions in the HS state will have a half filled t_2g level as we have seen in the orbital decomposed DOS analysis (see Fig. 10). It was also emphasized by Kanamori⁶⁰ that, the exchange interaction J^c–c_ij for the two half filled orbitals expected to be negative results in antiferromagnetic interaction. In consistence, the Mn⁴⁺ ions in Mn₅O₈ share edges with each other and hence the 90° superexchange interactions are responsible for the observed antiferromagnetic ordering. It may be noted that our experimentally measured Weiss constant θ value for Mn₅O₈ is −144.5 K²⁸ which further reiterates the antiferromagnetic superexchange interactions as mentioned above.

When we analyze orbital decomposed DOS for the oxygen p states, no noticeable p_z states are present between −2 eV to 0 eV (E_F). On the other hand, the orbital decomposed DOS for the d states of Mn3 ion shows that the majority of d states are present in this energy range. Hence, super-exchange path way is not possible between oxygen p_z states and Mn3 d states, as evident from Fig. 10 and angular momentum projected DOS (Fig. S1, ESI†). This could explain why the intralayer coupling between Mn atoms is of ferromagnetic in nature.

Mn1 and Mn2 d states are spread in the whole valence band from −8 eV to E_F with dominant contributions from d_xy and d_xz states near the E_F. The DOS analysis of Mn1 and Mn2 sites shows strong distribution in the energy range −4 eV to −2 eV in the valence band. Moreover, the orbital decomposed DOS for oxygen p states show that both p_x and p_y states are present in this energy range. Hence there is a possibility of superexchange antiferromagnetic interaction between oxygen p_x and p_y states with Mn1/Mn2 d states between the layer. As a result, one could expect AFM interaction between the layers and FM interaction within the layer leading to A-AFM ordering. Consistent with the conclusion arrived from DOS analysis, our total energy calculations also show that the A-AFM ordering is the lowest energy configuration in this system. The theoretical finding of A-AFM ordering in Mn₅O₈ could also support the experimentally observed negative Curie temperature value from the susceptibility measurements.²⁸

3.4 Bonding analysis through COHP

The crystal orbital Hamiltonian population (COHP) is calculated using VASP to analyze the bond strength and character of the bonding interactions between the constituents in Mn₅O₈.^61,62 COHP is constructed by weighing the DOS with the corresponding Hamiltonian matrix.⁶³ This approach provides a qualitative description of the bonding (negative COHP) and antibonding (positive COHP) interactions between atoms. Fig. 11 displays the calculated COHP for the Mn1–O1, Mn1–O2, Mn2–O1, Mn2–O2, Mn2–O3, Mn3–O1, Mn3–O2, Mn3–O3, Mn1–Mn2, and Mn2–Mn3 interactions in Mn₅O₈. The COHP curves reveal that the Mn–O bonding states are present strongly in the region −7.5 to −2.3 eV of the valence band. In the vicinity of the E_F (i.e., within −1 eV to E_F) in Mn–O COHP noticeable antibonding states are present. As the Mn–Mn interactions were screened by oxygen ions present between the Mn ions, the calculated Mn–Mn bonding states distribution is relatively small. We have calculated the bond strength between various constituents of Mn₅O₈ using the Integrated COHP (ICOHP) as we have done earlier.⁴⁸ The calculated ICOHP for various constituents of Mn₅O₈ reflecting the bond strength between the atoms are listed in Table 5. According to Table 5, Mn–O has the strongest bonding interaction in Mn₅O₈. The bonding interaction between Mn2–Mn3 is very weak since the bond distance between these atoms is relatively high (∼3 Å). The MnO₆ octahedra are highly distorted and hence the Mn2–O distances vary between 1.890 Å to 1.955 Å and correspondingly the calculated bond strength varies from −2.17 eV to −2.33 eV. The calculated bond length for Mn1–O_a is 1.993 Å and that for Mn2–O_a is 1.938 Å where, O_a is apical oxygen in the octahedra. Hence, one can expect that the Mn2–O_a bond will have a stronger bond strength than Mn1–O_a. In agreement, our calculated ICOHP value for Mn2–O3_a is larger than that for Mn1–O2_a. If there are strong bonds present between magnetic cations with anions, one can expect that the magnetic moment will quench. The calculated bond strength between constituents obtained based on ICOHP values listed in Table 5 are reflecting the variation in magnetic moments in the corresponding Mn atoms (see Table 4). Moreover the difference in the average bond strength for Mn1–O and Mn2–O indicates that the Mn atoms in Mn₅O₈ are in two different oxidation states, consistent with our DOS analysis.

Fig. 11 The calculated COHP for Mn1–O1, Mn1–O2, Mn2–O1, Mn2–O2, Mn2–O3, Mn3–O1, Mn3–O2, Mn3–O3, Mn1–Mn2 and Mn2–Mn3 in ground-state M4 configuration of Mn₅O₈.

Table 5 Calculated bond strength from Integrated COHP

Interaction	Bond strength (eV)
Mn1–O1	−2.18
Mn1–O2	−1.84
Mn2–O1	−2.27
Mn2–O2	−2.17
Mn2–O3	−2.33
Mn3–O1	−1.35
Mn3–O2	−1.27
Mn3–O3	−2.04
Mn1–Mn2	−0.26
Mn2–Mn3	−0.05

---

The formal oxidation states of the octahedral and trigonal-prismatic Mn atoms can be evaluated from bond-valence-sum (BVS) calculations, by using bond-valence parameters of R_ij(Mn²⁺) = 1.79, R_ij(Mn³⁺) = 1.76 and R_ij(Mn⁴⁺) = 1.753, and bond distances of d_ij, yielded from NPD analysis at 9 K, in the formula Σ exp[(R_ij − d_ij)/0.37]. The results indicate that octahedral coordinated Mn atoms at 2c (Mn1) and 4g (Mn2) sites are tetravalent and trigonal-prismatic coordinated Mn atom at 4i (Mn3) site is divalent (see Table 6), even though the BVS values for octahedral and trigonal-prismatic polyhedral deviate slightly from the ideal value of 3.7(2) and 2.3(2), respectively.

Table 6 Selected inter-atomic distances (Å) and bond valence sum (BVS) for Mn₅O₈ at 9 K. Calculated standard deviations are listed in parentheses

	Mn1	Mn2	Mn3
Note: BVS values were calculated by iteration from initial arbitrary mixed-valence value. The bond valence parameter was assumed by taking fraction of standard literature values; Mn^2+–O^2−, Mn^3+–O^2−, and Mn^4+–O^2− are 1.79, 1.76, and 1.753 respectively.
O1	1.91(2) × 4	1.89(2) × 2	2.15(2) × 4
O2	1.99(2) × 2	1.96(2) × 2	2.10(3)
O3		1.94(2) × 2	2.00(3)
BVS	3.7(2)	3.7(2)	2.3(2)

---

The valence states of Mn in Mn₅O₈ can be written as Mn₂²⁺Mn₃⁴⁺O₈, the spin-only magnetic moment for Mn₅O₈ can be calculated from the expression

An effective magnetic moment measured from magnetic susceptibility study is μ_eff = 4.803 μ_B. The calculated effective magnetic moment using μ_Mn(II₎ = 5.9 μ_B and μ_Mn(IV₎ = 3.87 μ_B is μ_eff = 4.786 μ_B. The close agreement between the calculated spin-only magnetic moment and the experimental moment confirms the presence of mixed valence states in Mn₅O₈. As the experimentally measured effective magnetic moment is close to the theoretically calculated spin-only value, it is apparent that the orbital angular moment is quenched due to the ligand field splitting. This is also evident from Table 2 showing that our calculated orbital moment is very small and the spin moment mainly contributes to the total magnetic moment.

In previous study,²⁸ we have mentioned the possibility of Mn₃O₄⁶⁴ as secondary phase in master Mn₅O₈ sample, based on the observed magnetic ferroic transition around 40 K. In present study, we have measured NPD at 70 (Fig. S2, ESI†) i.e. above 40 K but still below T_N = 133 K. However, no unique change is noticeable compared to the NPD data at 9 K. Therefore, we conclude that there is no major contribution from the secondary phase of Mn₃O₄ in the collected NPD data.

4 Conclusions

To summarize, magnetic ordering and the mixed valent nature of Mn₅O₈ have been reported using fully relativistic density functional theory calculations and Neutron powder diffraction measurements. From our total energy calculation we have predicted that Mn₅O₈ orders antiferromagnetically with the spin orientation along [100] direction in accordance with our NPD measurements. Among the four different magnetic models proposed from the experiments, M4 magnetic configuration is found to be the ground state magnetic structure in Mn₅O₈. Density of states analysis shows a large DOS at E_F in the ground state magnetic structure showing the metallic nature of Mn₅O₈. Calculations without the inclusion of Hubbard U leads to ferrimagnetic half metallic state as ground state, contradictory to the experimental findings, indicating the presence of strong Coulomb correlation effect in this material. However, by including Coulomb correlation effect in to the calculations we could correctly predict the ground state as antiferromagnetic metal. Presence of two different magnetic moments along with the different density of states distribution in the Mn sites illustrate the mixed valent behavior of Mn ions. Bond strength analysis based on COHP between constituents indicates strong anisotropy in the bonding behavior which results from layered nature of the crystal structure. The orbital decomposed DOS analysis of Mn d states shows that Mn ions in the Mn⁴⁺ and Mn²⁺ oxidation states with high spin magnetic configuration. Our bond valence sum analysis also supports the presence of two different oxidation states such as 4+ and 2+ in this compound. The calculated orbital moment using relativistic spin polarized calculation with orbital polarization correction yielded very small orbital moment and hence the spin-only moment is sufficient to account for the experimentally measured effective moment from susceptibility measurements. The over all results indicate that Mn₅O₈ can be described as a strongly correlated mixed valent antiferromagnetic metal.

Appendix: group theory analysis for Mn₅O₈

To determine magnetic structure of Mn₅O₈, the possible magnetic structures, which are compatible with the crystal symmetry, were investigated by the method described by Bertaut.⁶⁵ The magnetic structures are defined by the basis vectors of the irreducible representations of the little group Γ_k which for a propagation vector k = (−1, 0, 1) coincides with the crystallographic space group.

In the case of Mn₅O₈ the Mn atoms are in wyckoff sites at 2c, 4g, and 4i under space group of C2/m. The decomposition of the representation Γ, describing the transformation properties of the magnetic moments is given by Γ = Γ₁ + 2Γ₃ in Kovalev's notation.⁶⁶ The solutions defined by Γ₁ correspond to FM ordering within layers and AFM ordering between each layer with magnetic moments parallel to the b direction (M3 in Fig. 4). Γ₅ defines similar ordering with F1 in the ac plane (M4 in Fig. 4).

Acknowledgements

The authors are grateful to the Research Council of Norway for computing time on the Norwegian supercomputer facilities. This research was supported by the Indo-Norwegian Cooperative Program (INCP) via Grant No. F. No. 58-12/2014(IC) and Research Council of Norway, Grant No. 221905 (FRIPRO). One of the authors M. R. A. K. gratefully acknowledges the Central University of Tamil Nadu for the financial support.

References

1. J. Van Elp, R. Potze, H. Eskes, R. Berger and G. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 1530.
2. S. Geller, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 821–828.
3. T. Gao, H. Fjellvåg and P. Norby, Anal. Chim. Acta, 2009, 648, 235–239.
4. C. Franchini, R. Podloucky, J. Paier, M. Marsman and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195128.
5. P. Ravindran, A. Kjekshus, H. Fjellvåg, A. Delin and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064445.
6. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
7. M. M. Thackeray, Prog. Solid State Chem., 1997, 25, 1–71.
8. J. E. Post, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3447–3454.
9. R. Vidya, P. Ravindran, P. Vajeeston, A. Kjekshus and H. Fjellvåg, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 092405.
10. R. Vidya, P. Ravindran, A. Kjekshus and H. Fjellvåg, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144422.
11. C. Franchini, V. Bayer, R. Podloucky, J. Paier and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045132.
12. M. Imada, A. Fujimori and Y. Tokura, Rev. Mod. Phys., 1998, 70, 1039.
13. N. Mott, Rev. Mod. Phys., 1968, 40, 677.
14. W. A. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245103.
15. H. Shaked, J. Faber Jr and R. Hitterman, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 11901.
16. K. Dwight and N. Menyuk, Phys. Rev. B: Condens. Matter Mater. Phys., 1960, 199, 1470.
17. G. Jensen and O. Nielsen, J. Phys. C: Solid State Phys., 1974, 7, 409.
18. G. Srinivasan and M. S. Seehra, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1.
19. A. Yoshimori, J. Phys. Soc. Jpn., 1959, 14, 807–821.
20. H. Sato, K. Wakiya, T. Enoki, T. Kiyama, Y. Wakabayashi, H. Nakao and Y. Murakami, J. Phys. Soc. Jpn., 2001, 70, 37–40.
21. M. Sugawara, M. Ohno and K. Matsuki, Chem. Lett., 1991, 1465–1468.
22. C. Azzoni, M. Mozzati, P. Galinetto, A. Paleari, V. Massarotti, D. Capsoni and M. Bini, Solid State Commun., 1999, 112, 375–378.
23. J. H. Rask and P. R. Buseck, Am. Mineral., 1986, 71, 805–814.
24. G. B. Ansell, M. A. Modrick, J. Longo, K. Poeppeimeler and H. Horowitz, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 1795–1797.
25. A. Riou and A. Lecerf, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 1896.
26. N. Yamamoto, M. Kiyama and T. Takada, J. Appl. Phys., 1973, 12, 1827.
27. A. Punnoose, H. Magnone and M. Seehra, IEEE Trans. Magn., 2001, 37, 2150–2152.
28. T. Gao, P. Norby, F. Krumeich, H. Okamoto, R. Nesper and H. Fjellvåg, J. Phys. Chem. C, 2010, 114, 922–928.
29. S. Thota, B. Prasad and J. Kumar, Mater. Sci. Eng., B, 2010, 167, 153–160.
30. I. Uddin, P. Poddar and A. Ahmad, J. Nanoeng. Nanomanuf., 2013, 3, 91–97.
31. X. Zheng, C. Xu, K. Nishikubo, K. Nishiyama, W. Higemoto, W. Moon, E. Tanaka and E. S. Otabe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014464.
32. L. He, C. Chen, N. Wang, W. Zhou and L. Guo, J. Appl. Phys., 2007, 102, 103911.
33. Y.-F. Han, F. Chen, Z. Zhong, K. Ramesh, L. Chen and E. Widjaja, J. Phys. Chem. B, 2006, 110, 24450–24456.
34. D. Jeong, K. Jin, S. E. Jerng, H. Seo, D. Kim, S. H. Nahm, S. H. Kim and K. T. Nam, ACS Catal., 2015, 5, 4624–4628.
35. R. Vidya, P. Ravindran, H. Fjellvåg and A. Kjekshus, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 054422.
36. T. Gao, F. Krumeich, R. Nesper, H. Fjellvåg and P. Norby, Inorg. Chem., 2009, 48, 6242–6250.
37. B. C. Hauback, H. Fjellvåg, O. Steinsvoll, K. Johansson, O. T. Buset and J. Jørgensen, J. Neutron Res., 2000, 8, 215.
38. H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
39. J. Rodríguez-Carvajal, Physica B, 1993, 192, 55–69.
40. P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, An augmented plane wave + local orbitals program for calculating crystal properties, 2001.
41. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 78, 1396.
42. M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
43. V. Anisimov and O. Gunnarsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7570.
44. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943.
45. V. I. Anisimov, I. Solovyev, M. Korotin, M. Czyżyk and G. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929.
46. A. Liechtenstein, V. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467.
47. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
48. P. Ravindran, R. Vidya, A. Kjekshus, H. Fjellvåg and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224412.
49. S. M. Auerbach, K. A. Carrado and P. K. Dutta, Handbook of Layered Materials, Marcel Dekker, Inc., New York, 2004, pp. 475–508.
50. H. R. Oswald and M. J. Wampetich, Helv. Chim. Acta, 1967, 50, 2023.
51. H. Oswald, W. Feitknecht and M. Wampetich, Nature, 1965, 207, 72.
52. J. Haines, J. M. Leger and S. Hoyau, J. Phys. Chem. Solids, 1995, 56, 965–973.
53. R. Jeanloz and A. Rudy, J. Geophys. Res.: Solid Earth, 1987, 92, 11433–11436.
54. R. E. Cohen, I. Mazin and D. G. Isaak, Science, 1997, 275, 654–657.
55. P. Ravindran, A. Kjekshus, H. Fjellvåg, P. James, L. Nordström, B. Johansson and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 144409.
56. M. Brooks, Physica B, 1985, 130, 6–12.
57. O. Eriksson, B. Johansson and M. Brooks, J. Phys.: Condens. Matter, 1989, 1, 4005.
58. J. Goodenough, Magnetism and the Chemical Bond, Wiley, New York, 1963.
59. K. Motida and S. Miyahara, J. Phys. Soc. Jpn., 1970, 28, 1188–1196.
60. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
61. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
62. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
63. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
64. W. S. Seo, H. H. Jo, K. Lee, B. Kim, S. J. Oh and J. T. Park, Angew. Chem., Int. Ed., 2004, 43, 1115–1117.
65. E. Bertaut, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1968, 24, 217–231.
66. O. V. Kovalev, Irreducible representations of the space groups, Gordon and Breach, New York, 1985.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04170a

---