Thermal contact resistance across a linear heterojunction within a hybrid graphene/hexagonal boron nitride sheet

Abstract

Interfacial thermal conductance plays a vital role in defining the thermal properties of nanostructured materials in which heat transfer is predominantly phonon mediated. In this work, the thermal contact resistance (R) of a linear heterojunction within a hybrid graphene/hexagonal boron nitride (h-BN) sheet is characterized using non-equilibrium molecular dynamics (NEMD) simulations. The effects of system dimension, heat flux direction, temperature and tensile strain on the predicted R values are investigated. The spatiotemporal evolution of thermal energies from the graphene to the h-BN sheet reveals that the main energy carrier in graphene is the flexural phonon (ZA) mode, which also has the most energy transmissions across the interface. The calculated R decreases monotonically from 5.2 × 10⁻¹⁰ to 2.2 × 10⁻¹⁰ K m² W⁻¹ with system lengths ranging from 20 to 100 nm. For a 40 nm length hybrid system, the calculated R decreases by 42% from 4.1 × 10⁻¹⁰ to 2.4 × 10⁻¹⁰ K m² W⁻¹ when the system temperature increases from 200 K to 600 K. The study of the strain effect shows that the thermal contact resistance R between h-BN and graphene sheets increases with the tensile strain. Detailed phonon density of states (PDOS) is computed to understand the thermal resistance results.

---

1. Introduction

With the continued demand for shrinking the dimensions of nanodevices and increasing the density of nanocircuits in the electronic industry, the heat dissipation at the nanoscale heterojunctions has become a critical factor for the development and design of next generation nanoelectronics. To meet this continued demand, explorations of high performance thermal interface materials, such as two-dimensional (2D) atomic layered materials – graphene, hexagonal boron nitride (h-BN), phosphorene, and silicene – have been extensively undertaken. Among the 2D novel materials, graphene and h-BN have attracted the most attention due to their extraordinary thermophysical properties. The recent measurements of a partially suspended graphene sheet reveal its thermal conductivity (κ) being as high as 5300 W m⁻¹ K⁻¹ at room temperature.¹ Other experiments suggest that graphene has a thermal conductivity of 3000–5000 W m⁻¹ K⁻¹ for a length of ∼10 μm.² This high thermal conductivity exceeds that of graphite and is partially attributed to the strong sp² covalent bonding between C–C atoms and the long phonon mean-free path in carbon nanostructures. Due to their geometric resemblance, i.e., condensed honeycomb lattices and covalent sp² bonding, monolayer h-BN possesses similar physical properties to those of graphene, such as strong mechanical properties^3–5 and high chemical and thermal stability.^6–8

The miniaturization of devices and the critical need for improved heat dissipation rely on efficient thermal transport at the heterojunctions. Therefore, the phonon transport across an interface of a heterojunction has been of great interest. Using the molecular dynamics (MD) approach, the thermal contact resistance (R) at the graphene and silicon interface is calculated at 3.1–4.9 × 10⁻⁸ K m² W⁻¹.⁹ Hong et al.¹⁰ computed R between graphene and a copper substrate to be ∼2.61 × 10⁻⁸ K m² W⁻¹ at room temperature. It is found that by engraving the substrate with sub-nm surface roughness, the interfacial thermal resistance between graphene and copper can be reduced by 17%. Using a non-equilibrium molecular dynamics (NEMD) method, Li et al.¹¹ computed the R value between graphene and 4H-SiC to be ∼1 × 10⁻⁸ K m² W⁻¹. Zhang et al.¹² studied the thermal resistance between silicene and various substrates using a numerical pump–probe method. They found that the thermal conductance at amorphous interfaces was higher than that at crystalline interfaces. Thermal contact resistances between stacked 2D sheets such as graphene/silicene,¹³ graphene/h-BN¹⁴ and graphene/MoS₂¹⁵ have also been investigated. The calculation results suggest that the interfacial thermal conductance correlates positively with system temperatures and interaction strengths.

The aforementioned supported 2D structures are attached to the substrate via weak van der Waals interactions. But in a hybrid sheet, atoms located adjacent to the heterojunction are often connected by the strong covalent bonds. The thermal transport mechanism and phonon interactions of hybrid sheets differ from those of the stacked sheets and further investigations are needed. In this work, the thermal transport across the graphene/h-BN heterojunction is studied using MD simulations. The thermal energy dissipation at the contact areas is investigated comprehensively. The effects of system dimensions, heat flux direction, temperature and tensile strain on interfacial thermal resistance are explored. Detailed spatiotemporal isotherm and phonon spectrum analyses are conducted to assist the explanation of the computation results.

2. Models, physical basis, and computational approach

All simulations in this work are performed using the LAMMPS molecular dynamics simulator,¹⁶ which has been widely used for classical MD simulations. A schematic of the simulation domain is shown in Fig. 1. Periodic boundary condition is applied in the y direction, which is perpendicular to the heat flux q̇ direction, to eliminate the size effects. Free boundary conditions are applied in the in-plane x and out-of-plane z directions. A lattice mismatch of ∼1% is applied to both graphene and h-BN sheets to construct a supercell with a lattice constant of 2.485 Å. A comparable lattice mismatch between graphene/h-BN is confirmed by ab initio density functional calculations.¹⁷ Slightly larger lattice mismatches of 2.5% and 1.9% were reported in graphene/silicene¹³ and graphene/MoS₂¹⁸ hybrid sheets from previous computational studies. Compared with other graphene-based hybrid sheets,^19–22 the lattice mismatch considered in this study has negligible effects on the heterojunction's thermal properties.

Fig. 1 Atomistic configurations of the h-BN and graphene hybrid sheet. The outermost layers of atoms in the x direction are fixed. Heat bath (Q_in) and heat sink (Q_out) are placed at the two ends with four layers of atoms respectively.

The second generation of the Brenner potential,²³ namely, the reactive empirical bond-order (REBO) based on the Tersoff potential²⁴ with interactions between C–C bonds, is applied to model the graphene system. Interactions between boron atoms, nitrogen atoms and h-BN/graphene are described by the Tersoff potential,²⁵ similar to previous studies.^26–28 Non-equilibrium molecular dynamics simulations are conducted to characterize the interfacial thermal resistance. For thermal equilibrium simulations, the hybrid sheet is first placed in a canonical ensemble (NVT) for 600 ps (1 ps = 10⁻¹² s) and then turned into a microcanonical ensemble (NVE) for another 400 ps. After the system reaches thermal equilibrium at a given temperature, heat flux controls are applied to the heating/cooling groups constantly for another 7 ns, which is long enough for the temperature gradient to reach a steady state. The heat flux is calculated using the equation

where q̇ is the heat flux, Δε the imposed heat energy, A the cross-sectional area, and Δt the time step. It is worth noting that if the heat bath is positioned in the middle of the hybrid system and the heat sink is split at the two ends, a factor of 2 needs to be added to the denominator in eqn (1) since the heat flux will propagate in two opposite directions. The temperature gradient is computed by dividing the sample into n slabs along the heat flux direction. The temperature in each slab is calculated according to the energy equipartition theorem:where N is the number of atoms in each slab, k_B the Boltzmann constant, m_j and v_j the mass and velocity of atom j in the slab. The temperature drop occurring at the heterojunction can be used to determine the thermal resistance value according to the equation:where R is the interfacial thermal resistance and ΔT is the temperature difference/drop across the heterojunction. The phonon density of states (PDOS) G(ω) is computed from the Fourier transform of the velocity autocorrelation function (VACF):where ω is the vibrational wavenumber, Z(t) = 〈v(0)·v(t)〉/〈v(0)·v(0)〉 and v(t) denotes the atom velocity at time t. A higher value of PDOS for a phonon with frequency ω means that more states are occupied by it and zero PDOS means no phonon with frequency ω exists in the system. The phonon-power-spectrum analysis provides a quantitative means to assess the power carried by phonons in a system. Time steps are 0.5 fs (1 fs = 10⁻¹⁵ s) for all simulations.

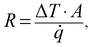3. Results and discussion

3.1 Effects of system dimension and heat flux direction

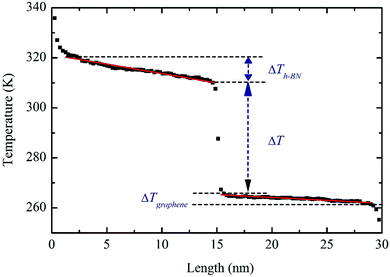
The classical NEMD method is applied for the interfacial thermal resistance characterization. Taking the 30.0 × 5.0 (x × y) nm² hybrid graphene/h-BN sheet as an example, the graphene and h-BN sheets each takes half of the length respectively, as shown in Fig. 1. After the system reaches thermal equilibrium at a temperature of 300 K, a constant heat flux Q_in = 1.85 × 10⁻⁷ W is added to the heat bath at each time step and the same amount Q_out is subtracted from the heat sink simultaneously for 1.4 × 10⁷ time steps. After the system reaches a steady state, another 4 × 10⁶ time steps are performed for data collection. The temperature distribution along the heat flux direction is shown in Fig. 2. It is observed that the temperature profiles near the thermal baths are nonlinear. During the NEMD process, kinetic energies are continuously added to/subtracted from the heating/cooling areas for temperature control. The kinetic energy and the potential energy within the heating/cooling regions are constantly changing (non-equilibrium state) and phonon boundary scattering is extremely rapid during this ultrafast energy exchange process. Therefore the temperature drop is nonlinear in these regions and should be excluded from the thermal conductivity computation.^29–32 The sharp temperature drop ΔT at the heterojunction is caused by the thermal contact resistance between h-BN and graphene. To obtain an accurate temperature difference, linear fittings are applied to the temperature profiles of the hybrid h-BN and graphene sheet, and the end values are used for ΔT calculations. The interfacial thermal resistance calculated using eqn (3) is 4.0 × 10⁻¹⁰ K m² W⁻¹ for the 30 nm length system. Previous studies by Li et al.¹¹ indicated that the interfacial thermal resistance between graphene and the substrate can be lowered by two orders of magnitude if the bonding type changes from van der Waals to covalent. The strong sp² bonds between B–N–C atoms facilitate the thermal energy dissipation at the h-BN/graphene heterojunction, which results in lower thermal contact resistances compared to those at the van der Waals interfaces.¹⁴

Fig. 2 Temperature distribution in the length direction of a 30.0 × 5.0 (x × y) nm² hybrid sheet at steady state. Temperature difference ΔT at the heterojunction is characterized by a linear fitting of the temperature profiles of each material and measuring the endpoint difference.

The phonon mean free path (MFP) of graphene is measured at ∼775 nm near room temperature.² The intrinsically long MFP induces a size dependent thermal conductivity in the graphene system. The confined dimension in the lateral directions will greatly affect the phonon behavior at the graphene/h-BN heterojunction. Thus, it is of great interest to investigate the effects of system dimensions on the interfacial thermal transport. Hybrid sheets with lengths ranging from 20 nm to 100 nm are used in the simulations. The predicted results are shown in Fig. 3. It can be seen that the R values are independent of the heat flux direction, but exhibit a decreasing trend with the increasing system lengths. The length dependence of R occurs if the system size is smaller than the phonon MFP. When the system size becomes larger, more phonon modes with longer wavelengths will be excited. Such phonons can pass through the interface with lower degrees of inelastic scattering and possess higher transmission rates, which can make additional contributions to the thermal conduction. The length dependence of R has also been observed in other hybrid systems.^33–35 Aside from the length effects on the interfacial thermal conductance, the in-plane thermal conductivities of the hybrid graphene/h-BN sheet are also dependent on system dimensions. It has been predicted that the system length has significant influence on the thermal conductivity of h-BN. The calculated thermal conductivity for infinitely long h-BN is 277.78 and 588.24 W m⁻¹ K⁻¹, respectively, along the armchair and zigzag directions.³⁶

Fig. 3 Dependence of interfacial thermal resistance on the system length. The calculated R values are independent of heat flux direction, i.e., there is no thermal rectification in the h-BN/graphene hybrid sheet.

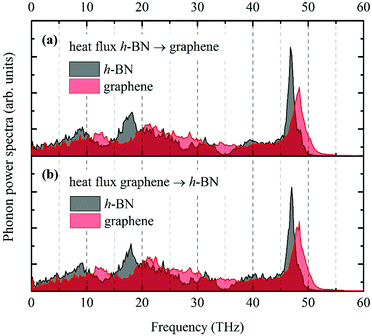
Phonon power spectrum analyses are conducted to assist the understanding of the predicted results. After the hybrid system reaches a steady state with a constant heat flux, atom velocities of the h-BN and graphene hybrid sheet are recorded continuously for 10 ps, which are then used for the PDOS computation according to eqn (4). The computed PDOS results are plotted in Fig. 4. When the heat flux flows from h-BN to graphene, the PDOS profiles shown in Fig. 4(a) are nearly identical to those in Fig. 4(b) where the heat flux is reversed from graphene to h-BN, indicating that the thermal transport is independent of the heat flux direction. One of the crucial factors in determining the interfacial thermal resistance is the overlap of phonon states. If the phonon population at a certain frequency ω is low or zero, the energy propagation by phonons of that wave vector would be highly restricted. To quantify this variation, an arbitrary unit variable, which is defined as , is introduced to help the analyses.¹¹A(ω) represents the intersection area at frequency ω. The area of integration is proportional to the amount of energy transported across the linear heterojunction by phonons at these frequency intervals. The calculated δ₁ for the heat flux from h-BN to graphene is 67.2% and δ₂ equals 67.1% in the opposite direction. The equivalent overlap areas further prove the nondependence of R on the heat flux direction.

Fig. 4 Phonon power spectra of the graphene/h-BN hybrid sheet. (a) Heat flux from h-BN to graphene. (b) Heat flux is from graphene to h-BN. The integrated PDOS overlapping areas are 67.2% and 67.1% respectively.

To take a further look at the thermal energy propagation within the hybrid sheet, the spatiotemporal temperature evolution is calculated for the 40 nm length hybrid sheet. After thermal equilibrium simulation at 300 K, an ultrafast thermal impulse with an interval of 50 fs is imposed at the end of the graphene. Atoms along the heat flux direction are divided into smaller slabs whose temperature is then calculated according to eqn (2). The isotherm contours are shown in Fig. 5. The pictures depict how heat flows from the origin to the entire field. Fig. 5(b)–(d) show the longitudinal (LA), transverse (TA) and flexural (ZA) components of graphene's thermal energies, respectively. Previous studies argued that the thermal conductivity in single layer graphene is mainly contributed by the in-plane TA and LA phonons, while the out-of-plane ZA phonon contribution can be ignored due to its small group velocity.³⁷ However, a recent study shows that for suspended graphene, the ZA phonon modes can contribute as much as 77% at 300 K and 86% at 100 K of the thermal conductivity due to high specific heat and longer mean phonon scattering time.³⁸ By formulating the ballistic thermal conductance of phonons in a 2D system and using the phonon dispersion relationship, Nakamura et al.³⁹ calculated the contribution of the TA, LA and ZA phonons to graphene's thermal conductance. They also concluded that the ballistic phonon conductance is determined by the ZA phonon modes below about 20 K but the contribution of the TA and LA phonon modes cannot be neglected above 20 K, while the ZA phonon contribution is still dominant. Besides, by numerically solving the phonon Boltzmann equation, Lindsay et al.⁴⁰ derived a symmetry-based selection rule which significantly restricts the anharmonic phonon–phonon scattering of the ZA phonons, and they showed that the lattice thermal conductivity of graphene is dominated by the ZA phonon modes.

Fig. 5 Thermal wave propagation from graphene to h-BN in the hybrid sheet. Here, the temperature scale on the far right for all the thermal maps is from 100 K to 1000 K, illustrated by gradual color change from blue to red. (a) Total temperature evolution in spatiotemporal space. (b)–(d) Decomposed thermal energies in x, y and z directions, respectively. A strong thermal wave is observed in the z direction, indicating that the flexural phonons are the main energy carriers in graphene and make the most contributions to interfacial thermal conductance.

Although many studies have been conducted to analyze the effect of ZA modes on the in-plane thermal conductivity of graphene, their effect on the interfacial thermal conductance has yet to be investigated. Here, one can clearly see from Fig. 5(d) that a strong thermal wave (ZA mode) propagates through the spatiotemporal isotherms, while from Fig. 5(b) and (c), no evident thermal waves (LA and TA modes) are seen. When the thermal relaxation time of phonons is relatively long, the thermal-wave effect becomes more prominent. Hence, it appears that the ZA mode is more significant than the LA and TA modes with respect to graphene's thermal energy dissipation. It can also be observed that the ZA phonons contribute the most energy transmission across the heterojunction towards the h-BN monolayer, indicating that the flexural phonons play a vital role in the interfacial thermal conductance of the hybrid graphene/h-BN sheet. The stress wavefront and thermal energy reflections at the interface are shown in Fig. 5(d).

3.2 Effects of temperature

Most thermal interface materials can be placed in various working environments under a wide range of temperatures. Thus, it is also of importance to investigate the effects of working temperatures on interfacial thermal resistance of the heterojunction. Temperatures from 200 to 600 K with an interval of 50 K are chosen and the calculated R values in both zigzag and armchair directions are displayed in Fig. 6, where the inset shows atomic structures of the system after reaching thermal equilibrium. Our results indicate that the interfacial thermal resistance decreases monotonically with the increasing temperature. Besides, the predicted R values are independent of the heat flux direction at different temperatures.

Fig. 6 Thermal resistance variations with temperature from 200 K to 600 K. The inset shows the fully relaxed atomic structure after the hybrid sheet reaches thermal equilibrium.

The decrease of R can be attributed to two major factors: (1) The increase of overall phonon population: At low temperatures, only a limited number of phonons are excited and involved in the thermal transport process. When the temperature increases, higher frequency phonons can be excited, giving more contributions to the interfacial thermal transport and thereby lowering the R values. (2) The increase of inelastic phonon scattering at the interface (heterojunction here), which further facilitates the phonon transmission and enhances the anharmonic coupling. The interfacial thermal resistance calculated using the conventional acoustic mismatch model (AMM) and the diffuse mismatch model (DMM) is independent of temperature within the classical high temperature limit. This is because the only temperature-dependent part for both models is the distribution function, whereas inelastic scatterings are not considered at the interfaces. The NEMD approach applied here accounts for both elastic and inelastic scattering at the interface. It has been proven that at van der Waals heterojunctions, inelastic scattering provides a major contribution to the energy transport surpassing that of elastic scattering at high temperatures.⁴¹ The second reason for the increase in the probability of inelastic scattering is that at high temperatures the high frequency phonons might break down into large volumes of low frequency phonons. These low frequency phonons have a higher probability of getting transferred through the interface when compared to the high frequency phonons, leading to higher phonon transmission coefficients and the reduction in the overall interfacial thermal resistance with the increasing temperature. Similar results have also been reported in previous studies of different nanostructure interfaces.^41–43

3.3 Effects of tensile strain

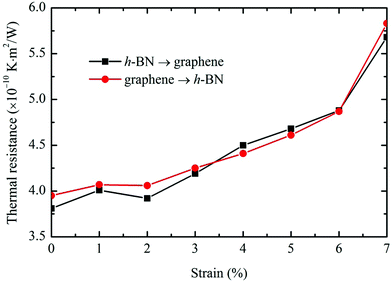
Mechanical strains have been proven to be an effective approach to tune the thermophysical properties of nanomaterials.^44–46 For pliable 2D materials, such as graphene and h-BN, the planar structures can be easily bent to fit the formation of various substrates. The deformation in the monolayer membranes can induce high local strains.^9,29 The effects of strains on the in-plane thermal conductivity of graphene,⁴⁷ silicene,⁴⁸ phosphorene⁴⁹ and other 2D materials^50–52 have been extensively studied. However, the effects of tensile strain on the interfacial thermal transport across hybrid sheets are still unclear, and hence the present study.

The definition of strain is given by ε = (l − l₀)/l₀, where l₀ is the original length and l is the final length. Interfacial thermal resistance computations are performed with strain values varying from 1% to 7%. The predicted R values are shown in Fig. 7. Our results show that the interfacial thermal resistance increases with the tensile strain. Phonon power spectra analyses are also performed to further understand the results. Fig. 8 shows the computed phonon spectra of the graphene at thermal equilibrium. A notable softening of the G-band is observed when the tensile strain increases from 1% to 7%. The red shift of the higher frequency peaks reduces the phonon group velocities and results in reduced thermal conductivity according to the classical lattice thermal transport theory.⁵³ The reduced phonon group velocities render less contribution from the phonon couplings to the interfacial heat flux, leading to higher thermal contact resistance between h-BN and graphene. A similar softening of the G-band was also seen in the Raman spectra of graphene flakes under uniaxial strain⁵⁴ and in few-layer graphene sheets under uniform in-plane strain.⁵⁵

Fig. 7 Dependence of interfacial thermal resistance on the tensile strain from 0–7%.

Fig. 8 Phonon power spectra of graphene under different tensile strains from 1–7%. The higher frequency peaks denote the G-bands. The red shift of the G-bands indicates group-velocity reduction in graphene.

4. Conclusion

Thermal transport across a linear heterojunction in a hybrid graphene/h-BN sheet is investigated using NEMD simulations. The effects of the system dimension, heat flux direction, temperature and tensile strain on interfacial thermal resistance R are explored comprehensively. It is found that the predicted R values are independent of the heat flux directions. When the hybrid sheet length increases from 20 nm to 100 nm, the interfacial thermal resistance decreased by 58% from 5.2 × 10⁻¹⁰ to 2.2 × 10⁻¹⁰ K m² W⁻¹. The spatiotemporal evolution of the thermal energies from graphene to h-BN indicates that the main energy carrier in graphene is the flexural phonon (ZA) mode, which also contributes to the highest energy transmission across the interface. Due to the increased phonon populations and higher inelastic phonon scattering rates, the R values decrease monotonically from 4.1 × 10⁻¹⁰ to 2.4 × 10⁻¹⁰ K m² W⁻¹ when the temperature increases from 200 K to 600 K. Lastly, we show that the interfacial thermal resistance increases with the tensile strain. Our study provides a fundamental understanding of thermal transport across the graphene/h-BN heterojunction, and a theoretical guidance for the design and development of hybrid sheet based nanodevices.

Acknowledgements

This work was supported by Nebraska Center for Energy Sciences Research and Holland Computing Center in the University of Nebraska-Lincoln.

References

1. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907.
2. S. Ghosh, I. Calizo, D. Teweldebrhan, E. P. Pokatilov, D. L. Nika, A. A. Balandin, W. Bao, F. Miao and C. N. Lau, Appl. Phys. Lett., 2008, 92, 151911.
3. X. Wang, A. Pakdel, J. Zhang, Q. Weng, T. Zhai, C. Zhi, D. Golberg and Y. Bando, Nanoscale Res. Lett., 2012, 7, 1–7.
4. L. Song, L. Ci, H. Lu, P. B. Sorokin, C. Jin, J. Ni, A. G. Kvashnin, D. G. Kvashnin, J. Lou, B. I. Yakobson and P. M. Ajayan, Nano Lett., 2010, 10, 3209–3215.
5. S. M. Kim, A. Hsu, M. H. Park, S. H. Chae, S. J. Yun, J. S. Lee, D. H. Cho, W. J. Fang, C. Lee, T. Palacios, M. Dresselhaus, K. K. Kim, Y. H. Lee and J. Kong, Nat. Commun., 2015, 6, 8662.
6. D. Golberg, Y. Bando, Y. Huang, T. Terao, M. Mitome, C. C. Tang and C. Y. Zhi, ACS Nano, 2010, 4, 2979–2993.
7. G. R. Bhimanapati, D. Kozuch and J. A. Robinson, Nanoscale, 2014, 6, 11671–11675.
8. X. M. Li, J. Yin, J. X. Zhou and W. L. Guo, Nanotechnology, 2014, 25, 105701.
9. J. Zhang, Y. Wang and X. Wang, Nanoscale, 2013, 5, 11598–11603.
10. Y. Hong, L. Li, X. C. Zeng and J. Zhang, Nanoscale, 2015, 7, 6286–6294.
11. M. Li, J. Zhang, X. Hu and Y. Yue, Appl. Phys. A, 2015, 119, 415–424.
12. J. Zhang, Y. Hong, Z. Tong, Z. Xiao, H. Bao and Y. Yue, Phys. Chem. Chem. Phys., 2015, 17, 23704–23710.
13. B. Liu, J. A. Baimova, C. D. Reddy, A. W.-K. Law, S. V. Dmitriev, H. Wu and K. Zhou, ACS Appl. Mater. Interfaces, 2014, 6, 18180–18188.
14. J. Zhang, Y. Hong and Y. Yue, J. Appl. Phys., 2015, 117, 134307.
15. B. Liu, F. Meng, C. D. Reddy, J. A. Baimova, N. Srikanth, S. V. Dmitriev and K. Zhou, RSC Adv., 2015, 5, 29193–29200.
16. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
17. G. Giovannetti, P. A. Khomyakov, G. Brocks, P. J. Kelly and J. van den Brink, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073103.
18. Y. Ma, Y. Dai, M. Guo, C. Niu and B. Huang, Nanoscale, 2011, 3, 3883–3887.
19. T. C. Nguyen, M. Otani and S. Okada, Phys. Rev. Lett., 2011, 106, 106801.
20. K. Kamiya, N. Umezawa and S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 153413.
21. M. H. Kang, S. C. Jung and J. W. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 085409.
22. B. Lee, S. Han and Y.-S. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075432.
23. W. B. Donald, A. S. Olga, A. H. Judith, J. S. Steven, N. Boris and B. S. Susan, J. Phys.: Condens. Matter, 2002, 14, 783.
24. J. Tersoff, Phys. Rev. Lett., 1988, 61, 2879–2882.
25. A. Kınacı, J. B. Haskins, C. Sevik and T. Çağın, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115410.
26. C. Sevik, A. Kinaci, J. B. Haskins and T. Çağın, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085409.
27. B. Mortazavi, L. F. C. Pereira, J.-W. Jiang and T. Rabczuk, Sci. Rep., 2015, 5, 13228.
28. I. Nikiforov, D.-M. Tang, X. Wei, T. Dumitricǎ and D. Golberg, Phys. Rev. Lett., 2012, 109, 025504.
29. J. Zhang and X. Wang, Nanoscale, 2013, 5, 734–743.
30. Y. Hong, J. Zhang, X. Huang and X. C. Zeng, Nanoscale, 2015, 7, 18716–18724.
31. J. Zhang, X. Wang and H. Xie, Phys. Lett. A, 2013, 377, 721–726.
32. J. Zhang, X. Wang and H. Xie, Phys. Lett. A, 2013, 377, 2970–2978.
33. R. E. Jones, J. C. Duda, X. W. Zhou, C. J. Kimmer and P. E. Hopkins, Appl. Phys. Lett., 2013, 102, 183119.
34. J. G. Park, Q. F. Cheng, J. Lu, J. W. Bao, S. Li, Y. Tian, Z. Y. Liang, C. Zhang and B. Wang, Carbon, 2012, 50, 2083–2090.
35. Z. Y. Ong, E. Pop and J. Shiomi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165418.
36. A. Tabarraei, Comput. Mater. Sci., 2015, vol. 108, Part A, pp. 66–71.
37. D. L. Nika, S. Ghosh, E. P. Pokatilov and A. A. Balandin, Appl. Phys. Lett., 2009, 94, 203103.
38. J. H. Seol, I. Jo, A. L. Moore, L. Lindsay, Z. H. Aitken, M. T. Pettes, X. Li, Z. Yao, R. Huang, D. Broido, N. Mingo, R. S. Ruoff and L. Shi, Science, 2010, 328, 213–216.
39. K. Saito, J. Nakamura and A. Natori, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115409.
40. L. Lindsay, D. A. Broido and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115427.
41. R. J. Stevens, L. V. Zhigilei and P. M. Norris, Int. J. Heat Mass Transfer, 2007, 50, 3977–3989.
42. M. Hu, P. Keblinski and B. Li, Appl. Phys. Lett., 2008, 92, 211908.
43. S. Vikas and T. Vikas, Nanotechnology, 2009, 20, 365701.
44. X. Han, H. Morgan Stewart, S. A. Shevlin, C. R. A. Catlow and Z. X. Guo, Nano Lett., 2014, 14, 4607–4614.
45. G. Zhang and Y. W. Zhang, Mech. Mater., 2015, 91, 382–398.
46. X. B. Li, K. Maute, M. L. Dunn and R. G. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245318.
47. T. Y. Guo, Z. D. Sha, X. J. Liu, G. Zhang, T. F. Guo, Q. X. Pei and Y. W. Zhang, Appl. Phys. A, 2015, 120, 1275–1281.
48. Q. X. Pei, Y. W. Zhang, Z. D. Sha and V. B. Shenoy, J. Appl. Phys., 2013, 114, 033526.
49. Y.-Y. Zhang, Q.-X. Pei, J.-W. Jiang, N. Wei and Y.-W. Zhang, Nanoscale, 2016, 8, 483–491.
50. Y. Y. Qin, Q. Y. Peng, Y. J. Ding, Z. S. Lin, C. H. Wang, Y. Li, J. J. Li, Y. Yuan, X. D. He and Y. B. Li, ACS Nano, 2015, 9, 8933–8941.
51. H. F. Zhan, G. Zhang, J. M. Bell and Y. T. Gu, Appl. Phys. Lett., 2014, 105, 153105.
52. J. W. Jiang, Carbon, 2015, 81, 688–693.
53. L. Shi, Nanoscale Microscale Thermophys. Eng., 2012, 16, 79–116.
54. O. Frank, G. Tsoukleri, J. Parthenios, K. Papagelis, I. Riaz, R. Jalil, K. S. Novoselov and C. Galiotis, ACS Nano, 2010, 4, 3131–3138.
55. J. Chen, J. H. Walther and P. Koumoutsakos, Nano Lett., 2014, 14, 819–825.

---