 Open Access Article
Open Access ArticleFeynman force components: basis for a solution to the covalent vs. ionic dilemma†
Justyna
Dominikowska
 *a,
Mirosław
Jabłoński
b and
Marcin
Palusiak
a
*a,
Mirosław
Jabłoński
b and
Marcin
Palusiak
a
aDepartment of Theoretical and Structural Chemistry, Faculty of Chemistry, University of Łódź, Pomorska 163/165, 90-236 Łódź, Poland. E-mail: justyna@uni.lodz.pl
bDepartment of Quantum Chemistry, Faculty of Chemistry, Nicolaus Copernicus University in Toruń, Gagarina 7, 87-100 Toruń, Poland
First published on 26th August 2016
Abstract
The Hellmann–Feynman theorem, when applied to nuclear coordinates in a molecular system, states that Feynman forces, i.e. forces acting on a nucleus in a molecule, are solely of an electrostatic nature. This theorem is described by Slater as “the most powerful” theorem applicable to molecules. However, its possibilities have hardly been harnessed. This work presents the use of the Hellmann–Feynman theorem in conjunction with the partitioning of the molecular space into atoms in the spirit of the quantum theory of atoms in molecules (QTAIM). Homopolar and heteropolar diatomic molecules of varying polarity are studied in the context of Feynman force components, i.e. the components exerted on each nucleus by the other nucleus and by the electron density distributions of each of the atoms. These results are further related to electronegativity differences used in the differentiation between covalent and ionic bond. The approach based on the directions of Feynman force components gives physical fundamentals for covalent vs. ionic bond distinction without referring to the electronegativity concept.
1. Introduction
This article is devoted to the distinction between covalent and ionic bond without directly referring to the vague electronegativity concept, instead making use solely of one of the most important theorems of chemistry – the Hellmann–Feynman theorem.1,2 The Hellmann–Feynman theorem1,2 states that for a system of total energy E, described by the time-independent Hamiltonian Ĥ, and a normalized wave function Ψ, the derivative of energy with respect to any parameter λ, appearing in the Hamiltonian, is equal to: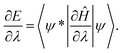 | (1) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) present in Ĥ depends on nuclear coordinates, eqn (1) takes the following form:
present in Ĥ depends on nuclear coordinates, eqn (1) takes the following form: | (2) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nA (please note that the notation used throughout the current study is presented in Scheme 1), into components corresponding to the repulsion by the nucleus of atom B,
nA (please note that the notation used throughout the current study is presented in Scheme 1), into components corresponding to the repulsion by the nucleus of atom B, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAnB, and to the attraction by the electron density of a whole molecule,
nAnB, and to the attraction by the electron density of a whole molecule, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAed. In addition, if one partitions the molecular space into atomic basins (according to the zero-flux gradient condition of space partitioning, as introduced in the quantum theory of atoms in molecules, QTAIM8), the force component,
nAed. In addition, if one partitions the molecular space into atomic basins (according to the zero-flux gradient condition of space partitioning, as introduced in the quantum theory of atoms in molecules, QTAIM8), the force component, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAed, can be further decomposed into the forces exerted on nucleus A by the electron density of atoms A,
nAed, can be further decomposed into the forces exerted on nucleus A by the electron density of atoms A, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA, and B,
nAedA, and B, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedB. Therefore, one may consider
nAedB. Therefore, one may consider ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nA using the formula:
nA using the formula:![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nA = nA = ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAnB + nAnB + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedB + nAedB + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA. nAedA. | (3) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB), and those coming from atom A (the electron density of atom A,
nAB), and those coming from atom A (the electron density of atom A, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA). If one applies this idea to eqn (3), the equation takes the form of eqn (4):
nAedA). If one applies this idea to eqn (3), the equation takes the form of eqn (4):![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nA = nA = ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB + nAB + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA. nAedA. | (4) |
Slater emphasized that the Feynman electrostatic theorem is one of “the most powerful theorems applicable to molecules”.9 Despite this, Fernandez Rico et al.10 observed that “the possibilities that it opens up have been scarcely exploited, and today the theorem is mostly regarded as a scientific curiosity”. At this time no studies have been devoted to the behavior of the components of the Feynman force. To fill this void, we analyze the Feynman force components present in eqn (3) for homopolar and heteropolar diatomic molecules in the present study. Our findings on the values and in particular on the directions of the Feynman force components allow us to establish a physical basis for the distinction between covalent and ionic bond without referring to the electronegativity concept.
2. Methodology
The geometries of all the systems investigated in the study were optimized without any symmetry constraints at the MP2 level of theory in conjunction with the aug-cc-pVTZ11 basis set. For equilibrium structures, a frequency analysis was carried out in order to verify whether optimized geometries correspond to potential energy surface minima. No imaginary frequencies were found. Both geometry optimization and frequency analysis were performed with the Gaussian 09 program.12 An analysis of electron density distribution in the framework of quantum theory of atoms in molecules (QTAIM)8 was carried out using the AIMAll program.13 Feynman forces were also computed with the use of AIMAll. It is important to note that for enhanced accuracy (resulting in much better zeroing of the sum of Feynman forces acting on each atom), formatted checkpoint files (*.fchk) from the Gaussian program were used as input files for AIMAll instead of the commonly used *.wfn or *.wfx wavefunction files. Since, in practice, forces obtained from an approximate wave function differ from those obtained from the corresponding gradient of energy (this difference manifests itself mainly in the force exerted on the nucleus of the atom by its own electron density), the “gradient-corrected” forces available in the AIMAll program were used in the study. The use of “gradient-corrected” forces led to much better Feynman force zeroing featuring the equilibrium geometries (the use of “gradient-corrected” forces improved the zeroing from the rank of 10−2 to 10−6 a.u.). It is worth noting that the QTAIM8 usage in this study was limited to the molecular space partitioning scheme based on the zero flux in the gradient vector field of the electron density. One should also note that both ionicity and covalency can be quantified14–16 within the quantum chemical topology (QCT)17 of which QTAIM8 is a part.3. Results and discussion
3.1. Homopolar diatomic systems
For the study of Feynman force components acting on nuclei in homopolar diatomic molecules, three systems are chosen, namely a helium dimer, a hydrogen molecule, and a nitrogen molecule. (For graphical representation of Feynman force components, see Fig. 1. The values of forces for those three systems are presented in Table S1 in the ESI.†) | ||
Fig. 1 Feynman force components acting on the nuclei in (a) He2, (b) H2 and (c) N2. The following arrow coloring is applied: red – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedB, blue – nAedB, blue – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAnB, green – nAnB, green – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA and gray – nAedA and gray – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB. nAB. | ||
In the case of a helium dimer, the force exerted on one helium nucleus by its own electron density – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHe1edHe1 – is very weak and directed towards the other He atom. The value of
nHe1edHe1 – is very weak and directed towards the other He atom. The value of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHe1edHe1 is lower by approximately three orders of magnitude than the forces exerted by the electron density or the nucleus of the second helium atom. Thus, in a helium dimer, the forces from the electron density and the nucleus of the other helium atom play a dominant role (their absolute value is 1.16 × 10−1 a.u.).
nHe1edHe1 is lower by approximately three orders of magnitude than the forces exerted by the electron density or the nucleus of the second helium atom. Thus, in a helium dimer, the forces from the electron density and the nucleus of the other helium atom play a dominant role (their absolute value is 1.16 × 10−1 a.u.). ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHe1edHe2 and
nHe1edHe2 and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHe1nHe2 nearly offset one another and
nHe1nHe2 nearly offset one another and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHe1He2 is a very small value (in the range of 10−4 a.u.). This is intuitive based on the fact that the binding energy in a helium dimer is extremely small, in the range of 10−6 kcal mol−1,18,19 and thus,
nHe1He2 is a very small value (in the range of 10−4 a.u.). This is intuitive based on the fact that the binding energy in a helium dimer is extremely small, in the range of 10−6 kcal mol−1,18,19 and thus, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHe1He2 in this system should also be weak. In the case of hydrogen and nitrogen molecules, the force directions are the same as in the case of a helium dimer, namely the force exerted on the nucleus of one atom by its own electron density is directed towards the other atom forming a molecule. This picture is in line with Berlin's theorem for diatomic molecules,20 in which the electron charge accumulation within the internuclear space provides a binding contribution. The nucleus of one atom is also attracted by the electron density of a neighboring atom and repulsed by its nucleus. The resultant force
nHe1He2 in this system should also be weak. In the case of hydrogen and nitrogen molecules, the force directions are the same as in the case of a helium dimer, namely the force exerted on the nucleus of one atom by its own electron density is directed towards the other atom forming a molecule. This picture is in line with Berlin's theorem for diatomic molecules,20 in which the electron charge accumulation within the internuclear space provides a binding contribution. The nucleus of one atom is also attracted by the electron density of a neighboring atom and repulsed by its nucleus. The resultant force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHe1He2 is repulsive and counteracts the force exerted on the nucleus by its own electron density. In the case of the hydrogen molecule, the force exerted on the nucleus of one hydrogen atom by its own electron density is of the same order of magnitude as the force exerted by the electron density of the other hydrogen atom, namely it is in the order of 10−1 a.u., which is less than the magnitude of the nucleus–nucleus repulsion (∼1 a.u.). In the case of a nitrogen molecule,
nHe1He2 is repulsive and counteracts the force exerted on the nucleus by its own electron density. In the case of the hydrogen molecule, the force exerted on the nucleus of one hydrogen atom by its own electron density is of the same order of magnitude as the force exerted by the electron density of the other hydrogen atom, namely it is in the order of 10−1 a.u., which is less than the magnitude of the nucleus–nucleus repulsion (∼1 a.u.). In the case of a nitrogen molecule, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nN1edN1 is in the range of 1 a.u. which is one order of magnitude lower than other forces acting on the nitrogen nucleus. Similar to the helium dimer and the hydrogen molecule,
nN1edN1 is in the range of 1 a.u. which is one order of magnitude lower than other forces acting on the nitrogen nucleus. Similar to the helium dimer and the hydrogen molecule, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nN1nN2 predominates the other forces. One may infer that, in the case of homopolar diatomic molecules, the repulsion between the nuclei is the greatest force because it counterbalances both the attractive force exerted on a nucleus of an atom by the electron density of the other atom and the force exerted on it by the atom's own electron density, which is also directed towards the other atom (see Fig. 1).
nN1nN2 predominates the other forces. One may infer that, in the case of homopolar diatomic molecules, the repulsion between the nuclei is the greatest force because it counterbalances both the attractive force exerted on a nucleus of an atom by the electron density of the other atom and the force exerted on it by the atom's own electron density, which is also directed towards the other atom (see Fig. 1).
3.2. Heteropolar diatomic systems
As representative examples of heteropolar diatomic molecules, three cases are chosen, namely HCl, HF and LiF. These three systems represent a variety of bond polarities. In the case of the least polar among them, HCl, the general pattern of Feynman forces is similar to the one found for the homopolar molecules (please compare Fig. 1 and 2(a)). For graphical representation of Feynman force components for heteropolar systems, see Fig. 2. Force values for these three systems are presented in Table S1 in the ESI.†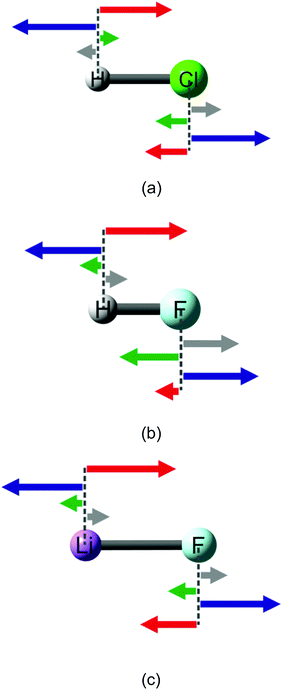 | ||
Fig. 2 Feynman force components acting on the nuclei in (a) HCl, (b) HF and (c) LiF. The following arrow coloring is applied: red – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedB, blue – nAedB, blue – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAnB, green – nAnB, green – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA and gray – nAedA and gray – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB. nAB. | ||
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHedH is nearly ten times weaker (in the range of 10−1 a.u.) than
nHedH is nearly ten times weaker (in the range of 10−1 a.u.) than ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHedCl. This means that
nHedCl. This means that ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHedCl and
nHedCl and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nHnCl are close to counterbalancing each other. In the case of forces acting on the chlorine nucleus (Fig. 2(a)), the attraction by its own electron density
nHnCl are close to counterbalancing each other. In the case of forces acting on the chlorine nucleus (Fig. 2(a)), the attraction by its own electron density ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nCledCl is nearly equal to the attraction by the hydrogen atom electron density
nCledCl is nearly equal to the attraction by the hydrogen atom electron density ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nCledH and the sum of those forces acting in the same direction is counterbalanced by the nucleus–nucleus repulsion
nCledH and the sum of those forces acting in the same direction is counterbalanced by the nucleus–nucleus repulsion ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nClnH (this repulsion among all the force components plays the dominant role). In the case of HCl, all Feynman force components acting on the chlorine nucleus are of the same order of magnitude, namely 1 a.u.
nClnH (this repulsion among all the force components plays the dominant role). In the case of HCl, all Feynman force components acting on the chlorine nucleus are of the same order of magnitude, namely 1 a.u.
When considering systems of higher polarity, the pattern of Feynman force components changes. In the case of either HF or LiF (Fig. 2(b) and (c), respectively), the force acting on the hydrogen or lithium atom nucleus by its own electron density, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA, is directed away from the fluorine nucleus. It can be intuitively explained with the formation of cation–anion bonding and significant electron density shift from either the hydrogen atom in HF or the lithium atom in LiF to the fluorine center (formation of a H or Li cation and a F anion). Relatively large negative net charge, derived from the anion and exerted on the cation, strongly polarizes the valence sphere of the cation, pushing its electrons ‘outside’ the molecule. Thus, in the case of ionic bonds, the dominant force, the attraction of a (formal) cation nucleus by the electron density of a fluorine (formal) anion, is counterbalanced by two forces, namely the repulsion of a cation nucleus by a nucleus of a fluorine anion and the force exerted on the cation nucleus by its own electron density. In both cases, the force exerted on the cation nucleus by its own electron density, being in the range of 10−1 a.u., is about one order of magnitude weaker than the other Feynman forces acting on the hydrogen or lithium nuclei in the respective fluorides.
nAedA, is directed away from the fluorine nucleus. It can be intuitively explained with the formation of cation–anion bonding and significant electron density shift from either the hydrogen atom in HF or the lithium atom in LiF to the fluorine center (formation of a H or Li cation and a F anion). Relatively large negative net charge, derived from the anion and exerted on the cation, strongly polarizes the valence sphere of the cation, pushing its electrons ‘outside’ the molecule. Thus, in the case of ionic bonds, the dominant force, the attraction of a (formal) cation nucleus by the electron density of a fluorine (formal) anion, is counterbalanced by two forces, namely the repulsion of a cation nucleus by a nucleus of a fluorine anion and the force exerted on the cation nucleus by its own electron density. In both cases, the force exerted on the cation nucleus by its own electron density, being in the range of 10−1 a.u., is about one order of magnitude weaker than the other Feynman forces acting on the hydrogen or lithium nuclei in the respective fluorides.
When considering forces acting on a fluorine nucleus in both HF and LiF, similarly to the chlorine nucleus in hydrogen chloride, the force exerted on the fluorine atom nucleus by its own electron density ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nFedF acts in the direction of the H or Li nucleus, respectively. An important difference between these systems is that, in the case of HF, the main factor counteracting the nucleus–nucleus repulsion is the attraction between the fluorine nucleus and the electron density of the fluorine atom, whilst in LiF, the attraction of the fluorine nucleus by the lithium atom electron density is the main factor. This can be explained with the fact that the hydrogen atom possesses no core electrons. Thus, the fluorine nucleus is less affected by the hydrogen atom electron density.
nFedF acts in the direction of the H or Li nucleus, respectively. An important difference between these systems is that, in the case of HF, the main factor counteracting the nucleus–nucleus repulsion is the attraction between the fluorine nucleus and the electron density of the fluorine atom, whilst in LiF, the attraction of the fluorine nucleus by the lithium atom electron density is the main factor. This can be explained with the fact that the hydrogen atom possesses no core electrons. Thus, the fluorine nucleus is less affected by the hydrogen atom electron density.
3.3. Physical basis for a solution to the covalent vs. ionic dilemma
According to the IUPAC definition21 electronegativity was introduced by Pauling as “the power of an atom to attract electrons to itself”. However, there is no unique definition of electronegativity. The most popular electronegativity scales are described by Pauling,22 Mulliken,23 Allred and Rochow,24 and Allen25 (it is worth noting that the units of the electronegativity scales differ from each other since they are based on different physical observables). Due to their definition, some Feynman force components may reflect “the power of an atom to attract electrons to itself”.21 To verify this intuitive hypothesis, for a set of nine heteropolar diatomic molecules, namely HF, HCl, HBr, LiF, LiCl, LiBr, NaF, NaCl and NaBr, electronegativity was compared to the![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB component of the Feynman force acting on the nucleus of an atom A. This component was chosen because it reflects the influence of the presence of atom B on nucleus A. The interrelation between the Pauling electronegativity difference, [χ(B) − χ(A)], and the value of force
nAB component of the Feynman force acting on the nucleus of an atom A. This component was chosen because it reflects the influence of the presence of atom B on nucleus A. The interrelation between the Pauling electronegativity difference, [χ(B) − χ(A)], and the value of force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is shown in Fig. 3 (note that the value of
nAB is shown in Fig. 3 (note that the value of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is considered to be negative when acting in the opposite direction to atom B, and positive otherwise).
nAB is considered to be negative when acting in the opposite direction to atom B, and positive otherwise).
In Fig. 3, it is clearly visible that there is an excellent correlation between electronegativity difference and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB force value for the three subsets of considered molecules, namely for HX, LiX and NaX, where X is a halogen atom. (Please see Table S3 in the ESI,† for the corresponding numerical data for
nAB force value for the three subsets of considered molecules, namely for HX, LiX and NaX, where X is a halogen atom. (Please see Table S3 in the ESI,† for the corresponding numerical data for ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB forces and for Pauling, Allred–Rochow and Allen electronegativity scales.) One may also notice that in the case of systems of the lowest electronegativity difference, namely for hydrogen bromide and hydrogen chloride, the value of
nAB forces and for Pauling, Allred–Rochow and Allen electronegativity scales.) One may also notice that in the case of systems of the lowest electronegativity difference, namely for hydrogen bromide and hydrogen chloride, the value of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is negative –
nAB is negative – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is directed away from atom B's nucleus. For the other systems the value of
nAB is directed away from atom B's nucleus. For the other systems the value of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is positive –
nAB is positive – ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is directed towards nucleus B. These results may be compared to the ones described in detail in Section 3.2, where Feynman force component patterns for hydrogen chloride and hydrogen fluoride are discussed.
nAB is directed towards nucleus B. These results may be compared to the ones described in detail in Section 3.2, where Feynman force component patterns for hydrogen chloride and hydrogen fluoride are discussed.
Electronegativity is a property allowing one to distinguish between the two important concepts in chemistry, namely the covalent and ionic bond. According to Pauling,26 the bond is ionic when the amount of its ionic character is greater than 50% (in other words, it is greater than the covalent character).21 The amount of ionic character (ionicity, fi) is defined with eqn (5) given by Pauling:26
| fi = 1 − e−¼[χ(B)−χ(A)]2. | (5) |
As was shown in Section 3.2, one may notice an important difference between the system of lower (HCl) and of much higher (HF and LiF) polarity. This difference is seen in the direction of the ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA force component and the direction of
nAedA force component and the direction of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB, where
nAB, where ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB = −
nAB = −![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAedA for diatomic molecules. For systems of higher polarity,
nAedA for diatomic molecules. For systems of higher polarity, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is directed towards the nucleus of atom B, whereas in the case of systems of lower polarity (also homopolar)
nAB is directed towards the nucleus of atom B, whereas in the case of systems of lower polarity (also homopolar) ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is directed away from atom B's nucleus. Since
nAB is directed away from atom B's nucleus. Since ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB reflects the influence of the presence of atom B on the nucleus of atom A, these opposite directions of
nAB reflects the influence of the presence of atom B on the nucleus of atom A, these opposite directions of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB may be interpreted as a physical basis for the distinction between covalent and ionic bond and can be compared to the distinction based on the percentage of ionic character. A straightforward relationship is found when instead of the
nAB may be interpreted as a physical basis for the distinction between covalent and ionic bond and can be compared to the distinction based on the percentage of ionic character. A straightforward relationship is found when instead of the ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB itself, as in Fig. 3, one considers the more general quantity
nAB itself, as in Fig. 3, one considers the more general quantity  . Similar to the sign of
. Similar to the sign of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB, this quantity, D, is positive when
nAB, this quantity, D, is positive when ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is directed towards atom B and negative otherwise. The value
nAB is directed towards atom B and negative otherwise. The value ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAnB is always negative by this convention, since this force is always repulsive when referring to the nucleus of atom B. This relationship is shown graphically in Fig. 4.
nAnB is always negative by this convention, since this force is always repulsive when referring to the nucleus of atom B. This relationship is shown graphically in Fig. 4.
 | ||
Fig. 4 Graphical representation of the interrelation between the Pauling electronegativity difference [χ(B) − χ(A)] and 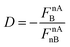 (gray circles – HX systems, blue circles – LiX, and green circles – NaX). (gray circles – HX systems, blue circles – LiX, and green circles – NaX). | ||
The correlation coefficient, R, for this interrelation is 0.974 (the coefficient of determination, R2, is close to 0.948). The plot shown in Fig. 4 directly links the change of the sign of D or the ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB direction (which is equivalent) with the covalent-ionic border based on the electronegativity difference. As mentioned previously there is no direct physical premise of this 50%-border distinction between the two types of bonding. Thus, instead of this a priori assumption, we propose the distinction based on a physical property, namely on the direction of the Feynman force component
nAB direction (which is equivalent) with the covalent-ionic border based on the electronegativity difference. As mentioned previously there is no direct physical premise of this 50%-border distinction between the two types of bonding. Thus, instead of this a priori assumption, we propose the distinction based on a physical property, namely on the direction of the Feynman force component ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB acting on the nucleus of an atom of a formal positive charge in a covalent or ionic bond. According to this new division, the bond is ionic when
nAB acting on the nucleus of an atom of a formal positive charge in a covalent or ionic bond. According to this new division, the bond is ionic when ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is directed towards atom B and the bond is covalent when
nAB is directed towards atom B and the bond is covalent when ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) nAB is directed away from atom B.
nAB is directed away from atom B.
4. Conclusions
In chemistry, the concepts of covalent and ionic bonds are of great importance. However, there has hitherto been no clear physical border between these two types of bonding. Feynman force components, coming directly from the Hellmann–Feynman theorem applied to nuclear coordinates, in conjunction with the partitioning of the molecular space into atoms allow distinction between covalent and ionic bonding. Thus, Feynman force components described in this study make a clear physically-grounded distinction between these two types of bonding instead of making use of e.g. a vague electronegativity concept.Acknowledgements
Calculations using the Gaussian 09 set of codes were carried out in Wrocław Center for Networking and Supercomputing (http://www.wcss.wroc.pl). Access to HPC machines and licensed software is gratefully acknowledged by JD and MP. MJ and MP acknowledge financial Grant OPUS9 2015/17/B/ST4/04050 from National Science Centre, Poland. JD additionally expresses her gratitude to Mrs Maria Hodorowicz, Mr Wojciech Gał-Pająk and Mrs Stanisław Frajcosz for their help during the revision process.References
- H. G. A. Hellmann, Z. Phys., 1933, 85, 180–190 CrossRef CAS.
- R. P. Feynman, Phys. Rev., 1939, 56, 340–343 CrossRef CAS.
- W. Pauli, Ann. Phys., 1922, 68, 177–240 CrossRef CAS.
- E. Schrödinger, Ann. Phys., 1926, 79, 361–379 CrossRef.
- M. Born and V. Fock, Z. Phys., 1928, 51, 165–169 CrossRef CAS.
- P. Güttinger, Z. Phys., 1931, 73, 169–184 CrossRef.
- R. F. W. Bader, J. Hernández-Trujillo and F. Cortés-Guzmán, J. Comput. Chem., 2007, 28, 4–14 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
- J. C. Slater, J. Chem. Phys., 1972, 57, 2389–2396 CrossRef CAS.
- J. Fernandez Rico, R. López, I. Ema and G. Ramírez, J. Chem. Theory Comput., 2005, 1, 1083–1095 CrossRef PubMed.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- T. A. Keith, AIMAll Professional, version 14.10.27, 2014, http://aim.tkgristmill.com Search PubMed.
- A. Martín Pendás, E. Francisco and M. A. Blanco, J. Phys. Chem. A, 2006, 110, 12864–12869 CrossRef PubMed.
- M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- M. García-Revilla, E. Francisco, P. L. A. Popelier and A. Martín Pendás, ChemPhysChem, 2013, 14, 1211–1218 CrossRef PubMed.
- P. L. A. Popelier, in The Chemical Bond II, ed. D. M. P. Mingos, Springer, 2016, ch. 2, pp. 71-117 Search PubMed.
- R. E. Grisenti, W. Schöllkopf, J. P. Toennies, G. C. Hegerfeldt, T. Köhler and M. Stoll, Phys. Rev. Lett., 2000, 85, 2284–2287 CrossRef CAS PubMed.
- M. Przybytek, W. Cencek, J. Komasa, G. Łach, B. Jeziorski and K. Szalewicz, Phys. Rev. Lett., 2010, 104, 183003 CrossRef CAS PubMed.
- T. Berlin, J. Chem. Phys., 1951, 19, 208–213 CrossRef CAS.
- IUPAC, Compendium of Chemical Terminology, 2nd edn (the “Gold Book”). Compiled by A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 1997. XML on-line corrected version: http://goldbook.iupac.org (2006-) by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins, ISBN 0-9678550-9-8, DOI: 10.1351/goldbook.
- L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1935, 3, 573–585 CrossRef CAS.
- A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264–268 CrossRef CAS.
- L. C. Allen, J. Am. Chem. Soc., 1989, 111, 9003–9014 CrossRef CAS.
- L. Pauling, The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, Cornell University Press, New York, 1960, pp. 97–102 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03774g |
| This journal is © the Owner Societies 2016 |


