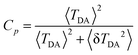Domain motions and electron transfer dynamics in 2Fe-superoxide reductase

Abstract

Superoxide reductases are non-heme iron enzymes that represent valuable model systems for the reductive detoxification of reactive oxygen species. In the present study, we applied different theoretical methods to study the structural dynamics of a prototypical 2Fe-superoxide reductase and its influence on electron transfer towards the active site. Using normal mode and essential dynamics analyses, we could show that enzymes of this type are capable of well-defined, electrostatically triggered domain movements, which may allow conformational proofreading for cellular redox partners involved in intermolecular electron transfer. Moreover, these global modes of motion were found to enable access to molecular configurations with decreased tunnelling distances between the active site and the enzyme's second iron centre. Using all-atom classical molecular dynamics simulations and the tunnelling pathway model, however, we found that electron transfer between the two metal sites is not accelerated under these conditions. This unexpected finding suggests that the unperturbed enzymatic structure is optimized for intramolecular electron transfer, which provides an indirect indication of the biological relevance of such a mechanism. Consistently, efficient electron transfer was found to depend on a distinct route, which is accessible via the equilibrium geometry and characterized by a quasi conserved tyrosine that could enable multistep-tunnelling (hopping). Besides these explicit findings, the present study demonstrates the importance of considering both global and local protein dynamics, and a generalized approach for the functional analysis of these aspects is provided.

---

Introduction

Reactive oxygen species (ROS) are partially reduced oxygen derivatives that are formed within the cell by reactions of molecular oxygen with radicals or transition metal sites. Despite their potential beneficial role, increased levels of ROS are known to severely harm essential cellular compounds. Consistently, ROS have also been associated with ageing and a wide range of diseases in humans.¹ Moreover, they can damage biological and synthetic transition metal compounds, and, as a consequence, detoxification of ROS is of major interest, both from chemical and medical points of view.

The superoxide anion radical, O₂˙⁻, is the most oxidized, one-electron reduced ROS. Superoxide effectively inactivates biological metal sites including FeS clusters that are vital constituents of many enzymes and electron transfer proteins.^2–7 Consequently, superoxide represents an important evolutionary factor, and most organisms have established molecular strategies for its detoxification.^2,3,8 In this respect, superoxide dismutase (SOD) represents a quasi ubiquitous class of enzymes that catalyse the disproportionation of superoxide, yielding O₂ and H₂O₂.^2,8,9 Superoxide reductase (SOR) represents an alternative detoxification system that catalyzes the one-electron reduction of superoxide to hydrogen peroxide:^2,8,10–22

O₂˙⁻ + 1e⁻ + 2H⁺ → H₂O₂

In all known SORs, this reaction takes place at a square-pyramidal Fe^II(His)₄(Cys)₁ non-heme iron centre that can transfer one electron via a well-characterized inner-sphere mechanism.^{2,8,20,23–40} Apart from a β-barrel fold harbouring this active site, the structures of different SOR enzymes may considerably differ, and only a few amino acids are strictly conserved.^2,8 While several SOR classes have been identified,^{8,15,19,41–43} most enzymes characterized so far can be described as canonical 1Fe- or 2Fe-SORs. While 1Fe-SORs are homotetrameric proteins containing four active site copies in a cube-shaped quaternary structure, we will focus on 2Fe-SORs, which form C₂-symmetric homodimers (Fig. 1).^2,8,44,45 In these enzymes, each of the two equal subunits is composed of two different iron-containing domains connected by a flexible loop of about 15 amino acids.^2,8 Here, the catalytic SOR-domain is characterized by the consensus β-barrel fold harbouring the active site (centre II), while a desulforedoxin-like DX-domain contains a distorted tetrahedral Fe^III/II(Cys)₄ site (centre I).^2,8,45,48

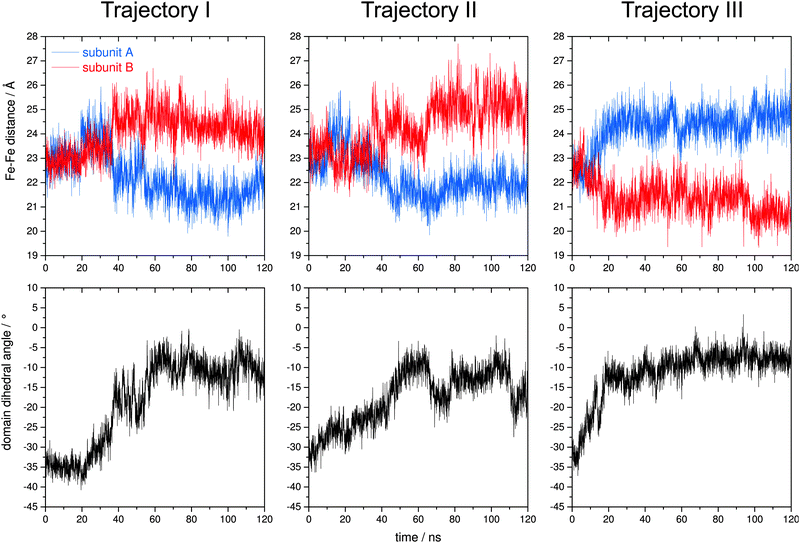
Fig. 1 Crystal structure of 2Fe-SOR from Dd (pdb entry: 1DFX).⁴⁵ The crystallographic C₂ axis is drawn as a dashed vertical line, and the different domains are indicated. The two equal subunits are colour-coded, and Fe atoms of centres I and II, depicted as green spheres, are labelled Fe1 and Fe2, respectively. Y115 indicates a quasi conserved tyrosine between both metals sites,^43,46,47 and approximate distances between Fe1, Fe2, and the Y115 side chain are displayed.

In contrast to superoxide disproportionation, the SOR reaction does not produce dioxygen, and the overall reducing power of the cell is decreased. Both aspects limit the (re-)formation of superoxide, and this may be crucial for anaerobic and microaerophilic organisms harbouring SOR.² On the other hand, the net reduction of superoxide requires an external thermodynamic driving force and efficient electron transfer to the active site. The latter may be accomplished by intermolecular electron transfer in both 1Fe- and 2Fe-SORs (Fig. 2A), and rubredoxin (RUB) and desulforedoxin (DX) have been identified as feasible electron shuttles.^{30,31,49–52} However, not all organisms harbouring SOR contain genes encoding RUB or DX.^2,8 In line with a pronounced lateral transfer of SOR genes,^2,8,43 this indicates alternative ways of electron donation that may not be uniform among different organisms.

Fig. 2 Schematic representation of possible electron transfer routes towards the active site of 2Fe-SOR. (A) Intermolecular electron transfer from a cellular electron shuttle, e.g. RUB or DX.^{30,31,49–52} (B) Intramolecular electron transfer between centres I and II, possibly mediated by a quasi conserved tyrosine residue between the two (Y115 in Dd 2Fe-SOR).^43,46,47 (C) Intermolecular electron transfer between centres I and II involving a cellular electron shuttle. (D) Intermolecular electron transfer between centres I and II of two different 2Fe-SOR molecules.⁴⁷ 2Fe-SOR domains are colour-coded, and Fe atoms of centres I and II, depicted as green spheres, are labelled Fe1 and Fe2, respectively. “Ext” refers to an external cellular electron shuttle.

For 2Fe-SOR, electron transfer to the active site may also proceed via centre I, which has a lower reduction potential than centre II^2,32,53,54 and a structure similar to the metal sites of electron shuttles RUB and DX.^2,8,20,25,45 Interestingly, both intra- and intermolecular electron transfer between centres I and II have been reported (Fig. 2B and D),^47,55 but natural and engineered variants lacking centre I have been found to be unimpaired in terms of superoxide reduction in vitro and in vivo.^19,56 While these latter findings indicate alternative ways of electron donation that may operate complementarily within the cell (vide supra), they do not exclude the above mechanisms per se. Another argument raised against intramolecular electron transfer between both metal centres refers to their large separation of about 22 Å (Fig. 1).² In principle, the rate of electron transfer decreases exponentially with the donor–acceptor distance;^57–60 however, examples of efficient biological electron transfer over similar distances have been reported.^58,60–62 In this respect, a quasi conserved tyrosine between the two metal sites (see S1, ESI†)^43,46,47 or cellular electron shuttles could serve as additional relay sites for electron/hole hopping in 2Fe-SOR (Fig. 1, 2B, and C).

It should also be stressed that the large interdomain Fe–Fe distance is inferred from crystal structure data (Fig. 1), which are not necessarily representative of the functional molecular configuration. First, the reported atomic coordinates may not reflect the native enzyme's equilibrium geometry in aqueous solution, and indeed X-ray diffraction data of SORs appear to suffer from photoreduction and structural constraints of the crystal lattice.^{2,24,25,44,63} In line with previous suggestions and the pronounced structural plasticity of these enzymes,^55,63,64 dynamic aspects may also enhance electron transfer between the two metal sites of 2Fe-SOR, e.g. by reducing the interdomain Fe–Fe distance. This may involve large-scale motions around the flexible regions between the DX and SOR domains, similar to proposals for other enzymes.^65–69

In the present study, we provide insights into the structural dynamics of 2Fe-SOR and its influence on a possible interdomain electron transfer between centres I and II, laying emphasis on an intramolecular mechanism (Fig. 2B). Using the enzyme from Desulfovibrio desulfuricans (Dd) as a model system, we applied elastic network model-based normal mode analysis (ENM-NMA),^70–76 molecular dynamics (MD) simulations,^77,78 and essential dynamics analysis (EDA)^75,76,79 to extract important molecular degrees of freedom. The impact of structural dynamics, individual amino acids, and other molecular properties on the electron transfer efficiency was then evaluated at the atomic level by the ‘pathways’ model described in the following.^80–86

The rate of biological electron transfer, k_ET, can be generally expressed as⁸⁷

where ℏ is the reduced Planck constant, k_B the Boltzmann constant, and T the temperature. While k_ET is also influenced by the driving force ΔG° and the reorganization energy λ, its exponential distance dependence is governed by T_DA,^{57–60,82,87} which can be interpreted as the electronic coupling between the electron donor (centre I) and acceptor (centre II). In a most basic scheme, T_DA is treated as a static or time-averaged property of a homogeneous tunnelling medium between the two. In contrast, the pathways model relates the electronic coupling to the protein structure at a given point of time, thereby revealing the effects of the backbone structure and individual amino acids in detail. Here, electron transfer is assumed to proceed via a sequence of steps through space, hydrogen bonds, and covalent bonds. The overall electronic coupling is then calculated as^82,86
where ε^C_i, ε^H_j, and ε^S_k are the decay parameters associated with tunnelling through the ith covalent bond, the jth hydrogen bond, and the kth space gap, respectively. Applying this approach to an ensemble of time-separated structures, the maximum electronic coupling for each configuration can be computed together with the associated electron transfer pathway, thereby revealing the influence of protein structural changes on these properties.⁸⁶ Note that a somewhat different approach has to be applied to evaluate the overall rate of electron tunnelling through a fluctuating medium.^88,89

Dynamic molecular properties of Dd 2Fe-SOR are visualized in Animations S1–S22 (ESI†), and an overview of all animated figures can be found in the ESI† (S2).

Computational details

Normal mode analysis

To evaluate relative atom displacements in low-frequency normal modes of Dd 2Fe-SOR by ENM-NMA, eigenvectors were calculated for the 100 smallest non-zero eigenvalues of the Hessian matrix by diagonalization. Calculations were performed on the NOMAD-Ref server (http://lorentz.immstr.pasteur.fr/nomad-ref.php),⁹⁰ which builds on the original force field by Tirion⁷⁰ extended by a distance weight function as first introduced by Hinsen.⁷⁴ The crystal structure of Dd 2Fe-SOR (pdb entry: 1DFX)⁴⁵ was used as the input equilibrium geometry, and all heavy atoms of the biological unit (homodimer) were considered in the elastic network. Distance-dependent atomic interactions were modelled from a global force constant of 100 kcal mol⁻¹ Å⁻², using a distance-weight and cut-off parameter of 5 and 10 Å, respectively. Normal mode amplitudes were scaled to an average root mean square deviation (RMSD) of 1 Å.

Molecular dynamics simulations

The crystal structure of Dd 2Fe-SOR (pdb entry: 1DFX)⁴⁵ was used as the input structure, and all heavy atoms of the biological unit (homodimer) were considered in the initial model. Hydrogen atoms were added according to neutral pH, and histidine and cysteine side chains were modelled as singly protonated and deprotonated, respectively.⁹¹ Histidine tautomers were guessed from the chemical environment of the side chains, i.e. for Fe-bound histidines, exchangeable hydrogen atoms were modelled as bound to the non-coordinated nitrogen atoms. Using VMD 1.9.1,⁹² the initial model was solvated in TIP3P water,⁹³ and Na⁺ and Cl⁻ ions were placed randomly to ensure neutrality and the presence of both positive and negative counterions (mimicking an ionic strength of 10 mM).

The system was simulated using NAMD 2.9 under periodic boundary conditions employing the CHARMM 27 force field.^94,95 In lack of adequate parameters describing the Fe centres, the distances between the corresponding metal ions and the coordinating amino acids were fixed to the values of the crystal structure during the MD simulations. While this simplification limits the analysis of (local) structural changes that involve metal ligand coordinates, the impact on global rearrangements that are robustly defined by the overall enzymatic architecture is expected to be small.^71–73 Metal ions of centres I and II were modelled as ferrous and ferric iron, respectively. After energy minimization and heating of the entire model to T = 300 K, water was equilibrated for 60 ps. The subsequent 120 ns production run was performed by Langevin piston dynamics⁹⁶ assuming a constant number of particles N, a constant temperature T = 300 K, and a constant pressure p = 1 atm (NpT ensemble). All bonds to hydrogen atoms were constrained by the SHAKE algorithm^97,98 to allow a time step of 2 fs. Short-range electrostatic and van-der-Waals interactions were cut at 12 Å. Long-range electrostatics were calculated using the Particle-Mesh Ewald summation.⁹⁹ Configurations were saved every 40 ps in the output trajectory.

Due to the size of the simulated system and the resulting computational cost, the number of MD production runs was limited to three. In this respect, a first repeat of the initial simulation (trajectory I) was initialized by a changed random seed to obtain different starting velocities (trajectory II). Moreover, a third run (trajectory III) was performed with a different initial distribution of Na⁺ and Cl⁻ ions to analyse environmental effects on the large scale protein dynamics.

Essential dynamics analysis

Using the ProDy program,¹⁰⁰ principal modes and their contribution to the overall atomic fluctuation were calculated by EDA based on C_α and Fe atoms for each MD trajectory as follows.⁷⁹ After filtering rotation and translation by aligning the trajectory to the first frame, the covariance matrix was constructed, using the average structure as a reference. Eigenvectors to the 20 largest eigenvalues of the covariance matrix were then calculated by diagonalization. Using the NMWiz plugin 1.0 in VMD 1.9.1,^92,100 principal mode amplitudes were scaled to an RMSD of 2 Å. For reasons outlined in the ESI† (S3), results from the EDA of trajectory III, as discussed in the manuscript, are based on the first 25 ns only. The results considering the entire trajectory are presented in S3 (ESI†) as well as Animations S7 and S8 (ESI†).

Pathways calculations

Maximum couplings and associated pathways were computed for all frames of the three MD trajectories, the biological unit of the Dd crystal structure (pdb entry: 1DFX, homodimer),⁴⁵ and the turning point geometries of selected low-frequency normal modes. All input structures included hydrogen atoms according to neutral pH and covalent bond information from the CHARMM topology file for proteins.^95,101 Histidine and cysteine side chains were modelled as singly protonated and deprotonated, respectively.⁹¹ Histidine tautomers were guessed from the chemical environment of the side chains, i.e. for Fe-bound histidines, exchangeable hydrogen atoms were modelled as bound to the non-coordinated nitrogen atoms. Covalent metal–ligand bonds not defined in the CHARMM topology file were added manually.

Pathways calculations were performed using a customized version of the pathways 1.2 plugin for VMD⁸⁶ that writes a detailed output for each frame during the evaluation of MD trajectories. Here, the penalty for tunnelling through the ith covalent bond, the jth hydrogen bond, and the kth space gap was calculated as ε^C_i = ε^C = 0.6, ε^H_j = (ε^C)² exp[−1.7(R_j − 2.8)], and ε^S_k = ε^C exp[−1.7(R_k − 1.4)], respectively, where R_j and R_k refer to the corresponding step distances in Å.^82,86,102 Through-space jumps were limited to 6 Å, while the cut-off angle and distance for hydrogen bond mediated steps was set to 30° and 3 Å, respectively. Fe atoms of centres I and II within one subunit were defined as electron donor and acceptor sites, respectively. Searches for pathways were performed by considering the entire enzyme as the tunnelling medium, and water molecules within a cut-off distance of 5 Å around the protein were included in the analyses where indicated. In the latter case, the molecule was centred within the periodic water box from the MD simulations prior to calculations using the PBCtools 2.6 plugin in VMD 1.9.1. Due to a limited number of native contacts within the elastic network, atom displacements within low-frequency normal modes were found to be overestimated for C_δ, C_ε, and N_ζ atoms of the surface exposed lysine K74. To avoid the inclusion of unreasonably extended covalent bond mediated steps, these atoms were excluded from pathways analyses of a domain torsional mode (vide infra).

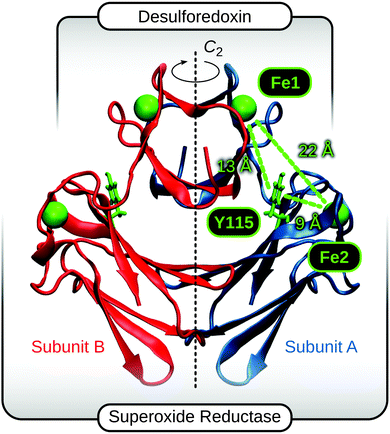
The coherence-like parameter C_p, evaluating the sensitivity of the maximum electronic coupling towards thermal fluctuations, was calculated within the pathways plugin as^86,103

where 〈T_DA〉² and 〈δT_DA²〉 are the squared arithmetic mean and the variance of T_DA, respectively. Further quantitative analyses of dominating tunnelling pathways and the involvement of the quasi conserved tyrosine Y115 were performed using a homemade program. For visualization purposes, all MD trajectories were aligned to the first frame prior to pathways calculations using the RMSD visualizer tool plugin in VMD 1.9.1.

Data evaluation and visualization

All quantities related to the molecular geometry were determined using VMD 1.9.1.⁹² For MD trajectories, RMSD values were calculated using the RMSD visualizer tool plugin in VMD 1.9.1 after aligning the whole trajectory to the first-frame reference structure of the protein. All molecular depictions were created in VMD 1.9.1,⁹² using the NMWiz plugin 1.0 for visualizing principal modes,¹⁰⁰ the VMD movie plugin 1.8 to generate animations, and STRIDE for the assignment of secondary structure motives.¹⁰⁴ Data evaluation and visualization, including the calculation of Spearman's rank correlation coefficient ρ, was performed using Origin 9.1.0 and OriginPro 8. All correlations with |ρ| > 0.05 are statistically significant at the 0.01 level. For reasons outlined in the ESI† (S3), correlation coefficients for trajectory III, as discussed in the manuscript, were based on the first 25 ns only. Results considering the entire trajectory are presented in Fig. S1 and S3–S8 (ESI†). All figures were prepared using Inkscape 0.47 and 0.48.

Results and discussion

Large scale domain motions of 2Fe-SOR

Normal mode analysis. To evaluate the influence of protein dynamics on a possible interdomain electron transfer in 2Fe-SOR, we first aimed at identifying internal modes of motion that could increase the electronic coupling between centres I and II. To this end, we used normal mode analysis based on an elastic network model (ENM-NMA) as a computationally cheap method that provides reasonable information on relative atom displacements in protein low-frequency normal modes.^70–76,90 While higher-frequency vibrations are often dominated by one or few internal coordinates, these thermally accessible modes involve domain motions and concerted atom movements that can be functionally relevant.^{63,64,71–73,75,76}

The electronic coupling decays with the donor–acceptor separation,^57–60,62 and, thus, the distance between centres I and II is expected to have a major influence on the rate of electron transfer between the two. Large scale motions associated with low-frequency normal modes^{70,71,73,75,76,105} could modulate the interdomain Fe–Fe distance, thereby providing access to molecular configurations that are more favourable in terms of interdomain electron transfer. To test this hypothesis, we evaluated the first 100 low-frequency normal modes of Dd 2Fe-SOR in terms of their interdomain Fe–Fe stretching amplitude. Here, the largest amplitude was observed for mode 11, which can be described as an interdomain hinge bend motion with a considerable out-of-phase Fe–Fe stretching character (Fig. 3, top; Animation S1, ESI†). This normal mode represents a reasonable candidate for intramolecular motions that could tune the protein structure for interdomain electron transfer.

Fig. 3 Effects of two low-frequency normal modes on the structure and electronic couplings of Dd 2Fe-SOR, as calculated by ENM-NMA and the pathways model.^86,90 (top) Front view schematic representation of interdomain Fe–Fe stretching mode 11. (bottom) Schematic representation of domain torsional mode 13, with the molecule viewed from the top along the crystallographic C₂ axis. Turning point structures where the Fe–Fe distance in subunit A and the Fe1–C1–C2–Fe2 dihedral angle is smallest (largest) are depicted on the left (right) for modes 11 and 13, respectively. The equilibrium geometry reflected by the crystal structure (pdb entry: 1DFX)⁴⁵ is shown as a reference in the centre. Electron transfer pathways corresponding to the two subunits are colour-coded, and Fe atoms of centres I and II, depicted as green spheres, are labelled Fe1 and Fe2, respectively. The quasi conserved tyrosine between both metals sites,^43,46,47 Y115 in Dd 2Fe-SOR, is shown in green. C1 and C2 are two points on the C₂ crystallographic axis (not shown). Mode amplitudes are scaled to an average RMSD of 1 Å, and dynamic representations of modes 11 and 13 are available as Animations S1 and S2 (ESI†), respectively.

Using the pathways model,^80–86 we then determined electronic couplings between the two metal sites for both classical turning points of mode 11 as well as the equilibrium molecular configuration reflected by the crystal structure. For the turning point structures, we found a larger (smaller) electronic coupling within the subunit exhibiting a decreased (increased) interdomain Fe–Fe distance (Fig. 3, top left and right). Taking the equilibrium structure as a reference (Fig. 3, top centre), a shortening of the Fe–Fe distance was found to exert a stronger influence on the electronic coupling than an equivalent elongation. This finding is in line with an exponential distance decay of T_DA and k_ET,^{57–60,82,87} providing a basis for a net gain in electron transfer efficiency upon distortion of the molecular geometry along this normal coordinate. With the current mode scaling, the calculated electronic couplings at the two turning points differ by an order of magnitude, which corresponds to a 100-fold increase in electron transfer efficiency. As a consequence, protein dynamics involving mode 11 might be biologically relevant for intramolecular electron transfer between centres I and II of 2Fe-SOR. With respect to this particular normal coordinate, Y115 appears to play a minor role in this mechanism (Fig. 3, top left and right), and its possible relevance for intramolecular electron transfer is seemingly limited to configurations close to the equilibrium geometry.

In proteins, which do not represent homogeneous tunnelling media,^{58,60,80–85} the internal degrees of freedom other than the donor–acceptor distance may affect the electronic coupling as well. In the case of 2Fe-SORs, any type of structural reorganization of the flexible region between the two metal-containing domains could, in principle, affect the electron transfer efficiency. Interestingly, the four Fe atoms of these enzymes do not lie in one plane according to crystal structure data (Fig. 3, bottom centre).^20,25,45 This can be interpreted as an equilibrium torsion with respect to the crystallographic C₂ axis (Fig. 1), and domain rotation around this symmetry element could affect electronic couplings in various ways. Such type of motion can be quantified by an Fe1–C1–C2–Fe2 dihedral angle, where Fe1 and Fe2 refer to the Fe atoms of centres I and II in one subunit, while C1 and C2 are two points on the C₂ axis. In Dd 2Fe-SOR, this dihedral angle is most strongly affected by normal mode 13, which is characterized by a pronounced C₂ rotation of the entire DX domain (Fig. 3, bottom; Animation S2, ESI†). Evaluating this mode, a different electron transfer pathway was found for increased dihedral angles, but no considerable changes in the electronic coupling were observed for either of the two turning point structures. In fact, the values are slightly smaller in both cases, indicating that the equilibrium structure represents the optimum configuration for electron transfer with respect to this normal coordinate. While domain torsion, as in mode 13, appears to be unfavourable for intramolecular electron transfer, it may be relevant for the overall dynamics of 2Fe-SOR and other mechanisms (vide infra).

Molecular dynamics simulations. Using ENM-NMA, we identified two modes of motion that could account for interdomain movements with a possible impact on electron transfer efficiencies in 2Fe-SOR. While pathways calculations revealed a notable influence of an interdomain Fe–Fe stretching mode on the electronic coupling, this finding should be interpreted with care, since ENM-NMA is subject to a number of limitations. In general, classical normal mode analysis is restricted to the harmonic approximation, and absolute mode amplitudes are not available.¹⁰⁶ Moreover, the influence of atom displacements on functional markers like T_DA can only be evaluated for one orthogonal degree of freedom at a time. As a consequence, the choice of functional mode candidates is somewhat arbitrary, the quantification of dynamic effects is ambiguous, and T_DA changes arising from molecular perturbations along multiple normal coordinates cannot be explored in a systematic manner. Additional limitations may arise from the simplified Hookean pair potential force field of the elastic network.⁷⁰ While this coarse-grained model is a suitable means to evaluate low-frequency modes in terms of collective motions,^70–76 its capability to describe individual atom displacements in detail is naturally limited. Moreover, solvent effects are not included, and the crystal structure is assumed to represent the equilibrium geometry,^70,74 which is not necessarily justified (vide supra).

Since the pathways model depends on atomic resolution molecular information, we next performed MD simulations using the crystal structure of Dd 2Fe-SOR as a starting geometry. This method uses an elaborate classical force field, and quantitative information on atom displacements is accessible by choosing adequate initial conditions.^77,78,107 Moreover, MD simulations are not restricted to harmonic motions, and solvent effects can be explicitly included. In the following, we will analyse three different MD trajectories with respect to encoded interdomain motions and their possible influence on electron transfer routes between the two metal centres of 2Fe-SOR. Here, trajectories I and II differ by the initial particle velocities only, while trajectory III uses a different starting distribution of Na⁺ and Cl⁻ ions.

MD simulations reveal atom displacements with respect to all degrees of freedom. While this is advantageous for evaluating the real-world dynamics of proteins, it complicates the identification of essential modes of motion that might be functionally relevant. To extract information on possible functional domain movements, we first compared all three trajectories to the above normal modes by analysing the time evolution of both the interdomain Fe–Fe distance and the domain torsion. Since the C₂ symmetry of Dd 2Fe-SOR is not retained during the MD simulations, the domain dihedral angle was redefined as Fe1–C1′–C2′–Fe2, where C1′ (C2′) specifies the centroid of the two Fe1 (Fe2) atoms. Evaluating the three trajectories with respect to these internal coordinates, we found that the interdomain Fe–Fe distance varies considerably during the simulations (Fig. 4, top). In all three cases, this quantity is increased in one subunit and simultaneously decreased in the other. Moreover, a clear out-of-phase motion is also reflected by a negative rank correlation ρ between Fe–Fe distances in subunits A and B (Fig. 5, top; Fig. S1, ESI†). This observation is reminiscent of mode 11, and Fe–Fe stretching amplitudes are comparable to the presented ENM-NMA results (2.5 Å with the current mode scaling). These findings indicate that this normal coordinate may indeed represent a dominating degree of freedom of potential functional relevance. Evaluating the domain dihedral angle, we also observe a considerable torsion of the DX domain by about 30° (Fig. 4, bottom). This value exceeds the amplitude of mode 13 (13.3° with the current mode scaling), highlighting the significance of this degree of freedom for 2Fe-SOR dynamics. For all three trajectories, the corresponding rearrangement yields a molecular geometry, where the four Fe atoms of Dd 2Fe-SOR reside nearly in one plane.

Fig. 4 Time evolution of selected internal coordinates of Dd 2Fe-SOR, plotted for all three MD trajectories. (top) Interdomain Fe–Fe distances for subunits A (blue) and B (red). (bottom) Domain dihedral angle defined as Fe1–C1′–C2′–Fe2, where Fe1 and Fe2 refer to the Fe atoms of centres I and II in one subunit, while C1′ (C2′) specifies the centroid of the two Fe1 (Fe2) atoms.

Fig. 5 Overview of the Spearman rank correlation coefficients ρ calculated for selected molecular properties of Dd 2Fe-SOR as extracted from the three MD trajectories. Entries are colour coded, where saturated red (blue) indicates a perfect positive (negative) correlation. Diagonal entries reflecting trivial self correlations are crossed out. For reasons outlined in the ESI† (S3), only the first 25 ns were considered in the calculation of ρ values for trajectory III. All correlations are statistically significant at the 0.01 level. (top) Correlations between selected internal coordinates (also see Fig. S1, ESI†). Fe–Fe A and Fe–Fe B refer to the interdomain Fe–Fe distances within the respective subunits. The interdomain torsion is defined as the dihedral angle Fe1–C1′–C2′–Fe2, where Fe1 and Fe2 refer to the Fe atoms of centres I and II in one subunit, while C1′ (C2′) specifies the centroid of the two Fe1 (Fe2) atoms. (bottom) Correlations between Fe1–Fe2 interdomain electronic couplings and selected geometric properties of the same subunit (also see Fig. S3–S8, ESI†). RMSD values were calculated with respect to the first trajectory frame. Electronic couplings were determined by the pathways model⁸⁶ in the presence (w/H₂O) and absence (w/o H₂O) of water.

Essential dynamics analysis. According to the above findings, interdomain rearrangements reflected by the MD trajectories may be expressed by a combination of normal modes 11 and 13; however, this conclusion is based on the evaluation of two internal marker coordinates only. To obtain a more representative picture of large scale rearrangements, we next used essential dynamics analysis (EDA)⁷⁹ to extract dominating modes of motion encoded in the MD trajectories. Technically, EDA is a principle component analysis (PCA) performed on a set of (time-separated) structures.^75,76,79 Similar to normal mode analysis (NMA), this technique yields a set of orthogonal modes of motion, called principal modes in the following. In both methods, each mode is characterized by an eigenvector of relative atom displacements, but the physical meaning of the corresponding eigenvalues is different.^75,76,79 In NMA, these quantities relate to the vibrational frequencies, and normal modes are listed according to increasing eigenvalues. In contrast, principal modes are listed in reverse order, and EDA eigenvalues reflect the contribution of each eigenvector to the overall mean square atomic fluctuation.§ Consistently, the first principal modes were reported to span an ‘essential’ configurational subspace, where few degrees of freedom describe large-scale concerted atom movements of potential functional relevance.^75,76,79

Using EDA, we calculated the first 20 principle modes of Dd 2Fe-SOR from the structural ensembles included in the individual MD trajectories. In all three cases, these few degrees of freedom were found to account for almost 90% of the overall atomic fluctuation, in line with expectations.⁷⁹ Even more, the first principle mode alone has a share of almost 60%, while each of the other modes contributes 10% at the most. This finding demonstrates that the first principle component represents an essential mode of motion encoded in the MD trajectories. Analysing the corresponding eigenvector for all three data sets, we found that the included interdomain motions resemble those of normal modes 11 and 13, as obtained by EDA-NMA (Animations S1–S10, ESI†). This is best illustrated by the first principal mode of trajectory III, which reflects a considerable rotation of the DX domain and clear out-phase changes of interdomain Fe–Fe distances (Animations S9 and S10, ESI†). Hence, these initially chosen coordinates represent valuable markers for large scale rearrangements in 2Fe-SOR, and the identified normal modes provide an easily accessible representation of the associated domain motions.

Electron transfer dynamics

Using different theoretical methods, we could show that 2Fe-SOR is capable of concerted large-scale motions that involve changes in the interdomain Fe–Fe distances and the rotation of the DX domain. In general, the structure of biological macromolecules is accepted to be evolutionary optimized, and this may apply to both static and dynamic properties.¹¹⁰ Thus, domain rearrangements of 2Fe-SOR are likely relevant for the enzymatic function, e.g. electron transfer to the active site.

Structural rearrangement and intermolecular electron transfer. While the concept of functional motions is most comprehensible for an intramolecular mechanism (Fig. 2B, vide infra), structural rearrangements might be beneficial for other types of interdomain electron transfers as well. Notably, mechanisms involving a second molecule of 2Fe-SOR (Fig. 2D) or an additional electron shuttle (Fig. 2C) are expected to depend on the formation of a well-defined protein–protein complex that enables efficient electronic coupling between the involved redox cofactors. Given the structural flexibility of 2Fe-SOR, the process of complex formation likely involves considerable rearrangements, triggered by protein–protein interactions. Evaluating the three MD trajectories, we found that the general appearance of large scale motions is comparable in all cases (vide supra). However, the direction of these movements is not uniform, as clearly reflected by the time evolution of interdomain Fe–Fe distances (Fig. 4, top; Animations S11–S22, ESI†). Here, MD trajectories I and II, which are identical except for the initial velocities, exhibit the same time evolution, i.e. subunit A evolves towards a closed configuration with a decreased Fe–Fe distance, while the opposite trend is observed for subunit B. Interestingly, these tendencies are reversed in simulation III, which includes a different starting distribution of Na⁺ and Cl⁻ ions. Thus, we propose that the observed domain rearrangement is electrostatically triggered, and similar effects can be expected upon interaction with a physiological redox partner. Reminiscent of the induced fit model for enzyme catalysis,¹¹¹ these structural rearrangements could facilitate the function of 2Fe-SOR by enhancing the specificity for suitable electron transfer partners, in line with the generalized concept of conformational proofreading.¹¹² Notably, this principle may play a role in all types of intermolecular electron transfer, including possible interdomain pathways (Fig. 2C and D) as well as the generally accepted direct route from a cellular electron shuttle to the active site (Fig. 2A).

Intramolecular electron transfer dynamics. According to ENM-NMA, motions that modulate the interdomain Fe–Fe distance could in principle enhance the efficiency of intramolecular interdomain electron transfer (Fig. 2B and 3, top). Given the intrinsic limitations of this method (vide supra), we next evaluated the electronic couplings of the three MD trajectories in order to obtain a comprehensive picture of electron transfer dynamics. Notably, the parameterization of the pathways model is optimized for covalent bond-mediated electron transfer through proteins. The results on electron transfer routes that are dominated by hydrogen bonds are less reliable, and, thus, the evaluation of pathways via water molecules is somewhat limited. Nonetheless, we also performed calculations including water in order to test the robustness of qualitative findings from the protein-only calculations.

Starting with an overall statistical evaluation, we found that average electronic couplings are comparable for all simulations, but different values are observed for the two subunits within one trajectory (Fig. 6). In all three cases, the subunit assuming a closed (open) configuration exhibits a higher (lower) average coupling. In line with correlation analyses (Fig. 5, bottom; S6, ESI†), this finding suggests that the electronic coupling decreases with the interdomain Fe–Fe distance in 2Fe-SOR. As expected, electron transfer in the open configuration is also more sensitive towards structural fluctuations, as indicated by lower values of the coherence-like parameter C_p (Fig. 6). Both qualitative conclusions are independent of the inclusion of water molecules in the analyses, supporting their relation to concerted domain rearrangements.

Fig. 6 Statistical analysis of interdomain electronic couplings between centres I and II within one subunit, as calculated by the pathways model⁸⁶ for all three MD trajectories. Data sets derived from analyses including (excluding) water are presented in blue (red). Arithmetic means, calculated from all time steps, are represented by vertical bars, while the corresponding standard deviations are indicated by whiskers. Values of the coherence-like parameter C_p are listed as white numbers. Subunits assuming a closed configuration during the MD simulations are indicated by an asterisk.

While these observations appear to support findings from ENM-NMA, the evaluation of time-averaged properties alone is insufficient to evaluate the possible functional role of the observed domain motions. To obtain more detailed insights, we next inspected the time evolution of electronic couplings for all MD trajectories and compared the observed values to those of equilibrium-like configurations, as observed in the initial time phase of the simulations (Fig. 7). Following this approach, we found that electronic couplings are clearly smaller than the equilibrium value, if an open configuration is assumed, in line with findings from ENM-NMA (Fig. 3, top). This effect is observed for subunit B in trajectories I and II as well as subunit A in trajectory III (Fig. 7). In these cases, the electronic coupling also exhibits a strong negative rank correlation with the interdomain Fe–Fe distance, the domain dihedral angle, and the RMSD value (Fig. 5, bottom; Fig. S6–S8, ESI†), which shows that the electron transfer efficiency in the open configuration decreases monotonically with increasing structural rearrangement. However, in contrast to expectations from ENM-NMA (Fig. 3, top), this trend is not inverted upon formation of a closed structure. Instead, we found that electronic couplings are barely increased for molecular configurations that exhibit sub-equilibrium interdomain Fe–Fe distances, as observed for subunit A in trajectories I and II as well as for subunit B in trajectory III (Fig. 4 and 7). Consistently, all rank correlations between the electronic coupling and the above structural markers are less pronounced in these cases (Fig. 5, bottom; Fig. S6–S8, ESI†). Both effects are observed for all three MD simulations and are independent of the inclusion of water molecules in the analyses.¶ Thus, we conclude that the observed domain rearrangements are not beneficial for a putative intramolecular electron transfer between centres I and II.

Fig. 7 Time evolution of interdomain electronic couplings between centres I and II within one subunit, as calculated by the pathways model⁸⁶ for all three MD trajectories. Values corresponding to subunit A (B) are plotted in blue (red), and datasets derived from pathways analyses including (excluding) water are presented at the bottom (top).

These unexpected observations provide a number of important implications for the pathways analysis of electron transfer dynamics and the possibility of an intramolecular mechanism in 2Fe-SOR. While domain rearrangements encoded in the MD trajectories are well described by two low-frequency normal modes, the corresponding pathways results are very different. This shows that the overall description of individual modes of motion, as provided by ENM-NMA, may be insufficient for the evaluation of electronic couplings and other properties that depend on precise information regarding all atomic coordinates. Specifically, ENM-NMA and MD data were found to differ in terms of the observed distance dependence of the electronic coupling. In this respect, pathways data obtained for normal mode 11 indicate that the electron transfer efficiency increases disproportionately with decreasing interdomain Fe–Fe distance (Fig. 3, top). In contrast, MD data show that large scale domain rearrangements in 2Fe-SOR yield electronic couplings that are equal to those of equilibrium-like configurations at the best, irrespective of the separation of centres I and II (Fig. 4 and 7). This observation is in contrast to the exponential distance dependence of the electron transfer efficiency expected for a homogeneous tunnelling medium. Thus, we propose that the equilibrium structure of 2Fe-SOR may be evolutionary optimized in terms of an intramolecular electron transfer between the two iron-containing domains.

According to this model, the electron transfer efficiency is expected to strongly depend on the local molecular configuration, i.e. the type and arrangement of amino acids within the intervening tunnelling medium. Thus, we next analysed the contribution of individual amino acids to the observed electron transfer pathways (S9, ESI†). If the aqueous solvent is explicitly included in these analyses, the relevance of specific side chains is generally decreased, as calculated electron transfer routes include mobile water molecules in most cases (Fig. S9 and S10, ESI;† see also footnote¶). Considering this finding and the fact that the associated electronic couplings may be less reliable (vide supra), we will focus on protein-only analyses in the following.

For all three MD trajectories, a single set of four amino acids accounts for more than 90% of the electron transfer pathways within the subunit assuming a closed configuration (Fig. 8 and Fig. S11, ESI†). This statement includes equilibrium-like configurations, as also reflected by the Dd 2Fe-SOR crystal structure (Fig. 3, centre). Besides mandatory cysteine residues involved in the metal centres (C10 and C116), dominating routes involve only two intervening amino acids, namely lysine K9 and the quasi conserved tyrosine Y115 that was previously proposed to mediate electron transfer between centres I and II.^46,47 This proposal is supported by the fact that Y115 is involved in 98, 90, and 100% of the pathways observed for trajectory I, II, and III, respectively. Even for the other subunit, assuming an open configuration, Y115 contributes to 80, 84, and 96% of the pathways, confirming the importance of this amino acid for intramolecular electron transfer (Fig. S12, ESI†). In contrast, the involvement of K9 and C10 is clearly decreased upon formation of an open configuration, while several other amino acids contribute more significantly. This demonstrates a shift to a different type of pathways, which is less efficient in terms of electron transfer (Fig. 6 and 7). Thus, we conclude that the rate of intramolecular electron transfer in Dd 2Fe-SOR is governed by the accessibility of feasible pathways involving the above amino acids rather than a simple distance dependence of the overall electronic coupling. For open configurations with large Fe–Fe distances, efficient electron transfer via this route is excluded by inappropriate arrangements of these amino acids. By contrast, this type of pathways is available in the apparently optimized equilibrium configuration, and global motions that decrease the Fe–Fe distance provide no access to more favourable electron transfer routes.

Fig. 8 Crystal structure of 2Fe-SOR from Dd (pdb entry: 1DFX)⁴⁵ visualizing the dominating route for intramolecular electron transfer between centres I and II within one subunit (green surface). The involved amino acids are shown in a liquorice representation and labelled in one letter code. The two equal subunits are colour-coded, and Fe atoms of centres I and II, depicted as green spheres, are labelled Fe1 and Fe2, respectively.

Conclusions and outlook

In the present study we applied several theoretical methods to explore the large scale dynamics of Dd 2Fe-SOR and its possible influence on electron transfer to the active site. We could show that enzymes of this type are capable of concerted atom movements, which can be described as a combined tilt-and-turn motion of the DX domain. The direction of these movements was found to depend on the initial distribution of external charges, indicating that domain rearrangement is induced electrostatically. Within the cell, protein–protein interactions may be the trigger, and large scale motions of 2Fe-SOR could facilitate the enzymatic function by conformational proofreading for redox partners involved in intermolecular electron transfer.

To specifically explore dynamic effects on intramolecular electron transfer rates, we evaluated the electronic coupling between centres I and II as a function of structural rearrangement. In contrast to expectations, we found that the electron transfer efficiency of equilibrium-like configurations is not exceeded, if the distance between the two metal centres is decreased. Apparently, an efficient electron transfer route is available via the equilibrium structure, and more feasible pathways are not accessible by protein dynamics – despite the large configurational space of the enzyme. Thus, the equilibrium structure may be evolutionary optimized for intramolecular electron transfer, which provides an indirect indication for the biological relevance of this mechanism. Consistently, a quasi conserved tyrosine, previously proposed as an electron relay between the two metal sites,^46,47 represents an integral constituent of the identified intramolecular route.

Large scale rearrangements observed for Dd 2Fe-SOR are determined by the overall architecture of the enzyme^71–73 and thus representative of canonical 2Fe-SORs in general. By contrast, intramolecular electron transfer efficiencies were found to depend on individual amino acids, and not all residues involved in the fast route through Dd 2Fe-SOR are conserved (K9, see S1, ESI†). Consequently, the realization and efficiency of intramolecular electron transfer between centres I and II may differ between individual 2Fe-SORs. In general, the in vivo feasibility of such a process depends on the local enzymatic structure and physiological redox partners available in the current host. Both aspects are neither uniform nor fully explored, which also implies that large scale protein dynamics with a beneficial effect on intramolecular electron transfer cannot be entirely excluded for other 2Fe-SORs.

In a more general sense, the present study revealed several fundamental aspects to be considered in the analysis of electron transfer and structural dynamics of proteins. We have demonstrated that electron transfer efficiencies may strongly depend on factors other than the donor–acceptor distance, including the type and arrangement of intervening amino acids as well as interactions with cellular electron shuttles. Thus, for protein classes with few conserved amino acids and a broad or heterogeneous spectrum of redox partners, the identification of a generalized electron transfer mechanism represents a demanding and probably misleading approach. In these cases, electron transfer routes and efficiencies may vary between or within individual proteins, which could explain seemingly contradictory results observed for 2Fe-SORs (vide supra).^19,47,55,56 Moreover, the dependence of electron transfer rates on individual amino acids also imposes considerable challenges to theoretical methods exploring the possible influence of protein dynamics since electronic couplings may depend both on the global and local molecular configuration. While global rearrangements are well-described by coarse-grained normal mode analysis, all-atom molecular dynamics simulations were found to be indispensable for exploring the influence of local fluctuations and concerted structural perturbations along more than one normal coordinate. The two types of information can be interrelated via essential dynamics analysis, and both capabilities and limitations of the individual techniques help to identify structural determinants of electron transfer efficiencies. In conclusion, we have introduced a generalized approach for the systematic evaluation of macromolecular dynamics and its influence on electronic couplings or other delicate properties.

In the future, this concept may be complemented by coarse-grained molecular dynamics simulations¹¹³ to further extend the accessible size- and time scales, thereby allowing the probing of large-scale multimolecular dynamics and related functional aspects in detail. Moreover, variational approaches for the identification of rigid protein subparts^114,115 and dynamics-based alignment strategies^116,117 could provide further insights into large-scale domain motions of proteins and their evolutionary conservation or convergence.

Acknowledgements

We thank Ilya Balabin for his dedicated support with regard to technical aspects of his ‘pathways’ plugin. This work was supported by the DFG (Cluster of Excellence ‘UniCat’). Molecular dynamics simulations were performed using resources provided by the North-German Supercomputing Alliance (HLRN).

References

1. M. Valko, D. Leibfritz, J. Moncol, M. T. D. Cronin, M. Mazur and J. Telser, Int. J. Biochem. Cell Biol., 2007, 39, 44–84.
2. Y. Sheng, I. A. Abreu, D. E. Cabelli, M. J. Maroney, A. F. Miller, M. Teixeira and J. S. Valentine, Chem. Rev., 2014, 114, 3854–3918.
3. J. A. Imlay, Annu. Rev. Microbiol., 2003, 57, 395–418.
4. J. A. Imlay, Mol. Microbiol., 2006, 59, 1073–1082.
5. A. Carlioz and D. Touati, EMBO J., 1986, 5, 623–630.
6. D. H. Flint, M. H. Emptage, M. G. Finnegan, W. Fu and M. K. Johnson, J. Biol. Chem., 1993, 268, 14732–14742.
7. P. R. Gardner and I. Fridovich, J. Biol. Chem., 1991, 266, 19328–19333.
8. A. F. Pinto, J. V. Rodrigues and M. Teixeira, Biochim. Biophys. Acta, 2010, 1804, 285–297.
9. J. M. McCord and I. Fridovich, J. Biol. Chem., 1969, 244, 6049–6055.
10. V. Niviere and M. Fontecave, JBIC, J. Biol. Inorg. Chem., 2004, 9, 119–123.
11. J. A. Imlay, JBIC, J. Biol. Inorg. Chem., 2002, 7, 659–663.
12. I. Moura, P. Tavares, J. J. Moura, N. Ravi, B. H. Huynh, M. Y. Liu and J. LeGall, J. Biol. Chem., 1990, 265, 21596–21602.
13. L. Chen, P. Sharma, G. J. Le, A. M. Mariano, M. Teixeira and A. V. Xavier, Eur. J. Biochem., 1994, 226, 613–618.
14. M. J. Pianzzola, M. Soubes and D. Touati, J. Bacteriol., 1996, 178, 6736–6742.
15. D. M. Kurtz, Jr., J. Inorg. Biochem., 2006, 100, 679–693.
16. D. M. Kurtz, Jr., Acc. Chem. Res., 2004, 37, 902–908.
17. S. I. Liochev and I. Fridovich, J. Biol. Chem., 1997, 272, 25573–25575.
18. F. E. Jenney, Jr., M. F. Verhagen, X. Cui and M. W. Adams, Science, 1999, 286, 306–309.
19. M. Lombard, D. Touati, M. Fontecave and V. Niviere, J. Biol. Chem., 2000, 275, 27021–27026.
20. G. Katona, P. Carpentier, V. Niviere, P. Amara, V. Adam, J. Ohana, N. Tsanov and D. Bourgeois, Science, 2007, 316, 449–453.
21. I. A. Abreu, L. M. Saraiva, J. Carita, H. Huber, K. O. Stetter, D. Cabelli and M. Teixeira, Mol. Microbiol., 2000, 38, 322–334.
22. E. D. Coulter, J. P. Emerson, D. M. Kurtz and D. E. Cabelli, J. Am. Chem. Soc., 2000, 122, 11555–11556.
23. J. V. Rodrigues, I. A. Abreu, D. Cabelli and M. Teixeira, Biochemistry, 2006, 45, 9266–9278.
24. M. D. Clay, F. E. Jenney, Jr., P. L. Hagedoorn, G. N. George, M. W. Adams and M. K. Johnson, J. Am. Chem. Soc., 2002, 124, 788–805.
25. V. Adam, A. Royant, V. Niviere, F. P. Molina-Heredia and D. Bourgeois, Structure, 2004, 12, 1729–1740.
26. C. Mathe, C. O. Weill, T. A. Mattioli, C. Berthomieu, C. Houee-Levin, E. Tremey and V. Niviere, J. Biol. Chem., 2007, 282, 22207–22216.
27. C. Mathe, T. A. Mattioli, O. Horner, M. Lombard, J. M. Latour, M. Fontecave and V. Niviere, J. Am. Chem. Soc., 2002, 124, 4966–4967.
28. C. Mathe, V. Niviere, C. Houee-Levin and T. A. Mattioli, Biophys. Chem., 2006, 119, 38–48.
29. J. V. Rodrigues, B. L. Victor, H. Huber, L. M. Saraiva, C. M. Soares, D. E. Cabelli and M. Teixeira, JBIC, J. Biol. Inorg. Chem., 2008, 13, 219–228.
30. J. P. Emerson, E. D. Coulter, R. S. Phillips and D. M. Kurtz, Jr., J. Biol. Chem., 2003, 278, 39662–39668.
31. J. V. Rodrigues, L. M. Saraiva, I. A. Abreu, M. Teixeira and D. E. Cabelli, JBIC, J. Biol. Inorg. Chem., 2007, 12, 248–256.
32. V. Niviere, M. Asso, C. O. Weill, M. Lombard, B. Guigliarelli, V. Favaudon and C. Houee-Levin, Biochemistry, 2004, 43, 808–818.
33. M. D. Clay, T. C. Yang, F. E. Jenney, Jr., I. Y. Kung, C. A. Cosper, R. Krishnan, D. M. Kurtz, Jr., M. W. Adams, B. M. Hoffman and M. K. Johnson, Biochemistry, 2006, 45, 427–438.
34. V. Niviere, M. Lombard, M. Fontecave and C. Houee-Levin, FEBS Lett., 2001, 497, 171–173.
35. I. A. Abreu, L. M. Saraiva, C. M. Soares, M. Teixeira and D. E. Cabelli, J. Biol. Chem., 2001, 276, 38995–39001.
36. J. P. Emerson, E. D. Coulter, D. E. Cabelli, R. S. Phillips and D. M. Kurtz, Jr., Biochemistry, 2002, 41, 4348–4357.
37. M. Lombard, C. Houee-Levin, D. Touati, M. Fontecave and V. Niviere, Biochemistry, 2001, 40, 5032–5040.
38. C. Mathe, V. Niviere and T. A. Mattioli, J. Am. Chem. Soc., 2005, 127, 16436–16441.
39. P. H.-L. Sit, A. Migliore, M.-H. Ho and M. L. Klein, J. Chem. Theory Comput., 2010, 6, 2896–2909.
40. T. A. Rokob, J. Chalupský, D. Bím, P. C. Andrikopoulos, M. Srnec and L. Rulíšek, JBIC, J. Biol. Inorg. Chem. DOI:10.1007/s00775-016-1357-8.
41. A. S. Pereira, P. Tavares, F. Folgosa, R. M. Almeida, I. Moura and J. J. G. Moura, Eur. J. Inorg. Chem., 2007, 2569–2581.
42. C. Kratzer, C. Welte, K. Dorner, T. Friedrich and U. Deppenmeier, FEBS J., 2011, 278, 442–451.
43. C. Lucchetti-Miganeh, D. Goudenege, D. Thybert, G. Salbert and F. Barloy-Hubler, BMC Microbiol., 2011, 11, 105.
44. A. P. Yeh, Y. Hu, F. E. Jenney, Jr., M. W. Adams and D. C. Rees, Biochemistry, 2000, 39, 2499–2508.
45. A. V. Coelho, P. Matias, V. Fülöp, A. Thompson, A. Gonzalez and M. A. Carrondo, JBIC, J. Biol. Inorg. Chem., 1997, 2, 680–689.
46. M. D. Clay, F. E. Jenney, Jr., H. J. Noh, P. L. Hagedoorn, M. W. Adams and M. K. Johnson, Biochemistry, 2002, 41, 9833–9841.
47. F. Bonnot, S. Duval, M. Lombard, J. Valton, C. Houee-Levin and V. Niviere, JBIC, J. Biol. Inorg. Chem., 2011, 16, 889–898.
48. M. Archer, R. Huber, P. Tavares, I. Moura, J. J. Moura, M. A. Carrondo, L. C. Sieker, J. LeGall and M. J. Romao, J. Mol. Biol., 1995, 251, 690–702.
49. M. J. Brumlik and G. Voordouw, J. Bacteriol., 1989, 171, 4996–5004.
50. F. Auchere, R. Sikkink, C. Cordas, P. Raleiras, P. Tavares, I. Moura and J. J. Moura, JBIC, J. Biol. Inorg. Chem., 2004, 9, 839–849.
51. J. V. Rodrigues, I. A. Abreu, L. M. Saraiva and M. Teixeira, Biochem. Biophys. Res. Commun., 2005, 329, 1300–1305.
52. F. Auchere, S. R. Pauleta, P. Tavares, I. Moura and J. J. Moura, JBIC, J. Biol. Inorg. Chem., 2006, 11, 433–444.
53. C. Berthomieu, F. Dupeyrat, M. Fontecave, A. Vermeglio and V. Niviere, Biochemistry, 2002, 41, 10360–10368.
54. P. Tavares, N. Ravi, J. J. Moura, J. LeGall, Y. H. Huang, B. R. Crouse, M. K. Johnson, B. H. Huynh and I. Moura, J. Biol. Chem., 1994, 269, 10504–10510.
55. F. Folgosa, C. M. Cordas, J. A. Santos, A. S. Pereira, J. J. Moura, P. Tavares and I. Moura, Biochem. J., 2011, 438, 485–494.
56. J. P. Emerson, D. E. Cabelli and D. M. Kurtz, Jr., Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3802–3807.
57. H. B. Gray and J. R. Winkler, Annu. Rev. Biochem., 1996, 65, 537–561.
58. H. B. Gray and J. R. Winkler, Biochim. Biophys. Acta, 2010, 1797, 1563–1572.
59. H. B. Gray and J. R. Winkler, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3534–3539.
60. H. B. Gray and J. R. Winkler, Q. Rev. Biophys., 2003, 36, 341–372.
61. J. R. Winkler and H. B. Gray, J. Am. Chem. Soc., 2014, 136, 2930–2939.
62. J. J. Warren, M. E. Ener, A. Vlcek, J. R. Winkler and H. B. Gray, Coord. Chem. Rev., 2012, 256, 2478–2487.
63. M. Horch, A. F. Pinto, T. Utesch, M. A. Mroginski, C. V. Romao, M. Teixeira, P. Hildebrandt and I. Zebger, Phys. Chem. Chem. Phys., 2014, 16, 14220–14230.
64. M. Horch, P. Hildebrandt and I. Zebger, Phys. Chem. Chem. Phys., 2015, 17, 18222–18237.
65. M. Sezer, R. Spricigo, T. Utesch, D. Millo, S. Leimkühler, M. A. Mroginski, U. Wollenberger, P. Hildebrandt and I. M. Weidinger, Phys. Chem. Chem. Phys., 2010, 12, 7894–7903.
66. A. Pacheco, J. T. Hazzard, G. Tollin and J. H. Enemark, JBIC, J. Biol. Inorg. Chem., 1999, 4, 390–401.
67. T. Utesch, M. Sezer, I. M. Weidinger and M. A. Mroginski, Langmuir, 2012, 28, 5761–5769.
68. T. Utesch and M. A. Mroginski, J. Phys. Chem. Lett., 2010, 1, 2159–2164.
69. T. C. Tan, D. Kracher, R. Gandini, C. Sygmund, R. Kittl, D. Haltrich, B. M. Hallberg, R. Ludwig and C. Divne, Nat. Commun., 2015, 6, 7542.
70. M. M. Tirion, Phys. Rev. Lett., 1996, 77, 1905–1908.
71. I. Bahar, T. R. Lezon, L. W. Yang and E. Eyal, Annu. Rev. Biophys., 2010, 39, 23–42.
72. E. C. Dykeman and O. F. Sankey, J. Phys.: Condens. Matter, 2010, 22, 423202.
73. I. Bahar and A. J. Rader, Curr. Opin. Struct. Biol., 2005, 15, 586–592.
74. K. Hinsen, Proteins, 1998, 33, 417–429.
75. S. Hayward and B. L. de Groot, Methods Mol. Biol., 2008, 443, 89–106.
76. S. Hayward and N. Go, Annu. Rev. Phys. Chem., 1995, 46, 223–250.
77. M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652.
78. S. A. Adcock and J. A. McCammon, Chem. Rev., 2006, 106, 1589–1615.
79. A. Amadei, A. B. Linssen and H. J. Berendsen, Proteins, 1993, 17, 412–425.
80. D. N. Beratan, J. N. Onuchic and J. J. Hopfield, J. Chem. Phys., 1987, 86, 4488–4498.
81. D. N. Beratan and J. N. Onuchic, Photosynth. Res., 1989, 22, 173–186.
82. D. N. Beratan, J. N. Betts and J. N. Onuchic, Science, 1991, 252, 1285–1288.
83. D. N. Beratan, J. N. Onuchic, J. R. Winkler and H. B. Gray, Science, 1992, 258, 1740–1741.
84. J. N. Onuchic and D. N. Beratan, J. Chem. Phys., 1990, 92, 722–733.
85. J. N. Onuchic, D. N. Beratan, J. R. Winkler and H. B. Gray, Annu. Rev. Biophys. Biomol. Struct., 1992, 21, 349–377.
86. I. A. Balabin, X. Q. Hu and D. N. Beratan, J. Comput. Chem., 2012, 33, 906–910.
87. R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322.
88. A. Troisi, A. Nitzan and M. A. Ratner, J. Chem. Phys., 2003, 119, 5782–5788.
89. S. S. Skourtis, I. A. Balabin, T. Kawatsu and D. N. Beratan, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3552–3557.
90. E. Lindahl, C. Azuara, P. Koehl and M. Delarue, Nucleic Acids Res., 2006, 34, W52–W56.
91. M. Horch, A. F. Pinto, M. A. Mroginski, M. Teixeira, P. Hildebrandt and I. Zebger, RSC Adv., 2014, 4, 54091–54095.
92. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
93. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
94. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
95. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
96. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
97. W. F. van Gunsteren and H. J. C. Berendsen, Mol. Phys., 1977, 34, 1311–1327.
98. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
99. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
100. A. Bakan, L. M. Meireles and I. Bahar, Bioinformatics, 2011, 27, 1575–1577.
101. A. D. MacKerell, M. Feig and C. L. Brooks, J. Comput. Chem., 2004, 25, 1400–1415.
102. G. L. Closs and J. R. Miller, Science, 1988, 240, 440–447.
103. I. A. Balabin and J. N. Onuchic, Science, 2000, 290, 114–117.
104. D. Frishman and P. Argos, Proteins, 1995, 23, 566–579.
105. N. Go, Biophys. Chem., 1990, 35, 105–112.
106. E. B. Wilson, P. C. Cross and J. C. Decius, Molecular Vibrations. The Theory of Infrared and Raman Vibrational Spectra., McGraw-Hill Book Company, 1955.
107. A. R. Leach, Molecular modelling: principles and applications, Pearson education, 2001.
108. S. Hayward, A. Kitao and N. Go, Protein Sci., 1994, 3, 936–943.
109. A. Kitao, F. Hirata and N. Go, Chem. Phys., 1991, 158, 447–472.
110. C. Micheletti, Phys. Life Rev., 2013, 10, 1–26.
111. D. E. Koshland, Jr., Proc. Natl. Acad. Sci. U. S. A., 1958, 44, 98.
112. Y. Savir and T. Tlusty, PLoS One, 2007, 2, e468.
113. M. G. Saunders and G. A. Voth, Annu. Rev. Biophys., 2013, 42, 73–93.
114. R. Potestio, F. Pontiggia and C. Micheletti, Biophys. J., 2009, 96, 4993–5002.
115. T. Aleksiev, R. Potestio, F. Pontiggia, S. Cozzini and C. Micheletti, Bioinformatics, 2009, 25, 2743–2744.
116. A. Zen, V. Carnevale, A. M. Lesk and C. Micheletti, Protein Sci., 2008, 17, 918–929.
117. R. Potestio, T. Aleksiev, F. Pontiggia, S. Cozzini and C. Micheletti, Nucleic Acids Res., 2010, 38, W41–W45.

---

Footnotes

† Electronic supplementary information (ESI) available: Sequence alignment for 2Fe-superoxide reductases; additional information on data treatment; supplementary data from molecular dynamics simulations and pathway analyses; and dynamic representations of normal modes, principal modes, molecular dynamics trajectories, and electron transfer pathways. See DOI: 10.1039/c6cp03666j

‡ These authors contributed equally.

§ The reverse ordering of modes in NMA and EDA is physically meaningful, since squared (effective) mode frequencies and (mass-weighted) mean square fluctuations are reciprocal in both methods.^76,105 Consistently, low-eigenvalue normal modes and high-eigenvalue principal modes were reported to span the same configurational subspace.^108,109

¶ If water is included, time traces in Fig. 7 exhibit stronger fluctuations, since electronic couplings are more sensitive to fast thermal motions (in line with lower C_p values, see Fig. 6). This can be explained by the additional degrees of freedom related to the rotation and translation of water molecules, which also reduce most rank correlations between the electronic coupling and the selected structural markers (Fig. 5, bottom and Fig. S6–S8, ESI†).

---