Open Access Article
Open Access ArticleDensity functional simulation of resonant inelastic X-ray scattering experiments in liquids: acetonitrile†
Johannes
Niskanen
*ab,
Kuno
Kooser
cd,
Jaakko
Koskelo
b,
Tanel
Käämbre
d,
Kristjan
Kunnus‡
ae,
Annette
Pietzsch
a,
Wilson
Quevedo
a,
Mikko
Hakala
b,
Alexander
Föhlisch
ae,
Simo
Huotari
b and
Edwin
Kukk
c
aInstitute for Methods and Instrumentation for Synchrotron Radiation Research, Helmholtz-Zentrum Berlin for Materials and Energy, Albert-Einstein-Str 15, D-12489, Berlin, Germany. E-mail: johannes.niskanen@helmholtz-berlin.de
bDepartment of Physics, University of Helsinki, Gustav Hällströmin katu 2a, FI-00014, Helsinki, Finland
cDepartment of Physics and Astronomy, University of Turku, Vesilinnantie 5, FI-20014 Turku, Finland
dInstitute of Physics, University of Tartu, W. Ostwaldi 1, EE-50411 Tartu, Estonia
eInstitut für Physik und Astronomie, Universität Potsdam, Karl-Liebknecht-Strasse 24/25, D-14476 Potsdam, Germany
First published on 9th September 2016
Abstract
In this paper we report an experimental and computational study of liquid acetonitrile (H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) by resonant inelastic X-ray scattering (RIXS) at the N K-edge. The experimental spectra exhibit clear signatures of the electronic structure of the valence states at the N site and incident-beam-polarization dependence is observed as well. Moreover, we find fine structure in the quasielastic line that is assigned to finite scattering duration and nuclear relaxation. We present a simple and light-to-evaluate model for the RIXS maps and analyze the experimental data using this model combined with ab initio molecular dynamics simulations. In addition to polarization-dependence and scattering-duration effects, we pinpoint the effects of different types of chemical bonding to the RIXS spectrum and conclude that the H2C–C
N) by resonant inelastic X-ray scattering (RIXS) at the N K-edge. The experimental spectra exhibit clear signatures of the electronic structure of the valence states at the N site and incident-beam-polarization dependence is observed as well. Moreover, we find fine structure in the quasielastic line that is assigned to finite scattering duration and nuclear relaxation. We present a simple and light-to-evaluate model for the RIXS maps and analyze the experimental data using this model combined with ab initio molecular dynamics simulations. In addition to polarization-dependence and scattering-duration effects, we pinpoint the effects of different types of chemical bonding to the RIXS spectrum and conclude that the H2C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH isomer, suggested in the literature, does not exist in detectable quantities. We study solution effects on the scattering spectra with simulations in liquid and in vacuum. The presented model for RIXS proved to be light enough to allow phase-space-sampling and still accurate enough for identification of transition lines in physical chemistry research by RIXS.
NH isomer, suggested in the literature, does not exist in detectable quantities. We study solution effects on the scattering spectra with simulations in liquid and in vacuum. The presented model for RIXS proved to be light enough to allow phase-space-sampling and still accurate enough for identification of transition lines in physical chemistry research by RIXS.
Photon-in—photon-out X-ray spectroscopies are highly useful tools for studying the electronic structure and chemistry of gaseous and condensed matter systems. One of the tools that carry most relevant information on the bonding and dynamics of molecular matter, is resonant inelastic X-ray scattering (RIXS) spectroscopy. A RIXS event stems from the coupling of the processes of X-ray absorption and emission.1–3 When performed at a K edge of an element, the RIXS technique provides a local probe of both the unoccupied and the occupied electronic orbitals in a single experiment, and in an element and site-selective manner. Due to the relative orientations of the absorption and emission transition dipoles, the scattering process also manifests polarization dependence in the angular distribution of the emitted photons4–7 which may be used to identify the symmetries of the participating states. Furthermore, the RIXS scattering duration can be modified by detuning the incident beam energy from the resonance,8–10 which may be used in studies of the nuclear motion and related potential energy surfaces in the femtosecond range. All these features of the method make it a good probe for physical chemistry.
RIXS process in polyatomic molecules can be simulated in numerous approaches including multiconfiguration self-consistent field method11–13 and density functional theory (DFT).14 Although accurate, multiconfiguration calculations are heavy if solvent effects or ensemble sampling are needed. On the other hand, absorption or emission simulations based on DFT,15 or many-body perturbation theory16,17 can be performed for simulation cells of up to few hundreds atoms. Such models make it possible to base the simulation on snapshots from structural simulations like molecular dynamics.18,19 DFT-based methods allow treating the solute and the solvent on equal footing in a periodically repeated simulation box, without the need to define the “solvent” and the “solute”.
In this study we present a DFT-based model for resonant inelastic scattering that leaves the system in an excited electronic state. We apply this model based on transition potential approximation, and perform spectrum calculations for snapshots from ab initio molecular dynamics simulations utilizing periodic boundary conditions for a supercell of ∼14 Å. The approach allows simulating the wavefunction of the whole cell on DFT level, both for the structural simulation and for the scattering process. We test the method in a statistical simulation of liquid acetonitrile at the nitrogen K-edge to explore the electronic structure and configurational diversity as seen in the RIXS spectra of the liquid phase. We also pinpoint the effects due to solvation by separate simulations. The molecule has been suggested to exist in H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and H2C
N and H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH isomers,20,21 which we study separately. We present an experiment performed at several incident energies and find basic agreement with a previous experiment performed at 400.45 eV.7 The spectral evidence does not support the proposed presence of H2C–C
NH isomers,20,21 which we study separately. We present an experiment performed at several incident energies and find basic agreement with a previous experiment performed at 400.45 eV.7 The spectral evidence does not support the proposed presence of H2C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH isomer in the system, because of the lack of its predicted spectral fingerprints in the experiment. Moreover, in accordance with Dierker et al.7 we observe incident-beam-polarization dependence of the spectra recorded in a fixed direction of detection, that the model is able to reproduce. To study the effect of the dynamics during the core-hole life time of 5 fs, we use a classical Z + 1 model and show that for the electronic excitation the effects are small. We find the loss features of the quasi-elastic line to be at the very limit or beyond the Z + 1 model. Most importantly, we show that density-functional-based statistical simulations of RIXS in molecular liquids can be performed accurately enough for reproduction of the main features in the RIXS spectrum.
NH isomer in the system, because of the lack of its predicted spectral fingerprints in the experiment. Moreover, in accordance with Dierker et al.7 we observe incident-beam-polarization dependence of the spectra recorded in a fixed direction of detection, that the model is able to reproduce. To study the effect of the dynamics during the core-hole life time of 5 fs, we use a classical Z + 1 model and show that for the electronic excitation the effects are small. We find the loss features of the quasi-elastic line to be at the very limit or beyond the Z + 1 model. Most importantly, we show that density-functional-based statistical simulations of RIXS in molecular liquids can be performed accurately enough for reproduction of the main features in the RIXS spectrum.
1 Methods
The RIXS experiment was performed at the BESSY II synchrotron facility of the Helmholtz Centre Berlin for Materials and Energy, at the UE52-SGM elliptically polarizing undulator beamline, using two polarizations of the incident beam: vertical (V) and horizontal (H). The resolution of the beamline monochromator was set to better than 0.12 eV at the N 1s edge for the X-ray absorption (XAS) measurements. The XAS were measured in total fluorescence yield (TFY) detection mode for the two polarizations, using a photodiode. The monochromator energy calibration was checked against the N 1s XAS of h-BN. The RIXS and XAS measurements were carried out on the liquid-jet setup of the FlexRIXS end-station,22 equipped with a Gammadata Scienta XES300 Nordgren-type soft X-ray grazing incidence grating spectrometer,23 which was positioned in the horizontal plane at normal angle to the incident light beam. The entrance slit of the spectrometer was vertical, parallel to the liquid jet. The overall energy resolution of the RIXS measurements was better than 0.4 eV.To study the effects of the solvent environment, we performed three different types of simulations: (i) liquid simulation based on snapshots from AIMD (ii) gas-phase calculation for the same snapshots by removing the solvent molecules (molecules that are not excited), and (iii) single point vacuum calculation with geometry optimization. For simulation of the RIXS spectra, we applied a model based on one by Gel'mukhanov and Ågren,24 where scattering cross section I(ω(out), ω(in), θ) of a randomly oriented sample in a static nuclear configuration R is derived from the Kramers–Heisenberg formula. At most general, the model describes a process via numerous coherently excited core–holes c (k in ref. 24) leading to a final state characterized by a hole in initially occupied valence orbital n and an electron on initially unoccupied orbital v: |R;c2n2〉 → |R;c1n2v1〉 → |R;c2n1v1〉. Each term in the resulting sum-over-states-and-core–holes formula is a product of an energy-dependent part and a dynamical part  , the latter of which contains information from the matrix elements of required transitions, rendered by the chosen scattering geometry θ and random orientation of the sample. We use one localized core hole (c = c′ = 1) and incident energy (ω(in)) – energy transfer (ω(tr)) mesh grid, which yields scattering cross section
, the latter of which contains information from the matrix elements of required transitions, rendered by the chosen scattering geometry θ and random orientation of the sample. We use one localized core hole (c = c′ = 1) and incident energy (ω(in)) – energy transfer (ω(tr)) mesh grid, which yields scattering cross section
 | (1) |
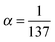 . The relation to emission energy ω(out) is simply ω(tr) = ω(in) − ω(out). Here ωvc is the energy of the core-to-valence transition in absorption, and ωcn the energy of the valence-to-core transition in emission. The function Φ is a Gaussian and corresponds to the energy spread of the incident light (a FWHM of 0.5 eV was used in the simulations) and Γc = 0.14 eV is the life-time broadening (FWHM) for the core-hole state. Moreover, from the model in ref. 24 we ignore the dependence of the decay amplitude and energy from the orbital v of the excited-electron: dcn(v) = dcn, ωcn(v) = ωcn. With these approximations we end up in eqn (1) and in a simplified form for ξvn(θ) for a randomly oriented sample:
. The relation to emission energy ω(out) is simply ω(tr) = ω(in) − ω(out). Here ωvc is the energy of the core-to-valence transition in absorption, and ωcn the energy of the valence-to-core transition in emission. The function Φ is a Gaussian and corresponds to the energy spread of the incident light (a FWHM of 0.5 eV was used in the simulations) and Γc = 0.14 eV is the life-time broadening (FWHM) for the core-hole state. Moreover, from the model in ref. 24 we ignore the dependence of the decay amplitude and energy from the orbital v of the excited-electron: dcn(v) = dcn, ωcn(v) = ωcn. With these approximations we end up in eqn (1) and in a simplified form for ξvn(θ) for a randomly oriented sample: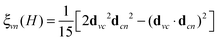 | (2) |
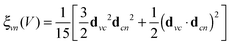 | (3) |
With the taken approach, studying the accessible configuration space R is feasible. We approximated the thermodynamic average in the canonical ensemble 〈I(ω(tr), ω(in), θ)〉NVT by sampling the phase space by ab initio molecular dynamics (AIMD) simulations. In addition a Gaussian of FWHM = 0.5 eV for the spectrometer resolution was used to generate the RIXS maps.
During the core hole lifetime (≈5 fs for N 1s), the system has the ability to readjust due to forces arising from the core level excitation.25,26 We studied these effects for liquid simulations in a model including the Z + 1 dynamics during 5 fs before the emission (microcanonical ensemble), by restarting the AIMD with the positions and velocities at the time of absorption. The Z + 1 dynamics simulations performed in this work only account for a decreased screening of the nitrogen nucleus and not the effects of the excited electron, which is ignored for equal treatment of all excited states.
The liquid simulations were performed for a box of 32 acetonitrile molecules for both AIMD and spectrum evaluation. The simulation box side length was chosen 14.125 Å, which yields the density of 773.65 g l−1, close to that of ref. 27. The box is depicted in Fig. 1 and in all simulations periodic boundary conditions were used. The system was thermalized first by running classical MD for 1 ns, then 5 ps velocity-rescaling AIMD, followed by 30 ps AIMD run using Nose thermostat at 300 K. In each studied case, 40 snapshots from the last 10 ps of the run was sampled. The AIMD runs and geometry optimization utilized TZVP-MOLOPT basis set28 for all atoms. Basis sets aug-cc-pV5Z (aug-cc-pVTZ)29 were used for the excited site and basis sets TZV2P-MOLOPT (TZVP-MOLOPT)28 were used for other sites in TP-HH (Δ-SCF) calculations, respectively. Goedecker–Teter–Hutter pseudopotentials (GTH-PP)30 were used with MOLOPT basis. All quantum-calculations were performed using the CP2K code15,31 and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.32 Classical MD was carried out using Gromacs package33–36 and the GAFF force field37 generated by the antechamber38 program and acpype39 utility software.
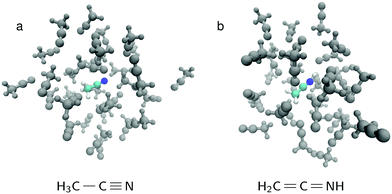 | ||
Fig. 1 The simulation box for (a) normal acetonitrile H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N (b) the isomer form H2C N (b) the isomer form H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH. In both cases, the other 31 molecules in the simulation box are H3C–C NH. In both cases, the other 31 molecules in the simulation box are H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N. N. | ||
2 Results and discussion
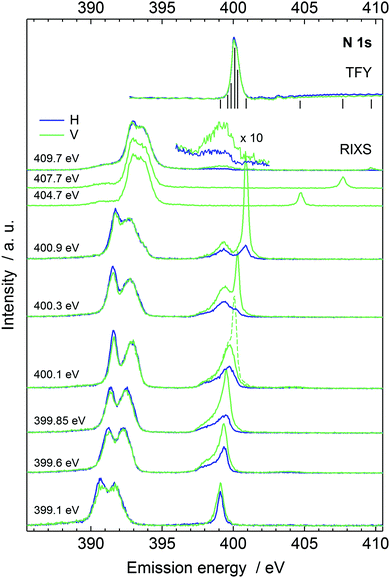
The recorded N 1s X-ray absorption spectrum is presented at top right in Fig. 2, complemented with vertical line markers at the excitation energies for the recorded RIXS spectra. The XAS spectrum has a strong resonance at 400.1 eV due to N 1s → πCN* excitation. The RIXS spectra are shown for the H and V scattering geometries. The RIXS spectra most notably consist of two main maxima separated by an energy interval of ca. 1.2 eV and located at ∼390–392 eV for excitation energies up to 400.9 eV. Molecular orbital calculations of Dierker and coworkers show that the higher emission energy feature consist of two 2e transitions, and the lower one of an 7a1 transition; a tail in emission energies below 390 eV originates from two 1e transition and a 6a1 transition.7 The acetonitrile molecule has been suggested to exist in isomers, both depicted in Fig. 1 with H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N solvent. The simulated RIXS maps are reported together with the experiment in Fig. 3, without dynamics, and with the 5 fs Z + 1 dynamics. The simulations for liquid H3C–C
N solvent. The simulated RIXS maps are reported together with the experiment in Fig. 3, without dynamics, and with the 5 fs Z + 1 dynamics. The simulations for liquid H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N reproduce the main features of the measured RIXS spectra.
N reproduce the main features of the measured RIXS spectra.
 | ||
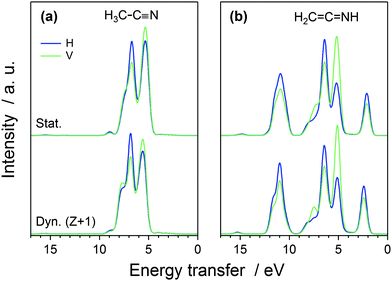
Fig. 3 The RIXS spectra in vertical (left) and horizontal (right) scattering geometry. (a) Experimental spectra with energy transfer range −1 to 15 eV normalized to TFY, (b) H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N in-vacuum single-point (SP) calculation, (c) H3C–C N in-vacuum single-point (SP) calculation, (c) H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N calculation without solvent at geometries of liquid simulation, (d) H3C–C N calculation without solvent at geometries of liquid simulation, (d) H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N liquid without excited state dynamics, (e) H3C–C N liquid without excited state dynamics, (e) H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N liquid with 5 fs Z + 1 dynamics, (f) H2C N liquid with 5 fs Z + 1 dynamics, (f) H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH isomer in liquid without excited state dynamics, and (g) H2C NH isomer in liquid without excited state dynamics, and (g) H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH isomer in liquid with 5 fs Z + 1 dynamics. Panels (h)–(n) present the same spectra in horizontal scattering geometry. The elastic line was left out from the simulation. The horizontal dashed lines indicate the locations of the sections corresponding to the simulated resonant RIXS spectra presented on Fig. 4 and 5. NH isomer in liquid with 5 fs Z + 1 dynamics. Panels (h)–(n) present the same spectra in horizontal scattering geometry. The elastic line was left out from the simulation. The horizontal dashed lines indicate the locations of the sections corresponding to the simulated resonant RIXS spectra presented on Fig. 4 and 5. | ||
The simulated spectra manifest different valence-orbital structure in H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and in H2C
N and in H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH. The changes in the molecular valence are due to the proton that requires changes in the bond orders and formation of a new single N–H bond. The simulated scattering spectrum shows these features as emergence of new emission lines (and orbitals) for H2C
NH. The changes in the molecular valence are due to the proton that requires changes in the bond orders and formation of a new single N–H bond. The simulated scattering spectrum shows these features as emergence of new emission lines (and orbitals) for H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH, whereas the lines are missing in the spectra of H3C–C
NH, whereas the lines are missing in the spectra of H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N. The simulation for H2C
N. The simulation for H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH yields intensities of comparable magnitude for all the line features, which leads to conclusion of very minor, if any, contribution of H2C
NH yields intensities of comparable magnitude for all the line features, which leads to conclusion of very minor, if any, contribution of H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH. We note that line around 398.5 eV in the emission spectra recorded with 409.7 eV incident photon energy (magnified in Fig. 2) most likely does not originate from H2C
NH. We note that line around 398.5 eV in the emission spectra recorded with 409.7 eV incident photon energy (magnified in Fig. 2) most likely does not originate from H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH. The line appears only in the two highest-incident-energy spectra and shows very strong angular distribution asymmetry. We attribute this feature to emission from an HOMO–LUMO shakeup state, which is reached with photon energies exceeding the N 1s ionization energy (404.9 eV for 50 mol% H3C–C
NH. The line appears only in the two highest-incident-energy spectra and shows very strong angular distribution asymmetry. We attribute this feature to emission from an HOMO–LUMO shakeup state, which is reached with photon energies exceeding the N 1s ionization energy (404.9 eV for 50 mol% H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N(aq)40) by the HOMO–LUMO gap energy, as such excitation would explain the threshold for the feature.
N(aq)40) by the HOMO–LUMO gap energy, as such excitation would explain the threshold for the feature.
Upon core-level excitation, the molecular system is not static, but develops in time.25 To study the life-time effects in the excited state, we applied a Z + 1 model simulating the nuclear dynamics in the presence of an N 1s core hole during 5 fs. The model ignores the excited electron and its effects on dynamics, but can be justified by the rapid increase of the nuclear repulsion being the dominant interaction during the short life-times of the core excited states. According to our simulation shown in Fig. 3 however, the effects of the dynamics are not expected to be very large. For H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, the nuclear dynamics is seen to give rise to an increase in the high-energy-transfer shoulder and for H2C
N, the nuclear dynamics is seen to give rise to an increase in the high-energy-transfer shoulder and for H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH to a change in the slope of highest-loss feature in the simulated spectra.
NH to a change in the slope of highest-loss feature in the simulated spectra.
The simulated H and V spectra at the π* resonance are depicted in Fig. 4, for the two liquid systems and for the two decay models. The spectra were normalized to the intensity maximum for H-polarization, no-Z + 1-dynamics spectrum for the isomer considered. The calculation is able to reproduce the experimentally observed polarization dependence.
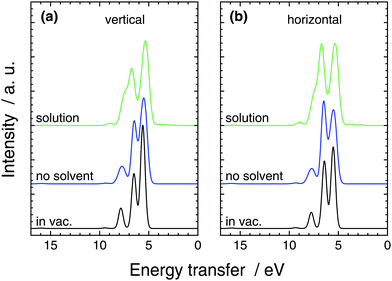
We studied the effects due to solvation in two additional simulations. First we removed all other molecules apart from the excited one from the simulation and performed an in-vacuum calculations. This simulation points out the effect of the solvent molecules, now treated quantum mechanically, in the RIXS spectra. Second, we performed an in-vacuum single point calculation in an optimized geometry. When compared to the previous simulation effects due to molecular structure changes and related statistics in the solution are underlined. The spectra are presented as maps in Fig. 3 and as cuts in Fig. 5.
Compared to the single point calculation, broadening of the lines is naturally seen in the solution simulation and the no-solvent simulation. Moreover, the intensity ratios of the lines are affected by the different geometries sampled in the no-solvent case leading the lower-transfer 2e (∼5.5 eV) line to lose peak height compared to the 7a1-originating peak (∼6.5 eV) in Fig. 5. We assign this to symmetry breaking of the molecule, that lifts the degeneracy in the 2e feature and spreads the intensity wider in the spectrum. The effect of QM-solvent is seen in comparison of the liquid and no-solution simulations that have exactly the same central-molecule structure. The “tail” feature of in-vacuum spectra and no-solvent spectra consists of 1e (∼8 eV) and a 6a1 (∼9.5 eV) transitions that move higher in energy transfer in QM-solvent. The two 1e states naturally split in energy and smear to the mostly 7a1 peak, whereas the single 6a1 peak is slightly boosted in intensity. Moreover the splitting of the two main features is slightly increased by the QM solvent, when compared to the no-solution case. Similar comparison also results in a lower peak height for the (mostly) 7a1 compared to the 2e peak at 5.5 eV. We note that, the in-solution spectrum consists of a large number of transitions and the simple gas-phase orbital picture breaks down due to orbital interaction with the QM-solvent: apart from the separated 6a1 line, peak spectra of individual lines do not necessarily resemble those of the no-solvent case. For the single-point in-vacuum calculation and the no-solvent simulation, linking the transitions is simpler.
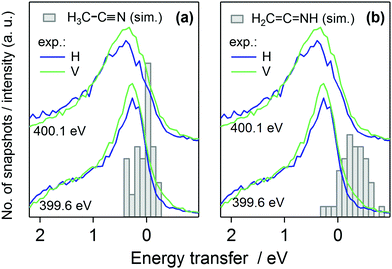
The quasi-elastic peak (Fig. 2) shows an energy loss side-band when the excitation energy is scanned over the absorption resonance. We assign the feature to vibrational excitations due to dynamics of the N 1s core-excited state in acetonitrile. The effective scattering time is longest at the resonance and decreases with detuning of the incident photon energy off (below) the resonance.8,10 Although the detuning phenomenon is quantum physical, it can be approximated as a classical effect.26 We applied the Z + 1 dynamics model (the excited electron is ignored) and evaluated the first core-excited state Δ-DFT energies for the 40 snapshots, presented as histograms in Fig. 6, where we have included the quasi-elastic line shape at the π* resonance (400.1 eV) as well. The figure shows that for H3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N the model explains the trend of the main peak but underestimates the shift at 400.1 eV. Even though such effect may be at the very limit of the applied model, we point out that our calculated shift actually is the lowest limit of the transfer. The model indeed assumes internal conversion of the electronic state to the lowest core-excited state in the new geometry. Naturally, different lifetimes are expected to yield different shifts also in the applied model, and as seen in Fig. 2 detuning from the resonance changes the shift of the quasielastic line. The simulation results with 5 fs lifetime agree better with the shift at detuned energy 399.6 eV, whereas the main resonance at 400.1 eV probably has longer scattering time and therefore longer relaxation and larger quasielastic shift. For the H2C
N the model explains the trend of the main peak but underestimates the shift at 400.1 eV. Even though such effect may be at the very limit of the applied model, we point out that our calculated shift actually is the lowest limit of the transfer. The model indeed assumes internal conversion of the electronic state to the lowest core-excited state in the new geometry. Naturally, different lifetimes are expected to yield different shifts also in the applied model, and as seen in Fig. 2 detuning from the resonance changes the shift of the quasielastic line. The simulation results with 5 fs lifetime agree better with the shift at detuned energy 399.6 eV, whereas the main resonance at 400.1 eV probably has longer scattering time and therefore longer relaxation and larger quasielastic shift. For the H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH, the Z + 1 simulation predicts slight anti-Stokes behaviour, which is highly unlikely although this result can not be tested. The effect is probably due to the fact that the dynamics takes place on the Z + 1 potential energy surface and not on the core-excited one, which allows dynamics leading to a configuration of higher core-excited-state energy. The validity of Z + 1 approximation in modeling core-excited dynamics is an interesting question and calls for further studies.
NH, the Z + 1 simulation predicts slight anti-Stokes behaviour, which is highly unlikely although this result can not be tested. The effect is probably due to the fact that the dynamics takes place on the Z + 1 potential energy surface and not on the core-excited one, which allows dynamics leading to a configuration of higher core-excited-state energy. The validity of Z + 1 approximation in modeling core-excited dynamics is an interesting question and calls for further studies.
3 Conclusions
The presented excitation-energy dependent resonant inelastic X-ray scattering spectra of liquid acetonitrile manifest dependence on the scattering geometry, i.e. dependence on the polarization of the incoming beam. We applied a transition-potential-DFT based approach to evaluate RIXS spectra for molecular liquids scattering-geometry-dependently, and applied the model together with ab initio molecular dynamics to simulate the N 1s RIXS of liquid acetonitrile using periodic boundary conditions. The main features of the scattering spectrum are reproduced and the solvation effects as well as effects due to statistics were pinpointed. In particular, the results show no support for presence of the H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH isomer, for which characteristic emission lines are predicted, but not observed in the experiment. The used approach for RIXS proved to be light enough to allow phase-space-sampling studies of molecular liquids and accurate enough to allow identification of RIXS transition lines for use of physical chemistry studies.
NH isomer, for which characteristic emission lines are predicted, but not observed in the experiment. The used approach for RIXS proved to be light enough to allow phase-space-sampling studies of molecular liquids and accurate enough to allow identification of RIXS transition lines for use of physical chemistry studies.
Acknowledgements
Finnish Centre for Scientific Computing (CSC) in Espoo is acknowledged for supercomputer resources for the project. Also The Academy of Finland (projects 1259599, 1260204), ESF (3.2.1101.12-0019) and the EU-TARI/HZB are gratefully acknowledged for the financial support. Dr M. Ianuzzi and Dr K. Jänkälä are thanked for helpful discussions.References
- W. Schulke, Electron Dynamics by Inelastic X-Ray Scattering, Oxford Series on Synchrotron Radiation, Oxford, 2007 Search PubMed.
- L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705–767 CrossRef CAS.
- J. Nordgren and J.-E. Rubensson, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 3–9 CrossRef CAS.
- Y. Luo, H. Ågren and F. Gel'mukhanov, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 1340–1348 CrossRef CAS.
- D. W. Lindle, P. L. Cowan, T. Jach, R. E. LaVilla and R. D. Deslattes, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 2353–2366 CrossRef CAS.
- Y. Horikawa, T. Tokushima, A. Hiraya and S. Shin, Phys. Chem. Chem. Phys., 2010, 12, 9165–9168 RSC.
- B. Dierker, E. Suljoti, K. Atak, K. M. Lange, N. Engel, R. Golnak, M. Dantz, K. Hodeck, M. Khan, N. Kosugi and E. F. Aziz, New J. Phys., 2013, 15, 093025 CrossRef.
- F. Gel'mukhanov, P. Salek, T. Privalov and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 380–389 CrossRef.
- P. Skytt, P. Glans, J.-H. Guo, K. Gunnelin, C. Såthe, J. Nordgren, F. Kh. Gel'mukhanov, A. Cesar and H. Ågren, Phys. Rev. Lett., 1996, 77, 5035–5038 CrossRef CAS PubMed.
- F. Hennies, A. Pietzsch, M. Berglund, A. Föhlisch, T. Schmitt, V. Strocov, H. O. Karlsson, J. Andersson and J.-E. Rubensson, Phys. Rev. Lett., 2010, 104, 193002 CrossRef PubMed.
- A. Cesar, F. Gel'mukhanov, Y. Luo, H. Ågren, P. Skytt, P. Glans, J. Guo, K. Gunnelin and J. Nordgren, J. Chem. Phys., 1997, 106, 3439–3456 CrossRef CAS.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P.h. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- Ph. Wernet, K. Kunnus, I. Josefsson, I. Rajkovic, W. Quevedo, M. Beye, S. Schreck, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. de Groot, K. J. Gaffney, S. Techert, M. Odelius and A. Föhlisch, Nature, 2015, 520, 78–81 CrossRef CAS PubMed.
- F. Hennies, S. Polyutov, I. Minkov, A. Pietzsch, M. Nagasono, H. Ågren, L. Triguero, M.-N. Piancastelli, W. Wurth, F. Gel'mukhanov and A. Föhlisch, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 032505 CrossRef.
- M. Ianuzzi and J. Hutter, Phys. Chem. Chem. Phys., 2007, 9, 1599–1610 RSC.
- K. Gilmore, J. Vinson, E. L. Shirley, D. Prendergast, C. D. Pemmaraju, J. J. Kas, F. D. Vila and J. J. Rehr, Comput. Phys. Commun., 2015, 197, 109–117 CrossRef CAS.
- J. Vinson, J. J. Rehr, J. J. Kas and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106 CrossRef.
- J. Vinson, J. J. Kas, F. D. Vila, J. J. Rehr and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045101 CrossRef.
- J. Niskanen, C. J. Sahle, K. O. Ruotsalainen, H. Müller, M. Kavčič, M. Žitnik, K. Bučar, M. Petric, M. Hakala and S. Huotari, Sci. Rep., 2016, 6, 21012 CrossRef CAS PubMed.
- G. de Petris, S. Fornarini, M. E. Crestoni, A. Troiani and P. M. Mayer, J. Phys. Chem. A, 2005, 109, 4425–4427 CrossRef CAS PubMed.
- E. Marotta and P. Traldi, Rapid Commun. Mass Spectrom., 2003, 17, 2846–2848 CrossRef CAS PubMed.
- K. Kunnus, I. Rajkovic, S. Schreck, W. Quevedo, S. Eckert, M. Beye, E. Suljoti, C. Weniger, C. Kalus, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, K. J. Gaffney, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, S. Techert, Ph. Wernet and A. Föhlisch, Rev. Sci. Instrum., 2012, 83, 123109 CrossRef PubMed.
- J. Nordgren, G. Bray, S. Cramm, R. Nyholm, J. E. Rubensson and N. Wassdahl, Rev. Sci. Instrum., 1989, 60, 1690–1696 CrossRef CAS.
- F. Gel'mukhanov and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 4378–4389 CrossRef.
- M. Odelius, H. Ogasawara, D. Nordlund, O. Fuchs, L. Weinhardt, F. Maier, E. Umbach, C. Heske, Y. Zubavichus, M. Grunze, J. D. Denlinger, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2005, 94, 227401 CrossRef PubMed.
- M. Blum, M. Odelius, L. Weinhardt, S. Pookpanratana, M. Bär, Y. Zhang, O. Fuchs, W. Yang, E. Umbach and C. Heske, J. Phys. Chem. B, 2012, 116, 13757–13764 CrossRef CAS PubMed.
- G. Moumouzlas, D. K. Panopoulos and G. Ritzoulls, J. Chem. Eng. Data, 1991, 36, 20–23 CrossRef.
- J. Van de Vondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. Van de Vondele, WIREs Comput. Mol. Sci., 2014, 4, 15–25 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1719 CrossRef CAS PubMed.
- E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317 CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367 CrossRef PubMed.
- K. A. Perrine, M. H. C. Van Spyk, A. M. Margarella, B. Winter, M. Faubel, H. Bluhm and J. C. Hemminger, J. Phys. Chem. C, 2014, 118, 29378–29388 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: The quasielastic line shape. See DOI: 10.1039/c6cp03220f |
| ‡ Current address: PULSE Institute, SLAC National Accelerator Laboratory, Stanford University, Menlo Park, California 94025, USA. |
| This journal is © the Owner Societies 2016 |