Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reaction cross sections and thermal rate constant for Cl− + CH3Br → ClCH3 + Br− from J-dependent quantum scattering calculations
Carsten
Hennig
and
Stefan
Schmatz
*
Institut für Physikalische Chemie, Universität Göttingen, Tammannstr. 6, D-37077 Göttingen, Germany. E-mail: sschmat@gwdg.de
First published on 6th July 2016
Abstract
Employing dimensionality-reduced time-independent quantum scattering theory and summation over all possible total angular momentum states, initial-state selected reaction cross sections for the exothermic gas-phase bimolecular nucleophilic substitution (SN2) reaction Cl− + CH3Br → ClCH3 + Br− have been calculated. The carbon–halogen bonds and the rotation of the methyl halides are taken into account. In agreement with previous calculations for J = 0, initial rotational motion of CH3Br decreases the reaction probability and consequently the cross sections. The experimentally obtained thermal rate constant for 300 K is reproduced within the experimental error. For lower temperatures, it is calculated to be below the experimental values but shows the same strong increase for T → 0.
I. Introduction
Nucleophilic bimolecular substitution (SN2) reactions1–4 which are characterized by the simultaneous making and breaking of two single bonds are not only of high practical interest but also can contribute to elucidate the very fundamentals of chemical reactions. In particular, this holds for gas-phase reactions which are not complicated by the surrounding solvent molecules. Extensive material, both experimental and theoretical, is available on the simple halogen exchange SN2 reactions| X− + CH3Y → XCH3 + Y−, | (1) |
While identity SN2 reactions (X = Y) are characterized by low reaction rates due to sharp barriers in the reaction profiles, exothermic halogen exchange reactions usually exhibit a barrier located below the reactant energy. From a naive point of view, ion-dipole capture theory should suffice to describe such a reaction, but even in statistical theories and classical mechanical treatments it is shown that a central barrier lower than the energy of the reactants influences the reaction due to large collision angular momenta and the corresponding large rotational energy (centrifugal) barriers which are added to the central barrier height.67 Comparisons between experiment, chemical dynamics, and ion-molecule capture rate constants are made for OH− + CH3I in ref. 68 and for OH−(H2O) + CH3I in ref. 69. Good agreement is found between experiment and chemical dynamics, and for OH− + CH3I it is quantitative. The ion-molecule capture rate constants are too large. For these reactions the central barrier is about 20 kcal mol−1 lower in energy than that for the reactants.
Quantum-mechanically the potential wells reflect incoming wave packets, thus setting high demands on the theoretical description. The wells support considerably long-lived metastable states bound by intermolecular ion-dipole forces which in the reaction probability vs. energy profiles show up as extremely narrow lines and strongly influence not only differential and total reaction cross sections but also the overall rate constant. These long-lived states can be of dynamical nature (energy stored in higher-frequency modes: Feshbach resonances) or, in exothermic systems, e.g. Cl− + CH3Br, additionally can be quasi-bound by the potential well (shape resonances). A quantum-mechanical approach is indispensable to calculate state-to-state reaction probabilities which then can be summed up to differential or integral cross sections and finally turned into rate constants.
In this paper, we present a quantum study of the exothermic reaction
| Cl− + CH3Br (α-channel) → ClCH3 + Br− (β-channel). | (2) |
Experimentally, Viggiano et al.12 found that in the Cl− + CH3Br reaction a higher CH3Br temperature does not increase the thermal rate constant, and Graul and Bowers11,13 reported that the products are vibrationally hot. Angel and Ervin21 found that the SN2 mechanism is ineffective compared with predictions from phase-space theory and ion-dipole capture theory. However, experiments on the detailed, state-selected dynamics of this reaction are scarce. The thermal rate constant down to 23 K was measured by LeGarrec et al.43 who also report a calculational result based on a dimensionality-reduced 3D quantum model, employing an approximate Hamiltonian for the umbrella bending mode of the methyl group and the rotating bond approximation (RBA), yielding a good, yet not perfect agreement with the experimental data. Reaction cross sections in a 2D model were calculated and analyzed by Schmatz and Clary.46 Even in these dimensionality-reduced models, the low intermolecular frequencies of the complexes, the heavy mass of the bromine nucleus and the far-reaching ion-dipole potentials render the Cl− + CH3Br SN2 system computationally very demanding because both memory and CPU time requirements set limits. The small rotational constants strongly increase the densities of both reactant and product states. Thus, one has to resort to dimensionality-reduced models42,48 where only those degrees of freedom are included which are absolutely indispensable for a qualitatively correct description of the reaction coordinate. In a second step, the influence of additional degrees of freedom can be investigated in detail. This analytical approach is only viable by theory whereas experiments deliver a more or less complete information, often in the form of highly averaged quantities like thermal rate constants. It has to be pointed out that the molecular beam ion-imaging experiments of the Wester research group have provided quite detailed non-thermal dynamics for SN2 reactions.22–29
While in our previous 4D calculations carried out under the constraint of C3v symmetry,55,57,59–61i.e. with inclusion of the umbrella bending and C–H stretching vibrations, a lot of information on mode-selectivity and the influence of the excitation of different internal degrees of freedom on the reactivity was obtained, the overall rate constant could not be reproduced exactly. The calculated value turned out to be too small57 because the computed reaction probabilities were determined to be too low, and important resonances, in particular broad ones were missing. As the employed model was exact within the dimensionality-reduced framework and all computations were well converged, the reason for the discrepancy can only be found just in this reduced dimensionality. Thus, in ref. 62 rotation of both reactant and product methyl halide molecules was included in state-to-state reaction probability calculations to properly take into account translation-to-rotation energy transfer. While the rotation around the axes perpendicular to the axes of molecular symmetry was included, the two internal totally-symmetric vibrational modes (C–H stretch and umbrella bend) were not longer taken into account. Particular numerical challenges in this type of calculation are (i) the number of energetically accessible states which is enhanced by one order of magnitude to 104–105, (ii) the necessity to propagate the wavefunctions out to much larger distances where the interaction between the reactant and product channels is zero, and finally (iii) the very fine energy resolution imposed by the narrow resonances.
In contrast to the reaction probability P(E), the cross section σ(E) is a quantity that is relatively easily accessible by appropriate experiments. State-selected reaction cross sections provide valuable information on both the influence of initial vibrational and/or rotational excitation. In the present work, we report on total angular-momentum dependent quantum scattering calculations for initial state-selected total cross sections σ(E) and the thermal rate constant k(T) for reaction (2). The cross sections are obtained as weighted sums over J-dependent reaction probabilities PJ(E) for given energy E and all possible total angular momentum quantum numbers J.
The paper is organized as follows: In Section II, we briefly report on the theoretical background, in particular the employed Hamiltonian, the reactive scattering formalism and the reduced-dimensionality theory to recover the full-dimensional thermal rate constant while in Section III numerical details of our computations are given. Section IV presents the results and their discussion and Section V contains our conclusions. Throughout, energies are quoted in wavenumber units.
II. Theory
We use only a single Jacobian coordinate system {R, r, γ} connected to the product channel with the angle γ describing the rotation of the pseudo-diatom CH3Cl or, in other words, the position of Br− with respect to this moiety. With the reduced masses μ1 = mBrmCH3Cl/(mBr + mCH3Cl) and μ2 = mClmCH3/mCH3Cl, the full four-dimensional Hamiltonian for this pseudo-triatomic system in the space-fixed frame70,71 can be simplified by transforming the wavefunction Ψ into ψ/(Rr), yielding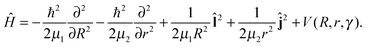 | (3) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) 2 (as a function of its two defining angles in the space-fixed coordinate system, θ and φ) is given by
2 (as a function of its two defining angles in the space-fixed coordinate system, θ and φ) is given by | (4) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) + ĵ, and changing to the body-fixed frame with reference axis z′ (along the Jacobi vector R, thus
+ ĵ, and changing to the body-fixed frame with reference axis z′ (along the Jacobi vector R, thus ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) z = 0) we use
z = 0) we use![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) 2 = (Ĵ − ĵ)2 = Ĵ2 + ĵ2 − 2Ĵz′2 − Ĵ+ĵ− − Ĵ−ĵ+ 2 = (Ĵ − ĵ)2 = Ĵ2 + ĵ2 − 2Ĵz′2 − Ĵ+ĵ− − Ĵ−ĵ+ | (5) |
Ĥ = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) J=0 + J=0 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) J + J + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , , | (6) |
 | (7) |
 | (8) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) = δk′k〈j′k|V(R, r, γ)|jk〉γ and
= δk′k〈j′k|V(R, r, γ)|jk〉γ and 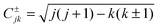 . Here, |jk〉 denotes a spherical harmonic function and 〈⋯〉γ indicates integration over γ, while J, j = |k|, |k| + 1,… and k = −J,…,J are the quantum numbers of the conserved total angular momentum, of the rotating diatom and of the projection of the total angular momentum Ĵ onto the body-fixed axis defined by the third atom and the center of mass of the diatom.
. Here, |jk〉 denotes a spherical harmonic function and 〈⋯〉γ indicates integration over γ, while J, j = |k|, |k| + 1,… and k = −J,…,J are the quantum numbers of the conserved total angular momentum, of the rotating diatom and of the projection of the total angular momentum Ĵ onto the body-fixed axis defined by the third atom and the center of mass of the diatom.
In this work, we treat the rotation of the reactive system for J ≥ 0. The infinite rotational energy of the third atom with respect to the center of mass of the diatom is responsible for a singularity. Only in the J > 0 setting, this is a coordinate singularity due to the non-Cartesian coordinate system (Eckart singularity).
In Jacobian coordinates each of two variables R and r can become infinite in different asymptotic configurations. Thus, a transformation to a single unbound reaction coordinate only, the coordinate-system independent hyperradius ρ (ref. 73–78) is applied,
 | (9) |
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) /
/![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ) is the corresponding hyperangle and R and r are scaled according to
) is the corresponding hyperangle and R and r are scaled according to 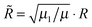 and
and  with
with  . The Hamiltonian operator then becomes
. The Hamiltonian operator then becomes | (10) |
 | (11) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) J=0surf +
J=0surf + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Jsurf +
Jsurf + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) with
with | (12) |
 | (13) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) = δk′k〈j′k|V(δ,γ;ρ)|jk〉γ. = δk′k〈j′k|V(δ,γ;ρ)|jk〉γ. | (14) |
We compute the wavefunctions based on only one of the (biased) hyperspherical coordinate systems in the interaction region, a method already employed directly in Jacobi coordinates for the standard reaction D + H2 → DH + H.79 All arrangement configurations still can be described accurately by a proper basis set adaptation. For an exact Hamiltonian, at fixed hyperradius ρ, all arrangement channel coordinates yield the same eigenstates (with different parametrization), such that matching onto the asymptotic coordinate systems is feasible once the interaction region is left. An additional intermediate region is used to smoothen the transition between these two regimes.
To describe the eigenfunctions of Ĥsurf, discrete variable representations (DVRs)80–82 are employed for δ and γ; while for the hyperangle δ, the “sinc-DVR”83,84 is chosen, for the physical angle γ the Legendre polynomial basis {Pj(γ)} is employed. As within each sector, the Ĥsurf matrices of size up to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 render a direct diagonalization very difficult, we employ an iterative method by taking advantage of the relative sparsity of the matrices in matrix-vector multiplications and calculate the eigenvalues and eigenvectors of the Ĥsurf matrices using Lanczos iteration.85,86 The basis for the matrix representations of Ĥsurf was constructed making use of potential-optimized DVRs (PODVRs)87 in both δ and γ.
000 render a direct diagonalization very difficult, we employ an iterative method by taking advantage of the relative sparsity of the matrices in matrix-vector multiplications and calculate the eigenvalues and eigenvectors of the Ĥsurf matrices using Lanczos iteration.85,86 The basis for the matrix representations of Ĥsurf was constructed making use of potential-optimized DVRs (PODVRs)87 in both δ and γ.
In the intermediate region, the wavefunctions up to the highest energy considered are fully separated, i.e. localized in α or β channel; the transition to the interaction region where just one of the coordinate systems is used, takes place at ρsep. The sector eigenfunctions ψ can be automatically grouped by the following criteria which imply vanishing overlap matrix elements between the α and β surface functions in adjacent sectors (λ = α, β):
 | (15) |
For given J and total energy E, the time-independent Schrödinger equation ĤJΨJ = EΨJ, is solved in two steps to obtain the partial waves ΨJ. After expanding the partial waves  for initial vibrational state n′ in close-coupling form with N channels,55,59 the eigenvalue equation for Ĥsurf is solved. The propagation of the wave functions in all three regions is carried out according to the R-matrix propagation algorithm.88 The eigenfunctions in hyperspherical coordinates and the corresponding R-matrices are projected from the representation in hyperspherical coordinates onto that in Jacobian coordinates89 and the propagation is continued in the specific Jacobian coordinates for the α and β configuration. In the asymptotic region, larger sector sizes can be chosen, and we used a step size algorithm similar to the description in ref. 88 to determine appropriate sector sizes. Finally, proper boundary conditions were applied to extract the complex S-matrix elements SJi,f(E), employing the single-sector projection method.
for initial vibrational state n′ in close-coupling form with N channels,55,59 the eigenvalue equation for Ĥsurf is solved. The propagation of the wave functions in all three regions is carried out according to the R-matrix propagation algorithm.88 The eigenfunctions in hyperspherical coordinates and the corresponding R-matrices are projected from the representation in hyperspherical coordinates onto that in Jacobian coordinates89 and the propagation is continued in the specific Jacobian coordinates for the α and β configuration. In the asymptotic region, larger sector sizes can be chosen, and we used a step size algorithm similar to the description in ref. 88 to determine appropriate sector sizes. Finally, proper boundary conditions were applied to extract the complex S-matrix elements SJi,f(E), employing the single-sector projection method.
When only reaction probabilities for J = 0 are available, the centrifugal term ĤJ = Ĥ + ℏ2J(J + 1)/2μρ2 can be added to ĤJ=0 in the propagation of the scattering wave function (rotating line approximation (RLA)90). To be more accurate, here we make use of probabilities PJi,f(E) = |SJi,f(E)|2 calculated employing ĤJ from eqn (10) for all possible values of J. Reactive scattering cross sections are then computed according to
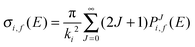 | (16) |
 | (17) |
While from the full-dimensional cumulative reaction probability the exact thermal rate constant could be obtained, the dimensionality-reduced theory based calculation of k(T) requires energy shifting procedures.89,91–95 However, since the saddle point in the Cl− + CH3Br reaction is located below the reactant energy, usual transition state theory cannot be applied due to a formally negative barrier height. However, characteristic data of the transition state as harmonic vibrational frequencies and rotational constants can be used in the calculation of partition functions. The azimuthal rotation in the transition state is included in the sum over the total angular momentum J. In a modification of eqn (13) from ref. 61, we calculate k(T) according to
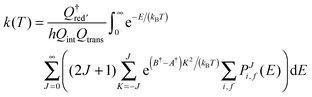 | (18) |
 denotes the partition function of the two non-degenerate totally symmetric modes (C–H stretch and umbrella bend) and the three doubly degenerate internal modes (antisymmetric C–H stretch, antisymmetric C–H bend and the “rocking motion”) in this transition state structure. Note that the degenerate bending mode is explicitly included in our treatment of the rotation. The difference of the zero-point energies between the saddle point structure and the reactants with respect to the two a1 modes and the three e modes is omitted due to the absence of a positive net barrier height. Qtrans denotes the three-dimensional translational partition function and Qint the partition function for all internal degrees of freedom of the reactants.
denotes the partition function of the two non-degenerate totally symmetric modes (C–H stretch and umbrella bend) and the three doubly degenerate internal modes (antisymmetric C–H stretch, antisymmetric C–H bend and the “rocking motion”) in this transition state structure. Note that the degenerate bending mode is explicitly included in our treatment of the rotation. The difference of the zero-point energies between the saddle point structure and the reactants with respect to the two a1 modes and the three e modes is omitted due to the absence of a positive net barrier height. Qtrans denotes the three-dimensional translational partition function and Qint the partition function for all internal degrees of freedom of the reactants.
III. Numerical details
The potential energy surface of Hase et al.34 was used and optimized with respect to the position of the CH3 group.62 A local symmetry approximation (LSA) was employed keeping the four nuclei of the methyl group always in the geometry of a right circular cone.62The final sector-dependent potential-optimized (PO) basis sets in δ and θ were constructed as described in ref. 62. The number of basis functions in both coordinates and the respective energies EPO for the interaction, intermediate and asymptotic regions are collected in Table 1 of ref. 62. The cutoff energy was set to Vcut = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. Depending on the region, we either employed the Hamiltonian (10) in hyperspherical coordinates with kinetic energy operators eqn (12) and (13) or Ĥ according to eqn (6) in scaled Jacobi coordinates (
000 cm−1. Depending on the region, we either employed the Hamiltonian (10) in hyperspherical coordinates with kinetic energy operators eqn (12) and (13) or Ĥ according to eqn (6) in scaled Jacobi coordinates (![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) ,
,![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) ) with kinetic energy operators according to eqn (7) and (8). All channels up to a total energy of Ediagmax = 2500 cm−1 have been computed and included in the R-matrix-propagation with a maximum number of Nch,max = 1466 channels. All channels below 4500 cm−1 were additionally included in each sector in computations with an energy below this limit. The calculations started at ρ = 6.5 a0 in the interaction region and switched to the intermediate region at ρ = 13.028 a0 (where the actual separation of the wave functions according to eqn (15) has already occurred at lower values of ρ and a minimum separation value of ρ = 13 a0 was imposed). At ρ = 40.889 a0, the transition to the asymptotic region took place. The wave functions were propagated to
) with kinetic energy operators according to eqn (7) and (8). All channels up to a total energy of Ediagmax = 2500 cm−1 have been computed and included in the R-matrix-propagation with a maximum number of Nch,max = 1466 channels. All channels below 4500 cm−1 were additionally included in each sector in computations with an energy below this limit. The calculations started at ρ = 6.5 a0 in the interaction region and switched to the intermediate region at ρ = 13.028 a0 (where the actual separation of the wave functions according to eqn (15) has already occurred at lower values of ρ and a minimum separation value of ρ = 13 a0 was imposed). At ρ = 40.889 a0, the transition to the asymptotic region took place. The wave functions were propagated to ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) asym = 3316.575 a0. The final S-matrix was computed at energy intervals of ΔE = 5 cm−1 from Emin = 300 cm−1 to Emax = 2000 cm−1. The convergence parameter for the localization of the wavefunctions, εsep, was set to 2 × 10−6. In the computation of k(T), the summation over K runs from −∞ to +∞. This has only a very small influence because the sum over K is fast converging (at least from J = 15) and the probabilities considerably decrease from J = 100. The summation over J is carried out until
asym = 3316.575 a0. The final S-matrix was computed at energy intervals of ΔE = 5 cm−1 from Emin = 300 cm−1 to Emax = 2000 cm−1. The convergence parameter for the localization of the wavefunctions, εsep, was set to 2 × 10−6. In the computation of k(T), the summation over K runs from −∞ to +∞. This has only a very small influence because the sum over K is fast converging (at least from J = 15) and the probabilities considerably decrease from J = 100. The summation over J is carried out until  . Unless stated otherwise, all energies are counted from the asymptotic potential energy value of CH3Br and are quoted in wavenumber units throughout. The convergence of the calculated cross sections was subject to careful examination, particularly with respect to the final value of the hyperradius and the number of partial waves considered in the expansion of the wavefunction. The geometrical parameters employed to calculate the symmetric top rotational constants as well as the vibrational frequencies used in the k(T) computation are given in Tables 1 and 2.
. Unless stated otherwise, all energies are counted from the asymptotic potential energy value of CH3Br and are quoted in wavenumber units throughout. The convergence of the calculated cross sections was subject to careful examination, particularly with respect to the final value of the hyperradius and the number of partial waves considered in the expansion of the wavefunction. The geometrical parameters employed to calculate the symmetric top rotational constants as well as the vibrational frequencies used in the k(T) computation are given in Tables 1 and 2.
| Reactant | Transition state | |
|---|---|---|
| r(C–H) | 1.0851 Å | 1.0718 Å |
| θ(H–C–Br) | 107.83° | 91.20° |
| R(C–Br) | 1.9452 Å | 2.422 Å |
| R(C–Cl) | ∞ | 2.354 Å |
| Reactant | Transition state | |
|---|---|---|
| C–Br stretch | 600 | — |
| Rocking motion | 972 | 972 |
| Umbrella bend | 1320 | 1020 |
| Antisymmetric C–H bend | 1492 | 1420 |
| Symmetric C–H stretch | 3052 | 3178 |
| Antisymmetric C–H stretch | 3197 | 3397 |
IV. Results and discussion
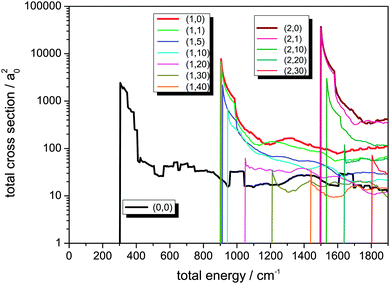
The integral cross sections for the reaction Cl− + CH3Br → ClCH3 + Br− for total energies up to 1900 cm−1, calculated within the dimensionality-reduced model, are graphically displayed in Fig. 1 and 2. Initial state-selected total cross sections, summed over all product states, | (19) |
The low-energy cross sections contribute most to the thermal rate constant. Consequently, a high resolution with respect to energy is necessary in the calculations.
Most of the cross sections show a typical well-known behaviour:49 An immediate rise when the channel opens and then a decay that behaves inversely proportional to km2 or Etrans, respectively. The sharp maximum of σ(E) is located close to that energy where the channel opens. The cross sections can thus very well be compared with respect to their magnitude, much better than the corresponding reaction probabilities.62 It is important to note the logarithmic scale in Fig. 1 and 2 when comparing the amplitudes of the cross sections.
As can be seen from Fig. 1, the integral reaction cross sections strongly decrease for rotational excitation in line with the observations made in ref. 62. It is remarkable that throughout the shapes of the different cross section curves in Fig. 1 are very similar, in line with the rotating line approximation that just shifts the energies by including a centrifugal term in the Hamiltonian which is proportional to the rotational energy of the whole system. This effect is clarified by considering the broad maximum in σ(0,0)(E) at about 1400 cm−1 that gradually shifts to higher total energies up to 1750 cm−1 for j = 40. The shifting towards higher energy, correlated with J(J + 1), defines a trend which, however, is somewhat too oversimplified. E.g., the respective maximum for j = 4 is found below that for j = 5. This indicates that the quantum character still prevails and that resonance effects between partial waves play a very important role, giving rise to deviations from the simple rotating line approximation picture.
Due to the data processing and averaging, the well-resolved resonance structure is lost. The plateau-like features seen in the plots originate from the data sampling. Interesting effects in the cross sections are the rectangular features in the cross sections for j = 0, j = 1 and j = 2. The plateau in the range around 1000 cm−1 does not show up in the comparable energy regimes for the other initial-state selected cross sections. The same holds for the broad peak located between 600 and 800 cm−1. On the other hand, the broad feature at about 1700 cm−1 is also found in the cross section for j = 2 at somewhat higher energies. In the curve for j = 1, however, this pattern is not seen in between these two energy values, but instead shows up at an even higher total energy.
A further interesting feature is that the overall shape of the reaction cross sections changes dramatically for very high angular momenta, e.g. for j = 40. Note that the cross sections for high rotational excitation do not show a pronounced rise directly at the opening of the channel. As the sharp rise is lost, the σ(E) curve resembles much more typical cross section vs. energy curves in neutral-neutral reactions.
In Fig. 2, reaction cross sections for additional excitation of the C–Br stretching vibration v, localized in the coordinate of the bond being broken, is shown. For comparison, the cross section out of the rovibrational ground state (0,0) is also displayed. For excitation in the C–Br stretching vibration with one or two quanta, the cross sections rise very strongly as known from our 2D calculation presented in ref. 49. The effect of rotational motion in the reactant molecule is the same as discussed before, i.e. in general a decrease is observed for higher initial j values. It is worth noting that for higher initial j, the maxima of the cross sections become smaller, but as a function of energy no further decay of the functions is observed. There is a sharp peak when the channel opens followed by a moderate decay, but then the cross section curves remain on average almost constant – apart from coarse oscillations – for a relatively broad energy interval.
The thermal rate constant for the reaction Cl− + CH3Br → ClCH3 + Br− as obtained from this work is graphically displayed in Fig. 3. The plot shows an atypical non-Arrhenius behavior with a negative temperature coefficient, which, however, strongly resembles that for ion-dipole reactions without a barrier. The older experimental thermal data, measured by Tanaka et al.,5 Olmstead and Brauman,6 Caldwell et al.,7 Bohme and Raksit8 as well as Viggiano et al.12 are very well met by the results of the previous calculation.
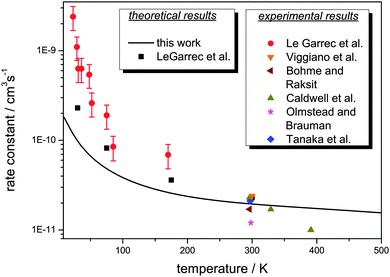 | ||
| Fig. 3 Thermal rate constant for the reaction Cl− + CH3Br → ClCH3 + Br− as calculated in this work (full line). Also shown are calculational results carried out by Clary43 and several experimental data.5–8,12,43 Note the logarithmic scale of the ordinate. | ||
For lower temperatures, however, quantitative agreement with the experimental data could not be reached. While experiment reveals a strong negative temperature dependence, a dramatic increase of the rate constant by more than two orders of magnitude going down from 300 K to 23 K, the calculations give only a one-order-of-magnitude increase. This is a similar behaviour as obtained by Clary in his RBA treatment43 which, however, yielded results somewhat closer to experiment. While Clary made use of the same potential energy surface34 as employed in our work, he scaled the geometries of the C–Br and C–Cl distances close to the saddle point structure.
The reasons for the discrepancies of both theoretical treatments are the relatively low quality of the potential energy surface which however is full-dimensional. Another potential surface, based on higher-level ab initio data may provide better results. As long as full-dimensional quantum scattering calculations are not possible, dimensionality-reduced settings have to be employed. These however rely on reduced-dimensional potential surfaces, optimized with respect to the remaining coordinates. The computation of optimized potential energies on the fly is still very costly.
A further point are the already mentioned approximations in theory. While Clary included the umbrella bend, we explicitly considered the degenerate transition-state bending vibration which has a much lower frequency leading to considerably more adiabatic channel curves in the scattering calculation. The respective other modes are taken into account by transition state theory, i.e. via the partition functions and zero-point-energy differences, as are the remaining modes which are often considered to be spectators. These have much higher frequencies and are relevant for higher temperatures.
Clary pointed out that the quantum treatment of the umbrella bend is responsible for increase of k(T) for low temperatures because the adiabatic curves can have activation energies which may become relevant at higher T. In this work, we showed that inclusion of the degenerate transition state bending motion has the same effect. This means that the general behaviour of the k(T) curve is dominated by the two-dimensional scattering, including only C–Br and C–Cl coordinates.49 The total cross sections reveal sharp peaks for low translational energies which are responsible for the behaviour of the rate constant that increases for lower temperatures. This can be explained by the scattering cross sections which in general become smaller for higher translational energies.
V. Conclusions
We have carried out time-independent quantum scattering calculations for the gas-phase reaction Cl− + CH3Br → ClCH3 + Br− for all possible total angular momentum values up to energies of about 2000 cm−1 above the asymptotic potential energy in the reactant channel. The converged S-matrices were used to compute initial-state selected total reaction cross section and therefrom, by thermal averaging, also rate constants. The latter are the only quantities for which reliable experimental data are available. In the past, several degrees of freedom have been included in addition to the distances of the bonds being formed and broken (which are indispensable for a quantum-mechanical description of the reaction): the umbrella bending mode (within an approximate treatment),42 the azimuthal rotation of the methyl halides,45 the symmetric C–H stretching mode and the umbrella bending mode (exact within in the reduced-dimensional treatment)55 and in the present paper the doubly-degenerate low-frequency bending mode.62 The latter, which corresponds to the rotational motion in the reactant or product molecules, should be expected to be most sensitive in a rate constant calculation due to its small vibrational frequency in the transition state which leads to a considerable population of excited internal states. However, it can be seen that the thermal rate constant is mostly influenced by the simple 2D picture which already yields the characteristic shapes of the reaction cross section curves.49 The additional degrees of freedom are responsible for a stepwise more and more accurate description of the rate constant. It is expected that the full cumulative reaction probability will give a rate constant that perfectly agrees with the experimental results. However, this cannot be the main target of the research within quantum scattering theory applied to molecular encounters. Much more valuable are the detailed features that originate from the individually investigated degrees of freedom. From a quantitative point of view, the most important issue will be the availability of a better potential energy hypersurface, at CCSD(T) quality or better. Further research could also explicitly include the umbrella bending mode.Acknowledgements
We are indebted to Prof. B. R. Rowe and Dr J. L. Le Garrec for providing us with the experimental data from Fig. 2 of ref. 43. Our work was financially supported by the Deutsche Forschungsgemeinschaft (DFG), grant SCHM 1651/1-3. Additional support from the Fonds der chemischen Industrie is gratefully acknowledged.References
- W. L. Hase, Science, 1994, 266, 998 CAS.
- M. L. Chabinyc, S. L. Craig, C. K. Regan and J. I. Brauman, Science, 1998, 279, 1882 CrossRef CAS PubMed.
- J. K. Laerdahl and E. Uggerud, Int. J. Mass Spectrom. Ion Processes, 2002, 214, 277 CrossRef CAS.
- S. Schmatz, ChemPhysChem, 2004, 5, 600 CrossRef CAS PubMed.
- K. Tanaka, G. I. MacKay, J. D. Payzant and D. K. Bohme, Can. J. Chem., 1976, 54, 1643 CrossRef CAS.
- W. N. Olmstead and J. I. Brauman, J. Am. Chem. Soc., 1977, 99, 4219 CrossRef CAS.
- G. Caldwell, T. F. Magnera and P. Kebarle, J. Am. Chem. Soc., 1984, 106, 959 CrossRef CAS.
- D. K. Bohme and A. B. Raksit, Can. J. Chem., 1985, 63, 3007 CrossRef CAS.
- J. A. Dodd and J. I. Brauman, J. Phys. Chem., 1986, 90, 3559 CrossRef CAS.
- S. E. Barlow, J. M. VanDoren and V. M. Bierbaum, J. Am. Chem. Soc., 1988, 110, 7240 CrossRef CAS.
- S. T. Graul and M. T. Bowers, J. Am. Chem. Soc., 1991, 113, 9696 CrossRef CAS.
- A. A. Viggiano, R. A. Morris, J. S. Paschkewitz and J. F. Paulson, J. Am. Chem. Soc., 1992, 114, 10477 CrossRef CAS.
- S. T. Graul and M. T. Bowers, J. Am. Chem. Soc., 1994, 116, 3875 CrossRef CAS.
- J. I. Brauman, J. Mass Spectrom., 1995, 30, 1649 CrossRef CAS.
- V. F. DeTuri, P. A. Hintz and K. M. Ervin, J. Phys. Chem., 1997, 101, 5969 CrossRef CAS.
- K. M. Ervin, Int. J. Mass Spectrom., 1999, 187, 343 CrossRef.
- S. Kato, G. E. Davico, H. S. Lee, C. H. DePuy and V. M. Bierbaum, Int. J. Mass Spectrom., 2001, 210/211, 223 CrossRef CAS.
- L. A. Angel and K. M. Ervin, J. Phys. Chem. A, 2001, 105, 4042 CrossRef CAS.
- L. A. Angel, S. P. Garcia and K. M. Ervin, J. Am. Chem. Soc., 2002, 124, 336 CrossRef CAS PubMed.
- L. A. Angel and K. M. Ervin, J. Am. Chem. Soc., 2003, 125, 1014 CrossRef CAS PubMed.
- L. A. Angel and K. M. Ervin, J. Am. Chem. Soc., 1014, 125, 2003 Search PubMed.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183 CrossRef CAS PubMed.
- J. Mikosch, R. Otto, S. Trippel, C. Eichhorn, M. Weidemüller and R. Wester, J. Phys. Chem. A, 2008, 112, 10448 CrossRef CAS PubMed.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534 CrossRef CAS PubMed.
- J. Xie, R. Sun, M. Siebert, R. Otto, R. Wester and W. L. Hase, J. Phys. Chem. A, 2013, 117, 7162 CrossRef CAS PubMed.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, J. Phys. Chem. A, 2013, 117, 8139 CrossRef CAS PubMed.
- J. Zhang, U. Lourderaj, R. Sun, J. Mikosch, R. Wester and W. L. Hase, J. Chem. Phys., 2013, 138, 114309 CrossRef PubMed.
- M. Kowalewski, J. Mikosch, R. Wester and R. de Vivie-Riedle, Eur. Phys. J. D, 2014, 68, 183 CrossRef.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960 CrossRef CAS PubMed.
- S. R. Vande Linde and W. L. Hase, J. Phys. Chem., 1990, 94, 2778 CrossRef CAS.
- S. R. Vande Linde and W. L. Hase, J. Chem. Phys., 1990, 93, 7962 CrossRef CAS.
- Y. J. Cho, S. R. Vande Linde, L. Zhu and W. R. Hase, J. Chem. Phys., 1992, 96, 8275 CrossRef CAS.
- W. L. Hase and Y. J. Cho, J. Chem. Phys., 1993, 98, 8626 CrossRef CAS.
- H. Wang, L. Zhu and W. L. Hase, J. Phys. Chem., 1994, 98, 1608 CrossRef CAS.
- H. Wang and W. L. Hase, J. Am. Chem. Soc., 1995, 117, 9347 CrossRef CAS.
- D. J. Mann and W. L. Hase, J. Phys. Chem. A, 1998, 102, 6208 CrossRef CAS.
- T. Su, H. Wang and W. L. Hase, J. Phys. Chem. A, 1998, 102, 9819 CrossRef CAS.
- G. Li and W. L. Hase, J. Am. Chem. Soc., 1999, 121, 7124 CrossRef CAS.
- L. Sun, W. L. Hase and K. Song, J. Am. Chem. Soc., 2001, 123, 5753 CrossRef CAS PubMed.
- Y. Wang, W. L. Hase and H. Wang, J. Chem. Phys., 2003, 118, 2688 CrossRef CAS.
- S. C. Tucker and D. G. Truhlar, Chem. Phys. Lett., 1989, 157, 164 CrossRef.
- D. C. Clary and J. Palma, J. Chem. Phys., 1997, 106, 575 CrossRef CAS.
- J. L. LeGarrec, J. B. A. Mitchell, J. L. Queffelec, B. R. Rowe and D. C. Clary, J. Chem. Phys., 1997, 107, 1021 CrossRef CAS.
- H. Wang, E. M. Goldfield and W. L. Hase, J. Chem. Soc., Faraday Trans., 1997, 93, 737 RSC.
- S. Schmatz and D. C. Clary, J. Chem. Phys., 1998, 109, 8200 CrossRef CAS.
- S. Schmatz and D. C. Clary, J. Chem. Phys., 1999, 110, 9483 CrossRef CAS.
- M. I. Hernández, J. Campos-Martinez, P. Villarreal, S. Schmatz and D. C. Clary, Phys. Chem. Chem. Phys., 1999, 1, 1197 RSC.
- H. G. Yu and G. Nyman, Chem. Phys. Lett., 1999, 312, 585 CrossRef CAS.
- S. Schmatz, Chem. Phys. Lett., 2000, 330, 188 CrossRef CAS.
- S. Schmatz, H. Stoll and P. Botschwina, Int. J. Mass Spectrom. Ion Processes, 2000, 291, 277 CrossRef.
- S. Schmatz, P. Botschwina, J. Hauschildt and R. Schinke, J. Chem. Phys., 2001, 114, 5233 CrossRef CAS.
- J. Hauschildt, R. Schinke, S. Schmatz and P. Botschwina, Phys. Chem. Chem. Phys., 2001, 3, 2275 RSC.
- S. Schmatz, P. Botschwina, J. Hauschildt and R. Schinke, J. Chem. Phys., 2002, 117, 9710 CrossRef CAS.
- S. Schmatz and J. Hauschildt, J. Chem. Phys., 2003, 118, 4499 CrossRef CAS.
- C. Hennig and S. Schmatz, J. Chem. Phys., 2004, 121, 220 CrossRef CAS PubMed.
- P. Botschwina, C. Hennig and S. Schmatz, Phys. Chem. Chem. Phys., 2004, 6, 4630 RSC.
- C. Hennig and S. Schmatz, Phys. Chem. Chem. Phys., 2005, 7, 1552 RSC.
- S. Schmatz, J. Chem. Phys., 2005, 122, 234306 CrossRef PubMed.
- C. Hennig and S. Schmatz, J. Chem. Phys., 2005, 122, 234307 CrossRef PubMed.
- C. Hennig and S. Schmatz, J. Phys. Chem. A, 2006, 110, 1524 CrossRef CAS PubMed.
- C. Hennig and S. Schmatz, Chem. Phys. Lett., 2007, 446, 250 CrossRef CAS.
- C. Hennig and S. Schmatz, J. Chem. Phys., 2009, 131, 224303 CrossRef PubMed.
- C. Hennig and S. Schmatz, Phys. Chem. Chem. Phys., 2012, 14, 12982 RSC.
- C. Hennig and S. Schmatz, Phys. Chem. Chem. Phys., 2015, 17, 26670 RSC.
- J. Zhang and W. L. Hase, J. Phys. Chem. A, 2010, 114, 9635 CrossRef CAS PubMed.
- L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875 CrossRef CAS PubMed.
- H. Wang and W. L. Hase, J. Am. Chem. Soc., 1995, 117, 9347 CrossRef CAS.
- J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019 CrossRef CAS PubMed.
- J. Xie, M. J. Scott, W. L. Hase, P. M. Hierl and A. A. Viggiano, Z. Phys. Chem., 2015, 229, 1747 CrossRef CAS.
- R. T Pack, J. Chem. Phys., 1974, 60, 633 CrossRef.
- G. C. Schatz and A. Kuppermann, J. Chem. Phys., 1976, 65, 4642 CrossRef CAS.
- J. R. Henderson, S. Miller and J. Tennyson, J. Chem. Soc., Faraday Trans., 1990, 86, 1963 RSC.
- A. Kuppermann, J. A. Kaye and J. P. Dwyer, Chem. Phys. Lett., 1980, 74, 257 CrossRef CAS.
- J. Römelt, Chem. Phys. Lett., 1980, 74, 263 CrossRef.
- G. C. Schatz, Chem. Phys. Lett., 1988, 150, 92 CrossRef CAS.
- D. C. Clary, J. Chem. Phys., 1991, 95, 7298 CrossRef CAS.
- J. Echave and D. C. Clary, J. Chem. Phys., 1994, 100, 402 CrossRef CAS.
- P. Honvault and J.-M. Launay, in Theory of Chemical Reaction Dynamics, ed. A. Lagana and G. Lendvay, Kluwer, Dordrecht, 2004, p. 187 Search PubMed.
- G. C. Groenenboom and D. T. Colbert, J. Chem. Phys., 1993, 99, 9681 CrossRef CAS.
- D. O. Harris, G. G. Engerholm and W. D. Gwinn, J. Chem. Phys., 1965, 43, 1515 CrossRef.
- A. S. Dickinson and P. R. Certain, J. Chem. Phys., 1968, 49, 4209 CrossRef CAS.
- J. C. Light, I. P. Hamilton and J. V. Lill, J. Chem. Phys., 1984, 82, 1400 CrossRef.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982 CrossRef CAS.
- J. T. Muckerman, Chem. Phys. Lett., 1990, 173, 200 CrossRef CAS.
- C. Lanczos, J. Res. Natl. Bur. Stand., 1950, 45, 255 CrossRef.
- H. D. Simon, Math. Comput., 1984, 42, 115 CrossRef.
- J. Echave and D. C. Clary, Chem. Phys. Lett., 1992, 190, 225 CrossRef CAS.
- E. B. Stechel, R. B. Walker and J. C. Light, J. Chem. Phys., 1978, 69, 3518 CrossRef CAS.
- R. B. Walker and E. F. Hayes, in The Theory of Chemical Reaction Dynamics, ed. D. C. Clary, Reidel, Dordrecht, 1986, p. 105 Search PubMed.
- M. S. Child, Mol. Phys., 1967, 12, 401 CrossRef CAS.
- J. M. Bowman, Adv. Chem. Phys., 1985, 65, 61 Search PubMed.
- J. M. Bowman and A. F. Wagner, in The Theory of Chemical Reaction Dynamics, ed. D. C. Clary, Reidel, Dordrecht, 1986, p. 47 Search PubMed.
- J. M. Bowman, J. Phys. Chem., 1991, 95, 4960 CrossRef CAS.
- J. M. Bowman and D. Wang, in Advances in Molecular Vibration and Collision Dynamics, ed. J. M. Bowman, JAI, Greenwich, 1994, vol. IIB, p. 187 Search PubMed.
- F. N. Dzegilenko and J. M. Bowman, J. Chem. Phys., 1996, 105, 2280 CrossRef CAS.
| This journal is © the Owner Societies 2016 |