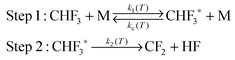Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting pressure-dependent unimolecular rate constants using variational transition state theory with multidimensional tunneling combined with system-specific quantum RRK theory: a definitive test for fluoroform dissociation†
Junwei Lucas
Bao
 b,
Xin
Zhang
*ab and
Donald G.
Truhlar
*b
b,
Xin
Zhang
*ab and
Donald G.
Truhlar
*b
aState Key Laboratory of Chemical Resource Engineering, Institute of Materia Medica, College of Science, Beijing University of Chemical Technology, Beijing, 100029, P. R. China. E-mail: zhangxin@mail.buct.edu.cn
bDepartment of Chemistry, Chemical Theory Center, and Supercomputing Institute, University of Minnesota, Minneapolis, Minnesota 55455-0431, USA. E-mail: truhlar@umn.edu
First published on 1st June 2016
Abstract
Understanding the falloff in rate constants of gas-phase unimolecular reaction rate constants as the pressure is lowered is a fundamental problem in chemical kinetics, with practical importance for combustion, atmospheric chemistry, and essentially all gas-phase reaction mechanisms. In the present work, we use our recently developed system-specific quantum RRK theory, calibrated by canonical variational transition state theory with small-curvature tunneling, combined with the Lindemann–Hinshelwood mechanism, to model the dissociation reaction of fluoroform (CHF3), which provides a definitive test for falloff modeling. Our predicted pressure-dependent thermal rate constants are in excellent agreement with experimental values over a wide range of pressures and temperatures. The present validation of our methodology, which is able to include variational transition state effects, multidimensional tunneling based on the directly calculated potential energy surface along the tunneling path, and torsional and other vibrational anharmonicity, together with state-of-the-art reaction-path-based direct dynamics calculations, is important because the method is less empirical than models routinely used for generating full mechanisms, while also being simpler in key respects than full master equation treatments and the full reduced falloff curve and modified strong collision methods of Troe.
1. Introduction
Unimolecular reactions, including isomerizations (A → B) and dissociation reactions (A → B + C) are widespread in chemical kinetics. Predicting unimolecular rate constants as functions of temperature and pressure is a longstanding goal in kinetics modeling.1,2 Methods developed for this purpose can also be used for association reactions (B + C → A), whose theoretical treatment involves common elements. The present article presents the validation of a recently proposed theoretical method for this problem that is simplified enough to be practically useful for mechanistic studies where rate constants need to be evaluated for a many-reaction mechanism over a range of temperature and pressure.Transition state theory (TST)3 assumes that all the trajectories originating from the reactant region cross a reactant/product dividing surface in phase space only once, and thus all forward-crossing trajectories lead directly to products; thus the dividing surface is assumed to be a dynamical bottleneck. This is the non-recrossing assumption, and the conventional TST dividing surface passes through a saddle point on the potential energy surface; generalized transition states may be placed at other locations. In variational transition state theory (VTST),4–7 the location of the dividing surface is variationally optimized either to maximize the Gibbs free energy of activation in a canonical ensemble or to minimize the number of states of the generalized transition state in a microcanonical ensemble, and therefore the non-recrossing assumption causes less error. VTST (including recent extensions such as multi-structural VTST8 and multi-path VTST9–12) has been widely applied in many chemically important systems (the reader may consult reviews3,13,14 or representative applications8–12,15–18 for examples). However, in both TST and VTST, the phase points in the reactant region are assumed to be in thermal equilibrium, and consequently Liouville's theorem guarantees that the Boltzmann distribution is also satisfied in the generalized transition state and eventually the product region as time evolves. This local equilibrium assumption is generally valid in gas-phase bimolecular reactions,19 except for diatomic dissociation,20 because inelastic collisions of the reactants are efficient enough to repopulate their rovibrational states and maintain local equilibrium in phase space, and in liquid-phase reactions, but not in gas-phase unimolecular reactions. In the latter case, unless the pressure is extremely high, the rovibrationally excited states at not in local equilibrium, and the rate constants depend on pressure, falling off as the pressure is lowered and the reactive states are depleted faster than they can be repopulated.
The reactive states of the unimolecular reactant can be populated by a chemical reaction or by thermal collisions; the former scenarios is called the chemical activation mechanism and the latter is called thermal activation or the Lindemann–Hinshelwood mechanism.21 In these mechanisms, only the rovibrational quantum states that are of the ground electronic state are populated; the atoms move on a single Born–Oppenheimer potential energy surface, and the whole chemical reaction is electronically adiabatic. In the chemical activation mechanism, the rovibrationally excited unimolecular states (which are denoted as P*) are generated by reactive collisions between reactants A and B, and P* can either be de-energized to form the product P (the stabilized adduct) by inelastic collisions with bath gas molecules or undergo further dissociation or isomerization to form product P′. The low-pressure rate constant of the formation of P is lower than the high-pressure-limit, while the dissociation/isomerization reaction rate constant is larger than the high-pressure-limit. In the Lindemann–Hinshelwood mechanism, thermally activated unimolecular states A* of a reactant A are created by thermal collisions between the reactant A and bath gas M; then A* reacts to form the products. The high-pressure-limit unimolecular rate constants are higher than the rate constants at lower pressures. The pressure-dependence of the unimolecular rate constant is known as the “falloff” effect because of the decrease of the thermal rate constant as the pressure decreases.
Modeling the falloff curves as functions of pressure p and temperature T has attracted considerable interest dating back to 1921.1,22–24 A complete solution to the problem would require solving the time-dependent kinetics equations for all state concentrations as functions of time; this is called the master equation.14,25 A simpler approach is the strong collision approximation that an energized molecule is completely deactivated by every collision and therefore every reactive state is produced in a single step from a molecule in an unactivated state.24 The classic work of Troe26 provided a detailed analysis of energy transfer processes during the collisional activation and de-activation, which he deduced based on approximate solutions to the master equation and from which he developed a modified strong collision model,27 which relates the collision efficiency to the amount of energy transferred and the energy dependence of the density of states. Jasper and co-workers28 carried out classical trajectory calculations for modeling the collisional energy transfer process, and concluded that Troe's modified strong collision model is a very good approximation to the real situation. In order to calculate the falloff curves, Troe and colleagues29 developed a central broadening factor (Fcent) based empirical method for computing the ratio of k(p; T) to the high-pressure-limit value as a function of pressure; in this treatment a number of parameters are required, and these parameters are either estimated empirically or fitted using the experimental data. This method has played an important role in interpolating or extrapolating limited experimental data points to a wider range of p and T.30
Attempts have been made to diminish empiricism for predicting falloff curves and to provide treatments simple enough for modeling reaction mechanisms of many-component mixtures, such as involved in combustion. Whereas solving a one-dimensional master equation is not a highly computationally demanding task, building the master equation involves providing microcanonical rate constants as input, and it could be very expensive to compute the required values of k(E) reliably. There are two aspects to nonempirical calculation of reliable rate constants: the level of dynamical theory employed and the potential energy surfaces on which that theory is based. The majority of applications of the master equation make the Rice–Ramsperger–Kassel assumption that the rate constants are functions of only the total energy (we call such rate constants microcanonical) and use conventional Rice–Ramsperger–Kassel–Marcus (RRKM) theory31 as the dynamical theory; this is the same as conventional transition state theory for a unimolecular reaction,32 rather than microcanonical variational transition state theory4 (μVT), but we note that the variational effect (which is a shorthand name for the difference of variational transition state theory from conventional transition state theory) is sometimes very important. Furthermore, the internal rotations are usually simply treated using 1D hindered rotors or even by the harmonic oscillator approximation, as contrasted to a more complete treatment33 of the contributions from multiple conformational structures. Also, the energy-resolved multidimensional tunneling is ignored in most treatments due to high computation cost. VTST, multidimensional tunneling calculations based on the directly calculated potential energy surface along the tunneling path, and multistructural treatments of torsions require more information about the potential energy surface than do conventional TST calculations, but in modern work canonical VTST can be carried out efficiently obtained by direct dynamics calculations8–12,15,17,33,34 with affordable, but reliable exchange–correlation density functionals35 to generate the input data. Microcanonical VTST calculations are also affordable but considerably more expensive, and so we would like to not require them for mechanism modeling.
Influential work done by Dean, Westmoreland, Bozzelli, and coworkers36 demonstrated the value of combining quantum Rice–Ramsperger–Kassel (QRRK) theory37 for microcanonical rate constants with the modified strong collision model. Although a master equation solver is widely implemented in many kinetics-modeling programs,38 Dean and Bozzelli showed that their QRRK approach could provide similar results with greater simplicity and lower cost and effort in generating the input data.39 In their earlier work, empirical methods, such as group additivity and Evans–Polanyi correlations, were used to estimate the Arrhenius pre-exponential factor A and thermodynamic functions because of the lack of reliable first-principles data. Although these empirical methods are tremendously helpful for rapidly providing the necessary thermochemical kinetics information as input for mechanistic studies, the accuracy of the so-produced data are sometimes unreliable. For example, the thermodynamic functions estimated by single-structure-based group additivity method can deviate significantly from values measured experimentally or computed using high-level theory for highly branched molecules;40 and estimating the energies of activation as temperature independent or depending linearly on temperature is inadequate over a wide temperature range because the activation energy at low temperature could be very much lower than the one at high temperature.41 The early QRRK work now has led to more advanced work. In recent studies by Dean and Bozzelli and coworkers,42 the CBS-QB3 electronic structure method is used for computing electronic energetics, thermodynamic functions are computed using 1-D hindered rotor with torsional potential scanned using the B3LYP density functional, and conventional TST rate constants with one-dimensional tunneling are computed, fitted (assuming a linear temperature-dependence of Ea) and serve as high-pressure-limit input for QRRK. Their work shows how one can diminish empiricism in fall-off calculations, and it motivated us to incorporate our own more complete high-pressure-limit rate constants into this kind of treatment.
Recently, we proposed the system-specific quantum RRK (SS-QRRK) method,43,44 which retains the theoretical and computational simplicity of the original QRRK model, yet is able to incorporate high-level electronic structure calculations into the potential energy surface and variational effects, multidimensional tunneling based on the directly calculated potential energy surface along the tunneling path, and torsional and other vibrational anharmonicity into the dynamical theory. Our SS-QRRK rate constants are calibrated by full high-pressure-limit canonical VTST direct dynamics calculations, and (aside from estimating collision rates with widely available Lennard–Jones parameters) the only empirical parameter needed for predicting falloff curves is the average energy transferred. A key advantage is that the VTST calculations based on the most accurate available electronic structure methods for the potential energy surface are required only for canonical rate constants, with SS-QRRK theory serving as a way to generate the required microcanonical data from the canonical rate constants.
In the present work, we tested our SS-QRRK method for the dissociation reaction of fluoroform (CHF3), whose dissociation products are difluoromethylene radical (CF2, with the electronic ground state being of 1A1 symmetry) and hydrogen fluoride (HF). Fluoroform is found in the atmosphere (where it is a greenhouse gas) as a consequence of its use for applications such as refrigeration, fire retardant, and plasma etching. Troe and coworkers45 pointed out that the decomposition of fluoroform is a unimolecular elimination without extraneous complications and that it can therefore serve as a test case for modeling the falloff behavior of a simple, rigid molecule. They noted that, whereas previous attempts to understand it, dating back 50 years,46 were unsuccessful or fragmentary, their new analysis “has brought about a complete consistency of measurements and modelling.”45 The reaction “therefore presents itself as an exemplary unimolecular thermal elimination reaction.” For this reason, and because of its simplicity and the availability of experimentally measured rate constants over a wide range of pressures and temperatures that are of interest in combustion chemistry, we believe it presents an ideal case to validate our new SS-QRRK approach. Troe and co-workers used conventional TST to compute the high-pressure-limit rate constants, and they fitted the experimental falloff data with reduced falloff curves, in which a number of parameters are estimated empirically or fitted. We carried out direct dynamics variational transition state theory calculations with multidimensional tunneling based on the directly calculated potential energy surface along the tunneling path; and we use the so-obtained high-pressure-limit data to calibrate SS-QRRK microcanonical rate constants. We will show that our computed falloff curves by the SS-QRRK approach is in excellent agreement with experimental results.
2. Theoretical methods
2.1. Choice of electronic structure method
We use CCSD(T)-F12a, which is explicitly correlated coupled cluster theory with single and double excitations and a quasiperturbative treatment of connected triple excitations,47 with the jun-cc-pVTZ48 basis set to obtain reference values of the classical barrier heights and classical reaction energies. (“Classical” barrier heights and energies of reaction are differences in potential energy without considering zero point energy, and reference values are highly accurate values used to validate more affordable levels of theory to be used for the dynamics calculations.) Single-point calculations were then carried out with various combinations of exchange–correlation density functionals and basis sets at geometries optimized by CCSD(T)-F12a/jun-cc-pVTZ. The results are presented in ESI.† These tests shows that the M08-HX49/aug-cc-pVTZ50 method is very accurate; its mean unsigned error (MUE) for the classical forward barrier height, reverse barrier height, and energy of reaction is 0.15 kcal mol−1. The reference values are respectively 77.75, 18.46, and 59.30 kcal mol−1, and the M08-HX/aug-cc-pVTZ values are 77.93, 18.67, and 59.25 kcal mol−1. Therefore this method was chosen for the direct dynamics calculations.All the electronic structure calculations (except for the coupled cluster calculations, which are performed using Molpro51) are performed using the locally modified Gaussian 09.52 Density functional calculations are computed with a numerical integration grid of 99 radial shells and 974 angular points per shell.
2.2. High-pressure-limit rate constants
Canonical variational transition state theory (CVT) is used for the first determination of the high-pressure-limit thermal rate constant of the reaction CHF3→CF2 + HF. This reaction has significant hydrogenic motion in the reaction coordinate, and therefore another set of calculations was carried out including tunneling; in particular the small-curvature tunneling approximation53 (SCT) is used for treating the underbarrier quantum mechanical tunneling and the overbarrier nonclassical reflection. The multidimensional SCT method incorporates the corner-cutting quantum centrifugal effect by using an effective mass that is dependent on the reaction-path-curvature, and it is based on the directly calculated potential energy surface along the tunneling path. Because the effective mass used in the imaginary action integral is less than the mass used to scale the coordinates, this is equivalent to shortening the tunneling path, and this increases the tunneling as compared to tunneling along the mass-scaled isoinertial minimum-energy path (MEP). The SCT tunneling approximation is a very well validated method that is applicable to large and complex systems,6,53,54 and one of the strengths of the method employed here is that it allows one to include this accuracy in falloff calculations at an affordable cost, as discussed in Section 2.3.The MEP, with a scaling mass of 1 amu, was computed from −2.75 Å to +2.75 Å with a step size of 1.06 × 10−3 Å by using the Page–McIver algorithm55 along with the reorientation of the dividing surface (RODS) algorithm56 for re-orienting the generalized-transition-state-theory dividing surface. The generalized normal mode analysis is carried out using non-redundant curvilinear coordinates;57 the Hessians are computed and diagonalized at every ninth step along the reaction coordinate. Vibrational anharmonicity is included along the reaction coordinate by scaling the generalized normal mode frequencies with a factor of 0.975.58
The high-pressure rate constant is fitted to the following formula appropriate to an endothermic reaction:12
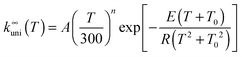 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−ECVT/SCTa(T)/RT]. The Arrhenius activation energy is defined as:
exp[−ECVT/SCTa(T)/RT]. The Arrhenius activation energy is defined as: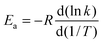 | (2) |
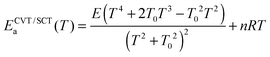 | (3) |
A∞uni(T) = k∞uni(T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[ECVT/SCTa(T)/RT] exp[ECVT/SCTa(T)/RT] | (4) |
Direct dynamic calculations were performed with Polyrate59 interfaced with Gaussian 09 via Gaussrate.60
2.3. Pressure-dependent rate constants
This section partially contains a brief review about the classic theories of unimolecular reactions because a review of the classical theory helps us make clear the connection between the way the old theory treats physical effects and the way the new theory does this; and we are able to clearly state the reasons for how and why we choose the physical parameters such as A and Ea that are used in SS-QRRK model.In the original Lindemann model, the rate constants are assumed to be temperature-dependent and energy-independent. The thermal activation rate constant k1 is modeled as:
k1 = Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E0/kBT) exp(−E0/kBT) | (5) |
| Z = πσ2〈νrel〉 | (6) |
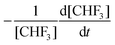 ) is:
) is: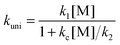 | (7) |
k∞uni = k1k2/kc = A∞uni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E0/kBT) exp(−E0/kBT) | (8) |
In our approach, k∞uni(T) is computed using CVT/SCT theory; and the threshold energy E0 of the unimolecular dissociation reaction (step 2) is set to be equal to the temperature-dependent high-pressure-limit Arrhenius activation energy ECVT/SCTa(T) computed as described in Section 2.2. The value of A∞uni(T) is now temperature-dependent and we shall call it the frequency factor when it is used in SS-QRRK theory (see below).
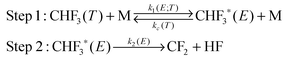
The energization and dissociation rate constants are treated as energy-dependent using SS-QRRK theory, and the collisional de-energization rate constant is computed based on modified strong collision model, which are discussed next. In particular, we consider the following thermal activation mechanism:
Step 1 is the thermal activation step, in which the thermally equilibrated fluoroform molecules (denoted as CHF3(T) in the mechanism) at temperature T collide with bath gas M to produce the rovibrationally excited reactant CHF3*(E) with total rovibrational energy E randomized among all modes. The rate constant of thermal activation k1 is a function of energy E and is parametrically dependent on T. The de-activation collisional rate constant kc is assumed to be temperature-dependent as in Lindemann–Hinshelwood theory; it is computed as
| kc(T) = Zβc | (9) |
To model k1(E;T) and k2(E), we use single-frequency quantum RRK theory (QRRK), in which rotation is not treated explicitly, and the molecule consists of s identical oscillators with vibrational frequency ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) , where we express
, where we express ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) in wave numbers (cm−1). In practice, we set s equal to number of vibrational degree of freedom (for CHF3, s is 9), and
in wave numbers (cm−1). In practice, we set s equal to number of vibrational degree of freedom (for CHF3, s is 9), and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) is chosen to be the reactant geometric mean frequency (for CHF3,
is chosen to be the reactant geometric mean frequency (for CHF3, ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = 1036.69 cm−1, which is computed by M08-HX/aug-cc-pVTZ). In the QRRK model of the microcanonical rate constant at energy E equal to nhc
= 1036.69 cm−1, which is computed by M08-HX/aug-cc-pVTZ). In the QRRK model of the microcanonical rate constant at energy E equal to nhc![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) (where h is Planck's constant, and c is the speed of light), a unimolecular reaction happens when a specific vibrational mode associated with the reaction coordinate possesses a critical energy (or threshold energy) E0 equal to mhc
(where h is Planck's constant, and c is the speed of light), a unimolecular reaction happens when a specific vibrational mode associated with the reaction coordinate possesses a critical energy (or threshold energy) E0 equal to mhc![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) . Note that n and m are not usually integers.
. Note that n and m are not usually integers.
First consider k1(E;T). The equilibrium constant for step 1 is the fraction of the molecules with n quanta of excitation, which is
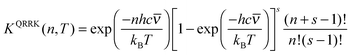 | (10) |
KQRRK(n,T) = kQRRK1(E = nhc![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ;T)/kc(T) ;T)/kc(T) | (11) |
Next consider the QRRK rate constant k2(E); this is equal to the frequency factor times the fraction of molecules with at least m quanta in one chosen mode, and for a quantum mechanical oscillator with s identical frequencies ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) and temperature T, this is given by30,61
and temperature T, this is given by30,61
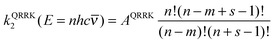 | (12) |
m = ECVT/SCTa(T)/hc![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) | (13) |
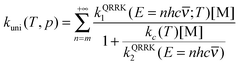 | (14) |
Now it can be shown why we choose the frequency factor and threshold energy by eqn (3) and (4). In the high-pressure-limit, eqn (14) reduces to:
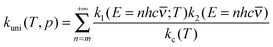 | (15) |
The variational effect can be very important in the computation of k(E), and ignoring it can be a significant source of error.43 The ability of the new method to incorporate variational effects in k(E) has been validated in our previous work43 by comparison to full microcanonical variational transition state theory calculations. To compute the energy-resolved quantum tunneling would involve using eqn (32) of ref. 43, and this would be very time consuming if based on the directly calculated potential energy surface along the tunneling path. The variational effect, multidimensional tunneling, and multi-structural torsional anharmonicity (MS-T) are usually ignored in current practice for falloff effects, but the present formalism allows their incorporation in falloff calculations with approximately the same affordable effort as is required for the canonical-ensemble high-pressure limit.
At high temperatures, the collision efficiency can be much smaller than unity, which means that only a small fraction of collisions lead to fully de-activated CHF3. The collision efficiency βc is computed using Troe's modified strong collision model:27
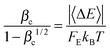 | (16) |
In this work, Whitten–Rabinovitch approximation27 is used to compute FE. Notice that in our approach, the threshold energy used in Whitten–Rabinovitch approximation is not the zero-point inclusive barrier height; instead, for consistency with the SS-QRRK treatment, we use the temperature-dependent CVT/SCT activation energy ECVT/SCTa(T) as the threshold energy. Our computed FE values at 298 K, 600 K, 800 K, 1000 K, 1600 K, and 2000 K are 1.060, 1.118, 1.162, 1.210, 1.365 and 1.477 respectively; the corresponding collision efficiency βc at these temperatures are 0.159, 8.76 × 10−2, 6.66 × 10−2, 5.31 × 10−2, 3.14 × 10−2, and 2.39 × 10−2. If the zero-point-included barrier had been used as threshold energy, the computed FE values at 298 K, 600 K, 800 K, 1000 K, 1600 K, and 2000 K would have been 1.056, 1.119, 1.164, 1.212, 1.378 and 1.510 respectively; we do not use these FE values in the paper, but we present them simply to show that the results in the present case are not sensitive to the choice of threshold energy in the FE calculation.
The single-structure Whitten–Rabinovitch approximation does not account for multistructural anharmonicity. This is not an issue in the present case, but when multi-structural torsional-potential anharmonicity (MS-T)33 is important, FE will be computed using Troe's definition:26
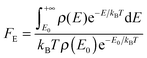 | (17) |
The collision efficiency can also be estimated as:63
 | (18) |
3. Results and discussion
3.1. Structure and energetics
We computed T1 diagnostic64 values by CCSD(T)-F12a/jun-cc-pVTZ level for CHF3, CF2, HF, and the transition state structure and obtained respectively 0.0112, 0.0164, 0.0084, and 0.0195, all of which are smaller than 0.02, which is the suggested65 criterion for closed-shell species having multireference character. Therefore, we concluded that our studied reaction CHF3 → CF2 + HF does not involve significant multireference character, and the energetics can be reliably computed using single-reference methods, such as Kohn–Sham density functional theory and coupled cluster theory.Both experimental and theoretical studies have confirmed that the electronic ground state of CF2 radical is 1A1.66 Our M08-HX/aug-cc-pVTZ calculation shows that the CF23B1 state is 2.39 eV energetically higher than its 1A1 state; this is in good agreement with the experimentally determined adiabatic excitation energy 2.46 eV.67
Absorption and microwave spectroscopy studies68 have revealed the equilibrium geometry of ground state CF2 to have RC–F = 1.300 Å and θ(F–C–F) = 104.94°. Our coupled cluster calculation gives RC–F = 1.300 Å and θ(F–C–F) = 104.8°; and our M08-HX/aug-cc-pVTZ calculation gives RC–F = 1.300 Å and θ(F–C–F) = 104.4°. Thus our calculated reactant geometries are quite accurate.
The dissociation of CHF3 is an endothermic reaction; the ZPE-inclusive energy of reaction as computed by M08-HX/aug-cc-pVTZ, CCSD(T)-F12a/jun-cc-pVTZ, CBS-QB3,69 and G4,70 is, respectively, 53.7, 53.3, 54.1, and 52.8 kcal mol−1. The ZPE-inclusive forward barrier heights computed at these levels are respectively 73.6, 73.1, 74.5 and 73.1 kcal mol−1. Thus M08-HX/aug-cc-pVTZ appears to be more accurate than CBS-QB3; and it has similar accuracy as G4, but M08-HX is computationally much less expensive than G4.
3.2. High-pressure-limit rate constants, variational effect and tunneling
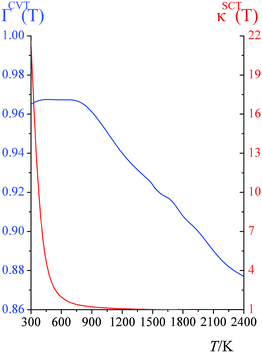
CVT/SCT computed high-pressure-limit unimolecular dissociation rate constants (s−1) are tabulated in the ESI†; they are fitted using eqn (1), which yields A = 3.020 × 109 s−1, n = 4.231, E = 54.7658 kcal mol−1, and T0 = 129.465 K.Fig. 1 shows the canonical variational recrossing transmission coefficients (i.e., the ratios of the CVT rate constant to the conventional TST ones) and the small-curvature tunneling transmission coefficients at various temperatures.
From 300 K to 900 K, the variational transmission coefficients are larger than 0.96 and hence, the canonical variational effect is not important at these temperatures; for temperatures higher than 900 K, the variational transmission coefficients decreases from 0.97 at 900 K to 0.88 at 2400 K. Fig. 2 shows the vibrationally adiabatic ground-state potential energy VGa (which is the sum, along the MEP, of the electronic potential energy and the zero-point vibrational energies of all the modes that are orthogonal to the reaction coordinate) along the minimum energy path (MEP), plotted with two key distances RC–H and RF–H (Å). At 300 K to 900 K, the variational transition state is very close to the saddle point; the location of the variational transition state at 300 K, 400 K, 600 K and 800 K are 0.025, 0.029, 0.037 and 0.045 Å away from the saddle point (in isoinertial coordinates6 scaled to 1 amu). As temperature increases, the variational transition state moves away from the conventional transition state; at 2400 K, the canonical variational transition state is 0.091 Å away from the conventional transition state.
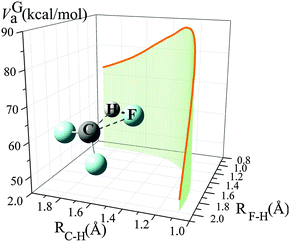 | ||
| Fig. 2 Vibrationally adiabatic ground-state potential energy (kcal mol−1) along the minimum energy path (MEP), depicted with distances of RC–H and RF–H (Å). | ||
The dissociation reaction of CHF3 is a hydrogen-transfer reaction; therefore quantum mechanical tunneling plays an important role. At 298 K, the small-curvature tunneling (SCT) accelerates the reaction rate by a factor of 21.7; at 550 K this has decreased to a factor of 1.9, and by 900 K it has decreased almost to 1.2. If reaction-path curvature had been ignored in computing the tunneling transmission coefficients, the tunneling effect would have been greatly underestimated. For example, at 298 K, the tunneling transmission coefficient would have been only 8.7. (The Wigner approximation71 for the tunneling transmission coefficient is even less accurate, giving a transmission coefficient that is 7 times smaller than the SCT tunneling transmission coefficient at 298 K).
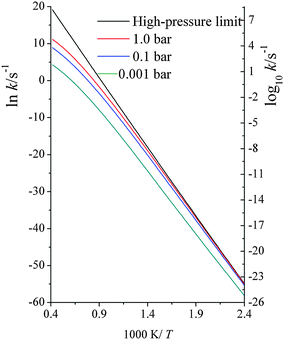 | ||
| Fig. 3 Computed unimolecular dissociation reaction rate constants (s−1) at various temperatures (K) at high-pressure-limit, 1.0 bar, 0.1 bar and 0.001 bar. | ||
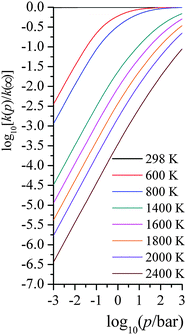 | ||
| Fig. 4 Computed falloff curves at various temperatures (K) with average energy transfer parameter being 58 cm−1. | ||
We compared our computed unimolecular rate constants with 34 experimentally measured data from 1490 K to 1960 K, with pressures ranging from 2.12 bar to 18.04 bar. With |〈ΔE〉| = 58 cm−1, the average ratio of computed to experimental rate constants is 0.76, with a standard deviation of 0.20. This excellent agreement indicates that our SS-QRRK methodology is a simple yet accurate way for predicting falloff behaviors, and this is the central result of the present paper.
The uncertainty of |〈ΔE〉| in real applications could be quite large because of the lack of available experimental values. In principle, trajectory calculations could be carried out to determine |〈ΔE〉|, but it is not clear if readily available approximations to the potential energy surface would be accurate enough to yield reliable values. In practice, |〈ΔE〉| values from similar systems, when available, are often used in modeling falloff. In fact there are three kinds of errors in the energy transfer. First, we do not know the mean value of |〈ΔE〉|. Second, even if we knew it at one temperature, the true value should be temperature dependent, even though most treatments used in combustion modeling treat it as temperature independent or energy independent. Third, even if we knew the correct value as a function of temperature, we would have errors from the assumption of the exponential-down model rather than using a full set of state-to-state vibrational-rotational energy transfer rates,72 not just a single average |〈ΔE〉|. In the combustion community, the |〈ΔE〉| value is often treated as a fitting parameter that is fitted to limited experimental data; alternatively, |〈ΔE〉| is adopted from other “similar” systems to approximately model the current system of interest.
Because of these uncertainties in the one empirical parameter needed in our treatment, and in order to test the sensitivity to this parameter and try to rationalize the possible reliability of the falloff calculations given the uncertainty of |〈ΔE〉| people used in the literature, we tested the sensitivity of the calculated rate constant to the value of |〈ΔE〉| used in our falloff calculations; full details are given in the ESI,† and here we just present key findings. Fig. 5 shows a scatter plot for the distribution of kcalc/kexptl at 34 data points, with different energy transfer parameter being used. For |〈ΔE〉| = 29, 58, 116, 232, and 464 cm−1, the average ratio of computed to experimental rate constants over 34 data points are 0.47, 0.76, 1.17, 1.72 and 2.41. In thermal activation mechanism, increasing the energy transfer parameter produces activated states more rapidly; therefore, the predicted unimolecular rate constants are larger and the falloff effect is smaller.
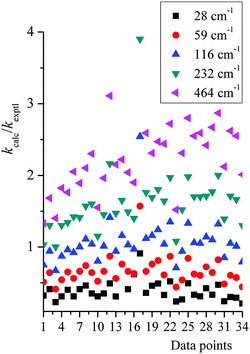 | ||
| Fig. 5 A scatter plot for the distribution of kcalc/kexptl at 34 data points, with different energy transfer parameter being used. Data point n on the x-axis corresponds to the n-th data point listed in Table S6 (in ESI†). | ||
At very low pressures, the rate constant, now bimolecular, increases with the magnitude of the average energy transfer, but more slowly than linearly. At the higher pressures of Fig. 5, a factor of 5.1 difference is observed in the unimolecular rate constant when |〈ΔE〉| ranges over a factor of 16 (from half the value (58 cm−1) of Troe and coworkers to eight times their value). On one hand, the sensitivity to |〈ΔE〉| is quite small; on the other hand, our deviation from experimental values is smaller than the sensitivity to the |〈ΔE〉| parameter. Our simpler treatment works well and allows one to avoid a more expensive master equation treatment. Note that a falloff calculation also requires the user to provide the energy transfer parameter in the input; if the error in using the SS-QRRK method is smaller than the error due to the uncertainty in the energy transfer parameter, there is no solid motivation for making the treatment more laborious. However, we do not want to imply that the master equation should be abandoned or avoided for treating reaction networks; our approach is an alternative way and computationally less expensive way, since E-dependent variational rate constants and microcanonical tunneling are not needed. Notice that, in the current master equation solvers, the microcanonical variational effects and energy-resolved tunneling are generally not included; and the thermally averaged quantum tunneling are treated using Eckart or Wigner models, which are not as accurate as SCT approximation.
3.4. Activation energies
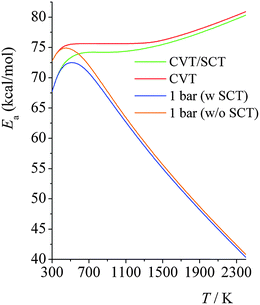
Arrhenius activation energies in the high-pressure-limit and at 100 bars, 10 bars, 1.0 bars and 0.01 bars are plotted in Fig. 6. In the high-pressure-limit, activation energy increases monotonically as temperature increases; the activation energy at 298 K is 12.7 kcal mol−1 smaller than the one at 2400 K; however at lower pressures, Fig. 6 shows non-monotonic behavior. At lower pressures and temperatures higher than 600 K, the activation energies decrease as pressure decreases; and higher the temperature, the more significant amount of the Ea decreases. This is consistent with what we showed in Fig. 3; the magnitude of the curvature of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k vs. 1/T curve (which is equal to, from the definition of Ea, the Arrhenius activation energy Ea multiplied by −1/R) decreases at higher temperatures and lower pressures. At temperatures lower than 600 K, the activation energy at 1.0 bars increases with the same trend as the one for the high-pressure-limit; the falloff effect is negligible at temperatures lower than 400 K. Then, as temperature increases, the activation energy starts decreasing, from 72.8 kcal mol−1 at 600 K to 40.4 kcal mol−1 at 2400 K; at 2400 K, the activation energy in the high-pressure-limit is 40.0 kcal mol−1 higher than the one at 1.0 bar.
k vs. 1/T curve (which is equal to, from the definition of Ea, the Arrhenius activation energy Ea multiplied by −1/R) decreases at higher temperatures and lower pressures. At temperatures lower than 600 K, the activation energy at 1.0 bars increases with the same trend as the one for the high-pressure-limit; the falloff effect is negligible at temperatures lower than 400 K. Then, as temperature increases, the activation energy starts decreasing, from 72.8 kcal mol−1 at 600 K to 40.4 kcal mol−1 at 2400 K; at 2400 K, the activation energy in the high-pressure-limit is 40.0 kcal mol−1 higher than the one at 1.0 bar.
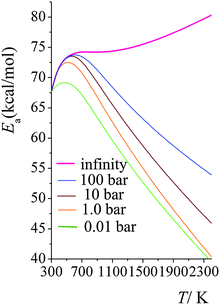 | ||
| Fig. 6 Calculated Arrhenius activation energies (kcal mol−1) at high-pressure-limit (infinity), 100 bar, 10 bar, 1.0 bar, and 0.01 bar at various temperatures (K). | ||
Fig. 7 shows the calculated Arrhenius activation energies in the high-pressure-limit, both with (green curve) and without (red curve) SCT tunneling; and it also shows the activation energies at 1.0 bar computed using SS-QRRK calibrated by CVT/SCT rate constants (blue line) and calibrated by high-pressure-limit CVT (without SCT) rate constants (orange line). The SS-QRRK method effectively includes the SCT tunneling into the microcanonical rate constants while avoiding the high computational cost of calculating energy-resolved microcanonical tunneling because SCT is only calculated rigorously for canonical ensembles in the high-pressure-limit. Quantum mechanical tunneling effectively lowers the activation energy, which is noticeable at low temperatures; at high temperatures, Ea computed by CVT/SCT and by CVT are very similar. At 1.0 bar, the maximum of the Ea curves arises from the balance between temperature-dependence of the high-pressure-limit activation energy (Ea increases as T increases) and the fall-off effects (Ea decreases as T increases).
4. Summary
In the current work, we applied the system-specific quantum RRK theory combined with Lindemann–Hinshelwood thermal activation mechanism to study the kinetics of dissociation reaction CHF3 → CF2 + HF, which is taken as a well understood reference case for validating the relatively new approach. The high-pressure-limit rate constants are computed using canonical variational transition state theory with the small-curvature tunneling approximation based on the directly calculated potential energy surface along the tunneling path. The predicted falloff curves and pressure-dependent unimolecular rate constants agree very well with experimentally measured values.Acknowledgements
This work was supported in part by the U. S. Department of Energy, Office of Basic Energy Sciences, under a grant number to be assigned by DOE.References
- M. J. Pilling and P. W. Seakins, Reaction Kinetics, Oxford University Press, Oxford, 1990 Search PubMed.
- S. J. Klippenstein, V. S. Pande and D. G. Truhlar, Chemical kinetics and mechanisms of complex systems: a perspective on recent theoretical advances, J. Am. Chem. Soc., 2014, 136, 528–546 CrossRef CAS PubMed.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, Current status of transition-state theory, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- B. C. Garrett, Generalized transition state theory. Classical mechanical theory and applications to collinear reactions of hydrogen molecules, J. Phys. Chem., 1979, 83, 1052–1079 CrossRef CAS.
- D. G. Truhlar and B. C. Garrett, Variational transition-state theory, Acc. Chem. Res., 1980, 13, 440–448 CrossRef CAS.
- D. G. Truhlar and B. C. Garrett, Variational transition state theory, Annu. Rev. Phys. Chem., 1984, 35, 159–189 CrossRef CAS.
- D. G. Truhlar, A. D. Isaacson and B. C. Garrett, Generalized transition state theory, in Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, 1985, pp. 65–137 Search PubMed.
- T. Yu, J. Zheng and D. G. Truhlar, Multi-structural variational transition state theory. Kinetics of the 1,4-hydrogen shift isomerization of the pentyl radical with torsional anharmonicity, Chem. Sci., 2011, 2, 2199–2213 RSC.
- T. Yu, J. Zheng and D. G. Truhlar, Multipath variational transition state theory: Rate constant of the 1,4-hydrogen shift isomerization of the 2-cyclohexylethyl radical, J. Phys. Chem. A, 2012, 116, 297–308 CrossRef CAS PubMed.
- J. L. Bao, R. Meana-Pañeda and D. G. Truhlar, Multi-path variational transition state theory for chiral molecules: the site-dependent kinetics for abstraction of hydrogen from 2-butanol by hydroperoxyl radical, analysis of hydrogen bonding in the transition state, and dramatic temperature dependence of the activation energy, Chem. Sci., 2015, 6, 5866–5881 RSC.
- J. L. Bao, P. Sripa and D. G. Truhlar, Path-dependent variational effects and multidimensional tunneling in multi-path variational transition state theory: rate constants calculated for the reactions of HO2 with tert-butanol by including all 46 paths for abstraction at C and all six paths for abstraction at O, Phys. Chem. Chem. Phys., 2016, 18, 1032–1041 RSC.
- J. Zheng and D. G. Truhlar, Multi-path variational transition state theory for chemical reaction rates of complex polyatomic species: ethanol + OH reactions, Faraday Discuss., 2012, 157, 59–88 RSC.
- B. C. Garrett and D. G. Truhlar, Variational transition state theory, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 67–87 Search PubMed.
- A. Fernández-Ramos, J. A. Miller, S. J. Klippenstein and D. G. Truhlar, Modeling the kinetics of bimolecular reactions, Chem. Rev., 2006, 106, 4518–4584 CrossRef PubMed.
- J. Zheng, R. Meana-Pañeda and D. G. Truhlar, Prediction of experimentally unavailable product branching ratios for biofuel combustion: The role of anharmonicity in the reaction of isobutanol with OH, J. Am. Chem. Soc., 2014, 136, 5150–5160 CrossRef CAS PubMed.
- R. Meana-Paxeda and A. Fernández-Ramos, Tunneling and conformational flexibility play critical roles in the isomerization mechanism of vitamin D, J. Am. Chem. Soc., 2012, 134, 346–354 CrossRef PubMed.
- J. L. Bao, P. Seal and D. G. Truhlar, Nanodusty plasma chemistry: a mechanistic and variational transition state theory study of the initial steps of silyl anion–silane and silylene anion–silane polymerization reactions, Phys. Chem. Chem. Phys., 2015, 17, 15928–15935 RSC.
- J. G. Lauderdale and D. G. Truhlar, Large tunneling effects in the migration of chemisorbed hydrogen on a metal, J. Am. Chem. Soc., 1985, 107, 4590–4591 CrossRef CAS.
- C. Lim and D. G. Truhlar, The effect of vibrational-rotational disequilibrium on the rate constant for an atom-transfer reaction, J. Phys. Chem., 1986, 90, 2616–2634 CrossRef CAS.
- H. S. Johnston and J. Birks, Activation energies for the dissociation of diatomic molecules are less than the bond dissociation energies, Acc. Chem. Res., 1972, 5, 327–335 CrossRef CAS.
- (a) H. H. Carstensen and A. M. Dean, The kinetics of pressure-dependent reactions, Compr. Chem. Kinet., 2007, 42, 101–184 Search PubMed; (b) J. W. Bozzelli, A. Y. Chang and A. M. Dean, Molecular density of states from estimated vapor phase heat capacities, Int. J. Chem. Kinet., 1997, 29, 161–170 CrossRef CAS; (c) A. Y. Chang, J. W. Bozzelli and A. M. Dean, Kinetic analysis of complex chemical activation and unimolecular dissociation reactions using QRRK Theory and the “oxidation state” modified strong collision approximation, Z. Phys. Chem., 2000, 214, 1533–1568 CrossRef CAS.
- (a) J. A. Christiansen, PhD thesis, University of Copenhagen, Copenhagen, Denmark, 1921; (b) F. A. Lindemann, Discussion on “the radiation theory of chemical action”, Trans. Faraday Soc., 1922, 17, 598–606 RSC.
- C. N. Hinshelwood, On the theory of unimolecular reactions, Proc. R. Soc. London, Ser. A, 1926, 113, 230–233 CrossRef CAS.
- W. Forst, Theory of Unimolecular Reactions, Academic Press, New York, 1973, p. 148 Search PubMed.
- (a) J. R. Barker, Multiple-well, multiple-path unimolecular reaction systems. I. MultiWell computer program suite, Int. J. Chem. Kinet., 2001, 33, 232–245 CrossRef CAS; (b) M. J. Pilling and S. H. Robertson, Master equation models for chemical reactions of importance in combustion, Annu. Rev. Phys. Chem., 2003, 54, 245–275 CrossRef CAS PubMed; (c) J. R. Barker, Energy Transfer in Master Equation Simulations: A New Approach, Int. J. Chem. Kinet., 2009, 41, 748–763 CrossRef CAS; (d) R. E. Weston, T. L. Nguyen, J. F. Stanton and J. R. Barker, HO + CO reaction rates and H/D kinetic isotope effects: Master equation models with ab initio SCTST rate constants, J. Phys. Chem. A, 2013, 117, 821–835 CrossRef CAS PubMed.
- (a) J. Troe, Theory of thermal unimolecular reactions at low pressures. I. Solutions of the master equation, J. Chem. Phys., 1977, 66, 4745–4757 CrossRef CAS; (b) J. Troe, Theory of thermal unimolecular reactions at low pressures. II. Strong collision rate constants. Applications, J. Chem. Phys., 1977, 66, 4758–4775 CrossRef CAS.
- J. Troe, Predictive Possibilities of Unimolecular Rate Theory, J. Phys. Chem., 1979, 83, 114–126 CrossRef CAS.
- (a) A. W. Jasper, J. A. Miller and S. J. Klippenstein, Collision efficiency of water in the unimolecular reaction CH4 (+H2O) ← CH3 + H (+H2O): One-dimensional and two-dimensional solutions of the low-pressure-limit master equation, J. Phys. Chem. A, 2013, 117, 12243–12255 CrossRef CAS PubMed; (b) A. W. Jasper, K. M. Pelzer, J. A. Miller, E. Kamarchik, L. B. Harding and S. J. Klippenstein, Predictive a priori pressure-dependent kinetics, Science, 2014, 346, 1212–1215 CrossRef CAS PubMed.
- (a) J. Troe, Theory of thermal unimolecular reactions in the fall-off range. I. Strong collision rate constants, Ber. Bunsen-Ges., 1983, 87, 161–169 CrossRef CAS; (b) R. G. Gilbert, K. Luther and J. Troe, Theory of thermal unimolecular reactions in the fall-off range. II. Weak collision rate constants, Ber. Bunsen-Ges., 1983, 87, 169–177 CrossRef CAS; (c) J. Troe and V. G. Ushakov, Revisiting falloff curves of thermal unimolecular reactions, J. Chem. Phys., 2011, 135 CrossRef CAS PubMed , 054304.
- K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions, John Wiley & Sons, New York, 2nd edn, 1996 Search PubMed.
- R. A. Marcus, Unimolecular dissociations and free radical recombination reactions, J. Chem. Phys., 1952, 20, 359–364 CrossRef CAS.
- (a) H. M. Rosenstock, M. B. Wallenstein, A. L. Wahrhaftig and H. Eyring, Absolute rate theory for isolated systems and the mass spectra of polyatomic molecules, Proc. Natl. Acad. Sci. U. S. A., 1952, 36, 667–678 CrossRef; (b) J. L. Magee, Theory of the chemical reaction rate constant, Proc. Natl. Acad. Sci. U. S. A., 1952, 38, 764–770 CrossRef CAS PubMed.
- (a) J. Zheng, T. Yu, E. Papajak, I. M. Alecu, S. L. Mielke and D. G. Truhlar, Practical methods for including torsional anharmonicity in thermochemical calculations on complex molecules: The internal-coordinate multi-structural approximation, Phys. Chem. Chem. Phys., 2011, 13, 10885–10907 RSC; (b) J. Zheng and D. G. Truhlar, Quantum Thermochemistry: Multistructural Method with Torsional Anharmonicity Based on a Coupled Torsional Potential, J. Chem. Theory Comput., 2013, 9, 1356–1367 CrossRef CAS PubMed.
- (a) K. K. Baldridge, M. S. Gordon, R. Steckler and D. G. Truhlar, Ab initio reaction paths and direct dynamics calculations, J. Phys. Chem., 1989, 93, 5107–5119 CrossRef CAS; (b) D. G. Truhlar and M. S. Gordon, From force fields to dynamics: Classical and quantal paths, Science, 1990, 249, 491–498 CAS.
- J. Zheng, Y. Zhao and D. G. Truhlar, The DBH24/08 database and its use to assess electronic structure model chemistries for chemical reaction barrier heights, J. Chem. Theory Comput., 2009, 5, 808–821 CrossRef CAS PubMed.
- (a) A. M. Dean, Predictions of pressure and temperature effects upon radical addition and recombination reactions, J. Phys. Chem., 1985, 89, 4600–4608 CrossRef CAS; (b) P. R. Westmoreland, J. B. Howard, J. P. Longwell and A. M. Dean, Prediction of rate constants for combustion and pyrolysis reactions by bimolecular QRRK, AIChE J., 1986, 32, 1971–1979 CrossRef CAS; (c) J. W. Bozzelli and A. M. Dean, Chemical activation analysis of the reaction of ethyl radical with oxygen, J. Phys. Chem., 1990, 94, 3313–3317 CrossRef CAS.
- L. S. Kassel, Studies in homogeneous gas reactions. II. Introduction of quantum theory, J. Phys. Chem., 1982, 32, 1065–1078 CrossRef.
- J. W. Allen, C. F. Goldsmith and W. H. Green, Automatic estimation of pressure-dependent rate coefficients, Phys. Chem. Chem. Phys., 2012, 14, 1131–1155 RSC.
- (a) C. Y. Sheng, J. W. Bozzelli, A. M. Dean and A. Y. Chang, Detailed kinetics and thermochemistry of C2H5 + O2: Reaction kinetics of the chemically-activated and stabilized CH3CH2OO˙ adduct, J. Phys. Chem. A, 2002, 106, 7276–7293 CrossRef CAS; (b) H. H. Carstensen, C. V. Naik and A. M. Dean, Detailed modeling of the reaction of C2H5 + O2, J. Phys. Chem. A, 2005, 109, 2264–2281 CrossRef CAS PubMed.
- P. Seal and D. G. Truhlar, Large entropic effects on the thermochemistry of silicon nanodusty plasma constituents, J. Am. Chem. Soc., 2014, 136, 2786–2799 CrossRef CAS PubMed.
- (a) J. Zheng, P. Seal and D. G. Truhlar, Role of conformational structures and torsional anharmonicity in controlling chemical reaction rates and relative yields: butanal + HO2, Chem. Sci., 2013, 4, 200–212 RSC; (b) J. Zheng and D. G. Truhlar, Kinetics of hydrogen-transfer isomerizations of butoxyl radicals, Phys. Chem. Chem. Phys., 2010, 12, 7782–7793 RSC.
- (a) K. Wang, S. M. Villano and A. M. Dean, Ab initio study of the influence of resonance stabilization on intramolecular ring closure reactions of hydrocarbon radicals, Phys. Chem. Chem. Phys., 2016, 18, 8437–8452 RSC; (b) K. Wang, S. M. Villano and A. M. Dean, Reactivity–structure-based rate estimation rules for alkyl radical H atom shift and alkenyl radical cycloaddition reactions, J. Phys. Chem. A, 2015, 119, 7205–7221 CrossRef CAS PubMed; (c) S. Yommee and J. W. Bozzelli, Cyclopentadienone oxidation reaction kinetics and thermochemistry for the alcohols, hydroperoxides, and vinylic, alkoxy, and alkylperoxy radicals, J. Phys. Chem. A, 2016, 120, 433–451 CrossRef CAS PubMed.
- J. L. Bao, J. Zheng and D. G. Truhlar, Kinetics of hydrogen radical reactions with toluene including chemical activation theory employing system-specific quantum RRK theory calibrated by variational transition state theory, J. Am. Chem. Soc., 2016, 138, 2690–2704 CrossRef CAS PubMed.
- J. L. Bao and D. G. Truhlar, Silane-initiated nucleation in chemically active plasmas: Validation of density functionals, mechanisms, and pressure-dependent variational transition state calculations, Phys. Chem. Chem. Phys., 2016, 18, 10097–10108 RSC.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Experimental and modelling study of the unimolecular thermal decomposition of CHF3, Z. Phys. Chem., 2011, 225, 1019–1028 CrossRef CAS.
- (a) E. Tschuikow-Roux and J. E. Marte, Thermal decomposition of fluoroform in a single-pulse shock tube, J. Chem. Phys., 1965, 42, 2049–2056 CrossRef; (b) E. Tschuikow-Roux, Thermal decomposition of fluoroform in a single-pulse shock tube. II. Pressure dependence of the rate, J. Chem. Phys., 1965, 42, 3639–3642 CrossRef; (c) A. P. Modica and J. E. LaGraff, Mass-spectrometer and ultraviolet absorption study of CHF3 decomposition behind shock waves, J. Chem. Phys., 1966, 44, 3375–3379 CrossRef CAS; (d) K. P. Schug, H. G. Wagner and F. Zabel, Gas phase α,α elimination of hydrogen halides from halomethanes. I. Thermal decomposition of chlorodifluoromethane, trifluoromethane, and trichloromethane behind shock waves, J. Phys. Chem., 1979, 83, 167–175 CAS; (e) Y. Hidaka, T. Nakamura and H. Kawano, High-temperature pyrolysis of trifluoromethane in shock waves, Chem. Phys. Lett., 1991, 187, 40–44 CrossRef CAS.
- (a) K. Raghavachari and J. B. Anderson, Electron correlation effects in molecules, J. Phys. Chem., 1996, 100, 12960–12973 CrossRef CAS; (b) T. B. Adler, G. Knizia and H. J. Werner, A simple and efficient CCSD(T)-F12 approximation, J. Chem. Phys., 2007, 127 CrossRef CAS PubMed , 221106; (c) G. Knizia, T. B. Adler and H. J. Werner, Simplified CCSD(T)-F12 methods: Theory and benchmarks, J. Chem. Phys., 2009, 130 CrossRef CAS PubMed , 054104.
- E. Papajak and D. G. Truhlar, What are the most efficient basis set strategies for correlated wave function calculations of reaction energies and barrier heights, J. Chem. Phys., 2012, 137 Search PubMed , 064110.
- Y. Zhao and D. G. Truhlar, Exploring the limit of accuracy of the global hybrid meta density functional for main-group thermochemistry, kinetics, and noncovalent interactions, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, M. Sch€utz, P. Celani, G. Knizia, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, version 2012.1, University of Birmingham, Birmingham, 2012 Search PubMed.
- (a) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision D. 01), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed; (b) Y. Zhao, R. Peverati, K. Yang, S. Luo, H. S. Yu, X. He and D. G. Truhlar, MN-GFM version 6.7 computer program module, University of Minnesota, Minneapolis, 2016 Search PubMed.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu and D. G. Truhlar, Molecular modeling of the kinetic isotope effect for the [1,5]-sigmatropic rearrangement of cis-1,3-pentadiene, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- (a) S. E. Wonchoba and D. G. Truhlar, Effect of phonon coupling on hydrogen tunneling rates at gas-surface interfaces, J. Chem. Phys., 1993, 99, 9637–9651 CrossRef CAS; (b) T. C. Allison and D. G. Truhlar, Testing the accuracy of practical semiclassical methods: Variational transition state theory with optimized multidimensional tunneling, in Modern methods for multidimensional dynamics computations in chemistry, ed. D. L. Thompson, World Scientific, Singapore, 1998, pp. 618–712 Search PubMed; (c) J. Pu and D. G. Truhlar, Validation of variational transition state theory with multidimensional tunneling contributions against accurate quantum mechanical dynamics for H + CH4 −> H2 + CH3 in an extended temperature interval, J. Chem. Phys., 2002, 117, 1479–1481 CrossRef CAS; (d) D. G. Truhlar, J. Gao, M. Garcia-Viloca, C. Alhambra, J. Corchado, M. L. Sanchez and T. D. Poulsen, Ensemble-averaged variational transition state theory with optimized multidimensional tunneling for enzyme kinetics and other condensed-phase reactions, Int. J. Quantum Chem., 2004, 100, 1136–1152 CrossRef CAS; (e) A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Variational transition state theory with multidimensional tunneling, Rev. Comput. Chem., 2007, 23, 125–232 CAS.
- M. Page and J. W. McIver Jr., On evaluating the reaction path Hamiltonian, J. Chem. Phys., 1987, 88, 922–935 CrossRef.
- J. Villà and D. G. Truhlar, Variational transition state theory without the minimum energy path, Theor. Chem. Acc., 1997, 97, 317–323 CrossRef.
- C. F. Jackels, Z. Gu and D. G. Truhlar, Reaction-path potential and vibrational frequencies in terms of curvilinear internal coordinates, J. Chem. Phys., 1995, 102, 3188–3201 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, Computational thermochemistry: Scale factor databases and scale factors for vibrational frequencies obtained from electronic model chemistries, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. F. Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, POLYRATE, version 2010-A, University of Minnesota, Minneapolis, 2010 Search PubMed.
- J. Zheng, S. Zhang, J. C. Corchado, Y. Y. Chuang, E. L. Coitiño, B. A. Ellingson and D. G. Truhlar, GAUSSRATE, version 2009-A, University of Minnesota, Minneapolis, 2010 Search PubMed.
- K. J. Laidler, Chemical Kinetics, McGraw-Hill, New York, 1965, 2nd edn, pp. 150–151 Search PubMed.
- H. Hippler, H. J. Wendelken and J. Troe, Collisional deactivation of vibrationally highly excited polyatomic molecules. II. Direct observations for excited toluene, J. Chem. Phys., 1983, 78, 6709–6717 CrossRef CAS.
- R. G. Gilbert and S. C. Smith, Theory of unimolecular and recombination reactions, Blackwell Science, Oxford, 1990 Search PubMed.
- T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- (a) J. C. Rienstra-Kiracofe, D. Wesley and H. F. Schaefer, The C2H5 + O2 reaction mechanism: high-level ab initio characterizations, J. Phys. Chem. A, 2000, 104, 9823–9840 CrossRef CAS; (b) S. R. Miller, N. E. Schultz, D. G. Truhlar and D. G. Leopold, A study of the ground and excited states of Al3 and Al3−. II. Computational analysis of the 488 nm anion photoelectron spectrum and a reconsideration of the Al3 bond dissociation energy, J. Chem. Phys., 2009, 130 CAS , 024304.
- (a) D. E. Milligan, D. E. Mann, M. E. Jacox and R. A. Mitsch, Infrared spectrum of CF2, J. Chem. Phys., 1964, 41, 1199–1203 CrossRef CAS; (b) D. E. Milligan and M. E. Jacox, Matrix-isolation study of the reaction of atomic and molecular fluorine with carbon atoms. Infrared spectra of normal and 13C-substituted CF2 and CF3, J. Chem. Phys., 1968, 48, 2265–2271 CrossRef CAS; (c) Z. L. Cai, Ab initio study of several electronic states of the CF2 radical, J. Phys. Chem., 1993, 97, 8399–8402 CrossRef CAS.
- S. Koda, Emission and energy transfer of triplet difluoromethylene produced in the reaction of oxygen atoms with tetrafluoroethylene, Chem. Phys. Lett., 1978, 55, 353–357 CrossRef CAS.
- (a) F. X. Powell and D. R. Lide, Microwave spectrum of CF2, J. Chem. Phys., 1966, 45, 1067–1068 CrossRef CAS; (b) W. H. Kirchhoff, D. R. Lide and F. X. Powell, Microwave spectrum, force field, and dipole moment of difluoromethylene, J. Mol. Spectrosc., 1973, 47, 491–498 CrossRef CAS; (c) A. Charo and F. C. De Lucia, The millimeter and submillimeter spectrum of difluoromethylene radical and its production in a dc glow discharge, J. Mol. Spectrosc., 1982, 94, 363–368 CrossRef CAS.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, A complete basis set model chemistry. VI. Use of density functional geometries and frequencies, J. Chem. Phys., 1999, 126, 084108 Search PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Gaussian-4 theory, J. Chem. Phys., 2007, 110, 2822–2827 Search PubMed.
- E. P. Wigner, Über das Überschrieten von potentialschwellen bei chemischen reaktionen, Z. Phys. Chem., Abt. B, 1932, 19, 203–216 Search PubMed.
- D. Rapp and T. Kassal, Theory of vibrational energy transfer between simple molecules in nonreactive collisions, Chem. Rev., 1969, 69, 61–102 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02765b |
| This journal is © the Owner Societies 2016 |