Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of the water dimer on the atmospheric reactivity of carbonyl oxides†
Josep M.
Anglada
*a and
Albert
Solé
b
aDepartament de Química Biològica i Modelització Molecular, (IQAC – CSIC), Jordi Girona, 18-26, E-08034 Barcelona, Spain. E-mail: anglada@iqac.csic.es
bDepartament de Ciència de Materials i Química Física, i Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, Martí i Franqués, 1, E-08028 Barcelona, Spain
First published on 31st May 2016
Abstract
The reactions of twelve carbonyl oxides or Criegee intermediates with the water monomer and with the water dimer have been investigated employing high level theoretical methods. The study includes all possible carbonyl oxides arising from the isoprene ozonolysis and the methyl and dimethyl carbonyl oxides that originated from the reaction of ozone with several hydrocarbons. These reactions have great significance in the chemistry of the atmosphere because Criegee intermediates have recently been identified as important oxidants in the troposphere and as precursors of secondary organic aerosols. Moreover, water vapor is one of the most abundant trace gases in the atmosphere and the water dimer can trigger the atmospheric decomposition of Criegee intermediates. Our calculations show that the nature and position of the substituents in carbonyl oxides play a very important role in the reactivity of these species with both the water monomer and the water dimer. This fact results in differences in rate constants of up to six orders of magnitude depending on the carbonyl oxide. In this work we have defined an effective rate constant (keff) for the atmospheric reaction of carbonyl oxides with water vapor, which depends on the temperature and on the relative humidity as well. With this keff we show that the water dimer, despite its low tropospheric concentration, enhances the atmospheric reactivity of Criegee intermediates, but its effect changes with the nature of carbonyl oxide, ranging between 59 and 295 times in the most favorable case (syn-methyl carbonyl oxide), and between 1.4 and 3 times only in the most unfavorable case.
Introduction
Alkene ozonolysis is one of the most important pathways for the degradation of unsaturated hydrocarbons in the Earth's atmosphere. The reaction follows the Criegee mechanism1 (reaction (1)) and proceeds, in a first step, by the 1,3-addition of ozone to the double bond of the unsaturated hydrocarbon producing a 1,2,3-trioxolane or a primary ozonide which decomposes, in a second step, into a carbonyl oxide (or Criegee intermediate) and a carbonyl compound. Carbonyl oxides are formed with an excess of vibrational energy and a part of them decomposes unimolecularly (about 37–50%),2–15 while the remaining fractions are stabilized vibrationally2,14–18 and can further react with other atmospheric trace gases. | (1) |
The reactivity of stabilized carbonyl oxides is also of great interest for atmospheric purposes. These species can react with tropospheric trace gases such as aldehydes, organic acids, NOx, NH3, SO2, HOx, O3, H2O, and with itself,11,35–67 and contribute to the formation of secondary organic aerosols.48,68–72 Among them the reaction with H2O is of major importance in the atmosphere because water vapor is the third most abundant trace gas in the troposphere. This reaction (2) with n = 1 produces σ-hydroxy-hydroperoxide (HHP),14,15,73 which has been detected in the atmosphere and has a direct impact in forest damage.74,75
| R1R2COO + H2O → R1R2C(OH)OOH | (2a) |
| R1R2COO + (H2O)2 → R1R2C(OH)OOH + H2O | (2b) |
| R(CH3)COO + H2O → R(CH2)C(OOH) + H2O → R(CH2)CO + HO + H2O | (3a) |
| R(CH3)COO + (H2O)2 → R(CH2)C(OOH) + (H2O)2 → R(CH2)CO + HO + (H2O)2 | (3b) |
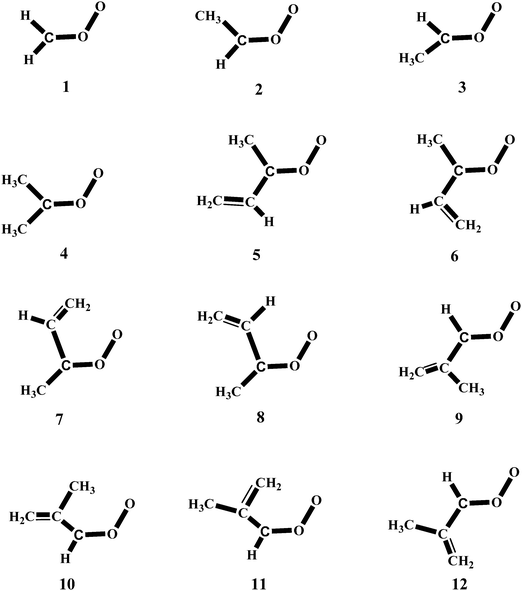
In a previous work42 we have carried out a systematic study on the reactivity of up to 15 carbonyl oxides with water and in this investigation we extend that study to the reaction of the twelve carbonyl oxides depicted in Fig. 1 with the water monomer and with the water dimer. The Criegee intermediates considered in this work are all possible carbonyl oxides arising from the isoprene ozonolysis and the methyl and dimethyl substituted products, arising from ozonolysis of several hydrocarbons. We aim to investigate whether the water dimer has a similar impact on the reactivity of all carbonyl oxides under different atmospheric conditions of temperature and relative humidity and in addition, we would also like to study if the reaction of carbonyl oxides with water will contribute to the atmospheric formation of hydroxyl radicals viareaction (3).
Technical details
All stationary points in the potential energy surface have been fully optimized with the hybrid density functional B3LYP method,85 employing the 6-311+G(2df,2p) basis set.86,87 At this level of theory we have also calculated the harmonic vibrational frequencies to verify the nature of the corresponding stationary point (minimum or transition state), to provide the zero point vibrational energy (ZPE) and the thermodynamic contributions to the enthalpy and free energy. Moreover, we have performed intrinsic reaction coordinate calculations,88–90 to ensure that the transition states connect the desired reactants and products.The final energies were obtained by performing, at the optimized geometries, single point energy calculations at the CCSD(T)91–94 level of theory using the more flexible aug-cc-pVTZ basis set.95,96 In order to obtain a better estimation on the stability of the different reactant complexes, we have also computed, at this level of theory, the basis set superposition error (BSSE) according to the counterpoise method by Boys and Bernardi.97 In addition, for some selected reactions we have carried out additional calculations in order to check the reliability of our computational scheme. Firstly, at the stationary points, we have performed single point energy calculations at the CCSD(T) level of theory employing the aug-cc-pVQZ basis set and we have also considered the extrapolation to the complete basis set (CBS) limit, according to the extrapolation scheme proposed by Helgaker et al.98 Secondly, we have re-optimized and characterized some elementary reactions at the QCISD level of theory99 using the 6-311+G(2df,2p) basis set and we have performed single point CCSD(T)/aug-cc-pVTZ calculations at the computed stationary points.
Finally, we have computed the rate constants using conventional (CTST) and variational (VTST) transition state theories. For this purpose, we have considered the energies obtained at the CCSD(T)/aug-cc-pVTZ//B3LYP/6-311+G(2df,2p) level and the partition functions computed at the B3LYP level of theory. In the case of the conventional transition state theory, the tunneling correction to the rate constants has been calculated using the zero-order approximation to the vibrationally adiabatic PES with zero curvature. In this case, the unsymmetrical Eckart potential energy barrier has been used to approximate the potential energy curve.100 In the calculations involving variational transition state theory, the tunneling effects have been obtained using the small curvature approach.
The quantum chemical calculations carried out in this work were performed by using Gaussian101 and ORCA program packages.102 The Molden program103 was employed to visualize the geometric and electronic features. The kinetic study was done by using the Polyrate program.104
Results and discussion
Reaction of carbonyl oxides with water and the water dimer
Reactions (2) and (3) show that there are two types of processes for the reaction of carbonyl oxides with water and the water dimer. The main process is reaction (2), and corresponds to the addition of the oxygen atom of water to the carbon atom of carbonyl oxide and simultaneously the transfer of one hydrogen atom of water to the terminal oxygen atom of the carbonyl oxide. This is a 1,3-dipolar-like interaction as shown schematically in Fig. 2. The product of the reaction is the corresponding hydroxy hydroperoxide (HHP). The process described by reaction (3) can occur in carbonyl oxides 2, 4, 5, and 6 (Fig. 1), which have a methyl substituent in syn-position. In this reaction water or the water dimer acts as a bridge for the transfer of one hydrogen atom from the methyl substituent to the terminal oxygen atom of the Criegee intermediate producing an hydroperoxide as shown schematically in Fig. 3. The hydroperoxide is produced with a vinyl group on the α-C and to distinguish it from the ROOH, another common species in the atmosphere, these species are commonly termed as vinyl hydroperoxide, and can lead to the formation of hydroxyl radicals.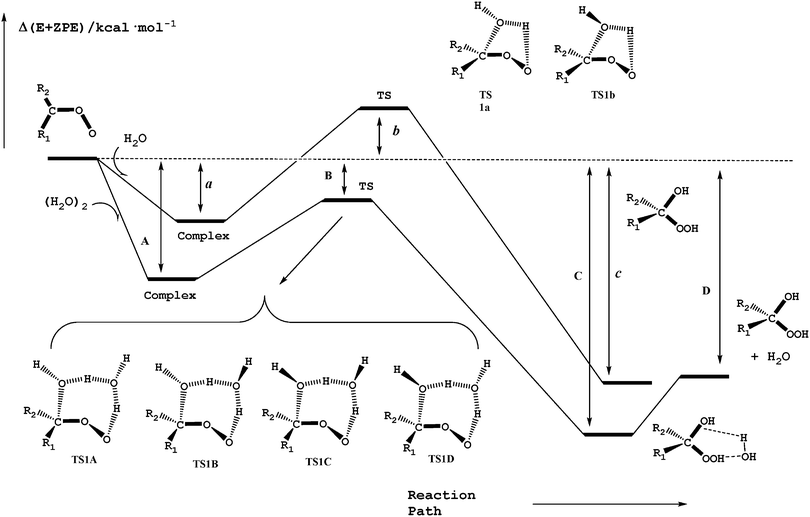 | ||
| Fig. 2 Schematic potential energy surface for the water addition to carbonyl oxides in reactions (2a) and (2b). | ||
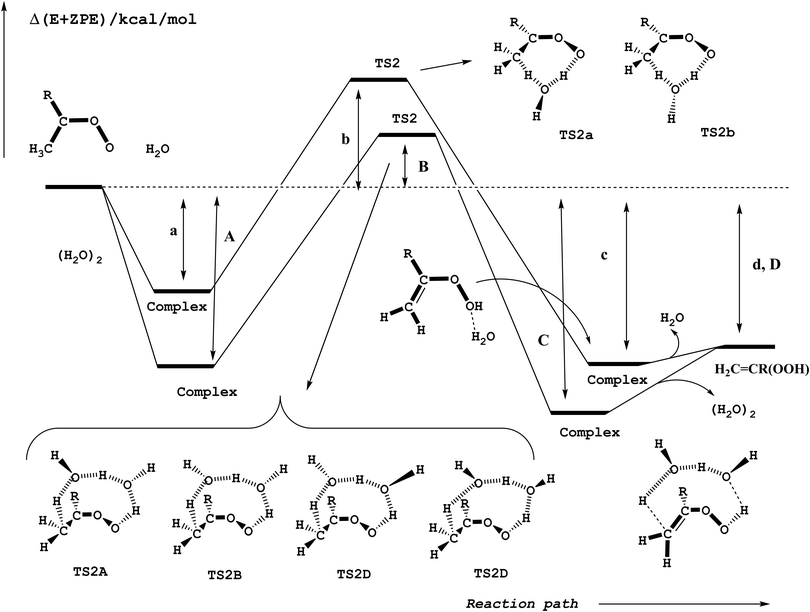 | ||
| Fig. 3 Schematic potential energy surface for the hydrogen atom transfer reactions of carbonyl oxides with water and with the water dimer in reactions (3a) and (3b). | ||
Addition of water to carbonyl oxides
Fig. 2 shows a schematic potential energy surface of the reaction of carbonyl oxides with water and with the water dimer. In all cases, each reaction begins with the formation of a pre reactive complex before the transition state and the release of the corresponding products. Table 1 contains the relative energy of the elementary reactions having the lowest energy barrier. The relative energies of all reactions are collected in Table S1 of the ESI.† In Fig. 2 and Table 1 the labels a, b, and c, correspond to the relative stability of the pre-reactive complex, the transition state and the product of the reaction with water and the labels A, B, C, and D correspond to the relative stability of the pre-reactive complex, the transition state, the post reactive complex and the product of the reaction with the water dimer.| Entry | R1b | R2b | R1R2COO + H2O | R1R2COO + (H2O)2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Path | a | b | c | Path | A | B | C | Dc | |||
| a Plain numbers correspond to CCSD(T)/aug-cc-pVTZ//B3LYP/6-311+G(2df,2p) relative energies. Values in parenthesis are without considering the BSSE correction, values in brackets correspond to CCSD(T)/CBS//B3LYP/6-311+G(2df,2p) relative energies, and values in braces correspond to CCSD(T)/aug-cc-pVTZ//QCISD/6-311+G(2df,2p) relative energies. b R1 stands for the substituent in syn-position and R2 stands for the substituent in anti-position. c It does not necessarily correspond to the most stable conformer. | |||||||||||
| 1 | H | H | TS1a | −6.14 (−6.88) | 1.50 | −42.69 | TS1B | −10.70 (−11.94) | −8.49 | −46.24 | −39.66 |
| [−6.66] | [2.22] | [−42.64] | [−11.38] | [−7.50] | [−45.95] | [−39.81] | |||||
| 2 | CH3 | H | TS1a | −6.58 (−7.46) | 5.34 | −36.67 | TS1A | −11.86 (−13.08) | −5.87 | −39.66 | −33.64 |
| {−7.29} | {5.98} | {−35.97} | |||||||||
| 3 | H | CH3 | TS1a | −7.70 (−8.54) | −1.20 | −41.20 | TS1D | −13.87 (−15.11) | −9.94 | −45.84 | −38.28 |
| 4 | CH3 | CH3 | TS1a | −7.63 (−8.58) | 3.57 | −34.93 | TS1A | −13.89 (−15.23) | −6.05 | −37.72 | −31.90 |
| 5 | CH3 |
t-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
TS1a | −6.45 (−7.36) | 6.82 | −30.46 | TS1A | −10.40 (−11.63) | −1.49 | −33.30 | −25.92 |
| 6 | CH3 |
c-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
TS1a | −6.62 (−7.54) | 5.24 | −31.50 | TS1A | −10.49 (−11.73) | −4.01 | −34.70 | −28.47 |
| 7 |
c-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
CH3 | TS1a | −5.19 (−5.96) | 5.84 | −32.04 | TS1A | −11.69 (−12.98) | −2.38 | −37.60 | −29.87 |
| 8 |
t-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
CH3 | TS1b | −6.50 (−7.40) | 4.31 | −31.69 | TS1A | −12.44 (−13.74) | −4.33 | −36.54 | −28.66 |
| 9 | H |
c-CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH3 CH3 |
TS1a | −6.89 (−7.73) | 1.85 | −34.15 | TS1D | −11.70 (−12.95) | −6.24 | −39.05 | −31.52 |
| 10 |
t-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
H | TS1a | −6.17 (−7.12) | 4.69 | −34.91 | TS1D | −10.73 (−11.98) | −4.91 | −39.02 | −31.88 |
| 11 |
c-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
H | TS1a | −4.54 (−5.19) | 6.82 | −33.12 | TS1A | −10.35 (−11.67) | −2.00 | −36.20 | −30.42 |
| 12 | H |
c-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
TS1a | −6.58 (−7.42) | 0.16 | −37.30 | TS1C | −12.06 (−13.37) | −7.95 | −40.84 | −34.27 |
For the reaction of each carbonyl oxide with a single water molecule there are two elementary reactions whose transition states have a five-membered ring structure. They have been labeled as TS1a and TS1b and differentiate from each other in the orientation of the dangling hydrogen atom of the water moiety (see Fig. 2). The reaction of each carbonyl oxide with the water dimer follows the same trends. Each pre-reactive complex is formed by the interaction between carbonyl oxide and the two water molecules. After the formation of pre-reactive complexes there are four possible elementary reactions whose transition states are labelled as TS1A, TS1B, TS1C, and TS1D. Fig. 2 shows that these transition states differentiate from each other in the orientation of the two dangling hydrogen atoms of the water dimer moiety. Each elementary reaction begins with the corresponding pre-reactive complex that has not been explicitly drawn in the figure for the sake of clarity, but has been considered throughout the work. The product of the reaction is the corresponding hydroxy hydroperoxide, as in the case of the reaction with the water monomer, but forming a hydrogen bond complex with the water molecule.
In order to assess the reliability of the theoretical approach employed in this work we have carried out some sets of calculations. Firstly, for the reaction of the parent carbonyl oxide 1 with water and the water dimer, we have performed, at all stationary points optimized at the B3LYP/6-311+G(2df,2p) level of theory, single point energy calculations at the CCSD(T) level of theory using the aug-cc-pVTZ and aug-cc-pVQZ basis sets, and also considering the extrapolation to the CBS basis set. These results, displayed in Table 1, show that for the reaction with the water monomer TS1a is computed to lie 1.50 kcal mol−1 above the energy of the separate reactants at the CCSD(T)/aug-cc-pVTZ level of theory, but 2.22 kcal mol−1 at the CCSD(T)/CBS level of theory, whereas for the reaction with the water dimer, the corresponding values are −8.49 kcal mol−1 at the CCSD(T)/aug-cc-pVTZ level of theory and −7.50 kcal mol−1 at the CCSD(T)/CBS level of theory. That is, the calculations at the CBS basis set predict relative energies for these transition states to be between 0.72 and 0.99 kcal mol−1 higher than the relative energies obtained using the aug-cc-pVTZ basis set. However, the pre reactive complexes are also destabilized by 0.2–0.6 kcal mol−1 so that the energy barriers for the transition states relative to the pre-reactive complexes change only by 0.4–0.5 kcal mol−1. Table 1 and Table S1 (ESI†) also show that the same trends are observed for the remaining elementary reactions whereas the relative stability of the reaction products changes by at most 0.3 kcal mol−1 when the basis set is extended from aug-cc-pVTZ to the CBS limit. Similar conclusions have been recently reported by Lin et al.,79 although these authors predict the relative energies of the transition state of the reaction of 1 with H2O and (H2O)2 to be 2.82 and −6.61 kcal mol−1 compared with the values of 2.22 and −7.50 kcal mol−1, respectively, computed in our work. The energy barriers obtained by Lin et al.79 are slightly higher than those predicted by our calculations, and these differences may be mainly attributed to the different basis sets employed in calculating the geometries of the stationary points. Secondly, for the reaction of the syn-methyl carbonyl oxide with water (entry 2), we have also optimized and characterized all stationary points at the QCISD/6-311+G(2df,2p) level of theory and we have performed single point energy calculations at the CCSD(T)/aug-cc-pVTZ level of theory. The results of Table 1 show differences of up to 0.5 kcal mol−1 with respect to the values obtained at the CCSD(T)/aug-cc-pVTZ//B3LYP/6-311+G(2df,2p) level of theory. According to these results, we estimate an error of the relative energies obtained at the CCSD(T)/aug-cc-pVTZ//B3LYP/6-311+G(2df,2p) level of theory of up to 1 kcal mol−1, but the error of the energy barriers relative to the reactants should be smaller, up to 0.5 kcal mol−1.
In a previous paper42 we have considered just one of these reaction paths for the reaction of each carbonyl oxide with a single water molecule, but we have disclosed that the corresponding reaction barrier, and consequently the reaction kinetics, depends on both, the nature of the substituents in the carbonyl oxide and on its position (syn or anti). We concluded that substituents with electron donating character hinder the nucleophilic attack of the oxygen atom of water to the carbon atom of the carbonyl oxide, increasing the energy barrier. In contrast, electron withdrawing substituents in the carbonyl oxide cause a decrease of the energy barrier. In addition, substituents in anti-position, produce a stabilization effect and substituents in syn-position produce a destabilization effect, which is caused by the hyperconjugative effects originated by the substituents. For a more detailed discussion on the nature of these effects we suggest the reader looks at ref. 42. This is the case, for instance, of the reaction of methyl carbonyl oxide with water. For the anti-conformer (entry 3) the pre-reactive complex has a binding energy of 7.70 kcal mol−1, (8.54 kcal mol−1 without BSSE) and the transition states lie 1.20 and 0.58 kcal mol−1 below the energy of the separate reactants. For the syn-conformer (entry 2) we have computed a binding energy of 6.58 kcal mol−1 for the reactive complex (7.46 kcal mol−1 without BSSE), while the transition states lie 5.34 and 6.74 kcal mol−1 above the energy of the separate reactants. The huge effect of the position of the substituent in carbonyl oxide is thus reflected in the energy barrier relative to the pre-reactive complex, which are computed to be 7.34 and 7.96 kcal mol−1 for the anti-carbonyl oxide, entry 3, but 12.8 and 14.9 kcal mol−1 for the syn-conformer, entry 2, (see Table 1 and Table S1, ESI†). Regarding the reaction with the water dimer, the results displayed in Table 1 and Table S1 (ESI†) show that all transition states lie below the energy of the separate reactants (between −3.95 and −5.87 kcal mol−1 for entry 2; and between −8.75 and −9.94 kcal mol−1 for entry 3), with a common stabilization energy of about 10–11 kcal mol−1 regarding the relative energies with respect to the corresponding values for the reaction with water monomers, whereas the pre-reactive complexes are stabilized by 5–7 kcal mol−1. Again our results are compared with the values recently reported by Lin and co-workers,79 although those authors predict slightly higher energy barriers in line with the above discussion on the parent carbonyl oxide 1.
As pointed out in a previous work,42 the results displayed also in Table 1 and Table S1 (ESI†) reveal very big differences in the relative energies of the remaining carbonyl oxides (entries 4 to 12), depending on the substituents in the carbonyl oxide and their position. The binding energy of the pre-reactive complexes range between 4.54 kcal mol−1 (entry 11) and 7.63 kcal mol−1 (entry 4), and the relative energy of the transition states with respect to the reactants runs between 0.16 kcal mol−1 (entry 12), and 6.82 kcal mol−1 (entry 11), whereas the reaction energies range between −30.46 kcal mol−1 (entry 5) and −37.30 kcal mol−1 (entry 12). The reaction with the water dimer follows the same trend as the reaction with the water monomer, regarding the nature and position of the substituents in carbonyl oxides. The transition states are roughly stabilized between 8 and 10 kcal mol−1 and the pre-reactive complexes are stabilized between 4 and 6 kcal mol−1 with respect to the relative energies of the corresponding stationary points of the reaction with a single water molecule. The differences in the distinct effects of the substituents are also clearly reflected in the computed energy barriers relative to the pre-reactive complexes, which change between 7.58 and 14.18 kcal mol−1 for the reaction of compounds 12 and 5 with the water monomer, respectively, and to differences between 5.42 and 8.48 kcal mol−1 for the reaction of the same carbonyl oxides with the water dimer.
Our calculations show differences with the reported values on the relative energies ranging between 2 and 3 kcal mol−1 with respect to previous theoretical studies carried out using less accurate theoretical approaches.39–41,63–65,105
In summary, the reaction with the water dimer follows the same trends as the reaction with the water monomer regarding the effect of the substituent and its position in the carbonyl oxide. In the case of reaction with the water monomer, the transition state forms a five-membered ring structure, but for the reaction with the water dimer, each transition state has a seven-membered ring structure in which the oxygen atom of one water molecule interacts with the carbon atom of the carbonyl oxide, one hydrogen atom of this water molecule is transferred to the second water molecule and simultaneously, one hydrogen atom of the second water molecule is also transferred to the terminal oxygen atom of the carbonyl oxide moiety. Therefore, this reaction can be envisaged as the reaction with the water monomer but catalyzed by a second water molecule.
Hydrogen atom transfer
Fig. 3 shows that there are two elementary reactions for the reaction of carbonyl oxides 2, 4, 5, and 6 (reaction (3)) with a single water molecule and four elementary reactions for the reaction with the water dimer. The corresponding transition states have been labeled as TS2a and TS2b for the reaction of carbonyl oxides with H2O and as TS2A, TS2B, TS2C, and TS2D for the reaction with (H2O)2. Fig. 3 shows that the different transition states differ from each other in the relative orientation of the dangling hydrogen atoms of the water monomer and dimer moieties, respectively. As discussed in the previous section, in Fig. 3 and Table 2 the labels a, b, c, and d, correspond to the relative stability of the pre-reactive complex, the transition state and the product of the reaction with water and the labels A, B, C, and D correspond to the relative stability of the pre-reactive complex, the transition state, the post-reactive complex and the product of the reaction with the water dimer. As pointed out in the section Addition of water to carbonyl oxides, each elementary reaction begins with a corresponding pre-reactive complex that has not been drawn for the sake of clarity, but has been considered along the work.| Entry | R1b | R2b | R1R2COO + H2O | R1R2COO + (H2O)2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Path | a | b | c | d | Path | A | B | C | D | |||
| a Plain numbers correspond to CCSD(T)/aug-cc-pVTZ//B3LYP/6-311+G(2df,2p) relative energies. Values in parenthesis are without considering the BSSE correction, values in brackets correspond to CCSD(T)/CBS//B3LYP/6-311+G(2df,2p) relative energies, and values in braces correspond to CCSD(T)/aug-cc-pVTZ//QCISD/6-311+G(2df,2p) relative energies. b R1 stands for the substituent in syn-position and R2 stands for the substituent in anti-position. | ||||||||||||
| 2 | CH3 | H | TS2b | −6.58 (−7.46) | 8.17 | −24.82 | −18.77 | TS2A | −11.86 (−13.08) | 2.06 | −29.66 | −18.77 |
| {−7.29} | {8.35} | {−24.39} | — | |||||||||
| 4 | CH3 | CH3 | TS2a | −7.63 (−8.58) | 7.52 | −22.39 | −16.45 | TS2A | −13.89 (−15.23) | 1.38 | −27.72 | −16.45 |
| 5 | CH3 |
t-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
TS2b | −6.45 (−7.36) | 10.10 | −19.14 | −12.82 | TS2A | −10.85 (−12.07) | 4.42 | −24.17 | −12.82 |
| 6 | CH3 |
c-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
TS2b | −6.62 (−7.54) | 8.70 | −22.80 | −16.37 | TS2A | −10.49 (−11.73) | 2.69 | −27.60 | −16.37 |
The relative energies for the processes with the lowest energy barrier have been collected in Table 1, while Table S2 of the ESI† contains the relative energies of all reactions investigated. For the reactions with the water monomer our calculations predict the transition states to lie between 7.52 and 10.10 kcal mol−1 above the energy of the separate reactants, whereas for the reaction with the water dimer the transition states lie between 1.38 and 4.42 kcal mol−1 with respect to the energies of the reactants, so that there is a common stabilization energy of roughly 6 kcal mol−1 in the relative position of the transition states in going from the reaction with the water monomer to the reaction with the water dimer. This stabilization is smaller by about 4 kcal mol−1 than that calculated for the water addition processes (reaction (2)) and discussed in the previous section.
Reaction kinetics
The kinetic model employed in the present calculations is the same that was used in a previous investigation on the reaction between carbonyl oxides and the water monomer, and is shown in eqn (4).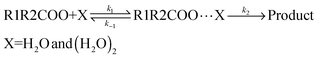 | (4) |
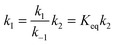 | (5) |
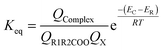 | (6) |
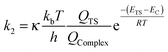 | (7) |
Moreover, the reliability of our kinetic study has been assessed computing, for all reactions involving carbonyl oxides 1, 2, 3, and 4, the rate constants employing the canonical variational transition state theory (CVTST) according to,106–108
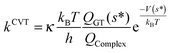 | (8) |
Table 3 contains the computed rate constants, at 298 K, for the reactions of the twelve carbonyl oxides considered in this work with water and the water dimer. In the previous section we have pointed out that in the reaction with the water monomer there are two elementary reactions for each process and in the reaction with the water dimer there are four elementary reactions. Therefore we have calculated the rate constant for each of these elementary reactions, so that the values contained in Table 3 correspond to the sum of the two and four rate constants for the reaction with the water monomer and the water dimer, respectively. Tables S3 and S4 of the ESI† collect the computed values for the reactions with the water monomer and the water dimer in the range of temperatures between 225 K and 325 K.
| Entry | R1R2COO + H2O | R1R2COO + (H2O)2 | ||||
|---|---|---|---|---|---|---|
| k TS1M | k TS2M | k M | k TS1D | k TS2D | k D | |
| a k M stands for the reaction with the water monomer and kD stands for the reaction with the water dimer. kTS1M = kTS1a + kTS1b; kTS2M = kTS2a + kTS2b; kTS1D = kTS1a + kTS1b + kTS1c + kTS1d; kTS2D = kTS2a + kTS2b + kTS2c + kTS2d. See text. b Plain values correspond to rate constants computed at the CTST level; values in parenthesis correspond to constants computed at the VTST level, and values in brackets are rate constants computed at the CTST level using CCSD(T)/CBS energies. c Theoretical values from the literature (in cm3 molecule−1 s−1) are: regarding the reaction with the water monomer for 1: 5.88 × 10−17ref. 40, 8.18 × 10−18ref. 64, and 3.60 × 10−16ref. 79; for 2: 4.23 × 10−20ref. 40, 1.17 × 10−20ref. 64 and 7.23 × 10−21ref. 105; for 3: 2.54 × 10−15ref. 40, 6.72 × 10−16ref. 64, and 2.87 × 10−16ref. 105; for 4: 7.49 × 10−19ref. 40 and 2.90 × 10−19ref. 64; for 5: 1.62 × 10−21ref. 105; and for 6: 3.43 × 10−20ref. 105. Regarding the reaction with the water dimer, for 1: 1.46 × 10−12ref. 64 and 5.44 × 10−12ref. 79; for 2: 1.51 × 10−15ref. 64 and 2.56 × 10−14ref. 79; for 3: 2.77 × 10−12ref. 64 and 1.60 × 10−11ref. 79. | ||||||
| 1 | 3.52 × 10−15 | — | 3.52 × 10−15 | 2.32 × 10−10 | — | 2.32 × 10−10 |
| [3.62 × 10−15] | [3.62 × 10−15] | [3.39 × 10−10] | — | [3.39 × 10−10] | ||
| (3.05 × 10−15) | — | (3.05 × 10−15) | (1.67 × 10−10) | — | (1.67 × 10−10) | |
| 2 | 2.06 × 10−18 | 5.26 × 10−19 | 2.58 × 10−18 | 1.29 × 10−12 | 1.05 × 10−17 | 1.29 × 10−12 |
| (1.42 × 10−18) | (1.47 × 10−18) | (2.89 × 10−18) | (4.82 × 10−13) | (1.78 × 10−16) | (4.83 × 10−13) | |
| 3 | 2.36 × 10−13 | — | 2.36 × 10−13 | 1.06 × 10−9 | — | 1.06 × 10−9 |
| (1.35 × 10−13) | — | (1.35 × 10−13) | (5.93 × 10−10) | — | (5.93 × 10−10) | |
| 4 | 3.89 × 10−17 | 1.63 × 10−18 | 3.97 × 10−17 | 6.96 × 10−13 | 2.79 × 10−17 | 6.96 × 10−13 |
| (1.91 × 10−17) | (5.00 × 10−18) | (2.41 × 10−17) | (3.72 × 10−13) | (2.00 × 10−17) | (3.72 × 10−13) | |
| 5 | 3.08 × 10−19 | 2.74 × 10−20 | 3.35 × 10−19 | 9.23 × 10−16 | 2.29 × 10−19 | 9.23 × 10−16 |
| 6 | 2.73 × 10−18 | 1.76 × 10−19 | 2.91 × 10−18 | 1.27 × 10−14 | 1.74 × 10−18 | 1.27 × 10−14 |
| 7 | 3.65 × 10−18 | — | 3.65 × 10−18 | 5.42 × 10−15 | 5.42 × 10−15 | |
| 8 | 1.87 × 10−17 | 1.87 × 10−17 | 4.71 × 10−14 | 4.71 × 10−14 | ||
| 9 | 2.91 × 10−15 | 2.91 × 10−15 | 3.31 × 10−12 | 3.31 × 10−12 | ||
| 10 | 6.87 × 10−18 | 6.87 × 10−18 | 1.08 × 10−13 | 1.08 × 10−13 | ||
| 11 | 2.25 × 10−19 | 2.25 × 10−19 | 2.39 × 10−15 | 2.39 × 10−15 | ||
| 12 | 1.67 × 10−14 | 1.67 × 10−14 | 2.21 × 10−11 | 2.21 × 10−11 | ||
In order to check the reliability of our calculations, regarding the effects of the theoretical approach, for the reaction of H2COO with the water monomer and the water dimer (entry 1) we have calculated the rate constants at the CTST level using the energies computed at CCSD(T) employing the aug-cc-pVTZ and CBS basis sets and we have calculated the rate constants at the VTST level using the energies computed at the CCSD(T)/aug-cc-pVTZ level of theory. In addition, for the reactions with compounds 2, 3, and 4, we have computed the rate constants at both CTST and VTST levels. Our results displayed in Table 3 show that, for the reactions of 1 with H2O and with (H2O)2, the rate constants calculated at the CTST level using the CCSD(T)/aug-cc-pVTZ and the more accurate CCSD(T)/CBS compare very well. On the other hand, the differences in the values of the rate constants computed using the CTST approach compared with more accurate VTST values are roughly within a factor of 2–3.
Regarding the reaction with the water monomer, our results displayed in Table 3, computed at 298 K, predict that the faster reaction corresponds to anti-methyl carbonyl oxide (entry 3), with a computed rate constant kM of 1.35 × 10−13 cm3 molecule−1 s−1, and the slower rate constant corresponds to the reaction with carbonyl oxide 11, with a computed rate constant kM of 2.29 × 10−19 cm3 molecule−1 s−1. There are differences of up to six orders of magnitude in the value of the rate constant depending on the nature of the carbonyl oxide, as has already been discussed in a previous work.42 Please note that the values reported in Table 3 for the reaction with the water monomer slightly differ from the values reported in ref. 42, which is mainly attributed to the fact that in this work we have considered the two reaction paths occurring for the reaction of each carbonyl oxide with water, whereas in the previous investigation only one reaction path was considered.
For the reaction of the parent carbonyl oxide with water (entry 1) our best calculation predicts a kM of 3.05 × 10−15 cm3 molecule−1 s−1 at 298 K, which compares very well with the value reported by Welz et al.21 (<4 × 10−15 cm3 molecule−1 s−1) measured by direct monitoring of the H2COO decay, and with the value of 1.3 ± 0.4 × 10−15 cm3 molecule−1 s−1 reported by Newland et al.,54 evaluated taking into account the SO2 removal at different RHs in ozonolysis experiments. However, indirect measurements of the rate constant predict values ranging between 3.2 ± 1.2 × 10−16 and <9 × 10−17 cm3 molecule−1 s−1.55,56,60 For the reaction of anti-CH3CHOO with H2O (entry 3), our calculations predict a rate constant of 1.35 × 10−13 cm3 molecule−1 s−1 at 298 K which is 13.5 times greater than the value obtained by Taatjes and co-workers (1.0 ± 0.4 × 10−14 cm3 molecule−1 s−1)57 but 5.6 times greater than the value reported by Sheps et al. (2.4 ± 0.4 × 10−14 cm3 molecule−1 s−1).58 For the reaction of dimethyl carbonyl oxide with water (entry 4) our calculations predict a rate constant of 2.41 × 10−17 cm3 molecule−1 s−1 at 298 K, compared to the value of <1.6 × 10−16 cm3 molecule−1 s−1 predicted by Huang and coworkers.84
Regarding the reaction with the water dimer, our results displayed in Table 3 predict rate constants that are between 1.14 × 103 and 1.67 × 105 times greater than the reaction with the water monomer. The fastest reaction corresponds to anti-methyl carbonyl oxide (entry 3) with a computed kD of 5.93 × 10−10 cm3 molecule−1 s−1 at 298 K and the smallest one corresponds to entry 5, with a computed kD of 9.23 × 10−16 cm3 molecule−1 s−1 at 298 K. Thus, our calculations predict differences of about five orders of magnitude between the largest and the smallest rate constants depending on the nature and position of the substituents in carbonyl oxide. For the reaction of H2COO + (H2O)2 (entry 1) we have computed a rate constant of 1.67 × 10−10 cm3 molecule−1 s−1 at 298 K, which is between 31 and 42 times greater than the experimental measurements, ranging between 4.0 ± 1.2 and 5.4 × 10−12 cm3 molecule−1 s−1.76–78 For the reaction of methyl carbonyl oxide with the water dimer we predict rate constants of 4.83 × 10−13 cm3 molecule−1 s−1 (syn, entry 2) and 5.93 × 10−10 cm3 molecule−1 s−1 (anti, entry 3) which are 14 and 37 times greater than the measured values of 3.40 × 10−14 and 1.60 × 10−11 cm3 molecule−1 s−1, respectively,79 and for the reaction of (CH3)2COO with (H2O)2 (entry 4) we have calculated a rate constant of 3.72 × 10−13 cm3 molecule−1 s−1, in line with the value of <1.3 × 10−13 cm3 molecule−1 s−1 reported by Huang et al.84 The differences between our calculated values and the experimental estimations can mainly rely on the theoretical approach used in this work. The use of optimized geometries and partition functions obtained by ab initio methods using a larger basis set will improve our results. However there are also significant differences in experimental data obtained through different measurements and we are confident that our calculations predict quite well the experimental trends regarding the reactivity of all carbonyl oxides with water and the water dimer.
For carbonyl oxides 2, 4, 5, and 6 the two reactions, water addition (reaction (2)) and hydrogen transfer (reaction (3)), can take place and the corresponding results are included in Table 3. Regarding the reaction with the water monomer, we have calculated almost the same rate constant for both reactions in the case of syn-methyl carbonyl oxide (1.42 × 10−18 and 1.47 × 10−18 cm3 molecule−1 s−1, respectively at 298 K, entry 2) whereas for the remaining carbonyl oxides the rate constant of reaction (2) is computed to be about one order of magnitude greater than the rate constant of reaction (3). It is worth mentioning that our values in Table 3 differ from those reported in a previous paper,42 which is due to the fact that the work we just considered is one of the reaction paths for each reaction. The corresponding values for each elementary reaction and for the whole reaction are reported in Tables S3 to S6 of the ESI.† The important point here is to look at the effect of the water dimer on the hydrogen transfer reaction (reaction (3)) compared with the water addition reaction (reaction (2)). The results from Table 3 show that the rate constants of reaction (3) with the water dimer are between 8 and 121 times greater than the reaction with the water monomer, whereas for reaction (2) the rate constant increases between 3.00 × 103 and 3.40 × 105 times when the water monomer is substituted by the water dimer. These results show clearly that there is a very big impact of the water dimer on the reactivity of carbonyl oxides via water addition reaction (reaction (2)), but the impact on the hydrogen transfer processes, and consequently on the production of hydroxyl radicals, is very small.
Finally, in Table 4 we have collected the Arrhenius parameters for all reactions investigated. There is a negative temperature dependence for all reactions with the water dimer and for reaction of carbonyl oxides 3 and 12 with the water monomer too, according to the relative energies of these reactions displayed in Table 1. The reaction of compounds 2, 4, 5, 6, 9, and 12 with the water monomer has a slight non-Arrhenius behavior (see footnote b in Table 4), which in the case of entries 2, 4, 5, and 6 is due to the strong non Arrhenius character of the hydrogen transfer reaction. Our calculated Arrhenius parameters of carbonyl oxides 1, 2, and 3, are in line with the theoretical values reported by Lin and co-workers79 (see footnote d in Table 4). For the reaction of H2COO with (H2O)2 (entry 1) our computed activation energy is 8.15 kcal mol−1, which compares very well with the experimental value of 8.1 ± 0.6 kcal mol−1 reported by Smith et al.77 and with the calculated value of 8.08 kcal mol−1 of Lin and co-workers.79
| Entry | R1R2COO + H2O | R1R2COO + (H2O)2 | ||
|---|---|---|---|---|
| A | E a | A | E a | |
| a Computed at the VTST level of theory for entries 1–4 and at the CTST level of theory for entries 5–12. b The reaction of carbonyl oxides 2, 4, 5, 6, 9, and 12 with the water monomer has some non-Arrhenius character. c The Arrhenius parameters of reaction (2) for the reactions of carbonyl oxides 2, 4, 5, and 6 with a single water molecule are: 1.43 × 10−14, −5.46; 1.30 × 10−14, −3.86; 8.11 × 10−16, −4.68; and 2.91 × 10−15, −4.13 corresponding to the pair A and Ea respectively. d The calculated parameters reported in ref. 79 are: (pairs of A and Ea, respectively) 1.24 × 10−14, −2.08; 3.14 × 10−15, −5.72; and 4.99 × 10−15, 1.14, for the reaction of 1, 2, and 3 with water, respectively, and 4.11 × 10−18, 8.08; 1.16 × 10−18, 5.93; and 1.63 × 10−18, 8.54 for the reaction of 1, 2, and 3 with the water dimer, respectively. | ||||
| 1 | 3.30 × 10−14 | −1.42 | 1.76 × 10−16 | 8.15 |
| 2 , | 1.78 × 10−16 | −2.44 | 4.44 × 10−17 | 5.50 |
| 3 | 2.58 × 10−14 | 0.98 | 7.51 × 10−17 | 9.40 |
| 4 , | 1.60 × 10−15 | −2.49 | 1.14 × 10−17 | 6.15 |
| 5 , | 1.17 × 10−16 | −3.50 | 2.21 × 10−18 | 3.57 |
| 6 , | 5.05 × 10−16 | −3.07 | 1.40 × 10−18 | 5.39 |
| 7 | 1.74 × 10−14 | −5.02 | 5.42 × 10−18 | 4.09 |
| 8 | 4.01 × 10−15 | −3.19 | 2.56 × 10−18 | 5.81 |
| 9 | 9.05 × 10−15 | −0.68 | 8.58 × 10−18 | 7.62 |
| 10 | 1.00 × 10−14 | −4.32 | 1.02 × 10−17 | 5.49 |
| 11 | 1.16 × 10−14 | −6.43 | 1.35 × 10−17 | 3.06 |
| 12 | 8.81 × 10−15 | 0.38 | 1.70 × 10−17 | 8.34 |
Atmospheric relevance
To gain more insight into the effect of the water dimer in the atmospheric reactivity of carbonyl oxides it is more convenient considering reaction rates rather than rate constants. The reaction rates for the reaction between carbonyl oxides and water and the water dimer can be written as| v1 = kM[R1R2COO][H2O] | (9) |
| v2 = kD[R1R2COO][(H2O)2] | (10) |
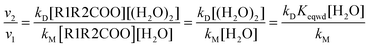 | (11) |
Thus, the atmospheric importance of the water dimer in enhancing the atmospheric degradation of carbonyl oxides by its reaction with water depends on the rate constant and on its concentration as well. In a previous work,82 we have calculated the rate constant for the formation of the water dimer and we have also estimated its concentration at different temperatures (between 275 and 310 K) and at different relative humidities (between 20 and 100% RH).82 Taking the water and water dimer concentrations reported in that work,82 and the rate constants kD and kM, computed in this investigation, we can calculate the relative reaction rates (eqn (11)).
In Fig. 4 we have plotted these values for the reactions of all Criegee intermediates considered in the present work, computed between 275 and 310 K temperature range, and between 20% and 100% RH. Table S7 of the ESI,† contains the corresponding values. Fig. 4 shows that for all reactions investigated the relative reaction rates have a quadratic behavior. They increase with the relative humidity but for a given RH the water dimer has a greater impact as the temperature decreases. Thus, for instance, considering the reactions of the parent carbonyl oxide 1, the water and water dimer concentrations at 20% RH (1.55 × 1017 and 5.44 × 1013 molecules cm−3), and at 100% RH (7.73 × 1017 and 1.36 × 1015 molecules cm−3),82 and taking the rate constants computed in this work, we see from Fig. 4 and Table S7 (ESI†) that the reaction rate with the water dimer is 16.2 times faster than the reaction with the water monomer at 310 K and 20% RH, but 81 times faster at the same temperatures and 100% RH. However, these relative rates are 27.1 times at 275 K and 20% RH and 136 times at 275 K and 100% RH. For the reactions of water and the water dimer with syn-CH3CHOO (entry 2) the relative reaction rates range between 49 times at 310 K and 20%RH and 378 times at 275 K and 100% RH whereas for the anti-CH3CHOO (entry 3) these values are just 1.41 times at 310 K and 20% RH and 9.29 times at 275 K and 100% RH. For the remaining carbonyl oxides considered in this work, Fig. 4 and Table S7 (ESI†) show that the impact of the water dimer is not as important as for entries 1 and 2, with values of the relative reaction rates up to 37 times.
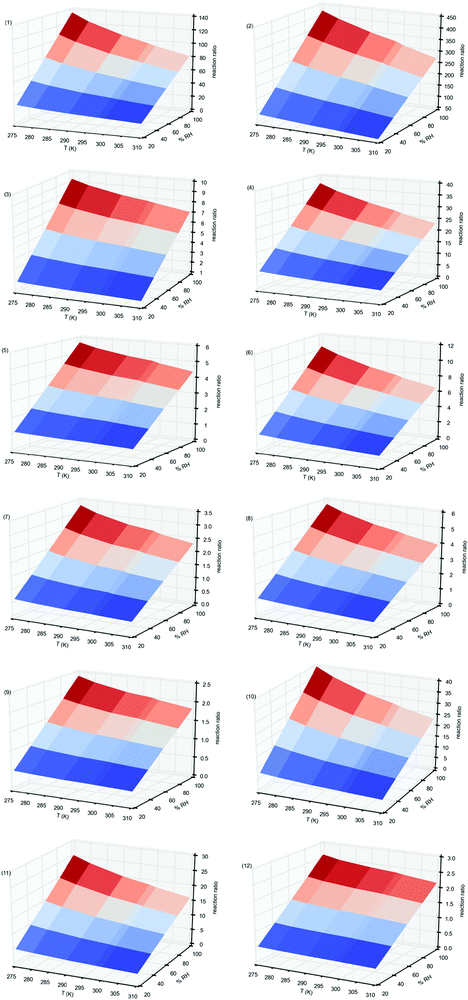 | ||
| Fig. 4 Relative reaction rates, computed according to eqn (11), at different temperatures and relative humidities, for the reaction of carbonyl oxides with water and with the water dimer. Values in parenthesis correspond to carbonyl oxide. | ||
Beyond analyzing the reaction rates of Criegee intermediates with water and with the water dimer, the results reported in this work allow us to calculate an effective rate constant (keff) that drives the kinetics of the atmospheric reaction of carbonyl oxides with water. Here we assume that both water and the water dimer play a role in the gas phase reactivity of carbonyl oxides, but no water trimer or water tetramer. This assumption is based on the fact that the atmospheric concentration of these water clusters is predicted to be very low81–83 and with the fact that the estimation that the reactivity with H2COO is even smaller than the reactivity with the water monomer.109 Accordingly, the reaction rate for the atmospheric degradation of carbonyl oxides by water can be written as:
| v = keff[R1R2COO][H2O]TOT = kM[R1R2COO][H2O] + kD[R1R2COO][(H2O)2] | (12) |
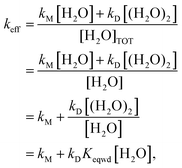 | (13) |
Eqn (13) shows that for each temperature, keff depends on the rate constant of the reaction of carbonyl oxides with the water monomer (kM) and with the water dimer (kD) but also on the actual concentration of water and the water dimer. Consequently the atmospheric reactivity of carbonyl oxides with water depends on the temperature (through kM and kD) and on the relative humidity too. In Table 5 we have collected the computed keff at 298 K and different RHs for all carbonyl oxides investigated in this work. The corresponding values computed in the 275–310 K range of temperatures and between 20% and 100% of RH are contained in Table S8 of the ESI.† At first glance, the results in Table 4 show a different influence of RH on keff. Thus, for instance, in the case of entry 9, we have calculated a keff at 100% RH two times greater than the value calculated at 20% of RH while for entries 1 and 2 this factor is about 5 times. It is also very interesting for atmospheric purposes to compare the keff values with the rate constants of the reaction with the water monomer. For instance, for the parent carbonyl oxide 1, we have computed a keff of 6.18 × 10−14 cm3 molecule−1 s−1 at 298 K and 20% RH and of 2.97 × 10−13 cm3 molecule−1 s−1 at 298 K and 100% RH, compared with the reaction of 1 with a single water molecule (3.05 × 10−15 cm3 molecule−1 s−1 at 298 K, see Table 3). Through these results we predict an enhancement of the atmospheric reactivity of 1 with water ranging between 20 and 100 times because of the effect of the water dimer. This enhancement is calculated to range between 59 and 295 times for syn-methyl carbonyl oxide (entry 2) but much smaller for the remaining Criegee intermediates. In the case of entry 9 these values drop to 1.40 and 3 times only.
| Entry | 20% RH | 40% RH | 60% RH | 80% RH | 100% RH |
|---|---|---|---|---|---|
| a Calculated according to eqn (13). | |||||
| 1 | 6.18 × 10−14 | 1.21 × 10−13 | 1.79 × 10−13 | 2.38 × 10−13 | 2.97 × 10−13 |
| 2 | 1.73 × 10−16 | 3.43 × 10−16 | 5.13 × 10−16 | 6.82 × 10−16 | 8.52 × 10−16 |
| 3 | 3.44 × 10−13 | 5.53 × 10−13 | 7.62 × 10−13 | 9.69 × 10−13 | 1.18 × 10−12 |
| 4 | 1.55 × 10−16 | 2.86 × 10−16 | 4.17 × 10−16 | 5.47 × 10−16 | 6.78 × 10−16 |
| 5 | 6.60 × 10−19 | 9.86 × 10−19 | 1.31 × 10−18 | 1.63 × 10−18 | 1.96 × 10−18 |
| 6 | 7.36 × 10−18 | 1.18 × 10−17 | 1.63 × 10−18 | 2.07 × 10−17 | 2.52 × 10−17 |
| 7 | 5.56 × 10−18 | 7.48 × 10−18 | 9.38 × 10−18 | 1.13 × 10−17 | 1.32 × 10−17 |
| 8 | 3.53 × 10−17 | 5.19 × 10−17 | 6.85 × 10−17 | 8.50 × 10−17 | 1.02 × 10−16 |
| 9 | 4.08 × 10−15 | 5.25 × 10−15 | 6.41 × 10−15 | 7.57 × 10−15 | 8.74 × 10−15 |
| 10 | 4.50 × 10−17 | 8.32 × 10−17 | 1.21 × 10−16 | 1.59 × 10−16 | 1.97 × 10−16 |
| 11 | 1.07 × 10−18 | 1.91 × 10−18 | 2.75 × 10−18 | 3.58 × 10−18 | 4.42 × 10−18 |
| 12 | 2.45 × 10−14 | 3.23 × 10−14 | 4.01 × 10−14 | 4.78 × 10−14 | 5.56 × 10−14 |
In summary, by the analysis of the values displayed in Fig. 4, Table 4, and Table S8 (ESI†) let us conclude that the water dimer enhances, in all cases, the reactivity of carbonyl oxides with water. However, the impact of (H2O)2 is very different depending on the nature and the position of the substituent in the carbonyl oxide. From Tables S5 and S8 (ESI†) we can deduce that the enhancement produced by the reaction of carbonyl oxides with the water dimer is huge for 1 and 2 (up to 137 and 379 times), moderate for 4, 10, and 11, (up to 26–41 times), minor for 3, 5, 6, and 8, (up to 6.7–10 times), and almost negligible for 7, 9, and 12 (less than 4 times under the most favorable conditions). These results have important atmospheric consequences, since it has been suggested that carbonyl oxides play an important role in the first nucleation steps in the formation of organic aerosols or in the oxidation of atmospheric species. Very recently, it has been suggested that the fast reaction of carbonyl oxides with water dimers may limit the impact of the simplest Criegee intermediates on atmospheric chemistry76,80 but our results clearly show that a very different impact is expected, depending on the nature of the carbonyl oxide but also on the temperature and on the relative humidity.
The last point of interest for atmospheric purposes refers to the possible atmospheric formation of OH radicals, viareaction (3), which is possible for the reaction of carbonyl oxides 2, 4, 5, and 6. If we take into account the reaction with the water monomer only, the values displayed in Table 3 show that for syn-methyl carbonyl oxide (entry 2) reaction (2) (viaTS1) and reaction (3) (viaTS2) have almost the same rate constant while for entries 4, 5, and 6, reaction (3) has a rate constant which is almost one order of magnitude smaller than reaction (2). However, this situation changes dramatically when water dimer is taken into account. We have just shown that water dimer has a big impact on the water addition reaction (reaction (2)) but a very small impact on the hydrogen transfer reactions (reaction (3)), so that the presence of water dimer hinders the atmospheric formation of hydroxyl radicals. Taking into account eqn (13), we can calculate a keff for reaction (3) and compared with the keff computed for the whole reaction (reaction (2) plus reaction (3), see Table 5 and Table S8 (ESI†)) we can estimate the branching ratio for the atmospheric OH production, which range between 0.01 and 0.04. That is, our calculations predict that the water dimer prevent the tropospheric formation of hydroxyl radicals viareaction (3). These results are in line with several studies showing that there is no influence of humidity on HO production in ozonolysis.105,110–114 although further studies conclude that the HO yields are increased in ozonolysis experiments conducted under humid conditions compared to experiments conducted under dry conditions.115,116
Conclusions
The results of the present investigation allow us to highlight the following points:(1) The reaction of carbonyl oxides with water and the water dimer takes place through a 1,3-dipolar interaction involving the carbon and terminal oxygen atoms of the Criegee intermediates. In all cases, the relative stability of the stationary points, and consequently the kinetics, depend on both the nature and the position of the substituents. Reactions with carbonyl oxides having electron donating character hinder the nucleophilic attack of the oxygen atom of water to the carbon atom of the carbonyl oxide, increasing the energy barrier. In contrast, electron withdrawing substituents in the carbonyl oxide produce a decrease of the energy barrier. In addition, substituents in anti-position produce a stabilization effect and substituents in syn-position produce a destabilization effect, which is caused by the hyperconjugative effects originated by the substituents. These findings imply differences up to 5–6 orders of magnitude in the rate constants between the fastest and the slowest reaction of carbonyl oxides with water and with the water dimer.
(2) With respect to reaction (2) that corresponds to the water addition process to carbonyl oxide, the substitution of the water monomer by the water dimer produces a relative stabilization of the transition states of roughly 8–11 kcal mol−1 in the relative energies with respect to the corresponding values for the reaction with water monomers. For reaction (3) that corresponds to the hydrogen atom transfer process, the relative stabilization of the transition states by substituting the water monomer by the water dimer is smaller, up to 6 kcal mol−1. As a consequence of this, the reaction with the water dimer is faster than the reaction with the water monomer. However, the impact of the water dimer on the atmospheric decomposition of carbonyl oxides changes very much depending on the nature of the Criegee intermediates. The rate constants of reaction (2) with the water dimer are between 1.14 × 103 and 3.40 × 105 times greater than the reaction with the water monomer, depending on the nature of the carbonyl oxide. In the case of reaction (3), these values range between 10 and 121 times.
(3) It is possible to define an effective rate constant (keff) for the atmospheric reactivity of carbonyl oxides with water. This keff depends on the rate constants of the reaction with water and the water dimer, and consequently on the temperature, but it also depends on the relative humidity. Through this effective rate constant we can estimate the enhancement of the atmospheric reactivity with water due to the effect of the reaction with the water dimer, which ranges between 59 and 295 times for the syn-methyl carbonyl oxide (entry 2), and between 1.40 and 3 times only for entry 9, depending on the temperature and relative humidity.
(4) The water dimer has a very different impact on the atmospheric reactivity of carbonyl oxides. It is huge for entries 1 and 2, moderate for 4, 10, and 11, minor for 3, 5, 6, and 8, and almost negligible for 7, 9, and 12. These results show that carbonyl oxides with a smaller keff last longer in the atmosphere and they are able to react with other tropospheric trace gases or contribute to the formation of aerosols.
(5) Our calculations show that the presence of the water dimer prevents the atmospheric formation of hydroxyl radicals viareaction (3).
Acknowledgements
This work was supported by the Spanish Secretaria de Estado de Investigación, Desarrollo e Innovación (CTQ2014-59768-P) and the Generalitat de Catalunya (Grant 2014SGR139). We also thank the Consorci de Serveis Universitaris de Catalunya (CSUC) for providing computational resources.References
- R. Criegee, Angew. Chem., Int. Ed. Engl., 1975, 14, 745–752 CrossRef.
- P. Neeb, O. Horie and G. K. Moortgat, J. Phys. Chem. A, 1998, 102, 6778–6785 CrossRef CAS.
- J. T. Herron and E. Huie, J. Am. Chem. Soc., 1977, 99, 5430–5435 CrossRef CAS.
- H. Niki, P. D. Maker, C. M. Savage, L. P. Breitenbach and M. D. Hurley, J. Phys. Chem., 1987, 91, 941–946 CrossRef CAS.
- R. I. Martinez and J. T. Herron, J. Phys. Chem., 1988, 92, 4644–4648 CrossRef CAS.
- D. Cremer, J. Gauss, E. Kraka, J. F. Stanton and R. J. Bertlett, Chem. Phys. Lett., 1993, 209, 547–556 CrossRef CAS.
- R. Gutbrod, R. N. Schindler, E. Kraka and D. Cremer, Chem. Phys. Lett., 1996, 252, 221–229 CrossRef CAS.
- R. Gutbrod, E. Kraka, R. N. Schindler and D. Cremer, J. Am. Chem. Soc., 1997, 119, 7330–7342 CrossRef CAS.
- J. M. Anglada, J. M. Bofill, S. Olivella and A. Solé, J. Am. Chem. Soc., 1996, 118, 4636–4647 CrossRef CAS.
- J. M. Anglada, J. M. Bofill, S. Olivella and A. Solé, J. Phys. Chem. A, 1998, 19, 3398–3406 CrossRef.
- J. M. Anglada, R. Crehuet and J. M. Bofill, Chem. – Eur. J., 1999, 5, 1809–1822 CrossRef CAS.
- S. E. Paulson, M. Y. Chung and A. S. Hasson, J. Phys. Chem. A, 1999, 103, 8127–8138 Search PubMed.
- K. H. Becker, I. Barnes, L. Ruppert and P. Wiesen, in Free Radicals in Biology and Environment, ed. F. Minisci, Kluwer Academic Publishers, Dordretch, 1996, pp. 365–385 Search PubMed.
- D. Johnson and G. Marston, Chem. Soc. Rev., 2008, 37, 699–716 RSC.
- O. Horie and G. K. Moortgat, Acc. Chem. Res., 1998, 31, 387–396 CrossRef CAS.
- O. Horie and G. K. Moortgat, Atmos. Environ., 1991, 25A, 1881–1896 CrossRef CAS.
- F. Su, G. Calvert and H. H. Shaw, J. Phys. Chem., 1980, 84, 239–246 CrossRef CAS.
- R. Atkinson, J. Phys. Chem. Ref. Data, 1997, 26, 215 CrossRef CAS.
- D. Cremer, T. Schmidt, J. Gauss and T. P. Radhakrishnan, Angew. Chem., Int. Ed. Engl., 1988, 27, 427–428 CrossRef.
- C. A. Taatjes, G. Meloni, T. M. Selby, A. J. Trevitt, D. L. Osborn, C. J. Percival and D. E. Shallcross, J. Am. Chem. Soc., 2008, 130, 11883–11885 CrossRef CAS PubMed.
- O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207 CrossRef CAS PubMed.
- M. Nakajima and Y. Endo, J. Chem. Phys., 2013, 139, 101103 CrossRef PubMed.
- Y.-T. Su, Y.-H. Huang, H. A. Witek and Y.-P. Lee, Science, 2013, 340, 174–176 CrossRef CAS PubMed.
- J. M. Beames, F. Liu, L. Lu and M. I. Lester, J. Am. Chem. Soc., 2012, 134, 20045–20048 CrossRef CAS PubMed.
- L. Sheps, J. Phys. Chem. Lett., 2013, 4201–4205 CrossRef CAS PubMed.
- W.-L. Ting, Y.-H. Chen, W. Chao, M. C. Smith and J. J.-M. Lin, Phys. Chem. Chem. Phys., 2014, 16, 10438–10443 RSC.
- H. Li, Y. Fang, J. M. Beames and M. I. Lester, J. Chem. Phys., 2015, 142, 214312 CrossRef PubMed.
- J. Li, S. Carter, J. M. Bowman, R. Dawes, D. Xie and H. Guo, J. Phys. Chem. Lett., 2014, 5, 2364–2369 CrossRef CAS PubMed.
- J. H. Lehman, H. Li, J. M. Beames and M. I. Lester, J. Chem. Phys., 2013, 139, 141103 CrossRef PubMed.
- P. Aplincourt, E. Henon, F. Bohr and M. F. Ruiz-López, Chem. Phys., 2002, 285, 221–231 CrossRef CAS.
- J. M. Beames, F. Liu, L. Lu and M. I. Lester, J. Chem. Phys., 2013, 138, 244307 CrossRef PubMed.
- F. Liu, J. M. Beames, A. M. Green and M. I. Lester, J. Phys. Chem. A, 2014, 118, 2298–2306 CrossRef CAS PubMed.
- M. C. Smith, W.-L. Ting, C.-H. Chang, K. Takahashi, K. A. Boering and J. J.-M. Lin, J. Chem. Phys., 2014, 141, 074302 CrossRef PubMed.
- M. Nakajima and Y. Endo, J. Chem. Phys., 2014, 140, 011101 CrossRef PubMed.
- R. A. Cox and S. A. Penkett, J. Chem. Soc., Faraday Trans. 1, 1971, 1753 Search PubMed.
- S. Hatakeyama, H. Bandow, M. Okuda and H. Akimoto, J. Phys. Chem., 1981, 85, 2249–2254 CrossRef CAS.
- P. Neeb, O. Horie and G. K. Moortgat, Tetrahedron Lett., 1996, 37, 9297–9300 CrossRef CAS.
- P. Neeb and O. Horie, Int. J. Chem. Kinet., 1996, 28, 721 CrossRef CAS.
- R. Crehuet, J. M. Anglada and J. M. Bofill, Chem. – Eur. J., 2001, 7, 2227–2235 CrossRef CAS.
- J. M. Anglada, P. Aplincourt, J. M. Bofill and D. Cremer, ChemPhysChem, 2002, 2, 215–221 CrossRef.
- P. Aplincourt and J. M. Anglada, J. Phys. Chem. A, 2003, 107, 5798–5811 CrossRef CAS.
- J. M. Anglada, J. Gonzalez and M. Torrent-Sucarrat, Phys. Chem. Chem. Phys., 2011, 13, 13034–13045 RSC.
- A. Mansergas and J. M. Anglada, ChemPhysChem, 2006, 7, 1488–1493 CrossRef CAS PubMed.
- A. Mansergas and J. M. Anglada, J. Phys. Chem. A, 2006, 110, 4001–4011 CrossRef CAS PubMed.
- A. Mansergas, J. Gonzalez, M. Ruiz-Lopez and J. M. Anglada, Comput. Theor. Chem., 2011, 965, 313–320 CrossRef CAS.
- T. Kurten, B. Bonn, H. Vehkamaki and M. Kulmala, J. Phys. Chem. A, 2007, 111, 3394–3401 CrossRef CAS PubMed.
- S. Jorgensen and A. Gross, J. Phys. Chem. A, 2009, 113, 10284–10290 CrossRef CAS PubMed.
- L. Vereecken, H. Harder and A. Novelli, Phys. Chem. Chem. Phys., 2012, 14, 14682–14695 RSC.
- L. Vereecken and J. S. Francisco, Chem. Soc. Rev., 2012, 41, 6259–6293 RSC.
- H. G. Kjaergaard, T. Kurten, L. B. Nielsen, S. Jorgensen and P. O. Wennberg, J. Phys. Chem. Lett., 2013, 4, 2525–2529 CrossRef CAS.
- Y.-T. Su, H.-Y. Lin, R. Putikam, H. Matsui, M. C. Lin and Y.-P. Lee, Nat. Chem., 2014, 6, 477–483 CrossRef CAS PubMed.
- R. Crehuet, J. M. Anglada, D. Cremer and J. M. Bofill, J. Phys. Chem. A, 2002, 106, 3917–3929 CrossRef CAS.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, D. L. Osborn, E. P. F. Lee, J. M. Dyke, D. W. K. Mok, D. E. Shallcross and C. J. Percival, Phys. Chem. Chem. Phys., 2012, 14, 10391–10400 RSC.
- M. J. Newland, A. R. Rickard, M. S. Alam, L. Vereecken, A. Munoz, M. Rodenas and W. J. Bloss, Phys. Chem. Chem. Phys., 2015, 17, 4076–4088 RSC.
- B. Ouyang, M. W. McLeod, R. L. Jones and W. J. Bloss, Phys. Chem. Chem. Phys., 2013, 15, 17070–17075 RSC.
- D. Stone, M. Blitz, L. Daubney, N. U. M. Howes and P. Seakins, Phys. Chem. Chem. Phys., 2014, 16, 1139–1149 RSC.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. F. Lee, J. M. Dyke, D. K. W. Mok, D. L. Osborn and C. J. Percival, Science, 2013, 340, 177–180 CrossRef CAS PubMed.
- L. Sheps, A. M. Scully and K. Au, Phys. Chem. Chem. Phys., 2014, 16, 26701–26706 RSC.
- T. Berndt, J. Voigtlander, F. Stratmann, H. Junninen, R. L. Mauldin Iii, M. Sipila, M. Kulmala and H. Herrmann, Phys. Chem. Chem. Phys., 2014, 16, 19130–19136 RSC.
- T. Berndt, R. Kaethner, J. Voigtlander, F. Stratmann, M. Pfeifle, P. Reichle, M. Sipila, M. Kulmala and M. Olzmann, Phys. Chem. Chem. Phys., 2015, 17, 19862–19873 RSC.
- D. L. Osborn and C. A. Taatjes, Int. Rev. Phys. Chem., 2015, 34, 309–360 CrossRef CAS.
- M. J. Newland, A. R. Rickard, L. Vereecken, A. Muñoz, M. Ródenas and W. J. Bloss, Atmos. Chem. Phys., 2015, 15, 9521–9536 CrossRef CAS.
- A. B. Ryzhkov and P. A. Ariya, Chem. Phys. Lett., 2003, 367, 423–429 CrossRef CAS.
- A. B. Ryzhkov and P. A. Ariya, Phys. Chem. Chem. Phys., 2004, 6, 5042–5050 RSC.
- A. B. Ryzhkov and P. A. Ariya, Chem. Phys. Lett., 2006, 419, 479–485 CrossRef CAS.
- J. D. Fenske, A. L. Hasson, A. W. Ho and S. E. Paulson, J. Phys. Chem. A, 2000, 104, 9921–9932 CrossRef CAS.
- T. B. Nguyen, G. S. Tyndall, J. D. Crounse, A. P. Teng, K. H. Bates, R. H. Schwantes, M. M. Coggon, L. Zhang, P. Feiner, D. O. Milller, K. M. Skog, J. C. Rivera-Rios, M. Dorris, K. F. Olson, A. Koss, R. J. Wild, S. S. Brown, A. H. Goldstein, J. A. de Gouw, W. H. Brune, F. N. Keutsch, J. H. Seinfeld and P. O. Wennberg, Phys. Chem. Chem. Phys., 2016, 18, 10241–10254 RSC.
- A. Sadezky, P. Chaimbault, A. Mellouki, A. Rompp, R. Winterhalter, G. Le Bras and G. K. Moortgat, Atmos. Chem. Phys., 2006, 6, 5009–5024 CAS.
- A. Sadezky, R. Winterhalter, B. Kanawati, A. Rompp, B. Spengler, A. Mellouki, G. Le Bras, P. Chaimbault and G. K. Moortgat, Atmos. Chem. Phys., 2008, 8, 2667–2699 CrossRef CAS.
- J. M. Anglada, S. Olivella and A. Sole, Phys. Chem. Chem. Phys., 2013, 15, 18921–18933 RSC.
- Y. Zhao, L. M. Wingen, V. Perraud, J. Greaves and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2015, 17, 12500–12514 RSC.
- E. Miliordos and S. S. Xantheas, Angew. Chem., Int. Ed., 2016, 55, 1015–1019 CrossRef CAS PubMed.
- F. Sauer, C. Schäfer, P. Neeb, O. Horie and G. K. Moortgat, Atmos. Environ., 1999, 33, 229–241 CrossRef CAS.
- S. Gäb, E. Hellpointner, W. V. Turner and F. Korte, Nature, 1985, 316, 535–536 CrossRef.
- K. H. Becker, K. J. Brockmann and J. Bechara, Nature, 1990, 346, 256–258 CrossRef CAS.
- W. Chao, J.-T. Hsieh, C.-H. Chang and J. J.-M. Lin, Science, 2015, 347, 751–754 CrossRef CAS PubMed.
- M. C. Smith, C.-H. Chang, W. Chao, L.-C. Lin, K. Takahashi, K. A. Boering and J. J.-M. Lin, J. Phys. Chem. Lett., 2015, 6, 2708–2713 CrossRef CAS PubMed.
- T. R. Lewis, M. A. Blitz, D. E. Heard and P. W. Seakins, Phys. Chem. Chem. Phys., 2015, 17, 4859–4863 RSC.
- L.-C. Lin, H.-T. Chang, C.-H. Chang, W. Chao, M. C. Smith, C.-H. Chang, J. Jr-Min Lin and K. Takahashi, Phys. Chem. Chem. Phys., 2016, 18, 4557–4568 RSC.
- M. Okumura, Science, 2015, 347, 718–719 CrossRef CAS PubMed.
- B. Ruscic, J. Phys. Chem. A, 2013, 117, 11940–11953 CrossRef CAS PubMed.
- J. M. Anglada, G. J. Hoffman, L. V. Slipchenko, M. M. Costa, M. F. Ruiz-López and J. S. Francisco, J. Phys. Chem. A, 2013, 117, 10381–10396 CrossRef CAS PubMed.
- J. Gonzalez, M. Caballero, A. Aguilar-Mogas, M. Torrent-Sucarrat, R. Crehuet, A. Solé, X. Giménez, S. Olivella, J. Bofill and J. Anglada, Theor. Chem. Acc., 2011, 128, 579–592 CrossRef CAS.
- H.-L. Huang, W. Chao and J. J.-M. Lin, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10857–10862 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, John Wiley, New York, 1986, pp. 86–87 Search PubMed.
- K. Ishida, K. Morokuma and A. Kormornicki, J. Chem. Phys., 1977, 66, 2153 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- J. Cizek, Adv. Chem. Phys., 1969, 14, 35–89 CrossRef CAS.
- R. J. Barlett, J. Phys. Chem., 1989, 93, 1963 CrossRef.
- J. A. Pople, R. Krishnan, H. B. Schlegel and J. S. Binkley, Int. J. Quant. Chem. XIV, 1978, 545–560 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- T. H. J. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 6769 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- K. L. Bak, J. Gauss, P. Jorgensen, J. Olsen, T. Helgaker and J. F. Stanton, J. Chem. Phys., 2001, 114, 6548–6556 CrossRef CAS.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- T. N. Truong and D. G. Truhlar, J. Chem. Phys., 1990, 93, 1761 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ocherski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.01, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- F. Neese, WIRes Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- G. Shaftenaar and J. H. Noordik, J. Comput. – Aided Mol. Des., 2000, 14, 123–134 CrossRef.
- D. H. Lu, T. N. Truong, V. S. Melissas, G. C. Lynch, Y.-P. Liu, B. C. Garrett, R. Steckler, A. D. Isaacson, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1992, 71, 235–262 CrossRef CAS.
- K. T. Kuwata, M. R. Hermes, J. Carlson and C. K. Zogg, J. Phys. Chem. A, 2010, 114, 9192–9204 CrossRef CAS PubMed.
- B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 1052–1078 CrossRef CAS.
- D. G. Truhlar and B. C. Garrett, Acc. Chem. Res., 1980, 13, 440–448 CrossRef CAS.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- A. B. Ryzhkov and P. A. Ariya, Chem. Phys. Lett., 2006, 419, 479–485 CrossRef CAS.
- R. Atkinson and S. M. Aschmann, Environ. Sci. Technol., 1993, 27, 1357–1363 CrossRef CAS.
- R. Atkinson, S. M. Aschmann, J. Arey and B. Shorees, J. Geophys. Res., 1992, 97, 6065–6073 CrossRef CAS.
- A. S. Hasson, M. Y. Chung, K. T. Kuwata, A. D. Converse, D. Krohn and S. E. Paulson, J. Phys. Chem. A, 2003, 107, 6176–6182 CrossRef CAS.
- D. Johnson, A. G. Lewin and G. Marston, J. Phys. Chem. A, 2001, 105, 2933–2935 CrossRef CAS.
- S. M. Aschmann, J. Arey and R. Atkinson, Atmos. Environ., 2002, 36, 4347–4355 CrossRef CAS.
- R. Wegener, T. Brauers, R. Koppmann, S. Rodriguez Bares, F. Rohrer, R. Tillmann, A. Wahner, A. Hansel and A. Wisthaler, J. Geophys. Res.: Atmos., 2007, 112, D13301 CrossRef.
- R. Tillmann, M. Hallquist, A. M. Jonsson, A. Kiendler-Scharr, H. Saathoff, Y. Iinuma and T. F. Mentel, Atmos. Chem. Phys., 2010, 10, 7057–7072 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02531e |
| This journal is © the Owner Societies 2016 |