Open Access Article
Open Access ArticleDiffusion and precipitation processes in iron-based silica gardens
F.
Glaab
a,
J.
Rieder
a,
J. M.
García-Ruiz
b,
W.
Kunz
*a and
M.
Kellermeier
*c
aInstitute of Physical and Theoretical Chemistry, University of Regensburg, Universitätsstrasse 31, D-93040 Regensburg, Germany. E-mail: werner.kunz@ur.de; Tel: +49 (0)941 943 4044
bLaboratorio de Estudios Cristalográficos, IACT (CSIC-UGR), Av. de las Palmeras 4, E-18100 Armilla, Granada, Spain
cMaterial Physics, BASF SE, Carl-Bosch-Strasse 38, D-67056 Ludwigshafen, Germany. E-mail: matthias.kellermeier@basf.com; Tel: +49 (0)621 60 43388
First published on 1st July 2016
Abstract
Silica gardens are tubular structures that form along the interface of multivalent metal salts and alkaline solutions of sodium silicate, driven by a complex interplay of osmotic and buoyant forces together with chemical reaction. They display peculiar plant-like morphologies and thus can be considered as one of the few examples for the spontaneous biomimetic self-ordering of purely inorganic materials. Recently, we could show that silica gardens moreover are highly dynamic systems that remain far from equilibrium for considerable periods of time long after macroscopic growth is completed. Due to initial compartmentalisation, drastic concentration gradients were found to exist across the tube walls, which give rise to noticeable electrochemical potential differences and decay only slowly in a series of coupled diffusion and precipitation processes. In the present work, we extend these studies and investigate the effect of the nature of the used metal cations on the dynamic behaviour of the system. To that end, we have grown single macroscopic silica garden tubes by controlled addition of sodium silicate sol to pellets of iron(II) and iron(III) chloride. In the following, the concentrations of ionic species were measured as a function of time on both sides of the formed membranes, while electrochemical potentials and pH were monitored online by immersing the corresponding sensors into the two separated solution reservoirs. At the end of the experiments, the solid tube material was furthermore characterised with respect to composition and microstructure by a combination of ex situ techniques. The collected data are compared to the previously reported case of cobalt-based silica gardens and used to shed light on ion diffusion through the inorganic membranes as well as progressive mineralisation at both surfaces of the tube walls. Our results reveal important differences in the dynamics of the three studied systems, which can be explained based on the acidity of the metal cations and the porosity of the membranes, leading to substantially dissimilar time-dependent solution chemistry as well as distinct final mineral structures. The insight gained in this work may help to better understand the diffusion properties and precipitation patterns in tubular iron (hydr)oxide/silicate structures observed in geological environments and during steel corrosion.
Introduction
The formation of “chemical gardens” is a phenomenon well known to any (chemistry) student.1 Simply by the addition of soluble metal salt crystals to alkaline silica sols, a variety of stunning structures reminiscent of living forms such as trees or aquatic plants can be generated.2 Their first record in the literature dates back to Glauber more than 300 years ago, who observed “iron trees” upon introducing ferrous chloride to solutions of potassium silicate.3 Resembling biogenic species though consisting entirely of inorganic matter, these structures aroused a flurry of interest around a century ago in the context of a search for the origin of life.4 While initially the growth of chemical gardens was thought to rely essentially on the chemistry of silica, later studies revealed that also a number of other anions (e.g. aluminate,5 oxalate,6 carbonate,7 phosphate,8 hydroxide9 or oxometalate10) can produce similar architectures with a broad range of multivalent metal cations.1,2,11–14The mechanism for the formation of the typically resulting tubular precipitates was found to be a complex interplay of osmosis, buoyancy and chemical reaction.2,15–17 In particular, it was shown that upon contact of the metal salt crystal and the silica solution, a layer of hydrous metal silicate is formed immediately at the interface. Osmotically driven inflow of water subsequently increases the enclosed volume, thus leading to the expansion of the flexible membrane until it bursts. This relieves the interior pressure and concentrated metal salt solution is ejected from the inside into the surrounding alkaline medium, ascending vertically due to the lower density. Instant precipitation of metal silicate and/or (hydr)oxide mineralises and seals the jet so that, in the following, the internal pressure re-increases. Driven by repeated events of membrane rupture and sealing, vertical hollow tubes are generated with typical final dimensions of a few millimeters in width and up to several centimeters in length (see Fig. 1A–C).18 At the end of the process, the formed tube wall (consisting of metal (hydr)oxides and silica(te))5 separates an inner volume of acidic metal salt solution from a surrounding, highly alkaline sol of sodium silicate, as illustrated in Fig. 1D.
In fact, most of the previous studies on silica gardens stopped at this point and analysed the structure and composition of the tubes19,20 or explored their possible application in fields like catalysis.21,22 However, in view of the substantial differences in conditions between the environments on both sides of the membrane (Fig. 1D), it is also of particular interest to study the temporal evolution of the chemical gradients created spontaneously in these systems. This has been impeded by the fact that classical silica garden tubes are relatively thin and thus it is inherently difficult to access the inner solution for analysis. Recently, we developed a procedure to grow single tubes with significantly larger dimensions and an open end on top in a reproducible manner.23 This was achieved by using pressed metal salt pellets instead of irregular crystals, and by adding the silicate solutions at a controlled rate. The resulting macroscopic tubes (cf.Fig. 1A–C) allowed a straightforward sampling of the two reservoirs separated by the membrane, hence enabling direct measurements of changes in species concentrations and pH over time. The corresponding data evidence that silica gardens operate far from equilibrium and relieve the initially generated gradients only slowly through a cascade of coupled diffusion and precipitation processes.23 Moreover, it was found that the concentration gradients caused by spontaneous compartmentalisation induce long-lasting electrochemical potential differences,23,24 which can be used as an energy source25 and may have played a key role in prebiotic chemistry scenarios.26
Our previously mentioned work23 focused on silica gardens prepared with cobalt salts as a first case study to establish the in situ characterisation methodology and to account for the relevance of cobalt compounds as catalysts.27 Here we extend this approach to systems based on iron salts and discuss differences in the dynamic behaviour as compared to cobalt, using both Fe2+ and Fe3+ to also assess the influence of the oxidation state of the metal cations. The choice of iron is due to its relevance for a number of natural processes as well as for practical applications. For instance, precipitation of iron silicates is a common geological phenomenon, nowadays occurring mainly in geothermally active regions like the Norris Geyser Basin in the Yellowstone National Park.28 Technologically, iron silicates are used among others as adsorbents,29 pigments,30 or catalysts.31 Another important field is the corrosion of iron or steel surfaces, where deposits with tubular morphologies reminiscent of chemical gardens have frequently been observed.32 Therefore, a better understanding of ion transport and precipitation processes across iron (hydr)oxide/silicate membranes is clearly of interest for various areas of research.
Results and discussion
Macroscopic growth behaviour
The first step in our study was to grow single macroscopic tubes of silica gardens based on iron salts. As in the case of cobalt,23 this was achieved by slow and controlled dosing of diluted water glass to pellets of FeCl2 and FeCl3, which were fixed at the bottom of the reaction vessel. In that way, vertical hollow tubes with ends open to the atmosphere and diameters in the range of several millimeters were obtained (Fig. 1). The relatively large dimensions of these structures allow facile access to the interior solution (for concentration measurements) and the direct immersion of microelectrodes (for monitoring pH and electrochemical potentials, see below).The rate of tube formation strongly depends on the kind of metal salt used and is by far the fastest for FeCl3. A possible explanation for this observation relies on the existence of distinct osmotic pressures in the three studied systems. The osmotic pressure (Π) of a salt solution is defined as Π = i·c·R·T, where i is the number of generated ions in case of complete dissociation. Consequently, Π should be proportionally higher in silica gardens based on FeCl3 (i = 4) than in those prepared with CoCl2 and FeCl2 (i = 3). As a result, the overall rate of exchange of species is propelled by reinforced pumping of exterior solution through the membrane. This effect is visible to the naked eye, as rapid increase of freshly created interior FeCl3 solution increases the possible speed of water glass dosing, whereas a less intense inflow of water into CoCl2- and FeCl2-based tubes requires significantly slower addition.
Concentration measurements
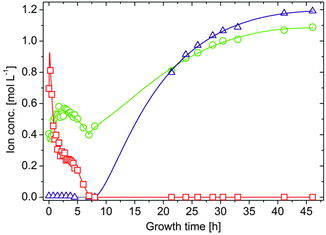
In order to probe diffusion and precipitation processes in the as-prepared tubular structures, samples were taken from the solutions on both sides of the membrane over extended periods of time (8–70 h) in intervals ranging from 2 min to 5 h. Subsequently, the concentrations of sodium, silicon and iron/cobalt were determined by atomic emission spectroscopy (AES). The results obtained for the three different types of silica gardens are presented in Fig. 2. In general, no significant changes in concentration could be detected for any of the elements in the outer silica solution (Fig. 2A), due to the large excess of water glass used for preparation and the poor solubility of multivalent cations in strongly alkaline environments. As opposed to that, the solution composition in the tube interior is subject to major changes over time (Fig. 2B–D). The concentrations of metal cations show a more or less pronounced initial increase – reflecting the still ongoing dissolution of the metal salt pellet – until a maximum is reached after different times (from 10 min in the case of FeCl3 to 10 h for FeCl2). In the following, an exponential decrease down to low and constant values can be observed – evidencing progressive and eventually quantitative precipitation of the cations into the tube wall (see below).23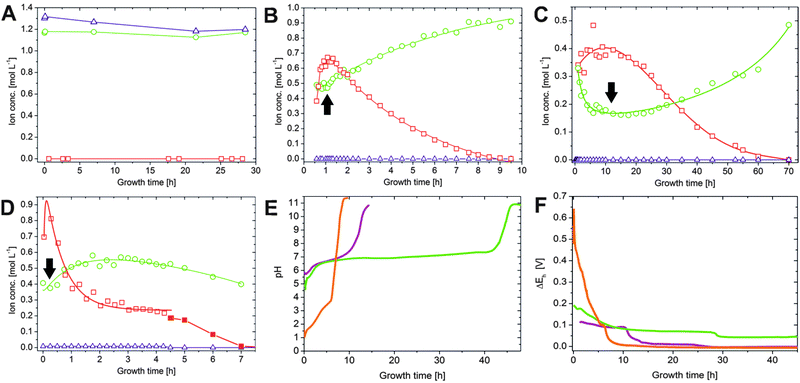 | ||
| Fig. 2 Spatiotemporal distribution of ionic species in silica gardens. (A) Iron (squares), sodium (circles) and silicate (triangles) ion concentrations measured in the outer water glass reservoir at different times after completed preparation of Fe3+-based silica gardens. Corresponding data for tubes prepared with FeCl2 and CoCl2 show essentially the same trends and are therefore omitted here. (B–D) Time-dependent concentration profiles for the metal cations (squares), sodium ions (circles), and silicate species (triangles) in the interior solution of tubes grown with pellets of (B) CoCl2, (C) FeCl2, and (D) FeCl3. Note the different time scales of the three graphs. Full squares in (D) indicate that the corresponding samples were taken after solidification of the interior solution had commenced. (E) Temporal evolution of the pH inside silica garden tubes prepared with CoCl2 (purple), FeCl2 (green) and FeCl3 (orange). (F) Electrochemical potential differences (ΔEh) measured across the tube membranes as a function of time (the same color code as in (E)). Note that the full lines in (B–D) are only meant to serve as a guide for the eye and do not rely on a distinct physical model. All data for cobalt-based silica gardens are reproduced for comparison from ref. 23 with permission by Wiley-VCH. | ||
The amount of sodium (which should in a first approximation be equally soluble in both compartments) inside the tube walls varies over similarly long periods of time, displaying quite complex behaviour that depends on the type of metal salt used. First, it is worth noting that the interior sodium concentration immediately after completion of the growth process is not zero, but already quite high (0.3–0.4 M in all systems). This indicates that significant amounts of sodium were transported along with water during the osmotic inflow that drives tube formation.23 In the following, [Na+]int runs through a more or less pronounced dip (marked by arrows in Fig. 2) that coincides with the maximum in the iron/cobalt concentration. This “dilution” effect can most likely be ascribed to the dissolution of the metal salt pellet, causing changes in ionic activity and concurrent osmotic forces. Subsequently, the inner sodium content increases gradually over (tens of) hours – a clear sign for slow diffusion of these (originally exterior) ions through the membrane. For silica gardens based on Fe3+ (Fig. 2D), [Na+]int levels off at ca. 0.55 M after about 2 h, before at around 4–5 h a slight decrease sets in. In contrast to sodium, silicate is not able to penetrate the membrane as long as acidic iron/cobalt ions are still present ([SiO2]int ≈ 0), which induce quantitative precipitation of amorphous silica or metal silicate on the outer surface of the tube wall.19
The most obvious difference in the progression of species concentrations between the distinct types of silica gardens studied is the actual period during which diffusion and/or precipitation processes are active. This period ranges from roughly 9 h for tubes based on FeCl3 (Fig. 2D) to several days in the case of FeCl2 (Fig. 2C). These substantial differences can be explained in terms of the distinct acidities33,34 of the used metal salts (Table 1): precipitation of metal silicate (and amorphous silica) should be accelerated by cations with higher acidity, given that the solubility of silica decreases steeply when approaching the near-neutral from the alkaline regime.35 These processes are expected to be fastest in the presence of the most acidic cation, i.e. Fe3+ (in line with the observed rapid macroscopic growth of Fe(III)-based tubes, as mentioned above). Therefore, the membranes formed in the corresponding silica gardens should be least dense and exhibit largest pores, which allow for a more efficient exchange between the two solutions surrounding them. As a consequence, the time needed for the system to equilibrate should be shortest in the case of Fe3+, which is in fact observed.
| Cation | Acidity | Solubility product |
|---|---|---|
| Co2+ | 9.6 (pK1) | 5.9 × 10−15 M3 |
| Fe2+ | 9.3 (pK1) | 4.9 × 10−15 M3 |
| Fe3+ | 2.4 (pK1), 5.7 (pK2) | 2.8 × 10−39 M4 |
In turn, the differences in the time-dependent evolution of silica gardens prepared with Co(II) and Fe(II) cannot readily be explained on that basis, suggesting that other factors (e.g. phase composition, particle size and/or morphology, and corresponding effects on the porosity and thus permeability of the membrane) also play an important role for diffusion and precipitation dynamics. Similar arguments can be put forward when considering the solubility of the respective metal hydroxides (see Table 1). Since Fe(OH)3 is orders of magnitude less soluble than the other two hydroxides, it will be removed most rapidly from the interior solution and hence accelerate the overall evolution of the corresponding silica garden (again reflected in the macroscopic growth rate).
A second major distinction between the three studied systems can be made concerning the progression of the inner metal ion concentrations at later times. While the amount of dissolved ions decreases exponentially and falls eventually below the detection limit in the case of both CoCl2 (after about 9–10 h, Fig. 2B) and FeCl2 (after about 70 h, Fig. 2C), the concentration of Fe3+ levels off at moderate values around 0.25 M after approximately 4 h (Fig. 2D, open squares). Visual observations confirmed that the interior solution starts to solidify at this point, presumably due to Fe(OH)3 precipitation, which complicates further extraction of samples. This phenomenon may also explain why the inner sodium concentration does not increase further as in the other two types of silica gardens. As precipitation proceeds, [Fe3+]int (and [Na+]int) decreases again in the following (Fig. 2D, full squares) and a yellow-brownish solid gradually fills the entire inner volume. After about 7 h, no more iron could be detected inside the tube. Careful removal of the parts of the precipitate with the aid of a pipette creates a small funnel within the open tube, which slowly becomes filled with a clear colourless liquid. Continued AES analyses of this solution revealed that the sodium and in particular also the silica concentration now slowly increase over a quite extended period of time (Fig. 3). Starting at ca. 0.4 M for [Na+]int and values below the detection limit for [SiO2]int after 7 h, the concentrations of the two species reach values of about 1.1 and 1.2 M, respectively, at the end of the experiment after 48 h. In both cases, final inner concentrations are thus only slightly lower than those determined experimentally for the outer water glass solution (cf.Fig. 2A).
This indicates that the system is close to equilibrium at this stage, and diffusion must succumb as concentration gradients vanish. The gradual increase of [Na+]int and [SiO2]int demonstrates that the walls were still intact after detaching pieces of the precipitate, as in the case of a leaking membrane a much faster increase would be expected. Therefore, we conclude that the traced time-dependent concentration changes are due to intimate ion diffusion processes across the tube walls. Similar observations were already made for cobalt-based silica gardens in our previous study.23 However, the present data highlight that the overall period over which such single tubes remain “active” (i.e. out of equilibrium) depends strongly on the chosen metal cation (note the still drastic concentration gradients prevailing after more than 70 h in the case of Fe(II), cf.Fig. 2C).
pH measurements
To shed more light on diffusion processes in the three studied silica garden systems, the pH of both the inner and outer solution was monitored continuously over time. Generally, the pH of the exterior water glass reservoir (ca. 11.2) was not found to be subject to noticeable changes, neither during growth nor after several days of maturation, due to the high excess and buffering ability of silica. The pH inside the tubes starts in the acidic range for all cations and subsequently increases in two distinct stages (Fig. 2E): first, a rather slow and continuous rise towards more or less neutral values (pH ≈ 7 for CoCl2 and FeCl2 and pH ≈ 4 for FeCl3) is observed over periods of roughly 6, 10 and 40 h for Fe3+, Co2+ and Fe2+, respectively. In the following, the pH increases more steeply and eventually, after another 2–5 h, reaches levels close to that of the outer reservoir, indicating that the initially generated pH gradients across the membrane ultimately vanish. A comparison of these pH profiles with the temporal progression of the inner metal ion concentrations (Fig. 2B–D) shows a clear correlation, i.e. the pH remains acidic as long as significant amounts of dissolved metal ions are present inside the tube. Previous studies have reported that the incorporation of metal ions into the inner surface of the forming membranes occurs mainly through precipitation as (amorphous) hydroxides.19,36 Our data support these observations and provide a quantitative picture for the precipitation process, which is driven by the existing pH gradient and the diffusion of hydroxide ions from the outer reservoir into the inner solution. Once arrived at the interior surface of the membrane, OH− ions precipitate as sparsely soluble metal hydroxides during the first stage when the interior solution is still rich in metal cations. This leads to a continuous decrease in the metal ion concentration and in parallel to a slight increase in pH. Figuratively speaking, the inner metal salt solution is thus “titrated” with a strong base by continuous diffusion of hydroxide ions along the pH gradient. As soon as all metal ions are consumed, i.e. the point of equivalence is reached, OH− diffusion becomes unhindered and provokes a much more distinct rise in pH until eventually the pH is the same on both sides of the membrane.As expected from the ion concentration measurements (Fig. 2B–D), there are significant differences between the studied metal salts. Most strikingly, the initial pH of the interior solution is much more acidic in the case of Fe3+ (pH ≈ 1–2) than for Fe2+ and Co2+ (pH ≈ 5–6). This can be ascribed to the higher acidity of FeCl3 as compared to FeCl2 and CoCl2 (cf.Table 1): while Fe2+ and Co2+ ions act as weak quasi-monoprotic acids in aqueous solution, hydrated Fe3+ ions are strong to medium-strong diprotic acids. Calculations of theoretically expected pH values for the inner solutions (based on the measured metal ion concentrations and their known acidities) show a more or less constant deviation of 1–1.5 pH units from the experimentally determined values before neutralisation is completed. This deviation suggests that a certain amount of hydroxide ions has entered the inner solution at the onset of tube growth along with water and sodium ions (as described above). This notion is confirmed by reference experiments, where the addition of small amounts of NaOH (ca. 1 mM) to aqueous metal salt solutions was found to increase the pH by more than one unit even at high metal ion concentrations (not shown). Most of the hydroxide ions transported into the interior volume during the early stages are likely to precipitate with the cations on the membrane, while those remaining in solution cause a slight increase in pH and thus account for the observed deviations between experimental and theoretical values.
The second main difference in the recorded pH profiles is the time required for the inner pH to ultimately become equal to that in the outer reservoir. As already observed for the ion concentrations, equilibration is fastest in silica gardens based on FeCl3 and by far slowest for FeCl2. In the case of Fe3+, one could argue that the larger initial gradient accelerates diffusion and precipitation processes. This argument does however not hold for the distinct behaviour of Fe2+ and Co2+, which have similar acidities (cf.Table 1). Here, the properties of the formed membrane must be substantially different (as discussed in more detail below). In light of the present data, it seems as if tubes grown with FeCl2 are either considerably thicker or denser than those obtained with FeCl3 and CoCl2. Larger pore sizes will clearly allow for faster transport through the membrane, both during the earlier stages where precipitation is still ongoing and later when the point of equivalence has been reached.
Electrochemical potential differences
Recent studies have shown that silica gardens represent systems that – due to spontaneous compartmentalisation and the concurrently generated drastic concentration gradients – create significant electrochemical potentials.2,23–25 In that regard, we have measured potential differences across the membranes formed with FeCl2 and FeCl3 by submerging platinum stick electrodes into the inner and outer solutions, according to a procedure already applied for CoCl2-based silica gardens in our earlier work.23 In all cases, considerable voltages could be detected immediately after tube preparation (Fig. 2F), followed by a decay with time that essentially reflects the progression of ion concentrations (Fig. 2B–D) and pH (Fig. 2E) in the respective system. We have previously shown that the potential differences existing across the tubular precipitates result from a combination of membrane and diffusion potentials (induced by gradients in ion concentrations and temporally changing permeabilities for the various species), and a third contribution originating from the persisting pH gradient.23 When comparing the ΔEh profiles recorded for different cations, it is evident that silica gardens prepared with FeCl3 produce much higher initial voltages (ca. 550 mV) than those formed by CoCl2 (ca. 120 mV) and FeCl2 (ca. 190 mV). Even though the nature of the cation will influence the magnitude of the membrane and diffusion potentials to some degree (essentially through the valency and ion mobility), the main reason for this observation is clearly the higher acidity of Fe3+, which significantly increases the pH-dependent contribution to the overall potential. Another interesting finding is the extended period over which potential differences persist in the silica garden system based on FeCl2. Indeed, ΔEh remains as high as 70 mV after one day (where the potential generated by the other two cations has already faded), and even at the end of the experiment after ca. 45 h there is still a notable voltage of about 40 mV being detected. This indicates that thermodynamic equilibrium is obviously not yet reached after almost two days, as also suggested by the corresponding ion concentration profiles (Fig. 2C). Again, we ascribe the distinct behaviour of Fe2+ to the porosity and/or composition of the tube wall. In any case, when it comes to the use of the spontaneously created potential differences as an energy source to drive chemical reactions, silica gardens formed with FeCl3 offer the strongest power at short times, whereas those grown with FeCl2 are more persistent and might be used for longer periods of time. Our results thus emphasise that the choice of the cation provides a straightforward means to tune chemical gardens with respect to their ability to act as batteries and/or catalysts.Ex situ characterisation
Having identified major differences between the dynamics of diffusion and precipitation processes in cobalt- and iron-based silica gardens in terms of solution chemistry, we now turn to investigate the composition and structure of the formed membranes. To that end, tubes grown with FeCl2 and FeCl3 were isolated at different times and subsequently (after washing with water/ethanol and drying) characterised using scanning electron microscopy (SEM), energy-dispersive X-ray (EDX) spectroscopy and X-ray powder diffraction (XRD). Corresponding analyses on silica gardens prepared with CoCl2 have already been presented in our previous study,23 where it was found that the inner wall of the tube is rich in crystalline cobalt hydroxychloride (Co2(OH)3Cl) with traces of Co(OH)2, whereas the outer surface proved to be constituted mainly of amorphous silica. Fig. 4 shows representative SEM images taken from the inner and outer surfaces of tubes formed with FeCl2 and FeCl3, while the results from corresponding EDX analyses are summarised in Table 2. | ||
| Fig. 4 Scanning electron micrographs showing the morphology and fine structure of the inner (top row) and outer (bottom row) surfaces of tubular membranes formed in silica garden systems based on FeCl3 (left) and FeCl2 (right). Samples were isolated from their growth solution after 3 h (FeCl3) and 24 h (FeCl2). Note that the wrinkled and ribbon-like patterns in (A) and (B) are oriented perpendicular to the vertical tube axis (cf.Fig. 1) and result from their pulsed growth behaviour. | ||
| Cation | Inner surface | Outer surface | ||||||
|---|---|---|---|---|---|---|---|---|
| Co/Fe | Si | Na | Cl | Co/Fe | Si | Na | Cl | |
| Co2+ | 32.5 | 0.9 | 3.1 | 7.2 | 14.2 | 7.0 | 4.0 | 1.4 |
| Fe2+ | 29.0 | — | — | 15.9 | 27.0 | — | — | 7.0 |
| Fe3+ | 24.7 | 2.5 | 1.3 | 1.0 | — | 26.2 | 1.9 | — |
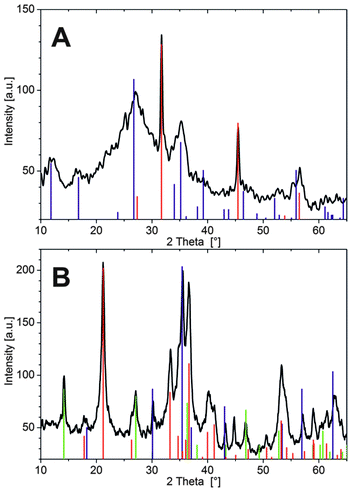
In the case of Fe3+, tubes were isolated after about 3 h in order to prevent complete solidification of the interior solution, as mentioned above. SEM micrographs reveal a wrinkled and ribbon-like structuring on the inner membrane wall (Fig. 4A), with multiple cracks that likely originate from the drying process. The outer surface has a dense and relatively smooth appearance (Fig. 4B), showing little distinct structural features except for some periodic banding textures caused by the pulsed growth behaviour of the tubes.18 Thus, both sides of the Fe3+-based membrane are rather compact and homogeneous, in contrast to the Co2+ case, where defined crystalline particles were observed on the inner surface.23 Nevertheless, the elemental composition as traced by EDX spectroscopy shows substantial differences (Table 2): while the outer part of the wall consists mainly of Si and O (with traces of Na, but no Fe), the tube interior is rich in Fe and O, along with minor fractions of Si, Na and Cl. Consequently, the outer membrane surface can be considered to be a pure silica layer, whereas the inner side predominantly consists of iron (hydr)oxide – giving a similar gradient in composition as observed for cobalt-based silica gardens.23 The fact that the two surfaces are smooth and non-faceted suggests that both components exist (mainly) in an amorphous state. Indeed, XRD patterns collected after 24 h (Fig. 5A) show a broad and undefined signal extending from about 20 to 40°, along with some weakly pronounced crystalline reflections that can be assigned to akaganeite (FeOOH).
In addition, relatively sharp peaks typical for halite (NaCl) are observed (in line with the EDX data), which could likely not be washed out quantitatively and crystallised upon drying (indicating that sodium and chloride ions are occluded/embedded in the tube wall). The absence of larger and more developed FeOOH crystals on the inner wall can be explained on the basis of the measured concentration profiles (Fig. 2D): since Fe3+ precipitates significantly faster than the other two cations, many small particles are formed under kinetic control, leading to amorphous oxyhydroxide species that only slowly transform into the thermodynamically favoured crystalline state.
The corresponding analyses of silica gardens grown with FeCl2 show a completely different picture. Here, the inner side of the tube wall is composed of spherical particles, typically 5–10 μm in diameter, which mostly have a rough appearance and are constituted by smaller subunits with plate- or needle-like shapes (Fig. 4C). Other spheres seem to be more compact and display angular facets (not shown). Both the observed morphologies strongly suggest the presence of a crystalline material on the interior membrane surface. SEM images of the outer side of the tube wall show an even structure, with large cracks spreading across the surface as a result of the drying process (Fig. 4D). Zooming into the texture of the material reveals a dense assembly of fairly uniform nanoplatelets, which are several hundreds of nanometers wide and about 50 nm thick. The shape of these building units indicates that the exterior membrane surface also has predominantly crystalline character in this case – in contrast to the unstructured and amorphous silica layers found on the outside of tubes formed with FeCl3 and CoCl2.23
As expected from the SEM images, EDX measurements show similar elemental compositions for the inner and outer side of the Fe2+-based tube wall (Table 2). In both cases, significant amounts of Fe and Cl (as well as O) were detected, but no Si. This confirms the absence of a distinct silica skin on the exterior side and shows that the membrane is more or less homogeneously composed of iron (hydr)oxide and/or (hydr)(oxy)chloride. We note that the nanotextured outer surface was frequently covered by loosely adhering, fluffy material (highlighted by arrows in Fig. 4D), which consisted of networks of coagulated silica nanoparticles (as verified by local EDX analysis) and may thus represent remnants of an initially present silica-rich layer. Indeed, visual observations during the early stages of tube growth suggest that a colourless, gelatinous material (presumably hydrated metal silicate) is formed first and subsequently turns green as the membrane gains in rigidity, indicating enhanced precipitation of Fe(II)/Fe(III) hydroxides (“green rust”). The fact that the initial silicate-rich gel is not found to be an integral part of the final membrane may imply that it re-dissolves as more and more iron (hydr)oxide species are formed. However, it is also possible that the isolation procedure caused significant structural changes, potentially leading to the deposition of flocculated silica on the membrane or conversely to partial disintegration of an originally continuous outer silica layer. In line with the SEM observations, X-ray powder diffraction patterns (Fig. 5B) evidence that the membrane material obtained with FeCl2 is considerably more crystalline than in the case of FeCl3. Occurring phases include the iron(III) oxyhydroxides goethite and lepidocrocite (both FeOOH), as well as magnetite (Fe(II)Fe(III)2O4) or maghemite (γ-Fe2O3), while no pure iron(II) compounds or noticeable fractions of NaCl (in agreement with EDX) could be detected. These results show that most of the incorporated Fe2+ ions were oxidised to Fe3+ by atmospheric O2 during ageing of the tube in contact with the surrounding solution and/or in the course of the isolation and drying process (which could be avoided by performing the experiments in an oxygen-free atmosphere, thus likely resulting in different behaviour). Moreover, the absence of any crystalline iron (hydr)oxychloride phases (as expected based on the large amounts of Cl detected by EDX, cf.Table 2) suggests that the membrane also contains amorphous components.
Taken together, our ex situ analyses demonstrate that open-tube silica gardens formed with CoCl2 and FeCl3 share a similar gradient in chemical composition, although the particular kinetics of precipitation lead to different microstructures and a lower degree of crystallinity in the case of iron(III). The observed gradient results from the distinct physicochemical conditions on the two sides of the membrane: metal cations trying to penetrate the tube wall from the inside precipitate as hydroxides due to the high pH in the outer reservoir, whereas silicate ions – moving in the opposite direction – polymerise as soon as they experience the low pH of the interior solution, forming the amorphous silica-rich layers on the outside of the membrane. Thus, metal (hydr)oxides and silica precipitate in spatially separated domains, explaining the absence of any (crystalline) metal silicate phases such as chrysolite or fayalite. In the case of FeCl2, the behaviour of the system is substantially different, as no outer silica layer is observed. The only reasonable explanation for this finding (apart from isolation artefacts) is that the tube wall is much denser (as already hypothesised above) and only allows small hydroxide ions to diffuse through, while larger silicate species are excluded and thus do not “feel” the strong pH gradient across the membrane. Accordingly, we could not detect any significant amounts of Si in the interior solution even at advanced stages when the inner pH was already high – in contrast to the Fe3+ case, where a clear increase in [SiO2]int was observed after about 10 h (cf.Fig. 3). For similar reasons, the diffusion of other ionic species (like Na+ or OH−) is dramatically slowed down in the iron(II) system.
Conclusions
In summary, our study has shown that the dynamic behaviour of silica gardens strongly depends on the type of metal cation used for their preparation. As diffusion and precipitation processes are intimately correlated in these systems, time-dependent concentration gradients and transport properties (i.e. membrane permeabilities) determine the final microstructure and composition of the tubular architectures. One key parameter identified in the present work is the acidity of the metal cations and, with it, the solubility of corresponding (hydr)oxides and silicates, as this is crucial for the rate of precipitation and hence also for the size and shape of the primary particles, which in turn influence membrane porosity. In the case of iron(III) chloride, this results in relatively fast equilibration and smooth membrane structures, along with initially drastic pH gradients that induce higher electrochemical potential differences than for the other two investigated cations. Iron(II) chloride represents an example for the other extreme in terms of behaviour. Here, concentration and pH gradients are generally less pronounced, and slow precipitation leads to dense and more crystalline tube walls with fundamentally different transport characteristics, which eventually give distinct (that is, homogeneous) membrane compositions and prevent equilibration even after days of maturation. Finally, cobalt(II) chloride can be considered as an intermediate case in that respect.Processes like those observed in the present work are likely to occur in natural environments,37 where iron-containing minerals get in touch with silica-rich waters, or in steel tubings upon progressive corrosion. The data collected in this study provide a quantitative basis for such phenomena and emphasise the importance of chemical gradients across self-assembled inorganic membranes.
Experimental
To prepare single macroscopic silica garden tubes with uniform shape, dry metal salt crystals (FeCl2·4H2O and FeCl3·6H2O; Merck, p.a.) were ground to fine powder and pressed into pellets with a diameter of 13 mm at 3.5 bar using a Perkin-Elmer hydraulic press. The pellets were then fixed at the bottom of a plastic beaker (120 mL) using a double-sided adhesive tape, and 10 mL of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (v/v) dilution of commercial water glass (Sigma-Aldrich, reagent grade) were added manually at a rate of ca. 1 mL s−1 using a plastic syringe. After a gel-like membrane was formed over the surface of the dissolving salt pellet, additional 30 mL of silicate solution were added automatically at a controlled constant rate of 1 and 10 mL min−1, respectively, for FeCl2 and FeCl3via a dosing apparatus (Unita I, Braun). The resulting tubes (cf.Fig. 1) had an open end towards the atmosphere and showed reproducible dimensions with lengths of ca. 20 mm and diameters of ca. 6 mm. The size of the tubes was mainly determined by the dimensions of the used metal salt pellets, with bigger pellets yielding larger tubes; the shape of the pellets (cylinders vs. disks) did not affect the size and morphology of the tubes to any noticeable degree. All experiments were performed under ambient conditions using water taken from a Millipore system.
4 (v/v) dilution of commercial water glass (Sigma-Aldrich, reagent grade) were added manually at a rate of ca. 1 mL s−1 using a plastic syringe. After a gel-like membrane was formed over the surface of the dissolving salt pellet, additional 30 mL of silicate solution were added automatically at a controlled constant rate of 1 and 10 mL min−1, respectively, for FeCl2 and FeCl3via a dosing apparatus (Unita I, Braun). The resulting tubes (cf.Fig. 1) had an open end towards the atmosphere and showed reproducible dimensions with lengths of ca. 20 mm and diameters of ca. 6 mm. The size of the tubes was mainly determined by the dimensions of the used metal salt pellets, with bigger pellets yielding larger tubes; the shape of the pellets (cylinders vs. disks) did not affect the size and morphology of the tubes to any noticeable degree. All experiments were performed under ambient conditions using water taken from a Millipore system.
For the determination of ion concentrations, samples were taken at different times from the interior (10 μL) and exterior (100 μL) solution, diluted with 10 mL water, and subsequently analysed by inductively coupled plasma atomic emission spectroscopy (ICP-AES) on a Spectroflame EOP instrument. Concentration calibration was achieved by measuring elemental standard solutions (obtained from Fluka and Aldrich), which were diluted with Millipore water at ratios ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 to 1
20 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 (v/v). For continuous pH measurements, a glass microelectrode (Mettler-Toledo InLab Micro; tip diameter: 3 mm) was immersed into either the inner or outer solution at a depth of 5 mm. The electrode was connected to a digital laboratory pH meter (Schott CG 843), which was read out by custom-designed software in intervals of 5 s. Electrochemical potential differences were monitored using a pair of identical Pt stick electrodes (diameter: 1 mm), which were immersed at a depth of 2 mm into both the inner and outer solution. Data were recorded every 0.3 s using two multimeters (Metex M-3890D USB) linked to a PC. We note that the presence of immersed electrodes may to some extent affect the dynamics of the systems due to perturbations and local concentration gradients. Moreover, the relatively large dimensions of the tubes will allow for enhanced convective flows in the interior solution, especially during the early stages of tube formation when the pellet is still dissolving and the forced inflow of water causes local density differences; while this effect could influence the resulting data at the beginning of the experiments, it is expected to become negligible during the later stages of slow diffusion and precipitation.
1000 (v/v). For continuous pH measurements, a glass microelectrode (Mettler-Toledo InLab Micro; tip diameter: 3 mm) was immersed into either the inner or outer solution at a depth of 5 mm. The electrode was connected to a digital laboratory pH meter (Schott CG 843), which was read out by custom-designed software in intervals of 5 s. Electrochemical potential differences were monitored using a pair of identical Pt stick electrodes (diameter: 1 mm), which were immersed at a depth of 2 mm into both the inner and outer solution. Data were recorded every 0.3 s using two multimeters (Metex M-3890D USB) linked to a PC. We note that the presence of immersed electrodes may to some extent affect the dynamics of the systems due to perturbations and local concentration gradients. Moreover, the relatively large dimensions of the tubes will allow for enhanced convective flows in the interior solution, especially during the early stages of tube formation when the pellet is still dissolving and the forced inflow of water causes local density differences; while this effect could influence the resulting data at the beginning of the experiments, it is expected to become negligible during the later stages of slow diffusion and precipitation.
In order to characterise the structure and composition of the formed silica gardens, fragments of the tubular precipitates were isolated after different periods of ageing and subsequently investigated by various ex situ techniques. To that end, the surrounding water glass reservoir and the solution inside the tubes were carefully removed using a syringe and replaced several times with water to wash out soluble salt remainders. Eventually, the tube material was isolated and thoroughly rinsed with water and ethanol, followed by drying at ambient temperature in a nitrogen atmosphere. The samples obtained in this way were first analysed with respect to elemental composition by EDX spectroscopy, using an EDAX Genesis 2000 system attached to a FEI Quanta 400F scanning electron microscope operating at a voltage of 20 kV. After sputter-coating with a thin Au layer, the microstructure was studied by SEM on a Zeiss Leo Gemini 1530 microscope at acceleration voltages of 2–5 kV and working distances ranging from 3 to 10 mm. Finally, XRD patterns were recorded on a Siemens D5000 diffractometer at a wavelength of 1.54 Å (CuKα radiation). The measured 2θ range was 8–80° in steps of 0.02–0.04°. The integration time per step was set to 15 s. The observed crystalline reflections were assigned to different mineral phases by using the reference library of the STOE WinXPOW software package.
Acknowledgements
J. M. G. R. is grateful to the European Research Council for financial support (FP7/2007-2013; ERC grant agreement No. 340863).References
- T. H. Hazelhurst, J. Chem. Educ., 1941, 18, 286 Search PubMed.
- L. M. Barge, S. S. S. Cardoso, J. H. E. Cartwright, G. J. T. Cooper, L. Cronin, A. De Wit, I. J. Doloboff, B. Escribano, R. E. Goldstein, F. Haudin, D. E. H. Jones, A. L. Mackay, J. Maselko, J. J. Pagano, J. Pantaleone, M. J. Russell, C. I. Sainz-Diaz, O. Steinbock, D. A. Stone, Y. Tanimoto and N. L. Thomas, Chem. Rev., 2015, 115, 8652 CrossRef CAS PubMed.
- J. R. Glauber, Furni Novi Philosophici, Amsterdam, 1646 Search PubMed.
- S. Leduc, The Mechanism of Life, Rebman, London, 1911 Search PubMed.
- R. D. Coatman, N. L. Thomas and D. D. Double, J. Mater. Sci., 1980, 15, 2017 CrossRef CAS.
- A. Baker, A. Toth, D. Horvath, J. Walkush, A. S. Ali, W. Morgan, A. Kukovecz, J. J. Pantaleone and J. Maselko, J. Phys. Chem. A, 2009, 113, 8243 CrossRef CAS PubMed.
- J. Maselko and P. Strizhak, J. Phys. Chem. B, 2004, 108, 4937 CrossRef CAS.
- C. J. S. Ibsen, B. F. Mikladal, U. B. Jensen and H. Birkedal, Chem. – Eur. J., 2014, 20, 16112 CrossRef PubMed.
- B. C. Batista and O. Steinbock, Chem. Commun., 2015, 51, 12962 RSC.
- C. Ritchie, G. J. T. Cooper, Y. F. Song, C. Streb, H. Yin, A. D. C. Parenty, D. A. MacLaren and L. Cronin, Nat. Chem., 2009, 1, 47 CrossRef CAS PubMed.
- D. D. Double and A. Hellawell, Nature, 1976, 261, 486 CrossRef CAS.
- D. Balköse, F. Özkan, U. Köktürk, S. Ulutan, S. Ülkü and G. Nisli, J. Sol–Gel Sci. Technol., 2002, 23, 253 CrossRef.
- J. H. E. Cartwright, B. Escribano and C. I. Sainz-Diaz, Langmuir, 2011, 27, 3286 CrossRef CAS PubMed.
- J. H. E. Cartwright, B. Escribano, S. Khokhlov and C. I. Sainz-Diaz, Phys. Chem. Chem. Phys., 2011, 13, 1030 RSC.
- J. H. E. Cartwright, J. M. Garcia-Ruiz, M. L. Novella and F. Otalora, J. Colloid Interface Sci., 2002, 256, 351 CrossRef CAS.
- S. Thouvenel-Romans and O. Steinbock, J. Am. Chem. Soc., 2003, 125, 4338–4341 CrossRef CAS PubMed.
- M. Kellermeier, F. Glaab, E. Melero-Garcia and J. M. Garcia-Ruiz, Experimental Techniques for the Growth and Characterization of Silica Biomorphs and Silica Gardens, in Research Methods in Biomineralization, ed. J. J. De Yoreo, Methods in Enzymology, 2013, vol. 532, p. 45 Search PubMed.
- J. Pantaleone, A. Toth, D. Horvath, J. R. McMahan, R. Smith, D. Butki, J. Braden, E. Mathews, H. Geri and J. Maselko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 046207 CrossRef CAS PubMed.
- J. Pagano, S. Thouvenel-Romans and O. Steinbock, Phys. Chem. Chem. Phys., 2007, 9, 110 RSC.
- K. Parmar, H. T. Chaturvedi, M. W. Akhtar, S. Chakravarty, S. K. Das, A. Pramanik, M. Ghosh, A. K. Panda, N. Bandyopadhya and S. Bhattacharjee, Mater. Charact., 2009, 60, 863 CrossRef CAS.
- C. Collins, R. Mokaya and J. Klinowski, Phys. Chem. Chem. Phys., 1999, 1, 4669 RSC.
- J. J. Pagano, T. Bansagi and O. Steinbock, Angew. Chem., Int. Ed., 2008, 47, 9900 CrossRef CAS PubMed.
- F. Glaab, M. Kellermeier, W. Kunz, E. Morallon and J. M. Garcia-Ruiz, Angew. Chem., Int. Ed., 2012, 124, 4393 CrossRef.
- L. M. Barge, I. J. Doloboff, L. M. White, M. J. Russell, G. D. Stucky and I. Kanik, Langmuir, 2012, 28, 3714 CrossRef CAS PubMed.
- L. M. Barge, Y. Abedian, M. J. Russell, I. J. Doloboff, J. H. E. Cartwright, R. D. Kidd and I. Kanik, Angew. Chem., Int. Ed., 2015, 54, 8184 CrossRef CAS PubMed.
- M. J. Russell, R. M. Daniel, A. J. Hall and J. A. Sherringham, J. Mol. Evol., 1994, 39, 231 CrossRef CAS.
- N. Li, X. Wang, S. Derrouiche, G. L. Haller and L. D. Pfefferle, ACS Nano, 2010, 4, 1759 CrossRef CAS PubMed.
- F. G. Ferris, T. J. Beveridge and W. S. Fyfe, Nature, 1986, 320, 609 CrossRef CAS.
- M. Maeda and M. Suzuki, National Institute of Advanced Industrial Science and Technology (AIST) Japan, 2014, p. 8 Search PubMed.
- M. B. Bogacki, I. Michalska and A. Krysztafkiewicz, Dyes Pigm., 2004, 61, 149 CrossRef CAS.
- D. A. Stone and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 11537 CrossRef CAS PubMed.
- A. Zecchina, M. Rivallan, G. Berlier, C. Lamberti and G. Ricchiardi, Phys. Chem. Chem. Phys., 2007, 9, 3483 RSC.
- C. F. Baes and R. E. Mesmer, The Hydrolysis of Cations, John Wiley & Sons, New York, 1976 Search PubMed.
- CRC Handbook of Chemistry and Physics, Taylor & Francis, USA, 2006 Search PubMed.
- R. K. Iler, The chemistry of silica, John Wiley & Sons, New York, 1979 Search PubMed.
- C. Collins, W. Zhou and J. Klinowski, Chem. Phys. Lett., 1999, 306, 145 CrossRef.
- H. Satoh, K. Tsukamoto and J. M. Garcia-Ruiz, Eur. J. Mineral., 2014, 26, 415 CrossRef CAS.
| This journal is © the Owner Societies 2016 |