Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Saturation dynamics and working limits of saturated absorption cavity ringdown spectroscopy
Ibrahim
Sadiek
a and
Gernot
Friedrichs
*ab
aInstitute of Physical Chemistry, University of Kiel, Max-Eyth-Str. 1, 24118 Kiel, Germany. E-mail: friedrichs@phc.uni-kiel.de
bKMS Kiel Marine Science – Centre for Interdisciplinary Marine Sciences, University of Kiel, Olshausenstr. 40, 24098 Kiel, Germany
First published on 29th July 2016
Abstract
Cavity ringdown spectroscopy (CRDS) in the linear absorption regime is a well-established method for sensitive trace gas detection, but only a few studies have addressed quantitative measurements in the presence of a saturated sample. In fact, saturation is usually avoided in order to escape from the required complex modeling of the saturation process that depends on the characteristics of the absorbing species, its interaction with the surrounding gas as well as on the temporal and spectral characteristics of the cavity excitation. Conversely, the novel saturated-absorption cavity ringdown spectroscopy approach (SCAR/Sat-CRDS) takes advantage of sample saturation in order to allow one to extract both the gas absorption and the empty cavity loss rates from a single ringdown event. Using a new continuous-wave infrared CRD spectrometer equipped with a tunable narrow-bandwidth high-power OPO laser system and a 18 bit digitizer, the transient dynamics of absorption saturation and the working limits of the Sat-CRDS approach in terms of its ability to extract reliable trace gas concentrations have been experimentally studied in this work. Using a strong methane transition as a test case, the excitation power P0 and saturation power PS have been systematically varied to explore a wide range of saturation regimes. At pressures 5 μbar < p < 2 mbar, the saturation intensity revealed a nearly linear pressure dependence showing that non-collisional processes contribute to the overall relaxation. A ratio of P0/PS ≈ 15 turned out to be optimal with working limits of 5 < P0/PS < 300. Moreover, the ratio of the absorption and empty cavity loss rates, γg/γc, has been varied to test the dynamic range of the method. At γg > γc, a pronounced coupling between the two parameters has been observed. Finally, a standard error analysis was performed revealing that the Sat-CRDS approach holds its advantages over conventional CRDS implementations in particular when the attainable ultimate detection sensitivity is limited by uncertainties in the empty cavity ringdown constant.
1 Introduction
Sensitive light absorption measurements by means of cavity ringdown spectroscopy (CRDS) have become a very well-established technique with widespread applications in trace gas detection, spectroscopy, and reaction kinetics.1–3 Almost all CRDS implementations are performed in the linear absorption regime where the difference between the measured ringdown time with absorber present in the cavity, τ, and the empty cavity ringdown time, τ0, is a direct measure of the concentration [c] of the detected species.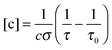 | (1) |
In Sat-CRDS the issue of non-exponential ringdown curves is overcome by properly modeling the whole ringdown curve taking into account an appropriate saturation model. In the simplest case, the sample is completely saturated and shows almost no net absorption at the beginning of the ringdown event and, with diminishing intracavity light intensity, is not saturated at all at its end. Then it is possible to directly measure the empty cavity decay constant τ0−1 at short ringdown times, whereas at long ringdown times the intensity decay is described by τ0−1 + cσ[c]. On the one hand, this approach makes the scanning of the laser frequency over the absorption line dispensable. In principle, this enhances the measurement speed by a factor of n and with it reduces the statistical noise by 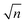 . Here, n is equal to the number of data points that would be needed to scan over the whole absorption line to determine a reliable spectrum baseline. Moreover, performing a single measurement at a fixed detection wavelength should significantly reduce the uncertainties related to baseline undulation and drift. On the other hand, the need for extracting at least two more or less correlated parameters from a single ringdown curve may cause additional uncertainty in parameter estimation, hence partly outweighing the outlined sensitivity enhancement. Recently, Lehmann20 introduced a theoretical error analysis trying to predict the ultimate sensitivity limits of Sat-CRDS. In his simulations, due to the strong parameter correlation, the standard error of the absorption extracted from the saturated ringdown curve turned out to be even one order of magnitude worse than that of a standard CRDS experiment. Moreover, it was pointed out that the standard error is a strong function of the initial degree of saturation and therefore a sensitive Sat-CRDS detection scheme would rely on a proper choice of the experimental conditions.
. Here, n is equal to the number of data points that would be needed to scan over the whole absorption line to determine a reliable spectrum baseline. Moreover, performing a single measurement at a fixed detection wavelength should significantly reduce the uncertainties related to baseline undulation and drift. On the other hand, the need for extracting at least two more or less correlated parameters from a single ringdown curve may cause additional uncertainty in parameter estimation, hence partly outweighing the outlined sensitivity enhancement. Recently, Lehmann20 introduced a theoretical error analysis trying to predict the ultimate sensitivity limits of Sat-CRDS. In his simulations, due to the strong parameter correlation, the standard error of the absorption extracted from the saturated ringdown curve turned out to be even one order of magnitude worse than that of a standard CRDS experiment. Moreover, it was pointed out that the standard error is a strong function of the initial degree of saturation and therefore a sensitive Sat-CRDS detection scheme would rely on a proper choice of the experimental conditions.
In the context of the current status of development and theoretical understanding of the Sat-CRDS approach, the aim of this study was to provide a systematic experimental assessment of the limiting factors that have to be taken into consideration for sensitive Sat-CRDS detection. First, a new IR-cw-CRDS experiment based on a high power OPO laser system has been setup that allowed us to easily vary the saturation conditions over a wide range. The saturation dynamics, which is controlled by the interplay of optical pumping and relaxation rate, has been investigated. The transition from the highly saturated absorption regime to a lower degree of saturation has been studied by varying both the intracavity intensity as well as the saturation intensity. The latter was tuned independently by setting the detection cell pressure. An experimental standard error analysis has been performed and compared to the theoretical predictions of Lehmann in order to determine the optimum working conditions. Finally, the ability of the model to retrieve the gas absorption decay rate for absorption lines with different line strengths has been examined.
2 Sat-CRDS model
2.1 Saturation and relaxation dynamics
Lee and Hahn6 have introduced an extensive theoretical analysis on the dynamic absorption saturation in pulsed CRDS. In their study, a broad dynamic range of saturation conditions covering the adiabatic and the non-relaxing regime has been simulated considering homogeneous and inhomogeneous broadening of the absorption line. Somewhat earlier, Brown et al.5 presented the equations governing the saturated ringdown decay for the adiabatic case assuming a homogeneous line broadening regime and, very recently, Giusfredi et al.21 depicted fitting strategies to retrieve quantitative absorption data from Sat-CRDS experiments at pressures resulting in absorption line profiles in the Voigt broadening regime.The saturation changes the population of the energy levels involved in the transition from the thermal Boltzmann equilibrium situation. For probing vibration–rotational transitions, a detailed treatment of this effect should be based on an open two-energy-level or multilevel relaxation scheme.22,23 However, the overall effect can be illustrated in a simple two-state model with ground state (g) and excited state (e). The population dynamics during a ringdown event can then be described by the population densities Ng(t) and Ne(t) and the decay of the intracavity spectral energy density ρν(t). For the non-degenerate case with statistical weights gg = ge = 1, the populations are changed by the excitation and deexcitation rates 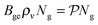 and
and 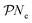 as well as the overall relaxation rate
as well as the overall relaxation rate 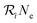 . Here, Bge is the Einstein-B coefficient of the respective transition and
. Here, Bge is the Einstein-B coefficient of the respective transition and 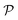 the absorption and stimulated emission probability. The relaxation probability
the absorption and stimulated emission probability. The relaxation probability 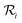 accounts for all other deexcitation processes such as spontaneous emission, A = 1/τnatural, collisional excitation and deexcitation, k = 1/τcollision as well as net population changes caused by diffusional or ballistic motion of ground state molecules into and excited state molecules out of the observation volume, k = 1/τdiffusion (including effects from transit-time broadening and wall quenching). In the adiabatic case, the saturation parameter
accounts for all other deexcitation processes such as spontaneous emission, A = 1/τnatural, collisional excitation and deexcitation, k = 1/τcollision as well as net population changes caused by diffusional or ballistic motion of ground state molecules into and excited state molecules out of the observation volume, k = 1/τdiffusion (including effects from transit-time broadening and wall quenching). In the adiabatic case, the saturation parameter 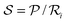 is related to the steady-state population difference
is related to the steady-state population difference 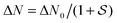 (for an homogeneously broadened absorption line) or
(for an homogeneously broadened absorption line) or 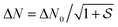 (for an inhomogeneously broadened absorption line; at line center) between the excited and the ground state. ΔN0 corresponds to the population difference without the light field
(for an inhomogeneously broadened absorption line; at line center) between the excited and the ground state. ΔN0 corresponds to the population difference without the light field 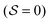 . Instead of using the saturation parameter
. Instead of using the saturation parameter 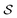 , it is common to express the saturation in terms of the saturation light intensity IS, where
, it is common to express the saturation in terms of the saturation light intensity IS, where 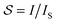 . Hence, in a closed two-level system, for
. Hence, in a closed two-level system, for 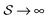 (i.e., I ≫ IS) both states become equally populated (ΔN = 0) and an absorbing sample becomes optical transparent at these high saturation levels.
(i.e., I ≫ IS) both states become equally populated (ΔN = 0) and an absorbing sample becomes optical transparent at these high saturation levels.
For a specific transition, the saturation intensity is determined by the relaxation rates of the involved energy states and, as many relaxation processes involve molecular collisions, it is a pressure dependent and collider specific quantity. Theoretically, IS ∝ τ−1g(ν)−1 (homogeneous broadening) or IS ∝ τ−1g(ν0)−1 (inhomogeneous broadening, ν0 is the line center frequency).22 Here, τ corresponds to the pressure dependent inversion lifetime (typically the lifetime of the upper level) with τ−1 = A + Q(p). Q(p) is the overall pressure-dependent quenching rate. Typically Q(p) ∝ p and with it τ−1 ∝ p holds for a quenching rate that is dominated by collisional processes. g(ν) corresponds to the normalized Lorentzian line shape function of the underlying homogeneous line profile with line width ΔνL. Considering a pressure broadened homogeneous line width with ΔνL ∝ p and using ΔνL × g(ν0) = const., it follows that g(ν0)−1 ∝ p. Therefore, at not too low pressures, the line center saturation intensity is expected to scale quadratically with pressure, IS ∝ p2. Note that for an inhomogeneously broadened line this holds for all ν. Towards lower pressures, however, g(ν0) eventually becomes pressure independent and, more important, diffusion, wall deexcitation and transit-time effects start to prevail the overall quenching. This results in a distinct deviation of IS from the anticipated p2 dependence. For example, gain saturation measurements of CO2 lasers at pressures from 133–267 mbar clearly showed24 that IS ∝ p2, whereas at pressures below 100 mbar the pressure exponent declined to values well below one.25 Similarly, for a Doppler-broadened transition of NH2D, the observed pressure dependence decreased from p1.4 at 150 μbar to p0.4 at 15 μbar.26 Hence, in order to elucidate the best working conditions for the Sat-CRDS method, the pressure dependence of the saturation intensity needs to be considered as well.
2.2 Ringdown equation
Under saturation conditions, the effective absorption coefficient of an inhomogeneous broadened line at steady-state condition becomes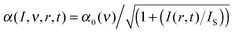 . α0(ν) is the non-saturated absorption coefficient at frequency ν and I(r,t) is the time dependent intensity of the cavity light field, which varies both radially,
. α0(ν) is the non-saturated absorption coefficient at frequency ν and I(r,t) is the time dependent intensity of the cavity light field, which varies both radially, 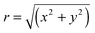 , and longitudinally along the propagation direction z. Considering that (i) the overall relaxation rate is faster than the empty cavity decay rate (adiabatic case, steady-state condition is fulfilled for all t), (ii) the displacement of a molecule with respect to the beam size is small during a time interval similar to the relaxation time (local approximation, allowing for spatial integration over the transverse Gaussian beam profile9,21), (iii) standing wave effects of the light field can be neglected, and (iv) averaging over the longitudinal field dependence of the light beam within the cavity is possible (i.e., the beam diameter remains nearly constant within the cavity), the power attenuation within the cavity for an inhomogeneously broadened absorption line can be written as9
, and longitudinally along the propagation direction z. Considering that (i) the overall relaxation rate is faster than the empty cavity decay rate (adiabatic case, steady-state condition is fulfilled for all t), (ii) the displacement of a molecule with respect to the beam size is small during a time interval similar to the relaxation time (local approximation, allowing for spatial integration over the transverse Gaussian beam profile9,21), (iii) standing wave effects of the light field can be neglected, and (iv) averaging over the longitudinal field dependence of the light beam within the cavity is possible (i.e., the beam diameter remains nearly constant within the cavity), the power attenuation within the cavity for an inhomogeneously broadened absorption line can be written as9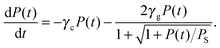 | (2) |
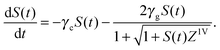 | (3) |
| f(t,γc,γg,Z1V) = S(t)/[S0 × exp(−γct)]. | (4) |
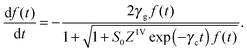 | (5) |
Numerical integration is needed to simulate the observed ringdown transient S(t) using eqn (3) and (5).
3 Experimental
IR-cw-CRDS setup
A continuous-wave single resonant optical parametric oscillator (cw-SR-OPO, Lockheed-Martin Aculight Argos 2400-SF Module C) pumped by 10 W of a fiber-amplified (IPG Photonics; YAR series) Yb-doped DFB fiber laser (NKT Photonics; Koheras Adjustik) operated at 1064 nm has been used as the light source. It was capable of producing >700 mW of continuously tunable idler output between 3.2 and 3.9 μm with a specified narrow linewidth of <60 kHz. Fig. 1 illustrates a schematic of the OPO coupled to the CRD spectrometer. Whereas the OPO signal and pump beams were dumped, the idler beam passed a ZnSe window acting as a beam splitter to measure the wavelength employing a Michelson type wavemeter (Bristol Instruments; Model 621A-IR) with a specified accuracy of ±0.2 ppm (i.e., ±0.0006 cm−1 or ±18 MHz at 3.3 μm) and a repeatability of ±6 MHz at a sampling frequency of 2.5 Hz. The main beam passed an acoustic optical modulator (AOM, Gooch & Housego Model MM040-5C11B38-5) acting as a fast optical switch with a rise time of 20 ns and a deflection efficiency of 60–70%. The deflected first order beam was guided into a commercial quartz-coated stainless steel ringdown cell (CRD Optics) equipped with multiple ports to establish a gas flow as well as to monitor the gas pressure (MKS Baratron; Model 622B 1 to 10−4 mbar) inside the cell. The test gas methane (99.5%) as well as the buffer gas argon (99.999%) were used as supplied.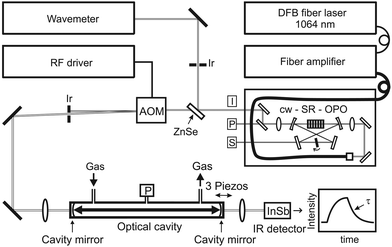 | ||
| Fig. 1 Schematic of experimental setup. I, P, S: idler, pump, and signal light beams; Ir: iris diaphragm; P: pressure transducer. | ||
A focal 50 cm in length Fabry–Perot resonator configuration with two 1 m radius of curvature ringdown mirrors (CRD Optics) with a specified reflectivity of 99.99% at 3.3 μm and a corresponding anti-reflection coating on the back surface has been used. A single 50 cm focusing lens was placed before the input CRD mirror to match both the beam waist position of the cavity as well as the TEM00 mode diameter on the mirror surfaces. Based on the resulting Gaussian beam transformation, neglecting the phase mismatch and the wavefront curvature, the theoretical mode matching coupling efficiency can be estimated to be around εmode = 0.58. Mirror adjustment was accomplished mechanically with mirror mounts equipped with 100 TPI lead screws providing 4 mm of coarse travel and electronically with three piezo elements offering 15 μm maximum travel. The frequency matching condition was achieved by modulating the length of the cavity by a triangle-wave voltage supplied to the three PZTs attached to the rear mirror using a three-channel piezo driver (MDT693B, Thorlabs) and a function generator (33210A, Agilent). Typically, a scanning speed of the cavity resonance frquency of 15 GHz s−1 has been used.
The geometry of the cavity corresponds to a round trip time of 3.33 ns, a Free Spectral Range FSR = c/2L of 300 MHz, and a transverse mode spacing of 100 MHz. At 3.3 μm, the TEM00 mode of the cavity has a 1/e beam waist radius of 0.674 mm and a beam diameter of 0.778 mm on the mirror surfaces, hence the variation of the beam cross section was merely 33% over the entire cavity (i.e., the Rayleigh range represents 86% of the cavity length). The Fresnel number F = a2/(λL) = 78, with 2a = 22.7 mm corresponding to the clear aperture of the mirrors, implies that diffraction losses were negligible. The actually measured ringdown time of the empty cavity was about 13.0 μs corresponding to a mirror reflectivity of 99.987% (including losses from scattering, coating absorption, etc.), an effective path length of 3.90 km, a Finesse 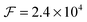 , and a cavity mode line width of 12.5 kHz. Finally, the laser light leaking through the rear mirror of the cavity was detected with a high-linearity liquid nitrogen cooled 2 mm InSb photodiode/preamplifier combination (SVS-VISTEK, KISDP-2-A-6/KA-05-CI) with a bandwidth of DC-5 MHz, corresponding to a rise time of 70 ns. The linearity of the detector has been checked by measuring single exponential transients of the empty cavity at different light levels impinging on the detector; for the experiment light levels were kept well below the saturation level of the used amplifier. A comparator circuit was used to trigger the AOM at a preset light level.
, and a cavity mode line width of 12.5 kHz. Finally, the laser light leaking through the rear mirror of the cavity was detected with a high-linearity liquid nitrogen cooled 2 mm InSb photodiode/preamplifier combination (SVS-VISTEK, KISDP-2-A-6/KA-05-CI) with a bandwidth of DC-5 MHz, corresponding to a rise time of 70 ns. The linearity of the detector has been checked by measuring single exponential transients of the empty cavity at different light levels impinging on the detector; for the experiment light levels were kept well below the saturation level of the used amplifier. A comparator circuit was used to trigger the AOM at a preset light level.
Data acquisition and numerical modeling
Sampling of the decay rates and continuous monitoring of the wavelength were achieved via National Instruments hardware and home-written LabView software. A high-resolution flexible digitizer (National Instrument, NI 5922) was used for digitizing the individual ringdown signals at a sampling rate of 10 MHz and a vertical resolution of 18 bit. High vertical resolution is crucial for Sat-CRDS experiment to prevent the digitized signal to fall below noise level before reaching the transition between the high saturation and the linear absorption regime. Each recorded ringdown transient consisted of 1300 points extending over about 10 decay times. For standard CRDS measurements, a single exponential function was fitted to the transient by a Levenberg–Marquardt nonlinear least-squares method, followed by averaging of typically 100 decay transients. For scanning the spectral line, the decay times were recorded as a function of the laser frequency. Sat-CRDS data acquisition was accomplished by first collecting a total of 400 decay transients, followed by sorting all measured ringdown transients as a function of the initial intensity I0 and then averaging the set of 100 signals with the highest and the set of 100 signals with the lowest I0 values. Despite the preset comparator level, due to a 0.7 μs delayed response of the AOM switch, this sorting procedure was necessary to confine the 7% variation of I0 levels to <1%.The versatile nonlinear programming solver fmincon implemented in MATLAB27 has been used as a fitting routine to extract the parameter vector x with γc, γg, Z1V, I0, and the detector offset SBg as adjustable parameters. fmincon seeks the minimizer of a scalar function of multiple variables subject to linear (and non-linear) constraints and bounds. The solver is called by
| x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,options). | (6) |
4 Results and discussion
In the following sections, (i) the ringdown characteristics under different degrees of initial saturation, (ii) the effective working limits of Sat-CRDS with respect to a variable relaxation rate, pumping rate as well as γg/γc ratio, and (iii) a standard error analysis are presented.4.1 Ringdown characteristics
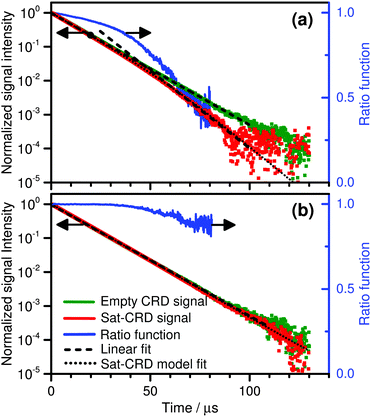
As a rule of thumb, optical saturation takes place when the rate of stimulated emission dominates the overall relaxation processes that refill the ground state. Consequently, the extent of optical saturation critically depends on the characteristics of the selected optical transition and on the interaction of the absorbing molecule with the surrounding buffer gas matrix. Moreover, the dynamics of sample saturation is determined by the ratio of relaxation rate and empty cavity decay rate. For fast relaxation the population dynamics can be assumed to be adiabatic all along the ringdown event, but the resulting high IS values require high intracavity intensities in order to clearly observe non-exponential ringdown curves.![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 3014.711728 cm−1 with a line intensity of 8.217 × 10−20 cm.28 As can be seen from the dashed black lines, the saturated ringdown signals are similar to the empty cavity signal at short ringdown times but start to deviate towards lower values at long ringdown times. At t > 100 μs the signals fall below noise level. Obviously, as the ringdown decay is dominated by the empty cavity decay constant at short times, the sample is nearly transparent showing that CH4 is highly saturated. The overall behavior can be seen even more clearly from the ratio of the Sat-CRD signal and the empty cavity signal (blue curves). In case (a), due to the higher pressure and hence higher relaxation rate, sample absorption starts to recover at t > 40 μs whereas in case (b) the pressure and with it the relaxation rate are so low that the whole saturated ringdown keeps similar to the empty cavity curve. A simulation with the Sat-CRD model (dotted curves) reveals that the ratio Z1Vb/Z1Va = 104 and with it the ratio of the saturation intensities is IS,a/IS,b = 104.
= 3014.711728 cm−1 with a line intensity of 8.217 × 10−20 cm.28 As can be seen from the dashed black lines, the saturated ringdown signals are similar to the empty cavity signal at short ringdown times but start to deviate towards lower values at long ringdown times. At t > 100 μs the signals fall below noise level. Obviously, as the ringdown decay is dominated by the empty cavity decay constant at short times, the sample is nearly transparent showing that CH4 is highly saturated. The overall behavior can be seen even more clearly from the ratio of the Sat-CRD signal and the empty cavity signal (blue curves). In case (a), due to the higher pressure and hence higher relaxation rate, sample absorption starts to recover at t > 40 μs whereas in case (b) the pressure and with it the relaxation rate are so low that the whole saturated ringdown keeps similar to the empty cavity curve. A simulation with the Sat-CRD model (dotted curves) reveals that the ratio Z1Vb/Z1Va = 104 and with it the ratio of the saturation intensities is IS,a/IS,b = 104.
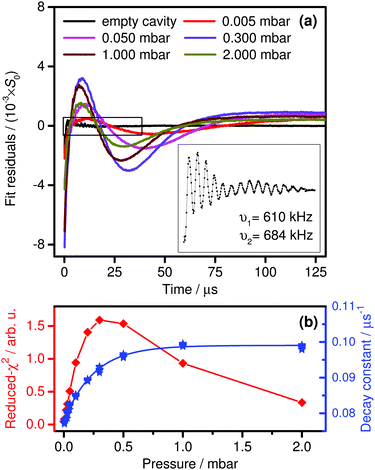
A reliable extraction of γc and γg relies on the measurements of non-exponential ringdown curves. Hence case (b) depicts an unfavorable scenario with too high intracavity light intensity and/or too low saturation intensity. The overall trend of non-exponential behavior upon variation of the cell pressure can be visualized in a comprehensible way by plotting the residuals of single-exponential fits to the Sat-CRDS transients.29Fig. 3a illustrates such an analysis for typical data of this work measured at variable cell pressures from 5 μbar to 2 mbar. The corresponding reduced χ2 values and single-exponential decay constants are shown in Fig. 3b. The resulting residuals are smallest for the experiment at 5 μbar showing that the signal behaves more or less like an empty cavity signal. Obviously, this is due to the achieved high degree of saturation, where at this low pressure the collision deactivation of the excited state is almost negligible. Addition of buffer gas results in an increase of molecular collisions that deactivate the excited state. Thus, the degree of saturation decreases and the transition to the linear absorption regime happens at earlier times during the decay transient. In Fig. 3a the increasing non-linearity shows up as a pronounced systematic deviation in the residuals and in Fig. 3b as an increase of the reduced χ2 values. Towards higher pressures χ2 passes through a maximum with the largest deviation obtained at a pressure about 300 μbar. Actually, at this pressure the transition from saturated to non-saturated behavior takes place in about the middle of the analyzed ringdown time window. At even higher pressures the saturation intensity continues to increase until it becomes comparable to the initial intensity within the cavity. Consequently, the ringdown curves approach a situation with an overall decay constant representing the single-exponential, non-saturated linear absorption regime.
To summarize, whereas at too low pressures the transition from saturated to non-saturated conditions takes place too late to be resolved within the dynamic range of the digitizer, at too high pressures the saturation effect is shifted to very short times and overall diminishes. Clearly, placing the transition between the two regimes on about the middle of the ringdown event is best for a reliable extraction of γc and γg. Moreover, in order to clearly separate both regimes it is of utmost importance to digitize the ringdown signals with high vertical resolution. 8 bit digitizers as used in many conventional CRD implementations are not suitable for Sat-CRDS measurements.
It is worth to mention here that nicely resolved oscillations have been observed in the residuals of the fits (inset of Fig. 3a). Overall, due to the low amplitude (<4 × 10−4 relative amplitudes with respect to the initial S0 signal level), these oscillations were clearly a minor effect that did not critically interfere with the ringdown fitting procedure. The frequency of the oscillations did not change with varied initial intensity I0 or cell pressure indicating that it is neither a molecular absorption nor a related acoustic effect resulting from thermal heating of the sample. The oscillation frequencies were found to be independent of the scanning speed of the cavity. Typically, the Fourier transform of the residual revealed two dominant frequency components of about 610 kHz and 684 kHz, hence noise components resulting from the operation of the AOM (50 MHz) and ringing effects of the detector/amplifier combination (5 MHz bandwidth) can be ruled out as well. Most likely, the oscillations are a result of a mode-beating of the predominantly excited TEM00 mode with a nearly degenerate higher transverse mode, which can be slightly excited during the fast scan of the cavity resonance as well. For a perfect focal cavity, degenerate transverse modes with n + m = 3, 6, 9,… (n and m are the mode indices) are present, however, already minor deviations from the focal condition removes this degeneracy. In addition, the two distinct frequency components could be explained by an astigmatism of the mirrors. For a cavity with two identical mirrors but small variations of the mirror curvature along the different transverse directions x and y, the astigmatic eigen-frequencies of the cavity are given by:30
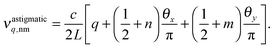 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arccos(1 − L/Rx,y) are round-trip Gouy phase shifts with a cavity length L and a mirror radius of curvature along the transverse dimension Rx,y. A deviation in the radius of curvature of |Ry − Rx|/R = 0.27% would be consistent with the observed frequency separation of 74 kHz.
arccos(1 − L/Rx,y) are round-trip Gouy phase shifts with a cavity length L and a mirror radius of curvature along the transverse dimension Rx,y. A deviation in the radius of curvature of |Ry − Rx|/R = 0.27% would be consistent with the observed frequency separation of 74 kHz.
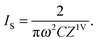 | (8) |
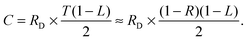 | (9) |
R D = S/Pout is the detector responsivity with Pout equal to the laser power impinging on the detector. RD = 1.29 × 105 V W−1 was determined experimentally using a thermal power meter (Thorlabs S302C/PM100D) and was found to be in very good agreement with a value of RD = r × G = 1.25 × 105 V W−1 estimated from the specifications of the photodetector responsivity r = 2.5 A W−1 and transimpedance amplifier gain G = 5.0 × 104 V A−1.
Eqn (9) also accounts for the conversion of Pout into the intracavity power P. Here, the transmission T of the rear mirror of the ringdown cavity has been set to (1 − R). In principle, the transmission of the mirrors could have been somewhat smaller in case absorption of the coating significantly contributed to the measured overall reflection loss. Allowance was made for an additional loss term (1 − L) and the factor of 2 accounts for intracavity light power in both propagation directions.6 For example, for an initial power of P0 of 0.20 W impinging on the cavity front mirror, a transmitted power of 32 μW was measured, corresponding to a 4.0 V detector signal level and a intracavity power of 0.50 W (only losses L resulting from surface reflections of the focusing lens in front of the detector with L = 0.06 have been considered). Hence, the overall experimental coupling efficiency with εtotal = 1.6 × 10−4 was much lower than expected for a perfectly impedance matched cavity with εtotal = 1. A quick estimate of the expected injection efficiency for our experimental setup can be based on the consideration that (i) the laser linewidth was five times the cavity mode linewidth (60 kHz versus 12.5 kHz), (ii) the passage time over the cavity resonance was short compared to the ringdown time (15 GHz s−1 cavity scan speed), and (iii) the mode coupling efficiency was about εmode = 0.58 as outlined in Section 3. Relying on the well elaborated effective injection efficiencies for a scanned cavity reported by Romanini et al.,32 an ideal coupling efficiency of about εtotal = 4 × 10−2 should have been possible in our case. Clearly, the experimental value was much lower. Possible reasons are a strongly overestimated mirror transmission T (e.g., by not accounting for significant scattering or absorption of the mirror coating), an underestimated loss term (1 − L) (e.g., by additional unidentified transmission/absorption losses of the CRD mirrors) or, probably more important, a larger than expected effective linewidth of the light source. The latter may have resulted from spectral noise components of the OPO seed laser, where noise of the piezo drive voltage directly translates to spectral noise. Note that a better coupling of light radiation into the cavity would allow for Sat-CRDS measurements at higher pressures, therefore future work is necessary to pin down the actual reason. Nevertheless, the achieved intracavity light levels with intensity ratios up to I0/IS = 1000 (see below) were high enough to investigate the full dynamic range of the Sat-CRDS model.
Fig. 4 shows the determined values of IS as a function of the cell pressure. The slope of the line in Fig. 4 reveals a p1.08 pressure dependence of the saturation intensity. As it has been pointed out in Section 2.1, the often assumed p2 dependence is not found at low pressures due to the fact that the overall relaxation becomes dominated by non-collision processes. From simple collision theory, assuming a collision cross section σAr–CH4 = 0.409 nm2, a cell temperature T = 295 K, and a rotational–translational energy transfer probability of 1/12,31 each methane molecule suffers a gas phase relaxation collision each 324 μs at p = 5 μbar and 809 ns at p = 2.0 mbar. These numbers can be compared with the collision-free transit time Tt = 2ω/vx = 4.3 μs of a molecule with 1D velocity vx passing through the Gaussian beam within the cavity. Hence, even at a cell pressure of 2 mbar, the relaxation process can be assumed to be significantly influenced by transit-time effects, which is consistent with the low pressure exponent. The estimated values with Tt being close to the observed ringdown decay times also reveal that the assumed adiabatic as well as the local approximation may not be fully satisfied under all experimental conditions. Relaxation rates slow compared to the ringdown decay have the effect that the ringdown transient stays longer saturated than in the adiabatic case. Consequently, fitting such ringdown curves with an adiabatic model yields too low IS values. This effect may have obscured an even weaker pressure dependence towards lower pressures that can be expected for a transit-time dominated relaxation scenario.
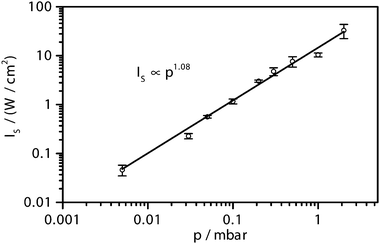 | ||
Fig. 4 Saturation intensity as a function of argon buffer gas pressure. 10 nanobar CH4 in argon, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 3014.712 cm−1 (0010 1F2 ← 0000 1A1). Reported IS values are based on a minimum loss term of L = 0.06 and a mirror transmission set to T = 1 − R (see text); assuming higher losses or lower transmission would result in higher IS values (see eqn (8) and (9)). = 3014.712 cm−1 (0010 1F2 ← 0000 1A1). Reported IS values are based on a minimum loss term of L = 0.06 and a mirror transmission set to T = 1 − R (see text); assuming higher losses or lower transmission would result in higher IS values (see eqn (8) and (9)). | ||
4.2 Working limits
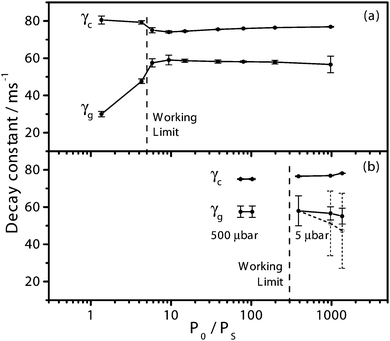
Since the initial degree of sample saturation P0/PS depends on both the relaxation and the pumping rates, the working regime of the Sat-CRDS has been investigated by changing both parameters independently. In addition, at very low pressures, inaccuracies of the Sat-CRDS model may become prominent due to the limiting adiabatic and local approximations. Finally, the ability of the Sat-CRDS model to retrieve the gas absorption decay rate at different absorber concentrations has been investigated.In the experiments shown in Fig. 5b, the P0/PS ratio has been controlled by changing the intracavity power P0 by adjusting the output power of the light source and/or the trigger level of the signal. These measurements were performed at pressures as low as 5 μbar in order to be able to achieve high P0/PS ratios. The aim was to explore the upper limit of P0/PS at which the Sat-CRDS model fails to extract γg due to the fact that throughout the dynamic range of the digitizer the sample essentially stays saturated. At P0/PS ≈ 970 already two signals out of 20 gave outliers for γg and at P0/PS ≈ 1360 three outliers have been observed. Including these outliers in the average, the mean value of γg yielded too low values with large error bars (dashed line with dashed error bars in Fig. 5b). By omitting the outliers, however, the model still predicted consistent γg values (solid line with solid error bars). Note that also at P0/PS ≈ 390 the uncertainty of the extracted γg was substantial showing that already at this ratio the model started to reach its working limit. Also in Fig. 5a the data point at P0/PS ≈ 1000 exhibits a comparably large uncertainty.
Interestingly, no obvious sign was found for the potential failure of the Sat-CRDS model towards the lowest experimental pressures caused by the possible breakdown of the adiabatic and local approximations. The weak trend of lower γg and higher γc values towards higher P0/PS is close to the error limits of the experiments and the effects related to parameter correlation seem to prevail.
Overall, to guarantee reliable parameter extraction, reasonable lower and upper working limits of 5 < P0/PS < 300 can be specified. Actually, the requirement of P0/PS > 5 can be a limiting factor for practical trace gas measurements at a given mixing ratio level of the absorbing species. As a trade-off between too low signal-to-noise ratio and a too broad absorption line (causing cross-sensitivity issues resulting from nearby absorption lines from interfering species), such measurements are often performed at cell pressures of several mbar. However, constantly evolving laser technology provides both narrow bandwidth (resulting in a better coupling efficiency to the high-finesse ringdown cavity) and high power lasers (such as modern quantum or interband cascade lasers or the cw-OPO used in this work), hence enabling high P0/PS ratios even at mbar pressure levels. Moreover, the problem is relaxed somewhat due to the fact that with higher pressures the absorption feature will no longer be in the inhomogeneously but homogeneously broadened line shape regime. Homogeneously broadened absorption lines, due to the 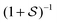 instead of
instead of 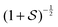 dependence of the absorption coefficient, are easier to saturate. For example, the 14CO2 Sat-CRDS measurements reported by Galli et al.10 were performed at a pressure of 11.6 mbar with an initial degree of saturation of about 30.
dependence of the absorption coefficient, are easier to saturate. For example, the 14CO2 Sat-CRDS measurements reported by Galli et al.10 were performed at a pressure of 11.6 mbar with an initial degree of saturation of about 30.
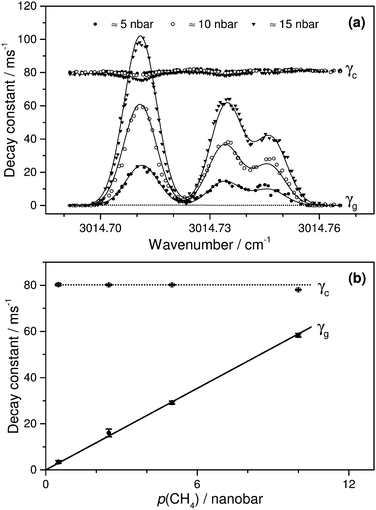 | ||
| Fig. 6 (a) CH4 absorption feature measured by Sat-CRDS method. ptotal = 200 μbar, P0/PS ≈ 67. The solid curve is based on relative line intensities adopted from the HITRAN database.28 (b) Linear response of Sat-CRDS. The solid curve represents a line fit of the γg data through the origin with R2 = 0.9991. | ||
4.3 Standard error analysis
A standard error analysis approach has been used to address the optimal Sat-CRDS detection conditions (i.e., the value of the initial degree of saturation that is corresponding to the smallest standard error σg for the extracted gas absorption decay rate γg). Recent simulations by K. Lehmann20 showed that the smallest standard error for γg extracted from the saturated signals is about one order of magnitude worse than that of a standard CRDS measurement. This interesting result, which was attributed to strong parameter correlation of γg and γc, eventually means that the ultimate sensitivity of Sat-CRDS is not expected to be better than for a standard CRDS approach. It is important to note, however, that in his simulations “ideal” noise conditions were assumed, not accounting for additional technical noise sources such as thermal drift, baseline undulations, acoustic interferences, etc. For a detector-noise-dominated situation, which is appropriate for the experimental setup used here, Huang and Lehman33 showed that an “ideal” standard error of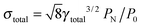 can be assumed. Based on this expression, they previously presented a very detailed analysis of the resulting sensitivity limits of non-saturated standard cw-CRDS for variable conditions (trigger level, detection system bandwidth, maximum repetition rate, fit interval, etc.). They also compared the theoretical “ideal” predictions with experimental ringdown data, which were recorded with their very well-characterized CRDS setup. Experimental sensitivities were reported to be about several times lower than the theoretical estimate.
can be assumed. Based on this expression, they previously presented a very detailed analysis of the resulting sensitivity limits of non-saturated standard cw-CRDS for variable conditions (trigger level, detection system bandwidth, maximum repetition rate, fit interval, etc.). They also compared the theoretical “ideal” predictions with experimental ringdown data, which were recorded with their very well-characterized CRDS setup. Experimental sensitivities were reported to be about several times lower than the theoretical estimate.
For practical purposes, the experimental standard error of γc is often assumed as a more reasonable, straightforward estimate of the detection limit of a standard CRDS experiment. Therefore, in the following discussion we normalize the standard error σg of the γg values extracted from the Sat-CRDS experiments with respect to the experimental standard error σc obtained for γc. In this way, the ratio σg/σc is a rough measure for the precision of the extracted γg value relative to the precision of the standard CRDS experiment. A corresponding standard error analysis is presented in Fig. 7. The experimental data are given as symbols (left axis) and are compared to the theoretically predicted trend curves reported by Lehmann33 for a γg/γc = 1.0 scenario, which is close to the experimental ratio of about 0.75 used in this work (right axis).
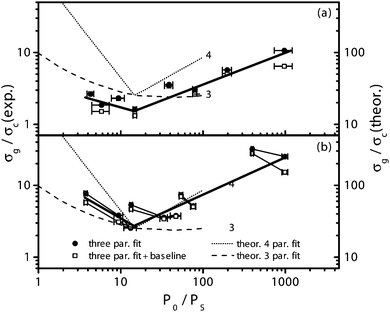 | ||
| Fig. 7 Plot of standard error σg of γg relative to the standard error σc of γc for (a) a variable PS and (b) variable PS and P0. Symbols with error bars (1σ standard deviation) refer to experimental values (left axis, referenced to the experimental σc). The thick solid lines depict the overall trend of the data. The dashed curves (right axis) are theoretical predictions for a detector noise limited scenario adopted from Lehmann.20 This prediction is referenced to the “ideal” σc value. For details see text. | ||
For the experimental data, σc was determined from empty cavity ringdown signals using the same number of ringdown events as for the determination of σg from the Sat-CRDS signals (20 experiments, each an average of 100 transients). In contrast, the theoretical values were referenced with respect to the “ideal” σc calculated by setting γtotal = γc in the expression for γtotal outlined above. The theoretical prediction have been included in Fig. 7 as dashed curves (right axis) for a three-parameter fitting scenario (i.e., γg, γc, P0; marked with “3” in the figure) as well as a four-parameter fitting scenario (i.e., γg, γg, P0, PS; marked with “4” in the figure). Yet another five-parameter fitting scenario with the baseline as an additional parameter was presented by Lehmann as well, but was found to yield essentially the same results as the four-parameter scenario. For our experimental data, a corresponding three-parameter fit (filled symbols) and a fit using the baseline as an additional parameter (open symbols) have been performed. In agreement with Lehmann we find that baseline fitting is not an important issue for the overall analysis.
Experimental values obtained by systematically changing the saturation power (variable cell pressure, P0 kept constant) are included in Fig. 7a whereas Fig. 7b illustrates data obtained by changing both the intracavity and saturation power. The connected points in Fig. 7b are measured at the same saturation intensity but different intracavity power. The systematically lower γg/γc ratios for the experiments with higher P0 can be understood by the higher signal-to-noise ratio of the corresponding ringdown transients. The thick solid lines in Fig. 7 reflect the overall trends of the experimental data. The trends are similar to the theoretically predicted ones with a somewhat more pronounced increase towards higher P0/PS values with respect to the theoretical 3-parameter fit. Moreover, comparable minima at about P0/PS ≈ 15 are obtained. The good agreement of experiment and theory suggests that this level of initial saturation can serve as a reliable guideline to the experimentalist when designing a sensitive Sat-CRDS detection scheme.
The absolute values of the experimental σg/σc ratios are about one order of magnitude lower than the theoretical prediction. As already outlined above this difference can be traced back to the different σc values used for the normalization. Hence the lower experimental ratios reflect the importance of technical noise contributions in a typical cw-CRDS implementation as used in this work. The experimental minimum value of about 2 further reveals that the precision of the σg extraction from the Sat-CRDS approach and with it the ultimate detection sensitivity is comparable to a standard CRDS approach.
However, as our experiments were performed at a fixed frequency, a fair comparison should also consider uncertainties in the empty cavity decay constant and the attainable repetition rate. On the one hand, due to the requirement of using high trigger levels in the Sat-CRDS approach to ensure high saturation levels, the latter tends to be lower. On the other hand, reliable empty cavity decay constant determination in a standard CRDS experiments typically requires scanning over the entire absorption line while the detection frequency can be kept fixed in the Sat-CRDS approach. For example, assuming that 25 spectral data points needs to be measured, the Sat-CRDS approach gains a sensitivity factor of up to 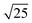 compared to the standard CRDS approach. Moreover, especially for spectrum acquisition over a wider wavelength range where baseline undulations resulting from etaloning effects become a more serious issue, the Sat-CRDS approach is advantageous. The same holds true when detecting species with dense spectra where, due to line overlapping issues, the precise determination of the empty cavity decay constant often is hardly possible. Altogether, the Sat-CRDS approach holds the potential to be more sensitive than a standard CRDS approach, especially in cases where the determination of the spectrum baseline is difficult. In other cases, as Lehmann20 pointed out, “the ‘price’ that parameter correlation will make the standard error in γg larger than that of γtotal, which is what is determined in a traditional CRDS experiment” may be too high and a well-designed standard CRDS measurement will prevail.
compared to the standard CRDS approach. Moreover, especially for spectrum acquisition over a wider wavelength range where baseline undulations resulting from etaloning effects become a more serious issue, the Sat-CRDS approach is advantageous. The same holds true when detecting species with dense spectra where, due to line overlapping issues, the precise determination of the empty cavity decay constant often is hardly possible. Altogether, the Sat-CRDS approach holds the potential to be more sensitive than a standard CRDS approach, especially in cases where the determination of the spectrum baseline is difficult. In other cases, as Lehmann20 pointed out, “the ‘price’ that parameter correlation will make the standard error in γg larger than that of γtotal, which is what is determined in a traditional CRDS experiment” may be too high and a well-designed standard CRDS measurement will prevail.
5 Conclusion
A new cw-IR-CRDS experimental setup based on a versatile OPO laser system has been established in order to investigate the saturation dynamics and working limits of the Sat-CRDS approach.The transient dynamics of absorption saturation depends on the interaction of the absorbing molecule with the buffer gas, the overall relaxation as well as the empty cavity decay rate. This behavior is well reflected in the experimentally observed saturated ringdown curves, which have been explored under different saturation conditions ranging from high to low initial degree of saturation and from the adiabatic close to the non-relaxing limit. An analysis of the residuals resulting from single-exponential fits of the non-exponential Sat-CRDS signals can be used as a quick estimate to determine a reasonable cell pressure for sensitive Sat-CRDS measurements.
For the selected absorption line of methane and with argon as the buffer gas, the pressure dependence of the saturation intensity has been determined at pressures of 5 μbar < p < 2 mbar. It turned out to be about p1.08 instead of the typically assumed p2 dependence showing that the relaxation is significantly influenced by non-collision induced processes such as the transit time.
The working limits of the Sat-CRDS approach, where the model fails to extract reliable gas absorption decay rates γg, have been investigated by changing the pumping rate (P0, laser power, trigger level), the saturation power (PS, variable cell pressure) and the γg/γc ratio. The working limits for the initial saturation are about 5 < P0/PS < 300 for our experimental setup, which is characterized by an empty cavity decay time of about 13 μs and 10 MHz/18 bit digitization of the ringdown signals. The Sat-CRDS approach was able to retrieve the absorption spectrum of several absorption lines with different intensities and exhibits linear response with respect to sample concentrations. Moreover, even at low pressures where the underlying adiabatic and local approximation starts to fail, reliable γg values were obtained showing that the Sat-CRDS model assumptions are robust. However, for γg/γc ≳ 1 a pronounced coupling of the fitting parameters was observed, hence limiting the dynamic range of Sat-CRDS.
Finally, a standard error analysis has been performed to elucidate an optimized value of the initial degree of saturation. A value of P0/PS ≈ 15 turns out to be optimal, in good agreement with theoretical predictions of Lehmann.20 The obtained best experimental value for the ratio σg/σc ≈ 2 reveals that the Sat-CRDS approach is not necessarily more sensitive than a standard CRDS detection scheme, however, with careful cavity and mode matching design as well as cavity stabilization measures a smaller relative standard error may be achieved for the Sat-CRDS method. The extra uncertainty resulting from the correlation of the fitting parameters γg and γc, however, is worth the extra “price” especially in cases where the determination of the empty cavity decay constant is difficult due to baseline instabilities and/or broad absorption features.
Acknowledgements
We would like to thank the Helmholtz Research School Ocean System Science and Technology (HOSST) at the Helmholtz Centre for Ocean Research Kiel – GEOMAR and the Cluster of Excellence “The Future Ocean” (DFG – EC80) at Kiel University for funding. Stimulating discussions with Doug Wallace (Transatlantic Ocean System Science and Technology (TOSST) research school, Dalhousie University, Canada), Arne Körtzinger (GEOMAR, Germany) and the entire HOSST-TOSST team were very helpful to sharpen the practical aspects of the project. Technical support and advice by Lockheed Martin Aculight, the supplier of the cw-OPO laser system, are gratefully acknowledged. We thank the anonymous referees for carefully reading the manuscript and their competent and constructive comments and suggestions for future work.References
- M. Mazurenka, A. J. Orr-Ewing, R. Peverall and G. A. D. Ritchie, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2005, 101, 100–142 RSC.
- G. Friedrichs, Z. Phys. Chem., 2008, 222, 31–61 CrossRef CAS.
- Cavity Ring-Down Spectroscopy, ed. G. Berden and R. Engeln, Wiley, Chichester, 2009 Search PubMed.
- A. P. Yalin and R. N. Zare, Laser Phys., 2002, 12, 1065–1072 Search PubMed.
- S. Brown, H. Stark and A. Ravishankara, Appl. Phys. B: Lasers Opt., 2002, 75, 173–182 CrossRef CAS.
- J. Lee and J. Hahn, Appl. Phys. B: Lasers Opt., 2004, 79, 653–662 CrossRef CAS.
- S. S. Brown, A. R. Ravishankara and H. Stark, J. Phys. Chem. A, 2000, 104, 7044–7052 CrossRef CAS.
- G. Friedrichs, M. Colberg, M. Fikri, Z. Huang, J. Neumann and F. Temps, J. Phys. Chem. A, 2005, 109, 4785–4795 CrossRef CAS PubMed.
- G. Giusfredi, S. Bartalini, S. Borri, P. Cancio, I. Galli, D. Mazzotti and P. De Natale, Phys. Rev. Lett., 2010, 104, 110801 CrossRef CAS PubMed.
- I. Galli, S. Bartalini, S. Borri, P. Cancio, D. Mazzotti, P. De Natale and G. Giusfredi, Phys. Rev. Lett., 2011, 107, 270802 CrossRef CAS PubMed; I. Galli, S. Bartalini, S. Borri, P. Cancio, D. Mazzotti, P. De Natale and G. Giusfredi, Phys. Rev. Lett., 2012, 108, 179902 CrossRef.
- I. Galli, S. Bartalini, P. Cancio, M. De Pas, G. Giusfredi, D. Mazzotti, N. Akikusa and P. De Natale, Optica, 2016, 3, 2334–2536 CrossRef.
- I. Galli, S. Bartalini, P. Cancio, P. De Natale, D. Mazzotti, G. Giusfredi, M. E. Fedi and P. A. Mando, Radiocarbon, 2013, 55, 213–223 CrossRef CAS.
- L. Lehr and P. Hering, IEEE J. Quantum Electron., 1997, 33, 1465–1473 CrossRef CAS.
- D. Romanini, P. Dupré and R. Jost, Vib. Spectrosc., 1999, 19, 93–106 CrossRef CAS.
- I. Labazan, S. Rudić and S. Milošević, Chem. Phys. Lett., 2000, 320, 613–622 CrossRef CAS.
- C. R. Bucher, K. K. Lehmann, D. F. Plusquellic and G. T. Fraser, Appl. Opt., 2000, 39, 3154–3164 CrossRef CAS PubMed.
- D. Lisak and J. T. Hodges, Appl. Phys. B: Lasers Opt., 2007, 88, 317–325 CrossRef CAS.
- A. A. Mills, B. M. Siller and B. J. McCall, Chem. Phys. Lett., 2010, 501, 1–5 CrossRef CAS.
- A. McIlroy and J. B. Jeffries, Applied Combustion Diagnostics, Taylor and Francis, New York, 2002, ch. 4 Search PubMed.
- K. K. Lehmann, Appl. Phys. B: Lasers Opt., 2014, 116, 147–155 CrossRef CAS.
- G. Giusfredi, I. Galli, D. Mazzotti, P. Cancio and P. De Natale, J. Opt. Soc. Am. B, 2015, 32, 2223–2237 CrossRef CAS.
- A. Yariv, Quantum Electronics, John Wiley & Sons, New York, 3rd edn, 1989 Search PubMed.
- W. Demtröder, Laser Spectroscopy: Experimental Techniques, Springer, Berlin, Heidelberg, 4th edn, 2008, vol. 2 Search PubMed.
- R. L. Abrams and W. B. Bridges, IEEE J. Quantum Electron., 1973, 9, 940–946 CrossRef CAS.
- K. Matsumoto, H. Shirahata and T. Fujioka, IEEE J. Quantum Electron., 1978, 14, 781–782 CrossRef.
- L. Thielman and L. W. Davis, Appl. Phys. Lett., 1974, 25, 461–463 CrossRef CAS.
- MATLAB and Optimization Toolbox, Version 8.5 (R2015a), The MathWorks Inc., Natick, Massachusetts, 2015.
- L. Rothman, I. Gordon, Y. Babikov, A. Barbe, D. C. Benner, P. Bernath, M. Birk, L. Bizzocchi, V. Boudon, L. Brown, A. Campargue, K. Chance, E. Cohen, L. Coudert, V. Devi, B. Drouin, A. Fayt, J.-M. Flaud, R. Gamache, J. Harrison, J.-M. Hartmann, C. Hill, J. Hodges, D. Jacquemart, A. Jolly, J. Lamouroux, R. L. Roy, G. Li, D. Long, O. Lyulin, C. Mackie, S. Massie, S. Mikhailenko, H. Müller, O. Naumenko, A. Nikitin, J. Orphal, V. Perevalov, A. Perrin, E. Polovtseva, C. Richard, M. Smith, E. Starikova, K. Sung, S. Tashkun, J. Tennyson, G. Toon, V. Tyuterev and G. Wagner, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 4–50 CrossRef CAS.
- P. Cancio, I. Galli, S. Bartalini, G. Giusfredi, D. Mazzotti and P. De Natale, Springer Series in Optical Sciences 179: Cavity-Enhanced Spectroscopy and Sensing, Springer, Heidelberg, 2014, ch. 4 Search PubMed.
- J. Courtois, A. Mohamed and D. Romanini, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 043844 CrossRef.
- P. G. Kistemaker, M. M. Hanna, A. Tom and A. E. De Vries, Physica, 1972, 60, 459–471 CrossRef CAS.
- D. Romanini, I. Ventrillard, G. Méjean, J. Morville and E. Kerstel, in Springer Series in Optical Sciences 179: Cavity-Enhanced Spectroscopy and Sensing, ed. G. Gagliardi and H.-P. Loock, Springer, Heidelberg, 2014, ch. 1 Search PubMed.
- H. Huang and K. K. Lehmann, J. Phys. Chem. A, 2013, 13399–13411 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |