Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Redox potentials of aryl derivatives from hybrid functional based first principles molecular dynamics
Xiandong
Liu
*a,
Jun
Cheng
*bc,
Xiancai
Lu
a,
Mengjia
He
a and
Rucheng
Wang
a
aState Key Laboratory for Mineral Deposits Research, School of Earth Sciences and Engineering, Nanjing University, Nanjing 210093, P. R. China. E-mail: xiandongliu@nju.edu.cn; Fax: +86 25 83686016; Tel: +86 25 89680700
bCollaborative Innovation Center of Chemistry for Energy Materials, State Key Laboratory of Physical Chemistry of Solid Surfaces, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, P. R. China. E-mail: chengjun@xmu.edu.cn; Tel: +86 5922181570
cDepartment of Chemistry, University of Aberdeen, Aberdeen AB24 3UE, UK. E-mail: jcheng@abdn.ac.uk
First published on 4th May 2016
Abstract
We report the redox potentials of a set of organic aryl molecules, including quinones, juglone, tyrosine and tryptophan, calculated using a first principles molecular dynamics (FPMD) based method. The hybrid functional HSE06 reproduces the redox potentials spanning from −0.25 V to 1.15 V within an error of 0.2 V, whereas the errors with the BLYP functional are much larger (up to 0.7 V). It is found that the BLYP functional predicts consistently lower electron affinities/ionization potentials than HSE06 both in gas phase and in an aqueous solution. In water, the ionization potentials are significantly underestimated by BLYP due to the exaggeration of the mixing between the solute states and the valence band states of liquid water. Hybrid HSE06 markedly improves both the solute levels and water band positions, leading to accurate redox potentials. This study suggests that the current FPMD based method at the level of hybrid functionals is able to accurately compute the redox potentials of a wide spectrum of organic molecules.
1. Introduction
Redox potential is a measure of the tendency of a species to gain electrons and therefore is a key thermodynamic quantity for characterizing electron transfer reactions. Redox potentials, together with acidity constants (i.e. the free energies of proton transfer reactions) are the basis for constructing pH-Eh diagrams, which are widely used to understand the stabilities of chemical species under various redox and pH conditions in many areas of chemistry.Computation of redox potentials is of great interest to the quantum chemistry communities and a number of methods have been developed. Solvation effects are often described by empirical methods such as implicit solvation models1,2 and the distribution of point dipoles.3 QM/MM methods can further include atomic detail of solvation shells by replacing the continuum solvent by classical force field models.4 Previous studies have shown that these methods can compute redox potentials accurately for many species, including inorganic compounds, organic compounds, and transition metal complexes.2
Alternatively, redox potentials can be calculated using first-principles molecular dynamics (FPMD), which treats solutes and solvents at the same quantum mechanical level and also accounts for the atomic level details of dynamical solvent effects.5 These can be important in many cases, for example, for the coordination spheres yielding drastic change upon reduction/oxidation, wherein entropic contributions could be significant to free energies. Another example is that at the elevated T-P conditions relevant to the Earth's interior, the solvent effects are hard to include in the implicit solvent protocols, because the models are usually parameterized for ambient conditions.1
The FPMD based vertical energy gap method developed by the Sprik group6–8 provides a feasible way to compute redox potentials and acidity constants. Extensive tests on molecular acids and metal cations indicate that acidity constants are reproduced within an error of 2 pKa units (approximately 0.1 eV) by GGA (generalized gradient approximation) functionals.9–14 In contrast, redox potentials calculated by GGA are much worse, for example, the values of benzoquinones (including benzoquinone, semi-benzoquinone and hydro-benzoquinone),15 tyrosine and tryptophan,6 are underestimated by 0.2–0.7 V. It has been found that GGA places the valence band of liquid water at a too high position and therefore exaggerates the mixing of the electronic states of the solute with the water valence band, leading to underestimation of the redox potential of the solute.16 Hybrid functionals such as HSE0617,18 improve the prediction of the band states of liquid water, which eventually leads to much better estimates of the redox potentials. This has been confirmed on some small inorganic molecules16 and transition metal aqua-cations.19 Very recently, random phase approximation and a double hybrid functional have been found to compute accurate water band positions and redox potentials for the oxidizing species of OH˙ and Cl˙.20
Redox chemistry of aryl derivatives, such as quinones, tyrosine and tryptophan, are of great importance in many research areas. In biology, tyrosyl and tryptophanyl radicals act as intermediates in the redox reactions of enzymes and quinones usually perform as the redox-active part of some cofactors.21 In geochemistry, it has been widely accepted that quinones are the major redox active groups in natural organic matters (NOMs),22 which, as important components of soils, take part in important supergene processes, e.g. the reduction and fixation of contaminants and metal cations. Independent small quinones (e.g. juglone, duroquinone and lawsone) and amino acids present in soils also play active roles in numerous electron transfer reactions.23 Therefore, accurate prediction of their redox potentials is very helpful for elucidating the redox reaction mechanisms in biological and geochemical processes.
In this study, hybrid functional based FPMD has been validated in the prediction of redox potentials of five organic molecules. We revisit the model systems used in the development of the method (i.e. benzoquinones, tyrosine and tryptophan) and test two other quinones, juglone and duroquinone, which have negative redox potentials. The solvation structures and solvent reorganization have been investigated using FPMD simulations. The redox potentials obtained using GGA and hybrid functionals have been compared in detail by analyzing the energy levels. The accurate computation of redox potentials with hybrid functionals suggests that the current FPMD based methodology has a wide range of potential applications in redox chemistry studies.
2. Methodology
2.1. Free energy perturbation theory and redox potential calculation
In the early study on transition metal cations,24–28 the computed redox potentials could not be directly compared with experimental measurements due to the lack of a physical potential reference. A molecular dynamics based computational standard hydrogen electrode (SHE) was developed to address this issue by Sprik et al.6,15 Herein, we present a brief introduction to the methodology and refer the interested readers to the original papers for more detail.The potential of a redox couple with respect to SHE corresponds to the free energy of the oxidation reaction in which the reduced state is oxidized by an aqueous proton:
| A−(aq) + H+(aq) → A˙(aq) + ½H2(g) | (1) |
| A−(aq) → A˙(aq) + e−(vac) | (2) |
| H+(aq) → H+(g) | (3) |
| H+(g) + e−(vac) → ½H2(g) | (4) |
| Hη = (1 − η)HR + ηHP | (5) |
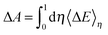 | (6) |
Thus, the computed free energies of eqn (2) and (3) can be expressed in the form of thermodynamic integrals, i.e., the oxidation integral of A−(aq) ((ΔoxAA−)) and the deprotonation integral of H3O+(aq) (ΔdpAH3O+), respectively. Note that in our implementation the desolvation of an aqueous proton (reaction (3)) is effectively replaced by the deprotonation of a solvated hydronium H3O+(aq). Including the free energy of the gas phase reaction (4) (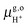 ), the formula for computing the redox potential is
), the formula for computing the redox potential is
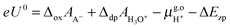 | (7) |
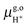 = 15.81 eV.6 It is important to note that the values of the individual thermodynamic integrals (ΔoxAA− and ΔdpAH3O+), which are associated with half reactions with a change of the net charge, do not bear physical meanings owing to the artificial offset in the potential reference under periodic boundary conditions (PBC). However, when combining the two in eqn (7), the potential offsets in the integrals are canceled, leading to the meaningful redox potentials vs. SHE. Strictly speaking, the complete cancelation is an assumption that the artificial potential offset is dominated by the solvent water. This should be rather safe for small ions; however, there might be some residual error for bulky solutes such as the organic molecules studied in this study. In a previous study,6 an empirical correction term of 0.3 eV was estimated by comparing the computed and experimental pKa's. However, the pKa's were computed with the BLYP functional and the reference integral ΔdpAH3O+ was taken as a value of 15.20 eV,6 but now the recommended value is 15.35 eV and will be used in this study.9,10 We, therefore, will not include this correction in computing the redox potentials of the organic molecules, and as will be observed below, the values obtained by using hybrid HSE06 are very close to experimental values.
= 15.81 eV.6 It is important to note that the values of the individual thermodynamic integrals (ΔoxAA− and ΔdpAH3O+), which are associated with half reactions with a change of the net charge, do not bear physical meanings owing to the artificial offset in the potential reference under periodic boundary conditions (PBC). However, when combining the two in eqn (7), the potential offsets in the integrals are canceled, leading to the meaningful redox potentials vs. SHE. Strictly speaking, the complete cancelation is an assumption that the artificial potential offset is dominated by the solvent water. This should be rather safe for small ions; however, there might be some residual error for bulky solutes such as the organic molecules studied in this study. In a previous study,6 an empirical correction term of 0.3 eV was estimated by comparing the computed and experimental pKa's. However, the pKa's were computed with the BLYP functional and the reference integral ΔdpAH3O+ was taken as a value of 15.20 eV,6 but now the recommended value is 15.35 eV and will be used in this study.9,10 We, therefore, will not include this correction in computing the redox potentials of the organic molecules, and as will be observed below, the values obtained by using hybrid HSE06 are very close to experimental values.
For the oxidation reaction, the vertical energy gaps at η = 0 and η = 1 have physical meanings, corresponding to the vertical ionization potential of the reduced state (IPA−) and the electron affinity of the oxidized state (EAA˙), respectively. They can also be aligned with respect to the SHE by using the following formulas, which are very similar to eqn (7),7
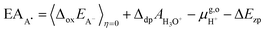 | (8) |
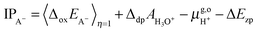 | (9) |
| λR = eU0 − EAA˙ | (10) |
| λO = IPA− − eU0 | (11) |
If the solvent response is linear, as assumed in the Marcus theory of electron transfer, the following relations hold; eU0 = (EAA˙ + IPA−)/2 and λR = λO, the deviation from which is a sign of nonlinearity in the solvent response. In particular, we will use the ratio λR/λO as a descriptor for measuring the asymmetry in the organization energies for the redox couples.
2.2. Model systems of organic molecules in water
Redox potential is a measure of the tendency of a species to gain electrons and therefore is a key thermodynamic quantity for characterizing electron transfer reactions. Redox potentials, together with acidity constants (i.e. the free energies of proton transfer reactions) are the basis for constructing pH-Eh diagrams, which are widely used to understand the stabilities of chemical species under various redox and pH conditions in many areas of chemistry. The molecular structures of the model systems are shown in Fig. 1. Benzoquinone, juglone, duroquinone, tyrosine anion and protonated tryptophan are denoted as Q, Jug, DQ, TyrO− and TrpH, respectively. The cell for all the simulations is a cubic box of the length of 12.43 Å. The number of solvent water molecules for each solute is listed in Table 1. The numbers were determined to approximately represent the density of liquid water under the ambient conditions. For Q, Tyro− and TrpH, the numbers of H2O are the same as those of previous simulations.6,15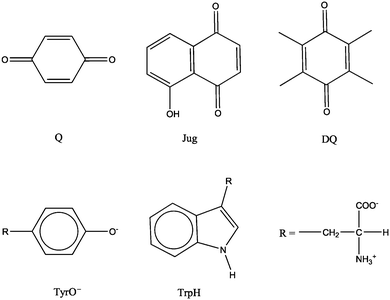 | ||
| Fig. 1 Structures of the model systems. Q = benzoquinone, Jug = juglone, DQ = duroquinone, TyrO− = tyrosine anion, TrpH = protonated tryptophan. | ||
| Oxidation | Number of H2O molecules |
|---|---|
| Q˙− → Q | 60 |
| Jug˙− → Jug | 57 |
| DQ˙− → DQ | 56 |
| TyrO− → TyrO˙ | 49 |
| TrpH → TrpH˙+ | 48 |
2.3. Computational setup
The simulations were performed using the freely available CP2K/QUICKSTEP package.30 In QUICKSTEP, the electronic structures were calculated with density functional theory implemented based on a hybrid GPW (Gaussian plane wave) technique.31 BLYP32,33 has been the favored GGA functional for FPMD simulations of aqueous systems and was widely used in previous calculations.6,15 While BLYP was used in this study for the sake of consistency, we do not expect the usage of other GGA functionals such as PBE to make any major difference in computing redox potentials. In the calculations with the hybrid functional HSE06,17,18 the exact exchange under PBC was implemented using the auxiliary density matrix method.34 Goedecker–Teter–Hutter (GTH) pseudopotentials were applied to represent the core electrons.35 Double-ζ basis sets augmented with polarization functions were employed for H, O, N and C. The cut off for expanding electron density in the reciprocal space was set to be 280 Ry. The convergence criteria for the electronic gradient and the energy difference between final SCF cycles were set to be 1.0 × 106 and 1.0 × 10−12 a.u., respectively.Born–Oppenheimer molecular dynamics simulations were carried out with a time step of 0.5 fs. The temperature was controlled at 330 K using the Nosé-Hoover chain thermostat. The elevated temperature is to avoid the glassy behavior at the lower temperatures.36 HSE06 MD runs were started from the BLYP equilibrated configurations. For each simulation, the production run was performed for over 6.0 ps, following a prior equilibration run for at least 2.0 ps.
To better understand the difference between BLYP and HSE06, we calculated the EA of DQ and TyrO and IP of DQ˙− and TyrO− in the gas phase. These calculations were carried out with a cubic box of the length of 25 Å. For charged ions, the electrostatic interaction was treated using the Martyna–Tuckerman method37 to effectively eliminate interactions between periodic images.
3. Results
3.1. Hydration structures
The H-bonding structures of the solutes have been characterized in previous BLYP FPMD calculations.6,15 The hydrophilic centers of quinones are the oxygen atoms. In addition to the ammonium and carboxyl groups, the indolic nitrogen and the oxygen atom are the hydrophilic centers of tryptophan and tyrosine, respectively.Taking DQ and Q as examples, the RDF-CN (radial distribution function-coordination number) curves for water H around quinone O derived from the HSE06 simulations are shown in Fig. 2. It is clearly observed that as oxidation proceeds, the H-bonds get weaker, as discussed in the previous study.15 For both DQ˙− and Q˙−, the H-bonds are peaked at around 1.65 Å and 1.70 Å, respectively, while for their oxidation states, the peaks shift to 1.85 Å. Similarly, for DQ˙− and Q˙−, the CNs are 2.1 and 2.2, respectively, while the CN is only 1.4 for DQ and Q (see the images of the DQ couple in Fig. 3). It is found that HSE06 and BLYP present similar H-bonding structures; for example, similar to HSE06, BLYP predicts the average H-bond distances for Q˙− and Q to be 1.70 Å and 1.90 Å, respectively.15
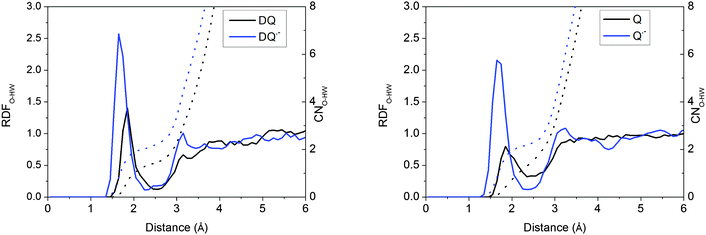 | ||
| Fig. 2 RDFs (radial distribution functions) and CNs (coordination numbers) for water H around the O of quinones derived from the HSE06 simulations. | ||
3.2. Vertical energy gaps and redox potentials
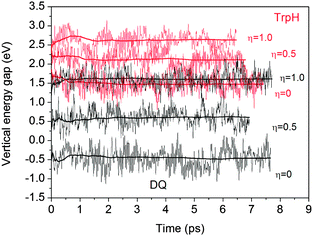
Table 2 lists the computed vertical energy gaps, thermodynamic integrals and redox potentials. All the vertical energy gaps converge within 0.1 eV in the MD simulations. This level of statistical uncertainty is consistent with the previous studies.6,15,19 The statistical accuracy can be shown by the accumulative averages of the vertical energy gaps of TrpH and DQ in Fig. 4.| η =0 (eV) | η = 0.5 (eV) | η = 1.0 (eV) | Integral (eV) | U 0Cal. (V) | U 0Exp. (V) | ||
|---|---|---|---|---|---|---|---|
| DQ | BLYP | −0.62 | 0.30 | 0.91 | 0.25 | −0.56 | −0.2438 |
| HSE06 | −0.46 | 0.6 | 1.61 | 0.59 | −0.22 | ||
| Jug | BLYP | −0.50 | 0.27 | 1.02 | 0.27 | −0.54 | −0.0939 |
| HSE06 | −0.22 | 0.63 | 1.50 | 0.63 | −0.18 | ||
| Q | BLYP15 | −0.33 | 0.45 | 1.40 | 0.48 | −0.33 | 0.1040 |
| HSE06 | −0.26 | 0.97 | 1.97 | 0.93 | 0.12 | ||
| TyrO | BLYP6 | 0.43 | 1.35 | 1.88 | 1.28 | 0.47 | 0.7221 |
| HSE06 | 0.81 | 1.61 | 2.38 | 1.60 | 0.79 | ||
| TrpH | BLYP6 | 1.00 | 1.55 | 2.01 | 1.53 | 0.72 | 1.1521 |
| HSE06 | 1.50 | 2.11 | 2.63 | 2.07 | 1.28 |
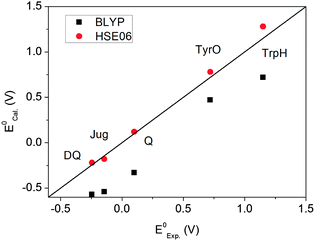
Fig. 5 plots the computed redox potentials against the experimental values. It is clear that BLYP underestimates all redox potentials and HSE06 significantly improves the predictions. Even for the lower end, i.e. DQ and Jug, the errors in BLYP are over 0.3 V. HSE06 increases all values relative to BLYP. Most redox potentials are reproduced within an error of ∼0.1 V. This error margin is of the same magnitude as the statistical errors in the MD simulations (Table 3). The overall accuracy of computation of redox potentials achieved by the current FPMD method is comparable to that of implicit solvation methods.2
| BLYP (eV) | HSE06 (eV) | |
|---|---|---|
| EA of DQ | 1.18 | 1.52 (0.34) |
| EA of TyrO | 1.71 | 1.95 (0.24) |
| IP of DQ˙− | 1.67 | 2.09 (0.42) |
| IP of TyrO− | 1.93 | 2.21 (0.28) |
3.3. Energy level diagram and solvent reorganization
The results of BLYP and HSE06 can be compared in more detail by analyzing the energy level diagrams. Vertical energy gaps are aligned to the SHE scale so that one can compare the coupling of the solute states with the band states of liquid water. As shown in the previous study, BLYP estimates the CBM (conduction band minimum) and VBM (valence band maximum) of liquid water to be −2.6 V and 2.3 V, respectively. Compared to experimental values of −3.2 V and 5.5 V, the BLYP VBM is very high by 3.2 V, in contrast to the relatively small error of 0.6 V in CBM.7 This will cause enhanced mixing of the solute states and the valence band of liquid water, leading to very high −IP levels of the solutes and therefore very high redox levels. HSE06 improves the computed VBM of liquid water by 1.3 V and places the CBM at the right position.7 This is also consistent with the observation from Fig. 6 that HSE06 significantly improves the −IP levels relative to those of BLYP by at least 0.48 V, while the differences in the –EA levels are much smaller. Therefore, the better description of the band structure of liquid water by hybrid HSE06 improves the accurate positioning of vertical and redox levels of the solutes.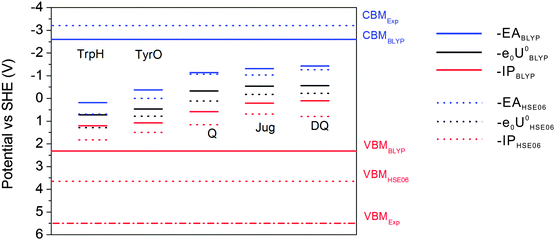 | ||
| Fig. 6 Energy level diagram calculated with HSE06 and BLYP. CBMHSE06 is overlapped with CBMExp. Solid lines: BLYP; Dashed lines: HSE06. | ||
As can be observed from the energetics in the gas phase (Table 3), the HSE06 results are consistently higher than the BLYP results by 0.2–0.4 eV. Note that the EA energy of DQ calculated by HSE06, 1.52 eV, agrees well with the experimental value of 1.60 eV.41 Similar underestimation by GGA has also been found in the comparison between BLYP and B3LYP in the previous publication.15 These results suggest that BLYP underestimates the attachment and detachment energies of these gas phase molecules compared to those of hybrid functionals. In water, the increases in the EA energies switching from BLYP to HSE06 are 0.16 eV and 0.38 eV for DQ and TyrO, respectively (see Table 2), close to the respective differences in vacuum (0.34 eV and 0.24 eV, respectively, from Table 3). In contrast, the increases in the IP differences are more obvious: from 0.42 eV and 0.28 eV in vacuum to 0.7 eV and 0.5 eV in water, respectively. The finding that the EA differences between BLYP and HSE06 in water and vacuum are close is consistent with the fact that the water VBM of BLYP and HSE06 differ by only 0.5 V. On the other hand, HSE06 significantly reduces the coupling of the HOMO of the solutes with valence band states of liquid water due to lowering of the water VBM by 1.3 eV compared to that using BLYP and therefore the IP differences between BLYP and HSE06 are more pronounced.16
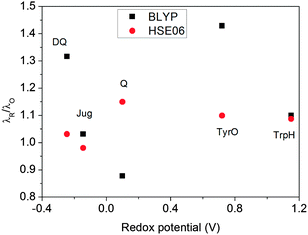
The ratios of λR/λO (Fig. 7) calculated by HSE06 are very close to 1.0 for all five redox couples, within a 15% deviation. This indicates that the solvent response to oxidation/reduction of these molecules predicted by HSE06 is rather linear, consistent with the Marcus theory of electron transfer.42 In contrast, the λR/λO ratios from BLYP are more scattered; Jug and TrpH deviate by 10%, while DQ and TyrO deviate by more than 30%. This asymmetry in the reorganization energies has been found previously to be much more pronounced for couples with very positive redox potentials such as OH−/OH˙ and Cl−/Cl˙; BLYP predicts λR/λO ratios to be close to 3, while HSE06 estimates are still about 1.4.8
4. Conclusion
This study shows that the FPMD based redox potential calculation method can accurately reproduce the redox potentials of a set of five aryl derivatives spanning from −0.25 V to 1.15 V at the level of hybrid HSE06, whereas BLYP results are too low. Including a fraction of exact exchange, HSE06 effectively improves the vertical energy levels of these organic solutes, which are underestimated by GGA functionals both in vacuum and in water. The test models in this study cover the redox potential range of NOMs (−0.3 to 0.15 V at pH = 7),22 and the computational settings used should be able to provide accurate estimates for NOMs. Considering also the previous successes in calculating transition metal cations,19 we are optimistic regarding application of this method to electron transfer reactions of transition metal–organic complexes. We hope our extensive test calculations demonstrate that equipped with hybrid functionals, the FPMD base method can be a powerful and reliable tool for investigating the redox chemistry in complex environments, including biological and geochemical systems.Acknowledgements
We acknowledge the National Science Foundation of China (No. 41222015, 41273074, 41572027 and 21373166), Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase), the Foundation for the Author of National Excellent Doctoral Dissertation of P. R. China (No. 201228), Newton International Fellowship Program and the financial support from the State Key Laboratory at Nanjing University. We are grateful to the High Performance Computing Center of Nanjing University for allowing us to use the IBM Blade cluster system.References
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2014, 16, 15068–15106 RSC.
- A. Warshel, P. K. Sharma, M. Kato and W. W. Parson, Biochim. Biophys. Acta, Proteins Proteomics, 2006, 1764, 1647–1676 CrossRef CAS PubMed.
- L.-P. Wang and T. Van Voorhis, J. Chem. Theory Comput., 2012, 8, 610–617 CrossRef CAS PubMed.
- D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, Cambridge, 2009 Search PubMed.
- F. Costanzo, M. Sulpizi, R. G. Della Valle and M. Sprik, J. Chem. Phys., 2011, 134, 244508 CrossRef PubMed.
- J. Cheng and M. Sprik, Phys. Chem. Chem. Phys., 2012, 14, 11245–11267 RSC.
- J. Cheng, X. Liu, J. VandeVondele, M. Sulpizi and M. Sprik, Acc. Chem. Res., 2014, 47, 3522–3529 CrossRef CAS PubMed.
- M. Sulpizi and M. Sprik, J. Phys.: Condens. Matter, 2010, 22, 284116 CrossRef PubMed.
- M. Sulpizi and M. Sprik, Phys. Chem. Chem. Phys., 2008, 10, 5238–5249 RSC.
- X. Liu, J. Cheng, M. Sprik and X. Lu, J. Phys. Chem. Lett., 2013, 4, 2926–2930 CrossRef CAS.
- X. Liu, J. Cheng, M. Sprik, X. Lu and R. Wang, Geochim. Cosmochim. Acta, 2013, 120, 487–495 CrossRef CAS.
- X. Liu, M. He, X. Lu and R. Wang, Chem. Geol., 2015, 411, 192–199 CrossRef CAS.
- M. Mangold, L. Rolland, F. Costanzo, M. Sprik, M. Sulpizi and J. Blumberger, J. Chem. Theory Comput., 2011, 7, 1951–1961 CrossRef CAS PubMed.
- J. Cheng, M. Sulpizi and M. Sprik, J. Chem. Phys., 2009, 131, 154504 CrossRef PubMed.
- C. Adriaanse, J. Cheng, V. Chau, M. Sulpizi, J. VandeVondele and M. Sprik, J. Phys. Chem. Lett., 2012, 3, 3411–3415 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- X. Liu, J. Cheng and M. Sprik, J. Phys. Chem. B, 2015, 119, 1152–1163 CrossRef CAS PubMed.
- J. Cheng and J. VandeVondele, Phys. Rev. Lett., 2016, 116, 086402 CrossRef PubMed.
- J. Stubbe and W. A. van der Donk, Chem. Rev., 1998, 98, 705–762 CrossRef CAS PubMed.
- J. T. Nurmi and P. G. Tratnyek, Environ. Sci. Technol., 2002, 36, 617–624 CrossRef CAS PubMed.
- M. Uchimiya and A. T. Stone, Chemosphere, 2009, 77, 451–458 CrossRef CAS PubMed.
- J. Blumberger, L. Bernasconi, I. Tavernelli, R. Vuilleumier and M. Sprik, J. Am. Chem. Soc., 2004, 126, 3928–3938 CrossRef CAS PubMed.
- J. Blumberger and M. Sprik, Theor. Chem. Acc., 2006, 115, 113–126 CrossRef CAS.
- J. Blumberger, I. Tavernelli, M. L. Klein and M. Sprik, J. Chem. Phys., 2006, 124, 64507 CrossRef PubMed.
- Y. Tateyama, J. Blumberger, M. Sprik and I. Tavernelli, J. Chem. Phys., 2005, 122, 234505 CrossRef PubMed.
- M. Sulpizi, S. Raugei, J. VandeVondele, P. Carloni and M. Sprik, J. Phys. Chem. B, 2007, 111, 3969–3976 CrossRef CAS PubMed.
- D. R. Lide, CRC handbook of chemistry and physics, CRC press, 2004 Search PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–487 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS.
- J. VandeVondele, F. Mohamed, M. Krack, J. Hutter, M. Sprik and M. Parrinello, J. Chem. Phys., 2005, 122, 014515 CrossRef PubMed.
- G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810–2821 CrossRef CAS.
- R. F. Anderson, Biochim. Biophys. Acta, Bioenerg., 1983, 722, 158–162 CrossRef CAS.
- T. Mukherjee, Radiat. Phys. Chem., 1987, 29, 455–462 CrossRef CAS.
- M. H. V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS PubMed.
- E. K. Fukuda and R. T. McIver Jr, J. Am. Chem. Soc., 1985, 107, 2291–2296 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
| This journal is © the Owner Societies 2016 |