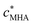Open Access Article
Open Access ArticleIntraparticulate speciation analysis of soft nanoparticulate metal complexes. The impact of electric condensation on the binding of Cd2+/Pb2+/Cu2+ by humic acids
Raewyn M.
Town
*a and
Herman P.
van Leeuwen
b
aDepartment of Physics, Chemistry and Pharmacy, University of Southern Denmark, Campusvej 55, 5230 Odense, Denmark. E-mail: raewyn.town@sdu.dk
bLaboratory of Physical Chemistry and Colloid Science, Wageningen University, Dreijenplein 6, 6703 HB Wageningen, The Netherlands
First published on 17th March 2016
Abstract
In aqueous dispersions of soft, charged nanoparticles, the physicochemical conditions prevailing within the particle body generally differ substantially from those in the bulk medium. Accordingly it is necessary to define intrinsic descriptors that appropriately reflect the chemical speciation inside the particle's microenvironment. Herein the speciation of divalent metal ions within the body of negatively charged soft nanoparticulate complexants is elaborated for the example case of humic acid association with Cd(II), Pb(II) and Cu(II). The electrostatic effects are described by a two-state model that accounts for counterion condensation in the intraparticulate double layer shell at the particle/medium interface and Donnan partitioning within the bulk of the particle body. Inner-sphere complex formation is defined by an intrinsic binding constant expressed in terms of local reactant concentrations as controlled by the pertinent electrostatic conditions. For the high particle charge density case (Debye length smaller than charged site separation), three distinct intraparticulate metal species are identified, namely free hydrated ions, electrostatically condensed ions, and inner-sphere metal–humic complexes. For all metal ions studied, the electrostatic contribution to the association of the metal ion with the oppositely charged particle is found to account for a substantial fraction of the total metal bound.
1 Introduction
Soft and permeable nanoparticles (NPs) are ubiquitous in environmental and biological systems where they play an important role in buffering concentrations of essential and toxic ions. A basic characteristic of an aqueous dispersion of such NPs is that the reactive sites are spatially confined to the particle body which is at an electric potential different from that in the bulk medium. Accordingly, the conditions prevailing within soft charged NPs, e.g. electric potential and ion concentrations, can differ strongly from those in the bulk medium. Furthermore, the rates of their reactions with oppositely charged ionic reactants can be orders of magnitude greater than those of the corresponding molecular counterparts.1,2 This property arises from the influence of the electrostatic field of the nanoparticle on (i) the local concentrations of ionic reactant species within the NP body, and (ii) the conductive acceleration of the diffusive rate of supply of ions with opposite charge sign. The magnitude of the nanoparticulate electric field also affects equilibrium binding properties, including the extent to which oppositely charged ions electrostatically associate with the NP entity as well as the distribution of the metal ion over its various species and over location within the particle body, i.e. their intraparticulate speciation. Equilibrium techniques for chemical speciation analysis, such as ion-selective electrode potentiometry, generally give a measure of the concentration of free M2+aq in the bulk medium; the remainder of the metal in the system is inferred to be associated with the complexant, i.e. “bound”. Conventional descriptors of metal complex formation, e.g. apparent stability constants![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app, are defined in terms of concentrations of chemical species that are averaged over the entire volume of the solution/dispersion, i.e. their smeared-out values. Evidently such parameters have limited meaning in the case of nanoparticulate complexants, where ‘bound’ metal stands for all physicochemical forms of M that are associated with the particle.
app, are defined in terms of concentrations of chemical species that are averaged over the entire volume of the solution/dispersion, i.e. their smeared-out values. Evidently such parameters have limited meaning in the case of nanoparticulate complexants, where ‘bound’ metal stands for all physicochemical forms of M that are associated with the particle.
Here we develop theoretical concepts to quantify intraparticulate speciation within charged soft nanoparticulate metal ion complexants and apply these to the binding of different types of divalent metal ions by the natural heterogeneous complexant, humic acid (HA). An aqueous HA “solution” actually is a dispersion of its natural NP entities with electrokinetic features that correspond to those of highly negatively charged NPs with the complexing sites distributed over the volume of the soft and permeable particle body.3 At a given metal/binding site ratio, the extent to which HA binds divalent cations, and the apparent stability of the pertaining complexes, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app, are generally dependent on the pH and ionic strength of the solution medium, which points to the involvement of both electrostatic and covalent contributions to the binding.4 The extent to which divalent cations associate with HA, as based on smeared-out equilibrium concentrations, generally follows the order Ca2+ < Cd2+ < Pb2+ ≈ Cu2+.4–6 Thus, on top of the electrostatic modes of association, there is an additional contribution to the binding for Cd(II), Pb(II) and Cu(II) due to the formation of covalent inner-sphere complexes. At the level of
app, are generally dependent on the pH and ionic strength of the solution medium, which points to the involvement of both electrostatic and covalent contributions to the binding.4 The extent to which divalent cations associate with HA, as based on smeared-out equilibrium concentrations, generally follows the order Ca2+ < Cd2+ < Pb2+ ≈ Cu2+.4–6 Thus, on top of the electrostatic modes of association, there is an additional contribution to the binding for Cd(II), Pb(II) and Cu(II) due to the formation of covalent inner-sphere complexes. At the level of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app values, the various equilibrium models for metal ion speciation, e.g. the NICA-Donnan7 and WHAM8 models, incorporate both electrostatic and covalent binding parameters for the M2+–HA interaction. Typically the electrostatic effects are modeled by assuming Donnan-type partitioning of any Mz+ into the HA body,8–14 with the relevant physicochemical parameters being the effective Donnan volume and the charge density of the HA particle.
app values, the various equilibrium models for metal ion speciation, e.g. the NICA-Donnan7 and WHAM8 models, incorporate both electrostatic and covalent binding parameters for the M2+–HA interaction. Typically the electrostatic effects are modeled by assuming Donnan-type partitioning of any Mz+ into the HA body,8–14 with the relevant physicochemical parameters being the effective Donnan volume and the charge density of the HA particle.
Recently, we have shown that Donnan-partitioning by itself is not sufficient to explain the extent to which Ca2+ associates with HA.15 For HA nanoparticles with a high structural charge density, ρp, and a radius rp well above the Debye screening length, κ−1, the bulk of the particle has zero net charge whilst the intraparticulate DL zone carries a strongly negative net charge in proportion to ρp.2 For the case of Ca2+, the net charge density in the intraparticulate part of the DL was shown to give rise to counterion condensation, analogous to that analysed by Manning for linear polyelectrolytes.16 The extent to which Ca2+ associates with a range of HA samples with different particle sizes at various ionic strengths, was well described by a simple two-state model that combines (i) purely electrostatic counterion condensation (CC) in the intraparticulate double layer (DL) at the particle/medium interface, and (ii) classical Donnan partitioning in the bulk of the HA particle.15 For the case with a 1-1 background electrolyte, the outcome is that divalent counterions may accumulate to quite high local concentrations in the DL zone. These findings are corroborated by e.g. the counterion condensation characteristics of polyelectrolytes such as DNA,17 and soft nanoparticles such as dendrimers,18–20 as well as the observation of strong counterion condensation in core–shell nanoparticles with a 3D structural charge in the shell.21
Since the associative reactions of Ca2+ with negatively charged ligands are dominated by electrostatics,22,23 the binding features of Ca2+ may be adopted as an approximate basis for discriminating between electrostatic and covalent contributions to binding of transition metal ions such as Cd2+, Pb2+, and Cu2+. The intraparticulate speciation then is more differentiated by the additional presence of inner-sphere complexes. In such cases, the application of a calcium salt as the background electrolyte is a useful means to eliminate the majority of the electrostatic contribution to the binding of the target M2+. In this paper we shall attempt to unravel the intraparticulate equilibrium metal speciation in terms of free hydrated ions, electrostatically condensed ions, and inner-sphere complexes, together with their spatial distribution within the particle body, for the case of a highly charged nanoparticulate complexant. The ensuing mode of interpretation will be applied to the humic acid complexes of Cd(II), Pb(II), and Cu(II). The type of HA selected features particles large enough to satisfy κrp > 1 for the ionic strengths investigated. This facilitates straightforward application of the two-state approach to particles with a Donnan type bulk core and a relatively thin double layer zone at the particle/medium interface.
2 Theory
2.1 Smeared-out vs. in situ stability constants
Conventional apparent stability constants,![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app, are expressed in terms of smeared-out concentrations and collectively include all factors that contribute to the overall stability of the association between a metal ion and a reactive site, S, i.e. both electrostatic and covalent chemical interactions. Since HA is a chemically heterogeneous complexant,4 the equilibrium relationship between the metal ion concentration and the various binding sites is described by a distributed affinity with the apparent stability constant
app, are expressed in terms of smeared-out concentrations and collectively include all factors that contribute to the overall stability of the association between a metal ion and a reactive site, S, i.e. both electrostatic and covalent chemical interactions. Since HA is a chemically heterogeneous complexant,4 the equilibrium relationship between the metal ion concentration and the various binding sites is described by a distributed affinity with the apparent stability constant ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app depending on the degree of occupation, θM, of the binding sites by M.4 Therefore, in comparing stabilities of metal–HA complexes it is usual practice to do so at a given θM value. Conventionally, θM is defined as the ratio of the concentrations of ‘bound metal’ and available reactive sites, where ‘bound metal’ denotes the total concentration of the metal ions that are somehow associated with the particle, via either electrostatic and/or covalent interactions where applicable. Analysis of the intraparticulate metal speciation enables θM to be defined in a more meaningful way as the ratio between the concentrations of inner-sphere metal complexes, MS, and reactive sites, i.e.
app depending on the degree of occupation, θM, of the binding sites by M.4 Therefore, in comparing stabilities of metal–HA complexes it is usual practice to do so at a given θM value. Conventionally, θM is defined as the ratio of the concentrations of ‘bound metal’ and available reactive sites, where ‘bound metal’ denotes the total concentration of the metal ions that are somehow associated with the particle, via either electrostatic and/or covalent interactions where applicable. Analysis of the intraparticulate metal speciation enables θM to be defined in a more meaningful way as the ratio between the concentrations of inner-sphere metal complexes, MS, and reactive sites, i.e. | (1) |
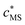 and
and 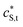 are the smeared-out counterparts. Under conditions of low coverage of binding sites by M2+, the total reactive site concentration is approximately equal to the concentration of free reactive sites, cS.
are the smeared-out counterparts. Under conditions of low coverage of binding sites by M2+, the total reactive site concentration is approximately equal to the concentration of free reactive sites, cS.
For simple molecular ligands, the conventional reported metal complex stability constants inherently include both electrostatic and covalent contributions to the binding. The overall metal ion complexation reaction often follows the Eigen mechanism, which involves formation of an outer-sphere ion pair M2+aq•S, between the metal ion M2+aq with an intact primary hydration shell and the reactive site S, followed by dehydration and formation of an inner-sphere complex MS.24 For simple ligands, the magnitude of the electrostatic attraction between a negatively charged reactive site and a positively charged metal ion is described by the outer-sphere stability constant, Kos, which is straightforwardly computed on the basis of Fuoss–Boltzmann electrostatics:25,26
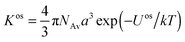 | (2) |
 | (3) |
The intrinsic stability constant, Kint, represents the inherent chemical affinity between a metal ion and a reactive site, after correction for the long-range electrostatics beyond those on the scale of atom–atom interactions. The intrinsic stability constant format is not often used for complexes with simple ligands, but for our present purposes of comparison with the high charge density NP complexant case, we may define Kint as:
| Kint = K/fos | (4) |
| f os = exp(−Uos/kT) | (5) |
Intrinsic stability constants have been used to describe metal ion complexation by soft charged nanoparticulate complexants, e.g. carboxymethyldextran28 and humic acids.7,8,29 For such complexants, the local physicochemical conditions prevailing within the particle body (pH, reactive site concentration, electrolyte ion concentrations and effective charge screening) can be very different from those in the surrounding aqueous medium. Eigen-type complex formation mechanisms have been elaborated for the nanoparticulate case, with rate constants for outer-sphere and inner-sphere complexation defined in terms of the conditions within the particle body.30 Accordingly, for soft charged NPs, it is more meaningful to define the intrinsic stability constant in terms of intraparticulate (in situ) conditions and reactant concentrations. This necessitates a detailed account for the electrostatic binding effects, as detailed below.
2.2 Electrostatic features of HA
Unless otherwise stated, we shall consider the case where a highly charged soft NP is equilibrated in an aqueous non-complexing background electrolyte, with a concentration well in excess over the smeared-out concentration of charged sites. In turn, the latter is in large excess over the target divalent cation, M2+, i.e. we consider the case of low coverage of binding sites by M2+. | (6) |
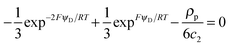 | (7) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) C, is small enough to satisfy the condition κ
C, is small enough to satisfy the condition κ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) C ≪ 1 (“high charge density” regime). The magnitude of ψD influences the equilibrium partitioning of any type of ion i, with valency zi, between the soft particle phase (with concentration ci,D) and the electrolyte solution (with concentration
C ≪ 1 (“high charge density” regime). The magnitude of ψD influences the equilibrium partitioning of any type of ion i, with valency zi, between the soft particle phase (with concentration ci,D) and the electrolyte solution (with concentration 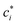 ) according to a Boltzmann factor,
) according to a Boltzmann factor, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B:32
B:32 | (8) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B for 1+ ions is 70 whilst that for 2+ ions is ca. 5 × 103, whereas in the 2-1 electrolyte the
B for 1+ ions is 70 whilst that for 2+ ions is ca. 5 × 103, whereas in the 2-1 electrolyte the ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B values are 10 and 105, respectively (eqn (7)). In the present work, the electrolyte concentration (at ionic strengths of either 10 or 100 mol m−3) is in great excess over that of the target M2+ ions (on the order of 10−3 mol m−3). Thus, in e.g. 10 mol m−3 1-1 electrolyte the local concentration of 1+ ions in the Donnan bulk is 700 mol m−3 whilst that of the 2+ ions is ca. 0.5 mol m−3. In spite of its much larger
B values are 10 and 105, respectively (eqn (7)). In the present work, the electrolyte concentration (at ionic strengths of either 10 or 100 mol m−3) is in great excess over that of the target M2+ ions (on the order of 10−3 mol m−3). Thus, in e.g. 10 mol m−3 1-1 electrolyte the local concentration of 1+ ions in the Donnan bulk is 700 mol m−3 whilst that of the 2+ ions is ca. 0.5 mol m−3. In spite of its much larger ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B, the local concentration of M2+ in this example is still insignificant compared to the 1+ ions in their neutralizing practically all of the structural charge of the particle body.
B, the local concentration of M2+ in this example is still insignificant compared to the 1+ ions in their neutralizing practically all of the structural charge of the particle body.
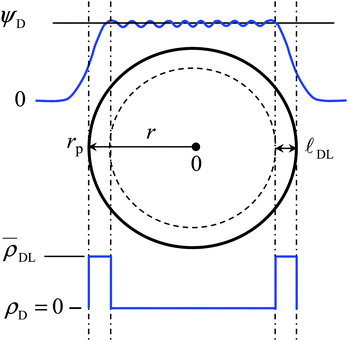
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL (and volume VDL).15 The model divides the volume of an individual particle, with radius rp and the center of the particle at r = 0, into two zones (Fig. 1) comprising:
DL (and volume VDL).15 The model divides the volume of an individual particle, with radius rp and the center of the particle at r = 0, into two zones (Fig. 1) comprising:
(i) an intraparticulate condensation shell, with thickness ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL, over which the complete intraparticulate double layer charge is evenly distributed (ρ =
DL, over which the complete intraparticulate double layer charge is evenly distributed (ρ = ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) DL), so that charge density driven counterion condensation may be invoked. The magnitude of
DL), so that charge density driven counterion condensation may be invoked. The magnitude of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL is related to the intraparticulate Debye length, κ−1p, for which values have been estimated by Duval.33 Within the model, the potential ψDL in the condensation zone has a linear profile as arising from the averaged net charge density,
DL is related to the intraparticulate Debye length, κ−1p, for which values have been estimated by Duval.33 Within the model, the potential ψDL in the condensation zone has a linear profile as arising from the averaged net charge density, ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) DL.
DL.
(ii) the remaining interior volume of the soft nanoparticle, with volume VD, carries no net charge and is considered to behave as a true Donnan phase with a constant potential, ψD, throughout.
Accordingly, the two-state approximation is formulated by the set of conditions for the condensation volume, eqn (9), and the Donnan volume, eqn (10):
(rp − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL) < r < rp: ρ = DL) < r < rp: ρ = ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) DL DL | (9) |
0 < r < (rp − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL): ρ = 0 and ψ = ψD DL): ρ = 0 and ψ = ψD | (10) |
2.3 Intraparticulate metal species
The reactive sites and inner-sphere complexes are physically present only within the nanoparticle body: their in situ concentrations, cS and cMS, respectively, are high, but their ratio is the same as that of the smeared-out concentrations,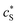 and
and 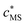 . The free metal ion exists both in the bulk aqueous medium and within the particle body, but its equilibrium concentration will be very different in the two domains. For a nanoparticulate complexant the intrinsic stability constant of the inner-sphere complex MS,
. The free metal ion exists both in the bulk aqueous medium and within the particle body, but its equilibrium concentration will be very different in the two domains. For a nanoparticulate complexant the intrinsic stability constant of the inner-sphere complex MS, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int, is defined as:
int, is defined as: | (11) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int signifies that, for the present case of a chemically heterogeneous complexant, the intrinsic stability represents a weighted average of all the inner-sphere complexes that are formed at the applicable θM. The computation of
int signifies that, for the present case of a chemically heterogeneous complexant, the intrinsic stability represents a weighted average of all the inner-sphere complexes that are formed at the applicable θM. The computation of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int uses the average intraparticulate concentrations of free Maq2+ and S, which in the high charge density regime (with κprp ≫ 1) are practically equal to the concentrations in VD; in VDL, that is near the interface with the aqueous medium, the concentration of hydrophilic sites may be somewhat higher and the free metal ion concentration will be lower due to the lower
int uses the average intraparticulate concentrations of free Maq2+ and S, which in the high charge density regime (with κprp ≫ 1) are practically equal to the concentrations in VD; in VDL, that is near the interface with the aqueous medium, the concentration of hydrophilic sites may be somewhat higher and the free metal ion concentration will be lower due to the lower ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B,M. The ensuing metal ion speciation scheme for high charge density soft NP complexants is given in Table 1.
B,M. The ensuing metal ion speciation scheme for high charge density soft NP complexants is given in Table 1.
| M(II) species | Bulk aqueous medium | Intraparticulate double layer | Donnan volume | Governing physicochemical features |
|---|---|---|---|---|
a The concentrations are denoted by: superscript * for smeared-out bulk solution concentration; superscript D or DL for local intraparticulate concentrations in the pertaining part of the particle volume; no superscript for the average intraparticulate concentration. The condensation limit for 2+ counterions in the DL with ρ = ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) DL is denoted by DL is denoted by ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) C.
b In the high charge density regime, with κprp ≫ 1, counterion condensation is confined to the intraparticulate double layer shell.
c See eqn (11). C.
b In the high charge density regime, with κprp ≫ 1, counterion condensation is confined to the intraparticulate double layer shell.
c See eqn (11).
|
||||
| Free M |

|

|

|
Donnan |
| Condensed M |
c
DLM,cond = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) CcDLS CcDLS |
0b | Counterion condensation | |
| Inner-sphere MSc |
c
MS = ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) intcScM,f intcScM,f |
Covalent binding | ||
| Total particle-associated M |
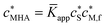
|
|||
3 Experimental
3.1 Properties of HA
The soil HA sample was from Aldrich and the particles have an approximately constant particle radius, rp, of ca. 80 nm over the pH range 5 to 8 and ionic strength range 0 to 400 mol m−3 KCl.34,35 In general, experimental estimates of the particle size of various types of HA by dynamic light scattering, capillary electrophoresis, and fluorescence correlation spectroscopy do not provide any evidence for significant changes in the particle size as a function of ionic strength in the range 0 to 200 mM.35–37 The chosen Aldrich HA entities conform to κprp ≫ 1, which facilitates straightforward application of the CC-Donnan approach (see Section 2). It is considered unlikely that the present HA entities, with rp of 80 nm, are composed of conglomerates of smaller entities, each with its own independent DL. The point is that such a situation should feature extensive aggregation/disaggregation upon changing pH and ionic strength, in contrast to experimental observation.34 The total carboxyl group content of this HA is ca. 3 mol per kg of HA.38,39 The effective charge density within the particle is ca. −700 mol e m−3 in an electrolyte medium at pH 6, corresponding to ca. 9 × 105 COO− per particle. Within the particle body the pH will be at least 1 unit below that in the bulk medium, and thus carboxylate groups will be the major structural charge carriers and reactive sites under our experimental conditions. By estimating the outer-sphere radius to be 0.6 nm,26 and taking into account that the COO− is attached to the HA structure, the outer-sphere volume/particle volume ratio nSVos/Vp comes to ca. 0.5. That is, approximately half of the intraparticulate free M2+aq is occupying an outer-sphere ion pair position, implying that each individual intraparticulate M2+aq spends about half of its time as an ion pair with COO−.3.2 Reagents and solution conditions
Solutions were buffered to pH 6 with 1 mol m−3 MES buffer (2-(N-morpholino)-ethanesulfonic acid) prepared from the solid (Fluka, MicroSelect, ≥99.5%): MES buffer has a low affinity for Cd(II), Pb(II) and Cu(II).40,41 Ionic strength was maintained at 10 mol m−3 or 100 mol m−3 with KNO3 or Ca(NO3)2 (BDH, AnalaR). M(II) solutions were prepared by dilution of standards: Cd(II) and Cu(II) standards were from Aldrich; Pb(II) standard was from Metrohm. In all experiments in this work, the concentration of HA in the dispersion was ca. 50 g m−3, corresponding to a volume fraction on the order of 10−4 (determined using the dry HA density of 1.66 kg m−3 and an 80% water content). The total concentration of M(II),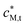 , was 4.6 × 10−3 mol m−3 so that there is a ca. 20 fold excess of binding sites over total metal in the dispersion. All solutions were prepared in ultrapure deionized water (resistivity >18 MΩ cm) from a Milli-Q gradient system.
, was 4.6 × 10−3 mol m−3 so that there is a ca. 20 fold excess of binding sites over total metal in the dispersion. All solutions were prepared in ultrapure deionized water (resistivity >18 MΩ cm) from a Milli-Q gradient system.
3.3 Electrochemical measurements
Stripping chronopotentiometry at scanned deposition potential (SSCP)42 and Absence of Gradients and Nernstian Equilibrium Stripping (AGNES)43 were used to determine the concentration of free M2+aq in the bulk medium, , and thus the total concentration of M associated with the HA particles,
, and thus the total concentration of M associated with the HA particles, 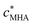 . Electrochemical measurements were performed with an Ecochemie μAutolab potentiostat coupled with a Metrohm 663 VA stand. The oxidation step was performed under complete depletion conditions (stripping current = 2 nA).44 The electrometer input impedance of these instruments is >100 GΩ. The working electrode was a Metrohm multimode mercury drop electrode, the auxiliary electrode was glassy carbon, and the reference electrode was Ag|AgCl|KCl(sat) encased in a 100 mol m−3 KNO3 jacket. Solutions were initially purged with oxygen-free N2, then a nitrogen blanket was maintained during measurements.
. Electrochemical measurements were performed with an Ecochemie μAutolab potentiostat coupled with a Metrohm 663 VA stand. The oxidation step was performed under complete depletion conditions (stripping current = 2 nA).44 The electrometer input impedance of these instruments is >100 GΩ. The working electrode was a Metrohm multimode mercury drop electrode, the auxiliary electrode was glassy carbon, and the reference electrode was Ag|AgCl|KCl(sat) encased in a 100 mol m−3 KNO3 jacket. Solutions were initially purged with oxygen-free N2, then a nitrogen blanket was maintained during measurements.
3.4 Intraparticulate speciation analysis
For CC-Donnan computations, the volume fraction of HA in the dispersion was used to convert smeared-out concentrations into local ones. The intraparticulate speciation (see Table 1) is computed by satisfying the electrostatic demands (counterion condensation and Donnan partitioning) and ascribing the remaining M to inner-sphere complexes. The electrostatic binding includes the accumulation of M2+ according to the pertaining![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) B for Donnan partitioning in VD (eqn (8)) and Boltzmann accumulation in the VDL, and the condensation of M2+ to compensate for some prescribed fraction of the charge in the DL. For the present experimental conditions, this fraction was shown to be about 80% of the available 700 mol m−3, corresponding to a local M2+ concentration of 280 mol m−3 (the contribution from monovalent cations is negligible45); see Results and Discussion below for details on this value of the condensation fraction for 2+ counterions. The presence of MS in the DL reduces the net charge therein, and thus the condensation demand is correspondingly decreased. Accordingly, the initial intraparticulate metal speciation is iterated with respect to the concentrations of inner-sphere complexes versus condensed metal ions in the DL zone until a consistent intraparticulate distribution over the Donnan bulk and DL zone is attained. Consistent values for cMS and cDLM,cond were attained after ca. 4 iterations in all cases.
B for Donnan partitioning in VD (eqn (8)) and Boltzmann accumulation in the VDL, and the condensation of M2+ to compensate for some prescribed fraction of the charge in the DL. For the present experimental conditions, this fraction was shown to be about 80% of the available 700 mol m−3, corresponding to a local M2+ concentration of 280 mol m−3 (the contribution from monovalent cations is negligible45); see Results and Discussion below for details on this value of the condensation fraction for 2+ counterions. The presence of MS in the DL reduces the net charge therein, and thus the condensation demand is correspondingly decreased. Accordingly, the initial intraparticulate metal speciation is iterated with respect to the concentrations of inner-sphere complexes versus condensed metal ions in the DL zone until a consistent intraparticulate distribution over the Donnan bulk and DL zone is attained. Consistent values for cMS and cDLM,cond were attained after ca. 4 iterations in all cases.
4 Results and discussion
4.1 Electrostatic contribution to the binding
The association of Ca2+ with HA is dominated by electrostatic binding.22,23 This feature provides us with a useful tool in the analysis of the HA complexes of transition metal ions that generally do involve covalent chemical bonds in addition to the electrostatic binding similar to that for Ca2+. Foremost, the analysis of data on the extent of association of Ca2+ with several HA samples under a range of pH and ionic strength conditions enables us to establish the magnitudes of the electrostatic parameters for the CC-Donnan model, i.e. the thickness of the DL shell,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL, and the extent of condensation in the DL zone,
DL, and the extent of condensation in the DL zone, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) C. Furthermore, the use of data for Cd/Pb/Cu with a calcium salt as the background electrolyte allows for the elimination of a great deal, if not all, of the electrostatic contribution to the binding of the target M2+: this strategy provides a means to test the consistency of our approach for the determination of
C. Furthermore, the use of data for Cd/Pb/Cu with a calcium salt as the background electrolyte allows for the elimination of a great deal, if not all, of the electrostatic contribution to the binding of the target M2+: this strategy provides a means to test the consistency of our approach for the determination of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int. These issues are elaborated in the following sections.
int. These issues are elaborated in the following sections.
For the given experimental conditions in the present work, the HA entities carry a charge density of approximately −7 × 107 C m−3, i.e. 0.7 mol e per dm3. For the chosen ionic strengths of 10 and 100 mol m−3, the HA charge density gives rise to Donnan potentials ψD of ca. −100 mV and −50 mV, respectively in 1-1 electrolyte (eqn (6)). The ensuing Boltzmann factors for equilibrium partitioning of the free metal ion between the bulk medium and the intraparticulate zones were computed using eqn (8). For the conditions considered herein, the amount of free M2+aq accumulated in the intraparticulate DL is an insignificant proportion of the total intraparticulate M, thus for present purposes it is sufficient to estimate the extent of Boltzmann accumulation in this zone by taking the potential at the particle/medium interface to be ca. 2/3 of the Donnan potentials.46,47 Conductivity data have shown that divalent ions such as Ca2+ and Ba2+ exhibit condensation behavior.48 In line with that, the two-state CC-Donnan model for electrostatic ion binding was applied to ion-selective electrode measurements of Ca2+ binding by a forest soil HA at pH 6 in 1-1 electrolyte at I = 10 and 100 mol m−3 (rpca. 30 nm),49 and Aldrich HA at pH 8, I = 80 mol m−3.50 An ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL of ca. 2 nm with 20% uncompensated charge remaining in the DL, together with Boltzmann accumulation in the intraparticulate DL and Donnan partitioning in the remainder of the particle body, provided a good description of the binding data at both ionic strengths and pH values. More specifically, an uncompensated charge of −140 mol e m−3 (20% of the structural charge) within a DL thickness,
DL of ca. 2 nm with 20% uncompensated charge remaining in the DL, together with Boltzmann accumulation in the intraparticulate DL and Donnan partitioning in the remainder of the particle body, provided a good description of the binding data at both ionic strengths and pH values. More specifically, an uncompensated charge of −140 mol e m−3 (20% of the structural charge) within a DL thickness, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL, of 2 nm in a particle of radius 80 nm corresponds to a surface charge, σs of −0.025 C m−2. The corresponding potential drop over the intraparticulate DL (=σs
DL, of 2 nm in a particle of radius 80 nm corresponds to a surface charge, σs of −0.025 C m−2. The corresponding potential drop over the intraparticulate DL (=σs![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) DL/εε0) of ca. −70 mV is of the correct order of magnitude, certainly if it is taken into account that the density of deprotonated carboxyl groups is highest in the more hydrophilic outer regions of the HA particle body.51 That is, the CC-Donnan approach describes the Ca2+–HA association purely in terms of an electrostatic partition equilibrium and provides a consistent description of Ca2+–HA association for various HA samples under different conditions of pH and ionic strength.15 The above parameters established for Ca2+ binding were then applied as input parameters to define the electrostatic contribution to the binding of Cd2+, Pb2+, and Cu2+.
DL/εε0) of ca. −70 mV is of the correct order of magnitude, certainly if it is taken into account that the density of deprotonated carboxyl groups is highest in the more hydrophilic outer regions of the HA particle body.51 That is, the CC-Donnan approach describes the Ca2+–HA association purely in terms of an electrostatic partition equilibrium and provides a consistent description of Ca2+–HA association for various HA samples under different conditions of pH and ionic strength.15 The above parameters established for Ca2+ binding were then applied as input parameters to define the electrostatic contribution to the binding of Cd2+, Pb2+, and Cu2+.
4.2 Smeared-out metal complexation parameters
Until now, metal ion binding by nanoparticulate complexants such as HA has been interpreted in terms of so-called smeared-out parameters. That is, the apparent stability constant,![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app, is defined in terms of the concentration of free metal ions in the bulk medium, together with the total smeared-out concentration of all forms of M that are associated with the particle, and the smeared-out reactive site concentration. At the level of the bulk solution parameters, clear differences are observed between the complexation behavior of various metal ions. E.g. for a given solution composition, the free metal ion concentration in the bulk medium follows the order Cd(II) > Pb(II) ≈ Cu(II). Also, the features of the SSCP waves (characteristic potential, shape, limiting signal) for the mentioned metal ions are modified to different extents in the presence of HA, indicating differences in the stability and lability of their HA complexes. Reported
app, is defined in terms of the concentration of free metal ions in the bulk medium, together with the total smeared-out concentration of all forms of M that are associated with the particle, and the smeared-out reactive site concentration. At the level of the bulk solution parameters, clear differences are observed between the complexation behavior of various metal ions. E.g. for a given solution composition, the free metal ion concentration in the bulk medium follows the order Cd(II) > Pb(II) ≈ Cu(II). Also, the features of the SSCP waves (characteristic potential, shape, limiting signal) for the mentioned metal ions are modified to different extents in the presence of HA, indicating differences in the stability and lability of their HA complexes. Reported ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app values typically follow the order Cd(II) < Pb(II) ≈ Cu(II), with values obtained at I = 10 mol m−3 being greater than those at 100 mol m−3.52,53 For Cd(II) binding with Aldrich HA at pH 6 at I = 100 mol m−3,
app values typically follow the order Cd(II) < Pb(II) ≈ Cu(II), with values obtained at I = 10 mol m−3 being greater than those at 100 mol m−3.52,53 For Cd(II) binding with Aldrich HA at pH 6 at I = 100 mol m−3, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app = ca. 20 m3 mol−1,54 and at I = 10 mol m−3,
app = ca. 20 m3 mol−1,54 and at I = 10 mol m−3, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app = ca. 100 m3 mol−1.55 The
app = ca. 100 m3 mol−1.55 The ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app values for Cu(II) and Pb(II) binding to various HA at pH 6, with a ca. 20-fold excess concentration of reactive sites over total metal ions, typically are in the range of 103 to 104 m3 mol−1.38,56–58 It should be noted, though, that the increase in
app values for Cu(II) and Pb(II) binding to various HA at pH 6, with a ca. 20-fold excess concentration of reactive sites over total metal ions, typically are in the range of 103 to 104 m3 mol−1.38,56–58 It should be noted, though, that the increase in ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app is not due to a corresponding increase in binding strength, but rather reflects the increase in intraparticulate free M with decreasing ionic strength. This is illustrated in Table 2 by the greater fraction of free M in VD at I = 10 mol m−3. Obviously, a more rigorous description of inner sphere M–HA complex formation requires knowledge of the speciation inside the HA particle entity.
app is not due to a corresponding increase in binding strength, but rather reflects the increase in intraparticulate free M with decreasing ionic strength. This is illustrated in Table 2 by the greater fraction of free M in VD at I = 10 mol m−3. Obviously, a more rigorous description of inner sphere M–HA complex formation requires knowledge of the speciation inside the HA particle entity.
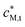 = 4.6 × 10−3 mol m−3;
= 4.6 × 10−3 mol m−3;  = 50 g m−3; pH = 6 in bulk electrolyte medium
= 50 g m−3; pH = 6 in bulk electrolyte medium
4.3 Intraparticulate speciation and intrinsic stability constants
The parameters defining the speciation scheme are given in Table 1. The CC-Donnan approach distinguishes between three types of intraparticulate metal species, namely free hydrated ions, electrostatically condensed ions, and inner-sphere complexes. Table 2 collates the concentrations of the various metal species and the intraparticulate![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values as derived from local concentrations after accounting for the electrostatic effects. The data show that at the given θM, the free hydrated metal ions generally are a minor proportion of the total intraparticulate M. The results for Cd(II) at I = 100 mol m−3 KNO3 show that 70% of the uncomplexed M is condensed in the intraparticulate double layer and 30% is inner-sphere bound, whilst Pb(II) and Cu(II) are approximately equally distributed between these two forms. However, the free M2+aq concentrations differ by orders of magnitude, and so does the ensuing intrinsic stability of the inner-sphere complexes,
int values as derived from local concentrations after accounting for the electrostatic effects. The data show that at the given θM, the free hydrated metal ions generally are a minor proportion of the total intraparticulate M. The results for Cd(II) at I = 100 mol m−3 KNO3 show that 70% of the uncomplexed M is condensed in the intraparticulate double layer and 30% is inner-sphere bound, whilst Pb(II) and Cu(II) are approximately equally distributed between these two forms. However, the free M2+aq concentrations differ by orders of magnitude, and so does the ensuing intrinsic stability of the inner-sphere complexes, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int. Notably, in contrast to the trend in
int. Notably, in contrast to the trend in ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) app, the
app, the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values are lower at lower ionic strength, even though the total intraparticulate metal concentrations are the same or greater for all metal ions. This phenomenon might be related to several differences in the intraparticulate environment, including a higher free metal ion concentration at lower ionic strength, a lower free energy difference between the free M2+aq and the inner-sphere complex MS at the more negative ψD, as well as differences in the effective charge screening.
int values are lower at lower ionic strength, even though the total intraparticulate metal concentrations are the same or greater for all metal ions. This phenomenon might be related to several differences in the intraparticulate environment, including a higher free metal ion concentration at lower ionic strength, a lower free energy difference between the free M2+aq and the inner-sphere complex MS at the more negative ψD, as well as differences in the effective charge screening.
The above observations highlight the significant role of electrostatic contributions in the binding of diverse metal ions by HA. For the purely electrostatic Ca2+ case, the condensed fraction represents the dominant intraparticulate species: ca. 90% of the particle-bound Ca2+ is condensed in the DL.15Table 2 shows that for Cd(II), Pb(II), and Cu(II) in KNO3 electrolyte the amounts of ions that are condensed in the DL are still a major proportion of the total, ranging from 50 to 70%. This largely explains the similarity observed in the total local concentrations for different types of metal ions with different inner sphere complexation strengths. We highlight that for the present high charge density case, there is significant profiling in the concentration of M within the particle: the condensed ions are located within a small proportion of the total particle volume (φDL = 0.07). The fraction of condensed ions corresponds to a local concentration on the order of 250 mol m−3 M2+aq,cond within the DL shell, i.e. a few % of the DL volume.59 This observation is in line with counterion condensation characteristics of polyelectrolytes such as DNA, for which divalent counterions may reach local concentrations on the order of 300 mol m−3 within a cylindrical condensation shell of thickness ca. 2 nm.17
If the electrostatic contribution to metal ion complexation by HA is properly taken into account, then the CC-Donnan derived ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values given in Table 2 will correspond to the truly intrinsic stability constant for the pertaining inner-sphere complex at the given intraparticulate conditions. As long as the ionic strength in the medium is well below the structural charge density inside the nanoparticle body,
int values given in Table 2 will correspond to the truly intrinsic stability constant for the pertaining inner-sphere complex at the given intraparticulate conditions. As long as the ionic strength in the medium is well below the structural charge density inside the nanoparticle body, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int is expected to be approximately constant for given conditions of θM, pH and I since the effective intraparticulate ionic strength is bound to be governed by the particle's charge density. To further explore the consistency of the CC-Donnan approach in its accounting for electrostatic contributions to the binding, experiments on Cd(II)/Pb(II)/Cu(II) HA complexes were performed in Ca(NO3)2 background electrolyte at the same ionic strengths as used for the measurements in KNO3 electrolyte. The concentration of Ca2+ then is a factor of several thousand times greater than that of the target M2+. Under these conditions it may be assumed that the purely electrostatic counterion condensation requirements of the HA entity are met by Ca2+ and thus the intraparticulate speciation of M2+ would comprise only Donnan-type partitioning in VD, Boltzmann accumulation in VDL and inner-sphere complexation in both VD and VDL. The results given in Table 2 indeed show that the
int is expected to be approximately constant for given conditions of θM, pH and I since the effective intraparticulate ionic strength is bound to be governed by the particle's charge density. To further explore the consistency of the CC-Donnan approach in its accounting for electrostatic contributions to the binding, experiments on Cd(II)/Pb(II)/Cu(II) HA complexes were performed in Ca(NO3)2 background electrolyte at the same ionic strengths as used for the measurements in KNO3 electrolyte. The concentration of Ca2+ then is a factor of several thousand times greater than that of the target M2+. Under these conditions it may be assumed that the purely electrostatic counterion condensation requirements of the HA entity are met by Ca2+ and thus the intraparticulate speciation of M2+ would comprise only Donnan-type partitioning in VD, Boltzmann accumulation in VDL and inner-sphere complexation in both VD and VDL. The results given in Table 2 indeed show that the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int values derived from measurements in Ca(NO3)2 are broadly comparable to those for measurements in KNO3. The remaining differences in
int values derived from measurements in Ca(NO3)2 are broadly comparable to those for measurements in KNO3. The remaining differences in ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int between the two media should be ascribed to side effects from the differences in the pertaining Donnan potentials, the ensuing differences in pH, the resulting small differences in θM, and in the effective local charge screening. Note for example that the differences in θM between the KNO3 and Ca(NO3)2 media are greater at the lower ionic strength due to the greater change in the electrostatic contribution to the binding (Table 2).
int between the two media should be ascribed to side effects from the differences in the pertaining Donnan potentials, the ensuing differences in pH, the resulting small differences in θM, and in the effective local charge screening. Note for example that the differences in θM between the KNO3 and Ca(NO3)2 media are greater at the lower ionic strength due to the greater change in the electrostatic contribution to the binding (Table 2).
5 Conclusions and outlook
The scheme developed herein for intraparticulate speciation is a rigorous and dedicated breakdown of the data into the properties of soft nanoparticulate multi-site metal ion complexants, tailored to their size and charge density. It establishes an operational basis for differentiating between electrostatic and covalent contributions to metal ion binding. The conceptual framework divides the particle body into the negatively charged intraparticulate double layer zone (volume VDL) that allows for counterion condensation to an extent dictated by the particle's structural charge density, and a uncharged bulk Donnan phase (volume VD). Three different physicochemical forms of M are identified, namely (i) free M2+aq, distributed within VD and VDL according to the electrostatic potential in each spatial zone, (ii) electrostatically condensed M2+aq within the DL, and (iii) inner-sphere MS, randomly distributed throughout the entire particle volume. The eventual intraparticulate speciation is a consequence of the interplay between the electrostatic and chemical binding options for M2+ at the given local densities of total charges and reactive sites. As long as the system is not at equilibrium, the timescale over which the electrostatic relaxation processes (both Donnan partitioning and counterion condensation) take place relative to that for the chemical reactions must be taken into account.60 Although the various ion redistribution processes may be limiting the rate of complex formation for Cd(II), Pb(II) and Cu(II), they do not affect the eventual equilibrium situation treated herein.Along with the analysis of in situ metal speciation for complexant particles with high structural charge density, we present an approach for the computation of intrinsic complex stability constants, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int. These are essentially free from long-range electrostatic contributions to the binding, i.e. they reflect the inherent strength of inner-sphere complexes in the local intraparticulate medium.
int. These are essentially free from long-range electrostatic contributions to the binding, i.e. they reflect the inherent strength of inner-sphere complexes in the local intraparticulate medium. ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int is expressed in terms of the concentrations that prevail within the soft nanoparticle body and thus facilitates insights into fundamental features of HAs. The distinction between
int is expressed in terms of the concentrations that prevail within the soft nanoparticle body and thus facilitates insights into fundamental features of HAs. The distinction between ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) int and smeared-out apparent complexation constants7–14 encompasses more than the Boltzmann correction of the free metal ion concentration and/or a volume fraction conversion. As confirmed by our comparison of experimental affinity data for transition metal ions in KNO3 and in Ca(NO3)2 background electrolyte, condensation of the target ion M2+ in the charged DL zone plays a major role if the HA particle charge density is high. The present analysis of the ensuing intraparticulate metal speciation might lead the way to more rigorous understanding of the chemical heterogeneity of particulate HA complexes, based on intrinsic stability constants and degrees of coverage representing the true ratios between inner-sphere bound metal and reactive site concentrations. Extension of the experimental work to a broad range of θM values will be crucial in that respect.
int and smeared-out apparent complexation constants7–14 encompasses more than the Boltzmann correction of the free metal ion concentration and/or a volume fraction conversion. As confirmed by our comparison of experimental affinity data for transition metal ions in KNO3 and in Ca(NO3)2 background electrolyte, condensation of the target ion M2+ in the charged DL zone plays a major role if the HA particle charge density is high. The present analysis of the ensuing intraparticulate metal speciation might lead the way to more rigorous understanding of the chemical heterogeneity of particulate HA complexes, based on intrinsic stability constants and degrees of coverage representing the true ratios between inner-sphere bound metal and reactive site concentrations. Extension of the experimental work to a broad range of θM values will be crucial in that respect.
The present study has considered the high charge density regime and particle sizes well above the Debye length. Extension of the CC-Donnan approach to lower charge densities and/or κrp around or below unity is underway and may unearth more fundamental issues pertinent for both equilibrium speciation modeling and dynamic aspects of M–HA complexes. Such developments necessarily call for a quantitative description of 3D condensation phenomena, as well as rigorous definition of the intraparticulate double layer thickness. Furthermore, fundamental knowledge of intraparticulate speciation is also a prerequisite for comprehensive interpretation of the chemodynamic features of M–HA systems, involving consideration of the various intraparticulate and extraparticulate diffusive and kinetic fluxes of metal species. The chemodynamics are relevant for the applicability of analytical techniques such as voltammetries including various stripping techniques,61 as well as for reactivity and bioavailability features.62–64
Symbols and abbreviations
References
- H. P. van Leeuwen, J. Buffle, J. F. L. Duval and R. M. Town, Langmuir, 2013, 29, 10297–10302 CrossRef CAS PubMed.
- H. P. van Leeuwen and J. Buffle, Environ. Sci. Technol., 2009, 43, 7175–7183 CrossRef CAS PubMed.
- J. F. L. Duval, K. J. Wilkinson, H. P. van Leeuwen and J. Buffle, Environ. Sci. Technol., 2005, 39, 6435–6445 CrossRef CAS PubMed.
- J. Buffle, Complexation Reactions in Aquatic Systems: An Analytical Approach, Ellis Horwood, Chichester, UK, 1988 Search PubMed.
- B. Manunza, S. Deiana, V. Maddau, C. Gessa and R. Seeber, Soil Sci. Soc. Am. J., 1995, 59, 1570–1574 CrossRef CAS.
- R. D. Guy and C. L. Chakrabarti, Can. J. Chem., 1976, 54, 2600–2611 CrossRef CAS.
- L. K. Koopal, T. Saito, J. P. Pinheiro and W. H. van Riemsdijk, Colloids Surf., A, 2005, 265, 40–54 CrossRef CAS.
- E. Tipping, Aquat. Geochem., 1998, 4, 3–48 CrossRef CAS.
- P. Warwick, A. Hall, S. J. King, J. Zhu and J. van der Lee, Radiochim. Acta, 1998, 81, 215–221 CrossRef CAS.
- A. P. Robertson and J. O. Leckie, Environ. Sci. Technol., 1999, 33, 786–795 CrossRef CAS.
- R. Marsac, M. Davranche, G. Gruau, M. Bouhnik-Le Coz and A. Dia, Geochim. Cosmochim. Acta, 2011, 75, 5625–5637 CrossRef CAS.
- A. C. Montenegro, S. Orsetti and F. V. Molina, Environ. Chem., 2014, 11, 318–332 CrossRef CAS.
- N. D. Bryan, D. M. Jones, M. Appleton, F. R. Livens, M. N. Jones, P. Warwick, S. King and A. Hall, Phys. Chem. Chem. Phys., 2000, 2, 1291–1300 RSC.
- M. F. Benedetti, W. H. van Riemsdijk and L. K. Koopal, Environ. Sci. Technol., 1996, 30, 1805–1813 CrossRef CAS.
- H. P. van Leeuwen and R. M. Town, Environ. Chem., 2016, 13, 76–83 CrossRef CAS.
- G. S. Manning, Acc. Chem. Res., 1979, 12, 443–449 CrossRef CAS.
- G. S. Manning, Biophys. Chem., 1977, 7, 95–102 CrossRef CAS PubMed.
- E. Garcia-Fernandez, P. M. R. Paulo and S. M. B. Costa, Phys. Chem. Chem. Phys., 2015, 17, 4319–4327 RSC.
- M. Majtyka and J. Kłos, Phys. Chem. Chem. Phys., 2007, 9, 2284–2292 RSC.
- Q. R. Huang, P. L. Dubin, C. N. Moorefield and G. R. Newkome, J. Phys. Chem. B, 2000, 104, 898–904 CrossRef CAS.
- Z. Li, A. K. van Dyk, S. J. Fitzwater, K. A. Fichthorn and S. T. Milner, Langmuir, 2016, 32, 428–441 CrossRef CAS PubMed.
- K. Krishnan and R. A. Plane, J. Am. Chem. Soc., 1968, 90, 3195–3200 CrossRef CAS.
- L. A. Clapp, C. J. Siddons, J. R. Whitehead, D. G. van Derveer, R. D. Rogers, S. T. Griffin, S. B. Jones and R. D. Hancock, Inorg. Chem., 2005, 44, 8495–8502 CrossRef CAS PubMed.
- M. Eigen, Pure Appl. Chem., 1963, 6, 97–115 CrossRef CAS.
- R. M. Fuoss, J. Am. Chem. Soc., 1958, 80, 5059–5061 CrossRef CAS.
- H. P. van Leeuwen, R. M. Town and J. Buffle, J. Phys. Chem. A, 2007, 111, 2115–2121 CrossRef CAS PubMed.
- P. G. Daniele, A. De Robertis, C. De Stefano, S. Sammartano and C. Rigano, J. Chem. Soc., Dalton Trans., 1985, 2353–2361 RSC.
- T. Miyajima, K. Yoshida, Y. Kanegae, H. Tohfuku and J. A. Marinsky, React. Polym., 1991, 15, 55–62 CrossRef CAS.
- R. F. M. J. Cleven, Heavy Metal/Polyacid Interaction. An Electrochemical Study of the Binding of Cd(II), Pb(II) and Zn(II) to Polycarboxylic Acids and Humic Acids, PhD thesis, Wageningen Agricultural University, 1984 Search PubMed.
- R. M. Town, J. Buffle, J. F. L. Duval and H. P. van Leeuwen, J. Phys. Chem. A, 2013, 117, 7643–7654 CrossRef CAS PubMed.
- H. Ohshima and T. Kondo, Biophys. Chem., 1990, 38, 117–122 CrossRef CAS PubMed.
- L. P. Yezek and H. P. van Leeuwen, Langmuir, 2005, 21, 10342–10347 CrossRef CAS PubMed.
- J. F. L. Duval, Langmuir, 2005, 21, 3247–3258 CrossRef CAS PubMed.
- R. Vermeer, Interactions Between Humic Acid and Hematite and Their Effects on Metal Ion Speciation, PhD thesis, Wageningen Agricultural University, 1996 Search PubMed.
- W. F. Tan, L. K. Koopal and W. Norde, Environ. Sci. Technol., 2009, 43, 591–596 CrossRef CAS PubMed.
- J. P. Pinheiro, A. M. Mota, J. M. R. d'Oliveira and J. M. G. Martinho, Anal. Chim. Acta, 1996, 329, 15–24 CrossRef CAS.
- M. Hosse and K. J. Wilkinson, Environ. Sci. Technol., 2001, 35, 4301–4306 CrossRef CAS PubMed.
- J. Puy, J. Galceran, C. Huidobro, E. Companys, N. Samper, J. L. Garcés and F. Mas, Environ. Sci. Technol., 2008, 42, 9289–9295 CrossRef CAS PubMed.
- G. Abate and J. C. Masini, Org. Geochem., 2002, 33, 1171–1182 CrossRef CAS.
- H. M. V. M. Soares, P. C. F. L. Conde, A. A. N. Almeida and M. T. S. D. Vasconcelos, Anal. Chim. Acta, 1999, 394, 325–335 CrossRef CAS.
- H. E. Mash, Y.-P. Chen, L. Sigg, R. Hari and H.-B. Xue, Anal. Chem., 2003, 75, 671–677 CrossRef CAS PubMed.
- R. M. Town and H. P. van Leeuwen, Electroanalysis, 2004, 16, 458–471 CrossRef CAS.
- J. Galceran, E. Companys, J. Puy, J. Cecília and J. L. Garcés, J. Electroanal. Chem., 2004, 566, 95–109 CrossRef CAS.
- R. M. Town and H. P. van Leeuwen, J. Electroanal. Chem., 2001, 509, 58–65 CrossRef CAS.
- M. A. G. T. van den Hoop, H. P. van Leeuwen and R. F. M. J. Cleven, Anal. Chim. Acta, 1990, 232, 141–148 CrossRef CAS.
- A. van der Wal, M. Minor, W. Norde, A. J. B. Zehnder and J. Lyklema, Langmuir, 1997, 13, 165–171 CrossRef CAS.
- H. Ohshima and S. Ohki, Biophys. J., 1985, 47, 673–678 CrossRef CAS PubMed.
- H. P. van Leeuwen, R. F. M. J. Cleven and P. Valenta, Pure Appl. Chem., 1991, 63, 1251–1268 CrossRef.
- I. Christl, Environ. Chem., 2012, 9, 89–96 CrossRef CAS.
- J. G. Hering and F. M. M. Morel, Environ. Sci. Technol., 1988, 22, 1234–1237 CrossRef CAS PubMed.
- R. von Wandruszka, Soil Sci., 1998, 163, 921–930 CrossRef CAS.
- I. Christl, A. Metzger, I. Heidmann and R. Kretzschmar, Environ. Sci. Technol., 2005, 39, 5319–5326 CrossRef CAS PubMed.
- A. Liu and R. D. Gonzalez, Langmuir, 2000, 16, 3902–3909 CrossRef CAS.
- E. Companys, J. Puy and J. Galceran, Environ. Chem., 2007, 4, 347–354 CAS.
- A. W. P. Vermeer, J. K. McCulloch, W. H. van Riemsdijk and L. K. Koopal, Environ. Sci. Technol., 1999, 33, 3892–3897 CrossRef CAS.
- C. Kolokassidou and I. Pashalidis, Radiochim. Acta, 2006, 94, 549–552 CrossRef CAS.
- J. Xiong, L. K. Koopal, W. F. Tan, L. C. Fang, M. X. Wang, W. Zhao, F. Liu, J. Zhang and L. P. Weng, Environ. Sci. Technol., 2013, 47, 11634–11642 CrossRef CAS PubMed.
- I. Christl, C. J. Milne, D. G. Kinniburgh and R. Kretzschmar, Environ. Sci. Technol., 2001, 35, 2512–2517 CrossRef CAS PubMed.
- Y. Marcus, Chem. Rev., 1988, 88, 1475–1498 CrossRef CAS.
- H. P. van Leeuwen, J. Buffle and R. M. Town, Langmuir, 2012, 28, 227–234 CrossRef CAS PubMed.
- R. M. Town and H. P. van Leeuwen, Environ. Chem., 2014, 11, 196–205 CrossRef CAS.
- H. P. van Leeuwen, J. Radioanal. Nucl. Chem., 2000, 246, 487–492 CrossRef CAS.
- P. D. Polyakov and J. F. L. Duval, Phys. Chem. Chem. Phys., 2014, 16, 1999–2010 RSC.
- S. Jansen, R. Blust and H. P. van Leeuwen, Environ. Sci. Technol., 2002, 36, 2164–2170 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |

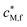
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)