 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A DFT-based comparative equilibrium study of thermal dehydration and hydrolysis of CaCl2 hydrates and MgCl2 hydrates for seasonal heat storage
Amar Deep
Pathak
*,
Silvia
Nedea
,
Herbert
Zondag
,
Camilo
Rindt
and
David
Smeulders
Energy Technology, P. O. Box 513 5600 MB Eindhoven, The Netherlands. E-mail: a.d.pathak@tue.nl
First published on 10th March 2016
Abstract
Salt hydrates store solar energy in chemical form via a reversible dehydration–hydration reaction. However, as a side reaction to dehydration, hydrolysis (HCl formation) may occur in chloride based salt hydrates (specially in MgCl2 hydrates), affecting the durability of the storage system. The mixture of CaCl2 and MgCl2 hydrates has been shown experimentally to have exceptional cycle stability and improved kinetics. However, the optimal operating conditions for the mixture are unknown. To understand the appropriate balance between dehydration and hydrolysis kinetics in the mixtures, it is essential to gain in-depth insight into the mixture components. We present a GGA-DFT level study to investigate the various gaseous structures of CaCl2 hydrates and to understand the relative stability of their conformers. The hydration strength and relative stability of conformers are dominated by electrostatic interactions. A wide network of intramolecular homonuclear and heteronuclear hydrogen bonds is observed in CaCl2 hydrates. Equilibrium product concentrations are obtained during dehydration and hydrolysis reactions under various temperature and pressure conditions. The trend of the dehydration curve with temperature in CaCl2 hydrates is similar to the experiments. Comparing these results to those of MgCl2 hydrates, we find that CaCl2 hydrates are more resistant towards hydrolysis in the temperature range of 273–800 K. Specifically, the present study reveals that the onset temperatures of HCl formation, a crucial design parameter for MgCl2 hydrates, are lower than for CaCl2 hydrates except for the mono-hydrate.
1 Introduction
Solar thermal energy can be stored in three forms: sensible heat, latent heat, and in thermochemical form. In a thermochemical storage system, energy is stored by bond breaking and reformation in a reversible reaction.1 Compared to sensible or latent heat, the energy storage density is higher in thermochemical form.2 This explains the enormous interest in thermochemical materials (TCMs) for seasonal heat storage applications.3 TCMs offer compact solar energy storage suitable for household applications. TCMs are widely available and inexpensive, and therefore appear to be an attractive material for seasonal heat storage. The cost of TCM is 30% of the total investment in the thermochemical heat storage system.3 Thus, the selection of TCMs is a key aspect in designing the heat storage system.Salt hydrates are one class of TCMs. Upon charging, these materials absorb solar energy and disintegrate into a lower hydrated or anhydrous form. Upon discharging, these dried salt hydrates recombine with H2O, forming hydrates while dissipating energy.
| Salt·nH2O ⇌ Salt + nH2O | (1) |
| MCl2·nH2O → MOHCl + (n − 1)H2O + HCl (M = Mg/Ca) | (2) |
Hydrolysis can be avoided in TCMs by mixing with other halides.6 Rammelberg et al.7 examined the performance of various salt mixtures. They observed that the mixture of CaCl2 hydrates and MgCl2 hydrates shows good cycle stability and improved kinetics compared to MgCl2 and CaCl2 hydrates alone. They have not described the chemical explanation for this extra stability. To assess the performance of the mixture of CaCl2 hydrates and MgCl2 hydrates, it is essential to investigate the dehydration and hydrolysis behavior of CaCl2 hydrates and compare these to MgCl2 hydrates.
CaCl2 hydrate has been used as a TCM.8–11 It has a very high crystalline energy storage density (2.82 GJ m−3), is readily available, inflammable and has high temperature lift during hydration.3,8,12 CaCl2 hydrates are also used in mobile storage of industrial waste.13 In domestic heat storage systems, TCMs are used in the temperature range of 300–500 K while in mobile storage of industrial heat, a much higher temperature range is used. Thus, it is important to investigate the equilibrium products of dehydration and hydrolysis reactions of CaCl2 hydrates over a wide temperature range. Next to the kinetics of dehydration/hydrolysis, the onset temperature of HCl formation in chloride based salt hydrates is a crucial parameter in designing heat storage systems.
Rammelberg et al.10 and Zondag et al.9 examined the kinetics of dehydration of CaCl2 hydrates using Thermogravimetric analysis (TGA) and did not observe hydrolysis. Fraissler et al.14 observed that the formation of HCl gas from the hydrolysis of CaCl2 occurs in a certain temperature range (683–1013 K). In these temperature regimes the preference of hydrolysis over dehydration reaction is ambiguous from experiments.
Computational models can be successfully used to investigate the in-depth behavior of salt hydrates in different temperature regimes.4,15–18 The hydration of Ca2+ ions has been successfully investigated using Density Functional Theory (DFT),19,20 molecular dynamics simulations18,21 and validated by experiments.22,23 Iype et al.4 characterized the H-bonds present in MgSO4 hydrates using DFT calculations. They observed that strong H-bonds affect the hydration kinetics of MgSO4 hydrates. Smeets et al.15 computationally investigated the dehydration and hydrolysis reactions for MgCl2 hydrates. They have reported the equilibrium curves for dehydration/hydrolysis of MgCl2 hydrates. We have explored the relative stability of various conformers of CaCl2 hydrates, ideal operating conditions of CaCl2 hydrates and compared them with MgCl2 hydrates.15 Nevertheless, to the best of our knowledge, currently no computational studies exist on the hydrolysis reaction of CaCl2 hydrates, the onset temperature of HCl formation and their comparison with MgCl2 hydrates. The system level complexity of salt hydrate mixtures like grain boundaries, grain sizes and their effect on the reaction kinetics could be addressed by multiscale integration of DFT results to the system level.24
In the present study, we would like to understand by means of DFT calculations, the temperature and pressure conditions under which hydrolysis precedes over dehydration. First we examine the molecular structure and vibrational frequencies of CaCl2 hydrates and their conformers. We investigate the strength of H-bonds present in CaCl2 hydrates, since strong H-bonds can result in sluggish hydration kinetics. We characterize the H-bonds using the Bond Valence (BV) sum rule. The BV sum rule is frequently used to correlate the structural properties of H-bonds and crystal structure determination.4,25,26 The enthalpy of the dehydration and hydrolysis reactions of CaCl2 hydrates is obtained from DFT calculations and compared to MgCl2 hydrates. The change in Gibbs free energy for dehydration and hydrolysis of all hydrates is obtained, followed by the equilibrium product concentration. The equilibrium properties obtained from the present DFT calculations can be used to calculate safety limits for thermal degradation of CaCl2 hydrates. These safety limits are compared with MgCl2 hydrates.
2 Computational model and validation
2.1 Density functional theory calculations
The molecular structures of various CaCl2 hydrates, their conformers, HCl, H2O, and CaOHCl are fully optimized in DFT using the Perdew–Wang exchange and correlation functional (PW91) under generalized gradient approximation (GGA)27 implemented in the Amsterdam Density Functional (ADF) program28 with the double-polarized triple-ζ basis set. A spin restricted Kohn–Sham method is used thus keeping the maximum integration accuracy. DFT-GGA has been used to study the salt hydrates like CaCl2, MgCl2, MgSO4.4,15–17 Iype et al.4 showed the applicability of GGA-DFT to study the H-bonds present in hydrates of MgSO4.2.2 Model validation
To validate the applicability of GGA-DFT using the PW91 functional, we have examined the binding enthalpy, Ca–O coordination length and vibrational frequency of [Ca(H2O)6]2+ ions. The successive binding enthalpy of hexahydrated Ca2+ ions is defined as
is defined as | (3) |
 | ||
| Fig. 1 Optimized structure of hydrated Ca2+ ions ([Ca(H2O)6]2+). Bader charges (black, italic) and Ca–O coordination lengths (in Å, blue) are shown. Color scheme: Ca = yellow, O = red, and H = white. | ||
In the present DFT study, the average coordination length of Ca–O in the first hydration shell of Ca2+ is 2.39 Å, which is in excellent agreement with past DFT results (2.37 Å),19 high order Car–Parrinello molecular dynamics results (2.41 Å)21 and experimental results (2.39 Å, XRD).29 Furthermore, we have calculated the vibrational frequencies of [Ca(H2O)6]2+. The IR peak position obtained from present calculations are in close agreement with Lei and Pan20 as shown in Fig. 2.
 | ||
| Fig. 2 The calculated IR spectra of the ground state structure of [Ca(H2O)6]2+. The represents the IR peak position of [Ca(H2O)6]2+ ions, as reported by Lei and Pan.20 | ||
2.3 Methodology
The harmonic frequencies of each optimized geometry are calculated to quantify the vibrational contribution of energy and entropy. The information of vibrational spectra, ground state geometry and Gibbs free energy (G) of all reactants and products are essential to calculate ΔG of dehydration and hydrolysis reaction.30 In the present study, we are interested in the following dehydration and hydrolysis reactions of CaCl2 hydrates:| CaCl2·nH2O ⇌ CaCl2·(n − 2)H2O + 2H2O [n = 6, 4] | (4) |
| CaCl2·nH2O ⇌ CaCl2·(n − 1)H2O + H2O [n = 2, 1] | (5) |
| CaCl2·nH2O → CaOHCl + (n − 1)H2O + HCl [n = 6, 4, 2, 1] | (6) |
 | (7) |
In this paper, the ΔG in dehydration and hydrolysis reactions is computed under ideal poly-atomic gas assumption30 assuming each reactant and product to be in the gaseous state. Gibbs free energy of a gaseous molecule at given temperature T and absolute pressure p can be given as
| G(T,p) = U + pV − TS | (8) |
| q = qtransqrotqvibqelec | (9) |
Internal energy U of poly-atomic gas can be expressed as
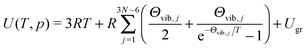 | (10) |
The entropy (S) of poly-atomic gas can be expressed as
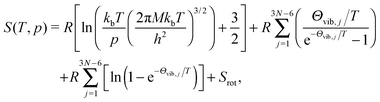 | (11) |
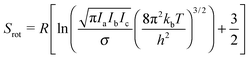 | (12) |
The H-bonds of CaC2 hydrates are analyzed in the gaseous phase. This is a valid analysis as the locus of H-bond parameters can be generalized irrespective of the system being in a condensed phase or the gaseous phase.4 The presence of H-bonds is identified by the non-bonded X⋯H (X = Cl and O) distance. When the non-bonded distance between O and H varies from 1.5 Å to 2.0 Å, we classify these H-bonds as OHO homonuclear type H-bonds, which is consistent with Iype et al.4 Similarly, when the non-bonded distance between Cl and H varies from 1.9 Å to 2.5 Å, we classify these H-bonds as a OHCl heteronuclear type H-bond. Bader charges on various atoms in the molecule are calculated to understand the charge distribution. We compared the charge distribution in all hydrates to observe charge transfer, the effect of Coulombic interactions on their stability and enthalpy of dehydration.
3 Results and discussions
The gaseous structures of CaCl2 hydrates are investigated to understand the H-bond network, relative stability of conformers and enthalpy change in the hydrolysis and dehydration reactions. The optimized structures are used to obtain vibrational frequencies, and their entropic and energy contribution from DFT calculations. In this section, we present the optimized structures of CaCl2 hydrates and their conformers.3.1 Molecular structures of CaCl2 hydrates and their conformers
 | ||
| Fig. 4 The optimized structure of CaCl2·4H2O conformers. Bader charges (black, italic) and coordination lengths (in Å, blue) are shown. Color scheme: Ca = yellow, Cl = green, O = red, and H = white. | ||
CaCl2·4H2O also exists in the β polymorph phase.33 The initial molecular structure is chosen close to the β phase structure. The optimized structure is shown in Fig. 4b. The optimized geometry is a distorted octahedral with 1.62 kcal mol−1 more stable than the α phase optimized geometry (Fig. 4a). The average Ca–O coordination length in the β phase optimized gaseous tetrahydrate is 2.405 Å, which is in agreement with the experimental β phase crystalline structure (2.46 Å).33 Similarly, the average Ca–Cl coordination of the gaseous phase tetrahydrate is 2.68 Å, which is in close agreement with the β phase crystalline structure (2.74 Å).33 There are two relatively strong H-bonds (OHCl) observed in the β phase optimized geometry compared to the α phase optimized geometry. There are intermolecular H-bonds (OHCl type) present in the β phase of the experimental crystalline structures,33 while intramolecular H-bonds are observed in the gaseous molecule. This is the reason for the slight discrepancy in the structure of a gaseous molecule and the β phase crystalline structure.
CaCl2·4H2O also occurs in the γ phase.34 The initial molecular structure is chosen close to the γ phase structure. The optimized structure is symmetrical and has almost a planar structure as shown in Fig. 4c. This structure is 19.24 kcal mol−1 less stable than the β phase optimized geometry. The average Ca–O coordination length is 2.26 Å in the γ phase optimized structure, which is in agreement with the γ phase crystalline structures (2.33 Å).34 The two H atoms of surrounded H2O molecules form a relatively strong H-bonds with the Cl compared to the α and the β phase optimized structures. The H2O takes away the Cl atom from the Ca, hence the Ca–Cl distance becomes 4.06 Å. The Bader charge on Cl is 0.07 less electronegative compared to the Cl of the β phase optimized structure. The Ca–Cl stretching and the lower atomic charge result in weaker electrostatic attraction between Ca–Cl pairs compared to α and β phase optimized structures. Thus, the γ optimized structure has lower stability over other conformers (α and β phase) despite having relatively strong H-bonds. The ∠Cl–H–O is 166.9°, which enables the greater availability of the Cl lone pairs for the anti-bonding Cl–H orbital overlap.
 | ||
| Fig. 5 The optimized structure of CaCl2·6H2O conformers. Bader charges (black, italic) and coordination lengths (in Å, blue) are shown. Color scheme: Ca = yellow, Cl = green, O = red, and H = white. | ||
CaCl2·6H2O exists experimentally in the γ phase.35 There are OHCl type intermolecular H-bonds present in the γ phase crystalline structures.35 Those H-bonds are between the H of the H2O of the hexahydrate and the Cl of the neighboring molecule of the hexahydrate in the crystal. The initial molecular structure is chosen close to the γ phase crystalline structure. In the optimized structure, the H2O forms an octahedral with the Ca as shown in Fig. 5b. The optimized structure (Fig. 5b) forms six H-bonds (2.00 Å) of OHCl type. The average Ca–O coordination length of γ phase optimized CaCl2·6H2O is 2.37 Å. The average Ca–Cl coordination length is 3.84 Å. There is a discrepancy of 26.6% in the Ca–Cl coordination length of the gaseous hexahydrate and the γ phase crystalline hexahydrate. There are intramolecular H-bonds present in the gaseous γ phase of hexahydrate (Fig. 5b) while intermolecular H-bonds in the γ phase crystalline structures,35 which explains the discrepancy.
The second stable conformer of the optimized CaCl2·6H2O is shown in Fig. 5c. This conformer is 4.12 kcal mol−1 less stable than the first conformer (Fig. 5a) and 4.41 kcal mol−1 less stable than the γ phase optimized structure (Fig. 5b). The average Ca–O coordination length is 2.45 Å. There are five intramolecular OHCl H-bonds (heteronuclear type) and one OHO type H-bond present in this conformer (Fig. 5c). Three H2O molecules are forming H-bonds (OHCl type) with one Cl, one H2O forms a H-bond (OHO type) with one of these H2O molecules and two H2O molecules form H-bonds with the other Cl atom. The average H⋯Cl H-bond length is 2.05 Å in the second stable conformer (Fig. 5c) while in the more stable γ phase optimized structure (Fig. 5b) it is 2.00 Å and 2.19 Å in the first conformer (Fig. 5a). The average O⋯H H-bond length is 1.88 Å in the second conformer (Fig. 5c) and in the first conformer, it is 1.83 Å. The O⋯H H-bonds are stronger in the first conformer, which explains the extra stability of the first conformer over the second conformer. The detailed explanation of H-bonds will be discussed in the section “Hydrogen bond in CaCl2 hydrate system”.
No conformer for MgCl2·4H2O and MgCl2·6H2O has been reported from DFT calculations.15 To rationally compare the structure of CaCl2 hydrates with MgCl2 hydrates, the average Bader charge on each atom is compared in Table 1. The Bader charges on Ca and Cl atoms of CaCl2 are lower in magnitude when compared with Mg and Cl in their analogous MgCl2 hydrates. The Bader charge on Ca and Mg atoms increases monotonically with the hydration number. The magnitude of the Bader atomic charge on Cl in CaCl2 hydrates decreases with hydration number whereas it increases from MgCl2 to MgCl2·2H2O and decreases till MgCl2·6H2O. The magnitude of average Bader atomic charges on O and H in CaCl2 hydrates is lower than MgCl2 hydrates. The Ca–Cl, Ca–O distance in CaCl2 hydrates is higher than MgCl2 hydrates. Thus, electrostatic attractions between Mg–O pairs in MgCl2 hydrates are stronger than Ca–O pairs in CaCl2 hydrates.
| Molecule | Ca (Mg) | Cl | O | H | Ca–O (Mg–O) | Ca–Cl (Mg–Cl) |
|---|---|---|---|---|---|---|
| CaCl2·6H2O (MgCl2·6H2O) | 1.633 (1.762) | −0.696 (−0.760) | −1.193 (−1.210) | 0.577 (0.575) | 2.37 (2.1) | 3.83 (3.76) |
| CaCl2·4H2O (MgCl2·4H2O) | 1.573 (1.700) | −0.755 (−0.802) | −1.180 (−1.188) | 0.582 (0.583) | 2.40 (2.15) | 2.68 (2.43) |
| CaCl2·2H2O (MgCl2·2H2O) | 1.558 (1.696) | −0.762 (−0.837) | −1.192 (−1.200) | 0.587 (0.590) | 2.36 (2.08) | 2.54 (2.26) |
| CaCl2·H2O (MgCl2·H2O) | 1.554 (1.650) | −0.770 (−0.826) | −1.202 (−1.204) | 0.594 (0.605) | 2.33 (2.05) | 2.49 (2.21) |
| CaCl2 (MgCl2) | 1.553 (1.621) | −0.776 (−0.811) | N.A. | N.A. | N.A. | 2.45 (2.18) |
3.2 Reaction enthalpies of CaCl2 hydrates
For reaction enthalpy calculations, we have considered the structure having minimum energy and no imaginary frequency. Table 2 describes the electronic ground state energy and various energy terms for all the studied hydrates. The binding energy (ΔEBinding) of a hydrate is defined as| ΔEBinding = ECaCl2·nH2O − (ECaCl2 + nEH2O) | (13) |
| Molecule | U gr/kcal mol−1 | ΔEBinding/kcal mol−1 | ΔEDehydration/kcal mol−1 | ΔEHydrolysis/kcal mol−1 |
|---|---|---|---|---|
| CaCl2·6H2O | −2319.15 | −104.65 | 14.56 (14.8) | 121.68 (119.3) |
| CaCl2·4H2O | −1630.28 | −75.52 | 16.57 (16.7) | 92.55 (89.7) |
| CaCl2·2H2O | −937.40 | −42.38 | 21.19 (15.7) | 59.41 (46.3) |
| CaCl2·H2O | −587.05 | −21.9 | 21.9 (22.4) | 38.93 (40.3) |
The enthalpy change during the dehydration reaction (ΔEDehydration) is defined as
| ΔEDehydration = 0.5 × [ECaCl2·(n−2)H2O + 2EH2O − ECaCl2·nH2O] (n = 4, 6) | (14) |
| ΔEDehydration = [ECaCl2·nH2O − ECaCl2·(n−1)H2O − EH2O] (n = 1, 2) | (15) |
| ΔEHydrolysis = [ECaOHCl + (n − 1)EH2O + EHCl − ECaCl2·nH2O] (n = 1, 2, 4, & 6) | (16) |
The enthalpy change during the dehydration and hydrolysis reaction of CaCl2 hydrates is compared with MgCl2 hydrates, as shown in Table 2. The dehydration enthalpy of CaCl2·6H2O, CaCl2·4H2O, and CaCl2·H2O is slightly lower than analogous MgCl2 hydrates. The dehydration enthalpy for CaCl2·2H2O is 26.8% higher than MgCl2·2H2O, thus CaCl2·2H2O dehydrates at higher temperature compared with MgCl2·2H2O. The CaCl2 hydrates (except mono hydrate) have high enthalpy of hydrolysis compared to MgCl2 hydrates (as given in Table 2) thus, CaCl2 hydrates are more resistant to hydrolysis reaction.
3.3 Hydrogen bond in the CaCl2 hydrate system
CaCl2 hydrates have the OHCl type heteronuclear H-bond and the OHO type homonuclear H-bond. The strong H-bond has a predominant covalent character while the moderate H-bond has mostly electrostatic character.38 The H-bond energy is a strong function of rX–H, rX⋯H, and rX–Y in XHX and XHY H-bonded systems.39 The Cl atom is larger in size compared to O and less electronegative thus the availability of the lone pair for H-bond formation is lower compared to the O. Thus the OHO type H-bond is stronger than the OHCl type H-bond.39In the present study, we observe the OHO type homonuclear H-bond in CaCl2·6H2O isomers (Fig. 5a and c). The strength of H-bonds depends on the distance between the donor H and the acceptor O distance (H-bond distance) and the ∠O–H⋯O (H-bond angle). The ∠O–H⋯O above 165° provides the complete lone pair availability in the O for the anti-bonding O–H orbital overlap4,40 therefore stabilizing the H-bond. The non-bonded O⋯H distance varies from 1.64 Å to 1.95 Å and ∠O–H⋯O 135.92° to 165.48°. The lengthening of the O–H bond varies from 0.017 Å to 0.041 Å. These OHO type H-bonds are moderate in strength and predominantly electrostatic in nature.38 In the first conformer of CaCl2·6H2O (Fig. 5a), three H-bonds of this type are present while in the second conformer of CaCl2·6H2O (Fig. 5c) only one H-bond is present. The first conformer of CaCl2·6H2O has one relatively strong but moderate strength H-bond (1.64 Å) thus provides 4.12 kcal mol−1 stability over the second conformer.
The CaCl2 hydrates have mostly OHCl type heteronuclear H-bonds. The H atoms of the hydrated CaCl2·XH2O molecule are attracted by adjacent Cl atoms and form OHCl type H bonds. In the present case, the Cl⋯H distance varies from 1.82 Å to 2.48 Å and the Cl–O distance varies from 2.86 Å to 3.15 Å. The lengthening of the OH bond varies from 0.01 Å to 0.08 Å. A similar bond length of H-bonds is observed in organic and organometallic crystals.41 Tommaso et al. also observed the OHCl type H-bond in the hydration of Ca2+ ions in salt solution.18 The bond valence is proportional to the electron density. The bond valence of the atom is distributed between the bonds which it forms. Each bond involves the same number of electrons. The BV sum rule is described as
| SH–O + SH⋯Cl = 1 | (17) |
3.4 Equilibrium product concentrations
The ΔG of a system is a function of pressure, temperature, and the system characteristics. At chemical equilibrium, the ΔG (from eqn (7)) should be zero and this will provide information about the equilibrium concentration of products. | ||
| Fig. 7 Equilibrium vapor pressure for the dehydration reactions of CaCl2 hydrates (green) at various temperatures and constant partial pressure of hydrate, p0 = 1 atm. The dashed red lines represent the dehydration curves of MgCl2 hydrates.15 The inset graph shows the comparison of enthalpy change during the dehydration reactions of CaCl2 and MgCl2 hydrates. | ||
Rammelberg et al.10 reported from thermal gravimetric analysis/differential scanning calorimetry (TGA/DSC) measurements 30% conversion of CaCl2·6H2O to CaCl2·4H2O at 336 K. In the present study, we observed 30% conversion of CaCl2·6H2O to CaCl2·4H2O only at around 340 K. There is an offset of 4 K is observed. The effect of temperature on the equilibrium dehydration curve of CaCl2·6H2O (slope = 0.035) is in agreement with the experiments (slope = 0.032)9,42 as shown in Fig. 7. An offset of 20 K is observed in the low vapor regime (<0.03 atm) for CaCl2·6H2O. The offset may be a consequence of the ideal polyatomic gas phase assumption. Another reason could be that the equilibrium product concentrations obtained from ΔG (DFT calculations) reports the static equilibrium properties while the experimental (TGA/DSC) kinetics reports the dynamic equilibrium properties. There is a similar offset observed in the equilibrium dehydration curve for CaCl2·4H2O to CaCl2·2H2O as well. The equilibrium partial vapor pressure (pH2O) of 1 atm is observed at 350.5 K for CaCl2·6H2O while at 490.5 K and 586.5 K for CaCl2·4H2O and CaCl2·2H2O as shown in Fig. 7.
The gradient of the dehydration curve for CaCl2·6H2O is 0.002 higher than MgCl2·6H2O while 0.007 lower for CaCl2·4H2O and CaCl2·2H2O when compared with their analogous MgCl2 hydrates. Thus, CaCl2·6H2O has the shortest range of dehydration temperature while CaCl2·4H2O and CaCl2·2H2O have a higher temperature range of operation. The dehydration enthalpy of CaCl2·6H2O is 0.25 kcal mol−1 lower than MgCl2·6H2O (as given in Table 2) thus it dehydrates at lower temperature compared to MgCl2·6H2O. The dehydration enthalpy of CaCl2·4H2O is 0.13 kcal mol−1 lower than MgCl2·4H2O while CaCl2·4H2O dehydrates at higher temperature than MgCl2·4H2O. This behavior can be explained from the role of the meta-stable conformer formed due to presence of strong H-bonds present in the CaCl2·4H2O isomer (Fig. 4c). The dehydration enthalpy of CaCl2·2H2O is 5.3 kcal mol−1 higher than MgCl2·2H2O (see inset graph of Fig. 7) so it dehydrates at higher temperature compared with MgCl2·2H2O.
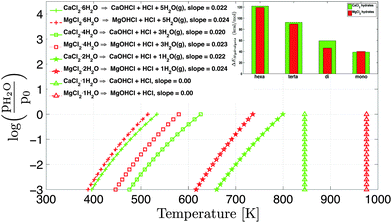 | ||
| Fig. 8 Equilibrium vapor pressure for the hydrolysis reactions of CaCl2 hydrates (green) at various temperatures and fixed HCl pressure pHCl = 1 × 10−3 atm and p0 = 1 atm. The dashed red lines represent the hydrolysis curves of MgCl2 hydrates.15 The inset graph shows the comparison of enthalpy change during the hydrolysis reactions of CaCl2 and MgCl2 hydrates. | ||
The equilibrium vapor pressure of 1 atm is observed from CaCl2·6H2O at 350.5 K and hydrolysis above the safety limit (pHCl = 1 × 10−3 atm) starts at 396 K. There is no overlapping temperature region between hydrolysis and dehydration for CaCl2·6H2O. The CaCl2·4H2O dehydrates into CaCl2·2H2O at 490.5 K (pH2O = 1 atm) while hydrolysis starts (above safety limit, pHCl > 1 × 10−3 atm) at 475.8 K. There is an overlap of around 14.7 K (from Fig. 7 and 8). Similarly the overlap for the CaCl2·2H2O is around 32.5 K. Fraissler et al.14 reported experimentally from TGA measurements that the HCl formation from thermal decomposition of CaCl2 salt hydrates occurs in the temperature range of 683−1013 K. We observe the starting point (pHCl = 1 × 10−3 atm, onset) of HCl formation for CaCl2·2H2O and CaCl2·H2O at 660 K and 845 K (pH2O = 1 × 10−3 atm) respectively. CaCl2·4H2O and CaCl2·6H2O will not be present in this temperature range. The offset in the onset of HCl formation temperature may be the consequence of the dynamic and static equilibrium comparison and the effect of the ideal polyatomic gas assumption. The hydrolysis of CaCl2·H2O is independent of the H2O vapor pressure as shown in Fig. 8.
Hydrolysis of MgCl2 hydrates starts at lower temperature in comparison to CaCl2 hydrates for hexa, tetra, and dihydrates, which is consistent with the enthalpy change in hydrolysis of MgCl2 and CaCl2 hydrates as given in Table 2. The slope of the MgCl2 hydrate hydrolysis curve is slightly higher compared to the CaCl2 hydrates so the hydrolysis of CaCl2 hydrates has a longer operating temperature range. Hydrolysis in MgCl2·6H2O, MgCl2·4H2O and MgCl2·2H2O starts at 388, 446, and 616 K (pH2O = 1 × 10−3 atm) respectively, which is lower than analogous CaCl2 hydrates. Hydrolysis in CaCl2·H2O starts at lower temperature (845 K) than MgCl2·H2O (976 K). Thus, CaCl2 hydrates have improved hydrolysis resistance if the operating temperature is less than 800 K.
Furthermore, the partial pressure of HCl (pHCl) is plotted with their equilibrium temperature at fixed H2O vapor pressure (pH2O = 4 × 10−3 atm) for MgCl2 and CaCl2 hydrates in Fig. 9. For any temperature (<761 K), MgCl2 will always have high partial pressure of HCl (pHCl) compared to CaCl2 hydrates. The slope of the equilibrium hydrolysis curve (Fig. 9) decreases from the hexahydrate to the monohydrate for both CaCl2 and MgCl2 hydrates. The slope of CaCl2 is slightly lower than analogous MgCl2 hydrates. Hence, the HCl concentration could be better controlled with temperature in CaCl2 hydrates over MgCl2 hydrates.
 | ||
| Fig. 9 Equilibrium vapor pressure for the hydrolysis reactions of CaCl2 hydrates (green) at various temperatures and fixed H2O pressure pH2O = 4 × 10−3 atm and p0 = 1 atm. The dashed red lines represent the hydrolysis curves of MgCl2 hydrates.15 The inset graph shows the comparison of enthalpy change during the hydrolysis reactions of CaCl2 and MgCl2 hydrates. | ||
For a given change in partial pressure of HCl (pHCl), the temperature changes maximum for the monohydrate. The reason for the change in the slope of the hydrolysis curve can be explained by the stoichiometric ratio between HCl and H2O. The stoichiometric ratio of HCl to H2O increases from 0.2 to 1 for the hexahydrate to the monohydrate. Thus, the molar ratio between HCl and H2O decreases from mono to hexahydrate, therefore, temperature varies maximum for the monohydrate for a given change in pHCl. The similar trend of slope is observed for MgCl2 hydrates.
4 Conclusions
To understand the equilibrium product concentrations of the dehydration and hydrolysis reactions of CaCl2·nH2O in comparison to MgCl2·nH2O, DFT calculations have been carried out. The structural properties of CaCl2 hydrates along with their atomic charges are analyzed. This study reveals the formation of many conformers due to the presence of various H-bonds. The relative stability of a conformer and dehydration enthalpy is dominated by electrostatic attraction and strength of H-bond formed. We observed a homonuclear H-bond (OHO) and a heteronuclear H-bond (OHCl) in the various hydrates of CaCl2. Most of the H-bonds (∼77%) in CaCl2 hydrate are of moderate strength. CaCl2·2H2O has two conformers due to the presence of an OHCl type H-bond. Similarly, three conformers of CaCl2·4H2O, and CaCl2·6H2O are observed. The most stable conformers are non-planar CaCl2·2H2O (Fig. 3d), β phase optimized CaCl2·4H2O (Fig. 4b), and γ phase optimized CaCl2·6H2O (Fig. 5b). These conformers are 4.78, 19.24, and 4.41 kcal mol−1 more stable than their lowest stable conformer. The relatively strong OHCl H-bonds provide 4.41 kcal mol−1 stability compared to its lowest stable conformer in CaCl2·6H2O. The H-bonds in CaCl2·4H2O destabilize the γ phase optimized structure by 19.24 kcal mol−1 compared with the β phase optimized structure. This implies that CaCl2·4H2O could form a metastable stage, and may have a sluggish hydration kinetics. Both CaCl2·2H2O and CaCl2·6H2O have less stable conformers, consequently they do not form metastable stages. Thus, the H-bonds should not markedly affect their hydration kinetics. The BV sum rule parameters for OHCl type H-bonds are 0.96 Å, 0.80 Å (for H⋯Cl pair) and 0.97 Å, 0.38 Å (for H⋯O pair). These parameters can be used to characterize the OHCl H-bonded system.The enthalpy change in the dehydration and hydrolysis reactions of CaCl2 hydrates is obtained from DFT and compared with MgCl2 hydrates. The equilibrium composition of dehydration and hydrolysis reactions is obtained by equating the ΔG to zero over a wide range of temperature and pressure conditions. The trend in the dehydration reaction is similar to the experiments for all the CaCl2 hydrates. The effect of temperature on the dehydration of CaCl2·6H2O (slope = 0.035) is in close agreement with experiments (slope = 0.032).9,10 We compared the equilibrium composition of dehydration and hydrolysis reactions for CaCl2 and MgCl2 hydrates. The CaCl2·6H2O dehydrates at lower temperature (as shown in Fig. 7) compared with MgCl2·6H2O while CaCl2·4H2O and CaCl2·2H2O dehydrates at higher temperature when compared to their analogous MgCl2 hydrates. The CaCl2 hydrates have better temperature control with the partial pressure of the products (pHCl, pH2O) when compared to the MgCl2 hydrates. We investigated hydrolysis and dehydration at different temperature, pressure regimes for CaCl2 and MgCl2 hydrates. The CaCl2 hydrates have better hydrolysis resistance over MgCl2 hydrates in the temperature range 273 to 800 K, which explains the higher stability in the mixture of CaCl2 and MgCl2 hydrates. Hydrolysis is very rare for CaCl2·6H2O because the onset of hydrolysis reaction at the safety limit (pHCl = 1 × 10−3 atm) is higher than the dehydration temperature of CaCl2·6H2O. Similarly CaCl2·4H2O and CaCl2·2H2O can undergo hydrolysis (pHCl = 1 × 10−3 atm) at 475.8 and 660 K respectively. The similar temperatures for MgCl2 hydrates are 446 and 616 K. CaCl2·H2O may undergo hydrolysis above 850 K. These temperature ranges should be treated as the safety limit range for hydrolysis reactions. The CaCl2 hydrates could be mixed with MgCl2 hydrates to improve the hydrolysis resistance and therefore durability of the system.
Acknowledgements
This work is part of the Industrial Partnership Programme (IPP) ‘Computational sciences for energy research’ of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO). This research programme is co-financed by Shell Global Solutions International B. V.References
- A. Sharma, V. Tyagi, C. Chen and D. Buddhi, Renewable Sustainable Energy Rev., 2009, 13, 318–345 CrossRef CAS.
- K. E. N'Tsoukpoe, H. Liu, N. Le Pierrès and L. Luo, Renewable Sustainable Energy Rev., 2009, 13, 2385–2396 CrossRef.
- K. E. N'Tsoukpoe, T. Schmidt, H. U. Rammelberg, B. A. Watts and W. K. Ruck, Appl. Energy, 2014, 124, 1–16 CrossRef.
- E. Iype, S. V. Nedea, C. C. M. Rindt, A. A. van Steenhoven, H. A. Zondag and A. P. J. Jansen, J. Phys. Chem. C, 2012, 116, 18584–18590 CAS.
- Y. Kirsh, S. Yariv and S. Shoval, J. Therm. Anal., 1987, 32, 393–408 CrossRef CAS.
- S. Shoval, S. Yariv, Y. Kirsh and H. Peled, Thermochim. Acta, 1986, 109, 207–226 CrossRef CAS.
- H. U. Rammelberg, M. Myrau, T. Schmidt and W. Ruck, IMPRES 2013, Fukuoka, 04.-06, 2013 Search PubMed.
- F. Trausel, A.-J. de Jong and R. Cuypers, Energy Procedia, 2014, 48, 447–452 CrossRef CAS.
- H. Zondag, M. van Essen, L. Bleijendaal, J. Cot, R. Schuitema, W. van Helden, W. Planje, T. Epema and H. Oversloot, Proceeding of IRES, 2008 Search PubMed.
- H. U. Rammelberg, T. Schmidt and W. Ruck, Energy Procedia, 2012, 30, 362–369 CrossRef CAS.
- C. C. Wilkins, N. W. Hunter and E. F. Pearson, J. Chem. Educ., 1992, 69, 753 CrossRef CAS.
- K. E. N'Tsoukpoe, H. U. Rammelberg, A. F. Lele, K. Korhammer, B. A. Watts, T. Schmidt and W. K. Ruck, Appl. Therm. Eng., 2015, 75, 513–531 CrossRef.
- A. Krönauer, E. Lävemann, S. Brückner and A. Hauer, Energy Procedia, 2015, 73, 272–280 CrossRef.
- G. Fraissler, M. Jöller, T. Brunner and I. Obernberger, Chem. Eng. Process., 2009, 48, 380–388 CrossRef CAS.
- B. Smeets, E. Iype, S. V. Nedea, H. A. Zondag and C. C. M. Rindt, J. Chem. Phys., 2013, 139, 124312 CrossRef CAS PubMed.
- C. M. Widdifield and D. L. Bryce, Can. J. Chem., 2011, 89, 754–763 CrossRef.
- C. M. Widdifield, I. Moudrakovski and D. L. Bryce, Phys. Chem. Chem. Phys., 2014, 16, 13340–13359 RSC.
- D. Di Tommaso, E. Ruiz-Agudo, N. H. de Leeuw, A. Putnis and C. V. Putnis, Phys. Chem. Chem. Phys., 2014, 16, 7772–7785 RSC.
- M. Pavlov, P. E. Siegbahn and M. Sandström, J. Phys. Chem. A, 1998, 102, 219–228 CrossRef CAS.
- X. Lei and B. Pan, J. Phys. Chem. A, 2010, 114, 7595–7603 CrossRef CAS PubMed.
- T. Todorova, P. H. Hünenberger and J. Hutter, J. Chem. Theory Comput., 2008, 4, 779–789 CrossRef CAS PubMed.
- M. Peschke, A. T. Blades and P. Kebarle, J. Phys. Chem. A, 1998, 102, 9978–9985 CrossRef CAS.
- A. A. Zavitsas, J. Phys. Chem. B, 2005, 109, 20636–20640 CrossRef CAS PubMed.
- S. Lan, H. Zondag, A. van Steenhoven and C. Rindt, J. Therm. Anal. Calorim., 2016, 1–10 Search PubMed.
- I. D. Brown, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS PubMed.
- L. Sobczyk, S. J. Grabowski and T. M. Krygowski, Chem. Rev., 2005, 105, 3513–3560 CrossRef CAS PubMed.
- J. P. Perdew, J. Chevary, S. Vosko, K. A. Jackson, M. R. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- M. M. Probst, T. Radnai, K. Heinzinger, P. Bopp and B. M. Rode, J. Phys. Chem., 1985, 89, 753–759 CrossRef CAS.
- D. A. McQuarrie, Statistical mechanics, Harper & Row, 1975 Search PubMed.
- A. Leclaire and M. M. Borel, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 1608–1610 CrossRef.
- A. Leclaire and M. Borel, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 585–588 CrossRef.
- A. Leclaire and M. Borel, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 902–904 CrossRef.
- A. Leclaire, M. Borel and J. Monier, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2757–2759 CrossRef.
- P. A. Agron and W. R. Busing, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 141–143 CrossRef.
- P. F. Weck and E. Kim, J. Phys. Chem. C, 2014, 118, 4618–4625 CAS.
- R. W. G. Wyckoff, Crystal Structures, 1963, vol. 1, pp. 239–444 Search PubMed.
- S. Grabowski, Hydrogen Bonding – New Insights, Springer Netherlands, 2006 Search PubMed.
- P. A. Kollman and L. C. Allen, Chem. Rev., 1972, 72, 283–303 CrossRef CAS.
- P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 1994, 116, 909–915 CrossRef CAS.
- T. Steiner, J. Phys. Chem. A, 1998, 102, 7041–7052 CrossRef CAS.
- http://www.prog-univers.com/IMG/pdf/CalciumChloridHandbook-2.pdf .
| This journal is © the Owner Societies 2016 |



