Open Access Article
Open Access ArticleInsights into enzyme point mutation effect by molecular simulation: phenylethylamine oxidation catalyzed by monoamine oxidase A
Gabriel
Oanca
ab,
Miha
Purg
c,
Janez
Mavri
a,
Jean C.
Shih
def and
Jernej
Stare
*a
aLaboratory of Biocomputing and Bioinformatics, National Institute of Chemistry, Ljubljana, Slovenia. E-mail: jernej.stare@ki.si
bFaculty of Physics, Alexandru Ioan Cuza University of Iasi, Iasi, Romania
cDepartment of Cell and Molecular Biology, Uppsala University, Uppsala, Sweden
dDepartment of Pharmacology and Pharmaceuticals Sciences, School of Pharmacy, University of Southern California, Los Angeles, USA
eUSC-Taiwan Center for Translational Research, University of Southern California, Los Angeles, USA
fDepartment of Cell and Neurobiology, Keck School of Medicine, University of Southern California, Los Angeles, USA
First published on 12th April 2016
Abstract
The I335Y point mutation effect on the kinetics of phenylethylamine decomposition catalyzed by monoamine oxidase A was elucidated by means of molecular simulation. The established empirical valence bond methodology was used in conjunction with the free energy perturbation sampling technique and a classical force field representing the state of reactants and products. The methodology allows for the simulation of chemical reactions, in the present case the breaking of the α-C–H bond in a phenylethylamine substrate and the subsequent hydrogen transfer to the flavin cofactor, resulting in the formation of the N–H bond on flavin. The empirical parameters were calibrated against the experimental data for the simulated reaction in a wild type protein and then used for the calculation of the reaction free energy profile in the I335Y mutant. In very good agreement with the measured kinetic data, mutation increases the free energy barrier for the rate limiting step by slightly more than 1 kcal mol−1 and consequently decreases the rate constant by about an order of magnitude. The magnitude of the computed effect slightly varies with simulation settings, but always remains in reasonable agreement with the experiment. Analysis of trajectories reveals a major change in the interaction between phenyl rings of the substrate and the neighboring Phe352 residue upon the I335Y mutation due to the increased local polarity, leading to an attenuated quadrupole interaction between the rings and destabilization of the transition state. Additionally, the increased local polarity in the mutant allows for a larger number of water molecules to be present near the active site, effectively shielding the catalytic effect of the enzyme and contributing to the increased barrier.
1. Introduction
The aim of this work is to improve the understanding of the role of point mutations in the catalytic function of monoamine oxidase (MAO), a flavoenzyme essential for the metabolism of biogenic monoamines, by using the multiscale empirical valence bond (EVB) methodology for molecular simulation, and link this information to changed rate constants for phenylethylamine decomposition. MAO degrades neurotransmitters such as serotonin and dopamine, which play a central role in the pathophysiology of major neuropsychiatric illnesses including anxiety and mood disorders, schizophrenia, autism-spectrum disorders, Parkinson's disease, epilepsy, and dementias.1 Serotonin and dopamine are important for neuronal development and regulation of immune response as was demonstrated in a study of a series of monoamine oxidase (MAO) gene knock-out (KO) mice, which are animal models for anxiety, aggression and autistic-like-behavior.2MAO A and B catalyze the oxidative deamination of monoamine neurotransmitters in both the brain and peripheral tissues and abnormal levels of these neurotransmitters result in a number of neurological and mental disorders.1 The molecular cloning of MAO A and MAO B genes provided the first unequivocal evidence that they are two distinct proteins encoded by different genes.3 The two MAO genes are closely linked and located on chromosome X,4 consisting of 15 exons with an identical exon–intron organization, and have evolved from the same ancestral gene by gene duplication, thus they are two isoenzymes.5 The expression of MAO A and B genes is regulated by some common and some unique transcription factors.6 MAO A and B share ∼70% amino acid sequence identity3 with different substrate specificities. MAO A prefers serotonin, norepinephrine and dopamine as substrates while MAO B prefers phenylethylamine and benzylamine as substrates.1 In human males, the MAO A deficiency causes a complex behavioral syndrome, exhibiting antisocial personality, impulsivity, stereotyped responses and mild cognitive impairments.7 The evidence suggests that psychotic symptoms in combat-related posttraumatic stress disorder are related to the increased MAO B activity.8 The elevated aggressiveness of MAO A KO mice provided the clearest genetic evidence that MAO A regulates behavior, establishing the link between genes and behavior for the first time.9 In addition, male MAO A KO mice exhibit an array of behavioral and neuromorphological alterations similar to all core features of autism-spectrum disorder.10 MAO B KO mice, on the other hand, do not show aggressive behavior.2
Both isoenzymes of MAO are assumed to have the same mechanism of action, though this assumption has been challenged lately.11 Both isoenzymes catalyze the oxidation of primary amines to imines by reducing the prosthetic group of the enzyme, namely flavin adenine dinucleotide (FAD). The resulting imine reacts with water nonenzymatically to give aldehyde and ammonia as final products.12 Regeneration of the enzyme is accomplished by a reaction with molecular oxygen, which is reduced to hydrogen peroxide. The mechanism of amine oxidation by MAO has been a subject of extensive experimental and theoretical research.11–32 While agreement has been achieved on the rate limiting step of the reaction – namely the C–H bond cleavage at the α-carbon atom of the amine leading to hydrogen transfer to the N5 atom of flavin (Fig. 1) – there has been much less consensus on the mechanism of this step. Specifically, it has been debated whether the hydrogen atom is transferred as a proton, a radical or a hydride ion. While published evidence for all three mechanisms exists, including a polar nucleophile (hydrogen transferred as proton)20 and a radical,25 we believe that the reaction proceeds through the hydride transfer mechanism,30,31,33,34 as recently supported by our mechanistic studies employing quantum calculations.26
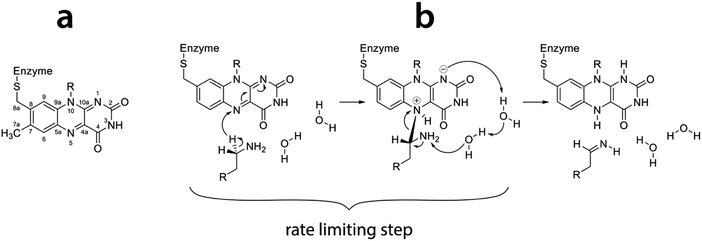 | ||
| Fig. 1 (a) Flavin moiety of FAD and atomic labels; (b) amine oxidation reaction scheme following the hydride transfer mechanism with the rate limiting step indicated (reproduced from ref. 26). | ||
The elucidation of chemical reactivity in enzymes remains a challenge for theoretical treatments, requiring both accuracy of quantum methods and long timescales of classical simulations. These requirements are commonly achieved by multiscale (QM/MM) modeling protocols encompassing quantum treatment of the subsystem of interest (e.g., the active site of an enzyme with its substrate) and classical treatment of the environment (the rest of the protein and the solvent) combining the advantages of both approaches.35–37 Perhaps the most efficient protocol in this regard available to date is Warshel's empirical valence bond (EVB) method.38–40 The basic idea is that the reactive subsystem is described on the level of a classical reactive force field augmented by the quantum treatment of valence states representing the reactants and products. The power of the EVB has been demonstrated for numerous enzymatic reactions and has led to significant development in the understanding of the functionality of enzymes.38,41–50
Among the experimental tools providing insight into the functionality of enzymes, point mutations are indispensable for the investigation of the origin of catalytic activity as well as substrate and inhibitor specificities at the residue level. The fact that MAO exists in two similar forms with different substrate specificities makes MAO particularly appealing for the identification of residues that contribute to catalytic activity and specificity. Indeed, a study involving one of the authors of the present work demonstrated that the residues Ile335 in MAO A and Tyr326 in MAO B (located at an equivalent position within the sequence) play a critical role in the specificity of the isoenzymes.51 Namely, the I335Y mutation makes MAO A more susceptible to substrates and inhibitors of MAO B while the Y326I mutation of MAO B makes its functionality similar to MAO A in the same regard. Other investigated point mutations only affected catalytic activity but not the specificity of MAO A and B.
The point mutation effect is reflected in the changed reaction rates for the oxidation of substrates. We focused our attention primarily to MAO A since it is clear that the deamination half reaction controls the overall rate constant in the A isoform. In the case of MAO B the rate constant depends also on the oxygen concentration and therefore the rate constants for reductive and oxidative half reaction are comparable, preventing the rate limiting step from being unambiguously attributed to the deamination half reaction.32 For phenylethylamine as a substrate the rate constant drops from 11.2 min−1 in the wild type (WT) MAO A to 1.8 min−1 in the I335Y mutant.51 The mutations C374S and C404S led to complete loss of the catalytic activity.52
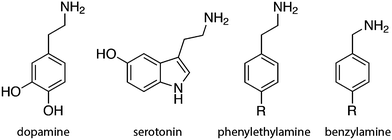
The present work includes the computational elucidation of the mutation effect on the rate of amine oxidation catalyzed by MAO A. As a substrate we chose phenylethylamine (PEA). Unlike dopamine and serotonin, PEA functions as a neuromodulator rather than an excitatory neurotransmitter, influencing several neurons in the brain through macroscopic diffusion and affecting brain plasticity. PEA is chemically similar to amphetamine and some studies suggest that it may be considered as an endogenous amphetamine. Its levels increase after physical exercise, resulting in a mood-enhancing effect.53 As such, PEA is a substrate of MAO and has been extensively used in the in vitro studies of the catalytic activity of MAO. The popularity of PEA derives from the fact that, apart from obvious similarity to endogenic neurotransmitters, various ring-substituted PEA analogs are available, facilitating the research of the effects of substituents and their electronic structure on the kinetics of amine oxidation catalyzed by MAO,22 thereby contributing to the improved understanding of the catalytic function of the enzyme. For the same reason, benzylamine is also a popular benchmark substrate of MAO, differing from PEA only in the length of the aliphatic amino group attached to the phenyl ring (Fig. 2).19,20,27,28 The present study using PEA will pave the way for more extensive studies of the mechanistic aspects of amine oxidation, involving substituents and their electronic structure effects. The most common biogenic and non-biogenic monoamine substrates of MAO are displayed in Fig. 2.
In this study we considered the I335Y mutation, because it is apparently related to the most crucial residue governing the specificity of MAO.51 Additionally, the impact of this mutation on kinetics is significant enough to ensure that the barrier change exceeds the computational precision, but at the same time it remains small enough not to imply that major structural changes of the protein could have occurred. The active site of MAO A with a docked PEA substrate molecule is displayed in Fig. 3.
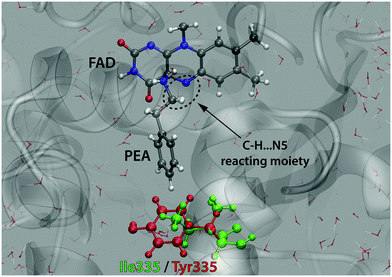 | ||
| Fig. 3 Active site of MAO A with the PEA substrate molecule and the reacting C–H⋯N5 moiety. The residue 335 subjected to mutation (Ile in the WT enzyme and Tyr in the mutant) is also indicated. | ||
Although under physiological conditions PEA mainly exists in a protonated form (pKa ∼ 9.8), the present study uses a neutral PEA molecule as a substrate, because it has been generally accepted on the basis of mechanistic postulates and experimental studies that the amine substrates react with MAO in the non-protonated form.20,27,54 In addition, recent computational studies provide evidence that mechanisms involving protonated amines as substrates are strongly disfavored.13,26 The computed barriers can be corrected for the reversible work of deprotonation, as governed by the difference between pKa of the substrate and physiological pH. However, we did not do so in the present study, because we believe that the pKa correction is circumvented due to the fact that the study is dealing with the same substrate in virtually the same environment – the reasonable assumption is that the difference in the pKa value of PEA between the WT enzyme and in the mutant is negligible.
This work uses a multiscale EVB simulation methodology for the calculation of the effect of I335Y mutation on the rate constant of phenylethylamine decomposition catalyzed by MAO A. The approach delivers the free energy profile of the rate limiting step of the reaction. While simulation of the reaction in the WT enzyme is used for the calibration of EVB parameters (see Section 2.1.), the simulation of the same reaction in the I335Y mutant yields the difference in the free energy barrier between WT MAO A and the mutant and the corresponding change of the reaction rate. The present study also investigates the effects of simulation parameters on the results.
2. Methods and models
2.1. EVB calculation of kinetic parameters of reactions
The two-state EVB Hamiltonian is expressed as a 2 × 2 matrix with the diagonal elements H11 and H22 representing the classical Hamiltonian of the valence state of reactants and products, respectively, whereas the off-diagonal term H12 corresponds to the coupling between the states. In general, the empirical formulation of H12 is an exponential function of interatomic distances, but it is often (also in this work) simplified to a constant. The Hamiltonian matrix is symmetric, hence H21 = H12. A quantity not included in the force field for H11 and H22 is the relative shift between the states representing their difference in heat of formation. By convention, the shift is added as a constant to the product Hamiltonian H22. The EVB free energy profile, Eg, is calculated from the secular equation pertinent to the EVB Hamiltonian:38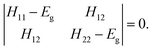 | (1) |
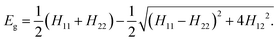 | (2) |
In terms of performance, the EVB approach is comparable to classical methods, allowing for long simulations and converged free energy profiles, while still including the quantum interaction between the valence states. The convenience of the approach is in that it can be done a posteriori on an existing classical simulation, provided that the simulation employs a two-state Hamiltonian, as described above. The common issues associated with the crossing of the barrier can be solved by the established sampling techniques such as umbrella sampling.55 In this work we used the free energy perturbation (FEP) approach56,57 based on gradual transformation between the reactant and the product state using the coupling parameter λ. At each stage of the simulation the effective Hamiltonian H(λ) is expressed as linear combination of the Hamiltonians corresponding to the state of reactants and products:
| H(λ) = λH11 + (1 − λ)H22. | (3) |
The reaction barrier ΔG‡ extracted from the computed free energy profile is related to the rate constant k through the Eyring–Polanyi equation (analogous to Arrhenius equation):
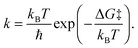 | (4) |
2.2. Computational details
The point mutation effect on the kinetics of PEA oxidation by MAO A was elucidated by the calculation of the free energy profile for the rate limiting step both in WT MAO A and in the I335Y mutant, by using the EVB approach. The simulations and EVB free energy calculations were performed using the program package Q v. 5,58 and the module qdyn as the MD engine.The model of solvated MAO A was built on the basis of the X-ray crystal structure of WT MAO A deposited in the Protein Data Bank (code 2Z5X).59 The simulations were built around the OPLS-AA force field60–62 and performed in a spherical cell with a radius of 30 Å centered at the flavin N5 atom (Fig. 1a and 3), encompassing most of the protein and 1884 water molecules. The parameters were acquired by the ffld_server utility assisted by the Maestro v. 9.7 graphical interface.63 In order to represent the two EVB states (reactants and products) the force field was adequately tuned on the reacting PEA and flavin moiety (36 atoms). The tuning included, among the rest, the replacement of harmonic potentials by Morse functions for breaking the C–H and forming the N–H bond, as well as the replacement of the standard 12-6 Lennard-Jones potential by a less proximity-prohibitive Buckingham-type potential (“soft-core repulsion”) on the reacting C⋯H and N⋯H atom pairs. For both states, atomic charges on the aforementioned 36 atoms were determined by fitting to the electrostatic potential computed by quantum calculations at the HF/6-31G(d) level of theory according to the RESP scheme, as implemented in AmberTools15.64 Due to practical issues related to the structure of the complex corresponding to products, the state of products was represented by the transient intermediate structure in which the flavin moiety remains planar, as was done in a previous study.24
The PEA molecule was manually docked into the active site of MAO A, the resulting model representing the state of reactants. The system was equilibrated in several steps by gradually elevating the temperature to 300 K and removing most of the position restraints. The total equilibration time was approximately 1.3 ns. The resulting relaxed structure was subjected to the I335Y mutation, i.e. the residue Ile335 was changed to Tyr. From this stage on, all the following steps were done independently for both the WT enzyme and the mutant.
The system was further relaxed for approximately 1 ns. Next, ten parallel MD runs were initialized by randomizing the atomic velocities and running short relaxation (typically 50 ps) resulting in ten independent sets of positions and velocities, all corresponding to the state of reactants. From these replicas ten independent sets of FEP simulations were carried out by running, for each replica, a series of consecutive simulations in which the coupling parameter λ was stepwise changed from 1 (reactants) to 0 (products) (eqn (3)). At each step an MD simulation was performed keeping the value of λ constant. The typical λ-step was 0.02, requiring 51 steps to complete the procedure. Depending on the length of MD at each step (see below), the total simulation time of the FEP procedure was between 255 picoseconds and 5.1 nanoseconds. By gradually transforming the model Hamiltonian from the state of reactants to the state of products, the rate limiting step of the reaction was simulated.
The EVB free energy profiles of the replicas were extracted from the simulation data by means of the qfep utility, a part of the Q program package. The two tunable EVB parameters involved in the expression of EVB free energy (coupling term and relative shift) were obtained for the simulated reaction in WT MAO A by fitting to the experimental barrier of 18.57 kcal mol−1 derived from the measured reaction rate of 11.2 min−1.51 The second target variable of the two-parameter fit was the free energy of the rate limiting step that was set to −1.00 kcal mol−1. This quantity cannot be measured experimentally, but the assumed value is in agreement with the previous mechanistic simulation of the oxidation of dopamine.24 While the fitting procedure exactly reproduces (by definition) the free energy barrier for the PEA oxidation in WT MAO A, the fitted EVB parameters were used for the calculation of the barrier for the same reaction in the I335Y mutant, yielding the kinetic effect of point mutation.
The accuracy of the approach was tested by using various combinations of simulation parameters, particularly the length of MD simulations comprising the FEP protocol and the geometric restraints. The typical simulation of the reaction starting from an equilibrated system included 50 ps of relaxation, 51 FEP steps of 10 ps and harmonic position restraints on the PEA and flavin atoms with a force constant of 0.5 kcal (mol−1 Å−2). Additionally, the donor–acceptor C⋯N5 distance in the reacting moiety (Fig. 3) was subjected to a distance restraint with a penalty harmonic potential with a force constant of 5 kcal (mol−1 Å−2) for distances above (but not below) 3 Å.
The construction of the topology, the preparation of inputs for the FEP protocol, the fitting of the EVB parameters and the analysis of the results were facilitated by scripts written by one of the authors (M. P.). The placement of PEA into MAO A and the mutation of MAO A was carried out using the UCSF Chimera program.65 Quantum calculations at the HF/6-31G(d) level yielding atomic charges were performed using the Gaussian09 package.66 All calculations were done at the computer center of the National Institute of Chemistry (16-core servers based on Intel E5-2660 CPUs), typically utilizing 4, 8 or 16 cores per MD run.
3. Results and discussion
3.1. Reaction path sampling issues and restraints
The FEP simulations were performed in ten parallel (replica) runs originating from the same equilibrated system and differing only in the starting conditions generated by randomization of velocities. The replicas represent the different pathways leading from reactants to products via the transition state; depending on whether they cover the same domain of the phase space or diverge into notably different regions of the phase space, the corresponding free energy profiles may exhibit smaller or larger variations between one another. The diversity of the replica reaction pathways can be in a large part controlled by the length of the simulation and by restraints. Ideally, the simulation should be to the greatest possible extent free of restraints and long enough in order to ensure that all statistically relevant parts of the phase space are adequately sampled, which would result in fully converged energy profiles. However, the problem is that the practically achievable simulation lengths are well too short to fulfill these criteria. This particularly holds for torsional degrees of freedom between the reacting entities, for which the corresponding correlation times can be exceedingly long even in the gas phase, let alone in a constrained macromolecular environment that imposes high barriers for torsional rearrangements. A picturesque description of the difficulty of transition path sampling postulates analogy with “throwing ropes over rough mountain passes in the dark,” which comprises the title of a highly cited review of transition path sampling techniques.67 Thus it is legitimate to confine torsional degrees of freedom between the reacting entities (presently enforced by positional restraints on PEA and flavin atoms). In such a way, the problem of long correlation times is in a large part circumvented at the expense of reduced phase space available for sampling. Such treatment has been routinely used in the investigation of macromolecular chemical reactions.24,68,69 The replicated simulations correspond to only slightly different sampling of the phase space, and variations between the profiles are reasonably small even with relatively short simulations. Still, differences between the profiles indicate that full convergence has not been attained; the average of the computed reaction and activation free energies is given as a final result.We examined the influence of restraints and found that it is essential to ensure that PEA and the flavin molecule assume alignment favorable for the reaction already during equilibration; this is best achieved by imposing restraints on both the C⋯N5 distance and the N5⋯H distance in the reacting moiety (see Fig. 3). Both distances were restrained by a harmonic potential with a force constant of 10 kcal (mol−1 Å−2) centered around the distance of 3 and 2 Å for C⋯N5 and N5⋯H, respectively. The restraint on the N5⋯H distance assures that the reacting α-C–H bond remains in the appropriate orientation (pointing towards N5), preventing it from flipping into the opposite direction (pointing away from N5). Such flipping of the C–H bond introduces noise into the free energy profiles, because it requires substantial time for the bond to flip back to the reacting orientation; despite this is sooner or later achieved during the FEP simulation (by increasing the weight of the products Hamiltonian), it is not done smoothly unless the FEP simulation consists of considerably longer MD runs. Once FEP was engaged, we did not find it reasonable to retain the restraint on the N5⋯H distance, since the reaction involves a major change in this geometry parameter. Also, due to sizable oscillations in the separation between PEA and flavin during the reaction, the C⋯N5 distance restraint was weakened by reducing the force constant to 5 kcal (mol−1 Å−2) and abandoning the penalty for distances below 3 Å. This scheme of restraints was found to yield smooth free energy profiles with reasonably small differences between the replicas. From this point on, investigation of the role of simulation settings will be limited to the length of the FEP simulation.
3.2. Free energy profiles
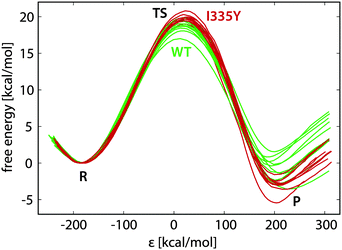
Typical free energy profiles (in batches of ten replicas for WT MAO A and for the I335Y mutant) are displayed in Fig. 4.In Fig. 4 the reaction coordinate is represented by the energy gap (ε), the difference between the Hamiltonians pertaining to reactants (H11) and products (H22): ε = H11 − H22. Such formulation of the reaction coordinate is routinely used in EVB calculations, and has the advantage of efficient mapping of the complex, multidimensional free energy surfaces onto a single coordinate. The profiles in Fig. 4 are reasonably similar to one another, the standard deviation in the free energy barrier being usually smaller than 1 kcal mol−1, but in certain cases reaching below 0.5 kcal mol−1 (Table 1). The diversity of the profiles is controlled by the length of the FEP simulation and by the restraints; therefore, the spread of the profiles and the barrier difference between WT and I335Y MAO A can vary with the simulation settings. However, the profiles are visually similar irrespective of the settings. Importantly, the average barrier for I335Y is always higher than for the WT enzyme.
| FEP step length [ps] | Total length [ps] | WT | I335Y | WT | I335Y | ||||
|---|---|---|---|---|---|---|---|---|---|
| ΔG‡ | σ | ΔG‡ | σ | ΔGR | σ | ΔGR | σ | ||
| 5 | 255 | 18.57 | 0.35 | 20.31 | 0.80 | −1.00 | 0.96 | −2.18 | 1.18 |
| 10 | 510 | 0.54 | 19.68 | 0.47 | 0.93 | −3.00 | 1.01 | ||
| 50 | 2550 | 1.57 | 20.45 | 0.67 | 2.26 | −0.51 | 1.53 | ||
| 100 | 5100 | 0.83 | 19.82 | 0.84 | 1.67 | −1.98 | 1.08 | ||
The simulations in WT MAO A were used for the calibration of EVB parameters; therefore, irrespective of the FEP simulation length the average activation barrier and reaction free energy for WT MAO A are always equal to 18.57 and −1.00 kcal mol−1, respectively. These are the prescribed target values used in the calibration. While the barrier of 18.57 kcal mol−1 is derived from the experimental kinetic data on PEA oxidation by MAO A,51 the reaction free energy of −1.00 kcal mol−1 is an arbitrary estimate implied by the previous EVB study of dopamine degradation by MAO B.24 We tested various target values of the reaction free energy (between −5 and +10 kcal mol−1) and, in agreement with that study, found that it only marginally influences the computed barrier in the I335Y mutant, hence the choice of the reference reaction free energy is of little practical importance, as long as it remains within the above limits.
The calibrated EVB parameters are the coupling term and the relative shift between the reactant and the product state (Section 2.1). In agreement with the postulated transferability, variations in the fitted parameters with simulation settings were small, the coupling term assuming values around 71–72 kcal mol−1 and the shift around 102–105 kcal mol−1. The fitted parameters were used to compute the free energy profiles in the I335Y mutant. In contrast to the WT enzyme, the so obtained replica-averaged activation barrier and the reaction free energy for the mutant vary with the simulation settings. Table 1 lists the computed barriers and free energies as a function of the length of the FEP simulation.
The average activation barrier for I335Y MAO A ranges from 19.68 to 20.45 kcal mol−1. Given that the measured kinetic data for PEA oxidation by I335Y MAO A translates into the barrier of 19.66 kcal mol−1, the agreement with the experiment is very good, although the computed barrier appears to be slightly overestimated. The just slightly exergonic character of the reaction (between −0.51 and −3.00 kcal mol−1 in the mutant) matches the general characteristics of enzymatic reactions; however, since the computed free energy in I335Y MAO A is derived from the arbitrarily postulated reference value of −1.00 kcal mol−1 in WT MAO A, this is of little significance. The increased barrier upon mutation but at the same time increased exergonicity looks counter-intuitive; however, as the computed reaction free energy is typically subjected to twice as large uncertainty as the barrier, we consider this issue to be rather minor.
The standard deviations indicative of the diversity of the FEP replicas are not exhibiting a steady trend with the FEP simulation length, but it can be assumed that they are influenced by two opposing effects, namely: (i) longer simulation improves thermal averaging and yields better convergence of the free energy profile; and (ii) longer simulation increases the possibility of exploring more diverse reaction pathways. While for sufficiently long simulations these effects are equivalent and synergistically lead to fully converged profiles, in the case of limited simulation lengths factor (ii) can eventually lead to poorer convergence and larger deviation between the replicas. If the system is given just enough time to start sampling the areas of phase space otherwise unexplored with shorter simulations, these new areas are possibly not sampled sufficiently, contributing to poorer statistics. Equivalently, the shorter simulation may be confined to a certain area of the phase space, thereby disregarding other areas, but the sampling within that area is sufficient for convergence. The determination of optimal simulation settings that would lead to the most reliable results for the presently studied reactions is in large part associated with the balance between the above outlined factors; it remains an open challenge and deserves further attention in our future research. The factor to be considered is also the CPU economy – the longest of the present simulations FEP (5.1 ns) – which requires about four days to complete, leaving room for improvements, but not allowing for dramatically increased simulation lengths.
Inspection of the plotted profiles (Fig. 4) shows that most of the difference between the profiles is built up in the close vicinity of the transition state. This is in agreement with the long correlation times characteristic of the transition state region. Consequently, since the main sources of diversity are on both sides of the transition state, variations between the replica profiles are typically larger near products than near the transition state. This is clearly reflected in the standard deviations reported in Table 1, the deviations in ΔGR being about twice as large compared to deviations in ΔG‡.
The point mutation effect is reflected in the changed activation barrier and, consequently, in the changed reaction rate of the catalyzed reaction. Converting the barriers computed for the I335Y mutant (Table 1) using eqn (4), Table 2 summarizes the corresponding quantities. While the agreement between the computed and experimental barriers can be proclaimed at least as good or even as excellent (the quantitative agreement of the 510 ps run being probably fortuitous), the agreement of the rate constants is somewhat poorer, but still satisfactory. This is due to the fact that the rate constant is an exponential function of the barrier (eqn (4)), thereby greatly magnifying variations that are considered to be small on the energy scale. For instance, a rate constant measured at 20% relative precision (as in the present case) translates into a precision of 0.1 kcal mol−1 for the free energy. Due to the limitations discussed above, such a precision is probably beyond the reach of the presently used simulations. Nevertheless, despite variations in the computed quantities, the simulations unambiguously demonstrate that the point mutation I335Y of MAO A increases the barrier and decreases the rate constant of PEA oxidation. The magnitude of the effect is reproduced very reasonably, at least at a qualitative level.
3.3. The source of the point mutation effect
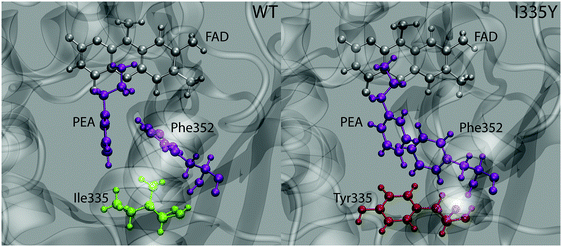
While good agreement between the computed free energy barriers and the experimental data partly validates the employed methodology as a prediction tool for changes in enzyme kinetics upon mutation, further analysis is needed to elucidate the origin of the observed point mutation effect. Geometry inspection of the trajectories reveals a plausible explanation of the barrier increase upon mutation. The most pronounced feature is that the alignment between the phenyl rings of PEA and the neighboring Phe352 residue differs between the WT MAO and the mutant, as displayed in Fig. 5. While in the WT protein the rings are aligned in a quasi T-shape (the angle between the ring planes being 60 degrees or larger), they are nearly parallel in the mutant, assuming displaced stacking alignment. In both cases the alignment does not change during the reaction.The alignment of aromatic rings is controlled by two types of interactions, namely polar quadrupole (favoring T-shape) and dispersion π⋯π (favoring parallel stacking) interactions. While the actual alignment between PEA and Phe352 is likely governed by both, it appears that the contribution of quadrupole interaction is more significant in WT MAO than in the mutant (and vice versa for the Van der Waals interactions). This is reasonable because polar interactions are affected by the polarity of surroundings, whereas dispersion interactions are not. Namely, the increased local polarity induced by the replacement of Ile335 by Tyr attenuates the quadrupole interaction between the phenyl rings of Phe352 and the PEA substrate, but does not alter the stacking interaction between these rings. The resulting change in alignment is due to the changed balance between both types of interaction. Importantly, part of stabilization due to quadrupole interaction between PEA and Phe352 rings is lost upon mutation. As the quadrupole interaction is stronger in the transition state than in the state of reactants (due to larger positive and negative charges on PEA ring hydrogens and carbons, respectively), the weakening of this interaction upon mutation destabilizes the transition state more than the reactants, resulting in the increased barrier. In contrast, we have not observed appreciable changes associated with the interaction between PEA and Ile/Tyr335 that could possibly lead to increased stability of reactants (and therewith increased barrier) due to mutation.
Another effect originating from mutation and possibly contributing to the increased barrier is the increased number of water molecules near the active site. Due to the increased local polarity caused by mutation the average number of water molecules present within 7 Å around PEA is increased by about two. As water near the active site shields the catalytic effect of the polar enzymatic environment, the increased amount of water molecules likely contributes to the increased barrier.
3.4. Notes on mechanistic aspects and geometry
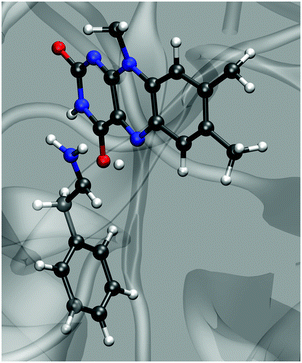
Any simulation of chemical reaction almost necessarily includes mechanistic aspects. Eventually, elucidation of a reaction mechanism is often the main scope of the simulation. Recent examples confirm that mechanistic computational investigations are also popular in the field of amine oxidation by MAO enzymes. These investigations mainly use cluster models treated by DFT and approximate the effects of the polar environment by implicit solvation models.18,26,29 A two-layer ONIOM quantum treatment combining DFT and semiempirical methods has also been used,30 as well as the QM/MM approach on a fully scaled solvated protein.13 All these studies provide valuable mechanistic insights, including geometry features and electronic structure effects. However, reaction path sampling in all these studies is severely limited due to the high complexity of electronic structure protocols. In this regard, the present study is rather peculiar and complementary, because it does not scrutinize mechanistic aspects but rather follows an assumed mechanism (hydride transfer in the present case). Unlike the approaches that rely on quantum treatment of the electron density, thereby facilitating mechanistic investigations from first principles, EVB rather uses pre-determined empirical valence states. Therefore, in EVB simulations, the reaction mechanism is patched into the simulation in the form of force fields and atomic charges of the reactant and the product state. As such, EVB does not yield the reaction mechanism as the output but rather uses one to sample the reaction phase space, making it unfit for first-principles mechanistic studies. In return, the relative simplicity of the protocol facilitates superior reaction phase sampling.Although the presently used methodology is unable to elucidate the reaction mechanism on its own, the fact that the simulations very reasonably reproduce the observed point mutation effect of MAO is encouraging, implying that the assumed mechanism is valid – or at least that it is not elementarily wrong. The hydride transfer proceeds in a similar way as proton transfer in hydrogen bonds – in the transition state (Fig. 6) the hydride ion is located near the midpoint between the α-C atom on PEA and N5 on FAD (but slightly closer to N5), the C⋯N distance reaches a minimum (∼2.8 Å), and fluctuations in the C⋯N distance are greatly reduced. At the same time the amine⋯C4a distance uniformly oscillates around the value of ∼3.2 Å with an upward and downward amplitude of ∼0.3 Å, showing no trend of change in the course of the reaction. This suggests that the proton transfer mechanism is not operational in our simulations, but given that the reaction parameters have been tuned to the hydride transfer mechanism, this is not surprising.
In our simulation setup we ensured that the selected mechanism is formally of a hydride transfer type by setting the charge of PEA and FAD entities in the state of products to be +1 and −1, respectively. Therefore, in the present setup ‘hydride transfer’ strictly means the H− entity (proton plus an electron pair). However, this is only an approximation of the quantities obtained by quantum calculations for that mechanism reported in the earlier work from our laboratory, in which the amount of transferred charge is below unity.26 Nevertheless, the fact that during the reaction a significant amount of negative charge is transferred between the reacting entities justifies the ‘hydride transfer’ term. Similar findings have been reported for an effectively similar ‘concerted asynchronous polar nucleophilic mechanism’, for which the transfer of the hydrogen nucleus and electron density is not perfectly synchronous, and the net amount of transferred charge is about 0.7 electrons.13 Evidently, the mechanisms of the present reaction elucidated by quantum calculations are rarely ‘pure’, and their designation is often debatable. Nevertheless, simulation techniques employed in this work are not intended to distinguish between the proposed mechanisms and judge their reliability, but the assumed mechanism generally matches the findings of recent computational mechanistic studies.
4. Conclusions
The EVB simulation of the I335Y point mutation effect on the catalytic decomposition of PEA by MAO A reasonably reproduces the experimentally observed change of the reaction rate of PEA degradation. The simulations correctly predict the increase of the free energy barrier upon mutation by slightly more than 1 kcal mol−1. On the average, the computed barrier is slightly overestimated and varies with the length of the simulation. A detailed investigation of the reaction pathway sampling can possibly yield improved precision and accuracy of the simulations, but the accuracy of the existing treatment is already good.In order to obtain smooth energy profiles, the torsions are confined by means of restraints, albeit at the expense of limited phase space. Also, it is essential to ensure that the orientation between PEA and flavin facilitates the reaction already at the equilibration stage; this is done by means of distance restraints. The impact of torsional degrees of freedom and therewith associated issues of simulation length, restraints and other factors determining the convergence of the free energy profiles clearly deserve further attention and will be investigated in our future work. Since part of these issues is inherent to the reaction and exists regardless of the environment, gas phase simulations may provide useful information, particularly due to their support for considerably longer simulations, as compared to the sizable model of a solvated protein.
The present simulations offer valuable insights into the origin of point mutation effect. Inspection of the trajectories reveals a significant change in the interaction between the phenyl rings of PEA and the neighboring Phe352 residue. The increased local polarity caused by mutation attenuates the quadrupole interaction between the rings, leading to destabilization that is more pronounced with the transition state than with the reactants. Also, the increased local polarity causes an increase in the number of water molecules present near the active site, contributing to the reduced catalytic effect of the enzyme.
The setup of the present simulations (force field, charges) is based on the assumption that the rate limiting step proceeds by the hydride transfer mechanism.70 While the present study does not scrutinize the mechanistic aspects, hence not providing per se evidence about the mechanism, good agreement with the experiment suggests that the assumed mechanism is reasonable and valid. It also supports the view that the I335Y point mutation preserves the structure of the protein. However, a more detailed investigation is required to provide proof of concept, probably including various substrates, mutations, and alternative mechanisms. Another crucial assumption undertaken in this study is that the I335Y mutation does not significantly alter the structure of the protein. In this view, mutations leading to a complete loss of the catalytic activity, such as C374S and C404S, should be taken with caution or avoided, since they may be associated with significant structural changes beyond the reach of the presently used simulation methodology. Examples of such changes are unfolding or detachment of the FAD cofactor. Further treatment of mutations represents a challenge, but requires this aspect be taken into account.
PEA is popular – together with benzylamine – for in vitro studies of the catalytic function of MAO enzymes, among the rest due to the fact that several ring substitution analogs are available (Fig. 2), facilitating mechanistic studies through the effects of the electronic structure originating from the substituents. In this view, various extensions of the present work are challenging for the future research, including detailed mechanistic aspects of the reaction, changes in the reaction rates upon ring substitution and therewith a related role of electronic structure and nonbonding interactions.
Acknowledgements
Financial support of Slovenian Research Agency (program grant P1-0012) is gratefully acknowledged. M. P. would like to thank his PhD supervisor Lynn Kamerlin and the Knut and Alice Wallenberg Foundation for funding and support. Tsai Family Fund and Boyd and Elsie Welin Professorship to J. C. Shih is also gratefully acknowledged. This work benefited from the Erasmus program scholarship (G. O.).References
- J. C. Shih, K. Chen and M. J. Ridd, Annu. Rev. Neurosci., 1999, 22, 197–217 CrossRef CAS PubMed.
- M. Bortolato, K. Chen and J. C. Shih, Adv. Drug Delivery Rev., 2008, 60, 1527–1533 CrossRef CAS PubMed.
- A. W. J. Bach, N. C. Lan, D. L. Johnson, C. W. Abell, M. E. Bembenek, S. W. Kwan, P. H. Seeburg and J. C. Shih, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 4934–4938 CrossRef CAS.
- N. C. Lan, C. Heinzmann, A. Gal, I. Klisak, U. Orth, E. Lai, J. Grimsby, R. S. Sparkes, T. Mohandas and J. C. Shih, Genomics, 1989, 4, 552–559 CrossRef CAS PubMed.
- J. Grimsby, K. Chen, L. J. Wang, N. C. Lan and J. C. Shih, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 3637–3641 CrossRef CAS.
- J. C. Shih, J. B. Wu and K. Chen, J. Neural Transm., 2011, 118, 979–986 CrossRef CAS PubMed.
- H. G. Brunner, M. Nelen, X. O. Breakefield, H. H. Ropers and B. A. Vanoost, Science, 1993, 262, 578–580 CAS.
- N. Pivac, J. Knezevic, D. Kozaric-Kovacic, M. Dezeljin, M. Mustapic, D. Rak, T. Matijevic, J. Pavelic and D. Muck-Seler, J. Affective Disord., 2007, 103, 131–138 CrossRef CAS PubMed.
- O. Cases, I. Seif, J. Grimsby, P. Gaspar, K. Chen, S. Pournin, U. Muller, M. Aguet, C. Babinet, J. C. Shih and E. Demaeyer, Science, 1995, 268, 1763–1766 CAS.
- M. Bortolato, S. C. Godar, L. Alzghoul, J. L. Zhang, R. D. Darling, K. L. Simpson, V. Bini, K. Chen, C. L. Wellman, R. C. S. Lin and J. C. Shih, Int. J. Neuropsychopharmacol., 2013, 16, 869–888 CrossRef CAS PubMed.
- R. Orru, M. Aldeco and D. E. Edmondson, J. Neural Transm., 2013, 120, 847–851 CrossRef CAS PubMed.
- M. Husain, D. E. Edmondson and T. P. Singer, Biochemistry, 1982, 21, 595–600 CrossRef CAS PubMed.
- E. Abad, R. K. Zenn and J. Kastner, J. Phys. Chem. B, 2013, 117, 14238–14246 CrossRef CAS PubMed.
- M. A. Akyuz, S. S. Erdem and D. E. Edmondson, J. Neural Transm., 2007, 114, 693–698 CrossRef CAS PubMed.
- R. Borstnar, M. Repic, S. C. L. Kamerlin, R. Vianello and J. Mavri, J. Chem. Theory Comput., 2012, 8, 3864–3870 CrossRef CAS PubMed.
- D. E. Edmondson, C. Binda, J. Wang, A. K. Upadhyay and A. Mattevi, Biochemistry, 2009, 48, 4220–4230 CrossRef CAS PubMed.
- S. S. Erdem and B. Buyukmenekse, J. Neural Transm., 2011, 118, 1021–1029 CrossRef CAS PubMed.
- S. S. Erdem, O. Karahan, I. Yildiz and K. Yelekci, Org. Biomol. Chem., 2006, 4, 646–658 CAS.
- S. MacMillar, D. E. Edmondson and O. Matsson, J. Am. Chem. Soc., 2011, 133, 12319–12321 CrossRef CAS PubMed.
- J. R. Miller and D. E. Edmondson, Biochemistry, 1999, 38, 13670–13683 CrossRef CAS PubMed.
- J. R. Miller and D. E. Edmondson, J. Biol. Chem., 1999, 274, 23515–23525 CrossRef CAS PubMed.
- R. K. Nandigama and D. E. Edmondson, Biochemistry, 2000, 39, 15258–15265 CrossRef CAS PubMed.
- M. Repic, M. Purg, R. Vianello and J. Mavri, J. Phys. Chem. B, 2014, 118, 4326–4332 CrossRef CAS PubMed.
- M. Repic, R. Vianello, M. Purg, F. Duarte, P. Bauer, S. C. L. Kamerlin and J. Mavri, Proteins, 2014, 82, 3347–3355 CrossRef CAS PubMed.
- R. B. Silverman, Acc. Chem. Res., 1995, 28, 335–342 CrossRef CAS.
- R. Vianello, M. Repic and J. Mavri, Eur. J. Org. Chem., 2012, 7057–7065 CrossRef CAS.
- M. C. Walker and D. E. Edmondson, Biochemistry, 1994, 33, 7088–7098 CrossRef CAS PubMed.
- J. Wang and D. E. Edmondson, Biochemistry, 2011, 50, 7710–7717 CrossRef CAS PubMed.
- G. Zapata-Torres, A. Fierro, G. Barriga-Gonzalez, J. C. Salgado and C. Celis-Barros, J. Chem. Inf. Model., 2015, 55, 1349–1360 CrossRef CAS PubMed.
- M. A. Akyuz and S. S. Erdem, J. Neural Transm., 2013, 120, 937–945 CrossRef PubMed.
- V. E. Atalay and S. S. Erdem, Comput. Biol. Chem., 2013, 47, 181–191 CrossRef CAS PubMed.
- A. K. Tan and R. R. Ramsay, Biochemistry, 1993, 32, 2137–2143 CrossRef CAS PubMed.
- K. A. Kurtz, M. A. Rishavy, W. W. Cleland and P. F. Fitzpatrick, J. Am. Chem. Soc., 2000, 122, 12896–12897 CrossRef CAS.
- P. F. Fitzpatrick, Arch. Biochem. Biophys., 2010, 493, 13–25 CrossRef CAS PubMed.
- S. F. Sousa, P. A. Fernandes and M. J. Ramos, Phys. Chem. Chem. Phys., 2012, 14, 12431–12441 RSC.
- M. W. van der Kamp and A. J. Mulholland, Biochemistry, 2013, 52, 2708–2728 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- J. Aqvist and A. Warshel, Chem. Rev., 1993, 93, 2523–2544 CrossRef.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- A. Warshel and R. M. Weiss, J. Am. Chem. Soc., 1980, 102, 6218–6226 CrossRef CAS.
- M. H. M. Olsson, J. Mavri and A. Warshel, Philos. Trans. R. Soc., B, 2006, 361, 1417–1432 CrossRef CAS PubMed.
- A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. B. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235 CrossRef CAS PubMed.
- A. J. Adamczyk, J. Cao, S. C. L. Kamerlin and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 14115–14120 CrossRef CAS PubMed.
- J. Aqvist and A. Warshel, Biochemistry, 1989, 28, 4680–4689 CrossRef CAS PubMed.
- J. Aqvist and A. Warshel, J. Am. Chem. Soc., 1990, 112, 2860–2868 CrossRef.
- J. K. Hwang, Z. T. Chu, A. Yadav and A. Warshel, J. Phys. Chem., 1991, 95, 8445–8448 CrossRef CAS.
- J. K. Hwang and A. Warshel, J. Phys. Chem., 1993, 97, 10053–10058 CrossRef CAS.
- A. V. Pisliakov, J. Cao, S. C. L. Kamerlin and A. Warshel, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17359–17364 CrossRef CAS PubMed.
- I. Feierberg, V. Luzhkov and J. Aqvist, J. Biol. Chem., 2000, 275, 22657–22662 CrossRef CAS PubMed.
- The Nobel Foundation, Nobel Prize in Chemistry – Advanced Information, 2013, http://www.nobelprize.org/.
- R. M. Geha, I. Rebrin, K. Chen and J. C. Shih, J. Biol. Chem., 2001, 276, 9877–9882 CrossRef CAS PubMed.
- H. F. Wu, K. Chen and J. C. Shih, Mol. Pharmacol., 1993, 43, 888–893 CAS.
- A. Szabo, E. Billett and J. Turner, Br. J. Sports Med., 2001, 35, 342–343 CrossRef CAS PubMed.
- T. Z. E. Jones, D. Balsa, M. Unzeta and R. R. Ramsay, J. Neural Transm., 2007, 114, 707–712 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- P. Kollman, Chem. Rev., 1993, 93, 2395–2417 CrossRef CAS.
- J. Marelius, K. Kolmodin, I. Feierberg and J. Aqvist, J. Mol. Graphics Modell, 1998, 16, 213–225 CrossRef CAS PubMed.
- S. Y. Son, A. Ma, Y. Kondou, M. Yoshimura, E. Yamashita and T. Tsukihara, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5739–5744 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed.
- Maestro, version 9.7, Schrödinger, LLC, New York, NY, 2014 Search PubMed.
- D. A. Case, J. T. Berryman, R. M. Betz, D. S. Cerutti, I. T. E. Cheatham, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. JanowskiJ. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, T. Luchko, R. Luo, B. Madej, K. M. Merz, G. Monard, P. Needham, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, R. Salomon-Ferrer, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, D. M. York and P. A. Kollman, AMBER 2015, University of California, San Francisco, 2015 Search PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS PubMed.
- B. A. Amrein, P. Bauer, F. Duarte, A. J. Carlsson, A. Naworyta, S. L. Mowbray, M. Widersten and S. C. L. Kamerlin, ACS Catal., 2015, 5, 5702–5713 CrossRef CAS PubMed.
- A. Barrozo, F. Duarte, P. Bauer, A. T. P. Carvalho and S. C. L. Kamerlin, J. Am. Chem. Soc., 2015, 137, 9061–9076 CrossRef CAS PubMed.
- R. Vianello, M. Repic and J. Mavri, Eur. J. Org. Chem., 2012, 7057–7065, DOI:10.1002/ejoc.201201122.
| This journal is © the Owner Societies 2016 |