Computational prediction of optimal metal ions to induce coordinated polymerization of muscle-like [c2]daisy chains

Abstract

Recently, a muscle-like organometallic polymer has been successfully synthesized using Fe²⁺ as a linker atom. The polymer exhibits acid–base controllable muscle-like expansion and contraction on the micrometer scale. Further development could be facilitated by revealing the polymerization mechanism and by searching for optimal linker atoms. In this work, we have examined possible equilibrium and intermediate polymer structures, which consist of [c2]daisy chains linked by divalent transition metal ions (Sc²⁺, Ti²⁺, Fe²⁺, Co²⁺, Ni²⁺ or Zn²⁺) with various hexa-coordination arrangements, based on calculations using density functional theory. We find that the metal linkers in polymers are weaker in acid than in base due to excess positive charges on the polymer, leading to their thermodynamical instability or even decomposition. This can explain the experimental difficulty in improving the degree of polymerization for metal-linked polymers. We also find that the polymers with either Fe²⁺ or Co²⁺ are the most favorable, with the latter extending 1.4% longer than with the former. Since Fe²⁺ has been confirmed experimentally to be a successful linker, Co²⁺ would function equally well and thus could be used as an alternative choice for polymerization.

---

1. Introduction

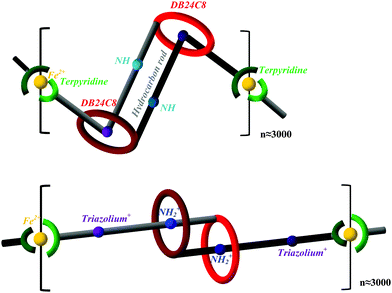
For decades, scientists have synthesized and examined muscle-like functional materials endowed with mechanical expansion and contraction triggered by chemical,^1–7 electrochemical,^1,8–15 or photochemical^10,16–21 stimuli under human control. In 2012, Giuseppone et al.²² successfully synthesized a polymer containing [c2]daisy chains and Fe²⁺ ions, which is acid–base controllable and micrometer-scale responsive while having muscle-like capability. As revealed by measurements of light scattering and small-angle neutron scattering,²² the unit lengths of the extended and contracted polymer units were found to be 5.4 and 3.2 nm, respectively. The 2.2 nm length difference in each unit is amplified in a linear polymer with about 3000 units to cause a stretch to 15 900 from 9400 nm, thus realizing muscle-like motion in a quasi-macroscopic regime. This achievement to some extent overcame the challenge of a low degree of polymerization and significantly advanced the technological prospect of practical muscle-like functional materials.²³

A [c2]daisy chain is a kind of doubly-threaded rotaxane. Each [c2]daisy chain supramolecule consists of two identical rod-and-ring molecules that are threaded to each other; they have the capability of telescoping as well as folding, which enables expansion and contraction (shown in Fig. 1) of each monomer. By adding the linking metal ion Fe²⁺, polymerization can be induced. As schematically shown in Fig. 1, the polymer unit is composed of one [c2]daisy chain and one Fe²⁺ ion, which are linked by organometallic hexa-coordination. The number of units (n) in the experimentally synthesized polymer was found to be about 3000 by Giuseppone's group.²² Each half of the [c2]daisy chain is threaded through the other half's dibenzo[24]-crown-8 (DB24C8) ether ring, while the bulky stopper (terpyridine group together with its adjacent ethinyl and phenyl species) prevents dethreading and also serves as a polymerizing linkage to the neighboring [c2]daisy chain by means of a bridging Fe²⁺. Each half of the [c2]daisy chain contains two recognition sites located in the thread, which serve as “docking stations” for the contracted vs. extended forms of the polymer: one is a triazolium ion (C₂N₃⁺) and the other is a neutral amino group (NH) at high pH, which changes to a secondary dialkyl ammonium ion (NH₂⁺) in a low pH environment. The length of each unit varies dynamically as the binding affinity of DB24C8 for the two docking stations changes with pH: in acidic solution (e.g., trifluoroacetic acid), the NH₂⁺ preferentially attaches to the crown ether, resulting in the extended form; in basic solution (e.g., sodium hydroxide), the deprotonated NH has lower affinity for the crown ether, which therefore binds with the triazolium ion, favoring the contracted form. The contraction/extension cycle of the above described single [c2]daisy chain²⁴ supramolecule has been studied in our previous computational simulations²⁵ using the monomer of this muscle-like polymer.^22,23 Our systematic quantum chemical and molecular dynamics calculations have revealed that the polymer length change is not only due to the linear telescoping between the two docking stations but also due to the folding/unfolding of the two bulky stoppers,²⁵ which is a striking difference as illustrated in Fig. 1 (top vs. bottom).

Fig. 1 Schematic representations of the polymerized [c2]daisy chain linked with Fe²⁺ ions (yellow balls). Each half of the [c2]daisy chain consists of a hydrocarbon rod (straight segments) with two docking stations (blue and purple balls), a crown ether ring DB24C8 (red ring), and a terpyridine end group (green arc). Two identical halves are mutually threaded to form a [c2]daisy chain unit, docked (top panel) at the triazolium⁺ station (in high pH) in the contracted state, or (bottom panel) at the NH₂⁺ station (in low pH) in the extended state.

Following a bottom-up strategy, the experimental quasi-macroscopic muscle-like behavior originates from the uniform change of many identical organometallic units. Thus, extending our prior study of the behavior of an individual [c2]daisy chain, investigations of the characteristics of the polymer containing different transition metal ions carried out in this work can clarify important aspects of this system and shed light on the mechanism of polymerization induced by the metal ions, which in turn can help in the design of optimal linkers.

2. Models and computational details

In this work, we choose Sc²⁺, Ti²⁺, Fe²⁺, Co²⁺, Ni²⁺ or Zn²⁺ to evaluate their effects on the polymer structures as they belong to the same period of elements with 3d¹, 3d², 3d⁶, 3d⁷, 3d⁸ or 3d¹⁰ valence electrons, respectively. It is known that the Lewis acidity^26,27 of Fe²⁺, Co²⁺, Ni²⁺ and Zn²⁺ ranges between soft and hard, giving some flexibility to coordinate with soft or hard Lewis bases. Nonetheless, their chemical characteristics may differentiate their role in inducing coordinated polymerization in our case and thus allow optimizing their use in applications. Although Sc²⁺ and Ti²⁺ are not the most frequent oxidation states of these elements, they are chosen to track the dependence of polymer energetics on the number of 3d electrons. Since Fe²⁺ or Zn²⁺ was used in experiment²² to induce polymerization, we use them as the comparative reference in this work.

This work uses the same approach and terminology as our previous study of the monomeric [c2]daisy chain.²⁵ Briefly, the extended and contracted [c2]daisy chains are still named ext⁴⁺ and cont²⁺, respectively. The configuration ext⁴⁺ (C₁₁₆H₁₃₄O₁₆N₁₄) carries four positive charges localized at two NH₂⁺ and two triazolium cations, while the two positive charges of cont²⁺ (C₁₁₆H₁₃₂O₁₆N₁₄) are localized at two triazolium cations. The acidic environment is represented by two protons attached to the nitrogen atoms of the amino groups and the basic environment is modeled through neutralizing the two protons (of NH₂⁺), which are then left out of the calculation. The metal ions are, before further optimization, inserted at equal distances (∼2 Å) from nearby nitrogen atoms of the terpyridines so as to hexa-coordinate with two [c2]daisy chains, which connect head-to-tail through a metal ion due to a periodic boundary condition. In the dimensions perpendicular to the chain, there are large intermolecular distances to avoid discernible interaction between parallel polymers.

In the experiment by Giuseppone et al.²² the cationic [c2]daisy chains and Fe²⁺ ions were polymerized in an ionic liquid, where stoichiometric PF₆⁻ and Cl⁻ counterions accompany the polymers to neutralize the charge in the environment of organic solvents (acetonitrile CH₃CN and chloroform CHCl₃ in a 1 : 1 mixture solution). The neutral polymer unit in acid or base is actually composed of C₁₁₆H₁₃₄O₁₆N₁₄Fe(PF₆)₄Cl₂ or C₁₁₆H₁₃₂O₁₆N₁₄Fe(PF₆)₂Cl₂. However, we do not include the PF₆⁻ and Cl⁻ counterions in our calculations as they usually interact only indirectly with the polymer and float around the cationic polymer in complexes with solvent molecules. We have previously²⁵ presented the stable complexes PF₆⁻(CH₃CN)_n or PF₆⁻(CHCl₃)_n (n = 1–8) and verified that these solvents provide a soft negative electrostatic potential environment for [c2]daisy chains, which thus avoids strong electrostatic interactions between the [c2]daisy chains and the surrounding counter-ions while keeping the [c2]daisy chain in a functioning state during the muscle-like motion. To simplify the calculation model, we thus feel justified to study the cationic polymer under vacuum.

Due to the fact that [c2]daisy chains are of large size and contain weak interactions such as hydrogen bonds and/or π–π stacking, the self-consistent charge density-functional tight-binding dispersion (SCC-DFTB-D) method^28–35 is first utilized to optimize the molecular and unit cell structure. Dispersion contributions are included via Lennard-Jones potentials, which take the parameters from the universal force field. The Slater–Koster (SK) potentials of metals with C, H, O, N are taken from the parameter sets trans3d^36,37 and znorg,^38–40 which have been well tested to predict comparably accurate geometries using DFT.

Applying periodic boundary conditions, the lattice component force is calculated together with the interatomic force during each SCC cycle. If the structure reaches the force optimization criterion but the lattice does not, the unit cell is automatically modified to other cell lengths until the lattice force converges. A global search is carried out to find the most favorable equilibrated and intermediate conformations of the polymer units corresponding to lowest total energies.

To verify the reliability of DFTB in predicting geometric structures in our work, we firstly study small complexes with hexa-coordination bonds formed between two terpyridines and one metal ion by SCC-DFTB-D and ωB97XD/6-31G* optimization, as listed in Table S1 (ESI†). The results confirm that SCC-DFTB-D can successfully predict similar hexa-coordination geometries as DFT and can deal with periodic and complicated polymer structures in this study. To obtain reliable molecular orbitals and energetic data, single-point calculations using the geometries derived at the SCC-DFTB-D level of theory are carried out using ωB97XD/6-31G*, a long-range hybrid density functional theory with dispersion corrections, available in the Gaussian 09 package.⁴¹ Note that the ωB97XD⁴² functional yields satisfactory accuracy for thermochemistry, kinetics, and non-covalent interactions.

3. Results and discussion

3.1 Polymer units

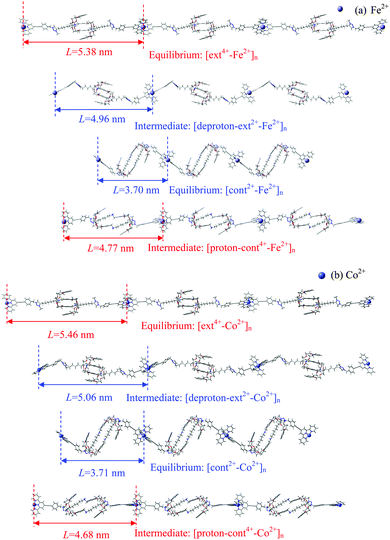
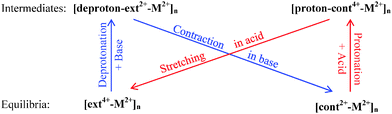
The combined optimization of geometry and cell parameters yields polymer structures containing transition metal ions (M²⁺: Sc²⁺, Ti²⁺, Fe²⁺, Co²⁺, Ni²⁺, or Zn²⁺). Fig. 2(a) and (b) and Fig. S1(a)–(d) (cf. ESI†) display two equilibrium structures and two intermediate polymer structures of three units of an infinite polymer chain for each of the six metal ions. Hereafter, the extended equilibrium and protonated intermediate polymers under acidic conditions are called [ext⁴⁺-M²⁺]_n and [proton-cont⁴⁺-M²⁺]_n, respectively, while the contracted equilibrium and deprotonated intermediates in base are denoted as [cont²⁺-M²⁺]_n and [deproton-ext²⁺-M²⁺]_n, respectively. Here n stands for infinite repetition in the polymers. The muscle-like motion cycles among four conformations follow the generic sequence shown in Scheme 1.

Fig. 2 The equilibrium and intermediate polymer structures in three linked units containing (a) Fe²⁺ or (b) Co²⁺, from SCC-DFTB-D calculations under vacuum. Gray, white, red, and blue atom colors represent C, H, O, and N, respectively. (Note that the terpyridine and benzene groups in the bulky stoppers are connected by –C≡C– groups, which in this representation look like abnormally long single bonds.)

Scheme 1 The cyclic process of acid-induced extension and base-promoted contraction among two equilibria and two intermediates in a simplified energy diagram. M²⁺ ions: Sc²⁺, Ti²⁺, Fe²⁺, Co²⁺, Ni²⁺, or Zn²⁺.

Interestingly, our calculations show that not all of the metal ions can induce stable muscle-like polymers. While polymerization is accomplished when using Sc²⁺, Fe²⁺ or Co²⁺, the use of Ti²⁺, Ni²⁺, or Zn²⁺ induces instabilities in the protonated intermediate polymer, as shown in Fig. S1(b)–(d) (ESI†). In [proton-cont⁴⁺-Ti²⁺]_n and [proton-cont⁴⁺-Ni²⁺]_n, the N–C bonds near NH₂⁺ break up, fragmenting the [c2]daisy chains and interrupting further extension. For example, the distances between N (of NH₂⁺) and the neighboring C (of CH₂) in [proton-cont⁴⁺-Ti²⁺]_n are increased to 2.055 and 2.057 Å, indicating bond breaking. In [proton-cont⁴⁺-Zn²⁺]_n, two DB24C8 rings are opened considerably and the hydrocarbon rods are no longer kept linear, counteracting the lengthening step. Thus, it appears that the conformations under the acidic conditions become unstable and may even decompose. The N–C bond cleavage phenomenon is worth noticing by the experimentalists as it probably impedes the smooth stretching of the polymer in its practical application.

To quantify the hexa-coordination behavior, we check the distances between the M²⁺ and the six N atoms to which the M²⁺ ion is coordinated in the terpyridine groups of [c2]daisy chains, as listed in Table 1. In most conformations, two shorter and four longer M²⁺–N bond lengths reflect reasonable metal coordination as suggested by the d²–sp³ orbital hybrid. However, one particularly long distance (>2.5 Å) appears in the systems [ext⁴⁺-Fe²⁺]_n, [proton-cont⁴⁺-Fe²⁺]_n, [proton-cont⁴⁺-Co²⁺]_n, [ext⁴⁺-Ni²⁺]_n, [proton-cont⁴⁺-Ni²⁺]_n, [cont²⁺-Ni²⁺]_n, and [deproton-ext²⁺-Ni²⁺]_n. This suggests that the conformations are becoming more distorted and weaker in acid than in base. Ni²⁺ is not a good linker ion for this muscle-like polymer as it cannot hexa-coordinate well with [c2]daisy chains, as shown by one unusual Ni²⁺–N distance (∼3 Å) in all its configurations. The more uneven hexa-coordination bonds via Ni²⁺ will probably make the polymer more easily disordered than other ions so as to fail in undergoing multiple muscle-like cycles. Fe²⁺–N bond lengths are in the range 1.9–2.1 Å (a distance larger than 2.5 Å is obtained in the unstable intermediate and not considered here), basically consistent with the experimental value of 2.06 Å, as reported in a similar complex.⁴³ This again reflects that SCC-DFTB-D can ensure comparable coordination bond lengths with the experiment.

Table 1 M²⁺–N distances in polymers calculated by SCC-DFTB-D; the six values in each situation correspond to the hexa-coordination of the ion to six N atoms; italic values are abnormally long, indicating instability of those conformations (unit: Å)

Extended polymer	M^2+–N distances	Contracted polymer	M^2+–N distances
[ext^4+-Sc^2+]n	2.349, 2.349, 2.372	[cont^2+-Sc^2+]n	2.342, 2.343, 2.372
	2.373, 2.375, 2.375		2.372, 2.373, 2.374
[deproton-ext^2+-Sc^2+]n	2.325, 2.326, 2.369	[proton-cont^4+-Sc^2+]n	2.349, 2.350, 2.372
	2.369, 2.373, 2.373		2.372, 2.375, 2.376
[ext^4+-Ti^2+]n	1.520, 1.935, 1.981	[cont^2+-Ti^2+]n	1.920, 1.983, 2.075
	2.028, 2.238, 2.304		2.120, 2.170, 2.258
[deproton-ext^2+-Ti^2+]n	2.040, 2.041, 2.118	[proton-cont^4+-Ti^2+]n	1.936, 1.942, 1.990
	2.119, 2.119, 2.121		1.991, 2.293, 2.301
[ext^4+-Fe^2+]n	1.921, 1.971, 1.980	[cont^2+-Fe^2+]n	1.934, 1.935, 2.042
	2.031, 2.032, 2.538		2.042, 2.043, 2.043
[deproton-ext^2+-Fe^2+]n	1.933, 1.935, 2.041	[proton-cont^4+-Fe^2+]n	1.920, 1.970, 1.979
	2.041, 2.042, 2.042		2.031, 2.031, 2.538
[ext^4+-Co^2+]n	1.888, 1.888, 1.950	[cont^2+-Co^2+]n	1.885, 1.886, 1.948
	1.950, 1.950, 1.951		1.948, 1.948, 1.948
[deproton-ext^2+-Co^2+]n	1.882, 1.882, 1.945	[proton-cont^4+-Co^2+]n	1.862, 1.915, 1.923
	1.945, 1.946, 1.946		1.928, 1.936, 2.784
[ext^4+-Ni^2+]n	1.953, 2.026, 2.027	[cont^2+-Ni^2+]n	1.951, 2.022, 2.028
	2.096, 2.109, 3.020		2.082, 2.106, 3.000
[deproton-ext^2+-Ni^2+]n	1.946, 2.018, 2.022	[proton-cont^4+-Ni^2+]n	1.953, 2.023, 2.028
	2.089, 2.099, 3.008		2.100, 2.102, 3.006
[ext^4+-Zn^2+]n	2.080, 2.081, 2.106	[cont^2+-Zn^2+]n	2.074, 2.076, 2.103
	2.107, 2.107, 2.108		2.105, 2.112, 2.114
[deproton-ext^2+-Zn^2+]n	2.064, 2.064, 2.110	[proton-cont^4+-Zn^2+]n	2.081, 2.081, 2.105
	2.110, 2.114, 2.114		2.105, 2.108, 2.108

---

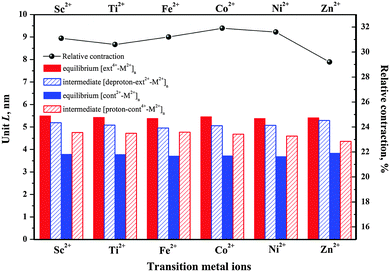
To examine the impact of the metal linker on the polymer length, we define the unit length (L) as the distance between two successive M²⁺ ions, as labeled in Fig. 2 and Fig. S1 (ESI†) and then compared in Fig. 3. The unit length data are all listed in Table S2 (ESI†). Firstly, it should be noted that the theoretical L value of [ext⁴⁺-Fe²⁺]_n is found to be 5.38 nm, in good agreement with the corresponding experimental value of 5.4 nm. Furthermore, the muscle-like motion is clearly exhibited by the unit length changes among these four conformations. Starting from the equilibrated state in acid, as the solution is changed from acidic to basic, the [ext⁴⁺-M²⁺]_n state (leftmost solid red bars in Fig. 3) converts to the [deproton-ext²⁺-M²⁺]_n state (next bars toward the right) with the lengths slightly decreasing by 0.3–0.4 nm. This change is induced by the slight folding of the bulky stoppers as displayed in Fig. 2 and Fig. S1 (ESI†). Next, the contraction process from the [deproton-ext²⁺-M²⁺]_n intermediate to the [cont²⁺-M²⁺]_n equilibrium (next blue bars toward the right) causes the unit length to greatly decrease by 1.3–1.5 nm. As the solution is changed from basic to acidic, [cont²⁺-M²⁺]_n becomes [proton-cont⁴⁺-M²⁺]_n (rightmost bars) and the unfolding of the bulky stoppers is clearly manifested as the unit length dramatically increases by 0.9–1.0 nm. The cycle is completed when the extension process from the [proton-cont⁴⁺-M²⁺]_n intermediate to the [ext⁴⁺-M²⁺]_n equilibrium (leftmost solid red bars) shows unit lengths increasing by 0.6–0.8 nm. This indicates that the pathway of the contraction and stretching in the polymer is basically consistent with our analysis for the individual [c2]daisy chain supramolecule and confirms that the folding of the two bulky stoppers occurs in the last phase of contraction while unfolding takes place in the first phase of stretching.²⁵ The response of the polymer to the acid is obvious at first, namely, the initial unfolding process significantly increasing the polymer length. Afterwards, the linear extension in the following process is hampered by a higher barrier and becomes difficult as revealed in our previous study.²⁵ By contrast, the structural response of the polymer to the base is not as apparent as to the acid at first, while the subsequent contraction is smoother than stretching with a lower energy barrier.

Fig. 3 Calculated polymer unit lengths of equilibria and intermediates and relative contraction between two equilibria containing Sc²⁺, Ti²⁺, Fe²⁺, Co²⁺, Ni²⁺, or Zn²⁺, from SCC-DFTB-D calculations under vacuum.

Notably, the unit length difference between [ext⁴⁺-M²⁺]_n and [cont²⁺-M²⁺]_n equilibria plays a key role in determining the relative polymer contraction under acid–base actuation. As shown in Fig. 3, the highest relative contraction, 31.9%, is found in the case of Co²⁺, while the second and third highest, are 31.6% and 31.2% for Ni²⁺ and Fe²⁺. Ni²⁺ is excluded here due to unsuccessful [proton-cont⁴⁺-Ni²⁺]_n configuration. The main advantage of Co²⁺ is that the [ext⁴⁺-Co²⁺]_n is perfectly extended 1.4% longer than [ext⁴⁺-Fe²⁺]_n, while [cont²⁺-Co²⁺]_n remains relatively as short as [cont²⁺-Fe²⁺]_n. Considering that Fe²⁺ has been successfully used in experiment, we thus conjecture that the polymer containing Co²⁺ might function equally well as that containing Fe²⁺.

3.2 Hexa-coordination of M²⁺ with [c2]daisy chains

Integrated muscle-like polymerization was realized in experiment by using metal ions to link daisy chains together. A single M²⁺ connects two [c2]daisy chains by forming the bis(terpyridine)-M²⁺ coordination complex with coordination of the metal ion to 6 N atoms in 6 pyridine rings. Increasing the degree of polymerization to lengthen the polymer is a key for enabling macroscopic expansion and contraction for large-scale mechanical applications. Hence, it is important to study the coordination of M²⁺ with rotaxanes at the molecular level.

It should be noted here that, compared to the [c2]daisy chain monomers, the polymerization reaction reorients 4 of the 6 pyridine rings in the two adjacent [c2]daisy chains such that 6 N atoms can bond to the linking metal ion: this converts the two adjacent terpyridines from trans to cis configuration. The trans form is a natural and stable state for [c2]daisy chains before polymerization and needs to be activated to the cis form and then to coordinate with M²⁺ for creating a polymer. This trans to cis conversion deforms the terpyridines moderately. For example, the N–C–C–N dihedral angle highlighted by enlarged balls in the trans and cis forms is shown in Fig. S2 (ESI†) for the four conformers of the monomer. While terpyridine is close to planar in the monomeric trans form, it is tilted by about 20° between two pyridine parts in the monomeric cis form, except for cont²⁺ which is planar, as shown in Fig. S3 (ESI†). The inevitable deformation will, to some extent, impact the coordination with metal ions in a symmetric coordination field. Nonetheless, the metal ions may try to flatten the terpyridine as they react with the [c2]daisy chains. The energy differences in the trans to cis conversions for the four states range from 151 to 156 kcal mol⁻¹ at the ωB97XD/6-31G* level of theory, cf. Fig. S3 (ESI†). This means that cis-terpyridine will be automatically converted to the trans form once the M²⁺–N coordination bond is broken and that more input energy is required to recover the polymerization reaction.

The formation of hexa-coordination bonds in an octahedral environment would require the use of the unoccupied 3d, 4s, 4p orbitals of the metal ions to interact with orbitals occupied by twelve electrons of the [c2]daisy chain. This is facilitated by two terpyridines each consisting of three nitrogen atoms each of which has a σ donor electron pair. Fig. S4 (ESI†) shows the twelve electrons localized at two terpyridine groups, confirming that the polymerization reaction occurs at the two ends. The six 3d electrons of Fe²⁺ fill the 3d_xy, 3d_xz and 3d_yz orbitals, leaving behind six empty 3d_z², 3d_x²−dy², 4s, 4p_x, 4p_y, 4p_z orbitals pointing at the N ligands. Six fully filled bonding orbitals and six empty anti-bonding orbitals will be formed in the Fe-based hexa-coordination compound. For Co²⁺, Ni²⁺ and Zn²⁺, one, two, or four more 3d electrons should fill the “anti-bonding” (e_g*) orbitals, destabilizing more the hexa-coordination compound than Fe²⁺. For Sc²⁺ and Ti²⁺, the only one or two 3d electrons should also fill the “non-bonding” (t_2g) orbitals but their relatively large ion radii may be not as favorable as Fe²⁺ for forming stable hexa-coordination bonds. Thus, Fe²⁺ is the best choice. On the other hand, the Sc²⁺ or Co²⁺ has an unpaired electron as it hexa-coordinates with [c2]daisy chains. Thus, the spin signal from the Sc-based and Co-based polymers may also help in probing some changes from the polar or non-polar environment provided by the ionic liquid.

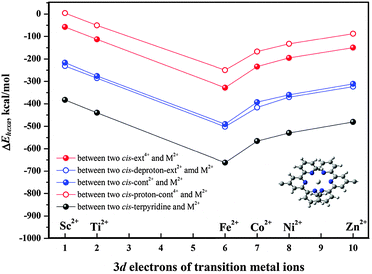
We have discussed above how the hexa-coordination is impacted by the conformational change. To examine the linking strength, i.e., the thermal stability of the organometallic coordinated polymers, we have calculated the hexa-coordination reaction heats (ΔE_hexa) between two [c2]daisy chains and M²⁺ according to the equation: ΔE_hexa = E_hexacoord − E_M²⁺ − 2E_{[c2]DaisyChain}. Here, all terpyridine groups in all hexa-coordination compounds are in cis form, and [c2]daisy chains can be cis-ext⁴⁺, cis-deproton-ext²⁺, cis-cont²⁺, and cis-proton-cont⁴⁺. The structures containing Co²⁺ are shown in Fig. S5 (ESI†) as an example, where the Co²⁺ and six coordinated N are highlighted by enlarged balls. The polymerization reaction heats (ΔE_hexa) for M²⁺ linking two [c2]daisy chains in four configurations were calculated at the ωB97XD/6-31G* level of theory based on the SCC-DFTB-D geometries, as shown in Fig. 4. The single-point energy corrections at the higher level of DFT based on the structures predicted by SCC-DFTB-D can guarantee a correct trend of the hexa-coordination thermal stability (see Fig. S6, ESI†). Among the metal ions that we studied, the linking strength is in the order: Fe²⁺ > Co²⁺ > Ni²⁺ > Zn²⁺ ≈ Ti²⁺ > Sc²⁺. The structure with Fe²⁺ presents the highest stability whereas the one with Sc²⁺ is the least stable. This leaves Co²⁺ as the theoretically next favorable choice for being applied in this muscle-like polymer. Our results in fact support the experimental observation²³ that, when Zn²⁺ instead of Fe²⁺ was used as the transition metal, the partial depolymerization of its extended polymer occurred while the contracted polymer was successfully obtained.

Fig. 4 Calculated hexa-coordination reaction heats (ΔE_hexa) at the level of ωB97XD/6-31G*.

Moreover, Fig. 4 indicates that the polymerization of [c2]daisy chains with M²⁺ occurs in the order: deproton-ext²⁺ > cont²⁺ > ext⁴⁺ > proton-cont⁴⁺. The contraction in base is energetically more favorable than the stretching in acid, with the reaction heats for the contracted case being about twice as large as for the extended case. A smaller reaction heat would easily lead to thermal decomposition of the extended polymer, especially for the protonated intermediates, and thus stops expansion during a cyclic motion. It is actually difficult to polymerize cationic monomers, as more positive charges on ext⁴⁺ or proton-cont⁴⁺ may hinder the polymerization reaction due to a larger electrostatic repulsion between the tetra-cationic [c2]daisy chains and the di-cationic M²⁺. We have verified this by calculating the reaction heat for two neutral cis-terpyridine molecules coordinating with one M²⁺, which represents the linking segment in all polymer structures. As shown in Fig. 4, their reaction heats are all increased by the same amount, much larger than for any polymerization. Clearly, in the experiment there are PF₆⁻ and Cl⁻ counterions in solution to compensate charged monomers and to help alleviate the Coulomb repulsion from its positive charges and ensure that polymerization occurs. Otherwise the hexa-coordination of M²⁺ with the [c2]daisy chains would be weakened considerably. However, from a different perspective, counterions are actually counter-productive because this polymer relies on two positive recognition sites to perform contraction and expansion. We believe that this is the main reason why in experiment it has been difficult to further improve the degree of polymerization. We note that Fig. 4 merely shows a general trend of the polymerization ability for a charged [c2]daisy chain monomer as the computational model does not include the accompanying counterions. Nevertheless, it tells us that further improvement of the thermal stability of the polymer by selecting an optimal metal ion such as Fe²⁺ and Co²⁺ or moving to neutral [c2]daisy chain supramolecules may help in increasing the degree of polymerization.

To further reflect the interaction strength between the metal ion and the [c2]daisy chain, we additionally calculate the Mayer bond order^44–46 (MBO) in each hexa-coordination compound, as shown in Fig. 5. It is surprisingly found that the MBOs from Co²⁺ are strongest except for coordinating with cis-deproton-ext²⁺, while those from Zn²⁺ are weakest. The MBO order is: Co²⁺ > Ti²⁺ > Fe²⁺ > Ni²⁺ > Sc²⁺ > Zn²⁺. It is seen that Co²⁺ is indeed an option for being applied to the muscle-like [c2]daisy chain polymer.

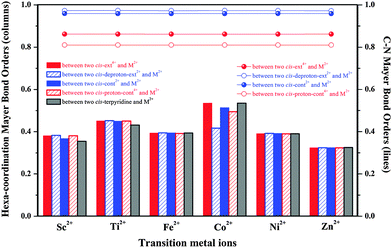Fig. 5 Calculated Mayer bond orders of the hexa-coordination bonds (in columns) and the C–N bonds at the C–N(H/H₂⁺)–C sites (in lines) at the level of ωB97XD/6-31G*.

Lastly, an MBO analysis can help reflect the N–C bond weakening in the C–N(H/H₂⁺)–C sites of all hexa-coordination compounds, as shown in Fig. 5. Under the basic conditions, the MBO values of the NH group with two neighboring alkyl C are 11–20% higher than those of NH₂⁺ under the acidic conditions, especially compared to the protonated intermediates. This indicates that the N–C bond strength is significantly reduced in the acidic environment, analogous to the hexa-coordination thermal stability. Since structural deformation in all hexa-coordination compounds is not as strong as in the realistic periodic polymers, we do not see the breakage of the N–C bond in compounds. However, it is expected from bond order results that the N–C breakage in the polymers will most likely occur in the most heavily distorted [proton-cont⁴⁺-M²⁺]_n, which is supported by the N–C cleavages in [proton-cont⁴⁺-Ti²⁺]_n and [proton-cont⁴⁺-Ni²⁺]_n. The N–C bond order change has no direct relationship with the metal type, see the four almost flat curves in Fig. 5, and will be significantly affected by the acid–base environment change.

4. Conclusions and perspectives

The study of equilibrium and intermediate polymer configurations in acid or base formed by linking muscle-like [c2]daisy chains with various transition metal ions reveals stable polymers linked by Sc²⁺, Fe²⁺ and Co²⁺ instead of Ti²⁺, Ni²⁺ and Zn²⁺. The conformations in acid suffer strong distortions quite easily and can even decompose, especially for the protonated contracted polymer. The bond between N (of NH₂⁺) and its neighbor C (of CH₂) is much weakened due to acid catalysis. The positive excess charges on the [c2]daisy chains greatly reduce the reaction heat for polymerization and weaken the hexa-coordination links with metal ions, showing the difficulty to improve the degree of polymerization to macroscale as experienced in experiment. In hexa-coordination compounds, the thermal stability vary with the order: Fe²⁺ > Co²⁺ > Ni²⁺ > Zn²⁺ ≈ Ti²⁺ > Sc²⁺, while the Mayer bond order has the order: Co²⁺ > Ti²⁺ > Fe²⁺ > Ni²⁺ > Sc²⁺ > Zn²⁺. Thus, Fe²⁺ and Co²⁺ are both optimal metal ions for polymerization by theoretical predictions. Furthermore, the extended polymer linked by Co²⁺ is 1.4% longer than that by Fe²⁺, producing a 0.7% higher relative contraction than with Fe²⁺. As Fe²⁺ has been shown in experiment to be a successful linker, Co²⁺ ions would function equally well and thus could be used as an alternative choice for polymerization.

Acknowledgements

We thank the High Performance Cluster Computing Centre, Hong Kong Baptist University, which receives funding from the Research Grants Council, University Grants Committee of the HKSAR and HKBU. This work was supported in part by project no. 9041650 of the Research Grants Council of HKSAR and the Scientific Research Foundation for the Returned Overseas Chinese Scholars, Ministry of Education of China (Grant No. [2013]693). MAVH and YLZ were supported in part by the HKBU Strategic Development Fund. CM acknowledges support from HKBU's Sabbatical Visitor scheme and partial support from the HKBU Strategic Development Fund. KH acknowledges support from HKBU's Distinguished Scholar scheme and partial support from the HKBU Strategic Development Fund.

References

1. R. A. Bissell, E. Crdova, A. E. Kaifer and J. F. Stoddart, Nature, 1994, 369, 133–137.
2. M.-V. Martínez-Díaz, N. Spencer and J. F. Stoddart, Angew. Chem., Int. Ed. Engl., 1997, 36, 1904–1907.
3. P. R. Ashton, R. Ballardini, V. Balzani, I. Baxter, A. Credi, M. C. T. Fyfe, M. T. Gandolfi, M. Gómez-López, M.-V. Martínez-Díaz, A. Piersanti, N. Spencer, J. F. Stoddart, M. Venturi, A. J. P. White and D. J. Williams, J. Am. Chem. Soc., 1998, 120, 11932–11942.
4. M. C. Jiménez, C. Dietrich-Buchecker and J.-P. Sauvage, Angew. Chem., Int. Ed., 2000, 39, 3284–3287.
5. J. Wu, K. C. Leung, D. Bentez, J.-Y. Han, S. J. Cantrill, L. Fang and J. F. Stoddart, Angew. Chem., Int. Ed., 2008, 47, 7470–7474.
6. P. G. Clark, M. W. Day and R. H. Grubbs, J. Am. Chem. Soc., 2009, 131, 13631–13633.
7. Z. Zhang, C. Han, G. Yu and F. Huang, Chem. Sci., 2012, 3, 3026–3031.
8. P. Gaviña and J.-P. Sauvage, Tetrahedron Lett., 1997, 38, 3521–3524.
9. L. Raehm, J.-M. Kern and J.-P. Sauvage, Chem. – Eur. J., 1999, 5, 3310–3317.
10. N. Armaroli, V. Balzani, J.-P. Collin, P. Gaviña, J.-P. Sauvage and B. Ventura, J. Am. Chem. Soc., 1999, 121, 4397–4408.
11. R. Ballardini, V. Balzani, W. Dehaen, A. E. Dell'Erba, F. M. Raymo, J. F. Stoddart and M. Venturi, Eur. J. Org. Chem., 2000, 591–602.
12. J.-P. Collin, C. Dietrich-Buchecker, P. Gaviña, M. C. Jimenez-Molero and J.-P. Sauvage, Acc. Chem. Res., 2001, 34, 477–487.
13. Y. Liu, A. H. Flood, P. A. Bonvallet, S. A. Vignon, B. H. Northrop, H.-R. Tseng, J. O. Jeppesen, T. J. Huang, B. Brough, M. Baller, S. Magonov, S. D. Solares, W. A. Goddard, C.-M. Ho and J. F. Stoddart, J. Am. Chem. Soc., 2005, 127, 9745–9759.
14. S. Saha, A. H. Flood, J. F. Stoddart, S. Impellizzeri, S. Silvi, M. Venturi and A. Credi, J. Am. Chem. Soc., 2007, 129, 12159–12171.
15. G. Fioravanti, N. Haraszkiewicz, E. R. Kay, S. M. Mendoza, C. Bruno, M. Marcaccio, P. G. Wiering, F. Paolucci, P. Rudolf, A. M. Brouwer and D. A. Leigh, J. Am. Chem. Soc., 2008, 130, 2593–2601.
16. A. C. Benniston and A. Harriman, Angew. Chem., Int. Ed. Engl., 1993, 32, 1459–1461.
17. A. C. Benniston, A. Harriman and V. M. Lynch, Tetrahedron Lett., 1994, 35, 1473–1476.
18. H. Murakami, A. Kawabuchi, K. Kotoo, M. Kunitake and N. Nakashima, J. Am. Chem. Soc., 1997, 119, 7605–7606.
19. P. R. Ashton, R. Ballardini, V. Balzani, A. Credi, K. R. Dress, E. Ishow, C. J. Kleverlaan, O. Kocian, J. A. Preece, N. Spencer, J. F. Stoddart, M. Venturi and S. Wenger, Chem. – Eur. J., 2000, 6, 3558–3574.
20. A. Harada, Acc. Chem. Res., 2001, 34, 456–464.
21. R. E. Dawson, S. F. Lincoln and C. J. Easton, Chem. Commun., 2008, 3980–3982.
22. G. Du, E. Moulin, N. Jouault, E. Buhler and N. Giuseppone, Angew. Chem., Int. Ed., 2012, 51, 12504–12508.
23. C. J. Bruns and J. F. Stoddart, Nat. Nanotechnol., 2013, 8, 9–10.
24. P. R. Ashton, I. Baxter, S. J. Cantrill, M. C. T. Fyfe, P. T. Glink, J. F. Stoddart, A. J. P. White and D. J. Williams, Angew. Chem., Int. Ed., 1998, 37, 1294–1297.
25. Y. L. Zhao, R. Q. Zhang, C. Minot, K. Hermann and M. A. Van Hove, Phys. Chem. Chem. Phys., 2015, 17, 18318–18326.
26. R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539.
27. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516.
28. G. Seifert, J. Phys. Chem. A, 2007, 111, 5609–5613.
29. B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684.
30. D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947–12957.
31. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
32. T. Frauenheim, G. Seifert, M. Elstner, Z. Hajnal, G. Jungnickel, D. Porezag, S. Suhai and R. Scholz, Phys. Status Solidi B, 2000, 217, 41–62.
33. M. Elstner, T. Frauenheim, E. Kaxiras, G. Seifert and S. Suhai, Phys. Status Solidi B, 2000, 217, 357–376.
34. T. Frauenheim, G. Seifert, M. Elstner, T. Niehaus, C. Köhler, M. Amkreutz, M. Sternberg, Z. Hajnal, A. D. Carlo and S. Suhai, J. Phys.: Condens. Matter, 2002, 14, 3015–3047.
35. W. J. Fan, J. Zeng and R. Q. Zhang, J. Chem. Theory Comput., 2009, 5, 2879–2885.
36. A. R. R. Neto and H. W. L. Alves, Phys. Status Solidi C, 2010, 7, 308–311.
37. W. Heckel, B. A. M. Elsner, C. Schulz and S. Müller, J. Phys. Chem. C, 2014, 118, 10771–10779.
38. N. H. Moreira, G. Dolgonos, B. Aradi, A. L. da Rosa and T. Frauenheim, J. Chem. Theory Comput., 2009, 5, 605–614.
39. N. H. Moreira, A. L. da Rosa and T. Frauenheim, Appl. Phys. Lett., 2009, 94, 193109.
40. A. Domínguez, N. H. Moreira, G. Dolgonos, T. Frauenheim and A. L. da Rosa, J. Phys. Chem. C, 2011, 115, 6491–6495.
41. M. J. Frisch, et al., Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009.
42. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
43. J. F. Berry, E. Bill, E. Bothe, S. D. George, B. Mienert, F. Neese and K. Wieghardt, Science, 2006, 312, 1937–1941.
44. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
45. A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, J. Chem. Soc., Dalton Trans., 2001, 2095–2108.
46. I. Mayer, J. Comput. Chem., 2007, 28, 204–221.

---

Footnote

† Electronic supplementary information (ESI) available: Figures of polymer structures containing Sc²⁺, Ti²⁺, Ni²⁺ or Zn²⁺, structures and energetic data of individual [c2]daisy chains in -cis and -trans forms, occupied molecular orbitals of [c2]daisy chains, and the table of calculated polymer unit lengths and contraction rate data are included. See DOI: 10.1039/c5cp07772a

---