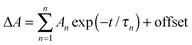Exploring photochemistry of p-bromophenylsulfonyl, p-tolylsulfonyl and methylsulfonyl azides by ultrafast UV-pump–IR-probe spectroscopy and computations

Abstract

The photochemistry of p-bromophenylsulfonyl azide (BsN₃), p-tolylsulfonyl azide (TsN₃) and methylsulfonyl azide (MsN₃) was studied by femtosecond time-resolved infrared spectroscopy with CH₂Cl₂ and CCl₄ as solvents along with quantum chemical calculations. The photolysis of these azides after 267 nm light excitation leads to the population of each respective azide S₁ excited state. Decay of the S₁ excited state gives rise to singlet nitrene formation. In the case of BsN₃, the decay was found to correlate with the formation of a pseudo-Curtius photoproduct (PCP) BrC₆H₄NSO₂. Transient electronic ground states of the three azides on their way to singlet nitrenes and PCPs were shown by locating the corresponding transition states on the potential energy surfaces. The lifetime of singlet ¹(BsN) and ¹(TsN) nitrenes is τ_S = ∼20 ps in CH₂Cl₂ and ∼700 ps in CCl₄. Singlet ¹(MsN) was not detected. Due to fast intersystem crossing (ISC), singlet nitrenes are converted into the triplet spin isomers lying lower in energy, the formation time constants being equal to the corresponding singlet nitrene lifetime. The formation of ³(MsN) was shown and the formation time constant in CH₂Cl₂ was found to be τ_ISC = 34 ± 3 ps. Internal conversion of the S₁ excited state to the ground state of the azide was low (Φ ≈ 0.15) for BsN₃ and TsN₃ and was not found in the case of MsN₃.

---

Introduction

Sulfonyl azides, RSO₂N₃, are important reagents in synthetic organic chemistry.^1–4 Similar to the reactions of the structurally related carbonyl azides,⁵ both thermal and photochemical decomposition reactions of sulfonyl azides have been extensively studied in solution^6–15 and demonstrated to exhibit rich and complex chemistry.^5,6,16–18

The photochemistry of 2-naphthylsulfonyl azide (2-C₁₀H₇SO₂N₃) was recently studied by femtosecond time-resolved infrared (fs-TRIR) spectroscopy and the azide S₁ excited state has been observed.⁶ This S₁ state decays to produce the singlet nitrene ¹(2-C₁₀H₇SO₂N) as a short-lived species (τ_S ≈ 0.70 ± 0.30 ns in CCl₄) that decays to the lower-energy and longer-lived triplet nitrene ³(2-C₁₀H₇SO₂N). The triplet spin state is the ground state for sulfonyl nitrenes which has been proved both theoretically^6,19,21 and experimentally by ESR and IR spectroscopy in matrices at low temperature.^16,17,20 However, neither singlet nor triplet sulfonylnitrenes are global minima, because the most stable species are N-sulfonylimines RNSO₂, which are formed with a large energy gain.²² So far, evidence for the formation of the pseudo-Curtius rearrangement product (PCP) after azide photolysis is still inconclusive.⁶

The possibility of concerted pseudo-Curtius Rearrangement In the Excited State (RIES) of sulfonyl azides as well as other sulfonylnitrene precursors has also been reported.²³N-Mesyl and N-tosyldibenzothiophene sulfimides were studied by ns-TRIR spectroscopy as the predecessors of MsN and TsN, respectively.²³ The time resolution (50 ns) of this experiment did not allow the authors to detect nitrenes, but sulfonoazepine was detected as a result of singlet nitrene attack on dibenzothiophene. Analysis of stable products formed upon photolysis of N-mesyldibenzothiophene sulfilimines suggests that triplet nitrene was produced upon irradiation. No evidence of pseudo-Curtius rearrangement of the sulfilimines precursor was found. This result suggests that neither singlet nor triplet nitrenes are the precursors of PCPs in solution at room temperature, as was concluded in ref. 6. However, the very recently studied photochemistry of trifluoromethylsulfonyl azide CF₃SO₂N₃ at low temperatures in matrices showed that the triplet nitrene ³(CF₃SO₂N) generated using the technique of post-pulse irradiation at 193 nm is converted to CF₃NSO₂ and CF₃S(O)NO by a Curtius-type rearrangement.¹⁶ Moreover, another new species CF₂N=SO₂F and FSNO were identified along with CF₂NF, SO₂, F₂CO, CF₃NO, and SO as side products. This experiment indicates that the possibility of the formation of the PCP as well as other products of rearrangement of nitrenes may depend on the substituent R (in RSO₂N).

Such a rich and diverse photochemistry of sulfonyl azides prompted us to investigate three sulfonyl azides that are structurally related to the aforementioned compounds, i.e. p-bromophenylsulfonyl azide (BsN₃), p-tolylsulfonyl azide (TsN₃) and the simplest member of the family, methylsulfonyl azide (MsN₃), by femtosecond time-resolved UV-pump–IR-probe spectroscopy in conjunction with computational studies.

Experimental and computational details

Synthesis

Sulfonylazides were synthesized by the reaction of the corresponding sulfonyl chlorides with sodium azide by known procedures.^24–26 Sodium azide was purified as in ref. 27. The structure of the azides was confirmed by ¹H, ¹³C NMR and IR spectroscopy (see ESI†).

Computational details

All calculations were performed with full geometry optimization using the Becke three-parameter hybrid exchange functional and the Lee–Yang–Parr correlation functional (B3LYP)^28,29 by employing 6-311++G(3df,3pd) and M06-2X³⁰ density functional theory with 6-311++G(d,p) basis sets. However, first singlet S₁ and triplet T₁ excited state energies and frequencies of azides were calculated using the single point methodology on the S₀ ground state geometry, all trials to optimize the excited states led to fragmentation of the species. Since the cost of S₁ state calculations by B3LYP/6-311++G(3df,3pd) was extremely high even for the smallest molecule MsN₃, we first calculated it using the 6-311++G(d,p) basis set. However, it led to principal errors in predicting the IR band shift: S₁ showed a blue shift with respect to the S₀, whereas a red-shift is observed experimentally.⁶ Changing the B3LYP by M06-2X functional gave the results which are in compliance with the experiment. Because the correspondence of calculation and experiment differs for each species, the results of both the B3LYP/6-311++G(3df,3pd) and M06-2X/6-311++G(d,p) computations are given where possible.

For each stationary point, second derivatives of the energy were calculated to confirm whether these structures were local minima or transition states. All transition state calculations were accompanied by intrinsic reaction coordinate (IRC) calculations³¹ to verify that each transition state connected the corresponding reactants and products. The calculated vibrational frequencies were not scaled. The calculated and experimental frequencies along with their assignment are summarized in Table S1 (ESI†).

Vertical excitation energies of azides were computed at the time-dependent TD-B3LYP and TD-M06-2X^32,33 levels of theory using the corresponding S₀ ground state geometries. To characterize the vertically excited states, electron density difference plots were computed (between S₀ and the S₁–S₃ states) as described previously.^6,34 All calculations were performed using the Gaussian09 suite of programs.³⁵

Ultrafast experiments

Ultrafast time-resolved UV-pump–IR-probe experiments were performed on an amplified Ti:sapphire laser system (100 fs pulse length, 800 nm laser wavelength and 1 kHz repetition rate). The amplified output is split into two beams and used to pump two optic parametric amplifiers (OPAs). One OPA was used to produce broad-band IR probe and reference pulses, and another OPA to generate UV pump pulses at 267 nm via third harmonic generation of the fundamental. The pump energy was set at 2 μJ, and the exposure dose was 40 J mol⁻¹ or 2 J ml⁻¹ solution (but 10 μJ for MsN₃, the exposure dose was 100 J mol⁻¹ or 10 J ml⁻¹ solution). The instrument response function was typically about 350 fs in the semiconductor GaAs (FWHM). To avoid contributions of rotational diffusion to the pump–probe signal, the polarization angle between pump and probe beams was set at the magic angle (54.7°). The pump and probe beam diameters were about 200 μm and 160 μm, respectively. Kinetic traces were analyzed utilizing single-trace fitting using a sum-of-exponentials instead of a global routine in view of the fact that the spectra of some species contained continuously shifting spectral bands which are related to vibrational cooling processes and difficult to model. The general equation for the used exponential terms is:
where ΔA is the experimental difference absorption signal (pump_on-minus-pump_off, in mOD); A_n – pre-exponential factor (in mOD); t – delay time between pump and probe beams (in ps); τ_n – formation/decay time constant (lifetime, in ps); offset – an ‘infinite’ spectrum at ‘infinite’ time (in mOD); n – integer number denoting the number of exponentials used. The featureless signal at −20 ps was subtracted as the background signal. In the ESI† the resulting paramaters required to fit the time evolution of discussed single wavenumbers can be found.

All experiments were performed at room temperature. The final sample concentration was 50 mM in the case of BsN₃ and TsN₃, and 100 mM for MsN₃. CCl₄ and CH₂Cl₂ (Sigma Aldrich) were used as nonpolar and polar solvents in order to estimate the solvent polarity effect on the reaction mechanism and on the time constants. The solution (about 6 ml) was constantly circulated between two 2 mm CaF₂ windows separated by a 50 μm spacer in a closed loop flow cell,³⁶ using a peristaltic pump at a speed of 4.4 ml min⁻¹. A comparison of the intensity of the N₃ stretch vibrations before and after the experiment via steady-state FTIR measurements reveals that about 8% of BsN₃ and TsN₃, and ∼20% of MsN₃ is photoconverted after 10 h and 14 h of laser experiments, respectively.

Results and discussion

Azide N₃ stretch region, 2000–2200 cm⁻¹

Irradiation at 267 nm of BsN₃ in CCl₄ produces a negative absorption signal at 2128 cm⁻¹ which, according to calculations, corresponds to the (bleached) N₃ stretch vibration of the azide S₀ ground state (Fig. 1 and 5 in the Computational results section for the complete FTIR spectrum). As was observed for 2-C₁₀H₇SO₂N₃,⁶ the bleach recovers after about 10 ps due to the repopulation of the azide ground state from its S₁ excited state. The internal conversion process (IC, i.e. the S₁ → S₀ transition) was found to have a time constant τ_IC(CCl₄) = 45 ± 2 ps for BsN₃ in CCl₄. Based on the fitting results we conclude that almost 15% of the excited molecules return to the azide ground state (corresponding to a quantum yield Φ_IC = 0.15 at 3 ns). The reaction rate R_IC = Φ_ICτ_IC⁻¹ is estimated to be (3.3 ± 0.3) × 10⁹ s⁻¹ in CCl₄. Percentages of recovery were the same for both BsN₃ and TsN₃ ground state νN₃ modes in both CCl₄ and CH₂Cl₂. However, the fitted recovery time constant at 2133 cm⁻¹ for BsN₃ in CH₂Cl₂ was different from that obtained in CCl₄ and was found to be τ_IC(CH₂Cl₂) = 31 ± 1 ps (see Fig. S1, ESI†). In the case of TsN₃τ_IC(CCl₄) = 33 ± 2 ps at 2127 cm⁻¹ in CCl₄ and 28 ± 3 ps at 2129 cm⁻¹ in CH₂Cl₂ were obtained (Fig. S1, ESI†). Temporal evolution of the signals did not show any dynamics after 200 ps up to 3 ns. Similarly, no recovery of the ground state was observed after photolysis of MsN₃ (Fig. S3, ESI†).

Fig. 1 Transient IR spectra produced upon BsN₃ photolysis in CCl₄ (λ_ex = 267 nm) at selected time delays (left). The (scaled) light-minus-dark FTIR difference spectrum is shown for comparison (spheres). Transient kinetics of BsN₃ ground state recovery at 2128 cm⁻¹ (right), also depicting the parameters resulting from the fit (continuous line) to the data curve (spheres).

As was shown previously, 330 nm excitation of 2-C₁₀H₇SO₂N₃ in the same solvents resulted in higher values of the ground state Φ_IC (up to 0.6 in CH₂Cl₂) and two times higher R_IC.⁶ In the case of BsN₃ and TsN₃ the internal conversion is low after irradiation at 267 nm. Its yield is not affected by the nature of the solvent and the R_IC is in the range of a few 10⁹ s⁻¹. In terms of the potential energy surface (PES) that means that S₁ and S₀ states of these azides have a rather large energy gap and obviously sufficiently separated PESs, so there is no conical intersection between them.

TD-B3LYP calculations predict that 267 nm light directly populates the S₁ excited state of BsN₃, TsN₃ and MsN₃ (vide infra). Unfortunately, we failed to experimentally detect any noticeable signal within 30 ps which could be assigned to the azide excited state S₁ in this spectral window for all studied azides. Interestingly, according to TD-M06-2X/6-311++G(d,p) results, the BsN₃ S₁ excited state is 56 cm⁻¹ red-shifted with respect to 2337 cm⁻¹ in S₀, and has eight times lower intensity than that for the S₀ state of azide, 83 vs. 691 km mol⁻¹ (Fig. S7 and Table S8, ESI†). That means that maximum ΔA of the S₁ signal is predicted to be ∼1.1 mOD since the S₀ state has a negative intensity signal of ∼−9 mOD. However, the S₁ state signal was not spectroscopically observed in the azide spectral window. The obtained experimental results allowed us to conclude that the S₁ states of BsN₃, TsN₃ and MsN₃ are probably weak IR-active species, showing signals which are even weaker than predicted, because otherwise they would have been detected. A similar behavior was recently observed in studying photochemistry of 5-azido-2-(N,N-diethylamino)pyridine.³⁷ The authors named the non-observable S₁ state a ‘spectroscopically dark’ excited state. It can be assumed that such a spectroscopic behavior of the S₁ state is due to identical or close symmetry of the ground and excited states rather than the n → π* nature of S₀ → S₁ transition of the compounds. However, a low-intense signal appearing within 30 ps in the 1500–1600 cm⁻¹ spectral window and its decay within 50 ps were observed for BsN₃ in CH₂Cl₂ (vide infra). We have found no evidence of triplet azide formation while the theory predicts strong signals (ε = ∼1000 km mol⁻¹) for such species.

Although the azide spectral region did not contain signals from azide's excited state S₁, it was clearly possible to observe intramolecular vibrational redistribution or ‘vibrational cooling’ (VC) of the hot azide ground state formed from the S₁ state for BsN₃ and TsN₃ in both CCl₄ and CH₂Cl₂ (Fig. S2, ESI† for BsN₃). VC typically exhibits itself by showing a time-dependent upshift in wavenumber of a vibrational mode. For instance, a vibrationally hot ground state of BsN₃ dissolved in CCl₄ was observed in the spectral range of 2110–2121 cm⁻¹ (2102–2119 cm⁻¹ in CH₂Cl₂, see Fig. S2, ESI†). The onset and decay time constants are 13 ± 5 ps at 2112 cm⁻¹ and 20 ± 19 ps at 2119 cm⁻¹ in CCl₄ for BsN₃ (and 15 ± 1 ps at 2102 cm⁻¹ and 16 ± 3 ps at 2119 cm⁻¹ in CH₂Cl₂). Similar VC values were obtained for TsN₃ while for MsN₃ no VC was found since no ground state recovery was observed.

In-ring C–C stretch region, 1500–1600 cm⁻¹

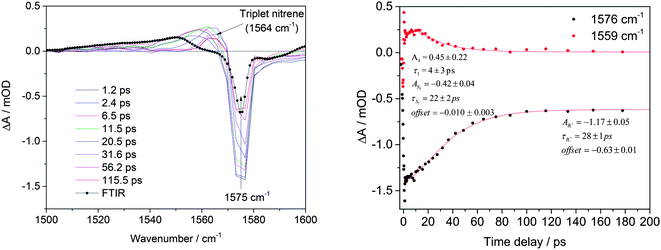
As was mentioned before, in the 1500–1600 cm⁻¹ spectral region it was possible to observe the S₁ excited state signal for the BsN₃ sample dissolved in CH₂Cl₂ (see Fig. 2). It was not possible to collect data in CCl₄ because the signal reproducibility was low. A negative absorption at 1575 cm⁻¹ was observed, which, based on the B3LYP results (calculated at 1607 cm⁻¹, ε = 65 km mol⁻¹), corresponds to the C–C ring stretch mode of the BsN₃ ground state. This band has a recovery time constant of τ_IC(CH₂Cl₂) = 28 ± 1 ps, which is similar to the time constant observed for the ground state N₃ stretch mode (2133 cm⁻¹, τ_IC(CH₂Cl₂) = 31 ± 1 ps, Fig. S1, ESI†). Calculations at the M06-2X level of theory predict the BsN₃ S₁ state vibration at 1625 cm⁻¹ (ε = 306 km mol⁻¹, Fig. S7 and Table S8, ESI†) which is 4.5 times more intense than that for the ground state and is 24 cm⁻¹ red-shifted. Indeed, a broad positive signal was detected within 30 ps after the laser pulse with maximum at 1559 cm⁻¹ corresponding to the azide S₁ state. The lifetime of the BsN₃ S₁ state in CH₂Cl₂ was found to be τ_S1(CH₂Cl₂) = 22 ± 2 ps. The decay constant nicely correlates with the τ_IC(CH₂Cl₂) = 28 ± 1 ps recovery time constant of the S₀. It also deserves to be mentioned that the BsN₃ S₁ lifetime is five times longer than that of 2-NpSO₂N₃ in the same solvent.⁶ This fact can be considered as a confirmation of the aforementioned assumption about weak intersection between the S₁ and S₀ PESs. A persistent signal with its maximum near 1564 cm⁻¹ is observed from 50 ps up to 3 ns and is assigned to triplet nitrene ³(BsN) based on vibrational calculations at the B3LYP level (1602 cm⁻¹, 177 km mol⁻¹, see Table S3, ESI†) and its absence in the FTIR spectrum (Fig. 2).

Fig. 2 Transient IR spectra in the range of 1500–1600 cm⁻¹ upon BsN₃ photolysis in CH₂Cl₂ at selected time delays (left). Transient kinetics at 1576 cm⁻¹ (BsN₃ ground state) and 1559 cm⁻¹ (BsN₃ S₁ state) in CH₂Cl₂ (right), also depicting the parameters resulting from the fits (solid line) to the data curves (dots).

SO₂ asymmetric stretch region, 1300–1400 cm⁻¹

Calculations suggest the presence of another interesting region where sulfonylnitrenes could be detected, which is the 1300–1400 cm⁻¹ spectral window (experiment in Fig. 3; see also calculated frequencies in Fig. S4–S9, ESI†). In this section we present a detailed discussion of the results obtained upon irradiation of BsN₃ in both CCl₄ and CH₂Cl₂ followed by a concise description of the results of TsN₃ and MsN₃.

Fig. 3 Transient kinetic surface plots for BsN₃ solution in CCl₄ in the range of 1320–1400 cm⁻¹ (a) and in CH₂Cl₂ in the range of 1300–1400 cm⁻¹ (b). Wavelength ranges in (a) and (b) are different due to solvent shifts. Transient IR spectra produced in the range of 1320–1400 cm⁻¹ (c and d) and 1140–1210 cm⁻¹ (e) upon BsN₃ photolysis in CCl₄ at selected time delays. See transient kinetics traces in Fig. 4 and transient IR spectra in Fig. S10 (ESI†) for more details. The time axes in (a) and (b) are linear up to 1 ps and logarithmic thereafter. Assignments are depicted by labels, arrows and lines that serve as guides to the eye.

BsN₃. Similar to the bands at 2128 and 1576 cm⁻¹, which are bleached in CH₂Cl₂, the ν^as(SO₂) band near 1377 cm⁻¹ vanishes upon photolysis due to depletion of the azide ground state (Fig. 3b and Fig. S10, ESI† for the spectral slices). The second higher wavenumber bleach corresponding to the S₀ state is the second νN₃ stretch band (1393 cm⁻¹). When CCl₄ was used as the solvent, the position of the two bands was reversed (Fig. 3b–d). As in the case of the N₃ stretch spectral window, the band at 1393 cm⁻¹ (in CH₂Cl₂) does not have a corresponding positive excited state signal at lower wavenumbers that appears within 30 ps and has a lifetime of around 20 ps. Interestingly, the M06-2X calculations predict the signal of the azide S₁ state of nearly but slightly less intensity and wavenumber to overlap with that of the S₀ state (around 1380 cm⁻¹, see Fig. S7, ESI†), explaining the absence of a measured S₁ signal.

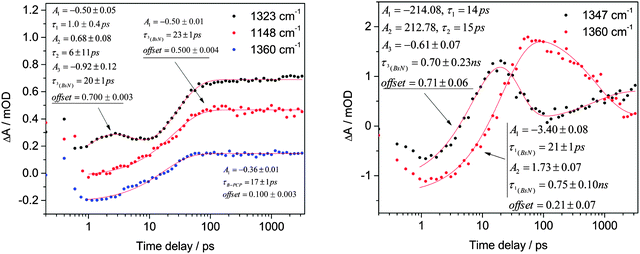
The 1377 cm⁻¹ feature in Fig. 3b shows little recovery (about 7%, but ∼20% in the case of CCl₄ as the solvent) and its time constant is 38 ± 9 ps (CH₂Cl₂). This is about 50% slower than τ_IC = 28 ± 1 ps (CH₂Cl₂) obtained from the trace at 1576 cm⁻¹. We believe that the observed behavior of this band is due to three different processes. One of them is the S₁ azide excited state formation absorbing at 1377 cm⁻¹, and the second one is its decay.⁶ Assuming that the S₁ decay and S₀ recovery time constants and extinction coefficients are equal they cancel each other, as predicted by the M06-2X calculations (see above). The third process, according to M06-2X calculations, is the formation of p-bromo-N-sulfonylaniline (BrC₆H₄NSO₂) as the pseudo-Curtius photoproduct (B-PCP). The evolution of the ν^as(SO₂) band at 1391 cm⁻¹ in CCl₄ shows ∼20% recovery of S₀, close to that for the azide ground state in the N₃ stretch region. This trace is well separated from the band assigned to the PCP (1365 cm⁻¹, see Fig. 3b and d). One point that remains unclear is why in CH₂Cl₂ the ground state ν^as(SO₂) band has two times less recovery than that in the N₃ stretch region.

Since the S₁ excited state of sulfonyl azides is a dissociative species capable of elimination of molecular nitrogen, singlet nitrene ¹(BsN) is observed in both CH₂Cl₂ and CCl₄. The singlet appears as a vibrationally hot species (see Fig. 3a–c, marked as ‘hot singlet nitrene’, and Fig. S10, ESI†), evident by a band shift from 1325 to 1350 cm⁻¹ in CH₂Cl₂ and from 1340 to 1357 cm⁻¹ in CCl₄. Fig. 3a–c show the results in CCl₄ because the kinetics of the vibrationally hot singlet nitrene cooling process is slower than that observed in CH₂Cl₂, and because the cooling process in the latter suffers from significant spectral overlap between hot singlet and triplet nitrenes (evident by the shifting isosbestic point in Fig. S10, ESI†). The time constant of hot ¹(BsN) formation is observed on a 2 ps timescale on the low wavenumber side of the signal, however, due to the spectral overlap of the cooling and formation processes, the actual formation timescale might actually be a bit slower; we conservatively estimate this value to be less than 20 ps. When CCl₄ is used as the solvent, the lifetime of singlet ¹(BsN) nitrene is substantially longer than that of VC. Thus, in CCl₄ the cooled singlet nitrene ¹(BsN) observed at 1360 cm⁻¹ has a formation time constant of τ_SN(CCl₄) = 20 ± 1 ps and its relaxation lifetime is τ_ISC(CCl₄) = 0.75 ± 0.10 ns.

Previous experimental and computational studies show that singlet sulfonyl nitrenes are unstable, highly reactive species that rapidly convert into more stable triplet isomers via intersystem crossing.^6,23 Recently, we confirmed that such transformation has an activation barrier of as low as 2 kcal mol⁻¹.²¹ That means that the formation of triplet nitrene is, apparently, the predominant if not the only process of transformation of the singlet nitrene and the two processes should occur with the same rate. Indeed, along with singlet ¹(BsN) nitrene decay, a new persistent (lifetime >3 ns) positive signal appears in CH₂Cl₂ at 1323 cm⁻¹ belonging to ³(BsN) with the time constant τ_ISC(CH₂Cl₂) = 20 ± 1 ps (see Fig. 3b and 4). A ‘rise-decay-rise’ profile of the 1323 cm⁻¹ curve in Fig. 4 results from the imposed exponentials for the appearance of hot singlet nitrene, its decay, and the formation of the triplet nitrene, as can also be followed by color changes at 1323 cm⁻¹ (yellow-orange-yellow-red) in Fig. 3b. A similar time constant of formation was also detected near 1148 cm⁻¹ in the ν^s(SO₂) region (Fig. 3e and 4). With CCl₄ as the solvent the band appears much later at 1347 cm⁻¹ and has a time constant of τ_ISC(CCl₄) = 0.70 ± 0.23 ns (Fig. 4). According to the B3LYP results (Fig. S4, Table S3, ESI†) the long-lived species may be assigned to either ³(BsN) (1342 cm⁻¹) or B-PCP (1354 cm⁻¹) or both. The B-PCP has also an additional predicted band at 1377 cm⁻¹ of double intensity. Experimentally, a low intensity band was observed at 1365 cm⁻¹ and 1360 cm⁻¹ in CCl₄ and CH₂Cl₂, respectively, and assigned to B-PCP. The calculated band at 1354 cm⁻¹ is therefore expected to exhibit an even lower intensity, leading us to assign the 1323 cm⁻¹ feature in CH₂Cl₂ to ³(BsN) nitrene.

Fig. 4 Transient kinetics at 1323 cm⁻¹ (triplet ³(BsN) and hot singlet nitrene peak), at 1148 cm⁻¹ (ν^s(SO₂), triplet ³(BsN)) and at 1360 cm⁻¹ (B-PCP) in CH₂Cl₂ (left). Transient kinetics at 1360 cm⁻¹ (assigned to vibrationally cooled singlet ¹(BsN)) and 1347 cm⁻¹ (with overlapping contributions from the hot singlet nitrene peak and triplet ³(BsN)) in CCl₄ (right). Both panels contain the parameters resulting from the fit (solid line) to the data curves (dots).

Fig. 5 FTIR spectra of BsN₃ (top), TsN₃ (centre) and MsN₃ (bottom) solved in CCl₄ (subtracted), a spacer thickness of 50 μm along with the B3LYP predicted vibration modes (red bars).

Singlet and triplet nitrenes are not the only products of photolysis derived from the azide S₁ excited state. For arylsulfonylazides, the formation of a PCP was postulated.^6,38 Both DFT functionals used here predict the presence of B-PCP, appearing as a 29 cm⁻¹ red-shifted signal to 1377 cm⁻¹ in the case of the B3LYP functional (Fig. S4, ESI;† it red-shifts only 8 cm⁻¹ to 1383 cm⁻¹ for M06-2X, see Fig. S7, ESI†) near ν^as(SO₂) of the azide ground state. For instance, for BsN₃ in CCl₄ and CH₂Cl₂ the signal of B-PCP was detected at 1365 and 1360 cm⁻¹, respectively. From the trace at 1365 cm⁻¹ in CCl₄ it is not possible to extract the parameters of B-PCP formation since it significantly overlaps with that of ¹(BsN). However, we were able to derive these time constants from the observed trace at 1360 cm⁻¹ (see Fig. 4), and to obtain τ_RIES(CH₂Cl₂) = 17 ± 1 ps. The B-PCP's formation time constant of 17 ± 1 ps correlates well with the time constant of the azide S₁ excited state depletion (at 1559 cm⁻¹, 22 ± 2 ps) as well as ¹(BsN)'s lifetime. However, previous studies have shown that singlet sulfonyl nitrene cannot be a precursor of the PCP since there is no evidence of PCP formation when a non-azide precursor is used²³ and that both B-PCP and ¹(BsN) are formed exclusively from the S₁ excited state of the azide.⁶ This conclusion was also confirmed by our unsuccessful attempts to locate a transition state between ¹(BsN) and the B-PCP (vide infra).

TsN₃. In general, due to the structural resemblance, the photochemistry of TsN₃ is similar to that of BsN₃. However, some differences deserve to be mentioned. In the SO₂ spectral region (Fig. S11–S13, ESI†) a bleach of the azide S₀ state was observed at 1379 cm⁻¹ in CH₂Cl₂ (1373 cm⁻¹ in CCl₄). The evolution of the azide S₀ state at 1379 cm⁻¹ reveals τ_IC(CH₂Cl₂) = 20 ± 3 ps (1373 cm⁻¹, 30 ± 7 ps in CCl₄) which correlates with that observed in the azide spectral region. The calculations also predict an intense signal of TolNSO₂ (T-PCP) which overlaps with the S₀ state of the azide. The recovery of the 1373 cm⁻¹ band was estimated from the curve fitting and found to be 25% (in CH₂Cl₂), which is 10% more than that for the 2129 cm⁻¹ trace (assigned to νN₃). This allows us to conclude that PCP formation also occurs for TsN₃. A high value of 1373 cm⁻¹ band recovery in CH₂Cl₂ is due to its overlap with the ν^as(SO₂) band of T-PCP (1353 cm⁻¹), and it has a formation time constant of τ_RIES(CH₂Cl₂) = 14 ± 3 ps. This value is similar to the recovery time constant of ν^as(SO₂) of the azide ground state (τ_IC(CH₂Cl₂) = 20 ± 3 ps at 1373 cm⁻¹). The formation time constants of ³(TsN) are somewhat different from those of ³(BsN) but equal to the singlet nitrene lifetime τ_ISC(CH₂Cl₂) = 25 ± 2 ps (1305 cm⁻¹) and τ_ISC(CCl₄) 0.44 ± 0.26 ns (1337 cm⁻¹), while lifetimes τ_S of ¹(TsN) were estimated to be ∼20 ps (CH₂Cl₂) and 0.67 ± 0.10 ns (1349 cm⁻¹, CCl₄), respectively.

MsN₃. Unfortunately, we found no signals in the SO₂ spectral window except for a bleach of the MsN₃ ground state at 1366 cm⁻¹ (CH₂Cl₂, see Fig. S14, ESI†) and 1378 cm⁻¹ (CCl₄) showing no IC process. Nevertheless, one persistent (>3 ns) signal at 1134 cm⁻¹ that is assigned to ν^s(SO₂) of triplet nitrene was observed in CH₂Cl₂ (Fig. S3, ESI†), where sulfonylazides showed fast transient dynamics. The signal has a formation time constant of 34 ± 3 ps. Based on the B3LYP results (Fig. S6, ESI†) this signal corresponds to a mixture of ³(MsN) and MeNSO₂ (M-PCP). Predicted wavenumber values are 1155 and 1157 cm⁻¹, respectively. The intensity ratio of the two species is about 5 : 1. However, the steady state FTIR spectrum does not show a permanent signal near 1134 cm⁻¹. Therefore, the observed signal at 1134 cm⁻¹ corresponds to the triplet nitrene ³(MsN).

Computational results

In order to assign the vibration bands of all species which could be formed by irradiation of azides we employed B3LYP/6-311++G(3df,3pd) and M06-2X/6-311++G(d,p) functionals/basis sets. FTIR spectra of azides along with the B3LYP predicted bands are shown in Fig. 5. The ground state N₃ vibrational frequencies are well reproduced by calculations; the error does not exceed 6%, while the M06-2X error is ∼10%. Previous studies showed that a better approximation of SO₂ frequencies may be obtained when large basis sets including d and f functions are used.^6,39 However, we have found that both DFT functionals provide a very good approximation of SO₂ frequencies, while 6-311++G(d,p) basis sets in combination with the M06-2X functional show an excellent agreement with experimental frequencies of the SO₂ group (Table 1).

Table 1 Calculated and experimental IR frequencies (in CCl₄, cm⁻¹) for BsN₃, TsN₃ and MsN₃ ground states using B3LYP/6-311++G(3df,3pd) and M06-2X/6-311++G(d,p) functionals

Method	Compound	N3 stretch			SO2 asym. stretch
		Calculated	Experiment	Error	Calculated	Experiment	Error
B3LYP	BsN3	2253	2128	125	1406	1392	14
	TsN3	2250	2123	127	1403	1384	19
	MsN3	2263	2135	128	1401	1373	28
M06-2X	BsN3	2337	2128	209	1391	1392	1
	TsN3	2331	2123	208	1383	1384	1
	MsN3	2351	2135	216	1367	1373	6

---

Since B3LYP/6-311++G(3df,3pd) calculations of the azide S₁ state are extremely time-consuming, we present the vibrational frequencies of S₁ states calculated at the M06-2X level for all azides and at the B3LYP level only for MsN₃. Full lists of the vibrational frequencies for the S₀, S₁ and T₁ states of azides (RSO₂N₃), singlet nitrenes ¹(RSO₂N), triplet nitrenes ³(RSO₂N) and pseudo-Curtius photoproducts (RN=SO₂) are given in Tables S2–S13 (ESI†) and plotted in Fig. S4–S9 (ESI†). It should be noted that M06-2X/6-311++G(d,p) adequately predicts PCP and azide ground state vibrational frequencies, but shows some inaccuracy in the prediction of singlet and triplet nitrenes while B3LYP/6-311++G(3df,3pd) adequately predicts the vibrational frequencies for the azide ground state, singlet and triplet nitrenes, but not for the PCP.

The B3LYP/6-31G(3df,3pd) optimized geometries of the azides were used for calculations of vertical excitations by the TD-B3LYP method. The lowest electronic transition occurs at 278, 277 and 258 nm in the case of BsN₃, TsN₃ and MsN₃, respectively, which corresponds to the HOMO–LUMO electronic transition. In MsN₃ the transition has a very low predicted oscillator strength f = 0.0001 at 258 nm. The predicted transitions are in good agreement with the ground-state electronic absorption spectra of the azides (Fig. 6). Note that the laser excitation wavelength was centered at 267 nm (having 1.2 nm FWHM), and because the difference in wavelength between the S₀ → S₁ and S₀ → S₂ electronic transitions is calculated to be >20 nm, the collected experimental data refer to the S₀ → S₁ transition.

Fig. 6 UV spectra of BsN₃ (top, 1 mM; 0.1 cm), TsN₃ (centre, 1 mM; 0.1 cm) and MsN₃ (bottom, 10 mM; 0.2 cm) in ethanol along with the B3LYP predicted vertical excitations (blue bars).

In addition, electron density difference plots of the singlet excited states were calculated at the TD-B3LYP/6-31G(3df,3pd) level of theory for the azides in order to identify the character of the excited states, according to ref. 6 (Fig. S15, ESI†). This approach shows that the S₁ excited state corresponds to the promotion of an electron from the sulfonyl oxygen lone pair to the π*-orbital of the azide group, and in the case of the aromatic compounds also to the in-plane π*-orbital of the aromatic system. Accumulation of electron density on the π*-orbital of the terminal N_β=N_γ moiety suggests that the S₁ excited state is a dissociative state and that the corresponding nitrene can be formed from the initially excited sulfonyl azide. This prediction is consistent with our experimental observations (vide supra).

If the pseudo-Curtius rearrangement products cannot be formed from the corresponding nitrenes (which we have experimentally confirmed, and as reported earlier^6,23), there must exist an alternative route to them from the original azides. Indeed, two independent transition states (TSs), each with only one imaginary mode, were located on the PESs of the studied azides. One of them leads to nitrene, while another one, lying ∼2 kcal mol⁻¹ (R = p-BrC₆H₄ and p-Tol) or ∼10 kcal mol⁻¹ (R = Me) higher, leads to the PCP. Although the structures of the two TSs depicted in Fig. 7 look similar, they are principally different as proved by IRC calculations and by the analysis of the imaginary modes. The first TS (top row in Fig. 7) leading to nitrenes is located mainly on the N_α⋯N_β bond and reflects the process of elimination of the N₂ molecule. The second TS (bottom row) leading to PCPs has a ∼150 cm⁻¹ higher imaginary wavenumber, suggesting a steeper reaction valley and being in line with a larger barrier.⁴⁰ Comparable contributions of the N_α⋯N_β bond elongation and simultaneous decrease of the C⋯N_α distance due to contraction of the NSC angle, together with notable C–S bond elongation, are clearly indicative of changes finally leading to the PCP formation. These results can be considered as an independent theoretical confirmation of the aforementioned conclusion that singlet sulfonyl nitrenes cannot be precursors for the PCP formation.

Fig. 7 Transition states connecting BsN₃, TsN₃ and MsN₃ ground states with the corresponding singlet nitrenes (top row, TS1) and PCPs (bottom row, TS2). Dark arrows show the principal displacement vectors. Several relevant angles (arched lines, in degrees) and atom–atom distances (dashed, in Angstroms) are also given.

We also tried to locate a transition state on the way from singlet or triplet nitrenes to PCPs. For singlet nitrenes no TS could be found. In contrast, we did locate a TS (with an energy of 42 kcal mol⁻¹; not shown in Table 2) for triplet ³(MsN) leading to triplet PCP. This is in agreement with the results of matrix isolation experiments of the triplet nitrene ³(CF₃SO₂N) and its further UV-promoted transformation into the final product CF₃NSO₂via the elusive ³(CF₃NSO₂).¹⁶

Photochemical reaction paths

Irradiation of BsN₃, TsN₃ and MsN₃ with 267 nm light directly populates the S₁ excited state of the azides (vide supra). The observed photochemical reaction paths are summarized in Fig. 8. The S₁ excited state of the azides is a short-lived dissociative species (k_S1(CH₂Cl₂) ∼ 45 × 10⁹ s⁻¹ for BsN₃) and expels the molecule of nitrogen to give singlet nitrene (¹(RSO₂N); with k_SN(CH₂Cl₂) of ∼50 × 10⁹ s⁻¹ for BsN₃), and the Curtius-like photoproduct RNSO₂, where R = p-BrC₆H₄, p-Tol or Me; with k_RIES(CH₂Cl₂) ∼ 59 × 10⁹ s⁻¹ for BsN₃/TsN₃. Singlet nitrenes were detected as vibrationally hot species since the experimental 267 nm excitation wavelength corresponds to 107.5 kcal mol⁻¹ of energy, whereas the energy required for the azide degradation is ca. 40 kcal mol⁻¹ (see Table 2 below). The excess energy absorbed by the azide molecule is therefore about 70 kcal mol⁻¹.

Fig. 8 Mechanism of photochemical transformations of sulfonyl azides upon 267 nm irradiation. The lifetime shown under a species corresponds to the overall decay of that species.

Table 2 B3LYP/6-311++G(3df,3pd) calculated energies (kcal mol⁻¹) of S₁ and T₁ states of azides with respect to the azide ground state, transition states (TSs), singlet and triplet nitrenes and pseudo-Curtius photoproducts

Species	Substituent, R
	p-BrC6H4	p-Tol	Me
* A ΔH^≠ value of 35.1 kcal mol^−1 was obtained for thermal decomposition of TsN3.^41
Azide S0 state	0.0	0.0	0.0
Azide S1 state	102.7	103.2	111.0
Azide T1 state	88.3	91.4	100.4
TS1 RSO2N3 → ^1(RSO2N) + N2	38.6	38.9*	39.4
Singlet nitrene ^1(RN) + N2	32.1	31.9	33.6
Triplet nitrene ^3(RN) + N2	17.5	17.2	19.8
TS2 RSO2N3 → RNSO2 + N2	40.5	40.3	49.8
RNSO2	−35.0	−34.1	−29.6
Singlet–triplet energy gap, ΔEST	14.6	14.7	13.8

---

As shown in Table 2, transformation of the azide S₀ state to ¹(RSO₂N) involves an energy barrier of ∼39 kcal mol⁻¹. Calculations show that the formation of a PCP from the azide S₀ state is influenced by the substituent at the SO₂ group and exhibits an energy barrier of ∼40 kcal mol⁻¹ for arylsulfonyl azides and 50 kcal mol⁻¹ for MsN₃. Thus, since the barriers of transformation of arylsulfonyl azides to singlet nitrenes and PCPs are similar, one could expect the formation of both species for all compounds. However, singlet nitrene formation from MsN₃ is ∼10 kcal mol⁻¹ more preferable than the formation of a PCP. The rest of the excitation energy of 107.5 kcal mol⁻¹ absorbed by the azide molecules is available for product formation. It also explains why the singlet nitrenes (and probably PCP as well) are formed as vibrationally hot species which subsequently cool down.

Vibrationally hot singlet nitrenes were detected only for BsN₃ and TsN₃ in both solvents but not for MsN₃. Subsequent relaxation of hot nitrene gives rise to the formation of a cooled singlet species ¹(RSO₂N). For ¹(RSO₂N) the B3LYP calculations predict ν^as = 1375, 1370 and 1382 cm⁻¹ for R = p-BrC₆H₄, p-Tol and Me, respectively. These wavenumbers are in good agreement with the experimentally observed absorption signals of relaxed singlet nitrenes ¹(BsN) and ¹(TsN) detected at 1360 and 1349 cm⁻¹ in CCl₄. Their decay constants were found to be k_ISC(CCl₄) = (1.3 ± 0.4) × 10⁹ s⁻¹ and (1.5 ± 0.4) × 10⁹ s⁻¹, respectively. Determination of singlet nitrene decay constants in CH₂Cl₂ is complicated by VC and we tentatively estimate it to be approximately 50 × 10⁹ s⁻¹.

Similar to the features observed for singlet nitrenes, weak persistent (>3 ns) bleaches of triplet ³(BsN) and ³(TsN) nitrenes were observed at 1347 and 1337 cm⁻¹ in CCl₄. The formation constants are k_ISC(CCl₄) = (1.4 ± 1.0) × 10⁹ s⁻¹ and (2.3 ± 1.7) × 10⁹ s⁻¹, respectively, which are comparable to the singlet nitrene decay constants, thus indicating that both transitions correspond to the same process.⁶ The decay constants of singlet nitrenes in CH₂Cl₂ are deduced from the formation constants of triplet nitrenes which were found to be k_ISC(CH₂Cl₂, ³(BsN)) = (50 ± 5) × 10⁹ s⁻¹ and k_ISC(CH₂Cl₂, ³(TsN)) = (40 ± 6) × 10⁹ s⁻¹, and therefore are significantly larger than in CCl₄. Note also that a persistent band (>3 ns) of ³(MsN) was detected at 1134 cm⁻¹ in CH₂Cl₂, which was assigned to the triplet nitrene formation with the formation constant k_ISC(CH₂Cl₂) = (29 ± 5) × 10⁹ s⁻¹. The latter value is slightly lower than that for ³(BsN) and ³(TsN), apparently due to the fact that two single time traces are compared, which do not necessarily need to represent the absorption of a single species (i.e. their transient absorptions could overlap). It is an indicator of a transient kinetic difference between aliphatic and aromatic azide photochemistry along with the absence of the azide ground state recovery.

Another permanent product of acyl- and sulfonylazide photochemistry is the PCP.^5,6,16 Its formation was clearly detected for BsN₃ and TsN₃ in CH₂Cl₂, while in CCl₄ the PCP's SO₂ band overlaps with that of the corresponding singlet nitrene. The trace near 1360 cm⁻¹ in CH₂Cl₂, corresponding to cooled B-PCP, was found to have the formation constant k_RIES(CH₂Cl₂, B-PCP) = (59 ± 7) × 10⁹ s⁻¹. The value correlates well with the azide S₁ state decay (k_ISC(CH₂Cl₂, BsN₃) = (46 ± 8) × 10⁹ s⁻¹ at 1559 cm⁻¹) and falls in the range of the singlet nitrene ¹(BsN) decay constants. Previous experiments showed that only azide, not singlet nitrene, is a predecessor of the PCP.^6,23 Furthermore, the transition state has been located to connect the ground state sulfonyl azide and PCP structures (Table 2). This transformation requires ∼41 kcal mol⁻¹ for the aromatic azides, a similar value as calculated here for TS1 leading to singlet nitrene formation. However, the energy of transition state TS2 leading to MeNSO₂ was calculated to be 10 kcal mol⁻¹ higher than that leading to ¹(MsN). According to calculations, the formation of ¹(MsN) is ∼3.3 × 10⁴ times faster than that of MeNSO₂ and one could expect exclusive formation of ¹(MsN) rather than MeNSO₂.

Conclusions

The photochemistry of p-bromophenylsulfonyl-, p-tolyl- and methylsulfonyl azides has been investigated experimentally by ultrafast time-resolved UV-pump–IR-probe spectroscopy and computationally at the B3LYP/6-311++G(3df,3pd) and M06-2X/6-311++G(d,p) levels of theory. All compounds showed the absence of spectral signatures corresponding to the azide S₁ and T₁ excited states in the regions of νN₃ or νSO₂. Only for BsN₃ the S₁ excited state with a lifetime of τ_S1(CH₂Cl₂) = 21 ± 3 ps was observed by a low intensity feature in the in-ring C–C stretch region. The internal conversion of the undetected S₁ excited state to the ground state of azide is low, representing an S₀ state recovery of ∼15%. Still, it represents an efficient way of the azide ground state recovery in BsN₃ and TsN₃, but was not observed for MsN₃. The used laser excitation wavelength provides more energy than that required for N₂ release, and the ¹(BsN) and ¹(TsN) singlet nitrenes were detected as vibrationally hot species in both CH₂Cl₂ and CCl₄. In the former solvent the lifetime τ_VC(CH₂Cl₂) is ∼20 ps. The lifetimes of relaxed singlet ¹(BsN) and ¹(TsN) nitrenes are τ_VC(CCl₄) = 0.75 ± 0.10 and 0.66 ± 0.10 ns, respectively. Corresponding triplet nitrenes were detected as persistent (>3 ns) species and their formation time constants correlate with the lifetime of singlet nitrenes. Singlet ¹(MsN) was not observed but its triplet spin isomer was detected. The formation of relaxed B-PCP correlates with the azide S₁ state decay and represents an example of rearrangement in the excited state. The assignment of the experimentally detected vibrational bands to species was supported by quantum chemical calculations.

In conclusion, for many years chemists believed that the formation of N-sulfonylamines RNSO₂ and their better known carbonyl analogues, isocyanates RNCO proceeds in two steps via generation of the corresponding nitrenes followed by their Curtius-type rearrangement.⁴² However, recent investigations^6,43 as well as the results of the present work employing ultrafast laser techniques call into question these notions and suggest an alternative, concerted mechanism of the Curtius-type rearrangement, at least as far as the formation of N-sulfonylamines from sulfonyl azides is concerned. Indeed, both our and other's experiments^6,43 prove the formation of PCPs and singlet nitrenes from the S₁ excited state of sulfonyl azides by comparing the formation/degradation time constants. Also, our calculations predict the existence of two different transition states, one connecting the azide and the singlet nitrene and another one connecting the azide and the pseudo-Curtius rearrangement product. This may encourage chemists to reinvestigate and reconsider the mechanism of other similar sextet rearrangements, like Lossen, Beckmann, Schmidt, Hofmann and Wolff rearrangements.

Acknowledgements

A. V. K. thanks the German Academic Exchange Service (Deutscher Akademischer Austauschdienst, DAAD) for financing the research stay in Germany and Dr Vladimir I. Meshcheryakov for his support in azide synthesis. C. N. thanks the Deutsche Forschungsgemeinschaft for funding of RTG 1986 “Complex Scenarios of Light Control”. J. B. acknowledges the Alexander von Humboldt Foundation for a Sofja Kovalevskaja award.

References

1. J. B. Sweeney, Synthesis of Aziridines, in Aziridines and Epoxides in Organic Synthesis, ed. A. K. Yudin, Wiley, Weinheim, 2006.
2. J. B. Sweeney, Chem. Soc. Rev., 2002, 31, 247–258.
3. A. I. Olivos-Suarez, H. Jiang, X. P. Zhang and B. de Bruin, Dalton Trans., 2011, 40, 5697–5705.
4. P. Muller and C. Fruit, Chem. Rev., 2003, 103, 2905–2919.
5. J. Kubicki, Y. Zhang, J. Xue, H. L. Luk and M. S. Platz, Phys. Chem. Chem. Phys., 2012, 14, 10377–10390.
6. J. Kubicki, H. L. Luk, Y. Zhang, S. Vyas, H.-L. Peng, C. M. Hadad and M. S. Platz, J. Am. Chem. Soc., 2012, 134, 7036–7044.
7. N. P. Gritsan, Properties of Carbonyl Nitrenes and Related Acyl Nitrenes, in Nitrenes and Nitrenium Ions, ed. D. E. Falvey and A. D. Gudmundsdottir, Wiley, New Jersey, 2013.
8. R. A. Abramovitch, T. D. Bailey, T. Takaya and V. Uma, J. Org. Chem., 1974, 39, 340–345.
9. R. A. Abramovitch and V. Uma, Chem. Commun., 1968, 797–798.
10. R. A. Abramovitch, G. N. Knaus and V. Uma, J. Am. Chem. Soc., 1969, 91, 7532–7533.
11. R. A. Abramovitch, G. N. Knaus and V. Uma, J. Org. Chem., 1974, 39, 1101–1106.
12. R. A. Abramovitch and T. Takaya, J. Org. Chem., 1972, 37, 2022–2029.
13. R. A. Abramovitch and G. N. Knaus, J. Org. Chem., 1975, 40, 883–889.
14. M. T. Reagan and A. Nickon, J. Am. Chem. Soc., 1968, 90, 4096–4105.
15. N. Torimoto, T. Shingaki and T. Nagai, J. Org. Chem., 1978, 43, 631–633.
16. X. Q. Zeng, H. Beckers, H. Willner, P. Neuhaus, D. Grote and W. Sander, J. Phys. Chem. A, 2015, 119, 2281–2288.
17. X. Q. Zeng, H. Beckers, P. Neuhaus, D. Grote and W. Sander, Z. Anorg. Allg. Chem., 2012, 638, 526–533.
18. C. E. Hoyle, R. S. Lenox, P. A. Christie and R. A. Shoemaker, J. Org. Chem., 1983, 48, 2056–2061.
19. E. Wasserman, Prog. Phys. Org. Chem., 1971, 8, 319–336.
20. G. Smolinsky, E. Wasserman and W. A. Yager, J. Am. Chem. Soc., 1962, 84, 3220–3221.
21. A. V. Kuzmin and B. A. Shainyan, J. Phys. Org. Chem., 2014, 27, 794–802.
22. B. A. Shainyan and A. V. Kuzmin, J. Phys. Org. Chem., 2014, 27, 156–162.
23. V. Desikan, Y. Liu, J. P. Toscano and W. S. Jenks, J. Org. Chem., 2008, 73, 4398–4414.
24. S. W. Pelletier, CI(L), 1953, 1034.
25. R. L. Danheiser, R. F. Miller, R. G. Brisbois and S. Z. Park, J. Org. Chem., 1989, 55, 1959–1964.
26. T. J. Curphey, New J. Org. Synth., 1981, 13, 112–115.
27. J. C. Kauer and W. A. Sheppard, J. Org. Chem., 1967, 32, 3580–3592.
28. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
29. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
30. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
31. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
32. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7434.
33. F. Furche and R. Ahlrichs, J. Chem. Phys., 2004, 121, 12772–12773.
34. V. Sichula, P. Kucheryavy, R. Khatmullin, Y. Hu, E. Mirzakulova, S. Vyas, S. F. Manzer, C. M. Hadad and K. D. Glusac, J. Phys. Chem. A, 2010, 114, 12138–12147.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci,G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.
36. J. Bredenbeck and P. Hamm, Rev. Sci. Instrum., 2003, 74, 3188–3189.
37. M. S. Panov, V. D. Voskresenska, M. N. Ryazantsev, A. N. Tarnovsky and R. M. Wilson, J. Am. Chem. Soc., 2013, 135, 19167–19179.
38. W. Lwowski, Azides and Nitrenes, Academic Press, Orlando, FL, 1984.
39. C. W. J. Bauschlicher and H. Patridge, Chem. Phys. Lett., 1995, 240, 533–540.
40. E. Kraka, J. Gauss and D. Cremer, J. Chem. Phys., 1993, 99, 5306–5315.
41. D. S. Breslow, M. F. Sloan, N. R. Newburg and W. B. Renfrow, J. Am. Chem. Soc., 1968, 91, 2273–2279.
42. S. B. Michael and J. March, March's Advanced Organic Chemistry, Wiley, Hoboken, New Jersey, 2007, 6th edn, p. 1609.
43. J. Wang, J. Kubicki, G. Burdzinski, J. C. Hackett, T. L. Gustafson, C. M. Hadad and M. S. Platz, J. Org. Chem., 2007, 72, 7581–7586.

---

Footnote

† Electronic supplementary information (ESI) available: FTIR and UV spectra of azides along with predicted bands, transient kinetics and transient IR spectra, calculated IR vibrational frequencies of all species, EDD plots, and geometries and energies of all molecules. See DOI: 10.1039/c5cp07636f

---