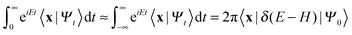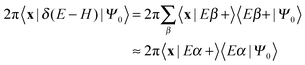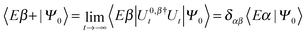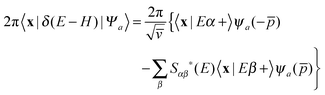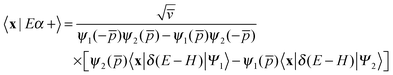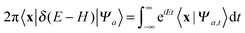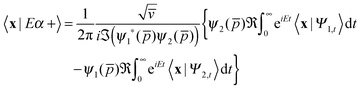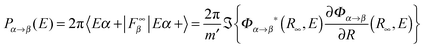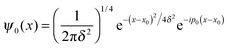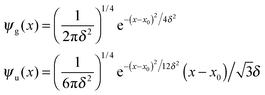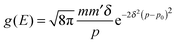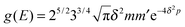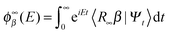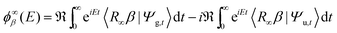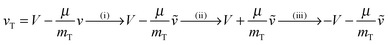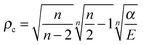Open Access Article
Open Access ArticleQuantum dynamical investigation of the isotope effect in H2 formation on graphite at cold collision energies
Marta
Pasquini
a,
Matteo
Bonfanti
a and
Rocco
Martinazzo
*ab
aUniversitá degli Studi di Milano, Dipartimento di Chimica, via Golgi 19, 20133 Milano, Italy. E-mail: rocco.martinazzo@unimi.it
bConsiglio Nazionale delle Ricerche, Istituto di Scienze e Tecnologie Molecolari, Milano, Italy
First published on 28th January 2016
Abstract
The Eley–Rideal abstraction of hydrogen atoms on graphitic surfaces at cold collision energies was investigated using a time-dependent wave packet method within the rigid-flat surface approximation, with a focus on hydrogen–deuterium isotopic substitutions. It is found that the marked isotope effect of collinear collisions disappears when the full dimensionality of the problem is taken into account, thereby suggesting that abstraction is less direct than commonly believed and proceeds through glancing rather than head-on collisions. In contrast, a clear isotope effect is observed for “hot-atom” formation, which appears to be strongly favored for heavy projectiles because of their higher density of physisorbed states. Overall, the dynamics is essentially classical and reasonably well described by quasi-classical trajectory methods at all but the lowest energies (≲10 meV). A comparison of the results obtained in the (substrate) adiabatic and diabatic limits suggests that the reaction is only marginally affected by the lattice dynamics, but highlights the importance of including energy dissipation processes in order to accurately describe the internal excitation of the product molecules.
1 Introduction
In recent years, hydrogen recombination on graphitic surfaces has been the subject of many theoretical investigations, largely motivated by the primary role that this process plays in the chemistry of the interstellar medium (ISM), the extremely cold and rarefied gas which fills the space between stars. H2 is in fact the most abundant molecular species in many interstellar environments, it takes part in most of the reactions forming complex molecular species and is the principal cooling agent during the gravitational collapse of the clouds that eventually leads to star formation.1 Efficient formation pathways for H2 are needed to explain its abundance since hydrogen molecules are continuously dissociated by the intense stellar UV radiation field and cosmic rays. It is now widely accepted that hydrogen formation has to occur on the surface of the interstellar dust grains.2–4 The latter are typically μm-sized and contain a silicate core covered by an “organic refractory” mantle, though the tiniest particles are entirely carbonaceous and most likely are simple polycyclic aromatic hydrocarbon (PAH) molecules.5 Hence, in all but the coldest (so-called molecular) clouds where H2O and CO2 ice mantles cover the silicate core, the surface where hydrogen recombination occurs is mainly carbonaceous, and this makes hydrogen–graphite a prototypical system for studying hydrogen formation in space.6–21In general, a reaction at the gas–surface interface may occur through three different mechanisms. In the Langmuir–Hinshelwood (LH) mechanism, both reactants adsorb onto the surface, thermalize with it and diffuse until they encounter each other and react. In the Eley–Rideal (ER) mechanism, on the other hand, only one of the reagents is adsorbed onto the surface, the second comes from the gas phase and forms the molecule in a direct collision process. A third, intermediate (“hot-atom”, HA) mechanism is possible, particularly when light atoms are involved: one of the two reactants is trapped on the surface but it is not equilibrated, rather hyperthermally diffuses until it finds its reaction partner. In the case of hydrogen recombination on graphite, the reaction mechanism strongly depends on the physical conditions, and several scenarios are possible, depending on whether physisorbed or chemisorbed species are involved.
Hydrogen atoms may be adsorbed onto the regular (0001) surface of graphite in the shallow (∼40 meV deep) physisorption well22 and diffuse quickly even in the zero temperature limit, thanks to efficient tunneling through the tiny (5 meV high) barrier between neighboring adsorption sites.23 Hydrogen recombination follows the physisorption of a H atom,24 and may occur through LH/HA25,26 or ER19,27 reactions. In this case, physisorption is facile – though rather inefficient24 – but desorption from the shallow well is a limiting factor, since refreshment of the surface is complete at a very small (surface) temperature, Ts ∼ 30–40 K.
Hydrogen atoms may also chemically adsorb onto the graphitic surface, and form a strong (covalent) bond with one of the substrate atoms, a process that has been extensively studied, both experimentally28–30 and theoretically.31,32 In this case, the binding carbon atom moves out of the surface plane by about 0.4 Å as a consequence of the sp2 → sp3 re-hybridization of its valence orbitals, “puckers” the surface and stores considerable energy (∼0.8 eV) which may be released into the lattice upon hydrogen abstraction. Importantly, a ∼0.20 eV barrier to chemisorption appears which prevents sticking of cold hydrogen atoms, as observed experimentally using cold atom beams,33 and recently confirmed theoretically by converged quantum scattering simulations of the sticking dynamics.34,35 The diffusion of chemisorbed H atoms is prevented by a large barrier that matches the desorption threshold – i.e. H atoms prefer to desorb rather than diffuse – thereby ruling out the possibility of a LH recombination. Hence, in this chemisorbed regime hydrogen species which manage to stick are stable on the surface up to high temperatures (Ts ∼ 400–500 K) and form H2 molecules either through an ER or a HA reaction mechanism.
In this article we focus on the Eley–Rideal recombination involving chemisorbed H species. The reaction is strongly exothermic and barrierless, and thus proceeds down to very low collision energies,33,36 forming vibrationally hot product molecules.37,38 It was thoroughly scrutinized theoretically on several aspects6–21 – namely, the rovibrational distribution of the products, the presence of steering effects in the dynamics, the dynamical role of the binding carbon atom, the effect of surface temperature, the competition with non-activated sticking to neighboring carbon atoms and the influence of non-zero surface coverage on the reaction – but only occasionally considered for the isotope effect.39,40 Here we reconsider this issue by focusing on the cold collision energy regime which is relevant for the chemistry of the interstellar clouds. We do this by employing a time-dependent wavepacket method within the sucessful rigid, flat-surface approximation41,42 that was already applied in the past to the present reaction system.11,18–20,27 The specific implementation that allows us to address collisions at such cold collision energies (down to ∼10−4 eV ≈ 1.2 K), – already applied to the H + H isotopic combination19 – makes use of two independent wavepacket propagations that, exploiting the linearity of the Schrödinger equation, remove the limitations of a standard, one-wavepacket propagation.43 The strategy is rather general for quantum simulations in the time domain, and is being used in larger dimensional quantum dynamical studies of the title process which includes the motion of surface atoms and, thus, energy dissipation to the surface.
The paper is organized as follows. Section 2 describes in detail our two-wavepacket method, Section 3 focuses on some methodological aspects specific to the Eley–Rideal recombination problem, Section 4 describes the results obtained for the four isotopic combinations considered, and Section 5 summarizes and concludes.
2 Time-energy mapping at cold collision energies
One of the main advantages of time-dependent wave packet methods over time-independent ones is that with a single propagation one obtains energy resolved information for a given initial internal state and a range of collision energies. This is accomplished with the help of a time-energy mapping of the dynamics which is made possible by enforcing two ‘asymptotic’ conditions on the initial wave packet: the wavepacket is chosen to be (i) localized in the asymptotic region of the reagents and (ii) with incoming momentum components only (i.e. momentum components towards the interaction region, p < 0). These conditions thus mimic the classical approach to a collision problem, where trajectories are started in the asymptotic region of the reagents with momentum vectors directed towards each other. They challenge the applicability of the time-dependent method to the cold collision energy regime since they severely limit the width Δp of the initial momentum wavefunction (Δp ≲ p0, if −p0 is the average initial momentum), hence the minimum width Δx of the initial wavepacket (Δx ≳ ℏ/Δp ≳ ℏ/p0). This is clearly unpleasant if one is interested in covering a large range of collision energies with a single calculation and, in addition, wants to keep the grid dimensions reasonably small.In order to make progress let us recall why the above conditions are crucial for the standard time-energy mapping. Firstly, they relate the forward propagation to the (differential) eigenprojector on the energy shell δ(E−H), namely through
Here |Eβ+〉 is a scattering (outgoing) eigenstate corresponding to the precollisional |Eβ〉 eigenstate, the sum runs over the open channels of every arrangement, and in the last step we have used
(U0,βt being the free-evolution operator for channel β) which holds, thanks to the conditions mentioned above. Finally, one obtains
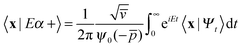 | (1) |
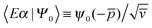 – and
– and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) and
and ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (≥0) are the entrance channel momentum and speed, respectively.
(≥0) are the entrance channel momentum and speed, respectively.
With this premise in mind, let us now show how to exploit the linearity of the Schrödinger equation and obviate condition (ii) by (independently) propagating two wavepackets in place of one.43 If ψa(p) is a generic (momentum) wavefunction for the motion in the entrance-channel scattering coordinate (to be used in |Ψa〉 = |ψaα〉 as initial state) we may write, under the sole condition (i) above,
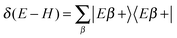 . The second term on the r.h.s. of the above expression represents the contribution of the outgoing components to the energy shell, i.e. the collision processes β → α which do have outgoing components in channel α and necessarily overlap with those contained in |Ψa〉. This term disappears, of course, in the traditional approach when condition (ii) is enforced. Now, using two (linearly independent) initial states (a = 1, 2), the above equation reduces to a 2 × 2 linear system in the variables X = 〈x|Eα+〉 and
. The second term on the r.h.s. of the above expression represents the contribution of the outgoing components to the energy shell, i.e. the collision processes β → α which do have outgoing components in channel α and necessarily overlap with those contained in |Ψa〉. This term disappears, of course, in the traditional approach when condition (ii) is enforced. Now, using two (linearly independent) initial states (a = 1, 2), the above equation reduces to a 2 × 2 linear system in the variables X = 〈x|Eα+〉 and 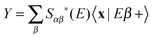 which can be easily solved to give
which can be easily solved to giveThis is the desired expression that we were looking for and that can be further re-expressed in terms of time-evolving wavepackets
using, in general, both the forward and the backward evolutions. The resulting equation generalizes eqn (1) without the requirement of condition (ii). It is easy to check that when enforcing this additional condition one wavepacket is sufficient to get the desired scattering eigenstate, and that the above expression does indeed reduce to eqn (1) (just use ψ1(
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ) ∼ 0 and consider x in the product region so that only the t > 0 evolution is required).
) ∼ 0 and consider x in the product region so that only the t > 0 evolution is required).
Finally, it is advantageous in practice to further simplify the above expression by employing time-reversal invariant initial states, i.e. states for which T|Ψa〉 = |Ψa〉 holds, T being the anti-unitary time-reversal operator. Indeed, in this case,
| 〈x|UtΨa〉 = 〈x|UtTΨa〉 = 〈x|TU−tΨa〉 = 〈x|U−tΨa〉* |
thereby involving only the forward evolution. Here, we can choose wavepackets for the translational motion that are ‘even’ or ‘odd’ with respect to a reflection on a plane passing through their average position x0, whose corresponding momentum wavefunctions are given by ψ1(p) = ϕg(p)e−ipx0 and ψ2(p) = −iϕu(p)e−ipx0, where ϕg(ϕu) is a real even (odd) function of p. This reduces the scattering amplitude to
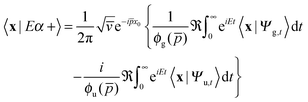 | (2) |
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) x0). This means that the two can be computed and managed independently of each other and stored as independent parts of a single complex array.
x0). This means that the two can be computed and managed independently of each other and stored as independent parts of a single complex array.
In this work we have used eqn (2) in place of eqn (1) in order to perform the time-energy mappings needed to extract energy resolved information from the time propagations. Thus, for example, the probability Pα→β for the collisional transition to a product internal state β reads as usual†
For completeness, Table 1 summarizes the main formulas used in the standard approach (with the common choice of a Gaussian wavepacket as the initial translational state) and in this work. Notice that the ‘even’ and ‘odd’ components in our approach correspond to the ground and the first excited states of a harmonic oscillator potential centered in x0; the choice 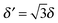 for the width appearing in ψu guarantees that the two wavefunctions have the same spread Δp in momentum space.
for the width appearing in ψu guarantees that the two wavefunctions have the same spread Δp in momentum space.
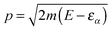 , where εα is the channel energy in the pre-collisional state, and the reaction probabilities are obtained from
, where εα is the channel energy in the pre-collisional state, and the reaction probabilities are obtained from 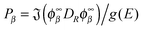 . Here, DRϕ∞β is analogous to ϕ∞β, and involves the derivate with respect to the scattering coordinate R evaluated at the large value R∞. In the table entries m and m′ are the reduced masses in the reagent and product arrangement, respectively, δ is the width of the initial wavepacket in the scattering coordinate and x0 (p0) the average position (momentum)
. Here, DRϕ∞β is analogous to ϕ∞β, and involves the derivate with respect to the scattering coordinate R evaluated at the large value R∞. In the table entries m and m′ are the reduced masses in the reagent and product arrangement, respectively, δ is the width of the initial wavepacket in the scattering coordinate and x0 (p0) the average position (momentum)
3 Dynamical model and methodology
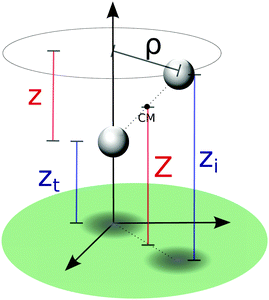
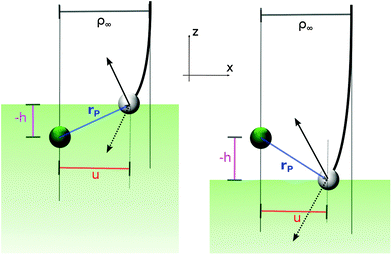
To simulate the Eley–Rideal process, we considered a projectile atom of mass mP and position xP which scatters off a chemisorbed target atom of mass mT and position xT. In line with our previous work17–20,27 a reduction of the number of relevant coordinates is achieved by invoking the rigid, flat surface approximation41,42 that makes P∥ (the total momentum parallel to the surface) and Jn (the projection of the total angular momentum on the surface normal) conserved quantities.§ In this simplified 3D description, the phonons of the graphitic surface are neglected and the interaction of the target/incident atoms with the surface is site-independent. On the other hand, the (important) role of the carbon binding the target can be included in the potential energy surface (PES) governing the dynamics in two opposite dynamical limits.11 In the (substrate) diabatic limit the reaction dynamics is supposed to be so fast that the C atom remains frozen in its puckered configuration, whereas in the adiabatic limit the substrate atom relaxes istantaneously during the (supposedly slow) recombination process. These limits give rise to two different PESs with rather different exothermicities (3.90 eV in the adiabatic potential and 3.03 eV in the diabatic one), on account of the energy left on the lattice in the diabatic model. Apart from this, though the energy landscape is rather similar in the two dynamical limits, and displays a downhill (barrierless) route to the molecular product.11In modeling the dynamics, the relevant dynamical variables are conveniently chosen to be either the height of the two atoms above the surface (zP,zT for the projectile and target atoms, respectively) and their separation on the surface plane (ρ), or the center of mass height Z = (mPzP + mTzT)/(mP + mT), the relative height z = zP − zT and ρ (see Fig. 1). The first is a “reagent” set of coordinates which best suits to compute energy resolved (in)elastic scattering, atom exchange and trapping probabilities, and the second is a “product” set which is ideal for determining the rovibrational populations of the reaction products.
As for the wavepacket propagation, a detailed description of our strategy, which stems from previous work reported by Lemoine and Jackson,42 has been presented elsewhere.18 Briefly, for the cartesian coordinates (either (zT,zP) or (Z,z)) the wavepacket is represented on a uniform grid, and the pseudospectral strategy involving the use of Fast Fourier Transforms (FFTs) is exploited to move efficiently back and forth between the coordinate and momentum space. For the cylindrical coordinate, the discrete Bessel transform (DBT) of Lemoine44 is used instead, since Bessel functions correctly handle the boundary conditions in the cylindrical radial coordinate and guarantee a numerically stable representation of the kinetic energy operator. The length of the grid along ρ (which sets the maximum value of the classical impact parameter) was set to 13 Å irrespective of the isotopic combination, after carefully testing that this value gives reasonably well converged cross-sections. The number of grid points, on the other hand, was chosen differently for each reaction in order to guarantee a common value of the maximum momentum on the ρ axis. The same consideration guided the choice for the grid spacing of the cartesian coordinates, for which an energy cutoff of ∼5.5 eV was introduced. Time propagation was performed using the split-operator method,45 using multithreaded routines for FFTs and linear algebra operations which are available in commercial packages.
The initial wavepackets were built as a product of three terms, namely (i) a wavepacket centered in the reagent asymptotic region and describing the motion of the incident atom normal to the surface (ψa(zP)), (ii) a vibrational wave function for the target atom bound to the surface (ϕv(zT)) and (iii) a quasi-plane wave for the relative motion parallel to the surface (ϕ∥(ρ)). We choose to consider only the vibrational ground state of the target atom (v = 0), since it is the only one relevant for the ISM chemistry, the excitation energy to ν = 1 being already too large for the typical diffuse cloud conditions. The translational component of the initial wavefunctions (two for each calculation) was 0.2 Å large in coordinate space and zero-centered in momentum space, in accordance with the methodology introduced in Section 2 (see Table 1). As for the motion along ρ, since we considered normal incidence only we picked up the lowest-momentum Bessel function supported by the adopted grid, i.e. a quasi-uniform initial state.
Practical application of the two-wavepacket strategy requires the use of a sufficiently large grid to accommodate both the longest wavelength of interest and a reasonably good absorbing potential. In practice, this is needed in the entrance arrangement only since product (open) channels benefit of the reaction exothermicity ultimately leading to short-wavelength outgoing components at all but the threshold energies. Following our previous experience, we adopted Manolopoulos' transmission-free absorbing potentials46 (APs). These were originally designed to completely remove transmission at high energy – provided the appropriate boundary conditions are enforced by the adopted discretization –, thereby allowing one to deal only with the low-energy reflection problem. These APs have one parameter only, the strength Emin of the potential, which sets both the energy scale (the lowest kinetic energy with a reflection probability less than 1%) and the AP length 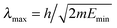 . In the typical applications we are interested in, i.e. hydrogen atoms at 10−3–10−4 eV, an absorption length of ∼30 Å is required, i.e. a rather smooth AP which is slowly absorbing. As a consequence, propagation requires rather long times19 (75–100 ps), which are anyhow necessary to obtain energy resolved results at low energies.
. In the typical applications we are interested in, i.e. hydrogen atoms at 10−3–10−4 eV, an absorption length of ∼30 Å is required, i.e. a rather smooth AP which is slowly absorbing. As a consequence, propagation requires rather long times19 (75–100 ps), which are anyhow necessary to obtain energy resolved results at low energies.
Probabilities were computed with the flux analysis outlined in Section 2. In particular, total Eley–Rideal cross-sections were obtained from the flux through the appropriate surfaces in both product and reagent coordinates, whereas the rovibrational H2 populations were conveniently determined in product coordinates. Cross-sections for hot-atom formation σHA were obtained from calculations in “reagents” coordinates, upon projecting the flux exiting along ρ onto the combined bound states of the incident and the target atoms. As a consequence, σHA describes the formation of pairs of atoms freely moving on the surface with an energy higher than the desorption threshold but channeled in the relative motion parallel to the surface. Specifically, the energy of the relative motion along ρ is given by 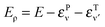 where εPν
where εPν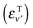 is the energy of the bound state in the surface-projectile (target) potential in which the incidon (targon) is found. Realistic surfaces present corrugation, fluctuations and dissipative effects, which make these “hot-atoms” metastable only – they either relax to stable species or desorb from the surface – nevertheless, the computed σHA represent reasonable order-of-magnitude estimates of the hot-atom formation cross-sections.
is the energy of the bound state in the surface-projectile (target) potential in which the incidon (targon) is found. Realistic surfaces present corrugation, fluctuations and dissipative effects, which make these “hot-atoms” metastable only – they either relax to stable species or desorb from the surface – nevertheless, the computed σHA represent reasonable order-of-magnitude estimates of the hot-atom formation cross-sections.
Table 2 summarizes the main parameters adopted for the simulations in reagent coordinates. Parameters of product coordinates were chosen to guarantee a similar accuracy down to a reasonably small collision energy (∼meV); at lower energies, only the reagent set can accommodate the large APs necessary to obtain converged results.19
| H + H/C | H + D/C | D + H/C | D + D/C | |
|---|---|---|---|---|
| t tot/ps | 100 | 100 | 100 | 100 |
| Δt/fs | 0.25 | 0.25 | 0.25 | 0.25 |
| z P(0)/Å | 15.0 | 15.0 | 15.0 | 15.0 |
| n P | 675 | 675 | 960 | 960 |
| ΔzP/Å | 0.06 | 0.06 | 0.0426 | 0.0426 |
| z P – flux line/Å | 16.0 | 16.0 | 16.0 | 16.0 |
| z P – EAPmin/meV | 0.14 | 0.14 | 0.06 | 0.06 |
| n T | 125 | 180 | 125 | 180 |
| ΔzT/Å | 0.06 | 0.0426 | 0.06 | 0.0426 |
| z T – flux line/Å | 5.0 | 5.0 | 5.0 | 5.0 |
| z T – EAPmin/meV | 14.2 | 6.1 | 14.2 | 6.1 |
| n ρ | 150 | 170 | 170 | 210 |
| ρ – flux line/Å | 11.0 | 11.0 | 11.0 | 11.0 |
| ρ – width/Å | 13.0 | 13.0 | 13.0 | 13.0 |
We further performed quasi-classical trajectory (QCT) calculations to single out genuine quantum effects in the reaction dynamics. Target vibrational energy levels were obtained, as in the wave packet calculations, by standard diagonalization of the adsorbate–substrate Hamiltonian in the sinc-discrete variable representation (DVR), and used to sample the target initial coordinate and momentum. The incident atom was placed at zP(0) = 8.0 Å, and propagation was carried out for sufficiently long times (up to 50 ps) to obtain converged results down to low collision energies (10−4 eV), running 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories for each selected energy.
000 trajectories for each selected energy.
4 Results and discussion
In the following, we describe the results of the quantum calculations that we performed on both the adiabatic and the diabatic models developed by Sha et al.11 to describe hydrogen recombination on graphite. We shall use “AonB” to indicate the process in which the A atom from the gas phase (the incidon) collides with the chemisorbed B atom (the targon):| A(g) + Bad → AB(g) |
4.1 2D calculations
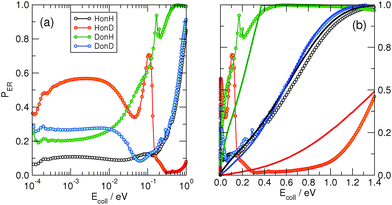
Fig. 2 reports the results of collinear reaction probabilities for the adiabatic potential, showing a clear isotope effect for each collision energy, though qualitatively different depending on the energy range considered. Similar results were obtained for the diabatic model (not shown).At high collision energy (Ecoll ≳ 0.2 eV) the behavior of the probability curves is rather classical and well-captured by a simple, quasi-classical impulsive model of the dynamics.¶ In this model, the projectile with mass mP and speed 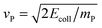 undergoes a binary collision with the target of mass mT and speed vT, slows down its motion, and gets captured by the targon after the latter elastically bounces off the surface. Reaction occurs when the final kinetic energy of the targon ET′ is larger than ER, a dynamical threshold which replaces the details of the dynamics and filters out those trajectories in which the targon is too slow to capture the projectile before leaving the reaction region (i.e. the surface).
undergoes a binary collision with the target of mass mT and speed vT, slows down its motion, and gets captured by the targon after the latter elastically bounces off the surface. Reaction occurs when the final kinetic energy of the targon ET′ is larger than ER, a dynamical threshold which replaces the details of the dynamics and filters out those trajectories in which the targon is too slow to capture the projectile before leaving the reaction region (i.e. the surface).
The final kinetic energy ET′ is determined by the post-collisional target velocity vT′, as results, in turn, by the acceleration provided by the strong H–H interaction and by the above two sequential collisions, that is through the sequence
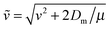 (Dm being the H–H well depth) and μ = mPmT/(mP + mT) is the reduced mass of the binary system. Hence, the reaction condition EfT(vT,vP) > ER determines a domain
(Dm being the H–H well depth) and μ = mPmT/(mP + mT) is the reduced mass of the binary system. Hence, the reaction condition EfT(vT,vP) > ER determines a domain ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (vP) of target velocities leading to reaction, and the reaction probability P follows by integrating the distribution of target velocities g(v) over
(vP) of target velocities leading to reaction, and the reaction probability P follows by integrating the distribution of target velocities g(v) over ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (vP) for each value of the collision energy Ecoll = mPvP2/2.
(vP) for each value of the collision energy Ecoll = mPvP2/2.
It then remains to establish which is the most appropriate velocity distribution function g(v) to be used. In the true impulsive limit g(v) would simply be g(v) = mT|ϕν(mTv)|2, where ϕν(p) is the momentum space wavefunction of the target initial vibrational state (v = 0 in our case). However, this limit does not strictly hold in our case since the (high-frequency) target vibration ω0 sets a bound to the collision time τ ≪ ω0−1 which only attains at some eV of collision energy, as can be seen upon noticing that 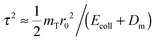 , where r0 is the potential range and ω02 = 2α2DT/mT (here, DT is the targon-surface well depth and α−1 is the length scale of the Morse potential used to represent the targon–surface interaction, α−1 ≈ r0). In other words, the targon atom performs one–two vibrations during the collision, and this makes the above-mentioned vibrational distribution particularly inadequate for the lightest targets. To remedy this deficiency, and keep the model as simple as possible, we assume that the appropriate momentum distribution keeps the same shape and average but is bound to describe the increase of the average kinetic energy due to the interaction with the projectile, i.e. 〈Δp2〉 = 〈Δp02〉 + 2mTDeff, where Deff is an effective interaction energy and 〈Δp02〉 is the width of the bare momentum distribution of the target. This amounts to replace the original targon frequency ω0 determining ϕν(p) with an effective frequency ω = ω0 + 4Deff/ℏ.
, where r0 is the potential range and ω02 = 2α2DT/mT (here, DT is the targon-surface well depth and α−1 is the length scale of the Morse potential used to represent the targon–surface interaction, α−1 ≈ r0). In other words, the targon atom performs one–two vibrations during the collision, and this makes the above-mentioned vibrational distribution particularly inadequate for the lightest targets. To remedy this deficiency, and keep the model as simple as possible, we assume that the appropriate momentum distribution keeps the same shape and average but is bound to describe the increase of the average kinetic energy due to the interaction with the projectile, i.e. 〈Δp2〉 = 〈Δp02〉 + 2mTDeff, where Deff is an effective interaction energy and 〈Δp02〉 is the width of the bare momentum distribution of the target. This amounts to replace the original targon frequency ω0 determining ϕν(p) with an effective frequency ω = ω0 + 4Deff/ℏ.
The results of such modeling for the adiabatic limit are given in Fig. 2 as full lines (panel (b)), color coded as the result of the quantum simulations. We set ET = 3.4 eV, Dm = 4.0 eV, and Deff = 0.124 eV to obtain a reasonable representation of the quantum results. A similar agreement was found for the diabatic model, using the same values of parameters except for Deff which had to be increased to 0.250 eV, in accordance with the larger frequency of the H-graphite motion in the diabatic limit.||
The model is rather crude but, as can be seen from Fig. 2, it captures the main aspects of the dynamics and reproduces the isotope effect observed at high energies. The increase of the reaction probability with increasing mP/mT is a consequence of the larger range of targon initial velocities leading to sufficiently fast post-collisional targon atoms. Thus, in this classical energy regime, the largest isotope effect (i.e. the largest overall difference in reactivitiy) occurs at the “threshold” energy of the mP/mT = 1 case, ∼0.6 eV in Fig. 2. This is the prototypical case where the projectile atom completely transfers its energy when the targon is at rest (vT = 0), and thus represents a sort of transition between two different dynamical behaviours.
At low energies (Ecoll ≲ 0.2 eV), on the other hand, the dynamical outcome is largely determined by the details of the interaction potential, and by the quantum character of the dynamics that becomes more and more marked the smaller the energy is. As a consequence, for instance, the HonD combination (barely reactive at high energies) becomes more reactive at low energies than the “references”, equal–mass combinations HoH and DonD. Thus, apart from the complicated details of the curves that appear to be tightly bound to the potential model (with sharp resonances dominating the outcome of the collision process), the only general conclusion that can be drawn for this energy range is that the collinear reaction probability is again highly affected by the mass of the incident and target atoms.
4.2 3D calculations
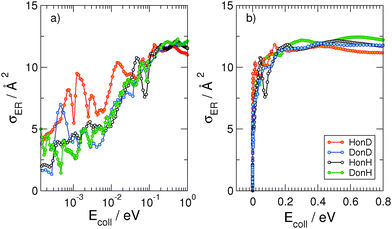
When the third spatial coordinate is added, the reactive cross-sections for the Eley–Rideal H2 recombination σER can be computed, as well as the cross-sections for non-reactive collisions giving rise to hot-atom species σHA. In Fig. 3, σER computed with the adiabatic model is plotted as a function of the collision energy for the four possible isotope combinations. The general behavior of such cross-sections was already extensively discussed in previous studies.11,17–19 At low energies, σER decreases as the collision energy decreases, likely because of the strong, short-range interaction potential between the two atoms that prevents low energy projectiles to enter the exit channel if their de Broglie wavelength is larger than the range of the potential. Thus, the cross-sections decay to zero for Ecoll → 0, though non-monotonically because of the presence of a number of sharp resonances. At moderate-to-high energy range, σER reaches large values (∼12 Å2) in all the considered cases, much larger than those observed on many metal surfaces,10 where σER barely reaches 1 Å2.** This feature is rather peculiar of the graphitic substrate where, in contrast to many metals, target hydrogen atoms are found at a larger height above the surface and projectile atoms experience a reduced interaction with the surface. At even higher energies (Ecoll > 0.2 eV), quantum oscillations appear in the cross-section, as a consequence of the particular reaction mechanism that – by featuring a rapidly decreasing internal excitation of the product for increasing energies – allows the low-lying product vibrational levels to be selectively populated.17,18,27Importantly, a rather striking feature of the results shown in Fig. 3 is the disappearance of the isotopic effect observed in the collinear case, in agreement with the findings of previous quantum studies at high collision energies on a crude model PES.39 This suggests that the dynamics is not as direct as the constrained collinear geometry forces it to be, and the reaction mechanism involves some energy “randomization” prior to reaction which hides the effect of different mass combinations. No real “tendency” can be discerned in the quantum results, and the effect of an unfavorable mass-ratio must be offset by some non-collinear dynamical effects. Such effects though must be of classical nature, since quasi-classical trajectory calculations reproduce quantum results very well over a large energy range, and do not show isotope effects either. This is shown in Fig. 4, where the QCT cross-sections, reported alongside with the quantum results, differ considerably from the latter only in the very low energy region, and are shown to reproduce rather well (on average) the quantum results. Notice, though, that different from the quantum results, the limiting classical cross-section at zero energy does not vanish, as expected for a barrierless classical reaction dynamics. For completeness, Fig. 4 also shows the results of the diabatic dynamical model (for clarity, only in the energy range where they are more reliable), which present a behavior similar to that obtained in the adiabatic limit, except for an overall reduction of the cross-section which correlates with the reduced exothermicity of the diabatic model.
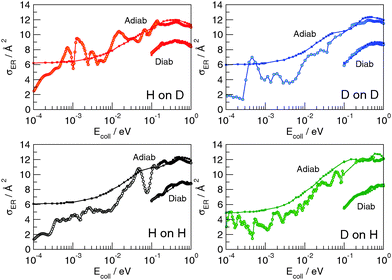 | ||
| Fig. 4 Comparison between quantum (circles) and quasi-classical results (squares). The size of the squares matches the estimated uncertainties in QCT results. | ||
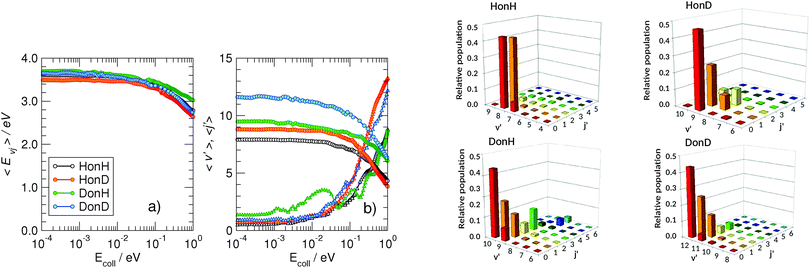
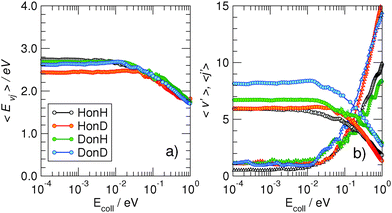
More information about the reaction dynamics can be obtained by looking at the rovibrational populations of the molecular product. The results obtained for the average internal energy, and average vibrational and rotational quantum numbers are shown in Fig. 5 (left). As is evident from that figure, and in agreement with previous studies at high energies,11,17,18 the nascent molecules are internally hot, with ca. 3.0–3.5 eV of the reaction exothermicity going in internal excitation of the Eley–Rideal product. In contrast to the behavior at high collision energies, though, internal excitation is mainly vibrational, the average rotational quantum number being rather small in the energy range 10−4–10−1 eV.†† This is not an artifact of the averaging procedure, since the detailed rovibrational distributions are rather peaked around few rovibrational states, as shown in Fig. 4 (right panel) at a representative energy of 2 meV. It is evident from that figure that the nascent molecule mostly appears in either one or two high-ν, low-j rovibrational states.
The behavior of the rotational excitation – which monotonically increases with the collision energy – correlates well with the reaction cross-sections, especially at high energies where the dynamics is classical. The rationale here is that, classically, the angular momentum j of the product molecule correlates well with the entrance orbital angular momentum l of the projectile–targon pair (i.e. j ∼ l), as discussed previously,18 hence 〈j〉 can be related to the reaction cross-section through the “maximum” impact parameter bmax, 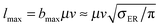 .
.
The above considerations suggest that in this realistic 3D case the reaction dynamics is determined by the relative motion in the entrance channel – similarly to what happens for the collinear approach –, but now the orbital angular motion of the colliding pair plays a primary role. If it were for the H–H potential only, “capture” of the projectile would not depend on the specific isotope combination, since the “capture radius” ρc reads as
This is best seen in a simple model where the targon is held fixed at a height h (h > 0 when the target atom lies above the surface) and the surface is represented by a hard wall that has the simple effect of reverting the normal component of the projectile velocity, vz → −vz (see Fig. 6). In this model, the orbital angular momentum of the projectile undergoes a sudden change l → l′ upon collision with the surface, namely
| Δl2 = l′2 − l2 = −4uhvxvz |
Real surfaces are not hard walls and display a more intricate competition with the targon field of forces than the one outlined above. Nevertheless, for the large-impact parameter trajectories we are interested in, the picture above is mainly modified only to the extent that the height of the turning point becomes energy dependent, the smaller the collision energy is, the higher the “altitude” where the projectiles revert their motion. In particular, the location of the physisorption well (relative to the chemisorption well) determines the limiting “height of the targon” at vanishing collision energies. Its negative value considerably reduces the size of the gas-phase capture radius and makes it finite at zero energy.
Overall, even though this argument does not explain the precise form that σER takes as a function of energy, it does suggest a reason why the reaction cross-section does not depend on the mass combination of the colliding pair: the reaction is dominated by the capture process – i.e. collisions are mainly glancing rather than head-on – and this is only marginally affected by isotopic substitutions.
Fig. 7 shows the average internal energy, and the average vibrational and rotational quantum numbers of the product molecules, as obtained from the diabatic model, similarly to Fig. 5 for the adiabatic limit. As can be seen from this figure, the dynamics is very similar in the two models, the only difference being the smaller reaction exothermicity described in the diabatic limit, which determines a corresponding decrease of the internal energy of the products. In other words, the change in the reaction energetics does not affect the translational energy of the products, only their internal content. This highlights the importance of including energy relaxation to the surface into the reaction dynamics in order to accurately assess the internal excitation of the product molecule – the “missing energy” of the diabatic model is just a crude way to describe such energy transfer, energy is stored in the puckered carbon atom and released into the substrate upon molecular formation.
In contrast with the ER reaction, the cross-section for the formation of hot-atom species is characterized by a strong isotopic effect. This is shown in Fig. 8, which reports σHA as a function of the energy of the incident atom for the four isotope combinations. As evident from the figure, when the incident atom is hydrogen (black and red curves), σHA barely reaches 2 Å2, whereas when the incident atom is deuterium (green and blue curves), the cross-section significantly increases and can be as large as ∼16 Å2. In our dynamical model, the HA formation corresponds to the situation in which the reactive event ends with a large momentum along ρ and with the incident atom bound (normal to the surface) in the physisorption well. Hence, the larger deuterium cross-sections are simply a consequence of the larger number of final physisorbed bound states available for the incident atom. The well is in fact only ∼7.75 meV in our model potential and supports only one state for H and two for D, but similar results are expected for a more realistic physisorption well depth.22,23 In any case, irrespective of the mass combination, σHA quickly vanishes for Ecoll ≳ 10−2 eV, when projectile energy becomes too large for trapping in the physisorption well.
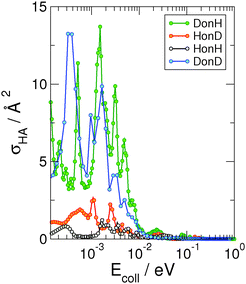 | ||
| Fig. 8 Quantum cross sections for the “hot-atom” formation for the four considered isotopic combinations as a function of collision energy, computed within the adiabatic model. | ||
A word of caution is appropriate here. Our dynamical model is not entirely adequate to simulate hot-atom formation, since within the flat surface approximation a free motion along ρ implies that both incidon and targon might be moving along the direction parallel to the surface. This situation should not be allowed in our problem since the target atom should be held in place by a strong, directional bond with the surface. The model though does capture the main effects of the presence of the target atom – i.e. the increase of surface corrugation and energy accommodation –, hence we are confident that it correctly describes the “initial” trapping cross section. After this step it is the dynamical response of the C–H bond that determines whether the trapped incidon species interacts again with the targon or is left free to move on the surface. In this respect, our results can be considered the limiting case where the targon rebounce (CH bending) is slow enough to not affect the projectile atom after the first collision.
5 Summary and conclusions
In this work we have used quantum dynamics to investigate isotope effects in collision induced processes involving hydrogen/deuterium atoms on graphite at the cold collision energies typical of the ISM. We focused on chemisorbed target atoms and analyzed the Eley–Rideal reaction and trapping dynamics for the four possible isotopic combinations, using a time-dependent “two-wavepacket” method and quasi-classical dynamics.Our simulations show that ER hydrogen formation is affected by isotopic substitutions only in the collinear approach. In this case, the PER curves for different mass combinations result from an intricate interplay of kinematic and quantum effects, but at high energies, are well rationalized by a simple quasi-classical impulsive model of the dynamics. In the 3D case, on the other hand, this marked isotopic effect disappears and the four considered reactions show almost identical trends and values for σER, likely as a consequence of the fact that the “capture” of the projectile does not depend on the specific mass combination. This suggests two different “mechanisms” for product formation, namely through either “head-on” or “glancing” collisions. The first presents a marked isotopic effect but has a limited weight in the cross-section while the second has the largest weight but is less sensitive to mass effects.
In contrast to the Eley–Rideal reaction, the mass of the projectile does strongly influence hot-atom formation. σHA reaches considerably large values (∼16 Å2) when the atom from the gas phase is the heaviest, and barely attains 2 Å2 for hydrogen. This is a direct consequence of the increased number of bound states in the physisorption well that can host the trapped incidon. This effect, likely occurring on different surfaces as well (e.g. those covered by ice mantles), might be responsible for some deuterium enrichment in the ISM grains, with impact on deuterium fractionation¶¶ through surface reactions. It is worth noticing though that such fractionation is mainly a gas-phase effect related to the efficient ‘primary’ fractionation in H3+([H2D+]/[H3+] ∼ 104[HD]/[H2]), and the primary role of surfaces is through accretion, which depletes H2D+-destroying molecules (notably CO) and makes the formation of higher deuterated species D2H+ and D3+ possible.48,49
A comparison of the results obtained in the adiabatic and in the diabatic limits suggests that the reaction is only marginally affected by the lattice dynamics – ab initio molecular dynamics simulations including the lattice dynamics indeed found cross-section values intermediate between these two limits21 – but for a correct description of the internal excitation of the product molecules it is essential to include energy transfer to the carbon atom holding the targon in place. Work is currently in progress to lift this static surface approximation and describe the dynamical role that the substrate carbon atoms (and the ensuing energy dissipation to the surface) play in the reaction.
Acknowledgements
This work has been supported by Regione Lombardia and the CINECA High Performance Computing Center through a LISA Initiative (2014) grant.References
- V. Wakelam, I. Smith, E. Herbst, J. Troe, W. Geppert, H. Linnartz, K. Öberg, E. Roueff, M. Agúndez and P. Pernot, et al. , Space Sci. Rev., 2010, 156, 13 CrossRef CAS.
- R. J. Gould and E. E. Salpeter, Astrophys. J., 1963, 138, 393 CrossRef CAS.
- D. Hollenbach and E. E. Salpeter, J. Chem. Phys., 1970, 53, 79 CrossRef CAS.
- D. Hollenbach and E. E. Salpeter, Astrophys. J., 1971, 163, 155 CrossRef CAS.
- B. T. Draine, Annu. Rev. Astron. Astrophys., 2003, 41, 241 CrossRef.
- P. Parneix and P. Brechignac, Astron. Astrophys., 1998, 334, 363 CAS.
- A. J. Farebrother, A. J. Meijer, D. C. Clary and A. J. Fisher, Chem. Phys. Lett., 2000, 319, 303 CrossRef CAS.
- A. J. H. M. Meijer, A. J. Farebrother, D. C. Clary and A. J. Fisher, J. Phys. Chem. A, 2001, 105, 2173 CrossRef CAS.
- M. Rutigliano, M. Cacciatore and G. D. Billing, Chem. Phys. Lett., 2001, 340, 13 CrossRef CAS.
- B. Jackson and D. Lemoine, J. Chem. Phys., 2001, 114, 474 CrossRef CAS.
- X. Sha, B. Jackson and D. Lemoine, J. Chem. Phys., 2002, 116, 7158 CrossRef CAS.
- S. Morisset, F. Aguillon, M. Sizun and V. Sidis, Phys. Chem. Chem. Phys., 2003, 5, 506 RSC.
- S. Morisset, F. Aguillon, M. Sizun and V. Sidis, J. Phys. Chem. A, 2004, 108, 8571 CrossRef CAS.
- D. Bachellerie, M. Sizun, D. Teillet-Billy, N. Rougeau and V. Sidis, Chem. Phys. Lett., 2007, 448, 223 CrossRef CAS.
- D. Bachellerie, M. Sizun, F. Aguillon, D. Teillet-Billy, N. Rougeau and V. Sidis, Phys. Chem. Chem. Phys., 2009, 11, 2715 RSC.
- M. Sizun, D. Bachellerie, F. Aguillon and V. Sidis, Chem. Phys. Lett., 2010, 498, 32 CrossRef CAS.
- R. Martinazzo and G. F. Tantardini, J. Phys. Chem. A, 2005, 109, 9379 CrossRef CAS PubMed.
- R. Martinazzo and G. F. Tantardini, J. Chem. Phys., 2006, 124, 124702 CrossRef PubMed (pages 14).
- S. Casolo, R. Martinazzo, M. Bonfanti and G. F. Tantardini, J. Phys. Chem. A, 2009, 113, 14545 CrossRef CAS PubMed.
- M. Bonfanti, S. Casolo, G. F. Tantardini and R. Martinazzo, Phys. Chem. Chem. Phys., 2011, 13, 16680 RSC.
- S. Casolo, G. F. Tantardini and R. Martinazzo, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6674 CrossRef CAS PubMed.
- E. Ghio, L. Mattera, C. Salvo, F. Tommasini and U. Valbusa, J. Chem. Phys., 1980, 73, 556 CrossRef CAS.
- M. Bonfanti, R. Martinazzo, G. F. Tantardini and A. Ponti, J. Phys. Chem. C, 2007, 111, 5825 CAS.
- B. Lepetit and B. Jackson, Phys. Rev. Lett., 2011, 107, 236102 CrossRef PubMed.
- S. Morisset, F. Aguillon, M. Sizun and V. Sidis, J. Chem. Phys., 2005, 122, 194702 CrossRef CAS PubMed (pages 8).
- D. Bachellerie, M. Sizun, F. Aguillon and V. Sidis, J. Phys. Chem. A, 2009, 113, 108 CrossRef CAS PubMed.
- R. Martinazzo and G. F. Tantardini, J. Chem. Phys., 2006, 124, 124703 CrossRef PubMed (pages 7).
- T. Zecho, A. Güttler, X. Sha, B. Jackson and J. Küppers, J. Chem. Phys., 2002, 117, 8486 CrossRef CAS.
- A. Güttler, T. Zecho and J. Küppers, Chem. Phys. Lett., 2004, 395, 171 CrossRef.
- T. Zecho, A. Güttler and J. Küppers, Carbon, 2004, 42, 609 CrossRef CAS.
- L. Jeloaica and V. Sidis, Chem. Phys. Lett., 1999, 300, 157 CrossRef CAS.
- X. Sha and B. Jackson, Surf. Sci., 2002, 496, 318 CrossRef CAS.
- E. Aréou, G. Cartry, J.-M. Layet and T. Angot, J. Chem. Phys., 2011, 134, 014701 CrossRef PubMed.
- M. Bonfanti, B. Jackson, K. H. Hughes, I. Burghardt and R. Martinazzo, J. Chem. Phys., 2015, 143, 124703 CrossRef PubMed.
- M. Bonfanti, B. Jackson, K. H. Hughes, I. Burghardt and R. Martinazzo, J. Chem. Phys., 2015, 143, 124704 CrossRef PubMed.
- A. Güttler, T. Zecho and J. Küppers, Carbon, 2004, 42, 337 CrossRef.
- F. Islam, E. R. Latimer and S. D. Price, J. Chem. Phys., 2007, 127, 064701 CrossRef PubMed.
- E. R. Latimer, F. Islam and S. D. Price, Chem. Phys. Lett., 2008, 455, 174 CrossRef CAS.
- A. J. H. M. Meijer, A. J. Farebrother and D. C. Clary, J. Phys. Chem. A, 2002, 106, 8996 CrossRef CAS.
- M. Rutigliano and M. Cacciatore, ChemPhysChem, 2008, 9, 171 CrossRef CAS PubMed.
- M. Persson and B. Jackson, J. Chem. Phys., 1995, 102, 1078 CrossRef CAS.
- D. Lemoine and B. Jackson, Comput. Phys. Commun., 2001, 137, 415 CrossRef CAS.
- R. Martinazzo and G. F. Tantardini, J. Chem. Phys., 2005, 122, 094109 CrossRef PubMed (pages 9).
- D. Lemoine, J. Chem. Phys., 1994, 101, 3936 CrossRef CAS.
- M. Feit, J. Fleck and A. Steiger, J. Comput. Phys., 1982, 47, 412 CrossRef CAS.
- D. E. Manolopoulos, J. Chem. Phys., 2002, 117, 9552 CrossRef CAS.
- S. Casolo, O. M. Lovvik, R. Martinazzo and G. F. Tantardini, J. Chem. Phys., 2009, 130, 054704 CrossRef PubMed.
- T. Millar, Planet. Space Sci., 2002, 50, 1189 CrossRef CAS , ISSN 0032-0633, special issue on Deuterium in the Universe.
- T. J. Millar, Astron. Geophys., 2005, 46, 2.29 CrossRef CAS.
Footnotes |
| † See, for example, the Appendix in ref. 18 for a time-dependent perspective. |
| ‡ The flux operator appearing here, F∞β, is defined as the Heisenberg derivative of the projector onto the product internal state β, F∞β = i[H,P∞β]. The latter reads as P∞β = h∞(R)|β〉〈β|, where R is the product scattering coordinate (operator), h∞(x) = {1 for x > R∞, 0 otherwise} is the usual Heaviside function centered on a large distance R∞ and β labels the relevant product internal state. |
| § Conservation of the angular momentum gives rise to a partial wave expansion. At normal incidence (the case considered in this work) only the zero angular momentum partial wave is required. |
| ¶ We term it quasi-classical because it makes use of the quantum distribution of the precollisional targon momenta. |
|| For the H-graphite surface oscillator the vibrational wavenumber ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = ω0/2πc turns out to be 1807 and 2252 cm−1 for the adiabatic and diabatic cases, respectively. = ω0/2πc turns out to be 1807 and 2252 cm−1 for the adiabatic and diabatic cases, respectively. |
| ** Notice though that a spin-statistical factor of 1/4 applies on graphitic substrates but not on metals. This is due to the fact that the spin of the chemisorbed H atom is not quenched on graphene(ite), see e.g., ref. 47. |
| †† The “isotope effect” which is apparent in the average vibrational quantum numbers just reflects the different level spacing of the H2, HD and D2 molecules, see Fig. 5, panel (a). |
‡‡ If needed, νx and νz can be expressed in terms of rP and the constants of motion in the targon field, namely as νx = (−νru + νωh)/rP and νz = (νrh + uνω)/rP, where 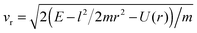 and νω = −l/mrPνω (U(r) being the projectile-targon spherical potential). and νω = −l/mrPνω (U(r) being the projectile-targon spherical potential). |
| §§ The case h = 0 with the targon “in the plane” of the surface does not modify l, hence in this case the rotational angular momentum of the product molecules exactly matches the angular momentum of the reagents. This is the correlation between angular momenta (j ∼ l) alluded to above. |
| ¶¶ That is, the observation of deuterated molecules well in excess (up to 1011) of the statistical predictions based on the cosmic D/H ratio ∼10−5. |
| This journal is © the Owner Societies 2016 |