Two reaction regimes in the oxidation of larger cationic tantalum clusters (Ta_n⁺, n = 13–40) under multi-collision conditions

Abstract

The reaction of cationic tantalum clusters (Ta_n⁺, n = 13–40) with molecular oxygen is studied under multi-collision conditions and at different temperatures. Consecutive reaction proceeds in several steps upon subsequent attachment of O₂. All cluster sizes exhibit fast reaction with oxygen and form a characteristic final reaction product. The time-dependent product analysis enables the fitting to a kinetic model with the extraction of all the rate constants. Determined rate constants reveal the existence of two different regimes, which are interpreted as a change in the reaction mechanism. Based on the temperature-dependent reaction behavior, it is proposed that the reaction changes from a dissociative to a molecular adsorption of oxygen on the clusters. It is found that both regimes appear for all cluster sizes, but the transition takes place at different intermediate oxides Ta_nO_x⁺. In general it is observed that transition occurs later for larger clusters, which is attributed to an increased cluster surface.

---

1 Introduction

Today tantalum is used for various applications ranging from electronics¹ to medical instruments.² Materials containing tantalum oxides are of special interest as they are utilized for example as optical³ and protective coatings for sensors⁴ or in electrochemical applications.^5–8 In the latter, efforts are made to find substitutes for purely Pt-based electrocatalysts in the oxygen reduction reaction (ORR). To this end, tantalum oxide materials that enhance redox reactions, especially towards oxygen, are studied. Pt particles embedded into a tantalum oxide framework, for instance, have been shown to be not only very durable but also highly active ORR electrocatalysts.⁸ TaO_x nanoparticles are also very stable and demonstrate a remarkable size-effect in the ORR activity, which may relate to an improved electroconductivity and a higher number of active sites for increasingly smaller particles.⁷ Basame et al. further showed that certain sites of a Ta/Ta₂O₅ electrode are chemically selective and it was speculated that selective redox activity occurred at sites with a very thin or entirely absent oxide film.⁶

All of these effects on the redox activity are caused by properties on the microscopic to nanoscopic scale that is preferentially studied under well-defined conditions. Ideal model systems for catalysis and reactions, in general, are found in small metal (oxide) clusters, particularly in the gas phase,⁹ and their study is inspired by their unique, often non-scalable properties.¹⁰ In the gas phase, neutral tantalum oxide clusters react readily with NO and NH₃.¹¹ Furthermore, tantalum cations have been found to mediate the coupling of methane and carbon dioxide.¹² Moreover, cationic clusters react with 1-butene, 1,3-butadiene and benzene by cracking of a C–C bond.¹³ For ethane and ethylene, association and molecular oxygen loss have been observed.¹⁴ In contrast to cluster oxides, relatively few studies on bare tantalum clusters exist. He and co-workers found that neutral tantalum clusters dehydrogenate unsaturated hydrocarbons.¹⁵ Cationic tantalum clusters have been observed to activate nitrogen¹⁶ and react with small alcohols by dehydrogenation or dissociation of the C–O bond.¹⁷

The reactivity of the tantalum cation with O₂ was previously studied in an argon matrix,¹⁸ a flow tube,¹⁹ a guided ion beam experiment,^20,21 and an RF ion trap²² and the exothermic formation of TaO⁺, TaO₂⁺ as well as higher oxides was observed. The consecutive reaction of tantalum (oxide) clusters with oxygen has not been investigated as of yet. A detailed investigation will, on a molecular level, provide insights relevant to the oxidation processes in complex tantalum oxide systems and reveal inherent cluster properties. Therefore, the aim of the present work is to study the reaction of size-selected tantalum cluster cations (Ta_n⁺, n = 13–40) with molecular oxygen. The reaction is followed over time under isothermal conditions at various temperatures. From these data kinetic parameters are extracted, which enable one to interpret the course of the reaction.

2 Experimental setup and methods

The experimental setup has been described elsewhere in detail.²³ In short, tantalum clusters of various sizes are produced by a laser vaporization cluster source.²⁴ Cationic clusters are size-selected by a quadrupole mass filter and subsequently stored in a ring electrode ion trap, which is based on the designs of Gerlich²⁵ and Asmis.²⁶ A home-built electronic control unit allows the application of square-wave voltages (100–750 kHz, 0–600 V_pp) to the electrodes of the trap. This setup permits the storage of ions at least between 200 u and 17 000 u for time spans of several milliseconds up to seconds.²³ As clusters created by a single 100 Hz laser pulse are stored and used for kinetic measurements, minimal reaction times of 10 ms and below can be investigated. A cryostat in combination with a heating cartridge enables the operation of the trap under isothermal conditions in a range between 20 K and 300 K. A buffer gas, usually helium, constantly streams into the trap and thermalizes the stored clusters within a few milliseconds.²⁷ These collisions additionally reduce the initial kinetic energy of the clusters so that they cannot overcome the confining potentials anymore. For all experiments the pressure inside the trap was set to 3 Pa. In a similar experiment Kappes and co-workers assumed that their pressure measurement has an error of 50%²⁸ and a similar error is assumed for the absolute pressure in this work. In order to study the oxidation of the clusters, a mixture of 100 ppm oxygen in helium (Westfalen, Helium 6.0, 100 ppm Oxygen 6.0) is used as buffer gas. This mixture is diluted even further with helium (Westfalen, Helium 6.0) in a home-built mixing chamber for concentration-dependent measurements. After a specific reaction time, the charged reaction products are ejected from the trap and analyzed on a home-built reflectron time-of-flight mass spectrometer with orthogonal ion extraction.²³ This mass spectrometer has a mass resolution of 3000 during operation of the ring electrode ion trap. A single measurement point typically represents an average of 100 measurement cycles.

3 Results

A detailed analysis of the oxidation reaction will be given on the example of Ta₂₀⁺ and the results are subsequently compared to selected cluster sizes up to n = 40. When Ta₂₀⁺ cations are exposed to oxygen, fast oxidation of the clusters occurs. As shown in Fig. 1, at a reaction time of 50 ms, a partial oxygen concentration of 100 ppm, and a temperature of 300 K, the vast majority of the clusters are oxidized and only a small amount of the bare clusters remains. The oxidation proceeds via the attachment of two oxygen atoms and only a negligible amount of cluster fragmentation occurs. After several consecutive oxidation steps, Ta₂₀O₂₆⁺ is formed as the final reaction product. The reaction is completed after 500 ms and all the clusters have reacted to this particular oxide. Similar reaction behaviors are found for different temperatures, the exception being reaction temperatures below 100 K (see ESI†). Here, additional oxygen molecules are bound to the clusters. As these species only appear at low temperatures, it is assumed that the surplus oxygen molecules are only weakly bound to the cluster (e.g. by van der Waals interactions). Similar effects have been found for silver dimers²⁹ or palladium clusters.³⁰

Fig. 1 Mass spectra of Ta₂₀⁺ clusters exposed to 100 ppm O₂ at 300 K for reaction times of (a) 10 ms, (b) 50 ms, (c) 200 ms and (d) 500 ms. The reaction proceeds via subsequent attachment of O₂ units, which eventually results in the formation of a single Ta₂₀O₂₆⁺ species. Peaks marked with + are due to a side reaction with water background, * mark peaks due to fragmentation of the tantalum cluster. Both species are disregarded in the following due to their very low abundance.

In order to evaluate the reaction, kinetic modeling is performed. As the simplest model, a set of consecutive oxidation steps neglecting any back reaction is assumed:

Ta₂₀⁺ → Ta₂₀O₂⁺ → Ta₂₀O₄⁺ ⋯ → Ta₂₀O₂₆⁺ (1)

This reaction scheme can be expressed by quasi-first order kinetics, as the oxygen concentration stays approximately constant over the course of the reaction. The resulting differential equations are fitted to the data points and for all species an excellent agreement is achieved (see Fig. 2). The as-obtained rate constants (k′) include the concentration of oxygen. Furthermore, when termolecular reactions (expressed by k⁽³⁾) due to collisional stabilization with helium are considered, k′ also includes the concentration of helium:³¹

k′ = k·[O₂] = k⁽³⁾·[O₂]·[He] (2)

Fig. 2 Normalized concentrations for Ta₂₀⁺, Ta₂₀O₂₆⁺ (final reaction product) and all reaction intermediates as a function of reaction time. The solid lines represent the result of the kinetic fit, which excellently matches the experimental data.

Normalizing to the oxygen concentration, the bimolecular rate constant (k) of the respective elementary reaction step is obtained. The assumption of eqn (2) is verified experimentally, as the observed rate constant k′ is found to depend linearly on the oxygen concentration (see Fig. S2 in the ESI†). Here it should be mentioned that the absolute oxygen concentration is subject to a rather large systematic error of about 50% due to the error of the pressure measurement. However, the comparison of the relative changes of the rate constants is subject to a measured relative error of about 10%.

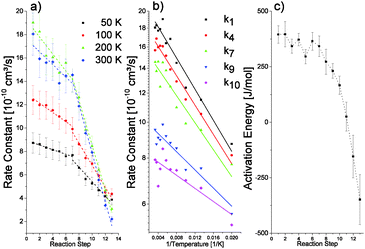
According to the fast nature of the reaction, large bimolecular rate constants ranging from about 1 × 10⁻⁹ cm³ s⁻¹ to more than 2 × 10⁻⁹ cm³ s⁻¹ are determined for the first reaction steps of all investigated cluster sizes (see Table T1 in the ESI†). These values are comparable to rate constants reported for the reaction of cationic vanadium clusters with oxygen, which are in the same range.³² Furthermore, the reaction rate may be compared to ion–molecule collision rates as described by Langevin theory,³³ which results in a calculated rate constant of 5.26 × 10⁻¹⁰ cm³ s⁻¹ for the association of O₂ to Ta₂₀⁺. This calculated value is obviously exceeded by the experimental value. However, Langevin theory models the interaction of a polarizable neutral molecule (i.e. an induced dipole) with a point charge. Accordingly, this description fails for larger clusters.³² When the experimental rate constants are plotted against the reaction step (Fig. 3), it is found that each reaction step is slower than the previous one. While for the first seven steps the rate constant decreases slowly, a steeper decrease is observed for the subsequent steps. This behavior is indicative of a change in the reaction mechanism and is similarly observed for the other cluster sizes; albeit the transition occurs at different reaction steps. Furthermore, the same observation is made at different reaction temperatures and both reaction regimes are reflected in the apparent activation energy, which is determined using an Arrhenius-like plot (Fig. 4). The activation energies are found to be considerably small, below 0.5 kJ mol⁻¹. During the first six reaction steps the apparent activation energy remains almost constant. However, from there on it decreases with each subsequent step, even reaching negative values. Similarly, relatively low but positive values were found for the reaction of silver dimers with oxygen.²⁹ The low activation energies reported in the same study were attributed to ion-induced dipole interactions, which result in a higher energy release upon adsorption.

Fig. 3 Rate constants determined for all reactions steps in the consecutive oxidation of Ta₂₀⁺. The two dashed lines represent a linear regression for reaction steps 1–7 and 7–13 respectively, demonstrating the existence of two reaction regimes.

Fig. 4 (a) Rate constants k of the oxidation of Ta₂₀⁺ as a function of the reaction step for 50 K, 100 K, 200 K and 300 K. (b) Arrhenius plot for selected reaction steps. (c) Apparent activation energy E_A for reaction steps 1 to 13. As observed in the trends of k and E_A, a transition occurs at the seventh reaction step during the oxidation of Ta₂₀⁺.

4 Discussion

The simple addition of O₂ is an insufficient description of the oxidation of larger cationic tantalum clusters. First of all, the observation of two reaction regimes, reflected by the different behavior of the rate constants and activation energies, indicates a change in the reaction mechanism. Secondly, the negative apparent activation energies for later reaction steps suggest a mechanism that is more complex than the straightforward addition of oxygen assumed beforehand. Formally negative activation energies have been determined previously in the reaction of small Ag, Au and Pd clusters with oxygen^29,30,34 and are the result of Lindeman-type reactions.³⁵ In the present case, Ta_nO_m⁺ (m ≥ 0) and O₂ react to form an activated complex Ta_nO_mO₂⁺* (given by k_a that can subsequently be stabilized) to Ta_nO_mO₂⁺ by collision with helium atoms (expressed by k_s), or dissociate again to Ta_nO_m⁺ and O₂ (k_b). The complex formation as well as the stabilization steps are described by ion–molecule collisions, which are barrierless and thus do not depend temperature.^33,36 Consequently only the back reaction (i.e. the dissociation of the complex) depends on temperature, resulting in larger apparent rate constants for lower temperatures. Analogously, the first reaction regime in the consecutive oxidation of Ta_n⁺ can be interpreted in a straightforward manner. We propose that in the first reaction regime the oxygen–oxygen bond cleavage occurs, as it has been found earlier that oxygen is bound to smaller tantalum clusters Ta_6–8⁺ as separate (bridging) atoms and not as an intact molecule.³⁷ Similar observations were made in the case of small palladium clusters.³⁰ This dissociation occurs in a fast reaction step prior to the collisional thermalization of the clusters:

The quick dissociation of O₂ followed by collisional stabilization with helium leads to a suppression of the back reaction, causing similar (i.e. small but finite) apparent activation energies for the first oxidation steps. The rate constant decreases for each subsequent reaction step while the activation energy roughly remains constant. Thus the lowered rate constant is attributed to a reduced steric factor, originating from the blocking of previously accessible reaction sites.

In the second reaction regime, apparent rate constants and activation energies are found to rapidly decrease at the same time, which initially seem to be counterintuitive. Therefore, another reaction mechanism must be responsible for the reaction behavior. After a transitional reaction step (in the case of Ta₂₀⁺: step seven), additional O₂ may be bound to the cluster as an intact molecule and the back reaction to the reactants becomes significant.

Here Ta₂₀O_x(O₂)⁺* (x ≥ 14) represents an activated complex that contains a molecularly adsorbed oxygen molecule. As a consequence the reaction scheme is now missing the dissociation step. The complex can then either evaporate a molecularly adsorbed O₂ or be stabilized by collisions with helium atoms. Due to the significant contribution of the back reaction, a decrease in overall rate constants and apparent activation energies is simultaneously observed for reaction steps in the second regime.

The transition from O₂ dissociation in the first regime to molecular adsorption in the second regime may, in principle, be related to electronic or geometric effects. Addressing the former, oxygen molecules serve as electron acceptors as can be observed in their reaction with gold clusters.³⁸ Similarly, each additional oxygen atom on the tantalum cluster may lead to a decrease of the electron density until the dissociation of another oxygen molecule is no longer possible. The decreased electron density may also weaken the subsequent binding of additional oxygen molecules. Thereby, an increase of the back reaction and consequently a decrease in the overall reaction rate is observed. Alternatively, the cluster geometry may play a role in the reaction with oxygen. A similar phenomenon was observed previously for nickel clusters reacting with CO.³⁹ There, a transition in the reaction kinetics was even used for the determination of the cluster structure. In the present work as well as in the previous study by Parks et al., the cluster size determines at which reaction step the transition from the first to the second reaction regime occurs. With the exception of Ta₁₆⁺ and Ta₁₇⁺ (Fig. 5), the transition shifts to a larger oxygen content. Accordingly, larger clusters exhibit more oxidation steps in the first reaction regime. In a spherical cluster the ratio of the surface to volume is proportional to n^−⅓. As crude as this approximation may be for smaller clusters, the ratio of oxygen atoms (x) at the transition reaction step to the cluster size (n) scales linearly with n^−⅓ (see Fig. 5b). Thus, the amount of oxygen reacted in the first regime correlates with the cluster surface. The cluster surface is given by the amount of accessible Ta–Ta bonds and therefore determines the number of oxygen molecules that can dissociate and bind as oxygen atoms bridging over said bonds. However, as mentioned before, electronic effects could also cause this behavior. In both cases, as the reaction progresses the bare cluster surface becomes saturated (i.e. an equivalent of passivation occurs on the nanoscale). At that point the reaction mechanism changes and additional oxygen atoms attach as intact molecules, which is the reaction pathway in the second reaction regime. Since oxidation seems to occur only on the cluster surface, the composition of the observed reaction products is different from metal oxide clusters formed inside of a laser vaporization source as such clusters contain a metal-oxide core.⁴⁰

Fig. 5 (a) Transition reaction step as a function of the cluster size. (b) Ratio of oxygen atoms (m) to tantalum atoms (n) within the cluster at the transition reaction step as a function of n^−⅓.

5 Summary

The reaction of cationic tantalum clusters (Ta_n⁺, n = 13–40) with molecular oxygen is studied under multi-collision conditions at several temperatures. All investigated cluster sizes are quickly oxidized in several consecutive reaction steps by the uptake of O₂ units. The reaction eventually yields a specific tantalum oxide cluster species, Ta_nO_m⁺ for every cluster size. The kinetic evaluation supplies rate constants and apparent activation energies for each reaction step. The existence of two regimes with different reaction mechanisms is observed, as rate constants and activation energies start to rapidly decrease at the same, size-dependent reaction step. For n = 20 the first regime covers the consecutive reactions from Ta₂₀⁺ to Ta₂₀O₁₄⁺. There, the reaction progresses the fastest, and apparent activation energies of 0.3–0.4 kJ mol⁻¹ are found. It is concluded that in the first regime the oxygen molecules quickly dissociate on the cluster surface, hindering the back reaction (i.e. an evaporation of O₂ molecules). In the second reaction regime (e.g. from Ta₂₀O₁₄⁺ to Ta₂₀O₂₆⁺) the apparent activation energies consecutively decrease, even to small negative values, and the rate constants decrease simultaneously. The adsorption of intact O₂ molecules on the tantalum oxide cluster surface in the second regime may require less activation energy (compared to the O–O bond cleavage) while the back reaction is still facilitated. As a consequence a decrease of the overall reaction rate is observed. Furthermore, the transition to the second regime occurs at later oxidation steps for larger clusters and the amount of oxygen reacted up to this point can be related to the surface-to-volume ratio. Consequently, we propose that the cluster surface is oxidized in the first regime and the subsequent interaction with additional oxygen molecules is less strong, leading to the adsorption of intact O₂ on the oxide surface.

Acknowledgements

This work was supported by an ERC Advanced Grant (ERC-2009-AdG 246645-ASC3).

References

1. S. Cardonne, P. Kumar, C. Michaluk and H. Schwartz, Int. J. Refract. Met. Hard Mater., 1995, 13, 187–194.
2. M. Ignatius, N. Sawhney, A. Gupta, B. Thibadeau, O. Monteiro and I. Brown, J. Biomed. Mater. Res., 1998, 40, 264–274.
3. G. Harry, T. P. Bodiya and R. DeSalvo, Optical coatings and thermal noise in precision measurement, Cambridge University Press, 2012.
4. C. Christensen, R. de Reus and S. Bouwstra, J. Micromech. Microeng., 1999, 9, 113.
5. F. Cardarelli, P. Taxil, A. Savall, C. Comninellis, G. Manoli and O. Leclerc, J. Appl. Electrochem., 1998, 28, 245–250.
6. S. B. Basame and H. S. White, Langmuir, 1999, 15, 819–825.
7. J. Seo, D. Cha, K. Takanabe, J. Kubota and K. Domen, Phys. Chem. Chem. Phys., 2013, 16, 895–898.
8. Z. Awaludin, J. G. S. Moo, T. Okajima and T. Ohsaka, J. Mater. Chem. A, 2013, 1, 14754–14765.
9. P. Armentrout, Annu. Rev. Phys. Chem., 2001, 52, 423–461.
10. A. Sanchez, S. Abbet, U. Heiz, W.-D. Schneider, H. Häkkinen, R. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573–9578.
11. S. Heinbuch, F. Dong, J. Rocca and E. Bernstein, J. Chem. Phys., 2010, 133, 174314.
12. R. Wesendrup and H. Schwarz, Angew. Chem., Int. Ed., 1995, 34, 2033–2035.
13. K. Zemski, R. Bell and A. Castleman, J. Phys. Chem. A, 2000, 104, 5732–5741.
14. K. Zemski, D. Justes and A. Castleman, J. Phys. Chem. A, 2001, 105, 10237–10245.
15. S. He, Y. Xie, F. Dong and E. Bernstein, J. Chem. Phys., 2006, 125, 164306.
16. Y. M. Hanrick and M. Morse, J. Phys. Chem., 1989, 93, 6494–6501.
17. K. Lange, B. Visser, D. Neuwirth, J. Eckhard, U. Boesl, M. Tschurl, K. Bowen and U. Heiz, Int. J. Mass Spectrom., 2015, 375, 9–13.
18. M. Zhou and L. Andrews, J. Phys. Chem. A, 1998, 102, 8251–8260.
19. G. K. Koyanagi, D. Caraiman, V. Blagojevic and D. K. Bohme, J. Phys. Chem. A, 2002, 106, 4581–4590.
20. C. S. Hinton, F. Li and P. Armentrout, Int. J. Mass Spectrom., 2009, 280, 226–234.
21. C. S. Hinton, M. Citir, M. Manard and P. Armentrout, Int. J. Mass Spectrom., 2011, 308, 265–274.
22. Y. Matsuo, H. Maeda and M. Takami, Chem. Phys. Lett., 1993, 201, 341–344.
23. D. Neuwirth, J. F. Eckhard, K. Lange, B. Visser, M. Wiedemann, R. Schröter, M. Tschurl and U. Heiz, Int. J. Mass Spectrom., 2015, 387, 8–15.
24. U. Heiz, F. Vanolli, L. Trento and W.-D. Schneider, Rev. Sci. Instrum., 1997, 68, 1986–1994.
25. D. Gerlich, Adv. Chem. Phys., 1992, 1–176.
26. D. J. Goebbert, G. Meijer and K. R. Asmis, 4th International Conference on Laser Probing LAP 2008, 2009, pp. 22–29.
27. J. Westergren, H. Grönbeck, S.-G. Kim and D. Tománek, J. Chem. Phys., 1997, 107, 3071–3079.
28. M. Neumaier, F. Weigend, O. Hampea and M. M. Kappes, J. Chem. Phys., 2005, 122, 104702.
29. L. D. Socaciu, J. Hagen, U. Heiz, T. M. Bernhardt, T. Leisner and L. Wöste, Chem. Phys. Lett., 2001, 340, 282–288.
30. S. M. Lang, I. Fleischer, T. M. Bernhardt, R. N. Barnett and U. Landman, J. Phys. Chem. A, 2014, 118, 8572–8582.
31. R. E. Leuchtner, A. C. Harms and A. W. Castleman, J. Chem. Phys., 1990, 92, 6527–6537.
32. M. Engeser, T. Weiske, D. Schröder and H. Schwarz, J. Phys. Chem. A, 2003, 107, 2855–2859.
33. G. Gioumousis and D. Stevenson, J. Chem. Phys., 1958, 29, 294–299.
34. T. M. Bernhardt, Int. J. Mass Spectrom., 2005, 243, 1–29.
35. J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical kinetics and dynamics, Prentice Hall, 1999.
36. A. Castleman Jr, K. Weil, S. Sigsworth, R. Leuchtner and R. Keesee, J. Chem. Phys., 1987, 86, 3829–3835.
37. A. Fielicke, P. Gruene, M. Haertelt, D. J. Harding and G. Meijer, J. Phys. Chem. A, 2010, 114, 9755–9761.
38. B. Salisbury, W. Wallace and R. Whetten, Chem. Phys., 2000, 262, 131–141.
39. E. K. Parks, K. P. Kerns and S. J. Riley, J. Chem. Phys., 2000, 112, 3384–3393.
40. K. S. Molek, T. D. Jaeger and M. A. Duncan, J. Chem. Phys., 2005, 123, 144313.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp07245j

---