Femtosecond predissociation dynamics of the methyl radical from the 3p_z Rydberg state

Abstract

The real time dynamics of electronic predissociation of the CH₃ radical (and its deuterated variant CD₃) from selected vibrational states of the 3p_z Rydberg state have been measured for the first time using a novel methodology based on a femtosecond three-color experiment to generate, two-photon excite and ionize methyl radicals as a function of time in combination with velocity map imaging detection. Subpicosecond lifetimes have been measured, showing a decreasing trend as vibrational excitation in the symmetric stretch and bending umbrella modes increases for both species. High-level ab initio calculations have been carried out in order to elucidate the CH₃ 3p_z predissociation mechanism and support the lifetime measurements. The observed lifetimes are relevant for the understanding of the resonance enhanced multiphoton ionization spectroscopy of this radical.

---

Introduction

The relevance of the methyl radical spans across both applied and fundamental areas of Chemistry. It is of great importance in processes like hydrocabon combustion,¹ the formation of complex hydrocarbons in the interstellar medium,² troposphere chemistry³ and chemical vapour deposition for diamond growth. Also, historically, as the simplest alkyl radical, it has been considered as a benchmark system in molecular orbital theory for the photochemistry of larger open-shell hydrocarbons. Still, some key questions relating to its spectroscopy and dynamics remain unanswered.

A crucial finding of Herzberg's seminal spectroscopic work⁴ is that the methyl radical is planar and, as a consequence, many excited states cannot be observed by one-photon spectroscopy, since one-photon transitions from the ground state are forbidden. It was not until multiphoton spectroscopy was made possible with intense lasers that the new techniques, especially resonance enhanced multiphoton ionization (REMPI), enabled the acquisition of new information on excited states,⁵ which are the result of exciting the unpaired electrons from an orbital with carbon 2p_z character into carbon-based orbitals with mostly Rydberg character. Out of the two-photon transitions of the methyl radical, the 3p_z and 4p_z states, in particular, have become widely used for the detection of the methyl radical in the gas-phase (see, for instance, ref. 6, 7–11 among others), but it was soon realized that the acquisition of highly resolved rovibrational data was not possible due to the rapid predissociation of all excited states, particularly in the undeuterated species. The state-dependent predissociation rates also preclude obtaining quantitative data for product state distributions in reactions where CH₃ is formed, and it is for this reason that direct comparisons have only been possible through transitions that share a common vibronic intermediate.¹²

The predissociation process of the vibrational levels of the 3p_z state of the methyl radical has been the subject of some studies, mainly aimed at quantifying its effect on their relative REMPI detection sensitivities, which would allow the measurement of the state distribution of the methyl radical formed in reactions of the type F + CH₄ → CH₃ + HF.^13,14 In ref. 13 the method employed consisted of the application of a kinetic model to characterize the (2 + 1) REMPI process in CD₃ through the 3p_z state. From fits to power dependencies obtained for each band, upper bounds for the predissociation rate of each state were estimated. This yielded an upper limit of 3 ps for the vibrational ground state, and this value decreased with increasing excitation in the umbrella mode, ν₂ (1 ps for ν₂ = 1, 0.8 ps for ν₂ = 2 and 0.4 ps for ν₂ = 3). From later work based on IR-UV double resonance,¹⁴ a 5 cm⁻¹ linewidth was observed for all single rovibronic transitions of the CH₃ radical, with which an estimated lifetime of ∼1 ps can then be inferred for the ν = 0 level and the symmetric stretch C–H mode ν₁ = 1 level.

The work of Black and Powis⁸ investigated the predissociation dynamics of CH₃ and CD₃ in the 4p_z Rydberg state in two ways: through rotationally dependent lifetime broadened linewidths of the (2 + 1) REMPI spectrum and through a modified band profile due to a reduction of the ionization yield by competing predissociation of the resonant intermediate. They found an important distinction between the behavior of CH₃ and CD₃ for the predissociation mechanism in the 4p_z state. While for CD₃ the evidence pointed only to homogeneous predissociation, for CH₃ the authors found a significant rotational level dependence of the measured linewidths in the (2 + 1) REMPI spectrum, indicating that, along with the homogeneous mechanism, a heterogeneous predissociation channel was active, which was attributed to a perpendicular Coriolis coupling. From a comparison of experimental and simulated (2 + 1) REMPI spectra, the authors proposed that an analogous situation should apply, at least qualitatively, for predissociation from the 3p_z Rydberg state. The authors also suggested a candidate state (3d ²E′′) whose interaction with the 4p_z Rydberg state could be responsible for the homogeneous predissociation.

The rovibrational dependence of the predissociation rate of the 3s Rydberg state of the methyl radical was investigated by resonance enhanced Raman spectroscopy by Westre et al.^15,16 and in this state the lifetime of CD₃ was found to halve upon adding one quantum of excitation in the umbrella mode, ν₂. In ref. 16, rotation-dependent subpicosecond lifetimes were obtained with a smooth J dependence. Later on, the photodissociation dynamics of CH₃ from the 3s Rydberg state at 193.3 nm was studied using photofragment translational spectroscopy.¹⁷ Only CH₂ and H(²S) fragments were observed and although it was not possible to assign the spin state of CH₂ unambiguously, it was suggested that it was produced predominantly in the ã ¹A₁ excited state. The measured translational energy distribution of the products was consistent with the presence of an exit barrier on the 3s potential energy surface and an anisotropy parameter of β = −0.9 ± 0.1 was determined corresponding to a perpendicular transition. Yang and co-workers^18,19 studied the photodissociation of CH₃ from the 3s Rydberg state at 212.5 nm using the H-atom Rydberg tagging time-of-flight technique with a pure CH₃ radical source generated by photolysis of CH₃I at 266 nm. Time-of-flight spectra of the H-atom products from the photolysis of both cold and hot CH₃ radicals were measured at different photolysis polarizations. The experimental results indicated that the photodissociation of the CH₃ radical in its ground vibrational state occurs on a very fast time scale in comparison with its rotational period. Experimental evidence also shows that photodissociation in the ν₂ = 1 vibrational state of the umbrella mode is characteristically different from that in the ground vibrational state.

Theoretical studies on the predissociation dynamics of the methyl radical are very scarce.^16,20,21 In the work of Yu et al.,²⁰ a small basis set RHF calculation was performed to obtain semiquantitative information about the relative barrier heights of radical (CH₃ → CH₂ + H) and molecular (CH₃ → CH + H₂) predissociation pathways from the ground, 3s and 3p states of the methyl radical. The group also used calculated relative energies of products and concluded that at the excitation energy of the 3p_z state, it is thermodynamically possible to form the X̃ ³B₁, 1 ¹A₁, 1 ¹B₁ and 2 ¹A₁ states of CH₂ as the product of radical predissociation, and CH(A ²Δ) and CH(X) as products of molecular predissociation. However, based upon orbital correlations it was predicted that the dominant reaction pathway for predissociation from the 3p_z state would be radical predissociation forming CH₂(1 ¹B₁) + H. This calculation predicted a much larger reaction barrier for radical predissociation at planar geometry from the 3p_z state than from the 3s state, which is in agreement with the higher resolution observed in REMPI spectra via the 3p_z state.

It is known that lifetimes extracted from spectral linewidths or indirect methods may have large errors due to competing experimental broadening effects which are difficult to quantify (e.g. Doppler and pressure broadening effects), and that the use of an appropriate femtosecond pump–probe scheme allows for the direct extraction of the time constant for the population decay of predissociative electronic excited states.^22–24 The method involves using the short pump pulse to excite the molecule to the vibronic state of interest and the probe pulse to ionize the state population after a variable delay.

In this work, we report the first direct, real-time measurements of the lifetimes of selected vibrational levels of the 3p_z Rydberg state of CH₃ and its deuterated form CD₃. In addition, high-level ab initio calculations of the electronic states involved in the CH₃ → CH₂ + H radical dissociation process have been carried out with the aim of interpreting and rationalizing the experimental findings. The resulting interpretation along with the accurate lifetime measurements obtained provide valuable information about one of the main dissociation pathways of this important radical system.

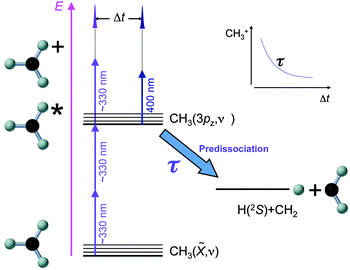
In contrast to more commonly used methods for CH₃ synthesis like pyrolysis of a suitable precursor¹⁷ or A-band photodissociation of CH₃I,^18,19 the method chosen for the generation of CH₃ (CD₃) radicals has been B-band photodissociation of CH₃I (CD₃I). The high cross section for this process in the precursor CH₃I (CD₃I) molecule (σ ≈ 600 × 10⁻¹⁸ cm² at 201.2 nm, the band origin²⁵) guarantees a high density of CH₃ radicals in the interaction region. Electronic predissociation in the precursor occurs via the route I*(²P_1/2) + CH₃(ν), the methyl fragment appearing in the ground electronic state and in a broad distribution of vibrational levels.²³ The experiment is then realized according to the scheme shown in Fig. 1, analogous to the scheme employed in ref. 26 for NH₃. A short pulse tuneable in the region of 330 nm (two-photon resonant with the 3p_z²A₂′′ ← X̃ ²A₂′′ transition) is used to transfer population to the 3p_z Rydberg state. A delayed pulse centered at 400 nm interacts with the excited sample, causing ionization. Methyl ions are detected as a function of the delay between the excitation (330 nm) and ionization (400 nm) pulses. As indicated in Fig. 1, the (2 + 1) REMPI (one-color) process coexists with the (2 + 1′) (two-color) process, and thus it is necessary to subtract the methyl ion signal caused by the excitation pulse alone to obtain transients like that sketched in the figure, from where the lifetimes can be readily obtained. By using a combination of vibrationally selective excitation and kinetic energy information provided by the velocity map imaging (VMI) detection of methyl fragments, lifetimes of the 3p_z state of the methyl radical have been measured with specificity in the ν₁ and ν₂ vibrational modes, as we will show below.

Fig. 1 Scheme of the experimental procedure to obtain lifetimes of the 3p_z vibrational levels in CH₃. A short, tuneable laser pulse centered at around 330 nm (two-photon resonant with the 3p_z²A₂′′ ← X̃ ²A₂′′ transition in CH₃) is used for excitation. A short pulse of 400 nm, delayed by Δt, probes the surviving population in the 3p_z Rydberg state by causing ionization, producing a signal that is proportional to the instantaneous population in the Rydberg state, schematically shown in the inset.

Methods

Experimental

The laser was an amplified Spectra Physics Ti:Sapphire system which delivers 50 fs pulses centered at 805 nm with an average pulse energy of 3.5 mJ and a repetition rate of 1 kHz. The output was split into three separate beams. The first beam was used for triggering the UV photodissociation of CH₃I (or CD₃I) as a precursor of the CH₃ (CD₃) radicals under study. The UV laser light was generated through frequency quadrupling of the fundamental, which passed through a frequency tripling unit followed by a sum-frequency mixing unit. This was tuned to 201.2 nm for the 0⁰₀ transition of the B-band in CH₃I (or 200.5 nm in CD₃I). The full width at half maximum (FWHM) bandwidth of the 201.2 nm beam was 0.3 nm, and the average pulse energy was below 1 μJ. Absorption is followed by predissociation yielding CH₃ (or CD₃) in a range of vibrational states. The second beam was passed through an optical parametric amplifier (OPA) which produced tunable light in the region of 1.2–1.3 μm, which is then frequency quadrupled to synthesize wavelengths at around 330 nm for two-photon excitation of methyl radicals into the 3p_z Rydberg state. The FWHM bandwidth of this arm is 2.5 nm, allowing vibrational selectivity in this step. The third part of the 804 nm fundamental beam was frequency doubled to produce pulses centered at 402 nm with average pulse energy <3 μJ, which is sufficient for one-photon ionization of the 3p_z state of the methyl radical. The polarization of all three pulses was horizontal and parallel to the face of the ion detector. The relative arrival times of the pulses were controlled with two mechanical delay stages with a time resolution of 1 fs, in the 330 nm and 400 nm arms. The position of the focal plane of the 200 nm and 400 nm beams was controlled using telescopes. The three beams were coupled collinearly into the vacuum chamber through a 25 cm focal length lens. The instrument temporal response was taken to be equal to the cross correlation of the 330 nm and 400 nm pulses, which was measured through multiphoton ionization of Xe to be 140 fs. The time delay between the 201.2 nm (or 200.5 nm) beam and the other beams, causing CH₃I dissociation, is not an important parameter, and it is simply fixed at a value that is sufficiently long so that the predissociation process is completed (30 ps).

CH₃I (or CD₃I), kept at 0 °C and seeded in He at a total pressure of 1.5 bar, was expanded into vacuum through a homemade 1 kHz piezoelectric pulsed valve with a 0.5 mm nozzle diameter. The molecular beam then passes through a skimmer which separates the source chamber from the ionization chamber. The ions formed in the interaction region are extracted perpendicularly by a set of open electrodes in velocity mapping configuration,²⁷ permitting 100% transmittance and detector-spot limited velocity resolution. The detector is situated at the end of a 50 cm time-of-flight (TOF) tube and consists of a pair of microchannel plates, in Chevron configuration, coupled to a phosphor screen. Typical repeller voltages were 5200 V for CH₃⁺ imaging and 4500 V for CD₃⁺ imaging, with optimal velocity mapping conditions found for V_extractor/V_repeller = 0.76. Mass selection is achieved by gating the gain of the front MCP plate. Phosphorescence is recorded on a Peltier-cooled 12 bit charge-coupled device camera. Typical image acquisition times were set at 800 ms, corresponding to 800 laser shots. The contribution of dissociative ionization was removed by subtracting the image obtained in the presence of 200 nm alone from the images obtained in the presence of all three laser beams. The images were inverted using the polar basis set expansion (pBasex) method.²⁸ The velocity calibration of images was carried out using the known kinetic energy of nascent CH₃(ν = 0) following 201.2 nm photodissociation of methyl iodide, which proceeds via the CH₃ + I*(²P_1/2) product channel, and (2 + 1) resonant multiphoton ionization at 333.45 nm.

Theoretical

Electronic structure computations of geometries and electronic states of CH₃ have been carried out using MOLPRO.²⁹ At the ground electronic state, the methyl radical is a planar molecule of D_3h symmetry. Since D_3h is not an Abelian group, all ab initio calculations were performed using the C_2v group representation, which is valid as long as the molecule remains in a planar configuration. In order to calculate the dissociation of the CH₃ radical along the C–H distance, geometry optimization in the ground state of CH₃ was carried out at different C–H distances using the complete active space self-consistent field (CASSCF) method^30,31 followed by the multireference perturbation theory CASPT2 method.³² In all cases, the augmented correlation consistent basis set (aug-cc-pVTZ)³³ was employed.

Using the optimized geometries, the ground and excited electronic state energies were computed using CASSCF followed by the internally contracted multi reference configuration interaction (MRCI)³⁴ approach. The orbitals included in the active space are (3–10)a₁, (1–4)b₁, and (1–3)b₂, while the 1a₁ and 2a₁ molecular orbitals (associated with the 1s and 2s orbitals of the carbon atom) were considered to be doubly occupied in all configurations. For the MRCI calculations the 1s orbital was kept frozen. Calculations were restricted to the first four states of A₁ and four first states of B₁ symmetries in C_2v. To establish the valence/Rydberg character of the states, the spatial extent was estimated through the computation of the quadrupolar moments. A threshold value of 40 a.u. was established for the valence/Rydberg distinction.

The obtained adiabatic potential energy curves have been diabatized for a more appropriate interpretation in terms of the dissociation of the radical along the C–H distance. For both A₁ and B₁ symmetry representations, we have applied a 3 × 3 diabatization model to get the diabatic potential energy curves and their diabatic electronic couplings for each symmetry. Considering three adiabatic states a₁, a₂ and a₃, we generate three diabatic states d₁, d₂ and d₃ following a sequential 2 × 2 diabatization scheme based on energy criteria. The assumptions made are, (a) if two states cross each other, they do it only once (valid in the present case); (b) total energy is conserved (i.e., a_i + a_j = d_i + d_j); (c) outside the interaction region I, diabatic potential energy curves match the adiabatic ones. I is defined as the region where ΔE < ΔE_min + ξ, where ΔE represents the energy difference between the two adiabatic states considered, ΔE_min is the minimum energy difference between them, and ξ is an arbitrary threshold to adapt in each case. Following those constraints, the d_i state is constructed by linking the left part of a_i and the right part of a_j by interpolation in the I region. The other diabatic curve is then built as d_j = a_i + a_j − d_i. When the first two diabatized states are obtained, the same procedure is repeated between both of them and the third adiabatic state, adapting ξ to the topology of the curves (in the present case, we considered 0.2 a.u. < ξ < 0.5 a.u.).

Results and discussion

Fig. 2 shows the measured methyl ion signals in the two-color experiment, i.e. after photolysis, only the pulse around 330 nm is employed in this case. The nascent CH₃ (CD₃) fragments from CH₃I photodissociation are detected via (2 + 1) REMPI by tuning the laser in the region of 330 nm and detecting the ions in VMI configuration. The vibronic transitions used in this experiment are the diagonal transitions corresponding to ν₂ = 0, 1, 2, 3. Due to the spectral proximity of these transitions to diagonal vibronic transitions of the ν₁ mode, it has been shown before^23,24 that activity in both modes can be detected simultaneously if the laser source possesses a sufficiently broad bandwidth.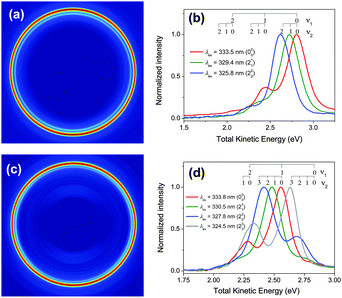

Fig. 2 Results of the (2 + 1) REMPI experiment of nascent CH₃ (CD₃) after B-band photodissociation of CH₃I (CD₃I). (a) Abel-inverted velocity map image of CH₃⁺ obtained at 333.5 nm. (b) Total kinetic energy distributions obtained from angular integration of Abel-inverted images at 333.5 nm (red, 0⁰₀ transition), 329.4 nm (green, 2¹₁ transition) and 325.8 nm (blue, 2²₂ transition). (c) Abel-inverted velocity map image of CD₃⁺ obtained at 333.8 nm. (d) Total kinetic energy distributions obtained from angular integration of Abel-inverted images at 333.8 nm (red, 0⁰₀ transition), 330.5 nm (green, 2¹₁ transition), 327.8 nm (blue, 2²₂ transition) and 324.5 nm (grey, 2³₃ transition). Transition wavelengths from ref. 35.

Fig. 2a shows a CH₃⁺ Abel-inverted image obtained under these conditions, where the excitation laser is tuned to a centre wavelength of 333.5 nm, resonant with the 0⁰₀ vibronic band of the 3p_z²A₂′′ ← X̃ ²A₂′′ transition. Together with the main ring, a dimmer ring appears, with a lower radius, i.e., lower kinetic energy; it corresponds to the 1¹₁ vibronic band of the 3p_z²A₂′′ ← X̃ ²A₂′′ transition, which can be detected due to the broadband character of the 333.5 nm laser.²³ Kinetic energy distributions obtained from this image and those corresponding to excitation of the 2¹₁ and 2²₂ vibronic bands, for which the excitation laser is retuned to 329.4 nm and 325.8 nm, respectively, are shown in Fig. 2b. The state distribution observed here for CH₃ produced by predissociation of CH₃I via the vibrational ground state of the ³R₁ Rydberg state includes ν₂ = 0, 1, 2 with ν₁ = 0, 1, in agreement with that observed by Gitzinger et al.²³

The analogous measurement for the case of CD₃ resulting from the predissociation of CD₃I at 200.5 (origin of the B-band), with (2 + 1) REMPI of CD₃ at 333.8 nm (resonant with the 0⁰₀ vibronic band of the 3p_z²A₂′′ ← X̃ ²A₂′′ transition), yields the Abel-inverted image of CD₃⁺ shown in Fig. 2c. Although the image may seem to be similar to that of CH₃⁺ in Fig. 2a, careful inspection indicates that the main ring does not correspond to the 0⁰₀ transition, as it did for CH₃, but instead, it corresponds to 1¹₁, and the dimmer, internal ring, to the 1²₂ transition. The complete set of kinetic energy distributions is shown in Fig. 2d. As can be seen, there is a marked vibrational population inversion in CD₃ as compared with CH₃, to the point that no CD₃ is formed in the ν₁ = 0, ν₂ = 0 vibrational state. This implies that lifetime measurements have not been possible for the vibrationless ν = 0 level of CD₃.

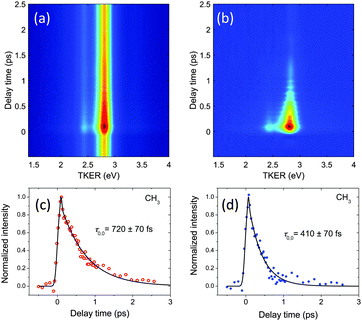
For the lifetime measurements, the third laser pulse at 400 nm was added after a controlled delay time. The methyl ion images were qualitatively analogous to those obtained with one-color REMPI, but signal levels were higher in a time window of a few hundred of femtoseconds. An example of the kinetic energy distributions obtained for each pump–probe delay time is shown in Fig. 3a in the form of a false color map for the case of CH₃ at 333.5 nm (0⁰₀ and 1¹₁ vibronic transitions). The two visible channels correspond, therefore, as in Fig. 2a, to the ν = 0 and ν₁ = 1 levels. Since CH₃⁺ signals thus measured are a result of both the (2 + 1′) and (2 + 1) REMPI processes, subtraction of the images obtained under 333.5 nm-only irradiation was necessary to isolate the (2 + 1′) processes that yielded information of lifetimes. The result of such subtraction is shown in Fig. 3b. No signal was observed in the (2 + 1) and (2 + 1′) experiments when the excitation laser was detuned from resonance.

Fig. 3 Measurement of vibrational state-dependent lifetimes of vibrational levels of the 3p_z Rydberg state in CH₃. (a) False color map representing the total kinetic energy distributions, obtained from Abel-inverted images, under two-color irradiation (333.5 nm + 400 nm) as a function of the delay time between the laser pulses. Two channels are visible, the main one corresponding to the 0⁰₀ transition, and the weaker, lower kinetic energy channel, to the 1¹₁ transition. (b) The same as (a), but after subtraction of the single color, 333.5 nm contribution. (c) Transient of the channel corresponding to the 0⁰₀ transition (revealing remaining population in ν = 0, obtained from the map shown in (b)). A lifetime of 720 ± 70 fs is obtained for the ν = 0 level of the 3p_z Rydberg state in CH₃. (d) Transient of the channel corresponding to the 1¹₁ transition (revealing remaining population in ν₁ = 1, obtained from the map shown in (b)). A lifetime of 410 ± 70 fs is obtained for the ν₁ = 1 level of the 3p_z Rydberg state in CH₃.

A two-dimensional nonlinear least squares fit to the maps was performed using the Levenberg–Marquardt algorithm following the procedure described in ref. 24. Each peak in the kinetic energy distribution was fit with a Gaussian function in the energy dimension such that the lifetimes of the individual states could be measured independently. The variation of the amplitude of these Gaussian functions with delay time was fit with an exponential decay convoluted with another Gaussian function to account for the instrument response. A third Gaussian contribution was also employed, centered at the temporal overlap of the two pulses, t₀, to describe two-color multiphoton ionization processes that may occur upon simultaneous absorption. The decrease in signal intensity observed with increasing delay was attributed to the population decay due to the predissociation of the intermediate 3p_z state. Transients obtained for the two channels visible in the maps in Fig. 3b are shown in Fig. 3c and d. Single exponential functions were proven to reproduce the time-varying signal levels within experimental error, and thus the time constants obtained from the fits for each of the channels are assigned to the lifetimes of each vibrational level.

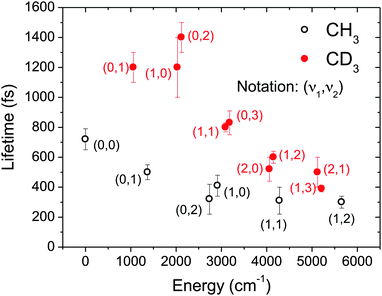
As was the case for the detection of the nascent CH₃ (CD₃) populations through (2 + 1) REMPI, measurement of the lifetimes of as many vibrational levels as possible required retuning the excitation laser to achieve population transfer to a broad set of (ν₁,ν₂) levels. Table 1 contains the results of the complete set of measurements for the 3p_z state of CH₃ and CD₃.

Table 1 Measured lifetime (τ) values (in fs) of the vibrational levels of the 3p_z state of the CH₃ and CD₃ radicals

ν 1	ν 2	CH3, τ (fs)	CD3, τ (fs)
0	0	720 ± 70	—
0	1	500 ± 50	1200 ± 100
0	2	320 ± 100	1400 ± 100
0	3	—	830 ± 80
1	0	410 ± 70	1200 ± 200
1	1	310 ± 90	800 ± 30
1	2	300 ± 40	600 ± 40
1	3	—	390 ± 20
2	0	—	520 ± 80
2	1	—	500 ± 100

---

It is somewhat unexpected that single exponential functions are capable of describing the temporal decays with sufficient accuracy. In principle, given that several transitions to a broad set of rotational levels can be coherently excited by the ultrashort pulses, contributing to the global ionization signal, multiexponential decays could be expected. In the analogous experiment by Dobber et al. in ammonia,²⁶ the authors found that biexponential decay functions were necessary to fit the observed decays for most vibrational levels. They attributed this result to different lifetimes of the low-lying versus the high-lying rotational levels. In our case, the fact that single exponential functions are always sufficient to obtain good fits to the data points to a mild rotational dependence of the lifetimes. The implication of this weak rotational dependence is a higher accuracy of the lifetimes obtained from the transients.

Lifetimes reported in Table 1 have been represented in graphic format in Fig. 4 for both CH₃ and CD₃ as a function of the energy of the level under consideration above the ν = 0 level. For CH₃, it was known that the 0⁰₀ vibronic transition was the only one where rotational structure could be resolved,⁵ consistently with the longest value found here for the predissociation lifetime of the ν = 0 level. The isotopic effect that favors rapid predissociation for the undeuteraded species is clear from the graph, lifetimes measured for CD₃ being more than twice as long as for CH₃ for all cases. Also, a rather monotonic trend is observed as a function of energy which seems to be irrespective of the vibrational mode or mode combination under consideration.

Fig. 4 Measured lifetimes of a set of (ν₁,ν₂) levels of the 3p_z Rydberg state of CH₃ (black empty circles) and CD₃ (solid red circles), plotted as a function of vibrational excess energy above the (0,0) level.

In order to shed light on the predissociation mechanism and the measured state selected lifetimes of the methyl radical from the 3p_z Rydberg state, high level electronic structure ab initio calculations have been performed for the CH₃ and CH₂ radicals. As mentioned above, ab initio calculations for electronically excited states of the CH₃ radical reported in the literature are very scarce due to the difficulties inherent to its open shell character. In the following, we present the first high-level MRCI calculations of excited states (up to energies of about 12 eV) which are involved in the photochemistry of CH₃. In Table 2, the vertical excitation energies (VEEs) from the ground state equilibrium geometry to the excited electronic states of A₁ and B₁ symmetries in C_2v for CH₃ are summarized and compared with the available previous calculations and experimental data. The VEEs to the different electronic excited states of CH₂ are also shown in the table. As can be seen, the correlation between the calculated VEE and the available experimental transitions is quite reasonable.

Table 2 MRCI vertical excitation energies (VEE) to the excited electronic states of methyl (CH₃) and methylene (CH₂)

Symmetry			CH3
D 3h	C 2v	Character	VEE (eV)	Prev. calc. (eV)	Expt. (eV)^36
X̃ ^2A2′′	X̃ ^2B1	Valence	0.0	0.0	0.0
3s ^2A1′	1 ^2A1	Rydberg	5.84	5.68^20	5.73
3px,y^2E′	2 ^2A1 + 1 ^2B2	Rydberg	6.87	6.92^20	—
^2E′	3 ^2A1 + 2 ^2B2	Valence	7.14	7.17^20	—
^3pz^2A2′′	2 ^2B1	Rydberg	7.65	7.19^20	7.43
3d ^2A1′	4 ^2A1	Rydberg	8.47	7.77^20	8.28
	3 ^2B1	Rydberg	11.08	—	—
	4 ^2B1	Valence	11.60	—	—

---

	C 2v		CH2
	X̃ ^3B1		0.0	0.0	0.0
	1 ^1A1		0.98	0.48^37	0.39
	1 ^1B1		1.48	1.54^37	1.43
	2 ^1A1		3.16	2.67^37	—
	1 ^3A1		6.35	—	—
	3 ^1A1		6.60	—	—
	1 ^3A2		7.34	—	—
	2 ^3B1		7.45	—	—
	1 ^3B2		7.57	—	—
	2 ^1B1		7.72	—	—
	3 ^3B2		7.93	—	—

---

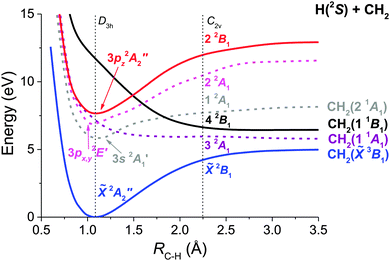
Ab initio potential energy curves as a function of the C–H distance have been calculated for the most relevant electronic states involved in the predissociation dynamics of CH₃ from the ³p_z²A₂′′ Rydberg state. Considering the large number of electronic states for CH₃ and that adiabatic curves are not easy to follow, all C_2v A₁ and B₁ states of interest have been diabatized following a three-state diabatic model to take into account the non-adiabatic interactions between electronic states, and the resulting curves are depicted in Fig. 5. The ground electronic state of CH₃ in D_3h symmetry, X̃ ²A₂′′, is a non-degenerate doublet. Considering the ab initio VEE values shown in Table 2, the first excited state of CH₃ is 3s ²A₁′, which presents a strong Rydberg character and lies 5.84 eV over the ground state. At around 7 eV, two states are observed, one associated with a 3p_x,y²E′ Rydberg state (not characterized experimentally), which presents A₁ character in C_2v, and a valence dissociative state of the same symmetry, ²E′. This valence state interacts with the 3p_x,y²E′ Rydberg state in the Franck–Condon region and also with the 3s ²A₁′ Rydberg state at a larger CH distance. Above in energy lies the 3p_z²A₂′′ Rydberg state at 7.65 eV, which is the one excited in the experiment by two-photon absorption. Finally, at around 12 eV, we find a valence dissociative state (the 4 ²B₁ in C_2v), which crosses the 3p_z²A₂′′ Rydberg state when the C–H bond is elongated.

Fig. 5 Diabatic ab initio potential energy curves of A₁ (dashed) and B₁ (solid) symmetry in C_2v relevant for predissociation of the 3p_z²A₂′′ Rydberg state of the methyl radical, along the C–H coordinate.

It is important to emphasize that if the ν₂ umbrella mode is active and the radical geometry is out of the planar configuration, then the D_3h/C_2v symmetry will break down to C_3v/C_s. This can alter the dissociation mechanism quite significantly, since the A₁ and B₁ representations in the C_2v symmetry group will both correlate with A′ in C_s (A₂′′ and A₁′ in D_3h correlate with A₁ in C_3v). In that case, all states shown in Fig. 5 will couple together.

Consequently, dissociation can follow several competing mechanisms. The fastest one is expected to be the direct predissociation from the 3p_z²A₂′′ Rydberg state to the valence dissociative 4 ²B₁ state (see Fig. 5). This state leads to CH₂ in the excited 1 ¹B₁ state. Since the crossing occurs at an elongated C–H distance of about 1.5 Å, the C–H stretch vibrational mode excitation in CH₃ would favor this mechanism, as confirmed by the shorter observed lifetimes when the ν₁ mode excitation increases. This 4 ²B₁ valence state also crosses the two lower 3s ²A₁′ and 3p_x,y²E′ Rydberg states. Therefore, the system can eventually relax to these states opening new routes of dissociation yielding CH₂ in different excited states. However, these alternative mechanisms would be expected to occur at longer time scales and they are probably not seen in the present experiment where we are monitoring the time-dependent depopulation of the CH₃ radical from the initially excited 3p_z²A₂′′ Rydberg state. In addition, as none of the excited states cross the ground state, it is unlikely that internal conversion can be thought as an effective mechanism for dissociation into the ground state.

The ab initio calculations of the different electronic states (and their corresponding couplings) involved in the CH₃ dissociation provide a valuable tool for elucidating the specific dissociation mechanism which the measured lifetimes are associated. Based on the ab initio results the following picture would be a consistent interpretation of the experimental findings of Table 1 and Fig. 4. As mentioned above, the ab initio calculations indicate that the 3p_z²A₂′′ Rydberg state initially excited in the experiment crosses the valence dissociative 4 ²B₁ state at around R_C–H = 1.5 Å (see Fig. 5). In the calculations these two states are found to be coupled nonadiabatically by a nearly Gaussian shape coupling that peaks at the crossing point. Such a coupling would be responsible for electronic predissociation from the 3p_z Rydberg state to the 4 ²B₁ state.

The monotonic decrease of the lifetimes of both CH₃ and CD₃ found experimentally with increasing vibrational excitation (Table 1) or energy (Fig. 4) can be explained as follows. The lifetime of an initially populated vibrational state ψ_ν1,ν2 of the 3p_z Rydberg state (with associated vibrational energy E_ν1,ν2) predissociating to a continuum state χ_E=Eν1,ν2 of 4 ²B₁ can be expressed as τ ∼ 1/C, where C = 〈ψ_ν1,ν2|V_coup|χ_E=Eν1,ν2〉, V_coup being the nonadiabatic coupling between the two electronic states. A monotonic increase of the magnitude of C is what causes the decrease of τ. Since both the magnitude and position of V_coup are fixed, regardless of the initial vibrational excitation, only changes in the shape of ψ_ν1,ν2 and χ_E=Eν1,ν2 with increasing vibrational excitation and energy can cause an increase (decrease) of C(τ).³⁸ Indeed, increasing the ν₁ stretching excitation causes an increase of the spatial spreading of ψ_ν1,ν2 toward larger R_C–H distances. Similarly, the corresponding increase of the energy E = E_ν1,ν2 causes also a larger delocalization of the continuum wave function χ_E=Eν1,ν2 toward shorter R_C–H distances. The result is a larger overlap between ψ_ν1,ν2, V_coup, and χ_E=Eν1,ν2, leading to a larger C value and a shorter τ. An increasing excitation of the ν₂ mode has a similar effect because it also contributes to a larger spatial (in the angular mode) delocalization of the wave functions, and thus also leads to a larger magnitude of C. However, the effect of the angular delocalization of the wave functions is expected to be smaller than in the case of the stretching mode, and this explains the smaller effect of ν₂ excitation on the lifetime found experimentally. The isotopic effect, reflected in the longer lifetimes found for CD₃, would have a similar explanation, being due to a larger spatial localization of the wave functions ψ_ν1,ν2 and χ_E=Eν1,ν2 because of the lower energies associated with the corresponding (ν₁,ν₂) vibrational states caused by the larger mass of CD₃, leading to longer values of C(τ) (i.e., longer lifetimes).

The above interpretation, supported by the ab initio results, associates the lifetimes measured with a direct predissociation process between the 3p_z²A₂′′ and 4 ²B₁ electronic states induced by a nonadiabatic coupling. This interpretation therefore precludes the possibility of dissociation by tunneling through a barrier between the two states. First, the typically subpicosecond lifetimes found experimentally for CH₃, and more remarkably also for CD₃, are clearly inconsistent with a slow tunneling mechanism. Second, the existence of a nonadiabatic coupling predicted by the ab initio simulations provides strong theoretical support to the direct predissociation mechanism.

Conclusions

Accurate subpicosecond lifetimes have been determined for selected vibrational states of the 3p_z Rydberg state of the methyl radical using a three-color femtosecond laser experiment in combination with ion imaging techniques. A clear isotopic effect (lifetimes are longer by a factor of about two for the deuterated species) is observed. Vibrational excitation (in the stretching and bending modes) produces a monotonic decrease of the lifetime. The high-level ab initio calculations carried out in this work help to rationalize the dynamics in terms of an electronic predissociation process induced by a nonadiabatic coupling between Rydberg and valence excited states. A strong impact of the present study for the understanding of the resonance enhanced multiphoton ionization spectroscopy of this relevant radical is envisioned.

Acknowledgements

This work has been financed by the Spanish Ministry of Economy and Competitiveness (MINECO) through grants CTQ2012-37404-C02-01, CTQ2012-36184, FIS2011-29596-C02-01 and FIS2013-40626-P and EU through the COST Actions Grant No. CM1401 and CM1405. This research was performed within the Unidad Asociada Química Física Molecular between Departamento de Química Física of Universidad Complutense de Madrid (UCM) and Consejo Superior de Investigaciones Científicas (CSIC). The facilities provided by the Centro de Asistencia a la Investigación de Láseres Ultrarrápidos at UCM are acknowledged. The Centro de Supercomputación de Galicia (CESGA, Spain) and CTI (CSIC) are acknowledged for the use of their resources.

References

1. K. C. Smyth and P. H. Taylor, Chem. Phys. Lett., 1985, 122, 518.
2. H. Feuchtgruber, F. P. Helmich, E. F. van Dishoeck and C. M. Wright, Astrophys. J., 2000, 535, L111.
3. R. P. Wayne, Chemistry of Atmospheres, Oxford University Press, Oxford, 2000.
4. G. Herzberg, Proc. R. Soc. A, 1961, 262, 291.
5. J. W. Hudgens, T. G. DiGuiseppe and M. C. Lin, J. Chem. Phys., 1983, 79, 571.
6. J. M. Jasinski, B. S. Meyerson and B. A. Scott, Annu. Rev. Phys. Chem., 1987, 38, 109.
7. D. H. Parker, Z. W. Wang, M. H. M. Janssen and D. W. Chandler, J. Chem. Phys., 1989, 90, 60.
8. J. F. Black and I. Powis, J. Chem. Phys., 1988, 89, 3986.
9. I. Powis and J. F. Black, J. Phys. Chem., 1989, 93, 2461.
10. B. Martnez-Haya, I. Zapater, P. Quintana, M. Menéndez, E. Verdasco, J. Santamara, L. Bañares and F. J. Aoiz, Chem. Phys. Lett., 1999, 311, 159.
11. P. Quintana, R. F. Delmdahl, D. H. Parker, B. Martnez-Haya, F. J. Aoiz, L. Bañares and E. Verdasco, Chem. Phys. Lett., 2000, 325, 146.
12. R. O. Loo, H.-P. Haerri, G. E. Hall and P. L. Houston, J. Chem. Phys., 1989, 90, 4222.
13. J. Zhou, J. J. Lin, W. Shiu, S.-C. Pu and K. Liu, J. Chem. Phys., 2003, 119, 2538.
14. W. Zhang, H. Kawamata, A. J. Merer and K. Liu, J. Phys. Chem. A, 2009, 113, 13133.
15. S. G. Westre, P. B. Kelly, Y. P. Zhang and L. D. Ziegler, J. Chem. Phys., 1991, 94, 270.
16. S. G. Westre, T. E. Gansberg, P. B. Kelly and L. D. Ziegler, J. Phys. Chem., 1992, 96, 3610.
17. S. W. North, D. A. Blank, P. M. Chu and Y. T. Lee, J. Chem. Phys., 1995, 102, 792.
18. G. Wu, B. Jiang, Q. Ran, J. Zhang, S. A. Harich and X. Yang, J. Chem. Phys., 2004, 120, 2193.
19. G. Wu, J. Zhang, S. A. Harich and X. Yang, Chin. J. Chem. Phys., 2006, 19, 109.
20. H. T. Yu, A. Sevin, E. Kassab and E. M. Evleth, J. Chem. Phys., 1984, 80, 2049.
21. P. Botschwina, E. Schick and M. Horn, J. Chem. Phys., 1993, 98, 9215.
22. A. P. Baronavski and J. C. Owrutsky, J. Chem. Phys., 1998, 108, 3445.
23. G. Gitzinger, M. E. Corrales, V. Loriot, G. A. Amaral, R. de Nalda and L. Bañares, J. Chem. Phys., 2010, 132, 234313.
24. G. Gitzinger, M. E. Corrales, V. Loriot, R. de Nalda and L. Bañares, J. Chem. Phys., 2012, 136, 074303.
25. S. Eden, P. Limao-Vieira, S. V. Hoffmann and N. J. Mason, Chem. Phys., 2007, 331, 232.
26. M. R. Dobber, W. J. Buma and C. A. de Lange, J. Phys. Chem., 1995, 99, 1671.
27. A. T. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477.
28. G. A. Garca, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989.
29. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, et al., MOLPRO, version 2012.1, a package of ab initio programs, 2012.
30. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259.
31. J. Heinze, N. Heberle and K. Kohse-Hoinghaus, Chem. Phys. Lett., 1994, 223, 305.
32. H.-J. Werner, Mol. Phys., 1996, 89, 645.
33. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
34. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
35. R. O. Loo, H. P. Haerri, G. E. Hall and P. L. Houston, J. Chem. Phys., 1989, 90, 4222.
36. National Institute of Standards and Technology, NIST Chemistry Webbook, 2010, http://webbook.nist.gov.
37. C. D. Sherrill, T. J. V. Huis, Y. Yamaguchi and H. F. Schaefer, J. Mol. Struct.: THEOCHEM, 1997, 400, 139.
38. A. Garca-Vela, J. Phys. Chem. A, 2014, 118, 6395.

---

Footnote

† Present address: Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK.

---