Vibrational anharmonicity of small gold and silver clusters using the VSCF method†
Luis A.
Mancera
*a and
David M.
Benoit
b
aInstitute of Theoretical Chemistry, University of Ulm, Albert-Einstein-Allee 11, D-89069 Ulm, Germany. E-mail: luis.mancera@uni-ulm.de
bThe University of Hull, Cottingham Road, Kingston Upon Hull HU6 7RX, UK
First published on 25th November 2015
Abstract
We study the vibrational spectra of small neutral gold (Au2–Au10) and silver (Ag2–Au5) clusters using the vibrational self-consistent field method (VSCF) in order to account for anharmonicity. We report harmonic, VSCF, and correlation-corrected VSCF calculations obtained using a vibrational configuration interaction approach (VSCF/VCI). Our implementation of the method is based on an efficient calculation of the potential energy surfaces (PES), using periodic density functional theory (DFT) with a plane-wave pseudopotential basis. In some cases, we use an efficient technique (fast-VSCF) assisted by the Voter–Chen potential in order to get an efficient reduction of the number of pair-couplings between modes. This allows us to efficiently reduce the computing time of 2D-PES without degrading the accuracy. We found that anharmonicity of the gold clusters is very small with maximum rms deviations of about 1 cm−1, although for some particular modes anharmonicity reaches values slightly larger than 2 cm−1. Silver clusters show slightly larger anharmonicity. In both cases, large differences between calculated and experimental vibrational frequencies (when available) stem more likely from the quality of the electronic structure method used than from vibrational anharmonicity. We show that noble gas embedding often affects the vibrational properties of these clusters more than anharmonicity, and discuss our results in the context of experimental studies.
1 Introduction
Many applications of gold clusters have been described in the literature covering different fields such as catalysis, sensors, and molecular electronics.1–3 In particular, Au clusters are interesting due to their significant catalytic activity as reported by Haruta,4 and some of their special properties are often rationalized by relativistic effects.2,3 Theoretical studies of Au clusters have used various methods to describe their electronic and structural properties, such as empirical many-body potentials,5–8 DFT,9–15 and ab initio methods.16–28 Although we consider only neutral clusters in this study, it should be remarked that an important amount of research has also been performed on ionic clusters, see for example the studies by Kappes and coworkers.29–32 Investigation of gold clusters is still a current and very active field of research, as can be seen from the large amount of studies in the last five years covering different aspects such as bonding,33,34 determination of minimum energy structures35–37 or development and application of new theoretical methods.38,39Silver clusters have also been widely studied in order to understand the size evolution of the cluster properties. They are interesting mainly due to their chemical reactivity relevant in heterogeneous catalytic reactions and to their optical properties. In addition, the characteristics of the sputtering mass spectra for Ag clusters allow for an unambiguous mass selection for several cluster sizes, in particular the odd-numbered clusters.40,41 Several theoretical studies of Ag clusters have been published either using DFT,42–46 or higher level electronic structure methods such as MP2, CCSD(T) or CI.46–49 Although there are not as many theoretical studies as for gold clusters, investigation of silver clusters is also a very active field of research nowadays. Most recent studies of silver clusters cover topics such as their physicochemical properties,50,51 applications,52–54 and theoretical modeling of interactions of the clusters with ligands.55,56 Due to their potential application in catalysis, the study of mixed Au–Ag clusters is also of particular interest.57–59
Au and Ag clusters are both interesting model systems to be investigated, not only due to their potential applications but also from a fundamental point of view. For example, various of the studies of Au clusters focus on predicting the transition from 2D to 3D structures. The predicted occurrence of this transition ranges between Au8 and Au15 depending on the method used, while the planar structures of Ag clusters are predicted only up to Ag5. For an understanding of the properties of metal clusters it is also relevant to investigate their vibrational frequencies, since they are a fingerprint of the cluster structure. Nevertheless, only few studies of Au and Ag clusters address this issue, and when vibrational frequencies are reported they only cover values obtained within the harmonic model. It has been shown that Au clusters behave differently to their lighter homologues, the Ag clusters.16 Therefore, we decided to investigate the vibrational properties of both neutral Au and Ag clusters in order to determine the magnitude of anharmonicity in their vibrational spectra.
Since for most oscillators a large dissociation energy is usually accompanied by a large force constant, the description of the interatomic potential by a harmonic model is better for bulk Au than for bulk Ag. Note that Au has an experimental bulk dissociation energy of −3.82 ± 0.02 eV per atom, larger than the one for Ag (−2.96 ± 0.01 eV per atom).60 Assuming a similar behaviour for their clusters, and since the experimental dissociation energy for Au2 is −1.15 ± 0.02 eV per atom, larger than the one for Ag2 (−0.83 ± 0.03 eV per atom),61 Au clusters are expected to be less anharmonic than silver clusters. In addition, as in both cases the binding energy for bulk is almost three times larger than for the clusters, we can expect a greater effect of anharmonicity for the clusters compared to the bulk.
The most used theoretical model to study vibrational properties of molecules is the harmonic approximation, which is implemented in almost every electronic structure program. There are many important processes that cannot be well described by the harmonic model, such as the bond dissociation in diatomic molecules. Since a harmonic representation of the vibrations neglects coupling between vibrational modes, it can also lead in many other cases to inaccuracies. Nevertheless, the advanced status of the electronic structure theory provides the basis for a more advanced vibrational structure theory beyond the pure harmonic model.62–67 Vibrational self-consistent field (VSCF),68–71 vibrational configuration interaction (VCI),72,73 vibrational Møller–Plesset theory (VMP),74 vibrational second-order perturbation theory (VPT2),75 and vibrational coupled cluster theory (VCC)76 are some of the methods developed to provide a better description of vibrational properties by including the effect of anharmonicity. These methods have been applied in various studies to calculate anharmonic vibrational spectra of molecules.77–82
In this study we combine VSCF/VCI and a DFT scheme using a plane-wave pseudopotential basis, in order to provide a magnitude and trend of the anharmonicity in neutral Au and Ag clusters. This allows us to obtain a more accurate solution to the vibrational problem by introducing the explicit correlation between modes. A fast-VSCF/VCI79 scheme is used to improve the overall speed of the frequency calculations. It works efficiently in the range of size which we consider and avoids the increasing computational cost as the cluster size increases. We have presented an overview of our VSCF/VCI implementation for adsorbates and metal clusters elsewhere, including RMSD values for anharmonic frequencies of the Au2–Au10 clusters.83 In another study, we have analyzed the harmonic and anharmonic spectra of Au7 in detail.84 In addition, we have addressed separately the effect of Kr embedding on the harmonic vibrational spectrum of the minimum energy structures of Aun clusters up to n = 9.85 Here we focus on the details of our VSCF/VCI implementation as well as on its discussion, extending the application to silver clusters.
The rest of this paper is organized in four sections: in Section 2 we present a brief description of the VSCF/VCI method together with the relevant computational details. Sections 3 and 4 contain the results and analysis of the vibrational properties for the minimum energy structures of Au and Ag clusters, respectively. Finally, we present our conclusions in Section 5. Detailed values of harmonic and anharmonic vibrational frequencies are presented in tables as a ESI.†
2 Methodology and computational details
In order to determine the global minimum energy structures of each size cluster, we use DFT to optimize a big set of planar and non-planar structures that were previously obtained using various empirical potentials with the procedure described in a recent study.86 In that study we have provided a detailed comparison of our minimum energy DFT structures with structures obtained using other DFT approaches and high-level theory methods. In general, our optimized global minimum energy structures obtained using DFT coincide in shape with the usual planar structures reported in various theoretical studies using other different DFT approaches, but additionally show the best approximation to the experimental values of the binding energy of Au2 and Au3. A separate discussion about challenges in describing the structure of the gold and silver trimers is presented in Sections 3.3 and 4.3, respectively, addressing the role of the Jahn–Teller and spin–orbit effects.For odd-sized (open-shell) structures, spin state and spin contamination could eventually affect the geometry and population analysis thus affecting the spin density. Although spin contamination is often seen in unrestricted Hartree–Fock and unrestricted Møller–Plesset calculations, it is less common in DFT calculations, even when unrestricted Kohn–Sham orbitals are used. A practical check for the presence of spin contamination consists in comparing the expectation value of the total spin, 〈S2〉 with s(s + 1) where s equals 1/2 times the number of unpaired electrons. For a difference between these two quantities of less than 10% the spin contamination is usually considered negligible. As the CPMD code calculates the total integrated absolute value of the spin density and not 〈S2〉 we cannot perform a direct check of spin contamination in our calculations. Spin contamination within DFT is not straightforward87 but can be approximately accessed using the absolute values of the spin density (as calculated by CPMD). In our cases those values are 1.12, 1.19, 1.15, and 1.17 for Au3, Au5, Au7, Au9 respectively, while the total integrated spin density is one in all cases. A view of the spin density for the odd-sized clusters can be obtained from the shape of the β-SOMO frontier orbitals. We have treated this already in detail for the gold clusters elsewhere,85 thus we do not include this discussion here.
2.1 The PBE/VDB approach
All calculations necessary for the optimization are performed using version 3.11.1 of CPMD code.88 By using periodic DFT within this code we mainly take advantage of the scaling of the technique (N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) which enables us to obtain better performance over more standard non-periodic codes. We use PBE89 as exchange–correlation functional, and the Vanderbilt (VDB) pseudo potentials90 with a low energy cutoff (30 Ry) for the plane-waves. The PBE functional is the most reliable DFT functional for describing basic properties in small metallic clusters.46 PBE/VDB resembles experimental binding energy values for Au2 and Au3 quite well, and is in good agreement with other DFT studies using full-potential basis sets. It is noteworthy that the geometries obtained with this approach are in very close agreement with geometries obtained using the multi-reference MRSDCI method, for the Au2–Au4 clusters.23,24
N) which enables us to obtain better performance over more standard non-periodic codes. We use PBE89 as exchange–correlation functional, and the Vanderbilt (VDB) pseudo potentials90 with a low energy cutoff (30 Ry) for the plane-waves. The PBE functional is the most reliable DFT functional for describing basic properties in small metallic clusters.46 PBE/VDB resembles experimental binding energy values for Au2 and Au3 quite well, and is in good agreement with other DFT studies using full-potential basis sets. It is noteworthy that the geometries obtained with this approach are in very close agreement with geometries obtained using the multi-reference MRSDCI method, for the Au2–Au4 clusters.23,24
Since most theoretical studies of vibrational spectra consider only harmonic frequencies, a number of studies have attributed discrepancies between theoretical frequencies and experimental spectra rightly or wrongly to anharmonic effects. However, without explicitly accounting for anharmonicity, assumptions based only on harmonic data can be misleading. In addition, in order to account for anharmonicity, harmonic values are usually scaled uniformly,91,92 even if there are also a number of non-uniform scaling techniques.93 We have already referred to this problem in our previous study of Au7.84 Since harmonic stretch frequencies (![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) are usually larger than anharmonic frequencies (
) are usually larger than anharmonic frequencies (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), possible scaling factor should be lower than one. Nevertheless, in the case of the Au7 cluster scaling factors larger than one are necessary in order to fit DFT results with the experimental vibrational frequencies. There we concluded that the larger deviation is due to a deficiency of DFT functionals in properly describing the electronic interactions in gold clusters. Nevertheless, in spite of the large difference in absolute values of the vibrational frequencies compared with experiments, using a DFT scheme can still give a relatively good description of the anharmonicity in relative values.
), possible scaling factor should be lower than one. Nevertheless, in the case of the Au7 cluster scaling factors larger than one are necessary in order to fit DFT results with the experimental vibrational frequencies. There we concluded that the larger deviation is due to a deficiency of DFT functionals in properly describing the electronic interactions in gold clusters. Nevertheless, in spite of the large difference in absolute values of the vibrational frequencies compared with experiments, using a DFT scheme can still give a relatively good description of the anharmonicity in relative values.
The VDB approach combines the pseudopotential approach with the very rapid plane-wave convergence, achieving good transferability and calculating forces in a more efficient way than other pseudopotentials. It needs cutoffs between 20–30 Ry, while with other pseudopotentials, cutoffs of more than 100 Ry are required. Relativistic effects, which are very important for gold, are included during the fitting of the pseudopotential. Nevertheless, including spin–orbit effects and calculating van der Waals (vdW) energy contributions explicitly is beyond the scope of the version of the CPMD code used in our study. In order to evaluate the effect of Ar atoms bounded to the silver clusters we also use norm-conserving Goedecker (GTH) pseudo potentials94–96 with a plane-wave energy cutoff of 100 Ry (1361 eV) for silver and argon. A similar methodology is described in our previous study of the binding of Kr atoms to gold clusters,85 but in the present study we do not include the analysis of van der Waals effects. We showed in our previous study, that vdW interactions are not relevant for the bare clusters themselves at these cluster sizes, and that for binding noble gas atoms to the gold clusters these interactions start to be significant only for cluster sizes from n = 7. In both cases VDB and GTH, relativistic effects are included in the pseudo potentials. Only the 5d106s1 valence electrons for Au, the 4d105s1 valence electrons for Ag, and the 3s23p6 valence electrons for Ar are considered.
2.2 The VSCF/VCI method
VSCF/VCI is the standard method implemented in our PVSCF code.97 We have shown in a previous study that anharmonicity for Au7 is quite small.84 If we presume that anharmonicity should be very small for all the clusters studied here, alternative and computationally cheaper methods could have been used in our study, for example, simple perturbative approaches as VMP74 or VPT2.75 Nevertheless, we cannot assume that all clusters behave the same, as catalytic experimental data indeed show that clusters of different sizes exhibit different behaviour. In addition, an important fluxional character has been suggested for Aun clusters recently,34,98 thus a perturbative approach could potentially miss some important features. There are also a number of examples in the literature that shows that perturbative approaches still have limitations. For example, very recently Oschetzki et al.82 have investigated (LiF)n clusters using the VSCF/VCI method, and by comparison with results obtained using VMP they show that anharmonic resonances cannot be properly described by the perturbative approach, while VSCF/VCI is more suitable to get a proper description. Therefore, we chose the VSCF/VCI method since its variational nature offers an important “safety net” for exploratory calculations such as ours, and in order to reduce its computational cost we have implemented a Fast-VSCF/VCI scheme, as explained in Section 2.3. We also have to admit that perturbative methods as VPT2 or VMP are not implemented in our PVSCF code at this stage.Although we have presented the main settings of our implementation of the method elsewhere,83,84 we recall here the main concepts in order to allow for a better understanding. VSCF provides an approximate solution to the vibrational wave function. It takes into account the deviation of the potential energy surface (PES) from harmonicity and the coupling between normal modes, using a mean-field approach. This method is based upon the assumption that the total wave function of the system is separable and can be described by a product of single-mode wave functions φ(k)kj(Qj). Here, Q = {Q1,…,Qn} is a set of mass-weighted normal coordinates, and n is the number of vibrational modes determined by the number of atoms, N. The excitation quanta of each vibrational state is expressed by a collective index k ≡ kj ≡ {k1, k2,…,kn}. The fully coupled vibrational Schrödinger equation is replaced by a set of single mode equations with an effective potential V(k)j(Qj) for each vibrational state k and for each mode j, which accounts for mode–mode interactions in a mean-field manner. This corresponds to the effective potential seen by each normal mode due to the presence of the other normal modes for a given vibrational state. Since this effective potential depends implicitly on the wave function of all modes i ≠ j, the set of single-mode equations needs to be solved iteratively until self-consistency is achieved. The PES of the system is explored using a hierarchical many-body expansion, limited to the second order in V (pairwise approximation),78,79
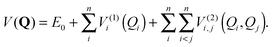 | (1) |
The 1D-VSCF equations are solved using the Fourier grid Hamiltonian (FGH) method proposed by Balint-Kurti et al.99,100 This is a special case of a discrete variable representation (DVR), and has the advantage that is a variational method where the wave functions or eigenfunctions of the Hamiltonian operator are generated directly as the amplitudes of the wave function on the grid points, thus they are not given as a linear combination of any set of basis functions.99 We use a truncated Watson operator101 that neglects the Coriolis coupling term of the molecular Hamiltonian. As we are interested in the pure vibrational spectra, neglecting coupling between vibrational and rotational modes should not be an issue to get reliable values of the vibrational anharmonicity. We support this argument on various facts: (i) due to the geometry of these clusters most vibrations are restricted to the plane, so that we cannot consider rotations, although for a few out-of-plane modes this could eventually occur, (ii) the relatively large mass of these clusters will further decrease the possible effect of Coriolis coupling compared with light molecules, (iii) at lower excitations of the vibrational angular momentum, the contribution of these couplings to the total energy may be small. In the VCI basis we include all one-mode and two-mode excitations up to seven virtual excitation quanta for each vibrational mode. The diagonalization part of the VCI procedure accounts for a significant part of the time required to solve the correlation problem. Therefore, an iterative diagonalization procedure of the VCI matrix using our own implementation of the direct Davidson algorithm102–104 is performed for each VSCF-optimized state as described by Scribano and Benoit.81 This was originally introduced by Carter et al.73 in order to diagonalize efficiently large vibrational VCI matrices. As we use a state-specific approach,77 the need for a block-Davidson approach is not as crucial as it could be in other methods. In our hands, the current approach which tracks the desired state performs very well even for dense spectra.
2.3 Computation of the PES and anharmonic frequencies
After a full optimization of the structures using PBE/VDB, we calculate the harmonic frequencies and corresponding normal modes at the minimum energy structures obtained for each cluster size, also using the CPMD code. In all cases, the minimum energy structures are planar. With this we proceed to compute the potential energy surfaces (PES). The PES construction is performed using the PVSCF code97 which drives the CPMD code in order to evaluate the total energy for a given number of points. Starting from an optimized structure and its corresponding Hessian matrix, we evaluate the DFT total energy for a fixed number of points on a grid (here 16) to obtain the 1D potential energies, and for a regular grid with 256 points (16 × 16) to obtain the 2D PES. We transform the Qj mass-weighted normal coordinates into dimensionless coordinates qj = Qjλj−1/4 such as proposed by Gregurick et al.105 in order to have an adjustable grid, sensitive to each mode, where the factor λj corresponds to the jth eigenvalue of the Hessian. In addition, to calculate the potential at each normal mode point, a transformation back to Cartesian coordinates is made, and the potential energy is then calculated at this displaced geometry. The 16 regularly spaced grid points along each normal coordinate are interpolated to a finer-meshed representation of the PES using a cubic-spline algorithm. The 256 regularly spaced grid points for each mode–mode coupling term are interpolated on a finer mesh using a bicubic interpolation.106Calculating 2D PES increases the computational cost as the cluster size increases, since the number of pair-couplings elements growths as n(n − 1)/2 with n the number of vibrational modes. Therefore, we calculate complete PES for Aun and Agn clusters with n ≤ 5 only. For Aun with n > 5 we calculate PES using a reduced scheme of pair-couplings (Fast-VSCF). For Fast-VSCF/VCI,79 we select a set of relevant pair-couplings, based on the analysis of the coupling strength. Although empirical models are not accurate enough to give a good description of those structures, they can used as a cheap method to get approximate geometries for further high-level calculations. Therefore, we use the Voter–Chen empirical potential,107–109 which is a version of the embedded-atom model (EAM), in order to pre-scan the complete PES previously to apply DFT. The choice of this potential is based on our previous study that assesses the quality of various empirical potentials,86 and shows this potential as comparatively better suited to reproduce PES of small gold clusters. This strategy reduces the computing time dramatically. It should be remarked the importance of having a good prediction of the couplings in order to get accurate results: while neglecting strong couplings in the calculations can lead to wrong results, predicting of weak couplings as strong can lead to waist computational efforts.
The normal modes obtained from the Hessian matrix constructed using PBE/VDB in each case are used as an input to carry out the PES pre-scanning. In order to determine which mode–mode couplings contribute most to the vibrational dynamics, we define a measure in terms of the potential evaluated on a number mmax of grid points, ζ2Dij:
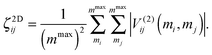 | (2) |
This measure provides a magnitude for each element of the pre-scanned 2D PES. Since the maximum elongation does play a role in the coupling strength, we use a systematic criterion for determining the maximum extent of the displacement where we try to ensure that each modal potential supports 7 or 8 bound states. This provides a coherent set of elongations that can be different for each mode but overall survey a similar vibrational space. We choose the couplings where ζ2Dij is higher than a given threshold value, which is obtained from a statistical analysis based on box-and-whisker plots.110 We show the coupling maps corresponding to the pre-scanned 2D PES as ESI† (Fig. A1). These maps are colour-coded so that a white square corresponds to low coupling strength and a black square to a very strong coupling. In those cases in which we only calculate partial 2D PES (Au6–Au10), modes not considered within the selected pair-couplings show anharmonic contributions coming from the diagonal potential only, since they are not coupled. Once the complete or partial PES have been generated, the vibrational VSCF/VCI analysis is carried out using the PVSCF code,97 in order to obtain the values of the anharmonic frequencies for each normal mode.
2.4 Analytical models for anharmonicity
In contrast to the harmonic case, where the solution of the 3N-dimensional oscillator is given in terms of the 1D harmonic solutions for each one of the 3N − 6 normal vibrational modes, the quantum anharmonic oscillator cannot be exactly solved analytically. Thus, it is necessary to resort to approximations that are functions with an analytical or a closed analytical expression. By fitting computed 1D-PES, we determine the relation between parameters obtained from these functions and the shape of PES, in order to classify the type of anharmonicity of some interesting single vibrational modes.In order to include the effect of anharmonicity, the expression for the harmonic oscillator is modified using the phenomenological Dunham's expansion111 which is traditionally written in dimensions of wave numbers:
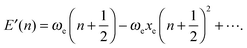 | (3) |
| V(x) = De[1 − e−a(x−xe)]2, | (4) |
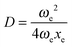 , a = (2ωexe)1/2, and ν0 = ωe − 2ωexe. Morse potential is suitable to model only those cases in which a positive anharmonicity occurs (ν0 < ωe).
, a = (2ωexe)1/2, and ν0 = ωe − 2ωexe. Morse potential is suitable to model only those cases in which a positive anharmonicity occurs (ν0 < ωe).
Another methodology to obtain an expression for the anharmonic oscillator resorts to an approximate solution by using perturbation theory. The Hamiltonian for the quantum anharmonic oscillator is expressed as the one for the harmonic oscillator113 with a perturbation up to the second-order Ĥ = Ĥ0 + λŴ.114,115 A widely used function is the generalized quartic potential, which is a potential including all odd and even terms for the polynomial expansion up to the fourth power. Since its analytic solutions116,117 are not suitable for the purposes of this study, we use the pure quartic and modified quartic potential which are simplified functions of it.
The pure quartic oscillator118 is suitable for modeling modes with negative anharmonicity (ν0 > ωe) where the potential resembles a quasi-parabolic symmetric shape. It is obtained by considering only the perturbation in q4:
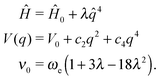 | (5) |
A modified quartic potential with an additional term in q3 is more convenient for the study of negative anharmonicity (ν0 > ωe), in those cases in which the anharmonic potential stays above the harmonic one, but the symmetric shape around the minimum is lost by the effect of the odd q3 term.
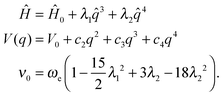 | (6) |
3 Vibrational anharmonicity in gold clusters
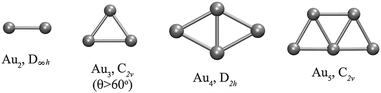
Fig. 1 shows the optimized planar structures, which represent the global DFT minimum energy structures of the Au clusters as computed using PBE/VDB. For Au2 the corresponding symmetry is D∞h and the bond length is 2.5 Å. For Au3, the global minimum is an obtuse triangle C2v with structural parameters 2.53 Å/138.1°. For Au4, the global minimum is a trapezoid D2h with structural parameters 2.67 Å/58.6°. The other global minimum structures are as follows: a “W-shape” planar trapezoid C2v for Au5 with a main structural parameter L = 2.6 Å (at the basis of the trapezoid), a triangle D3h for Au6 with a main structural parameter L = 2.61 Å (any of the external bonds), a capped triangle Cs for Au7, a D4h structure for Au8, a C2v structure for Au9, and a planar enlarged hexagonal structure with D2h symmetry for Au10. The Au–Au binding energy for those structures are −1.16, −1.24, −1.55, −1.70, −1.94, −1.90, −2.02, −2.01, and −2.09 eV per atom, from Au2 to Au10 respectively as obtained using PBE/VDB.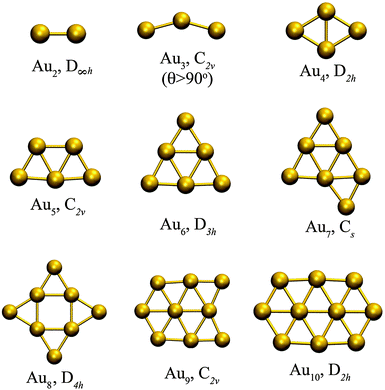 | ||
| Fig. 1 Global minimum energy structures studied for Au2–Au10 clusters, showing the point group symmetries, as computed using PBE/VDB. | ||
3.1 Experiments
The accepted reference value of the fundamental vibrational frequency of Au2 (190.1 cm−1) has been taken from the value reported by Ruamps.119 It should be remarked that for this experiment, an interaction of the noble gas atoms (Ar) with the clusters during the measure of the vibrational spectrum is excluded. Vibronic spectra for Au2 and Au3 have been reported by Bishea et al.120,121 describing transitions originated from the ground vibronic level of the ground electronic state, although only little can be ascertained about the ground state. Most of the experiments covering larger Au clusters in the gas phase have been restricted to charged clusters. Only very recent studies covering neutral clusters have been reported, using far-infrared multiphoton-dissociation spectroscopy (FIR-MPD) for Au7, Au19 and Au20,122 and for Au3 and Au4.98 Differently to the experiment reported by Ruamps for Au2,119 for the FIR-MPD technique an interaction of the neutral cluster with the embedded noble gas atom (Kr) is supposed to occur. We have shown elsewhere that for Au7 the Kr atom causes a larger effect on signal IR intensities than on vibrational frequencies84 (see also Ghiringhelli et al.98). In another study we have also systematically studied the role of the Kr embedding in small neutral gold clusters.85 We coincide with Ghiringhelli et al. that for Au2, Au3 and Au4 the Kr atoms are moderately bound to the clusters. As in that study we have already described the Kr embedding in detail, we report in the following our results of anharmonicity of the bare clusters only.3.2 Au2
Based on optical spectroscopy measurements119,123 and on the Dunham's expansion,111 Morse61 reports the following spectroscopic constants for the ground state of the gold dimer: D0 = 2.29 ± 0.02 eV, ωe = 190.9 cm−1, ωexe = 0.420 cm−1, and re = 2.4719 Å. The values ωe and ωexe correspond to the harmonic frequency and the first anharmonic constant, respectively. The anharmonic frequency for the same model can be calculated as ν0 = ωe − 2ωexe = 190.1 cm−1. Using PBE/VDB we obtain a harmonic frequency of![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) = 176.2 cm−1 and an anharmonic frequency of
= 176.2 cm−1 and an anharmonic frequency of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 175.3 cm−1. These values are ∼8% lower than the harmonic and anharmonic experimental frequencies, ωe = 190.9 cm−1 and ν0 = 190.1 cm−1, respectively. Nevertheless, the calculated anharmonic frequency is 0.9 cm−1 lower than the calculated harmonic frequency, keeping almost the same difference as the experimental values.
= 175.3 cm−1. These values are ∼8% lower than the harmonic and anharmonic experimental frequencies, ωe = 190.9 cm−1 and ν0 = 190.1 cm−1, respectively. Nevertheless, the calculated anharmonic frequency is 0.9 cm−1 lower than the calculated harmonic frequency, keeping almost the same difference as the experimental values.
Almost all schemes shown in Table 1 underestimate the experimental frequency of Au2. Our chosen approach PBE/VDB does it by ∼15 cm−1. Even more accurate calculations at the CCSD(T) level still underestimate the experimental value by ∼4 cm−1. MP2 and LDA predicts the harmonic frequency of Au2 better than PBE/VDB, compared to the experimental value. Nevertheless, in both cases this relative good agreement originates from a fortuitous cancelation of errors as we have already shown elsewhere for gold clusters using MP2.84 Since anharmonicity decreases the harmonic frequency of Au2 by ∼1 cm−1, any correction assigned to anharmonicity should yield still lower frequencies. It indicates that anharmonicity is not the cause of the large discrepancy between theory and experiment.
| Method | E b | r e |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) − − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) |
|---|---|---|---|---|---|
| PBE/VDB | 1.16 | 2.50 | 176.2 | 175.3 | −0.9 |
| LDA/VDB | 1.50 | 2.43 | 195.9 | … | … |
| MP2/SDD16 | 1.21 | 2.46 | 199 | … | … |
| MP2/HW VDZ17 | 0.98 | 2.63 | 186 | … | … |
| CCSD(T)/SDD16 | 1.06 | 2.51 | … | … | … |
| CCSD(T)/PJHN19 | 1.10 | 2.49 | 187 | … | … |
| MCPF/HW MB21 | 0.94 | 2.56 | 172 | … | … |
| MRSDCI/EC23 | 1.03 | 2.52 | 193 | … | … |
| Experimental61,120 | 1.15 | 2.47 | 190.9 | 190.1 | −0.9 |
Table 1 also shows that good agreement of the theoretical binding energy and bond length with the experimental value does not necessarily imply good agreement of the harmonic frequency. By comparing the various studies, we see that the CCSD(T) calculations reported by Hess et al.19 show the best prediction for the three magnitudes. MRSDCI calculations reported by Balasubramanian et al.23 show the best prediction for the harmonic frequency, a reasonable prediction for the bond length but a larger difference for the binding energy.
Contrary to the accepted fact that neutral gold clusters have still planar structures even for cluster sizes above 10 atoms, MP2 and LDA predict 3D structures from Au7 on, mainly due to a wrong description of the dissociation energy of these clusters. The shortcomings of MP2 to properly describe the structures of the small neutral clusters have been attributed to the tendency of MP2 to overestimate binding energies,124 to the usual large basis set superposition error (BSSE) that artificially shortens the bond length,19 and to the fact that the correlation energy calculated by means of an n-body expansion using MP2 for gold clusters does not converge smoothly.20 In the frame of DFT and in particular for LDA, there are significant errors in the exchange and correlation energies. As the exchange energy is generally underestimated and the correlation energy is overestimated, these errors tend to cancel, thus LDA is relatively successful at describing the harmonic frequency of Au2. Nevertheless, this is obtained at the cost of a wrong description of the binding energy. GGA and further developed functionals improve significantly on the description of the binding energy of molecules but not necessarily profit that much of cancelation of errors as LDA does, although they are though to provide a better overall performance. Therefore, the main reasons to use DFT with the PBE functional in our study instead of MP2 or LDA, although they provide a better value of the frequency of Au2, is that PBE/VDB does offer a better computational scaling than standard MP2 and also it has been shown that PBE gets other things right (such as dissociation energy) in comparison with both MP2 and LDA. A strong reason to not use MP2 is that using a large basis set or introducing counterpoise corrections would deteriorate that cancellation of errors that make that method apparently better. Using MP2 or LDA would also imply dealing with the wrong minimum energy structures for clusters larger than Au6.
Fig. 2 shows a plot of our results for the harmonic and the anharmonic potentials of Au2 using PBE/VDB. This represents a typical case in which the anharmonic frequency is lower than the harmonic frequency. The zero point energy (ZPE), as calculated for the harmonic oscillator, corresponds to ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) /2 = 88.1 cm−1. From the anharmonic calculation the ZPE is 88.0 cm−1, 0.1 cm−1 lower than for the harmonic case.
/2 = 88.1 cm−1. From the anharmonic calculation the ZPE is 88.0 cm−1, 0.1 cm−1 lower than for the harmonic case.
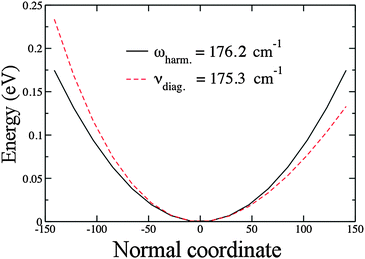 | ||
| Fig. 2 Harmonic and anharmonic potentials for the stretching mode of Au2. Results obtained using PBE/VDB. The normal coordinate is in a dimensionless variable as explained in Section 2.3. | ||
We apply the Morse potential oscillator model in order to fit this stretching mode. Values obtained directly from the harmonic and anharmonic calculations, and from the fitting of the potential energy curve are reported in Table 2. Since fitted values agree with the values obtained directly from the PVSCF code, the Morse potential is suitable to obtain the spectroscopic values for the stretching mode of the gold dimer. The largest discrepancy occurs for the dissociation energy, while the fitted first anharmonic constant ωexe is close to the reported experimental value.
| Parameter | Units | Calculated | Fitted value ± error |
|---|---|---|---|
(![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) ωe ) ωe |
cm−1 | 176.2 | 176.3 ± 0.3 |
(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ν0 ) ν0 |
cm−1 | 175.3 | 175.4 ± 0.3 |
| D e | eV | 2.14 | 2.200 ± 0.003 |
| w e x e | cm−1 | 0.45 | 0.440 ± 0.001 |
| a | (cm−1)1/2 | 0.95 | 0.940 ± 0.001 |
3.3 Au3
The global minimum energy structure of Au3 is still a matter of controversy. As a consequence, predictions of vibrational frequencies for this cluster vary depending on the structure assumed as the global minimum. Analysis of the electronic states show that Au3 with its three valence s-electrons should give rise to a 2E′ ground state configuration in D3h symmetry. Nevertheless, different structures very close in energy in a complex PES result as the high symmetric structure is distorted by the Jahn–Teller effect,125i.e. a non-linear molecule in an orbitally degenerate state will undergo a distortion which lowers its energy and removes the degeneracy of the state, when the molecule is in any state whose orbital degeneracy is ≥2. For homonuclear trimers, such as the neutral gold cluster, the distortion is from D3h to C2v symmetry. This splits the 2E′ state (equilateral triangle in D3h) into 2B2 (acute triangle C2v with θ > 60°) and 2A1 (acute triangle C2v with θ < 60°) states.16,126 Other effects can affect the subtle relation between the different states of the gold trimer. This is the case of the spin–orbit coupling that accounts for the interaction of the electron's spin with its motion, causing shifts in the electron's atomic energy levels. Vibrational anharmonicity itself may induce splitting of the spectra in highly symmetrical molecular species. In addition, the Born–Oppenheimer approximation used for the vibrational analysis may break down for the case of different electronic configurations close to each other. This is due to the dependence of the electronic wave function on the motion of the nuclei.At room temperature Au3 does certainly not correspond to a single defined structure, but to a changing structure adopting various shapes according its complex PES. The relation in energy between the 2A1 and the 2B2 states varies depending on the method used to compute it, as can be seen in Table A2 of the ESI.† For example, most DFT approaches show a 2B2 geometry (obtuse C2v triangle with θ > 90°) as the global minimum energy structure for this cluster. For MP2 the minimum energy structure is the acute triangle (θ > 60°), very close in energy to the another acute triangle (θ < 60°).17 We found that the obtuse structure calculated using PBE/VDB is 40 meV lower in energy than the acute structures, while using MP2/SBKJC1f it is 50 meV per atom higher (see Table A2 of the ESI†). Using CCSD(T), both acute structures are very close in energy,16,126 and any of them can be the minimum depending on the basis set used. Although high-level theory methods include multi-reference effects, which are important in particular for description of open-shell structures like Au3, studies using CCSD(T) sometimes report on vibrational frequencies that are far away from reported experimental values, and there are no available reports considering the obtuse structure with that method. Various theoretical studies using CCSD(T) have already investigated the balance between the Jahn–Teller effect and spin–orbit effect in Au3. For example Wesendrup et al.16 show that the splitting of the equilateral structure in two acute structures is due to a predominant Jahn–Teller effect. Shen and BelBruno126 get the same conclusion when they use CCSD, but they also show that using DFT including explicitly spin–orbit effect, this quenches the splitting induced by the Jahn–Teller effect. A similar mechanism has been suggested in an experimental study by Guo et al.127 Therefore, there are no conclusive results about the right minimum structure of Au3 provided by those methods.
Since our present study is based in a DFT scheme, inclusion of multi-reference effects in our calculations is limited to that of those effects that could be reproduced by the DFT functional and the corresponding basis set. Although some limitations of DFT exist in comparison with high-level electronic structure methods, it has been shown that DFT can cover in some extent multi-reference effects, either implicitly via the exchange–correlation functional or explicitly via the form of the Kohn–Sham wave function.128 In addition, although explicitly treatment of spin–orbit effects are out of the scope of the version of the CPMD code used in our study, some features such as relativistic effects are indirectly included in DFT during the fitting of the pseudopotential. The DFT approach we use in this study (PBE/VDB) also shows a better approximation to the experimental values of the binding energy of Au2 and Au3 than other DFT approaches and high-level method studies reported in the literature. Therefore, even given its limitations, we think that DFT still offers a suitable and practical manner to gain insight into the Au3 cluster and can be used to study the larger clusters in a systematical way.
A slightly bent linear structure, corresponding to an obtuse triangle C2v, has been suggested by Howard et al.129 as the ground state for Au3, from measurements using electron-spin resonance. A vibronic spectrum of Au3 has been determined by Bishea et al.121 from resonant two-photon ionization spectroscopy measurements. This experiment describes transitions which originate from the ground vibronic level of the ground electronic state. The analysis of the experimental spectrum shows a totally symmetric stretching vibration at 179.7 cm−1 and a second vibration at 61.9 cm−1. The existence of an obtuse geometry is not proven, but due to difficulties in assigning certain modes, it has not been absolutely excluded. Bishea et al.121 analyze different possible transitions between the ground and excited states, and show a transition in the equilateral D3h point group, with both the ground and excited states undergoing Jahn–Teller effect, as the most likely assignment. This is performed by considering a linear Jahn–Teller effect with spin–orbit splitting. Guo et al.,127 using matrix-infrared spectroscopy assign the global minimum energy structure to an equilateral triangle, D3h, with two vibrational frequencies, 172 cm−1 and 118 cm−1. By doing relativistic configuration interaction (RCI) calculations, they argue that the spin–orbit effect stabilizes the D3h structure and quenches Jahn–Teller distortion. They suggest that anharmonicity appears to play a greater role in higher combinations involving the antisymmetric stretching mode than the symmetric mode.
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) and anharmonic (
) and anharmonic (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) frequencies for the minimum energy structure of Au3 calculated using PBE/VDB in comparison to experimental values, in cm−1. For the anharmonic frequencies, diagonal and VSCF/VCI results considering all three pair-couplings are reported. RMSD values of the frequencies are referred to experimental values
) frequencies for the minimum energy structure of Au3 calculated using PBE/VDB in comparison to experimental values, in cm−1. For the anharmonic frequencies, diagonal and VSCF/VCI results considering all three pair-couplings are reported. RMSD values of the frequencies are referred to experimental values
Table A2 of the ESI† shows that both acute Au3 structures have roughly the same minimum energy with differences of about 5 meV (one −1.195 eV with θ = 65.6° and the other −1.190 eV with θ = 56.7°), while the obtuse structure (−1.236 eV with θ = 138.1°) is separated by approx. 40 meV from the acute structures. To promote an overlap of the 1D PES of both acute Au3 structures, the vibration of the bending mode should cause changes in the bending angle larger than −5.6° (when θ > 60°) and than 2.3° (when θ < 60°). Nevertheless, we do not observe any overlap. In addition, the vibration of the bending mode for the obtuse structure (θ = 138.1°) is far away of reaching angles close to 60°. It seems that an overlap between acute structures due to vibrations, if it occurs, should take place at the 2D PES level, i.e. not through the bending mode itself but through the coupling between different modes. Since for Au3 we only calculate the 2D PES of the obtuse structure and this is 40 meV lower in energy than the acute structures, we did not experience any convergence problem caused by overlap, neither with the acute structures nor with the obtuse and the acute structures. We show in Section 4.3 that convergence problems occur when we calculate the 2D PES of one of the acute structures of the Ag3 cluster that prevent us from computing a complete 2D PES. This means that although our method provides a measure of the anharmonicity in almost all cases, it has shortcomings for those open-shell structures where a complex PES with almost degenerate geometries is present.
In contrast to the interpretation by Guo et al.,127 who attribute discrepancies between theory and experiment to the anharmonicity involving the stretching mode (mode 1), Table 3 shows that vibrational anharmonicity is more significant for the bending mode (mode 3) of the obtuse structure, even if it is still too small (∼1.6 cm−1). The argument of Bishea et al.,121 that vibrational anharmonicity may contribute to the splitting of the equilateral triangle into acute structures, seems to be reasonable. In Section 4.3, we show that computing the 2D PES for the acute structures of the silver trimer is cumbersome, since the narrow difference in energy between these two structures leads to an overlap of the PES. This implies that the vibrational motions, even with the low anharmonicity, may lead to a changeable structure with a variable bending angle around θ = 60°.
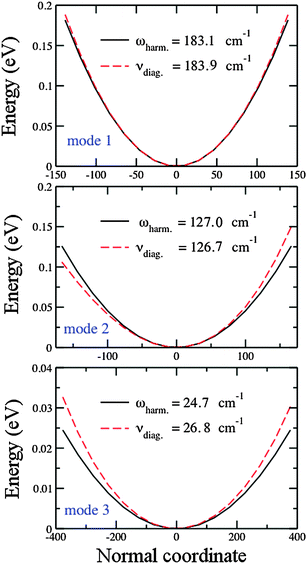
Table 4 shows the vibrational frequencies for the three normal modes of the obtuse Au3 cluster. Only the antisymmetric mode (mode 2), which has a positive anharmonicity, is fitted to the Morse potential. The symmetric mode (mode 1) is fitted to the pure quartic potential (perturbation in q4) and the bending mode (mode 3) is fitted to the modified quartic potential (perturbations in q3 and q4). The pure quartic and generalized quartic potential do not allow for calculation of parameters other than the frequencies. Both mode 1 and 3 show negative anharmonicity. Fitting for mode 2 fairly reproduces the calculated values. For modes 1 and 3, the ω0 fitted values resemble very well the calculated values, but for mode 3 the ωe fitted value differs from the calculated harmonic frequency. This is a presumable consequence of the strong hyperharmonicity of this mode.
| Parameter | Units | Calculated | Fitted value ± error |
|---|---|---|---|
| Mode 1 (pure quartic) | |||
(![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) ωe ) ωe |
cm−1 | 183.1 | 183.3 ± 0.1 |
(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ν0 ) ν0 |
cm−1 | 183.9 | 183.9 ± 0.1 |
| Mode 2 (Morse) | |||
(![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) ωe ) ωe |
cm−1 | 127.0 | 126.9 ± 0.3 |
(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ν0 ) ν0 |
cm−1 | 126.7 | 126.7 ± 0.3 |
| ω e x e | cm−1 | 0.14 | 0.120 ± 0.001 |
| D e | eV | 3.56 | 4.26 ± 0.01 |
| a | (cm−1)1/2 | 0.53 | 0.480 ± 0.001 |
| Mode 3 (mod. quartic) | |||
(![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) ωe ) ωe |
cm−1 | 24.7 | 26.5 ± 0.1 |
(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ν0 ) ν0 |
cm−1 | 26.7 | 26.8 ± 0.1 |
3.4 Au4
The vibrational frequencies of the global minimum energy structure for Au4 (trapezoid D2h) are reported in Table A4 of the ESI.† The harmonic frequencies are in the range of 34.5 cm−1 to 167.2 cm−1, with exception of mode 6 all modes are in-plane. For this structure the complete 2D potential energy surface was calculated. VSCF/VCI calculations show the largest anharmonicity of −1.8 cm−1 (−1%) for the largest frequency mode (mode 1), which corresponds to the breathing mode. This cannot be rationalized by just considering diagonal contributions, showing the importance of including the effect of the pair-couplings. In all cases the VSCF/VCI anharmonic frequency is lower than the harmonic one, and the change in ZPE due to anharmonicity is −0.1%. Changes in vibrational frequency due to anharmonicity are very small (RMSD = 0.9 cm−1) compared to the changes induced by Kr binding, which largely alters the structure (see ref. 85).3.5 Au5
The harmonic frequencies of Au5 are in the range of 24.9 cm−1 to 180.8 cm−1, with the exception of modes 8 and 9 all modes are in-plane (see Table A5 of the ESI†). For this structure, the complete 2D potential energy surface was calculated. The largest anharmonicity, −2.1 cm−1 (−2.3%), was obtained for mode 5, which corresponds to a stretching mode. Large changes between the diagonal results and the correlation-corrected values for certain modes indicate that such modes are more strongly correlated, i.e. strongly coupled with other modes. For example, by including the pair-couplings, the difference between VCI and diagonal frequencies for modes 1 and 5 are −1.7 cm−1 and −2.0 cm−1, respectively. In all cases, the VSCF/VCI anharmonic frequencies are lower than the harmonic ones. The change in ZPE due to anharmonicity considering pair-couplings is −0.3%. The RMSD between harmonic and anharmonic frequencies is 1.1 cm−1, larger than for Au4.3.6 Au6–Au10
Harmonic and anharmonic frequencies of these clusters are presented in detail in Tables A6–A10 of the ESI.† The harmonic frequencies for the Au6 cluster are in the range of 33.5 cm−1 to 184.4 cm−1, and there are four doubly degenerate frequencies. For the anharmonic frequencies, the 2D PES was computed using 15 of 66 possible pair-couplings. The calculated couplings have a coupling strength higher than 49.7%. With the exception of modes 10, 11 and 12, all modes are in-plane. The largest anharmonicity, −1.6 cm−1 (−1.4%), is obtained for mode 5, corresponding to a bending mode with anharmonic frequency of 111.5 cm−1. This mode is the strongest coupled mode, since the frequency changes by −1.6 cm−1 when the effect of the couplings is included. In contrast to the former clusters studied here, Au6 shows various modes with almost zero anharmonicity. These modes (6, 7, 10, 11 and 12) are weakly coupled to other modes.The Au7 cluster shows harmonic frequencies in the range of 16.3 cm−1 to 189.6 cm−1, where modes 12 to 15 are out-of-plane. The 2D PES was computed using only 9 of 105 possible pair-couplings. The calculated couplings have a coupling strength higher than 51.2%. The anharmonicity is very low, in comparison to the former clusters. The largest anharmonicity, 0.8 cm−1 (0.4%), was obtained for mode 1, which corresponds to a stretching mode. The RMSD between harmonic and anharmonic frequencies is 0.4 cm−1. We have studied this cluster in detail elsewhere,84 and showed that the effect of Kr embedding changes its harmonic frequencies with a RMSD of 1.5 cm−1. Anharmonicity calculated for the minimum energy configuration of Au7Kr shows changes in frequency with a RMSD of 0.7 cm−1.
The harmonic frequencies for the Au8 cluster are in the range of 6.9 cm−1 to 202.8 cm−1, there are four doubly degenerate frequencies, and modes 13 to 18 are all out-of-plane. The 2D PES was computed using 12 of 153 possible pair-couplings. In contrast to the former clusters studied, less than 8% of the couplings for Au8 contain the higher coupling strengths, with values above 28.52%. Only 9 modes are strongly coupled to the others. With the exception of modes 4, 5, 17 and 18, all modes show almost zero anharmonicity. It is noticeable that the two lowest frequency modes (17 and 18), which are out-of-plane, show the largest anharmonicity, −2.6 cm−1 and 1.8 cm−1, respectively.
The harmonic frequencies for the Au9 cluster are in the range of 12.3 cm−1 to 187.0 cm−1, where modes 16 to 21 are all out-of-plane. The 2D PES was computed using 10 of 210 possible pair-couplings. The selected pair-couplings have coupling strengths higher than 72%. With the exception of a few modes, anharmonicity is almost zero. The largest anharmonicity, −2.0 cm−1, is observed for mode 4, which represents a predominant bending motion of the molecule. This large total anharmonicity is attributed to pair-couplings, since diagonal anharmonicity for the same mode is almost zero. The harmonic frequencies for the Au10 cluster are in the range of 16.3 cm−1 to 176.1 cm−1, and modes 19 to 24 are all out-of-plane. The calculated couplings have a coupling strength higher than 44.26%. The largest anharmonicity occurs for modes 1, 2, 3, 8 and 24 with values close to −1.0 cm−1.
In general, the prediction of the strongest couplings for the Au6–Au10 clusters given by the Voter–Chen potential was satisfactory, i.e. all strong couplings predicted by the empirical potential correspond to strong couplings calculated with PBE/VDB, with a very few exceptions. Couplings obtained with the empirical potential as strong but calculated with PBE/VDB as very weak are considered as badly predicted, and therefore they are not included in the reduced 2D PES used to calculate the anharmonic frequencies. This is remarkable only for the Au10 cluster, where 4 of 18 couplings were wrong predicted, and it presumably indicates that at that size the cluster is reaching a regime in which the non-planarity is close to occur, since the performance of the two methods shows larger qualitative differences.
3.7 Discussion on Au clusters
Table 5 shows for each cluster the maximum difference between anharmonic and harmonic mode as well as the mode for which this occurs. We have found a small vibrational anharmonicity for Au2 of about −0.9 cm−1 that agrees with the reported value from experiment. For larger Au clusters, anharmonicity seems to be small, with a few larger values for some specific vibrational modes. The RMSD value allows us to have a measure of the overall deviation of the differences. In all cases these RMSD values are quite small with the maximum value around 1.2 cm−1. In most cases, the maximum absolute differences occur for higher modes. Nevertheless, for Au8 and Au10 the modes with the larger anharmonicity are low frequency and out-of-plane modes. Because of the large amount of data, we have provided for each cluster size a comparison mode by mode of harmonic and anharmonic frequencies in a tabular form in the ESI.† Since ambiguous results for gold cluster structures and their vibrational properties have been usually attributed to vibrational anharmonicity, we consider that the outcome of our study substantially contributes to this discussion by providing explicitly calculated values of its magnitude. Although we have found that vibrational anharmonicity is small in absolute value, the larger relative anharmonicity values can be attributed to different types of modes, depending on the cluster size, i.e. to the only stretching mode for Au2, to a bending mode for Au3, to a breathing mode for Au4, etc. (as reported in Table 5). This can be reasonably expected due to the particular geometries of these small clusters that lead to different strength of the bonds.| Cluster size | Mode/type |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) − − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) |
|
|---|---|---|---|
| Max | RMSD | ||
| 2 | 1/stretching | −0.9 | 0.9 |
| 3 | 3/bending | 1.6 | 1.2 |
| 4 | 1/breathing | −1.8 | 0.9 |
| 5 | 5/stretching | −2.1 | 1.1 |
| 6 | 5/bending | −1.6 | 0.6 |
| 7 | 1/stretching | 0.8 | 0.4 |
| 8 | 17/out-of-plane | −2.6 | 0.8 |
| 9 | 4/bending | −2.0 | 0.6 |
| 10 | 24/out-of-plane | −1.2 | 0.5 |
It should be remarked that although we have successfully found a magnitude of the anharmonicity, the absolute values of the vibrational frequencies are shifted to low values when compared with available experimental reports. This is mainly due to shortcomings in the performance of current DFT functionals. Since the purpose of this study has been to find a quantitative measure of the anharmonic effects, using the standard PBE functional allowed us to obtain a reliable value of the anharmonicity that is comparable with the one reported in available experiments, such as for Au2. Therefore, we extended this procedure to larger clusters.
For comparison of theoretical frequencies with experimental spectra of these clusters, anharmonicity and the electronic structure method are not the only issues to be considered, but also the possible effect of noble gas atom ligands. Classical experiments on Au2 and Au3 declare no interaction between the cluster and the noble gas atoms used in the experiment, while recent experimental reports of gold122 and silver40 clusters using far-infrared multiple-photon dissociation spectroscopy (FIR-MPD) declare the interaction with noble gas atoms. Since we calculated anharmonicity for the bare clusters only, a comparison with the FIR-MPD spectra is more challenging. We have treated the effect of noble gas atoms on the gold clusters previously,85 showing that binding of a noble gas atom does strongly affect the harmonic vibrational frequencies of these clusters in some particular cases. In the present study we include a similar discussion on the effect of noble gas atoms on the harmonic frequencies of the silver clusters.
Improving the description of the absolute values of the frequencies of these clusters is not as simple as using a more sophisticated high-level electronic structure method, if anharmonicity and the effect of ligands are not taken into account within the analysis. Indeed, for very small clusters as Au2 and Au3 that have been widely studied with high-level electronic structure methods,28,120,121 there is not complete agreement about their real structures and/or behavior. Also for a larger cluster such as Au8 various studies using high-level theory do not offer conclusive answers, since there are still limitations to use excessively large wave function basis sets.130 A combined strategy consisting in using a high-level electronic structure method beyond DFT, calculating anharmonicity and including the effect of noble gas atoms for each cluster size, all at the same time, could become a cumbersome task which is out of the scope of this study. Nevertheless, our results provide a good approximation to the issue of anharmonicity in these clusters, that combined with the outcome of our previous studies are intended to contribute to the understanding and stimulate further investigation of small metal neutral clusters.
4 Vibrational anharmonicity in silver clusters
Fig. 4 shows the optimized planar structures for the bare Agn clusters with 2 ≤ n ≤ 5. These represent the global DFT minimum energy structures as computed using PBE/VDB. For Ag2 the corresponding symmetry is D∞h and the bond length is 2.57 Å. For Ag3, the global minimum is an acute triangle C2v with structural parameters 2.63 Å/69.3°. For Au4, the global minimum is a trapezoid D2h with structural parameters 2.74 Å/123.1°. For Au5, the global minimum is a “W-shape” planar trapezoid C2v with a main structural parameter L = 2.69 Å (at the basis of the trapezoid). The Ag–Ag binding energy for those structures are −0.89, −0.89, −1.18, and −1.28 eV per atom, respectively as obtained using PBE/VDB.We calculate harmonic and anharmonic frequencies at the minimum energy structures of the bare clusters. Since only silver clusters up to Ag5 are studied, the pre-scanning of the PES using the Voter–Chen potential is not employed here. In all cases the diagonal anharmonic frequencies are calculated, but VSCF/VCI frequencies are calculated only for Ag4. The narrow energy differences between two nearly degenerate acute structures and one obtuse structure of Ag3 make the calculation of the 2D PES for this cluster size cumbersome. Overlap of these two PES does not allow the computation of the anharmonic frequencies including pair-couplings. For Ag5 it was also not possible to obtain the 2D-PES due to convergence issues.
We also calculate the harmonic frequencies of the same Ag clusters with attached Ar atoms. The effect of Ar embedding on the harmonic frequencies of these clusters is considered using PBE/GTH. For the bare clusters, the binding energies obtained using PBE/GTH vary slightly from the values found with PBE/VDB. We obtained −0.87, −0.86, −1.14, and −1.25 eV per atom, for Ag2 to Ag5, respectively. Fig. 5 shows the different configurations of the AgnKr clusters studied here. In general, larger strengths of the Ag–Ar interaction are associated with shorter Ag–Ar distances.
4.1 Experiments
An overview of experimental results for the silver dimer has been given by Morse.61 A complete overview for larger silver clusters has been given by Lombardi and Davis.41 Vibrational spectroscopy of small silver clusters in noble gas matrices was first reported by Schulze et al.131 for Ag2 and Ag3. Moskovitz et al. report Raman spectra of silver clusters deposited in solid argon for Ag3,132 Ag5,133 Ag7 and Ag9.134 Resonant two-photon ionization spectra (R2PI) have been used by Cheng et al.135 to study the Ag2Ar cluster. Ag3 has also been studied by Hartmann et al.49 using femtosecond pump–probe spectroscopy. They studied the vibrational properties in terms of intramolecular vibrational redistribution (IVR). More recently, Fielicke et al.40 carried out a study of Ag3 and Ag4 clusters in the gas phase with argon embedding, using far-infrared multiple-photon dissociation spectroscopy (FIR-MPD).4.2 Ag2
Experimental values for dissociation energy, bond length and vibrational frequency of the Ag2 cluster have been highlighted in various reviews.41,61 Spectroscopic constants for the ground state of the silver dimer are reported by Morse: D0 = 1.65 ± 0.03 eV for dissociation energy and r0 = 2.480 Å for bond length.61 Further studies show that the bond length is larger, for example Simard et al. report r0 = 2.533 ± 0.001 Å.136 Concerning vibrational frequencies, one of the fundamental experimental studies was performed by Srdanov and Pesic137 evaporating silver under argon pressure. They report ωe = 192.4 ± 0.2 cm−1 for harmonic frequency and ωexe = 0.60 ± 0.02 for the first anharmonic constant. It implies that the anharmonic frequency for the Dunham's model can be calculated as ν0 = ωe − 2ωexe = 191.2 cm−1.
Table 6 shows the calculated values for binding energy, bond length and harmonic vibrational frequency of the Ag2 cluster compared to selected theoretical values reported by other authors using different methods, and to experimental values. The harmonic and anharmonic frequencies obtained using PBE/VDB are ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) = 180.9 cm−1 and
= 180.9 cm−1 and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 179.6 cm−1, respectively. This indicates an anharmonicity of −1.3 cm−1 that reproduces very well the anharmonicity of −1.2 cm−1 estimated from the experiment. Thus, Ag2 shows only a slightly larger difference in anharmonicity compared to the Au2 cluster, which has an anharmonicity of −0.9 cm−1 (see Section 3.2).
= 179.6 cm−1, respectively. This indicates an anharmonicity of −1.3 cm−1 that reproduces very well the anharmonicity of −1.2 cm−1 estimated from the experiment. Thus, Ag2 shows only a slightly larger difference in anharmonicity compared to the Au2 cluster, which has an anharmonicity of −0.9 cm−1 (see Section 3.2).
| Method | E b | r e |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) − − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) |
|---|---|---|---|---|---|
| PBE/VDB | 0.89 | 2.56 | 180.9 | 179.6 | −1.3 |
| BLYP/SDD46 | 0.83 | 2.61 | 176.0 | … | … |
| BP86/SDD46 | 0.87 | 2.57 | 187.0 | … | … |
| MP247 | 0.70 | 2.63 | … | … | … |
| CCSD(T)47 | 0.80 | 2.64 | … | … | … |
| Exp.61,136,137 | 0.83 | 2.53 | 192.4 | 191.2 | −1.2 |
Fig. 5 shows two possible configurations of the Ag2 cluster considering Ar embedding, as obtained using PBE/GTH. Similar to gold clusters, the orientation of the Ar atoms can be described by the characteristics of the electrostatic potential. The binding energies of the Ar atoms to Ag2 are however, significantly smaller than those of Ar binding to Au2. The argon binding energy to Au2 is 90 meV while to Ag2 is only 25 meV. Therefore, changes in harmonic frequencies due to Ar embedding are very small for Ag2, compared to the changes induced in Au2. One and two Ar atoms increase the harmonic frequency of the Au2 cluster by 6.2 cm−1 and 10.8 cm−1. The harmonic frequencies of Ag2, Ag2Ar and Ag2Ar2 are 181.1 cm−1, 181.8 cm−1 and 183.4 cm−1, respectively, calculated using PBE/GTH. This means that one and two Ar atoms increase the harmonic frequency of Ag2 by 0.7 cm−1 and 2.2 cm−1, respectively.
4.3 Ag3
The general considerations presented at the beginning of Section 3.3 about the difficulties to compute a complex PES as for Au3 also applies for Ag3. It means, that Jahn–Teller and orbit-effects should be taken into account for the analysis, although we have admitted that including explicitly these effects is out of the scope of our calculations. In contrast to Au3, DFT predicts an acute triangle with θ > 60° as the global minimum energy structure of Ag3. Table A12 of the ESI† shows that the three Ag3 structures have roughly the same minimum energy with differences smaller than 10 meV, although their angles are quite different (55.6°, 69.3° and 133.6°). To promote an overlap of the 1D PES, changes of the bending angle induced by the bending mode should be larger than −9.3° (when θ > 60°) and than 3.4° (when θ < 60°), even larger than for the Au3 acute structures. Since no overlap is observed, this would imply a rather flat 2D PES easily connecting the three local minima, not through the bending mode itself but through the coupling between different modes. This makes the calculation of the 2D PES more challenging for the acute minimum energy structure of this cluster. Our attempts to compute reliable 2D PES for this system remained unsuccessful. For this reason, we report for Ag3 only diagonal anharmonic frequencies. On the other hand, similar to the case of Au3, various experiments lead to different conclusions about the vibrational frequencies of Ag3. In the following we briefly describe some relevant experimental studies and afterwards present our calculated frequencies in the context of some of those experimental results.Experimental results for Ag3 are considered ambiguous. In particular, there are large disagreements between gas-phase studies and matrix isolation studies. Haslett et al.132 used matrix isolation resonance Raman spectroscopy and obtained frequencies 119 cm−1 and 99 cm−1 for the totally symmetric and for the bending mode, respectively. This is in good agreement with the study by Schulze and Becker,131 who obtained 120.5 cm−1 in matrix isolation. Vibrational spectra of Ag3 have also been derived from fluorescence studies and from resonant two photon ionization spectra (R2PI). A detailed overview of experimental results for Ag3 is given by Lombardi and Davis.41 Fielicke et al.40 recently studied the vibrational frequencies of Ag3 using far-infrared multiple photon dissociation (FIR-MPD). This technique has also been successfully applied to other neutral metal clusters at different cluster sizes. In this experiment, Ag3Arm complexes were produced with one up to four bound argon atoms. Although the signal-to-noise ratio is low, several depletion bands are observed. Due to the dissociation of the cluster under far-infrared excitation, the original spectrum should be corrected. Such a dissociation causes that Ag3Arm complexes affect the signal of Ag3Arm−1 complexes. By correcting and fitting Gaussian profiles of the depletion signals, Fielicke et al.40 assigned 182.8 cm−1 to the highest frequency mode and 113 cm−1 to the degenerate mode of Ag3Ar. This methodology leads to uncertainties of ±1 cm−1. By binding more Ar atoms the highest frequency mode remains unchanged, but the lowest frequency mode changes slightly. Frequencies obtained for the lowest mode of Ag3Ar, Ag3Ar2, Ag3Ar3, and Ag3Ar4 are 113.0 cm−1, 116.8 cm−1, 119.1 cm−1 and 120.5 cm−1, respectively.
In Table A12 of the ESI† we report structural and harmonic frequency results obtained using PBE/VDB and PBE/GTH for the different Ag3 isomers. Table 7 shows the calculated harmonic and diagonal anharmonic frequencies for the minimum energy structure of Ag3 (acute triangle with θ > 60°), using PBE/VDB. Similarly to the gold trimer, Ag3 shows the largest anharmonicity in the bending mode (mode 3) but in this case it is almost three times larger than for Au3. This contrasts with the suggestion given by Hartmann et al.48 that anharmonicity may affect the antisymmetric mode (mode 1) the most.
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) and anharmonic (
) and anharmonic (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) frequencies for the global minimum energy structure of Ag3, the acute triangle with θ > 60°, in cm−1. Values obtained using PBE/VDB
) frequencies for the global minimum energy structure of Ag3, the acute triangle with θ > 60°, in cm−1. Values obtained using PBE/VDB
| n |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) diag.
diag.
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) diag. −
diag. − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) |
|---|---|---|---|
| 1 | 173.3 | 172.2 | −1.2 |
| 2 | 118.9 | 119.8 | −0.1 |
| 3 | 55.2 | 50.5 | −4.7 |
| ZPE | 174.2 | 172.5 | −1.7 |
| RMSD | 2.8 |
Due to the convergence problems mentioned above, the anharmonic frequencies reported here do not include the pair-couplings between modes. For a more complete analysis including the effect of the Ar atoms in the experiment, we perform in the following section a comparison of theoretical and experimental frequencies at the harmonic level. In that case the effect of the Ar atom is not as big as the effect of a Kr atom on Au3, so that Ag3 vibrational anharmonicity could have a more significant role.
Fig. 5 shows various possible configurations of the minimum energy structure of the Ag3 cluster considering Ar embedding, as obtained using PBE/GTH, and Table 8 shows the harmonic frequencies obtained for the minimum energy structures of Ag3 and Ag3Arm complexes. They are compared to the experimental values. Ar embedding does not change the geometry of the minimum configuration, but slightly distorts it. As a consequence, the frequency of the lowest frequency mode changes. These changes partially reproduces the trends observed by Fielicke et al.40 in the experimental spectrum. The RMSD between the theoretical values and those reported by Fielicke are of ∼7 cm−1. Our results are also very similar to those reported by Hartmann et al.,48 using full CI calculations.
In various studies of Raman spectra for Ag3 in rare gas matrices,131,132 a band of ∼119 cm−1 is assigned to the symmetric mode of an equilateral triangle. This value coincides better with the frequency of mode 2 of the acute structures. It seems that in these Raman spectra the highest frequency mode is screened and only the band corresponding to the next frequency mode is detectable. This has been well explained by Fielicke et al.40 based on comparisons of various experimental results.
4.4 Ag4
Even-numbered neutral silver clusters have been less studied than the odd clusters. Therefore, only a few experimental spectra for Ag4 are available. Felix et al.138 studied Ag4 cluster using fluorescence spectroscopy but the lack of vibrational resolution in these experiments did not allow to obtain vibrational constants for the ground state. Hess et al.,139 using femtosecond pump–probe spectroscopy, only identified a vibrational mode at ∼45 cm−1. Fielicke et al.40 studied the vibrational spectrum of this cluster using far-infrared multiple-photon dissociation spectroscopy (FIR-MPD). They obtained more suitable results for the vibrational frequencies than previous studies. In this experiment, Ag4Arm complexes are produced, having between two and five argon atoms bound. By correcting and fitting Gaussian profiles of the depletion signals, in the same way as for the silver trimer, Fielicke et al. identified two bands at 192.7 cm−1 and 162.7 cm−1, independent of the number of argon atoms attached. They also suggest the possible existence of a third band at ∼120 cm−1, but this is not conclusive due to the low resolution of the spectrum in this range.Table 9 shows the harmonic and anharmonic frequencies of Ag4 calculated using PBE/VDB. The RMSD between anharmonic and harmonic frequencies is only 1 cm−1. The largest anharmonicity affects the breathing mode (mode 1). The overall magnitude of the anharmonicity for the Ag4 is similar to the one calculated for Au4 (see Table A4 of the ESI†). Nevertheless, two noticeable differences from Au4 are observed: (i) difference between the anharmonic and harmonic frequencies for the largest frequency mode has different sign. (ii) The variation in the zero point energy (ZPE) due to anharmonicity is slightly larger (by ∼1 cm−1 and with opposite sign) for Ag4 than for Au4. This shows that total anharmonicity for this silver cluster is mainly negative (the cluster is hyperharmonic).
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) and anharmonic (
) and anharmonic (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) frequencies for the global minimum energy structure of Ag4 calculated using PBE/VDB, in cm−1. For the anharmonic frequencies both the diagonal and VSCF/VCI results are reported. For VSCF/VCI all 15 possible pair-couplings are considered
) frequencies for the global minimum energy structure of Ag4 calculated using PBE/VDB, in cm−1. For the anharmonic frequencies both the diagonal and VSCF/VCI results are reported. For VSCF/VCI all 15 possible pair-couplings are considered
| n |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) − − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) |
|
|---|---|---|---|---|
| Diagonal | VCI | |||
| 1 | 183.7 | 183.0 | 185.1 | 1.5 |
| 2 | 157.6 | 158.1 | 156.7 | −0.9 |
| 3 | 104.1 | 104.5 | 103.4 | −0.7 |
| 4 | 89.5 | 90.4 | 88.4 | −1.1 |
| 5 | 80.5 | 80.7 | 81.0 | 0.5 |
| 6 | 37.5 | 36.9 | 36.6 | −0.9 |
| ZPE | 326.5 | 326.6 | 327.7 | 1.2 |
| RMSD | 1.0 | |||
Fig. 5 shows various possible configurations of the minimum energy structure of the Ag4 cluster considering Ar embedding, as obtained using PBE/GTH. Table 10 shows the harmonic frequencies of Ag4 and the Ag4Arm complexes. These are compared to the experimental values reported by Fielicke et al.40 and to theoretical values reported by other authors. PBE/GTH better matches the experimental frequencies compared to BP86 or MP2 calculations reported by other authors. The best prediction occurs for Ag4Ar2, with a RMSD between experiment and theory of 6.2 cm−1. A reported study by Hartmann et al.,49 using the BLYP functional, shows the best predictions for the two modes reported in the experiment, with an overestimation of the frequencies. Nevertheless, we have shown that BLYP does not give optimal results for gold and in general for transition metal clusters.84 Moreover, most DFT approaches underestimate the frequencies. Therefore, the good performance of BLYP in predicting these two frequencies in Hartmann's calculations may rely more on the constructed basis set than on the functional itself.
| Ag4 | Ag4 | Ag4Ar | Ag4Ar2 | Ag4 | ||
|---|---|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp
40
exp
40
|
PBE/GTH | BP8644 | MP247 | BLYP49 | ||
| 192.7 | 183.8 | 183.7 | 185.2 | 181.3 | 166.1 | 196 |
| 162.7 | 158.3 | 158.0 | 158.1 | 140.1 | 147.6 | 165 |
| 105.5 | 105.7 | 106.0 | 110.2 | 97.7 | 114 | |
| 91.6 | 93.9 | 97.4 | 106.6 | 81.5 | 90 | |
| 81.7 | 81.0 | 82.3 | 90.0 | 75.4 | 81 | |
| 48.6 | 49.8 | |||||
| 45.1 | ||||||
| 29.8 | 28.6 | 28.8 | 23.3 | 32.5 | 36 | |
| 20.1 | 23.0 | |||||
| 16.4 | ||||||
| RMSD | 7.1 | 7.2 | 6.2 | 17.9 | 21.6 | 2.8 |
It is observed that anharmonicity does not correct the large discrepancy between theoretical and experimental frequencies. The RMSD between the VSCF/VCI frequencies and the experiment is 6.8, very close to that of the harmonic frequencies.
4.5 Ag5
Haslett et al.133 investigated the matrix isolation Raman spectrum of mass-selected Ag5 clusters. In their experiment, cationic clusters were co-deposited with Ar on a polished aluminum substrate. Then, a re-neutralization process was accomplished with a low-energy electron flux in order to obtain neutral clusters. They propose the planar trapezoidal cluster as the most probably structure to give rise the experimental spectrum, with assigned vibrational bands at 174, 162, 136, 126, 105, 100, 80 and 68 cm−1. They did not find evidence of a second isomer contributing to the spectrum but found evidence of a photofragmentation of the pentamer into a trimer and a dimer. Based on the photofragmentation kinetics, they concluded that the planar structure of Ag5 exists in at least two kinds of matrix sites. For the assignment of the bands, they ignore a band at 189 cm−1 which is believed to correspond to Ag2. Peaks at 105 cm−1 and 100 cm−1 are believed to belong to a single mode, which is split due to the deposition of the cluster in two different types of sites in the matrix. The same assumption is used for the bands at 126 cm−1 and 136 cm−1.133Table 11 shows the harmonic and anharmonic frequencies of Ag5 calculated using PBE/VDB. Only diagonal anharmonic frequencies are reported, which have a RMSD with respect to the harmonic frequencies of 1.9 cm−1.
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) and anharmonic (
) and anharmonic (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) frequencies for the global minimum energy structure of Ag5 calculated using PBE/VDB, in cm−1. For the anharmonic frequencies only diagonal results are reported
) frequencies for the global minimum energy structure of Ag5 calculated using PBE/VDB, in cm−1. For the anharmonic frequencies only diagonal results are reported
| n |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) diag
diag
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) diag −
diag − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) |
|---|---|---|---|
| 1 | 182.0 | 182.5 | 0.5 |
| 2 | 151.9 | 151.4 | −0.5 |
| 3 | 144.0 | 143.4 | −0.7 |
| 4 | 117.5 | 118.0 | 0.4 |
| 5 | 97.9 | 97.6 | −0.3 |
| 6 | 78.6 | 78.4 | −0.2 |
| 7 | 71.0 | 71.4 | 0.5 |
| 8 | 27.4 | 31.7 | 4.3 |
| 9 | 23.7 | 27.2 | 3.5 |
| ZPE | 447.0 | 450.4 | 3.4 |
| RMSD | 1.9 | ||
Although we have not calculated accurate VSCF/VCI anharmonic frequencies, the diagonal values already show that the large discrepancies between the experimental frequencies and the theoretical frequencies for Ag5 do not originate from vibrational anharmonicity. Only the modes 8 and 9 show anharmonicity of ∼4 cm−1, but these correspond to out-of-plane modes. The large discrepancies between theory and experiment may be more related to a non-adequate assignment of the frequencies caused by a contribution of various cluster sizes to the signal, and to the possible effect of the matrix on the splitting of certain modes. The possible assignment of the experimental frequencies to a non-planar structure is also excluded, based on calculation of the harmonic frequencies.
Table 12 shows the harmonic frequencies of Ag5 and Ag5Ar5 complex, calculated using PBE/GTH. In the latter case, one argon atom is attached to each silver atom, following the orientations shown in Fig. 4. The harmonic frequencies are compared to the experimental values reported by Haslett et al.133 and to theoretical values reported by other authors. Table 12 follows the assignment and criteria given by Haslett et al. for the comparison, i.e. peaks at 100 cm−1 and 105 cm−1 are assumed as corresponding to only one single mode.
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp-mod) with a suggested assignment of the experimental frequencies taking into account a mode at 189 cm−1 originally excluded by the author of the experiment
exp-mod) with a suggested assignment of the experimental frequencies taking into account a mode at 189 cm−1 originally excluded by the author of the experiment
| Ag5 | Ag5 | Ag5Ar5 | Ag5 | ||
|---|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp
133
exp
133
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp-mod
exp-mod
|
PBE/GTH | SCF140 | CCSD(T)140 | |
| 174 | 189 | 180.4 | 181.5 | 189.3 | 186.9 |
| 162 | 174 | 151.4 | 151.4 | 160.9 | 158.2 |
| 136 | 162 | 144.5 | 143.4 | 155.1 | 151.3 |
| 126 | 136 | 118.2 | 118.4 | 122.5 | 124.3 |
| 105 | |||||
| 100 | 105 | 98.1 | 99.1 | 103.2 | 101.7 |
| 80 | 100 | 79.9 | 78.3 | 90.2 | 85.7 |
| 68 | 80 | 72.6 | 71.7 | 75.6 | 74.5 |
| … | |||||
| 19.0 | 19.5 | 19.0 | 23.5 | ||
| 18.4 | 18.1 | 17.0 | 21.9 | ||
| RMSD | 6.7 | 6.5 | 10.6 | 8.4 | |
From the comparison, PBE/GTH shows the smallest RMSD values between theoretical and experimental frequencies. In addition, argon embedding does not significantly change the harmonic frequencies of the bare cluster. Large changes induced by the argon embedding are ∼1 cm−1 but the overall RMSD only changes from 6.7 to 6.5. Therefore, care has to be taken with the assignment proposed by Haslett et al.133 They ignore a band at 189 cm−1 which is believed to correspond to Ag2, but none originating from Ag3 was discarded. They suggest splitting of one mode into 105 cm−1 and 100 cm−1, and splitting of another mode into 126 cm−1 and 136 cm−1, as a consequence of the matrix effect. For the comparison they used the two latter, 126 cm−1 and 136 cm−1, as they were two different modes, but they did not do the same with 105 cm−1 and 100 cm−1.
From the study of gold clusters presented in Section 3 and from the previous silver clusters studied in this section, PBE/GTH is always found to underestimate the harmonic frequencies compared to the experimental frequencies. If it is assumed that this trend should be also valid for Ag5, the band neglected by the authors of the experiment at 189 cm−1 should in fact belong to the vibrational spectrum of Ag5 or to both Ag2 and Ag5. Although this seems to be reasonable, a definitive assignment of the frequencies is more challenging, if the products of the photofragmentation, Ag2 and Ag3, are considered to contribute to the experimental spectrum.
4.6 Discussion on Ag clusters
Table 13 shows for each silver cluster the maximum difference between anharmonic and harmonic frequency as well as the mode for which this occurs. Due to the already mentioned convergence problems on the calculation of the 2D PES for Ag3 and Ag5, we report only diagonal anharmonic frequencies (including 1D PES only) for these two clusters. We have found a small vibrational anharmonicity for Ag2 of about −1.3 cm−1 that agrees with the reported value from experiment. While for the Ag4 anharmonicity is also small, the odd-sized clusters Ag3 and Ag5 shows significant larger anharmonicity. In the same manner as for the gold clusters, anharmonicity is larger for some specific vibrational modes: the only stretching mode for Ag2, the bending mode for Ag3, a breathing mode for Ag4, and an out-of-plane mode for Ag5.| Cluster size | Mode/type |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) − − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) * * |
|
|---|---|---|---|
| Max | RMSD | ||
| 2 | 1/stretching | −1.3 | 1.3 |
| 3 | 3/bending | −4.7 | 2.8 |
| 4 | 1/breathing | −1.5 | 1.0 |
| 5 | 8/out-of-plane | 4.3 | 1.9 |
Similar to gold clusters, the absolute values of the vibrational frequencies are shifted to low values when compared with available experimental reports. Nevertheless the agreement of the computed anharmonicity with the experiment for Ag2 is remarkable. The fact that most experimental studies of Ag clusters declare an interaction of the cluster with argon atoms, implies the necessity of performing the comparison of vibrational frequencies including those effects. At the harmonic level, Ar atoms modify the vibrational frequencies although not as much as krypton atoms do with the Au clusters. For Ag2, one or two Ar atoms increase the harmonic frequency by 0.7 cm−1 and 2.2 cm−1, respectively. For Ag3, the mode 3 (bending mode) is largely affected by 2.6 cm−1 when three Ar atoms are bound. For Ag4, binding two Ar atoms affects largely the mode 4 (bending mode) by 5.8 cm−1. For Ag5, changes in the harmonic frequencies induced by binding five Ar atoms are not larger than 1.0 cm−1 for all modes. Although the changes are less pronounced that for the case of gold atoms with Kr atoms bound,85 the larger changes also occur in the size range n = 1–4. Slightly larger vibrational anharmonicity and smaller effect of noble gas embedding show that the anharmonic effects would be more significant for silver than for gold clusters. Since various DFT approaches predict 3D structures for Ag clusters from Ag6, it is remarkable that for Ag5 the larger anharmonicity occurs for a out-of-plane mode. Similar to gold clusters, the larger anharmonicity in out-of-plane modes could be an indicator of a close transition from 2D to 3D clusters.
5 Conclusions
In this study, we have shown a method to compute anharmonic frequencies in small gold and silver clusters, supported by the use of a plane-wave-based DFT approach with an efficient pseudopotential to calculate potential energy surfaces. While maintaining a good accuracy, our methodology is based on a Fast-VSCF scheme that allows us to reduce the computing time tremendously. Even if a semi-empirical model is not accurate enough to reproduce all properties of these clusters, we have used the Voter–Chen version of the embedded-atom model satisfactorily in order to pre-scan the 2D PES. We have previously assessed this empirical potential and found it suitable to predict the relevant couplings of the 2D PES. We are aware of larger systems being studied with similar methods but considering complete PES and in some cases including higher order coupling interactions. Nevertheless, as the time required for the computation of the 2D PES increases with the number of atoms, we considered convenient to use a reduced-coupling method in order to provide a systematic way of keeping computational cost down as much as the cluster size increases. In this way, we got to reduce the estimated time to calculate all the 2D PES of the Au clusters by ∼89%.In general, our methodology to calculate the anharmonic frequencies shows a great performance and could in principle be extended to larger systems. Nevertheless, problems in convergence during the calculation of 2D-PES for Ag3 and Ag5 make us aware about the possible consequences of neglecting multi-reference effects in DFT. This could be an issue affecting the performance or the accuracy of the method, in particular for the case of open-shell structures. Although it has been shown that some multi-reference effects can be covered by DFT, determining in what extent DFT itself or the quality of the pseudopotential basis set used here are responsible for these convergence problems is out of the scope of this study.
Modeling 1D PES for some interesting normal modes using analytical expressions allowed us to distinguish different types of anharmonicity. It shows that a positive anharmonicity (ν0 < ωe) can be well represented by the Morse potentials. A negative anharmonicity (ν0 > ωe) instead requires the use of the pure quartic or the modified quartic potential, depending on how symmetric the potential energy curve is. Here ν0 denotes the anharmonic frequency and ωe the harmonic frequency as computed from the models. Note that this convention for the sign of anharmonicity applies for the single normal modes only. Considering vibrational pair couplings can eventually change the sign of the anharmonicity, as seen for mode 1 of Au3.
In general, PBE/VDB and PBE/GTH yield underestimated harmonic frequencies of Au and Ag clusters in comparison to the experimental values. Although this is a known feature of current DFT functionals, PBE with the plane-wave basis sets chosen provides well behaved relative values that account for an accurate magnitude of the anharmonicity, in those cases in which experimental values of the anharmonicity are available such as for the dimers. Even if gold clusters do not show large overall anharmonicity (maximum RMSD of 1 cm−1), some specific vibrational transitions are slightly more anharmonic (∼2–3 cm−1). The Au7 and Au8 clusters are the ones which show less anharmonicity.
Although a larger anharmonicity for Ag clusters is expected than for Au clusters, the differences are too small. For both silver and gold dimers, the anharmonicity is negative but slightly larger for Ag2 with respect to the one of Au2 (by ∼0.3 cm−1 using PBE/VDB) which is in agreement with experimental results. The diagonal frequencies of Au3 and Ag3 show similar anharmonicity for the symmetric and antisymmetric modes, but for the bending mode, anharmonicity of Ag3 is almost three times the one for Au3, also with opposite sign. However, it cannot be said that this difference is translated to the more accurate VSCF/VCI frequencies since for Ag3 these were not calculated due to the complex 2D PES of this cluster. For the tetramer, overall anharmonicity is similar for silver and gold (∼1 cm−1). The larger anharmonicity occurs for the breathing mode but with opposite sign than for gold. For the pentamer, the differences between diagonal and harmonic frequencies are larger for both silver than for gold clusters, in particular for the low frequency modes. Since it was not possible to obtain a converged 2D PES for Ag5, a comparison at the VSCF/VCI level for the pentamers is not possible.
For Ag2 and Ag3 the effect of anharmonicity is lower than the effect of the Ar embedding. This is also valid for Au2 and Au3 under Kr embedding as we showed in a previous study. Nevertheless, for Ag4 and Ag5 the effect of Ar embedding is rather small so that anharmonicity plays comparatively a more significant role. Anharmonicity is often invoked to explain the vibrational spectrum of the silver trimer. This is due to the shortcomings of the theoretical models used to interpret the ambiguous experimental results obtained using different techniques for this cluster. The suggestion given by Hartmann et al.48 that anharmonicity may affect more the antisymmetric mode of the silver trimer is contradicted by the results obtained here that show the bending mode being more affected by vibrational anharmonicity. A difficulty in assigning frequencies to the experimental spectra of certain silver clusters is that they are affected by the signal of smaller clusters which are product of photofragmentation. This phenomenon has been observed for Ag3 and Ag5. We also concluded that the assignment of frequencies given to the spectrum of Ag5 by Haslett et al.133 is not adequate since they ignore the largest frequency band. This is based on the presumed effect of a spurious signal originating from the silver dimer. Nevertheless, it is only possible for the experimental frequencies to be in agreement with the trends of the theoretical frequencies calculated here if we include this band.
Acknowledgements
This work was supported by a grant (SFB-569/TP-N1) from the German Science Foundation (DFG) through the Special Research Unit “Hierarchical Structure Formation and Function of Organic–Inorganic Nanosystems”.References
- P. Schwerdtfeger, Gold goes nano: from small clusters to low-dimensional assemblies, Angew. Chem., Int. Ed., 2003, 42, 1892–1895 CrossRef CAS PubMed
.
- P. Pyykkö, Theoretical chemistry of gold, Angew. Chem., Int. Ed., 2004, 43, 4412–4456 CrossRef PubMed
.
- P. Pyykkö, Theoretical chemistry of gold. II, Inorg. Chim. Acta, 2005, 358, 4113–4130 CrossRef
.
- M. Haruta, Size- and support-dependency in the catalysis of gold, Catal. Today, 1997, 36, 153–166 CrossRef CAS
.
- N. T. Wilson and R. L. Johnston, Modelling gold clusters with an empirical many-body potential, Eur. Phys. J. D, 2000, 12, 161–169 CrossRef CAS
.
- K. Michaelian, N. Rendon and I. L. Garzon, Structure and energetics of Ni, Ag and Au nanoclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2000–2010 CrossRef CAS
.
- I. L. Garzon, K. Michaelian, M. R. Beltran, A. Posada-Amarillas, P. Ordejon, E. Artacho, D. Sanchez-Portal and J. M. Soler, Lowest energy structures of gold nanoclusters, Phys. Rev. Lett., 1998, 81, 1600–1603 CrossRef CAS
.
- C. Rey, L. J. Gallego, J. Garcia-Rodeja, J. A. Alonso and M. P. Iniguez, Molecular-dynamics study of the binding energy and melting of transition-metals clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 8253–8262 CrossRef CAS
.
- B. Soule, M. Ford and M. Cortie, Low energy structures of gold nanoclusters in the size range 3–38 atoms, THEOCHEM, 2004, 686, 193–205 CrossRef
.
- E. M. Fernandez, J. M. Soler, I. L. Garzon and L. C. Balbas, Trends in the structure and bonding of noble metal clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 165403 CrossRef
.
- V. Bonacic-Koutecky, J. Burda, R. Mitric, M. Ge, G. Zampella and P. Fantucci, Density functional study of structural and electronic properties of bimetallic silver–gold clusters: comparison with pure gold and silver clusters, J. Chem. Phys., 2002, 117, 3120–3131 CrossRef CAS
.
- H. Häkkinen and U. Landman, Gold clusters (AuN, 2 ≤ N ≤ 10) and their anions, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R2287–R2290 CrossRef
.
- H. Grönbeck and P. Broqvist, Comparison of the bonding in Au8 and Cu8: a density functional theory study, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 073408 CrossRef
.
- J. C. Idrobo, W. Walkosz, S. F. Yip, S. Ögüt, J. Wang and J. Jellinek, Static polarizabilities and optical absorption spectra of gold clusters (Aun, n = 2–14 and 20) from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 205422 CrossRef
.
- P. Koskinen, H. Häkkinen, G. Seifert, S. Sanna, T. Frauenheim and M. Moseler, Density-functional based tight-binding study of small gold clusters, New J. Phys., 2006, 8, 1–11 CrossRef
.
- R. Wesendrup, T. Hunt and P. Schwerdtfeger, Relativistic coupled cluster calculations for neutral and singly charged Au3 clusters, J. Chem. Phys., 2000, 112, 9356–9362 CrossRef CAS
.
- G. Bravo-Perez, I. L. Garzon and O. Novaro, An initio study of small gold clusters, THEOCHEM, 1999, 493, 225–231 CrossRef CAS
.
- G. Bravo-Perez, I. L. Garzon and O. Novaro, Non-additive effects in small gold clusters, Chem. Phys. Lett., 1999, 313, 655–664 CrossRef CAS
.
- B. A. Hess and U. Kaldor, Relativistic all-electron coupled-cluster calculations on Au2 in the framework of the Douglas–Kroll transformation, J. Chem. Phys., 2000, 112, 1809–1813 CrossRef CAS
.
- A. Hermann, R. P. Krawczyk, M. Lein, P. Schwerdtfeger, I. P. Hamilton and J. J. P. Stewart, Convergence of the many-body expansion of interaction potentials: from van der Waals to covalent and metallic systems, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 013202 CrossRef
.
- C. W. Bauschlicher, S. R. Langhoff and H. Patridge, Theoretical study of the structures and electron affinities of the dimers and trimers of the group IB metals (Cu, Ag, and Au), J. Chem. Phys., 1989, 91, 2412–2419 CrossRef CAS
.
- C. W. Bauschlicher, S. R. Langhoff and H. Patridge, Theoretical study of the homonuclear tetramers and pentamers of the group IB metals (Cu, Ag, and Au), J. Chem. Phys., 1990, 93, 8133–8137 CrossRef CAS
.
- K. Das and K. Balasubramanian, Spectroscopic properties of low-lying electronic states of Au2, J. Mol. Spectrosc., 1990, 140, 280–294 CrossRef CAS
.
- K. Balasubramanian and K. Das, Excited electronic states of Au3, Chem. Phys. Lett., 1991, 186, 577–582 CrossRef CAS
.
- K. Balasubramanian, P. Y. Feng and M. Z. Liao, Geometries and energy separations of 14 electronic states of Au4, J. Chem. Phys., 1989, 91, 3561–3570 CrossRef CAS
.
- D. Liao and K. Balasubramanian, Electronic structure of Cu6, Ag6, Au6 and their positive ions, J. Chem. Phys., 1992, 97, 2548–2552 CrossRef CAS
.
- S. A. Serapian, M. J. Bearpark and F. Bresme, The shape of Au8: gold leaf or gold nugget?, Nanoscale, 2013, 5, 6445–6457 RSC
.
- K. R. Geethalakshmi, F. Ruiperez, S. Knecht, J. M. Ugalde, M. D. Morse and I. Infante, An interpretation of the absorption and emission spectra of the gold dimer using modern theoretical tools, Phys. Chem. Chem. Phys., 2012, 14, 8732–8741 RSC
.
- S. Gilb, P. Weis, F. Furche, R. Ahlrichs and M. M. Kappes, Structures of small gold cluster cations (Aun+, n < 14): ion mobility measurements versus density functional calculations, J. Chem. Phys., 2002, 116, 4094–4101 CrossRef CAS
.
- F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, The structures of small gold cluster anions as determined by a combination of ion mobility measurements and density functional calculations, J. Chem. Phys., 2002, 117, 6982–6990 CrossRef CAS
.
- A. Lechtken, D. Schooss, J. R. Stairs, M. N. Blom, F. Furche, N. Morgner, O. Kostko, B. von Issendorff and M. M. Kappes, Au34−: a chiral gold cluster?, Angew. Chem., Int. Ed., 2007, 46, 2944–2948 CrossRef CAS PubMed
.
- M. P. Johansson, A. Lechtken, D. Schooss, M. M. Kappes and F. Furche, 2D–3D transition of gold cluster anions resolved, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 053202 CrossRef
.
- X.-G. Xiong, W.-H. Xu, J. Li and P. Pyykkö, Aspects of bonding in small gold clusters, Int. J. Mass Spectrom., 2013, 354–355, 15–18 CrossRef CAS
.
- E. C. Beret, L. M. Ghiringhelli and M. Scheffler, Free gold clusters: beyond the static, monostructure description, Faraday Discuss., 2011, 152, 153–167 RSC
.
- J. A. Hansen, P. Piecuch and B. G. Levine, Communication: determining the lowest-energy isomer of Au8: 2D, or not 2D, J. Chem. Phys., 2013, 139, 191101 CrossRef PubMed
.
- Z. Liu, Z. Qin, H. Xie, R. Cong, X. Wu and Z. Tang, Structure of Au40/−1 in the gas phase: a joint geometry relaxed ab initio calculations and vibrationally resolved photoelectron imaging investigation, J. Chem. Phys., 2013, 139, 094306 CrossRef PubMed
.
- M. P. Johansson, I. Warnke, A. Le and F. Furche, At what size do neutral gold clusters turn three-dimensional?, J. Phys. Chem. C, 2014, 118, 29370–29377 CAS
.
- J. Xian, S. Baroni and P. Umari, Approximate treatment of semicore states in GW calculations with application to Au clusters, J. Chem. Phys., 2014, 140, 124101 CrossRef PubMed
.
- E. Fabiano, L. A. Constantin and F. D. Sala, Exchange–correlation generalized gradient approximation for gold nanostructures, J. Chem. Phys., 2011, 134, 194112 CrossRef CAS PubMed
.
- A. Fielicke, I. Rabin and G. Meijer, Far-infrared spectroscopy of small neutral silver clusters, J. Phys. Chem. A, 2006, 110, 8060–8063 CrossRef CAS PubMed
.
- J. R. Lombardi and B. Davis, Periodic properties of force constants of small transition-metal and lanthanide clusters, Chem. Rev., 2002, 102, 2431–2460 CrossRef CAS PubMed
.
- R. Santamaria, I. G. Kaplan and O. Novaro, A comparative theoretical study of stable geometries and energetic properties of small silver clusters, Chem. Phys. Lett., 1994, 218, 395–400 CrossRef CAS
.
- I. G. Kaplan, R. Santamaria and O. Novaro, Non-additive forces in atomic clusters. The case of Agn, Mol. Phys., 1995, 84, 105–114 CrossRef CAS
.
- R. Poteau, J. L. Heully and F. Spiegelmann, Structure, stability, and vibrational properties of small silver clusters, Z. Phys. D: At., Mol. Clusters, 1997, 40, 479–482 CrossRef CAS
.
- R. Fournier, Theoretical study of the structure of silver clusters, J. Chem. Phys., 2001, 115, 2165–2177 CrossRef CAS
.
- S. Zhao, Z.-H. Li, W.-N. Wang, Z.-P. Liu, K.-N. Fan, Y. Xie and H. F. Schaefer, Is the uniform electron gas limit important for small Ag clusters? assessment of different density functionals for Agn (n ≤ 4), J. Chem. Phys., 2006, 124, 184102 CrossRef PubMed
.
- M. N. Huda and A. K. Ray, A correlation study of small silver clusters, Eur. Phys. J. D, 2003, 22, 217–227 CrossRef CAS
.
- M. Hartmann, J. Pittner, V. Bonacic-Koutecky, A. Heidenreich and J. Jortner, Theoretical exploration of femtosecond multi-state nuclear dynamics of small clusters, J. Chem. Phys., 1998, 108, 3096–3113 CrossRef CAS
.
- M. Hartmann, R. Mitric, B. Stanca and V. Bonacic-Koutecky, Theoretical investigation of the ultrafast NeNePo spectroscopy of Au4 and Ag4 clusters, Eur. Phys. J. D, 2001, 16, 151–155 CrossRef CAS
.
- C. P. Joshi, M. S. Bootharaju and O. M. Bakr, Tuning properties in silver clusters, J. Phys. Chem. Lett., 2015, 6, 3023–3035 CrossRef CAS PubMed
.
- I. Chakraborty, J. Erusappan, A. Govindarajan, K. S. Sugi, T. Udayabhaskararao, A. Ghosh and T. Pradeep, Emergence of metallicity in silver clusters in the 150 atom regime: a study of differently sized silver clusters, Nanoscale, 2014, 6, 8024–8031 RSC
.
- S. M. Copp, D. E. Schultz, S. Swasey and E. G. Gwinn, Atomically precise arrays of fluorescent silver clusters: a modular approach for metal cluster photonics on DNA nanostructures, ACS Nano, 2015, 9, 2303–2310 CrossRef CAS PubMed
.
-
I. Diez and R. H. Ras, in Advanced Fluorescence Reporters in Chemistry and Biology II, ed. A. P. Demchenko, Springer Series on Fluorescence, Springer, Berlin, Heidelberg, 2010, vol. 9, pp. 307–332 Search PubMed
.
- S. Bellucci, I. Bolesta, I. Karbovnyk, I. Kolych, S. Martyniv and S. Velgosh, Influence of silver clusters on the light absorption in CdBr2-Ag crystals, J. Nanophotonics, 2010, 4, 049503 CrossRef
.
- S. Klacar, A. Hellman, I. Panas and H. Grönbeck, Oxidation of small silver clusters: a density functional theory study, J. Phys. Chem. C, 2010, 114, 12610–12617 CAS
.
- N. T. Cuong, H. M. T. Nguyen and M. T. Nguyen, Theoretical modeling of optical properties of Ag8 and Ag14 silver clusters embedded in an LTA sodalite zeolite cavity, Phys. Chem. Chem. Phys., 2013, 15, 15404–15415 RSC
.
- S. Heiles, A. J. Logsdail, R. Schafer and R. L. Johnston, Dopant-induced 2D-3D transition in small Au-containing clusters: DFT-global optimisation of 8-atom Au-Ag nanoalloys, Nanoscale, 2012, 4, 1109–1115 RSC
.
- G. Barcaro, M. Broyer, N. Durante, A. Fortunelli and M. Stener, Alloying effects on the optical properties of Ag–Au nanoclusters from TDDFT calculations, J. Phys. Chem. C, 2011, 115, 24085–24091 CAS
.
- A. Shayeghi, R. Schäfer, D. M. Rayner, R. L. Johnston and A. Fielicke, Charge-induced dipole vs. relativistically enhanced covalent interactions in Ar-tagged Au–Ag tetramers and pentamers, J. Chem. Phys., 2015, 143, 024310 CrossRef CAS PubMed
.
-
CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, 72nd edn, 1991–1992 Search PubMed
.
- M. Morse, Clusters of transition-metal atoms, Chem. Rev., 1986, 86, 1049–1109 CrossRef CAS
.
- L. S. Norris, M. A. Ratner, A. E. Roitberg and R. B. Gerber, Møller–Plesset perturbation theory applied to vibrational problems, J. Chem. Phys., 1996, 105, 11261–11267 CrossRef CAS
.
- G. M. Chaban, J. O. Jung and R. B. Gerber,
Ab initio calculation of anharmonic vibrational states of polyatomic systems: electronic structure combined with vibrational self-consistent field, J. Chem. Phys., 1999, 111, 1823–1829 CrossRef CAS
.
- O. Christiansen, Vibrational structure theory: new vibrational wave function methods for calculation of anharmonic vibrational energies and vibrational contributions to molecular properties, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953 RSC
.
- O. Christiansen, Response theory for vibrational wave functions, J. Chem. Phys., 2005, 122, 194105 CrossRef PubMed
.
- T. Hrenar, H.-J. Werner and G. Rauhut, Accurate calculation of anharmonic vibrational frequencies of medium sized molecules using local coupled cluster methods, J. Chem. Phys., 2007, 126, 134108 CrossRef PubMed
.
- T. Hrenar, G. Rauhut and H.-J. Werner, Impact of local and density fitting approximations on harmonic vibrational frequencies, J. Phys. Chem. A, 2006, 110, 2060–2064 CrossRef CAS PubMed
.
-
G. D. Carney, L. L. Sprandel and C. W. Kern, Variational approaches to vibration–rotation spectroscopy for polyatomic molecules, John Wiley & Sons, Inc., 2007, ch. 6, vol. 37, pp. 305–379 Search PubMed
.
- J. M. Bowman, K. Christoffel and F. Tobin, Application of SCF-SI theory to vibrational motion in polyatomic molecules, J. Phys. Chem., 1979, 83, 905–912 CrossRef CAS
.
- J. M. Bowman, The self-consistent-field approach to polyatomic vibrations, Acc. Chem. Res., 1986, 19, 202–208 CrossRef CAS
.
- J. M. Bowman, Self-consistent field energies and wavefunctions for coupled oscillators, J. Chem. Phys., 1978, 68, 608–610 CrossRef CAS
.
- K. M. Christoffel and J. M. Bowman, Investigation of self-consistent field, SCF CI and virtual state configuration interaction vibrational energies for a model three-mode system, Chem. Phys. Lett., 1982, 85, 220–224 CrossRef CAS
.
- S. Carter, J. M. Bowman and N. C. Handy, Extensions and test of multimode: a code to obtain accurate vibration/rotation energies of many-mode molecules, Theor. Chem. Acc., 1998, 100, 191–198 CrossRef CAS
.
- O. Christiansen, Møller–Plesset perturbation theory for vibrational wave functions, J. Chem. Phys., 2003, 119, 5773–5781 CrossRef CAS
.
- V. Barone, Anharmonic vibrational properties by a fully automated second-order perturbative approach, J. Chem. Phys., 2005, 122, 014108 CrossRef PubMed
.
- O. Christiansen, Vibrational coupled cluster theory, J. Chem. Phys., 2004, 120, 2149–2159 CrossRef CAS PubMed
.
- G. Rauhut, Efficient calculation of potential energy surfaces for the generation of vibrational wave functions, J. Chem. Phys., 2004, 121, 9313–9322 CrossRef CAS PubMed
.
- N. J. Wright and R. B. Gerber, Direct calculation of anharmonic vibrational states of polyatomic molecules using potential energy surfaces calculated from density functional theory, J. Chem. Phys., 2000, 112, 2598–2604 CrossRef CAS
.
- D. M. Benoit, Fast vibrational self-consistent field calculations through a reduced mode–mode coupling, J. Chem. Phys., 2004, 120, 562–573 CrossRef CAS PubMed
.
- D. M. Benoit, Efficient correlation-corrected vibrational self-consistent field computation of OH-strech frequencies using a low-scaling algorithm, J. Chem. Phys., 2006, 125, 244110 CrossRef PubMed
.
- Y. Scribano and D. M. Benoit, Calculation of vibrational frequencies through a variational reduced-coupling approach, J. Chem. Phys., 2007, 127, 164118 CrossRef PubMed
.
- D. Oschetzki and G. Rauhut, Pushing
the limits in accurate vibrational structure calculations: anharmonic frequencies of lithium fluoride clusters (LiF)n, n = 2–10, Phys. Chem. Chem. Phys., 2014, 16, 16426–16435 RSC
.
- D. M. Benoit, B. Madebene, I. Ulusoy, L. A. Mancera, Y. Scribano and S. Chulkov, Towards a scalable and accurate quantum approach for describing vibrations of molecule–metal interfaces, Beilstein J. Nanotechnol., 2011, 2, 427–447 CrossRef CAS PubMed
.
- L. A. Mancera and D. M. Benoit, Towards an understanding of the vibrational spectrum of the neutral Au7 cluster, Phys. Chem. Chem. Phys., 2013, 15, 1929–1943 RSC
.
- L. A. Mancera and D. M. Benoit, The nature and role of the gold–krypton interactions in small neutral gold clusters, J. Phys. Chem. A, 2015, 119, 3075–3088 CrossRef CAS PubMed
.
- L. A. Mancera and D. M. Benoit, An alternative methodology to assess the quality of empirical potentials for small gold clusters, Comput. Theor. Chem., 2015, 1067, 24–32 CrossRef CAS
.
- J. Wang, A. D. Becke and V. H. Smith, Evaluation of 〈S2〉 in restricted, unrestricted Hartree–Fock, and density functional based theories, J. Chem. Phys., 1995, 102, 3477–3480 CrossRef CAS
.
-
CPMD Code, version 3.11.1., IBM Corp. and MPI Stuttgart, 2005, Car–Parrinello Molecular Dynamics Search PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef
.
- A. P. Scott and L. Radom, Harmonic vibrational frequencies: an evaluation of Hartree–Fock, Moller–Plesset, quadratic configuration interaction, density functional theory, and semiempirical scale factors, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS
.
- J. P. Merrick, D. Moran and L. Radom, An evaluation of harmonic vibrational frequency scale factors, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS PubMed
.
- G. Rauhut and P. Pulay, Transferable scaling factors for density functional derived vibrational force fields, J. Phys. Chem., 1995, 99, 3093–3100 CrossRef CAS
.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS
.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS
.
- M. Krack, Pseudopotentials for H to Kr optimized for gradient-corrected exchange–correlation functionals, Theor. Chem. Acc., 2005, 114, 145–152 CrossRef CAS
.
-
D. M. Benoit, I. Respondek, B. Madebene, Y. Scribano and D. M. Lauvergnat, PVSCF Code, latest version, 2009 Search PubMed
.
- L. M. Ghiringhelli, P. Gruene, J. T. Lyon, D. M. Rayner, G. Meijer, A. Fielicke and M. Scheffler, Not so loosely bound rare gas atoms: finite-temperature vibrational fingerprints of neutral gold–cluster complexes, New J. Phys., 2013, 15, 083003 CrossRef
.
- C. C. Marston and G. G. Balint-Kurti, The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions, J. Chem. Phys., 1989, 91, 3571–3576 CrossRef CAS
.
- G. G. Balint-Kurti, C. L. Ward and C. C. Marston, Two computer programs for solving the Schrödinger equation for bound-state eigenvalues and eigenfunctions using the Fourier grid Hamiltonian method, Comput. Phys. Commun., 1991, 67, 285–292 CrossRef CAS
.
- J. K. Watson, Simplification of the molecular vibration-rotation hamiltonian, Mol. Phys., 1968, 15, 479–490 CrossRef CAS
.
- E. R. Davidson, The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices, J. Comput. Phys., 1975, 17, 87–94 CrossRef
.
- E. R. Davidson, Super-matrix methods, Comput. Phys. Commun., 1989, 53, 49–60 CrossRef
.
- C. W. Murray, S. C. Racine and E. R. Davidson, Improved algorithms for the lowest few
eigenvalues and associated eigenvectors of large matrices, J. Comput. Phys., 1992, 103, 382–389 CrossRef
.
- S. K. Gregurick, G. M. Chaban and R. B. Gerber, Ab Initio and improved empirical potentials for the calculation of the anharmonic vibrational states and intramolecular mode coupling of N-Methylacetamide, J. Phys. Chem. A, 2002, 106, 8696–8707 CrossRef CAS
.
- H. Akima, Algorithm 760: rectangular-grid-data surface fitting that has the accuracy of a bicubic polynomial, ACM Trans. Math. Software, 1996, 22, 357–361 CrossRef
.
-
A. F. Voter, Embedded atom method potentials for seven FCC metals: Ni, Pd, Pt, Cu, Ag, Au, and Al, 1993, unclassified Search PubMed
.
- A. F. Voter and S. P. Chen, Accurate interatomic potentials for Ni, Al and Ni3Al, Mater. Res. Soc. Symp. Proc., 1987, 82, 175–180 CrossRef CAS
.
-
A. F. Voter, Intermetallic Compounds, Wiley, 1994, ch. 4, vol. 1, the embedded-atom method Search PubMed
.
- I. Respondek and D. M. Benoit, Fast degenerate correlation-corrected vibrational self-consistent field calculations of the vibrational spectrum of 4-mercaptopyridine, J. Chem. Phys., 2009, 131, 054109 CrossRef PubMed
.
- J. L. Dunham, The energy levels of a rotating vibrator, Phys. Rev., 1932, 41, 721–731 CrossRef CAS
.
- P. M. Morse, Diatomic molecules according to the wave mechanics. II. Vibrational levels, Phys. Rev., 1929, 34, 57–64 CrossRef CAS
.
- A. Pathak and S. Mandal, Classical and quantum oscillators of quartic anharmonicities: second order solution, Phys. Lett. A, 2001, 286, 261–276 CrossRef CAS
.
-
C. Cohen-Tannoudji, B. Diu and F. Laloe, Quantum Mechanics, Wiley, 2nd edn, 2005 Search PubMed
.
-
J. L. Powell and B. Crasemann, Quantum Mechanics, Adisson-Wesley Publishing, 1965 Search PubMed
.
- L. Skala, J. Dvorak and V. Kapsa, Analytic solutions of the Schrödinger equation for the modified quartic oscillator, Int. J. Theor. Phys., 1997, 36, 2953–2961 CrossRef
.
- J. L. Chen, L. C. Kwek and C. H. Oh, Quartic anharmonic oscillator and non-Hermicity, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 012101 CrossRef
.
- E. Z. Liverts, V. B. Mandelzweig and F. Tabakin, Analytic calculation of energies and wave functions of the quartic and pure quartic oscillators, J. Math. Phys., 2006, 47, 062109 CrossRef
.
- J. Ruamps, Production and study of the optical spectrum of diatomic metallic molecules and contribution to theoretical computation of intensities, Ann. Phys., 1959, 13, 1111–1157 Search PubMed
.
- G. Bishea and M. Morse, Spectroscopic studies of jet-cooled AgAu and Au2, J. Chem. Phys., 1991, 95, 5646–5659 CrossRef CAS
.
- G. A. Bishea and M. D. Morse, Resonant two-photon ionization spectroscopy of jet-cooled Au3, J. Chem. Phys., 1991, 95, 8779–8792 CrossRef CAS
.
- P. Gruene, D. M. Rayner, B. Redlich, A. F. G. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Structures of neutral Au7, Au19 and Au20 clusters in the gas phase, Science, 2008, 321, 674–676 CrossRef CAS PubMed
.
- L. L. Ames and R. F. Barrow, Rotational analysis of bands of the gaseous Au2 molecule, Trans. Faraday Soc., 1967, 63, 39–44 RSC
.
- R. M. Olson, S. Varganov, M. S. Gordon, H. Metiu, S. Chretien, P. Piecuch, K. Kowalski, S. A. Kucharski and M. Musial, Where does the planar-to-nonplanar turnover occur in small gold clusters?, J. Am. Chem. Soc., 2005, 127, 1049–1052 CrossRef CAS PubMed
.
- H. A. Jahn and E. Teller, Stability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235 CrossRef CAS
.
- Y. Shen and J. J. BelBruno, Density functional theory study of the Jahn–Teller effect and spin–orbit coupling for copper and gold trimers, J. Phys. Chem. A, 2005, 109, 512–519 CrossRef CAS PubMed
.
- R. Guo, K. Balasubramanian, X. Wang and L. Andrews, Infrared vibronic absorption spectrum and spin–orbit calculations of the upper spin–orbit
component of the Au3 ground state, J. Chem. Phys., 2002, 117, 1614–1620 CrossRef CAS
.
- D. Cremer, M. Filatov, V. Polo, E. Kraka and S. Shaik, Implicit and explicit coverage of multi-reference effects by density functional theory, Int. J. Mol. Sci., 2002, 3, 604–638 CrossRef CAS
.
- J. Howard, R. Sutcliffe and B. Mile, ESR spectrum of matrix isolated Au3, J. Chem. Soc., Chem. Commun., 1983, 23, 1449–1450 RSC
.
- R. M. Olson and M. S. Gordon, Isomers of Au8, J. Chem. Phys., 2007, 126, 214310 CrossRef PubMed
.
- W. Schulze, H. U. Becker, R. Minkwitz and K. Manzel, Matrix Raman spectra of Ag2 and Ag3, Chem. Phys. Lett., 1978, 55, 59–61 CrossRef CAS
.
- T. L. Haslett, K. A. Bosnick, S. Fedrigo and M. Moskovits, Resonance Raman spectroscopy of matrix-isolated mass-selected Fe3 and Ag3, J. Chem. Phys., 1999, 111, 6456–6461 CrossRef CAS
.
- T. L. Haslett, K. A. Bosnick and M. Moskovits, Ag5 is a planar trapezoidal molecule, J. Chem. Phys., 1998, 108, 3453–3457 CrossRef CAS
.
- K. A. Bosnick, T. L. Haslett, S. Fredigo, M. Moskovits, W.-T. Chan and R. Fournier, Tricapped tetrahedral Ag7: a structural determination by resonance Raman spectroscopy and density functional theory, J. Chem. Phys., 1999, 111, 8867–8870 CrossRef CAS
.
- P. Cheng, K. Willey and M. Duncan, Vibronic spectroscopy of Ag2Ar, Chem. Phys. Lett., 1989, 163, 469–474 CrossRef CAS
.
- B. Simard, P. A. Hackett, A. M. James and P. R. Langridge-Smith, The bond length of silver dimer, Chem. Phys. Lett., 1991, 186, 415–422 CrossRef CAS
.
- V. Srdanov and D. Pesic, Analysis of the E-X and C-X band system isotopically enriched of Ag2, J. Mol. Spectrosc., 1981, 90, 27–32 CrossRef CAS
.
- C. Felix, C. Sieber, W. Harbich, J. Buttet, I. Rabin, W. Schulze and G. Ertl, Fluorescence and excitation spectra of Ag in an argon matrix, Chem. Phys. Lett., 1999, 313, 105–109 CrossRef CAS
.
- H. Hess, K. Asmis, T. Leisner and L. Wöste, Vibrational wave packet dynamics in the silver tetramer probed by NeNePo femtosecond pump–probe spectroscopy, Eur. Phys. J. D, 2001, 16, 145–149 CrossRef CAS
.
- M. Warken and V. Bonacic-Koutecky, Quantum mechanical treatment of stationary and dynamical properties of bound vibrational systems. Application to the relaxation dynamics of Ag5, after an electron photodetachment, Chem. Phys. Lett., 1997, 272, 284–294 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information about the computed vibrational frequencies for all clusters studied. See DOI: 10.1039/c5cp05283a |
| This journal is © the Owner Societies 2016 |