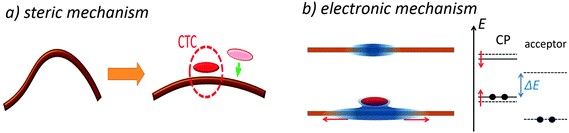Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Threshold-like complexation of conjugated polymers with small molecule acceptors in solution within the neighbor-effect model†
Andrey Yu.
Sosorev
a,
Olga D.
Parashchuk
a,
Sergey A.
Zapunidi
a,
Grigoriy S.
Kashtanov
a,
Ilya V.
Golovnin
a,
Srikanth
Kommanaboyina
b,
Igor F.
Perepichka
b and
Dmitry Yu.
Paraschuk
*a
aFaculty of Physics and International Laser Center, M.V. Lomonosov Moscow State University, Moscow 119991, Russia. E-mail: paraschuk@gmail.com
bSchool of Chemistry, Bangor University, Bangor LL57 2UW, UK
First published on 14th January 2016
Abstract
In some donor–acceptor blends based on conjugated polymers, a pronounced charge-transfer complex (CTC) forms in the electronic ground state. In contrast to small-molecule donor–acceptor blends, the CTC concentration in polymer:acceptor solution can increase with the acceptor content in a threshold-like way. This threshold-like behavior was earlier attributed to the neighbor effect (NE) in the polymer complexation, i.e., next CTCs are preferentially formed near the existing ones; however, the NE origin is unknown. To address the factors affecting the NE, we record the optical absorption data for blends of the most studied conjugated polymers, poly(2-methoxy-5-(2-ethylhexyloxy)-1,4-phenylenevinylene) (MEH-PPV) and poly(3-hexylthiophene) (P3HT), with electron acceptors of fluorene series, 1,8-dinitro-9,10-antraquinone (DNAQ), and 7,7,8,8-tetracyanoquinodimethane (TCNQ) in different solvents, and then analyze the data within the NE model. We have found that the NE depends on the polymer and acceptor molecular skeletons and solvent, while it does not depend on the acceptor electron affinity and polymer concentration. We conclude that the NE operates within a single macromolecule and stems from planarization of the polymer chain involved in the CTC with an acceptor molecule; as a result, the probability of further complexation with the next acceptor molecules at the adjacent repeat units increases. The steric and electronic microscopic mechanisms of NE are discussed.
Introduction
Blends of conjugated polymers (CPs) with small-molecule acceptors are the heart of the state-of-the-art plastic solar cells. In some of the blends, a pronounced charge-transfer complex (CTC) is formed between the polymer donor and the acceptor molecules in the electronic ground state.1–4 The CP CTCs can significantly absorb in the red/near-IR regions1,5,6 and generate mobile charges7,8 making them promising for photovoltaics. As the lowest electronic excited states in the donor–acceptor blends, the excited CTCs (usually called charge-transfer states) are key intermediates on the pathway from excitons to free charges9 even in CP blends with fullerenes where the CTC is very weak.10–12 As a result, the CTCs strongly affect the solar cell performance.13–15 The ground-state donor–acceptor interaction in CTCs can also influence the conformation of the polymer chains,6,16 the phase separation in the blend,3,17 and enhance the photooxidation stability.8,18 All these CTC features could be exploited to improve the performance of organic solar cells.4CTCs in small-molecule donor–acceptor blends have been thoroughly investigated. However, if one of the CTC constituents, e.g. donor, is a CP, its macromolecular nature and electron delocalization over the conjugated segment can significantly affect the CTC formation and properties. Specifically, the CTC concentration in solution of poly(2-methoxy-5-(2-ethylhexyloxy)-1,4-phenylenevinylene), MEH-PPV, and 2,4,7-trinitrofluorenone, TNFon, increases in a clear threshold-like fashion:6 when the acceptor concentration is below a threshold value, the CTC concentration is low; however, when the threshold is exceeded, an intensive CTC formation starts. This is contrasting with the small-molecule blends, where the CTC concentration increases gradually with an acceptor addition, and the plot of the CTC concentration versus the acceptor concentration is convex. To explain the threshold-like CTC formation in MEH-PPV:TNFon blends, the neighbor effect (NE) model was recently proposed.6,19 According to this model, the CTC binding energy increases if two or more acceptor molecules are complexed with the polymer chain nearby each other. Fig. 1 illustrates this NE effect: the binding energy of an isolated (individual) CTC is E0, and it increases by ENE or 2ENE (E0, ENE > 0) if one or both of the neighboring segments are also complexed, respectively. Hence, successive CTCs are preferentially formed near the existing ones, i.e. the CTC formation is a cooperative phenomenon. For MEH-PPV:TNFon blends, it was found that ENE can be comparable to E0 so that the NE can play a key role in the CP complexation.19 The NE should result in the formation of intrachain CTC aggregates that can explain photoluminescence quenching in MEH-PPV:TNFon blends.20 Furthermore, these aggregates seem to be inherited in film allowing explanation of ordered polymer nanodomains in MEH-PPV:TNFon blends.21 Therefore, the NE can lead to blend self-organization. Unraveling the mechanisms of cooperative phenomena and self-organization in polymers is a long-standing challenge in the polymer science; moreover, the cooperative effects in CPs involving their π-conjugated system are practically not studied. Accordingly, the NE in CP complexation is worth detailed investigation. Specifically, it is not known whether the NE is a general feature of CTC formation in CP donor–acceptor blends, or it occurs only in MEH-PPV:TNFon blends. Consequently, the physical factors that drive the NE and its microscopic mechanism should be addressed.
There are several factors that can influence the CTC formation in solution. According to the Mulliken model,22 the CTC binding energy depends on the difference between the donor ionization potential corresponding, in a one-electron model, to the highest occupied molecular orbital (HOMO) energy, and the acceptor electron affinity corresponding to the lowest unoccupied molecular orbital (LUMO) energy. This energy difference is called the “effective HOMO–LUMO gap”.23 The lower the effective HOMO(D)–LUMO(A) gap, the higher the CTC binding energy. As a result, for the same donor and various acceptors, the binding energy should depend on the acceptor electron affinity. The second main factor that determines the CTC binding energy in the Mulliken model is the donor–acceptor electronic coupling, HDA, which in turn depends on the compatibility of the donor and acceptor π-conjugated systems at their molecular skeletons. In addition, since the CTC formation in solution is affected by the donor–solvent and acceptor–solvent interactions, the solvent is also expected to affect the CTC binding energy. Finally, as shown in ref. 24, the CTCs serve as interchain links, and it is not clear whether CTCs can be formed on a single chain. Therefore, the CTC formation could depend on the polymer concentration.
In this work, we address the influence of the effective HOMO–LUMO gap, solvent, polymer concentration, and molecular skeletons of the donor and acceptor on the CTC formation in blends of CPs with small-molecule acceptors. We study CTC optical absorption in blended solutions of MEH-PPV and poly(3-hexylthiophene) (P3HT) with various electron acceptors: acceptors of the fluorene series, 1,5-dinitro-9,10-anthraquinone (DNAQ), and 7,7,8,8-tetracyanoquinodimethane (TCNQ). Then we fit the data by the analytical NE model for CP complexation19 and obtain the isolated CTC binding energy, E0, and the NE energy gain, ENE, as fitting parameters. Finally, we investigate how E0 and ENE are affected by the factors mentioned above and discuss the possible microscopic mechanisms of the NE in CP complexation.
Experimental
Materials
Fig. 2 shows the structural formulae of studied polymer donors and small-molecule electron acceptors used in this study. MEH-PPV (Mw = 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Mn = 420
000, Mn = 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma-Aldrich) and P3HT (regioregular electronic grade, #4002-EE Reike Metals) were used as received. TCNQ was recrystallized twice from acetonitrile. Various fluorene-type electron acceptors have been synthesized and used in this study. These acceptors contain from two to three nitrogroups (NO2 in positions 2,4,7-) in their structure and the carbonyl oxygen atom or the dicyanomethylene group at the C-9 position. In addition, some acceptors contained a –CO2R ester group with long chain solubilizing linear alkyl substituents R = n-C4H9, n-C5H11, n-C7H15 (see the ESI† for the details of their synthesis). These variations in the chemical structure of the acceptors allowed us to vary their electron affinities and solubility. 2,4,7-Trinitrofluorenone (TNFon) and 2,4,7-trinitro-9-dicyanomethylenefluorene (DTNF) were synthesized according to procedures described previously.25
000, Sigma-Aldrich) and P3HT (regioregular electronic grade, #4002-EE Reike Metals) were used as received. TCNQ was recrystallized twice from acetonitrile. Various fluorene-type electron acceptors have been synthesized and used in this study. These acceptors contain from two to three nitrogroups (NO2 in positions 2,4,7-) in their structure and the carbonyl oxygen atom or the dicyanomethylene group at the C-9 position. In addition, some acceptors contained a –CO2R ester group with long chain solubilizing linear alkyl substituents R = n-C4H9, n-C5H11, n-C7H15 (see the ESI† for the details of their synthesis). These variations in the chemical structure of the acceptors allowed us to vary their electron affinities and solubility. 2,4,7-Trinitrofluorenone (TNFon) and 2,4,7-trinitro-9-dicyanomethylenefluorene (DTNF) were synthesized according to procedures described previously.25
Computational procedures
DFT computations of the geometries of studied electron acceptors were carried out with the Gaussian 0926 package of programs by using Pople's 6-31G split valence basis set supplemented by d-polarization functions and diffusion functions for heavy atoms. Becke's three-parameter hybrid exchange functional27,28 with the Lee–Yang–Parr gradient-corrected correlation functional (B3LYP)29 was employed. The restricted Hartree–Fock formalism was used. No constraints were used and all structures were free to optimize in a gas phase or in solutions in various solvents using the polarizable continuum model (PCM).30 Thus, the geometries were optimized at the B3LYP/6-31+G(d) level and the electronic structures were calculated at the same level of theory. The electron affinities (EA) were approximated as the negative of the LUMO energies (EA = −ELUMO) in accordance with DFT-Koopman's theorem.Optical absorption spectroscopy
The donor and acceptor were dissolved separately in solvent [chlorobenzene (CB), o-dichlorobenzene (DCB), toluene (Tol), chloroform (CF) or tetrahydrofuran (THF)] and then mixed. The color of the mixture stabilized within ca. 10–20 seconds, the mixture was kept for at least 3–5 min before measurements. The MEH-PPV concentration in CB was kept constant at 1.00 g l−1 (3.84 mM) except for blends with TNFon where it was either 2.00 g l−1 (7.68 mM) or 0.010 g l−1 (38.4 μM). The P3HT concentration was 5.00 g l−1 (30.1 mM). In solvents effect measurements, the MEH-PPV concentration was kept 2.00 g l−1 (7.68 mM) in CB or 0.50 g l−1 (1.92 mM) in other solvents. Optical absorption spectra of the mixed solutions were recorded using a fiber-coupled spectrophotometer (Avantes) in quartz cuvettes of 0.10 mm path length (for blends with TNFon, HeptCTNFon, BuCDDNF, AmCDTNF and DNAQ) or 10 mm path length (for blends with DTNF and TCNQ, and P3HT:TNFon). The CTC absorption coefficients, αCTC = absorbance/path length [cm], were calculated at 630 nm (for MEH-PPV blends with TNFon, HeptCTNFon, BuCDDNF, AmCDTNF and DNAQ) or at 800 nm (for MEH-PPV blends with DTNF and TCNQ, and P3HT:TNFon blends), measurements at other wavelengths are given in the ESI.†Results
Synthesis of fluorene acceptors
Syntheses of fluorene acceptors – derivatives of nitrofluorene-4-carboxylic acids – are depicted in Scheme 1. Diphenic acid (1) is quantitatively cyclized by concentrated sulfuric acid into fluorenone-4-carboxylic acid (2) at ca. 110–140 °C.31,32 Nitration of the latter by a mixture of fuming nitric and concentrated sulfuric acid results in 2,7-dinitro-(3)33,34 or 2,5,7-trinitro-9-fluorenone-4-carboxylic acids (4).33,35 From this point of view, an isolation of acid 2 is not necessary and we have elaborated high-yield (>70% after purification) one-pot syntheses of acids 3 and 4 directly from compound 1 by directly adding fuming acid to the solution of 2 formed in sulfuric acid (deep-red solution of protonated form of 2 at its carbonyl oxygen) and performing nitration reactions at room temperature (for 3) or at 105–110 °C (for 4) (see the ESI†). Thus obtained acids 3 and 4 were converted into corresponding esters (3 → BuCDNFon; 4 → AmCTNFon, HeptCTNFon) by reaction with thionyl chloride in the presence of a catalytic amount of N,N-dimethylformamide (DMF) followed by esterification of formed acyl chlorides with corresponding alcohols (n-butanol, n-pentanol or n-heptanol, accordingly). Ester BuCDNFon was also obtained by an alternative route: fluorenone-4-carboxylic acid (2) obtained by heating of diphenic acids (1) in sulfuric acid was involved in situ, without isolation, into the next step of esterification by n-butanol to afford n-butyl ester 5. The nitration of the latter by a mixture of fuming nitric acid and concentrated sulfuric acid at room temperature gave ester BuCDNFon in an excellent yield of 84%, without hydrolysis of the ester group. Conversion of fluorenone BuCDNFon into stronger electron acceptor BuCDDNF was done by triethylamine-catalyzed condensation with malononitrile in methanol solution, the method which was initially proposed for condensation of polynitro-9-dicyanomethylenefluorenes.36,37 We also applied for this reaction another, more convenient method of condensation, previously proposed by us, which is based on using DMF as a solvent.25,38–41 This method does not require a basic catalyst that allows performing the reaction under milder conditions, and it normally gives higher yields and better purity of 9-dicyanomethylenefluorenes. The latter method was also used in the synthesis of AmCDTNF from AmCTNFon, and in both cases it gave excellent yields of the products (84–88% after purification).DFT calculations of orbital energies and electron affinities of acceptors
DFT computations have been performed at the B3LYP/6-31+G(d) level of theory for both geometry optimizations and calculations of the electronic structures of all acceptors. The effect of the solvent was incorporated using the polarizable continuum model (PCM) to match the results with spectroscopic measurements in these solvents. Kohn–Sham frontier orbital energies of acceptors together with HOMO–LUMO energy gaps and electron affinities are collated in Table 1 (more details on B3LYP/6-31+G(d) calculations are given in the ESI†). An incorporation of the solvent effect is important for an accurate estimation of acceptor frontier energy levels and electron affinities, as solvation (from a gas phase to highly polar acetonitrile) changes e.g. LUMO energies of acceptors by 0.2–0.5 eV while the actual solvent effect on EA depends on the structure of the acceptor (Fig. S1 and S2 in the ESI†). In this work we used B3LYP/6-31+G(d) calculated EA values for studied electron acceptors, which was recently shown to correlate well (r = 0.97–0.98) with the experimental data on EA estimations from cyclic voltammetry experiments in the same solvent (see Fig. S3 in the ESI†).25| Compound | E HOMO (eV) | E LUMO (eV) | E g (eV) | EAc (eV) |
|---|---|---|---|---|
| a DFT B3LYP/6-31+G(d) calculations in chlorobenzene solution using the PCM model. Calculations for other solvents (and for the gas phase) are given in the ESI, Fig. S1. b E g = EHOMO − ELUMO. c EA = −ELUMO. | ||||
| DNAQ | −8.00 | −3.82 | 4.18 | 3.82 |
| TCNQ | −7.30 | −4.76 | 2.54 | 4.76 |
| TNFon | −7.90 | −4.12 | 3.78 | 4.12 |
| HeptCTNFon | −7.98 | −4.21 | 3.77 | 4.21 |
| BuCDDNF | −7.71 | −4.21 | 3.50 | 4.21 |
| DTNF | −7.94 | −4.42 | 3.52 | 4.42 |
| AmCDTNF | −8.00 | −4.49 | 3.51 | 4.49 |
Charge-transfer complexation of MEH-PPV and P3HT with small-molecule electron acceptors
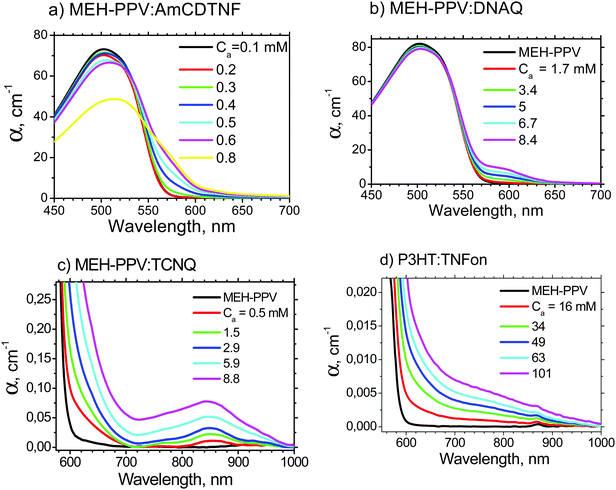
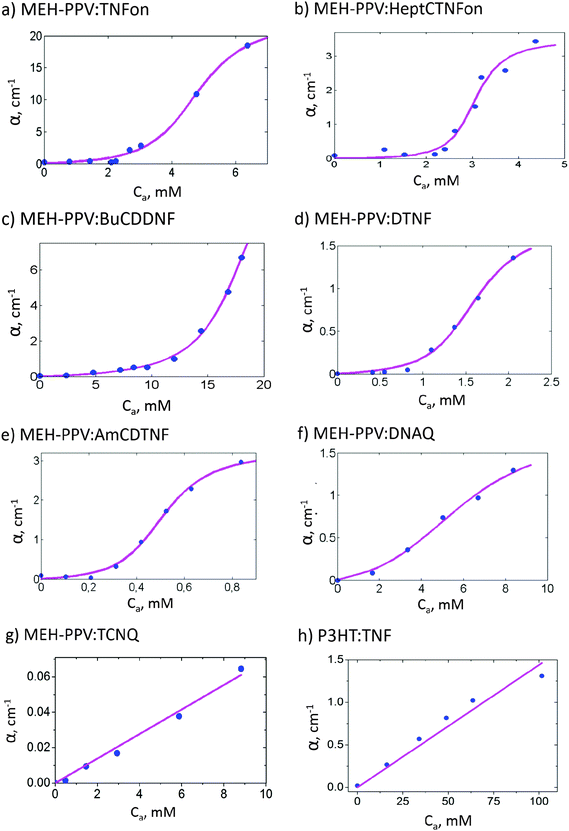
Fig. 3 shows the absorption spectra of MEH-PPV:AmCDTNF (a representative fluorene acceptor), MEH-PPV:DNAQ, MEH-PPV:TCNQ, and P3HT:TNFon blends in chlorobenzene. The spectra of MEH-PPV blends with different fluorene-type acceptors are similar to that of MEH-PPV:AmCDTNF and are shown in the ESI.† Upon acceptor addition, new absorption features in the polymer band gap arise in all the blends, and their intensity is increased with the acceptor content. For MEH-PPV blends with TNFon and DNAQ, this subgap absorption was previously attributed to the CTC.1,4 The MEH-PPV:TCNQ blend shows intragap absorption very similar to that observed in ref. 42 for a slightly different PPV derivative, poly(2-methoxy-5-(3,7-dimethyloctyloxy)-1,4-phenylenevinylene) (MDMO-PPV), and this absorption was attributed to CTC. Note that the absorption spectra for different MEH-PPV blends in Fig. 3 show different shapes indicating that the subgap absorption can hardly be assigned to polymer aggregation (for other acceptors see Fig. S4 in the ESI†). In ref. 42, the subgap absorption in P3HT blends with various acceptors was also attributed to the CTC. We therefore assign the subgap absorption features observed in all the studied blends to the CTC between polymer donors and small-molecule electron acceptors.Fig. 4 presents dependencies of the blend absorption coefficients, α, on the acceptor concentration, Ca, for various MEH-PPV:acceptor (a–g) and P3HT:TNFon (h) blends at selected wavelengths within the polymer bandgap (the data at other wavelengths are given in Fig. S5, ESI†). These absorptions correspond to the polymer–acceptor CTC. All the blends, excluding MEH-PPV:TCNQ and P3HT:TNFon, show similar S-type shapes of α(Ca) dependencies with an inflexion point indicating more or less threshold-type character of polymer complexation. Therefore, we conclude that the threshold-like complexation is not a unique feature of MEH-PPV:TNFon blends. The thresholds in the α(Ca) dependences could originate from the threshold-like behavior of the CTC concentration, molar extinction, and/or stoichiometry. For MEH-PPV:TNFon blends, the CTC extinction and stoichiometry were shown to be independent of the acceptor content, and the threshold in the CTC absorption was attributed to the threshold-like concentration behavior.6 Consequently, we assume that the S-type α(Ca) dependencies in the other MEH-PPV:acceptor blends are also determined mainly by threshold-like behavior of the CTC concentration, CCTC.
While an extension of the Ca range to higher concentrations to reach the saturation of the α(Ca) dependencies in Fig. 4 would be desirable for better fitting the experimental data by the NE model (see below), we are limited by solubility issues. Some acceptors, e.g.DNAQ and TCNQ, have limited solubility in the used solvents. Moreover, at high MEH-PPV and acceptor concentrations, precipitation of the complexed polymer was sometimes observed. This potentially could contribute to the S-shape α(Ca) dependencies. To exclude this possibility, we have performed experiments at a very low MEH-PPV concentration of 0.01 g l−1 (38.4 μM) and have nicely observed full saturation of α(Ca) dependencies at high acceptor concentrations (see Fig. S7 in the ESI† and discussion of the complexation model below).
Below we discuss how different factors affect the CTC formation in CP:acceptor blends.
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 M−1 cm−1) was used. Fig. 6 demonstrates that the 〈N〉(Ca) dependencies for the blends with the substantially different donor concentrations are very close indicating that CTC formation is not sensitive to the polymer concentration and hence to the inter-macromolecular interactions. Therefore, we conclude that the latter do not play a major role in the CP complexation and the polymer complexation operates mainly at individual polymer chains. Notably, the curve shape and the threshold acceptor concentration (Fig. 6) are not affected by the polymer concentration indicating that the threshold-like behavior does not originate from the inter-macromolecular interactions.
700 M−1 cm−1) was used. Fig. 6 demonstrates that the 〈N〉(Ca) dependencies for the blends with the substantially different donor concentrations are very close indicating that CTC formation is not sensitive to the polymer concentration and hence to the inter-macromolecular interactions. Therefore, we conclude that the latter do not play a major role in the CP complexation and the polymer complexation operates mainly at individual polymer chains. Notably, the curve shape and the threshold acceptor concentration (Fig. 6) are not affected by the polymer concentration indicating that the threshold-like behavior does not originate from the inter-macromolecular interactions.
Discussion
Neighbor effect model
To fit the experimental data, we will use the NE model19 briefly outlined in this section. According to the model, the CTC is formed between an acceptor molecule and a polymer segment expanded to several repeat units of the polymer main chain. The binding energy of a CTC is E0 if both the neighboring polymer segments are uncomplexed (Fig. 1). It increases by ENE if one of them is complexed and by 2ENE if both are complexed. Note that, according to the binding energy definition, ENE corresponds to the total energy gain for the whole system if two CTCs are formed nearby, i.e., the effective binding energy per acceptor molecule increases by ENE/2. The model gives a dependence of the average CTC number per chain, 〈N〉, on the acceptor concentration, Ca. Since 〈N〉 is proportional to the CTC concentration in solution (eqn (1)), the model gives the CCTC(Ca) dependence as well. The NE model is analytical and has three fitting parameters: (i) the number of sites available for the CTC formation per chain (L), (ii) the binding energy of an isolated CTC (E0), and (iii) the energy gain for two CTCs formed nearby (ENE). In this work, we use a simplified version of the NE model that neglects a decrease in the acceptor concentration due to its involvement in CTCs; the reasons for this will be specified below. Interestingly, in this simplified NE model, the 〈N〉(Ca) curve shape is determined solely by ENE and does not depend on L or E0 within a reasonable range of the parameters.19 The two remaining model parameters are responsible only for axes scaling: L determines the “y” scale, and the “x” scale is determined by E0 + ENE. Fig. 7 shows the average share of complexed segments 〈N〉/L as a function of the acceptor concentration for different ENE values (the “x” scale is normalized to the acceptor concentration at which the half of the chain is complexed). One can see that the larger the ENE, the steeper the threshold. Therefore, since 〈N〉 is proportional to CCTC, the shape of the experimental CCTC(Ca) curve provides information about the NE strength in terms of ENE. The threshold acceptor concentration Cta that corresponds to the beginning of the CTC concentration increase is defined in the model as shown in Fig. 7. Since the scale of the “x” axis (acceptor concentration) is determined by E0 + ENE, the threshold acceptor concentration is also associated with E0 + ENE. As a result, analysis of the CCTC(Ca) data with the NE model allows us to estimate the isolated CTC binding energy and NE in various CP:acceptor blends.Fitting the data with the NE model
The model described above deals with the CTC concentration as a function of the acceptor concentration, CCTC(Ca). We can obtain CCTC(Ca) from the measured CTC absorption, α: CCTC(Ca) = α(Ca)/ε, where ε is the CTC molar extinction. However, the CTC molar extinction was determined only for one blend, i.e. MEH-PPV:TNFon,6 and it is unknown for the blends of other acceptors studied in this work. Unfortunately, Benesi–Hildebrand and related linear regression methods,41,48,49 used for determination of CTC molar extinction coefficients that are usually applied for small-molecule CTC and the method proposed in ref. 6 for threshold-like α(Ca) are inapplicable. The first methods are inappropriate since α(Ca) in our polymer donor–acceptor mixtures is not described by the standard association constant model.6 The latter method assumes that the ratios between the CTC molar extinction at some wavelength and the polymer molar extinction are the same in solution and in film. However, this assumption is not solid for most of our blends as we found that the film spectra differ significantly from those in solutions (see Fig. S6b in the ESI†). Accordingly, for using the assumption of constant ratio between the CTC and polymer molar extinctions, one needs to separate the polymer and the CTC absorptions in the solution and film spectra. Because this is not an easy task (if possible at all), we considered the CTC molar extinction as an additional fitting parameter and applied the model directly to the experimental α(Ca) dependencies. Doing that, we supposed that the CTC molar extinction for a pair MEH-PPV:acceptor is weakly affected by the number of acceptor molecules (one, two or more) involved in CTC on the same polymer chain. This seems reasonable taking into account that variations in extinctions of low-molecular π–π CTC are not high. Thus, for CTC of various fluorene acceptors with low-molecular donors, e.g. anthracene,41N-ethylcarbazlole,49 or N-propylcarbazole,39 in different solvents (1,2-dichloroethane, dioxane), the molar extinction coefficients vary from 800 to 1900 M−1 cm−1 only, whereas variations in the equilibrium constants is much higher, from 1.07 to 12.1 M−1. In line with this, in MEH-PPV:TNFon blends, the CTC molar extinctions are independent of the CTC concentration.6 For non-complicated molecular complexation of D + A = CTC, an isobestic point is generally observed evidencing only two spectroscopically resolvable species. Isobestic points are also observed for some of our complexes (see Fig. 3a, b and Fig. S4a, b in the ESI†), although not always for full concentration regions. This could be understood taking into account the flexibility of the MEH-PPV backbone and its conformation changes induced by an environment (e.g. by solvent as discussed above, but one would expect the same effect on CTC formation). This would result in an intensity change of the main MEH-PPV absorption band and its bathochromic shift due to planarization of the polymer backbone43–47,50 so that the isobestic point can be smeared. Yet, an observation of relatively clear isobestic points in many cases of MEH-PPV:acceptor complexations allow us to consider that just one type of CTC would be sufficient to analyze the data in the NE model.We use here the simplified NE model (described above) as it is much less sensitive to the CTC concentration and unknown CTC molar extinction. As mentioned above, the shape of the CCTC(Ca) curve and its x-axis scaling are practically independent of the chain length L in the simplified NE model. In other words, the average share of the complexed segments, η(Ca) = 〈N〉/L, is independent of L for its reasonable values and has only two parameters, E0 and ENE. As a result, the CTC concentration and therefore the CTC absorption are nearly linearly proportional to L (eqn (2)):
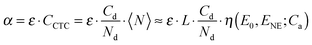 | (2) |
The results of the data fitting are presented in Fig. 4 by solid lines. The model fits well the experimental data providing reasonable estimates for E0 in the range of 2–6 kT and for ENE in the range of 0–4 kT. The E0 values are of the same order as the CTC binding energy in small-molecule donor:acceptor blends.51 Remarkably, in some of the blends, ENE can be close to or even larger than E0, as we have earlier found for MEH-PPV:TNFon blends.19 Therefore, the NE can play a key role in the CTC formation in CP:acceptor blends. On the other hand, for MEH-PPV:TCNQ and P3HT:TNFon blends, the experimental data do not show any S-type features and can be fitted well by a straight line (Fig. 4g and h). Moreover, some degree of negative curvature is observed for P3HT:TNFon blends at high acceptor concentrations (Fig. S5h, ESI†) so that the data can be fitted by common models for low-molecular CTCs. Therefore, assuming that a significant part of the CP chains is complexed (see above), we suggest a negligibly small NE (see Fig. 7) in MEH-PPV:TCNQ and P3HT:TNFon blends.
In the next section, using the results of α(Ca) fitting, we summarize how the isolated-CTC binding energy (E0) and NE extra binding energy (ENE) depend on the acceptor electron affinity, solvent, polymer concentration, and molecular skeletons of the donor and acceptor.
Factors governing the CTC binding energy and the NE
The effect of the acceptor electron affinity on E0 and ENE was investigated in MEH-PPV blends with various fluorene acceptors. Fig. 8a demonstrates the best-fit values for E0versus the acceptor electron affinity, EA. Note that the E0 value (in combination with ENE) relates to the threshold acceptor concentration Cta:19 the higher the E0, the lower the Cta. The observed up to 50-fold difference in Cta corresponds to the variation of E0 by several times (cf.BuCDDNF and AmCDTNF in Fig. 4 and 8a). One can see that E0 has a trend of growth with increasing the acceptor electron affinity (at least for structurally related fluorene acceptors), in accordance with the Mulliken model.22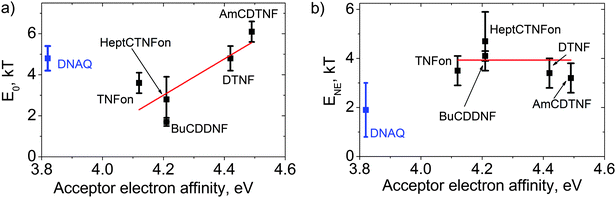 | ||
| Fig. 8 Binding energy of an isolated CTC (a) and NE energy gain (b) obtained from the fits of the absorption data (Fig. 4). The lines are a guide to the eye for the fluorene acceptors. | ||
Fig. 8b presents the calculated ENE values versus the electron affinity of the studied acceptors. Unexpectedly, all MEH-PPV:fluorene acceptor blends show near the same ENE values within the fitting error. This corresponds to a similar α(Ca) shape for these blends (Fig. 4a–e) as the latter is determined solely by ENE in the NE model (see above). Therefore, one can conclude that the NE does not depend on the acceptor electron affinity within the studied range.
As shown above, the α(Ca) dependencies for MEH-PPV:TNFon blends in various solvents differ by both curvature of the S-shaped profiles and threshold acceptor concentration, Ca (Fig. 5). As a result, fitting the data with the NE model gives different E0 and ENE parameters. Fig. 9 shows the best-fit values of E0 (panel a) and ENE (panel b) in different solvents, obtained from the data in Fig. 5, versus the Lippert–Mataga index, Δf. While the regression is weak, the general trend is obvious: the larger the Δf, the lower the binding energy of an isolated CTC (E0), and the higher the NE (ENE).
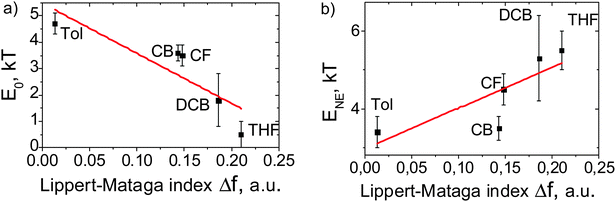 | ||
| Fig. 9 E 0 and ENE values in different solvents obtained from the data in Fig. 5versus Lippert–Mataga index Δf = [(ε − 1)/(2ε + 1) − (n2 − 1)/(2n2 + 1)], where ε is the dielectric permittivity and n is the refraction index. The error bars are given at a confidence level of 80%. The lines are a guide to the eye. | ||
The experimental data in Fig. 6 show that the α(Ca) curves practically coincide for MEH-PPV:TNFon blends with the donor concentration differing by 200 times. As a result, the best-fit parameter values for the blend with the low Cd (E0 = 3.6 ± 0.8 kT, ENE = 3.3 ± 0.8 kT) coincide within the experimental and fitting errors with those for the blend with the high Cd (E0 = 3.6 ± 0.5 kT, ENE = 3.5 ± 0.6 kT). This indicates that the CTC binding energy and the NE do not depend on the polymer concentration and hence on the inter-macromolecular interactions.
For MEH-PPV blends with DNAQ and TCNQ, whose conjugated molecular skeletons considerably differ from the fluorene ones, and P3HT:TNFon blends, in which the donor has a conjugated skeleton different from that of MEH-PPV, the α(Ca) shapes are significantly different from those of the MEH-PPV blends with fluorene acceptors (see Fig. 4). The NE model attributes this to much weaker NE in the former blends (see Fig. 7). For DNAQ, ENE = 1.9 ± 1.1 kT, which is about 1.5 times lower than the average ENE for the MEH-PPV blends with fluorene acceptors. This indicates that the NE is sensitive to the size and the shape of conjugated molecular core of an acceptor. For MEH-PPV:TCNQ and P3HT:TNFon blends, the linear α(Ca) dependencies can be treated as evidence for weak or absent NE in these blends assuming that the majority of polymer conjugated segments is complexed at the maximum acceptor concentration (see above). Therefore, we conclude that the NE is very sensitive to the shape and size of conjugated molecular cores of both the donor and acceptor. The isolated CTC binding energy for the MEH-PPV:DNAQ blend is E0 = 5.0 ± 0.7 kT, which is relatively large as compared to the values for the MEH-PPV:fluorene acceptors, taking into account the lower electron affinity of DNAQ. This underlines that E0 is also sensitive to the structures of the donor and acceptor conjugated molecular cores.
Table 2 summarizes our findings on the CTC energetics in the studied polymer:acceptor blends. Both energies E0 and ENE are insensitive to the polymer concentration indicating that the complexation can operate at a single chain and the NE is an intra-macromolecular effect. While the isolated CTC binding energy E0 depends on the solvent quality, acceptor electron affinity, and molecular skeletons of the donor–acceptor pair, only two of the investigated factors, namely the type of donor and acceptor conjugated molecular skeletons and the solvent, determine the NE energy gain in CP complexation, ENE. In the next section, we rationalize and discuss a possible microscopic mechanism that could be responsible for the NE.
| Factor | Sensitivity of the NE model parameters | |
|---|---|---|
| E 0 | E NE | |
| Polymer concentration | No | No |
| Solvent | Yes | Yes |
| Electron affinity | Yes | No |
| Conjugated molecular skeleton | Yes | Yes |
Microscopic picture of the neighbor effect
The current NE model is one-dimensional (1D) and does not take into account directly any 3D effects as, e.g., changes in the conformational state of the polymer and its aggregation, which can affect the CTC formation and seem to be essential in CP CTCs. Nevertheless, the NE model can be a starting point to analyze the microscopic mechanism underlying the CTC formation in CPs. We suggest that the NE stems from chain planarization upon CTC formation. While only a few repeat units of the polymer can directly contact a short acceptor molecule in a CTC (via overlapping of the polymer and acceptor orbitals), the electronic and conformational state of the rest of the conjugated segment (ca. 5–7 units in MEH-PPV7,52,53) is also affected by complexation.16,54 Specifically, using Raman spectroscopy, the CTC formation was shown to increase the chain planarity and torsional rigidity16,55 that can be explained by more quinoid character of the complexed polymer chain, which is stiffer and more planar. The NE can then be attributed to the two mechanisms: steric and/or electronic. First, the complexed polymer segment is more planar and therefore sterically more favorable for the subsequent CTC formation with a planar acceptor as illustrated in Fig. 10a (steric mechanism). Indeed, the planarized chain can provide larger orbital overlapping with the π-electron conjugated orbitals of the planar acceptor increasing the electronic coupling between the donor HOMO and acceptor LUMO, HDA, and hence the CTC binding energy. In addition, because of more quinoid character, the effective conjugation length of the complexed chain is less limited by the thermally activated torsional deformations,55 and hence it is longer than that of the free (uncomplexed) chain. Fig. 10b (left) illustrates an increase of the effective conjugation length of a CP after CTC formation with an acceptor molecule. The increased conjugation length results in a higher/lower local HOMO/LUMO level as illustrated in Fig. 10b (right). Note that the increase in the HOMO energy due to planarization can overwhelm its decrease due to CTC formation. According to the Mulliken model, the lower the energy difference between the donor HOMO and the acceptor LUMO, the larger the CTC binding energy (electronic mechanism).22 Therefore, the latter can be higher for CTCs formed at a conjugated segment that already has a CTC, i.e., at the repeat units adjacent to the complexed ones.We suggest that the chain planarization upon CTC formation originates from the more quinoid character of the complexed chain, and hence is determined by the degree of charge transfer in a CTC. In the Mulliken model, the degree of charge transfer is determined by two factors: donor–acceptor electronic coupling, HDA, and the effective HOMO(D)–LUMO(A) gap. The observed strong dependence of the NE on the donor and acceptor molecular structure is in complete accordance with the chain planarization hypothesis since the molecular structures determine HDA. However, we observed that the EA does not affect the NE in CP complexation that seems to be in some contradiction with the hypothesis. In order to reconcile the data with the hypothesis, we assume that with EA increase the charge density on the acceptor shifts from the fluorene core to the substituents, and this shift in turn can decrease HDA and limit the net charge transfer degree making the latter less sensible to EA. With this assumption, the chain planarization hypothesis appears to agree with the experimental data; however, the more detailed analysis of the suggested NE mechanism is beyond the scope of the current study. Consequently, we suggest that the chain planarization hypothesis describes a possible microscopic mechanism of the NE in the CP complexation. One can expect that the NE will be strong in blends where the CTC formation substantially increases the chain planarity. This would require a planar acceptor with an extended π-system (and reasonably low LUMO) for strong orbital overlap and pronounced π–π CT interaction with polymer donor moieties. In contrast, the NE is expected to be negligible in polymer:fullerene blends, e.g. P3HT:PCBM or MEH-PPV:C60, as well as in blends with very small acceptors (e.g. tetracyanoethylene, TCNE). Indeed, as the fullerene molecules are not planar, and the size of the conjugated system of very small acceptors is much smaller than the polymer conjugated length, overlapping between the polymer HOMOs and the acceptor LUMOs should be very weak, and the chain planarity and the electronic structure will be slightly affected by the CTC formation thus resulting in a weak NE. We also argue that the NE should operate stronger for CPs with semi-flexible chains where the complexation could noticeably increase the chain planarity.
Additional contribution to the NE can stem from cross-chain π–π aggregation that was initially suggested in ref. 6. Following this suggestion, a CTC could be a link between two distant segments of a single polymer chain. The formation of the CTC-link and subsequent planarization of the two segments would result in approaching their monomer units adjacent to the link and an increased probability for successive CTC-links to be formed nearby the first one (Fig. 3 in ref. 6). Note that the NE was found to be independent of the polymer concentration (the latter was changed by 200 times, Fig. 6), which determines the number of interchain contacts. Therefore, the interaction of different macromolecules does not affect the NE, which operates within an individual macromolecule.
A strong NE should result in high inhomogeneity of the CTC distribution over the chains so that large CTC aggregates can be formed.19 These aggregates can be inherited in film, where microscopic ordered domains of the complexed polymer were observed.21 The morphology and photophysics are completely different in the domains of neat and complexed CP.2 The NE strength can determine the size of the CTC domains and thus could be used to control the film morphology. Moreover, blend self-organization as a result of the NE can be a route to overcome the intrinsic disorder of CPs and result in improved performance of polymer electronic devices. Therefore, search for CP blends with strong NE deserves further studies.
Conclusions
We have found that in a number of MEH-PPV blends with various molecular π-electron acceptors, the charge-transfer complex (CTC) absorption shows threshold-like dependence on the acceptor concentration, while in the other MEH-PPV and P3HT-based blends this dependence resembles that typical for small-molecule donor–acceptor blends. The optical absorption data were analyzed within a model that takes into account the neighbor effect (NE) in conjugated polymer (CP) complexation. We conclude that the NE can play a key role in this complexation. The binding energy of an isolated CTC was found to be sensitive to the acceptor electron affinity, the solvent, and the type of donor and acceptor conjugated molecular skeletons, while the NE depends only on the skeletons and the solvent. We suggest that the NE in CP complexation operates within an individual macromolecule and stems from the planarization of the conjugated chain upon CTC formation. We expect that the NE should be weak in CP blends with non-planar acceptors (e.g. fullerene derivatives), acceptors with relatively small π-delocalized orbitals, and blends with relatively rigid CPs, whereas it is expected to be more pronounced in blends of semi-flexible CPs with acceptors having an extended π-conjugated system suitable for efficient orbital overlap with polymer donor moieties.Acknowledgements
This work was supported by Russian Foundation of Basic Research (projects #13-02-01313 and 13-03-12472). This work was done using equipment purchased under the Lomonosov Moscow State University Program of Development. S.K. thanks the Bangor University for 125 Anniversary PhD Scholarship.References
- A. A. Bakulin, S. G. Elizarov, A. N. Khodarev, D. S. Martyanov, I. V. Golovnin, D. Y. Paraschuk, M. M. Triebel, I. V. Tolstov, E. L. Frankevich, S. A. Arnautov and E. M. Nechvolodova, Synth. Met., 2004, 147, 221–225 CrossRef CAS
.
- A. Y. Sosorev and D. Y. Paraschuk, Isr. J. Chem., 2014, 54, 650–673 CrossRef CAS
.
- D. Y. Paraschuk, S. G. Elizarov, A. N. Khodarev, A. N. Shchegolikhin, S. A. Arnautov and E. M. Nechvolodova, JETP Lett., 2005, 81, 467–470 CrossRef CAS
.
-
A. A. Bakulin, M. S. Pshenichnikov, P. H. M. van Loosdrecht, I. V. Golovnin and D. Y. Paraschuk, in Physics of nanostructured solar cells, ed. V. Badescu and M. Paulescu, Nova Science Publishers, 2010, pp. 463–504 Search PubMed
.
- A. A. Bakulin, A. N. Khodarev, D. S. Martyanov, S. G. Elizarov, I. V. Golovnin, D. Y. Paraschuk, S. A. Arnautov and E. M. Nechvolodova, Dokl. Chem., 2004, 398, 204–206 CrossRef CAS
.
- O. D. Parashchuk, V. V. Bruevich and D. Y. Paraschuk, Phys. Chem. Chem. Phys., 2010, 12, 6021–6026 RSC
.
- A. A. Bakulin, D. S. Martyanov, D. Y. Paraschuk, M. S. Pshenichnikov and P. H. M. van Loosdrecht, J. Phys. Chem. B, 2008, 112, 13730–13737 CrossRef CAS PubMed
.
- A. E. Ozimova, V. V. Bruevich, T. Dittrich and D. Y. Paraschuk, Macromol. Symp., 2010, 296, 138–143 CrossRef CAS
.
- A. A. Bakulin, S. A. Zapunidy, M. S. Pshenichnikov, P. H. M. van Loosdrecht and D. Y. Paraschuk, Phys. Chem. Chem. Phys., 2009, 11, 7324–7330 RSC
.
- J. J. Benson-Smith, L. Goris, K. Vandewal, K. Haenen, J. V. Manca, D. Vanderzande, D. D. C. Bradley and J. Nelson, Adv. Funct. Mater., 2007, 17, 451–457 CrossRef CAS
.
- T. Drori, C. X. Sheng, A. Ndobe, S. Singh, J. Holt and Z. V. Vardeny, Phys. Rev. Lett., 2008, 101, 037401 CrossRef CAS PubMed
.
- T. Drori, J. Holt and Z. V. Vardeny, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075207 CrossRef
.
- C. Deibel, T. Strobel and V. Dyakonov, Adv. Mater., 2010, 22, 4097–4111 CrossRef CAS PubMed
.
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767 CrossRef CAS PubMed
.
-
K. Vandewal, K. Tvingstedt and O. Inganäs, in Semiconductors and Semimetals, eds. M. T. Uli Wüerfel and R. W. Eicke, Elsevier, 2011, vol. 85, pp. 261–295 Search PubMed
.
- V. V. Bruevich, T. S. Makhmutov, S. G. Elizarov, E. M. Nechvolodova and D. Y. Paraschuk, J. Chem. Phys., 2007, 127, 104905 CrossRef CAS PubMed
.
- S. G. Elizarov, A. E. Ozimova, D. Y. Paraschuk, S. A. Arnautov and E. M. Nechvolodova, Proc. SPIE, 2006, 6257, 293–302 Search PubMed
.
- I. V. Golovnin, A. A. Bakulin, S. A. Zapunidy, E. M. Nechvolodova and D. Y. Paraschuk, Appl. Phys. Lett., 2008, 92, 243311 CrossRef
.
- A. Sosorev and S. Zapunidi, J. Phys. Chem. B, 2013, 117, 10913–10919 CrossRef CAS PubMed
.
- A. Y. Sosorev, O. D. Parashchuk, S. A. Zapunidi, G. S. Kashtanov and D. Y. Paraschuk, J. Phys.
Chem. C, 2013, 117, 6972–6978 CAS
.
- O. D. Parashchuk, S. Grigorian, E. E. Levin, V. V. Bruevich, K. Bukunov, I. V. Golovnin, T. Dittrich, K. A. Dembo, V. V. Volkov and D. Y. Paraschuk, J. Phys. Chem. Lett., 2013, 4, 1298–1303 CrossRef CAS PubMed
.
- R. S. Mulliken, J. Am. Chem. Soc., 1952, 74, 811–824 CrossRef CAS
.
- D. Veldman, S. C. J. Meskers and R. A. J. Janssen, Adv. Funct. Mater., 2009, 19, 1939–1948 CrossRef CAS
.
- O. D. Parashchuk, T. V. Laptinskaya and D. Y. Paraschuk, Phys. Chem. Chem. Phys., 2011, 13, 3775–3781 RSC
.
- V. G. Pavelyev, O. D. Parashchuk, M. Krompiec, T. V. Orekhova, I. F. Perepichka, P. H. M. van Loosdrecht, D. Y. Paraschuk and M. S. Pshenichnikov, J. Phys. Chem. C, 2014, 118, 30291–30301 CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed
.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
.
- S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef CAS
.
- M. S. Newman, T. B. Patrick, R. S. Darlak and E. A. Zuech, J. Org. Chem., 1969, 34, 1904–1906 CrossRef CAS
.
- E. H. Huntress, K. Pfister and K. H. T. Pfister, J. Am. Chem. Soc., 1942, 64, 2845–2849 CrossRef CAS
.
- G. I. Migachev, N. G. Grekhova and N. S. Dokunikhin, Zh. Org. Khim., 1978, 14, 2380–2387 CAS
(in Russian).
-
H. E. Hinderer and R. W. Smith, US patent 3,467,623, 1969
.
- T. Sulzberg and R. J. Cotter, J. Org. Chem., 1970, 35, 2762–2769 CrossRef CAS
.
- T. K. Mukherje and L. A. Levasseu, J. Org. Chem., 1965, 30, 644–646 CrossRef
.
- T. K. Mukherje, J. Phys. Chem., 1966, 70, 3848–3852 CrossRef
.
- I. F. Perepichka, A. F. Popov, T. V. Orekhova, M. R. Bryce, A. N. Vdovichenko, A. S. Batsanov, L. M. Goldenberg, J. A. K. Howard, N. I. Sokolov and J. L. Megson, J. Chem. Soc., Perkin Trans. 2, 1996, 2453–2469 RSC
.
- I. F. Perepichka, L. G. Kuz'mina, D. F. Perepichka, M. R. Bryce, L. M. Goldenberg, A. F. Popov and J. A. K. Howard, J. Org. Chem., 1998, 63, 6484–6493 CrossRef CAS
.
- I. F. Perepichka, A. F. Popov, T. V. Orekhova, M. R. Bryce, A. M. Andrievskii, A. S. Batsanov, J. A. K. Howard and N. I. Sokolov, J. Org. Chem., 2000, 65, 3053–3063 CrossRef CAS PubMed
.
- D. D. Mysyk, I. F. Perepichka and N. I. Sokolov, J. Chem. Soc., Perkin Trans. 2, 1997, 537–546 RSC
.
- P. Panda, D. Veldman, J. Sweelssen, J. J. A. M. Bastiaansen, B. M. W. Langeveld-Voss and S. C. J. Meskers, J. Phys. Chem. B, 2007, 111, 5076–5081 CrossRef CAS PubMed
.
- T.-Q. Nguyen, V. Doan and B. J. Schwartz, J. Chem. Phys., 1999, 110, 4068–4078 CrossRef CAS
.
- D. Wang, Y. Yuan, Y. Mardiyati, C. Bubeck and K. Koynov, Macromolecules, 2013, 46, 6217–6224 CrossRef CAS
.
- H. Yamagata, N. J. Hestand, F. C. Spano, A. Köhler, C. Scharsich, S. T. Hoffmann and H. Bässler, J. Chem. Phys., 2013, 139, 114903 CrossRef PubMed
.
- R. Traiphol, P. Sanguansat, T. Srikhirin, T. Kerdcharoen and T. Osotchan, Macromolecules, 2006, 39, 1165–1172 CrossRef CAS
.
- D. Hu, J. Yu, K. Wong, B. Bagchi, P. J. Rossky and P. F. Barbara, Nature, 2000, 405, 1030–1033 CrossRef CAS PubMed
.
- H. A. Benesi and J. H. Hildebrand, J. Am. Chem. Soc., 1949, 71, 2703–2707 CrossRef CAS
.
- S. A. Grebenyuk, I. F. Perepichka and A. F. Popov, Spectrochim. Acta, Part A, 2002, 58, 2913–2923 CrossRef
.
- Y. Ebihara and M. Vacha, J. Phys. Chem. B, 2008, 112, 12575–12578 CrossRef CAS PubMed
.
- R. S. Mulliken and W. B. Person, J. Am. Chem. Soc., 1969, 91, 3409–3413 CrossRef CAS
.
- R. Chang, J. H. Hsu, W. S. Fann, K. K. Liang, C. H. Chang, M. Hayashi, J. Yu, S. H. Lin, E. C. Chang, K. R. Chuang and S. A. Chen, Chem. Phys. Lett., 2000, 317, 142–152 CrossRef CAS
.
- T. E. Dykstra, E. Hennebicq, D. Beljonne, J. Gierschner, G. Claudio, E. R. Bittner, J. Knoester and G. D. Scholes, J. Phys. Chem. B, 2008, 113, 656–667 CrossRef PubMed
.
- V. V. Bruevich, T. S. Makhmutov, S. G. Elizarov, E. M. Nechvolodova and D. Y. Paraschuk, J. Exp. Theor. Phys., 2007, 105, 469–478 CrossRef CAS
.
- M. O. Osotov, V. V. Bruevich and D. Y. Paraschuk, J. Chem. Phys., 2009, 131, 094906 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis and characterization of studied fluorene acceptors with respective 1H and 13C NMR spectra, mass-spectra, infrared spectra, melting points and elemental analyses. Additional optical absorption data for polymer:acceptor blends in solutions and in films. DFT calculations for fluorene acceptors and correlations between computational DFT data and CV experiments. See DOI: 10.1039/c5cp05266a |
| This journal is © the Owner Societies 2016 |