Open Access Article
Open Access ArticleSerpentine polymorphism: a quantitative insight from first-principles calculations†
Raffaella
Demichelis
*a,
Marco
De La Pierre
a,
Mainak
Mookherjee
b,
Claudio M.
Zicovich-Wilson
c and
Roberto
Orlando
d
aNanochemistry Research Institute, Curtin Institute for Computation and Department of Chemistry, Curtin University, U1987, 6845 Perth, Western Australia, Australia. E-mail: raffaella.demichelis@curtin.edu.au
bEarth, Ocean and Atmospheric Sciences, Florida State University, Tallahassee, FL 32036, USA
cCentro de Investigación en Ciencias-(IICBA), Universidad Autónoma del Estado de Morelos, Av. Universidad 1001, 62209 Cuernavaca, Morelos, Mexico
dDipartimento di Chimica, Università degli Studi di Torino, Via Giuria 7, 10125 Torino, Italy
First published on 30th March 2016
Abstract
Single-walled chrysotile nanotubes [Mg3Si2O5(OH)4] of increasing size (up to 5004 atoms per unit cell, corresponding to a radius of 205 Å) have been modelled at the Density Functional level of theory. For the first time, it is demonstrated that the (n, −n) and (n, n) series present a minimum energy structure at a specific radius (88.7 and 89.6 Å, respectively, referring to the neutral surface), corresponding to a rolling vector of (60, −60) and (105, 105), respectively. The minima are nearly overlapped and are lower in energy than the corresponding slab of lizardite (the flat-layered polymorph of chrysotile) by about 3.5 kJ mol−1 per formula unit. In both cases, the energy profile presents a shallow minimum, where radii in the range of 63 to 139 Å differ in energy by less than 0.5 kJ mol−1 per formula unit. The energy of larger nanotubes has a trend that slowly converges to the limit of the flat lizardite slab. Structural quantities such as bond distances and angles of nanotubes with increasing size asymptotically converge to the flat slab limit, with no discontinuities in the surrounding of the minimum energy structures. However, analysis of the elongation of a rectangular pseudo-unit cell along the nanotube circumference indicates that the main factor that leads lizardite to curl in tubes is the elastic strain caused by the mismatch between the lattice parameters of the two adjacent tetrahedral and octahedral sheets. It is also shown in this study that the curvature of the layers in one of the lately proposed models of antigorite, the “wavy-layered” polymorph of chrysotile, falls within the range of radii of minimum energy for the nanotubes. These findings provide quantitative insights into the peculiar polymorphism of these three phyllosilicates. They show also that chrysotile belongs to those families of inorganic nanotubes that present a minimum in their strain energy profile at a specific range of radii, which is lower in energy with respect to their flat equivalent.
1 Introduction
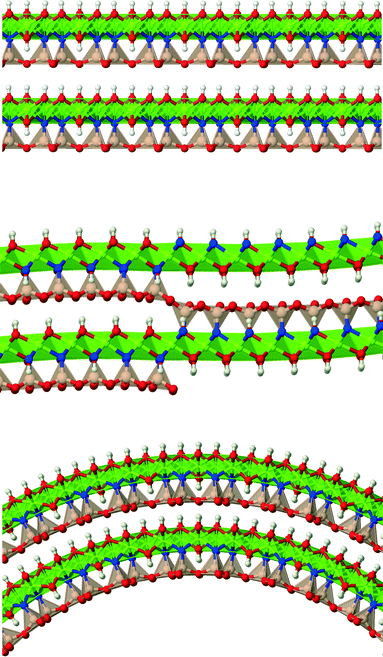
Lizardite, chrysotile and antigorite represent one of the most fascinating, yet not fully understood, cases of polymorphism.1 They are hydrous phyllosilicate minerals belonging to the group of serpentines, and have an ideal formula unit corresponding to Mg3Si2O5(OH)4. Their crystal structure consists of TO layers, where a brucite-type octahedral sheet (O) is attached to a silica tetrahedral sheet (T, made of di-trigonal rings formed by SiO4 tetrahedra units) through sharing one oxygen atom (an “apical” oxygen, Oa). What makes their structures so peculiar and difficult to determine is the bending flexibility of these slabs (Fig. 1), which can give rise to a range of layered structures where the layers can be flat (like in lizardite), modulated or “wavy” (like in antigorite, whose periodicity and features along the ab plane is still a matter of debate2–7), or curled in the form of concentric or spirally-wrapped nanotubes (chrysotile8–13).While lizardite has been characterized with a high level of accuracy for a range of temperature and pressure conditions (despite the fact that discriminating between the many possible polytypes is still a challenging task),14–21 the other two polymorphs are still a matter of study, together with the reasons that cause such a diverse range of structures.22 Owing to its relevance and the role it might play in transporting water into the Earth's interior, some physical properties of antigorite have been examined as well.23–26
A number of qualitative hints on what could be the cause of the high flexibility of the TO slab27–30 are present in the literature, suggesting that curling is a result of the lattice parameter misfit between the O and the T sheets and that this adjustment is facilitated by a balance between the high flexibility of the Mg–O bonds and the high rigidity of the Si–O bonds.
A first attempt to quantify the lattice parameter misfit was made by D'Arco et al.,31 where electronic structure calculations were carried out on relatively small chrysotile single-walled fibres with a radius of up to about 35 Å (corresponding to the tiniest fibre found in nature). The lattice parameters of the ideal isolated T and O sheets were calculated, confirming that the a lattice parameter of lizardite falls in between the T and O lattice parameters that differ by around 0.1 Å. The aforementioned study also shows that one additional main structural factor that allows the slab to curl is the rotational freedom of the SiO4 tetrahedra around the Si–Oa axis.
Due to the limited extent of the investigated range of radii, these results could not provide final indications about the behaviour of the strain energy profile of chrysotile against lizardite (i.e. the energy difference between the tube and the flat slab as a function of the tube radius), and in particular, about the existence of a minimum at large radii. This hypothesis has also been recently explored by Krasilin and Gusarov30 by theoretical modeling based on Young's modulus data collected in a number of other experiments; here, it is the spread of experimental data that has not permitted conclusions on this point.
The implementation of a number of tools in the past few years allowed for an extension of the analysis by D'Arco et al.,31 where the (n, −n) series was modelled only up to the smallest observed nanotube n = 24.‡ In particular, what made the present study feasible in terms of computing time and resources were the exploitation of helical symmetry (including symmetry planes that were not yet implemented at the time of ref. 31) up to any number of symmetry operators (in this case, it means modelling unit cells with thousands of atoms while maintaining an asymmetric unit of only 12 atoms),32 improved exploitation of symmetry in algorithms operating on Fock and density matrices (resulting in both shorter computing times and reduced memory requirements),33–35 and the geometry guess option described in ref. 36 that dramatically reduces the number of optimisation steps required to reach structural convergence.
In this work, we have modeled chrysotile as a series of 58 single-walled (n, −n) nanotubes with a radius between 13 and 205 Å (measured with reference to the neutral surface, NS, i.e. the ideal cylinder surface whose size is equal to that of a flat, unrolled lizardite slab), and a second series of 14 single-walled (n, n) nanotubes with a radius in the range of 24–101 Å. Lizardite and one of the latest proposed models for antigorite5 were modeled, too, for structural comparison with chrysotile. After a brief summary on the computational methods that we have adopted, the following sections will present and discuss the results.
2 Computational methods
Periodic models of different dimensionalities were adopted to describe the various structures investigated in this work: 3D for lizardite bulk 1T, lizardite bulk 2H1 and antigorite (m = 16); 2D for the flat lizardite slab and the free-standing flat T and O sheets; 1D for the chrysotile nanotubes.Calculations were performed at the Density Functional Theory (DFT) level as implemented in the CRYSTAL14 public package.37,38 Maximum advantage is taken of the highly symmetric helical groups of chrysotile nanotubes at all stages of the electronic structure calculation, direct transformations are performed between the bases of Atomic Orbitals (AOs) and Symmetry Adapted Molecular Orbitals, and allocation of full matrices in the basis of AOs is always avoided. Performance in terms of CPU time and memory allocations is discussed in detail in ref. 33–35.
The B3LYP functional was used, as previous studies on lizardite and on chrysotile demonstrated its accuracy in describing the structural features and the properties of these polymorphs.21,31 The well-known inaccuracy of DFT methods in predicting relative energies, due to short- and long-range dispersion interactions not being properly accounted for, will not represent a major issue in this study, since the atomic coordination, the density within a slab, and the spacing between subsequent slabs is quite similar between the three polymorphs.39
6-31G* basis sets from ref. 40 and 41 were adopted, with the most diffuse exponents reoptimised for chrysotile in the work by D'Arco et al.31 Thresholds controlling the accuracy of the Coulomb and exchange series and of their approximation were set more strictly than default values (TOLINTEG 13 13 13 13 26, NOBIPOLA; see ref. 37 for further details). While thresholds adopted in a previous publication31 were tight enough to guarantee convergence on the smaller tubes (n of up to 24), more strict values were required to reach convergence on bigger tubes, most probably because of the very large number of symmetry operators and then symmetry equivalent atoms within a unit cell. Similarly, the accuracy of the grid used to evaluate the DFT exchange–correlation contribution via numerical integration over the unit cell volume was increased with respect to the one adopted in the work by D'Arco et al.:31 the XXLGRID keyword was used,37 corresponding to a pruned grid with 99 radial and 1454 angular points. With this grid, the error on the numerically integrated density is as small as 4 × 10−5|e| on a total of 2520 |e| and 9 × 10−3|e| on a total of 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 |e| for the (9, −9) and (139, −139) structures, respectively.
920 |e| for the (9, −9) and (139, −139) structures, respectively.
The reciprocal space was sampled according to a Monkhorst–Pack mesh with a shrinking factor of 6, corresponding to 4, 7, 34, 28 and 68 independent k vectors in the irreducible part of the Brillouin zone for chrysotile nanotubes, flat lizardite slab, lizardite bulk 1T, lizardite bulk 2H1 and antigorite (m = 16), respectively.
The threshold on the self consistent field energy was set to 10−8Eh. Structure optimisation was performed by use of analytical energy gradients with respect to atomic coordinates and unit cell parameters, within a quasi-Newton scheme combined with the Broyden–Fletcher–Goldfarb–Shanno42–45 scheme for Hessian updating. The default optimisation convergence criteria were used for energy, gradient components and nuclear displacement. In order to compute the elastic modulus for isotropic unit cell distortions of the slabs, optimisation of the atomic coordinates was repeatedly performed while keeping the cell parameters fixed across a range of values.
3 Structure and properties of lizardite
As mentioned in the introduction, bulk lizardite has a well-known layered structure where each layer consists of one T and one O sheets joined together through apical oxygen atoms. This layer, or slab, will represent the reference model for most of our discussion on serpentine polymorphs.Given this layered structure, a number of possible polytypes have been identified in the past,14 with the one-layer trigonal (1T) and the two-layer hexagonal (2H1) being the most likely in nature. They differ by minor distortions in the angles between the oxygen-sharing tetrahedra.46 The electronic energy difference at 0 K between the two polytypes as calculated within the current computational framework is very small, 0.6 kJ mol−1 per formula unit in favour of the 2H1 structure. Despite this datum being in apparent disagreement with the fact that 1T-lizardite is most commonly detected in the experiments, it should be considered as just an estimation, which does not include any temperature or pressure effect. Temperature has indeed been found to play a crucial role in determining structural changes (and therefore stability) for values >300 K.15 Being a comparison between multi-layered systems, the Basis Set Superposition Error47 (BSSE) should in principle be taken into account for the energy per layer; however, the structure and spacing between the layers are so similar that we can reasonably assume that the BSSE will cancel nearly exactly when calculating the relative energy, as well as all those interactions that are not properly accounted for when using DFT. As a further check, calculations repeated with different choices of computational parameters, with a more accurate basis set48 and with a different DFT functional (PBEsol49) give results that fall within the range of 0.6–0.8 kJ mol−1 per formula unit in favour of the 2H1 polytype.
The calculated and experimental structural parameters of 1T and 2H1 lizardite are reported in Table 1, together with those for antigorite (m = 16 polysome; see the following sections for further details on antigorite). The observed slight overestimation of distances is a known feature of the B3LYP functional. Overall, the agreement between the calculated and experimental structures is excellent, including the inter-layer atomic arrangement and spacing (c lattice parameter, O⋯O distance).
| 1T-lizardite | 2H1-lizardite | Antigorite (m = 16) | ||||
|---|---|---|---|---|---|---|
| Calc. | Exp. | Calc. | Exp. | Calc. | Exp. | |
| a | 5.350 | 5.325 | 5.348 | 5.318 | 81.977 | 81.664 |
| b | — | — | — | — | 9.298 | 9.255 |
| c | 7.318 | 7.259 | 14.644 | 14.541 | 7.302 | 7.261 |
| β | — | — | — | — | 91.013 | 91.409 |
| V | 181.4 | 178.3 | 362.7 | 356.2 | 5565 | 5486 |
| Si–Omax | 1.665 | 1.651 | 1.666 | 1.648 | 1.665 | 1.668 |
| Si–Omin | 1.608 | 1.577 | 1.608 | 1.602 | 1.607 | 1.595 |
| Mg–Omax | 2.151 | 2.139 | 2.150 | 2.125 | 2.248 | 2.210 |
| Mg–Omin | 2.026 | 2.024 | 2.064 | 2.021 | 2.025 | 2.003 |
| O⋯Omax | 3.06 | 3.04 | 3.08 | 3.09 | 3.16 | 3.14 |
| O⋯Omin | — | — | — | — | 2.99 | 3.00 |
This first analysis has shown that the method, basis set and computational parameters adopted here are accurate and predictive for serpentine polymorphs. Further validation is provided by Prencipe et al.,21 whose full analysis of 1T-lizardite vibrational properties shows an excellent agreement with the available experimental values.
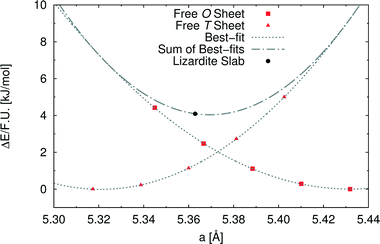
In order to investigate the role of the lattice mismatch between T and O sheets in determining the equilibrium structure of a lizardite slab, we performed a set of calculations on free-standing, flat sheets of the two types, using hydrogen to saturate the dangling bonds (see also work by D'Arco et al.31). In this way, the O sheet corresponds to a layer of brucite, whereas the T sheet has no equivalent in nature. The computed equilibrium lattice parameters of the T and O sheets are 5.317 and 5.432 Å, respectively, to be compared with the simulated value for the lizardite slab, 5.363 Å. Next, we computed the dependence of electronic energy on the isotropic variation of the unit cell (see Fig. 2), so that we could estimate through best-fit the corresponding moduli, 753 (T) and 584 (O) kJ/(mol Å2). The parameters from these best-fits predict that the lattice parameter value that minimises the combined strain energy of the two sheets is 5.369 Å, which is only 0.006 Å larger than the actual lizardite value from the simulations. This simple calculation confirms that the most important factor in determining the structure of the lizardite bi-layer is actually the elastic strain related to the lattice mismatch. It then seems reasonable to try and exploit similar arguments in estimating the minimum energy curvature of chrysotile in the following discussion.
4 Structure and energy of chrysotile nanotubes
Bulk chrysotile presents a very high level of structural complexity, in terms of both large unit cells, the full details of which are partly unknown, and relatively low space group symmetry. A detailed model for spirals and for the possible stacking sequences of concentric cylinders is currently unavailable. All these factors make the simulation of the bulk structures of chrysotile polymorphs/polytypes currently unaffordable with the first-principles approach adopted here. For these reasons, with the aim of making a first step forward in building a realistic model of this system, we carried out extensive investigation on a large set of individual nanotubes with different radii and rolling directions.Single-walled chrysotile nanotubes were constructed as described in ref. 31, by rolling-up a mono-layer of lizardite along the 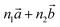 vector, where
vector, where 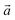 and
and 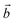 are lizardite's unit cell vectors with an equal module
are lizardite's unit cell vectors with an equal module 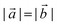 and an angle of 120°, and n1 and n2 are the nanotube indices (n1 = −n2 in (n, −n), or n1 = n2 in (n, n)). The only periodic lattice vector is parallel to the nanotube axis and has a length in the ranges 5.28–5.36 Å (see Fig. S1(d) in the ESI†) and 9.23–9.28 Å along the (n, −n) and (n, n) series, respectively.
and an angle of 120°, and n1 and n2 are the nanotube indices (n1 = −n2 in (n, −n), or n1 = n2 in (n, n)). The only periodic lattice vector is parallel to the nanotube axis and has a length in the ranges 5.28–5.36 Å (see Fig. S1(d) in the ESI†) and 9.23–9.28 Å along the (n, −n) and (n, n) series, respectively.
Fig. 3(a) reports the computed strain energy ΔE of a structurally relaxed single-walled chrysotile as a function of the radius of its neutral surface rNS, i.e. the energy difference between the nanotube and the flat slab. It can easily be observed that the energy curve presents a shallow minimum around a radius of 88.7 Å (n = 60) for the (n, −n) series and of 89.6 Å (n = 105) for the (n, n) series which is 3.5 kJ mol−1 per formula unit lower in energy with respect to the flat structure. Structures with radii in the range of 63–139 Å differ by no more than 0.5 kJ mol−1, indicating that these curled structures are energetically favoured in a wide range of sizes.§
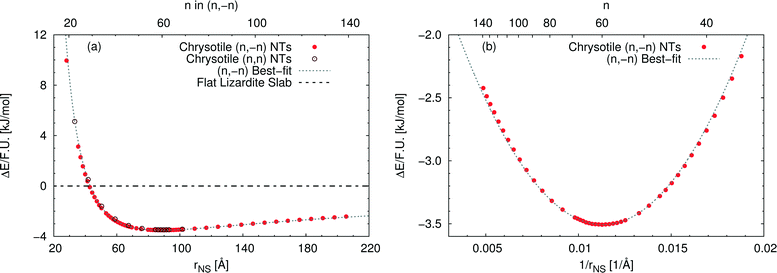 | ||
| Fig. 3 Energy difference per formula unit of (n, −n) single-walled chrysotile nanotubes with respect to the flat lizardite slab [kJ mol−1], as a function of (a) NS radius [Å] and index n, and (b) inverse NS radius [Å−1] and index n. The superimposed curve has been obtained through quadratic best-fit over a set of 16 points around the energy minimum. In (a), data for the (n, n) series are also shown. In (b), only the subset of (n, −n) data in the energy range of −3.6–−2 kJ mol−1 is shown. All the corresponding (n, −n) data are reported in Table S1 in the ESI.† | ||
Notably, Whittaker10,12,50 observed that the average between the inner and the outer radius was 84 Å and 96 Å for clino- and para-chrysotile, respectively, and predicted that the strain-free layer of lizardite would have a radius of 88 Å on the basis of X-ray diffraction data.
As (n, n) nanotubes have a lattice vector about 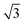 times larger than that of (n, −n) ones, for a given radius value, the (n, n) tube has about 70% more atoms, resulting in much more expensive calculations. A smaller set of points was then computed along this series, which are reported in Fig. 3(a). Despite (n, −n) being generally assumed as the preferred rolling direction, the (n, n) family of tubes actually shows the same trend with radius and turns out to be only 0.1 kJ mol−1 per formula unit less stable.
times larger than that of (n, −n) ones, for a given radius value, the (n, n) tube has about 70% more atoms, resulting in much more expensive calculations. A smaller set of points was then computed along this series, which are reported in Fig. 3(a). Despite (n, −n) being generally assumed as the preferred rolling direction, the (n, n) family of tubes actually shows the same trend with radius and turns out to be only 0.1 kJ mol−1 per formula unit less stable.
D'Arco et al.31 performed some best fits on energy vs. radius data for the (n, −n) family, based on two different formulas; notably, one of them predicted the presence of a shallow minimum at −3.1 kJ mol−1 for n = 58. However, data in that study were collected only up to n = 24 and therefore the extrapolated result was not enough at that time to claim the actual presence of a minimum in the energy profile.
Fig. 3(b) shows the strain energy as a function of the curvature, i.e. inverse radius, and clearly suggests nearly parabolic behaviour. In fact, a quadratic best-fit of the energy values around the minimum (16 points were considered) provides a very good description of the dataset along a much wider range of radii. The curvature parameter obtained from the fit permits an estimation of the bending modulus of the slab, 20.6 eV. A closer look at the figure reveals that the best-fit overestimates energies below the minimum-energy radius, whereas it underestimates values above this radius. This points towards a non-linear elastic effect such that the bending modulus is dependent on the tube radius. To try and estimate this effect, we performed a second best-fit using a quartic function; this time the whole dataset, except for the smallest tube, could be included in the fit. The resulting bending modulus spans a range of values between 17.6 and 22.5 eV, when considering radii included between 35.5 and 205.5 Å, with a percent variation larger than 20%. At the radius of minimum energy, this second model gives a bending modulus of 20.7 eV, which is in close agreement with our first evaluation. We could also try and extrapolate an estimate for the flat slab (i.e. infinite radius), which amounts to 24.1 eV.
A wide range of structural data can be extracted from our calculations, and analysed as a function of the index n (or tube radius). For example, Fig. 4 plots values for slab thickness and surface area per formula unit for selected atomic layers. Both quantities reveal monotonic behaviour, either increasing or decreasing, as a function of n, with asymptotical convergence towards the values found in the flat lizardite slab. Similar monotonic trends can be found for a wide set of other structural properties, including lattice parameter, sheet thicknesses, bond distances and angles; the corresponding data can be found in Fig. S1 and S2 and Tables S2 and S3 in the ESI.† None of these quantities shows discontinuities around the n values corresponding to the minimum strain energy.
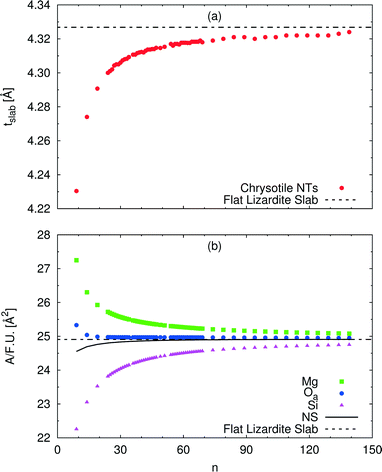 | ||
| Fig. 4 Dependence of selected structural parameters of single-walled (n, −n) chrysotile nanotubes on the index n: (a) total slab thickness (measured from inner to outer oxygen atoms); (b) surface area per formula unit for a set of atomic layers. Values for the flat lizardite slab are reported, too. Distances are in Å, areas are in Å2. The number of formula units and of atoms in the unit cell is equal to 2n and 36n, respectively. The corresponding data are reported in Table S2 in the ESI.† | ||
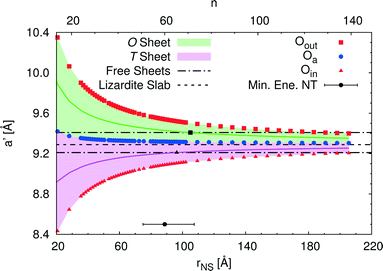
An alternative rectangular unit cell can be defined for the lizardite slab. This is relevant to our discussion because (n, −n) chrysotile nanotubes are wrapped by rolling the flat slab along the longest side of this unit cell, a′, and by keeping the shortest side as their cell parameter. Visual representation of a' and its geometrical relationship with a lizardite unit cell is reported and discussed in ref. 31. In the tubes, a′ is not a repeating unit (that is why we refer to it as a “pseudo”-unit cell parameter). However, being aligned with the tube circumference, it gives a direct measure of the structural strain as a function of the tube radius compared to the flat slab. Fig. 5 reports a′ as a function of the radius rNS and of the index n, for a set of atomic layers: outer, apical and inner oxygen atoms. The first and the second sets of oxygen atoms delimit the O sheet, whereas the second and the third ones delimit the T sheet. Like the other quantities, all a' curves exhibit monotonic behaviour converging to the value for lizardite, 9.289 Å.
Let us now consider the a′ values for the free-standing flat O and T sheets: they are 9.408 and 9.210 Å, respectively, lying for both sheets between the data for small-radius nanotubes and the datum for flat lizardite, which represents the asymptotic limit at infinite radius. If elongation along a′ were a relevant factor, we would then expect a lower nanotube strain energy at radii corresponding to the a′ values of the O and T sub-sheets that lie closer to the values for their free-standing homologues; also, the minimum strain energy would be determined by combination of the effects for the two sheets. Given that the O and T sheets in the nanotubes have a finite thickness and, beside elongation, they also incur in bending, correct calculation of their strain energy would be demanding. Nonetheless, we can get a simplified insight by looking at what happens at half-thickness (darker straight lines in Fig. 5): here, O and T sheets cross the free-standing sheet a′ values around a radius of 105 and 96 Å, respectively. In this picture, one would then expect the minimum strain radius to fall within this range, which is extremely close to the actual radius of minimum energy, 88.7 Å (actually closer than 0.1 kJ mol−1 per formula unit on the energy scale). This finding provides a strong evidence of the main role played by elastic strain due to the lattice mismatch in determining the minimum energy radius in chrysotile nanotubes.
5 The structure of antigorite
The bulk structure of antigorite has been debated for a long time and there are a few models in the literature that are claimed to best describe its features.2,4–6,51 These models refer to different “polysomes”, i.e. structures that differ by the number of silicate tetrahedra spanning a wavelength along the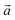 lattice vector.5m = 17 and m = 16 polysomes were found in several samples by Capitani and Mellini,5 with m = 17 being the most common. These two polysomes have 17 and 16 silicate tetrahedra per wavelength, respectively, and present 4- and 8-membered rings of tetrahedra at the position where the tetrahedral sheets reverse their orientation.6
lattice vector.5m = 17 and m = 16 polysomes were found in several samples by Capitani and Mellini,5 with m = 17 being the most common. These two polysomes have 17 and 16 silicate tetrahedra per wavelength, respectively, and present 4- and 8-membered rings of tetrahedra at the position where the tetrahedral sheets reverse their orientation.6
Full analysis of the structure of antigorite is not within the scope of this paper. Rather, antigorite is considered here for structural comparison with its cylindrically wrapped polymorph, chrysotile. For this reason, since there are no major structural differences between the two polysomes, we have decided to refer to the m = 16 structure here, as its unit cell is smaller and features higher symmetry than the m = 17 model. This results in a largely reduced computational cost, in terms of time and memory resources, and also simplifies the analysis of the structure. The main structural data are reported in Table 1.
Here, it is interesting to observe that the imaginary arc containing the silicon atoms in each of the silicate half-waves of antigorite has a radius falling in the range of 83–88 Å. Besides, the radius of the atomic layer of silicon atoms in the minimum energy (n, n) chrysotile nanotube is 88.2 Å. The proximity of these values establishes a clear link between the peculiar structure of antigorite and that of chrysotile. Similar results can be expected for the m = 17 polysome, although the lower symmetry might result in a wider range of values for the radius.
6 Conclusions and perspectives
This paper quantitatively demonstrates that lizardite slabs have an intrinsic tendency to curl at a specific range of radii by using state-of-the-art first-principles methods. In fact, the (n, −n) and (n, n) series of single-walled chrysotile nanotubes present a minimum energy structure at a radius of 88.7 and 89.6 Å, respectively, referring to the neutral surface, with index (60, −60) and (105, 105), respectively. The plot of the energy vs. tube radius for the (n, n) series nearly overlaps with that of the (n, −n) series. The electronic energy in the minima is about 3.5 kJ mol−1 per formula unit lower with respect to the corresponding flat slab of lizardite. While tubes with a radius in the range of 63 to 139 Å differ in energy by no more than 0.5 kJ mol−1 per formula unit, the energy of the series slowly converges for very large radii to the limit of the lizardite slab. Similar behaviour is observed for the structural parameters.Notably, the curvature of the half-waves in the m = 16 polysome of antigorite has a radius that falls around the same value as that of the chrysotile minimum energy structures. The m = 17 polysome has not been explicitly considered in this paper, but its experimental structure suggests that a similar comment is likely to hold for its structure as well.
Analysis of the elongation of lizardite and chrysotile unit cell parameters provides clear evidence that the elastic strain caused by the mismatch between the lattice parameters of the T and the O sheets is the main driving factor towards the curling of the slab.
While much research is being devoted in investigating the stability and phase diagram of these phases on the Earth's crust and mantle, little attention has been paid so far to providing a satisfactory description of their structures and properties at the atomic level, despite the fact that the occurrence of a given polymorph is intrinsically related to interplay of fundamental interactions. While the calculations presented here are currently at the limit of feasibility at such an accurate level of theory, further steps will be required towards better atomic understanding of serpentine polymorphism, which involve adding further levels of complexity to our systems. Among these, substitution of Mg and Si with other elements (Al and Fe, for instance) can importantly affect the lattice structure, and thus its curling and stability. Moreover, multi-walled and spirally-wrapped chrysotile fibres need to be considered to account for inter-layer interactions, which include strong hydrogen bonds and could play a role in stabilising one phase with respect to the others.
Acknowledgements
The authors thank Siobhan Wilson (Monash University) for providing the SEM images of lizardite, chrysotile and antigorite that have been used in the graphical abstract. RD acknowledges financial support from Curtin University through the Curtin Research Fellowship scheme. CZW acknowledges financial support from Mexican CONACyT, through project CB-178853, and from the Crystal code funds. MM is supported by US NSF (1639552 and 1634422). RD and MD acknowledge both the Pawsey Supercomputing Centre (Perth) and the Australian National Computational Infrastructure (NCI, Canberra) for the provision of computer time.References
- B. W. Evans, K. Hattori and A. Baronnet, Elements, 2013, 9, 99–106 CrossRef CAS.
- I. Dódony, M. Pósfal and P. R. Buseck, Am. Mineral., 2006, 91, 1831–1838 CrossRef.
- M. T. Otten, Am. Mineral., 1993, 78, 75–84 CAS.
- G. C. Capitani and M. Mellini, Am. Mineral., 2004, 89, 147–158 CrossRef CAS.
- G. C. Capitani and M. Mellini, Am. Mineral., 2006, 91, 394–399 CrossRef CAS.
- G. C. Capitani, L. Stixrude and M. Mellini, Am. Mineral., 2009, 94, 1271–1278 CrossRef CAS.
- M. Mellini, Y. Fuchs, C. Viti, C. Lemaire and J. Linareès, Eur. J. Mineral., 2002, 14, 97–104 CrossRef CAS.
- E. J. W. Whittaker, Acta Crystallogr., 1953, 6, 747–748 CrossRef CAS.
- E. J. W. Whittaker, Acta Crystallogr., 1955, 8, 571–574 CrossRef CAS.
- E. J. W. Whittaker, Acta Crystallogr., 1956, 9, 855–862 CrossRef CAS.
- E. J. W. Whittaker, Acta Crystallogr., 1956, 9, 862–864 CrossRef CAS.
- E. J. W. Whittaker, Acta Crystallogr., 1956, 9, 865–867 CrossRef CAS.
- K. Yada, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1971, 27, 659–664 CrossRef CAS.
- M. Mellini and P. F. Zanazzi, Am. Mineral., 1987, 72, 943–948 CAS.
- S. Guggenheim and W. Zhan, Can. Mineral., 1998, 36, 1587–1594 CAS.
- A. L. Auzende, I. Daniel, B. Reynard, C. Lemaire and F. Guyot, Phys. Chem. Miner., 2004, 31, 269–277 CrossRef CAS.
- A. L. Auzende, R. J. M. Pellenq, B. Devouard, A. Baronne and O. Grauby, Phys. Chem. Miner., 2006, 33, 266–275 CrossRef CAS.
- E. Balan, M. A. Saitta, F. Mauri, C. Lemaire and F. Guyot, Am. Mineral., 2002, 87, 1286–1290 CrossRef CAS.
- N. Hilairet, I. Daniel and B. Reynard, Phys. Chem. Miner., 2006, 33, 629–637 CrossRef CAS.
- M. Mookherjee and L. Stixrude, Earth Planet. Sci. Lett., 2009, 279, 11–19 CrossRef CAS.
- M. Prencipe, Y. Noël, M. Bruno and R. Dovesi, Am. Mineral., 2009, 94, 986–994 CrossRef CAS.
- B. W. Evans, Int. Geol. Rev., 2004, 46, 479–506 CrossRef.
- G. C. Capitani and L. Stixrude, Am. Mineral., 2012, 97, 1177–1186 CrossRef CAS.
- M. Mookherjee and G. C. Capitani, Geophys. Res. Lett., 2011, 38, L09315 Search PubMed.
- N. Ghaderi, H. Zhang and T. Sun, J. Geophys. Res.: Solid Earth, 2015, 120, 4831–4842 CrossRef CAS.
- L. Bezacier, B. Reynard, H. Cardon, G. Montagnac and J. D. Bass, J. Geophys. Res.: Solid Earth, 2013, 118, 527–535 CrossRef CAS.
- L. Pauling, Proc. Natl. Acad. Sci. U. S. A., 1930, 16, 578–582 CrossRef CAS.
- E. Foresti, M. F. Hochella, H. Kornishi, I. G. Lesci, A. S. Madden, N. Roveri and H. Xu, Adv. Funct. Mater., 2005, 15, 1009–1016 CrossRef CAS.
- T. F. Bates, L. B. Sand and J. F. Mink, Science, 1950, 111, 512–513 CAS.
- A. A. Krasilin and V. V. Gusarov, Russ. J. Gen. Chem., 2014, 84, 2359–2363 CrossRef CAS.
- P. D'Arco, Y. Noël, R. Demichelis and R. Dovesi, J. Chem. Phys., 2009, 131, 204701 CrossRef PubMed.
- Y. Noël, P. D'Arco, R. Demichelis, C. M. Zicovich-Wilson and R. Dovesi, J. Comput. Chem., 2010, 31, 855–862 Search PubMed.
- C. M. Zicovich-Wilson, Y. Noël, A. M. Ferrari, R. Orlando, M. De La Pierre and R. Dovesi, AIP Conf. Proc., 2012, 1456, 248–255 CrossRef CAS.
- R. Orlando, M. De La Pierre, C. M. Zicovich-Wilson, A. Erba and R. Dovesi, J. Chem. Phys., 2014, 141, 104108 CrossRef PubMed.
- M. De La Pierre, R. Orlando, M. Ferrabone, C. M. Zicovich-Wilson and R. Dovesi, Sci. China: Chem., 2014, 57, 1418–1426 CrossRef CAS.
- R. Demichelis, Y. Noël, P. D'Arco, L. Maschio, R. Orlando and R. Dovesi, J. Mater. Chem., 2010, 20, 10417–10425 RSC.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà and Y. Noël, CRYSTAL 2014 User's Manual, 2014 Search PubMed.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317 CrossRef CAS.
- S. Casassa and R. Demichelis, J. Phys. Chem. C, 2012, 116, 13313–13321 CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222 CrossRef CAS.
- M. M. Francl, W. J. Petro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- C. G. Broyden, J. Inst. Math. Its Appl., 1970, 6, 76–90 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Math. Com., 1970, 24, 23–26 CrossRef.
- D. F. Shanno, Math. Com., 1970, 24, 647–656 CrossRef.
- S. W. Bailey, Clays Clay Miner., 1969, 17, 355–371 CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459 CrossRef CAS PubMed.
- J. Perdew, A. Ruzsinsky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- E. J. W. Whittaker, Acta Crystallogr., 1957, 10, 149–156 CrossRef CAS.
- I. Dódony, M. Pósfal and P. R. Buseck, Am. Mineral., 2002, 87, 1143–1457 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ce00190d |
‡ Here, the standard (n1, n2) notation is used for nanotubes, according to which the rolling vector is defined as 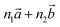 , where , where 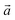 and and 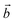 are the lattice parameters of the hexagonal 2D unit cell of lizardite. are the lattice parameters of the hexagonal 2D unit cell of lizardite. |
| § Different DFT functionals and basis sets may give slightly different radii and the position of the minimum may vary by a few n units. |
| This journal is © The Royal Society of Chemistry 2016 |