Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crystal structure landscape of conformationally flexible organo-fluorine compounds†
Pradip Kumar
Mondal
and
Deepak
Chopra
*
Department of Chemistry, IISER Bhopal, Bhopal, India. E-mail: dchopra@iiserb.ac.in
First published on 17th November 2015
Abstract
The crystal structure landscape of an unsubstituted benzanilide was generated and a number of hypothetical structures were accessed with experimentally obtained crystal structures of mono-, di-, tetra- and penta-fluorobenzanilides. Thus, chemical modification allows us to access the “high energy” forms of the parent compound, thereby delineating the significant role of weak intermolecular interactions.
Crystal structure prediction (CSP) methods for organic molecules have attracted tremendous interest in recent years.1 These are based on searches for the most thermodynamically feasible crystal structure, and such an evaluation neglects the role of entropy and the kinetics of crystallization.1 The role of the solvent, temperature, pressure and other related kinetic factors may lead to the formation of alternative crystalline polymorphs.2 The existence of all possible polymorphic forms in experimentally determined crystal structures is difficult to predict using empirical methods practiced in the prediction of crystal structures of an organic molecule. CSP, once conceived to be a challenging exercise,3 has been successfully performed on rigid molecules and the success achieved from the first four blind tests is a testimony to this fact (CSP1999 (1st blind test), CSP2001 (2nd blind test), CSP2004 (3rd blind test) and CSP2007 (4th blind test)). For a conformationally flexible molecule (2–3 internal degrees of freedom), the fourth blind test was able to successfully predict the crystal structure of N-(dimethylthiocarbamoyl)benzothiazole-2-thione.4 However, the fifth blind test (CSP2010) attempted to predict the crystal structure of a highly flexible molecule (8 internal degrees of freedom) and the tests resulted in a successful prediction.5 Interestingly, Leusen and co-workers successfully predicted the crystal structure of another molecule in 2011, which could not be predicted in the 2001 blind test.6 In this study, we have introduced as a new challenge a moderately flexible organic molecule,7 namely an unsubstituted benzanilide [Scheme 1], and we have evaluated its crystal structure landscape (CSL).8 The CSL of a given compound is generated on account of the variations in molecular conformation and the arrangement of different packing motifs during the crystallization process. The possible crystal structures lie in a narrow range of energies. In our case, this molecule is moderately flexible with three internal degrees of freedom [Scheme 1] and contains 26 atoms [only the elements C, H, N, O, and F]. For our target molecule, the landscape was generated with Z' = 1 only and the relevant space groups, namely, P1, P
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , P21, Pc, P21/c, C2/c, P212121, Pna21, and Pca21 were only investigated. It should be kept in mind that the experimentally realized crystal structures of fluorinated benzanilides were observed to crystallize in the above-mentioned space groups and hence only these have been considered in the current study. The number of generated crystal structures in the potential energy landscape of the crystal is more than five thousand. Only one hundred lowest energy structures, under thermodynamic considerations, were analyzed. To map the CSL generated by this molecule, we have synthesized a series of different molecules wherein we have introduced fluorine atoms (as an isosteric replacement of the hydrogen atom/atoms) and their experimentally realized crystal structures did enable us to access the “hypothetical” structures predicted for the parent compound. One such study on benzoic acid and co-crystals of benzoic acid, wherein the role of replacement of H with F in accessing “hypothetical” structures of benzoic acid and its co-crystals, has been performed.8 It is noteworthy to extend the use of CSL to relatively flexible molecules containing organic fluorine. This is on account of the fact that such molecules exhibit dynamic disorder9 in the crystalline lattice. Furthermore, compounds containing fluorine have tremendous applications in all fields of science.10 It is interesting to note that the simplest possible chemical modification of a molecule can lead to the formation of altered crystal structures wherein the associated difference in energetics is extremely negligible. This has been observed in the case of the deuterated form of pyridine.11 Thus, the predicted crystal structures need to be verified with the experimental structures, and this requires performing a large number of crystallization trials to get the required crystal structure as a polymorph12 for a particular compound of interest. Finally, similar exercises were done on the CSP of paracetamol by Neumann and Perrin in 2009 (ref. 13) and its validity with the experimental structures (four polymorphic forms) was also realized paving the pathway to “polymorph instantiation”.
, P21, Pc, P21/c, C2/c, P212121, Pna21, and Pca21 were only investigated. It should be kept in mind that the experimentally realized crystal structures of fluorinated benzanilides were observed to crystallize in the above-mentioned space groups and hence only these have been considered in the current study. The number of generated crystal structures in the potential energy landscape of the crystal is more than five thousand. Only one hundred lowest energy structures, under thermodynamic considerations, were analyzed. To map the CSL generated by this molecule, we have synthesized a series of different molecules wherein we have introduced fluorine atoms (as an isosteric replacement of the hydrogen atom/atoms) and their experimentally realized crystal structures did enable us to access the “hypothetical” structures predicted for the parent compound. One such study on benzoic acid and co-crystals of benzoic acid, wherein the role of replacement of H with F in accessing “hypothetical” structures of benzoic acid and its co-crystals, has been performed.8 It is noteworthy to extend the use of CSL to relatively flexible molecules containing organic fluorine. This is on account of the fact that such molecules exhibit dynamic disorder9 in the crystalline lattice. Furthermore, compounds containing fluorine have tremendous applications in all fields of science.10 It is interesting to note that the simplest possible chemical modification of a molecule can lead to the formation of altered crystal structures wherein the associated difference in energetics is extremely negligible. This has been observed in the case of the deuterated form of pyridine.11 Thus, the predicted crystal structures need to be verified with the experimental structures, and this requires performing a large number of crystallization trials to get the required crystal structure as a polymorph12 for a particular compound of interest. Finally, similar exercises were done on the CSP of paracetamol by Neumann and Perrin in 2009 (ref. 13) and its validity with the experimental structures (four polymorphic forms) was also realized paving the pathway to “polymorph instantiation”.
Starting from a simple chemical diagram, computations related to CSL were performed with Materials Studio 6.1 using the COMPASS26 force field. We chose a default set up entitled “fine quality” for packing, geometry optimization, and clustering. This procedure is a crystal structure generation tool to obtain closely related crystal structures of the parent compound which qualify as polymorphs. Our analysis is thus based on the 100 most stable close-packed structures. The lattice energy of all the experimental crystal structures was calculated by the PIXELC module in the CLP computer program.14 The plot of the lattice energy versus density depicts that the space group P21/c gives the most efficient packing, as is reflected in the relatively high magnitudes of the density of the compounds [see ESI† Fig. S3].
To understand the formation of organic solids, it is important to recognize the role of non-covalent interactions in the study of the CSL. In this regard, the presence of a strong and well-defined N–H⋯O hydrogen bond is highly effective in the assembly of benzanilide structures.15 Crystal structures also display the formation of C–H⋯O, C–H⋯π and π⋯π intermolecular interactions in the crystalline lattice. An isosteric replacement of the hydrogen atom with the fluorine atom on the phenyl ring results in the formation of C–H⋯F intermolecular interactions and these are classified as H-bonds when the interaction distance is short16 and are associated with directional characteristics. Our study involves the formation of alternative packing modes in these isomeric molecules through the process of CSP. We intend to simplify the relation between the theoretically predicted structures of the unsubstituted benzanilide and the experimentally realized crystal structures. These are obtained by the ongoing change in the position of the fluorine atoms from ortho to meta to para in different isomeric molecules.
To verify such a study, based on prediction, with the experimental structure, we divided the results obtained into a total of nine groups in accordance with their space group and unit cell type. The experimental unsubstituted benzanilide P0000 [CSD code: BZANIL02] has the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and the following lattice parameters: a = 5.352 Å, b = 7.971 Å, and c = 12.471 Å. This structure belongs to group 1 with the unit cell type 5-8-12 and is ranked at the 4th and 11th positions in the CSL [Table 1]. This structure is held by strong N–H⋯O hydrogen bonds and multiple weak C–H⋯π interactions. We further consider monofluorobenzanilides P4000 (P
and the following lattice parameters: a = 5.352 Å, b = 7.971 Å, and c = 12.471 Å. This structure belongs to group 1 with the unit cell type 5-8-12 and is ranked at the 4th and 11th positions in the CSL [Table 1]. This structure is held by strong N–H⋯O hydrogen bonds and multiple weak C–H⋯π interactions. We further consider monofluorobenzanilides P4000 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 5.369 Å, 7.862 Å, and 12.892 Å) and P0040 (P
, 5.369 Å, 7.862 Å, and 12.892 Å) and P0040 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 5.349 Å, 7.599 Å, and 12.945 Å). The crystal structures of these molecules match with those obtained from the CSL of benzanilide, ranked at the 4th and 11th positions in the energy–density plot [Fig. 1] in the same group. We further consider difluorobenzanilides (two fluorine atoms present in one or both of the phenyl rings), P4040 (P
, 5.349 Å, 7.599 Å, and 12.945 Å). The crystal structures of these molecules match with those obtained from the CSL of benzanilide, ranked at the 4th and 11th positions in the energy–density plot [Fig. 1] in the same group. We further consider difluorobenzanilides (two fluorine atoms present in one or both of the phenyl rings), P4040 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 5.460 Å, 7.693 Å, and 13.038 Å), P0034 (P
, 5.460 Å, 7.693 Å, and 13.038 Å), P0034 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 5.4385 Å, 7.5939 Å, and 12.8178 Å), P0035 (P
, 5.4385 Å, 7.5939 Å, and 12.8178 Å), P0035 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 5.1300 Å, 8.8893 Å, and 11.6782 Å) and P3400 (P
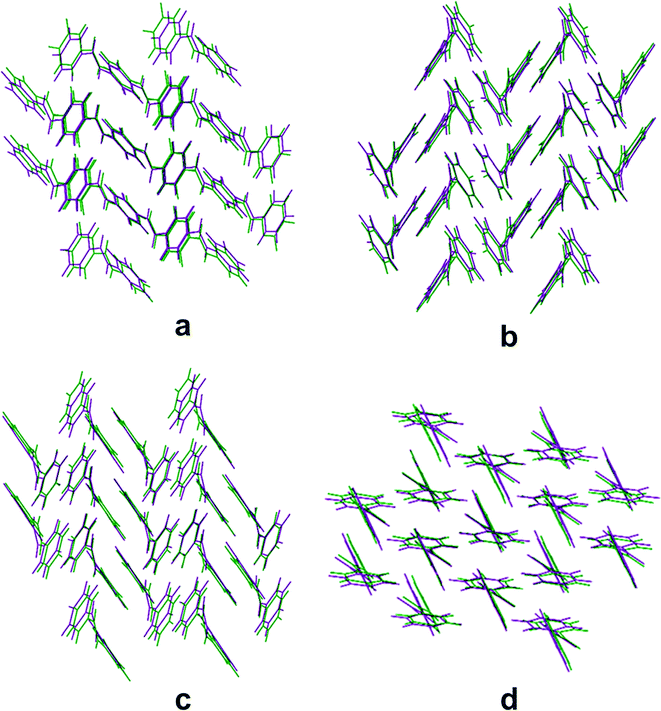
, 5.1300 Å, 8.8893 Å, and 11.6782 Å) and P3400 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 5.4838 Å, 7.7928 Å, and 12.6887 Å), which are also similar and their crystal structures are also comparable with the CSL of benzanilide. It is interesting to note that the overlay diagrams for P4000, P4040, P0034 and P3400 are almost similar to the 4th ranked structure [Fig. 2]. In continuation of our hypothesis, we now consider the case of tetrafluorobenzanilide (two fluorine atoms in each of the two phenyl rings) P2334 (P
, 5.4838 Å, 7.7928 Å, and 12.6887 Å), which are also similar and their crystal structures are also comparable with the CSL of benzanilide. It is interesting to note that the overlay diagrams for P4000, P4040, P0034 and P3400 are almost similar to the 4th ranked structure [Fig. 2]. In continuation of our hypothesis, we now consider the case of tetrafluorobenzanilide (two fluorine atoms in each of the two phenyl rings) P2334 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 4.9918 Å, 9.3610 Å, and 12.0172 Å), which belongs to the same group (see the ESI† for the overlay and RMS deviation, Fig. S2(a–h)). These structures are also constructed via N–H···O hydrogen bonds, but the crystal structures are arranged utilizing other related weak interactions. In P0034, P3400, P4000, P0040 and P4040, the C–H⋯π interactions are present in the crystal packing. In the case of P0035 and P2334, C–H⋯F and π⋯π are the more significant interactions.
, 4.9918 Å, 9.3610 Å, and 12.0172 Å), which belongs to the same group (see the ESI† for the overlay and RMS deviation, Fig. S2(a–h)). These structures are also constructed via N–H···O hydrogen bonds, but the crystal structures are arranged utilizing other related weak interactions. In P0034, P3400, P4000, P0040 and P4040, the C–H⋯π interactions are present in the crystal packing. In the case of P0035 and P2334, C–H⋯F and π⋯π are the more significant interactions.
| Group | Compound code | Unit cell type | Rank | Space groups |
|---|---|---|---|---|
| Group 1 | P0000, P0034, P0035, P2334, P3400, P4000, P0040, P4040 | 5-8-12 | 4th and 11th |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Group 2 | P3500 | 10-5-20 | 15th and 65th | P21/c |
| Group 3 | P0024, P3423, P3435, QUKVUN, P2324, P2423, P3000 | 5-8-25 | 48th, 88th, and 93rd | P21/c |
| Group 4 | P2323 | 5-9-23 | 68th | P212121 |
| Group 5 | P2040 (Form 2), P0020 | 5-5-19 | 14th, 17th, and 26th | P21 |
| Group 6 | P2335 | 5-5-12 | 73rd | P1 |
| Group 7 | P0026 | 10-21-5 | 23rd | Pna21 |
| Group 8 | P2500, P2040 (Form 1), P3020 | 24-5-8 | 2nd, 6th, 39th, 50th, and 52nd | Pca21 |
| Group 9 | P2400 | 5-5-19 | 24th | Pc |
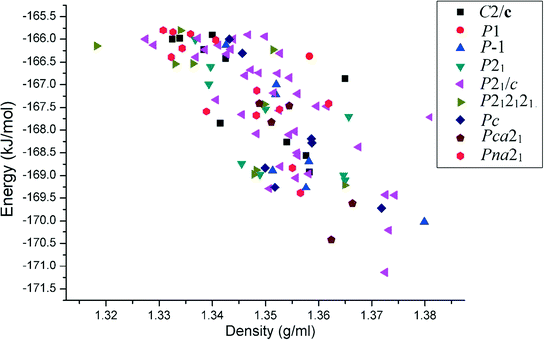 | ||
| Fig. 1 Plot of the relative lattice energies versus densities of the top 100 predicted crystal structures for the unsubstituted benzanilide in different space groups. | ||
The isomeric difluorobenzanilide P3500 (P21/n, 10.179 Å, 5.150 Å, and 20.053 Å) belongs to group 2 in the centrosymmetric P21/c space group and its crystal structure is similar to that of the 15th and 65th ranked benzanilide in the energy–density landscape. The third group is the 5-8-25 structure type in the same centrosymmetric P21/c space group. Monofluorobenzanilide P3000 (P21/c, 8.069 Å, 5.391 Å, and 23.238 Å), difluorobenzanilide P0024 (P21/n, 5.4223 Å, 7.6977 Å, and 25.4353 Å), tetrafluorobenzanilides P3423 (P21/n, 5.1818 Å, 8.312 Å, and 25.739 Å), P3435 (P21/n, 5.1818 Å, 8.312 Å, and 25.517 Å) P2324 (P21/n, 9.456 Å, 4.7786 Å, and 24.253 Å), and P2423 (P21/n, 8.8818 Å, 4.9233 Å, and 24.9499 Å) and pentafluorobenzanilide (five fluorine atoms in one ring) QUKVUN (P2/c, 4.982 Å, 9.724 Å, and 25.775 Å) belong to this structure type with ranks 48th, 88th and 93rd as obtained from the energy–density ranking [see ESI† Fig. S2(i–k)]. The third group with the P21/c space group is primarily seen in the experimentally determined crystal structures of highly fluorinated benzanilides, P3423, P3435, QUKVUN, P2324 and P2423, wherein C–H⋯F and π⋯π are the decisive interactions. The π⋯π interaction is mainly predominant in substituted benzanilides containing a higher number of fluorine atoms. This is because the incorporation of such an electronegative atom changes the uniform electron density distribution on the benzene ring [Fig. 4]. The C–H⋯π interactions are significant for the crystal structure of P0024. A detailed investigation of the energetics and topological characteristics of different supramolecular constructs utilizing weak interactions for this class of molecules shall be reported separately.17
The fourth group belongs to the orthorhombic crystal system and the P212121 space group. The molecule containing tetrafluorinated benzanilide (two fluorine atoms in each ring) P2323 (P212121, 5.0295 Å, 8.838 Å, and 24.4547 Å) occupies the 68th position in the energy–density ranking list (see ESI† Fig. S2(l)). The crystal structure is arranged via C–H⋯F and π⋯π interactions. Monofluorinated benzanilide P2040 (form 2) (P21, 4.9617 Å, 5.4859 Å, and 19.174 Å) as well as the higher difluorobenzanilide P0020 (P21, 5.421 Å, 6.258 Å, 15.534 Å, and 97.45 Å) belong to group 5 which present specific positions in the ranking list, namely 14th, 17th and 26th, respectively [see ESI† Fig. S2(m–o) for the overlay diagrams]. The overlay diagram for P2040 (form 2) is almost similar to the 26th ranked structure [Fig. 3].
Only one theoretically predicted crystal structure out of the hundred obtained structures, containing the triclinic P1 space group and ranked 73rd in the CSL (corresponding to group 6) was observed. This nicely matches with the crystal structure landscape of tetrafluorobenzanilide (two fluorine atoms in each ring) P2335 (P1, 4.6457 Å, 5.0544 Å, and 11.8597 Å) [Fig. 3]. The 23rd position in the rank list is occupied by difluorobenzanilide P0026 (Pna21, 9.914 Å, 21.812 Å, and 4.923 Å) in group 7 [see ESI† Fig. S2(p)] crystallizing in the orthorhombic crystal system.
Difluorobenzanilides (two fluorine atoms may be present in one ring or both rings) P2500 (Pca21, 24.3084 Å, 5.0243 Å, and 8.4598 Å), P2040 (form 1) (Pca21, 25.563 Å, 4.969 Å, and 8.250 Å) and P3020 (Pca21, 24.660 Å, 5.203 Å, and 8.244 Å) belonging to the Pca21 space group are present at specific positions in the ranking list [Fig. 3], namely 2nd, 6th, 39th, 50th, and 52nd in group 8 [see ESI† Fig. S2(q–s)]. It is indeed interesting to obtain a short contact to the fluorine atom in the case of P2500, [C13–H13⋯F1 hydrogen bond (neutron value: 2.09 Å, 154°)] [Fig. 4]. Finally, in group 9, difluorobenzanilide P2400 (Pn, 5.535 Å, 5.035 Å, and 19.29 Å) is similar to the 24th rank predicted crystal structure on the CSL [see ESI† Fig. S2(t)]. The short C12A–H12A⋯F1A hydrogen bond (neutron value: 2.29 Å, 174°) is responsible for the crystal packing along with the presence of the C3–H3⋯O1 hydrogen bond (neutron value: 2.66 Å, 146°) [Fig. 4].
To further substantiate our understanding of the CSL in fluorine-containing molecules, we have undertaken the exercise of obtaining the landscape of crystal structures of a decafluoro-substituted benzanilide, wherein all the ten hydrogen atoms on the two phenyl rings are replaced with fluorine atoms. These molecules also provide the required crystal energy landscape for experimental realization of the crystal structures of mono-, di-, tetra-, or related polyfluoro-substituted benzanilides [see ESI† Table S4]. These compounds generate a very similar group of crystal structure types and unit cell configurations. It was observed that the CSL generated for the deca-fluorinated benzanilide does not produce the required overlay diagram when mapped to the experimentally determined crystal structures. Hence, no values of the “similarity index (RMS deviation)” are reported. This may be on account of the variations in the crystal density of the calculated landscape for the decafluorinated benzanilide which lies in the range of 2.09 g ml−1 to 2.21 g ml−1, whereas the densities for the experimentally determined crystal structures (corresponding to the presence of different fluorine atoms) lie in the range of 1.30–1.71 g ml−1 which is closer to the range of density (1.31 g ml−1 to 1.39 g ml−1) obtained from the CSL of the unsubstituted benzanilide. The energy density graph [ESI† Fig. S3], the table [ESI† Table 5] and the CIF of the first 100 predicted structures corresponding to the deca-fluorinated benzanilide are provided in the ESI.†
In conclusion, the landscape depends on the number of fluorine atoms and the position of the fluorine atoms. When the number of fluorine atoms is low, i.e. one or two, then the crystal packing is primarily guided by C–H⋯π interactions and in the case of a higher number of fluorine atoms, the prevalence of C–H⋯F, F⋯π, and π⋯π interactions is important for the formation of the crystal structures. This is a subtle, yet important structural feature responsible for the formation of crystals utilizing weak interactions. The position of fluorine is also important in considering the factors that are instrumental in the finally obtained crystal structure (for example, [P0034 and P3400], [P2324 and P2423], and [P4000 and P0040] are present in the same group). This entire exercise reflects a pivotal point in the crystal chemistry of organic solids which is equivalent to stating the fact that “chemical modification” leads to the experimental realization of different “forms” of a compound which otherwise are not accessible under routine crystallization conditions for the molecule of interest. The isolation of polymorphs for the poly-fluorinated benzanilides is expected to render deeper insights into the role of weak interactions and facilitates a greater degree of mapping the crystal structure landscape of the parent compound.
Acknowledgements
PKM and DC thank the reviewers for their suggestions towards the improvement of the manuscript. PKM thanks CSIR for the senior research fellowship. We are also thankful to IISER Bhopal for the research facilities and infrastructure. DC acknowledges funding from the DST-SERB Scheme.Notes and references
- (a) S. L. Price, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC; (b) S. L. Price, Phys. Chem. Chem. Phys., 2008, 10, 1996–2009 RSC; (c) G. M. Day, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 1023–1033 CrossRef CAS; (d) G. M. Day, Crystallogr. Rev., 2011, 17, 3–52 CrossRef; (e) D. E. Braun, M. Orlova and U. J. Griesser, Cryst. Growth Des., 2014, 14, 4895–4900 CrossRef CAS; (f) D. E. Braun, J. A. McMahon, L. H. Koztecki, S. L. Price and S. M. Reutzel-Edens, Cryst. Growth Des., 2014, 14, 2056–2072 CrossRef CAS; (g) A. T. Hulme, S. L. Price and D. A. Tocher, J. Am. Chem. Soc., 2005, 127, 1116–1117 CrossRef CAS PubMed.
- S. L. Price, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 313–328 CrossRef CAS PubMed.
- (a) A. Gavezzotti, CrystEngComm, 2002, 4(61), 343–347 RSC; (b) A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314 CrossRef CAS.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. D. Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125 CAS.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. D. Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551 CAS.
- (a) M. A. Neumann, F. J. J. Leusen and J. Kendrick, Angew. Chem., Int. Ed., 2008, 47, 2427–2430 CrossRef CAS PubMed; (b) H. C. S. Chan, J. Kendrick and J. J. Leusen, Angew. Chem., Int. Ed., 2011, 50, 2979–2981 CrossRef CAS PubMed.
- C. Ouvrard and S. L. Price, Cryst. Growth Des., 2004, 4, 1119–1127 CAS.
- (a) R. Dubey, M. S. Pavan and G. R. Desiraju, Chem. Commun., 2012, 48, 9020–9022 RSC; (b) R. Dubey and G. R. Desiraju, Chem. Commun., 2014, 50, 1181–1184 RSC.
- S. K. Nayak, M. K. Reddy, D. Chopra and T. N. G. Row, CrystEngComm, 2012, 14, 200–210 RSC.
- K. Muller, C. Faeh and F. Diederich, Science, 2007, 317, 1881–1886 CrossRef PubMed.
- S. Crawford, M. T. Kirchner, D. Bläser, R. Boese, W. I. F. David, A. Dawson, A. Gehrke, R. M. Ibberson, W. G. Marshall, S. Parsons and O. Yamamuro, Angew. Chem., Int. Ed., 2009, 48, 755–757 CrossRef CAS PubMed.
- D. Chopra and T. N. G. Row, Cryst. Growth Des., 2005, 5, 1679–1681 CAS.
- M. A. Neumann and M. A. Perrin, CrystEngComm, 2009, 11, 2475–2479 RSC.
- (a) A. Gavezzotti, New J. Chem., 2011, 35, 1360 RSC; (b) A. Gavezzotti, J. Phys. Chem. B, 2003, 107, 2344 CrossRef CAS; (c) A. Gavezzotti, J. Phys. Chem. B, 2002, 106, 4145 CrossRef CAS.
- D. Chopra and T. N. G. Row, CrystEngComm, 2008, 10, 54–67 RSC.
- P. Panini and D. Chopra, Cryst. Growth Des., 2014, 14, 3155–3168 CAS.
- P. K. Mondal and D. Chopra, CrystEngComm, 2015 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1407974–1407988. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ce01721a |
| This journal is © The Royal Society of Chemistry 2016 |