Using simulation to understand the structure and properties of hydrated amorphous calcium carbonate†
Riccardo
Innocenti Malini
*a,
Yuriy G.
Bushuev
bc,
Shaun A.
Hall
a,
Colin L.
Freeman
a,
P. Mark
Rodger
bc and
John H.
Harding
a
aDepartment of Materials Science and Engineering, University of Sheffield, Mappin St., Sheffield S1 3JD, UK. E-mail: mta08ri@sheffield.ac.uk
bDepartment of Chemistry, University of Warwick, Gibbet Hill Rd., Coventry CV4 7AL, UK
cCentre for Scientific Computing, University of Warwick, Gibbet Hill Rd., Coventry CV4 7AL, UK
First published on 26th November 2015
Abstract
We report results from studies using four different protocols to prepare hydrated amorphous calcium carbonate, ranging from random initial structures to melting hydrated mineral structures. All protocols give good agreement with experimental X-ray structure factors. However, the thermodynamic properties, ion coordination environments, and distribution of water for the structures produced by the protocols show statistically significant variation depending on the protocols used. We discuss the diffusivity of water through the various structures and its relation to experiments. We show that one protocol (based on melting ikaite) gives a structure where the water is mobile, due to the presence of porosity in the amorphous structure. We conclude that our models of hydrated amorphous calcium carbonate do give a range of behaviour that resembles that observed experimentally, although the variation is less marked in the simulations than in experiments.
1 Introduction
The process of biomineralisation has intrigued the scientific community for nearly a century.1 Living systems can fine-tune the precipitation of minerals, leading to structures with both remarkable morphologies over various length scales and unusual physical properties.2 These structures are often formed through the initial precipitation of hydrated amorphous precursors, as has been observed in both vertebrates and invertebrates.3–5 Hydrated amorphous calcium carbonate is an example of such a phase and is the precursor to calcite (usually),6 aragonite7 and vaterite8 in many living organisms. Control over structures, polymorph selection and properties is achieved by a complex interplay between the solution chemistry,9 the presence of inorganic10,11 or organic12–14 molecules and the physical conditions15,16 under which the phase precipitates. These processes have inspired new synthetic methods including the replication of the sea urchin skeletal plate using solid substrates17 or the fabrication of micro-lens arrays by self-assembly from amorphous calcium carbonate (ACC) mediated by organic molecules.18 However, before being able to use such approaches effectively, the mechanisms of morphological control and polymorph selection must be fully understood. Indeed, since ACC is a common starting point from which polymorph selection occurs in carbonate biominerals, a deeper knowledge of the structure and properties of ACC is a key step in gaining this understanding.Experimental evidence, from analysis of either biologically or synthetically prepared samples, indicates that ACC, CaCO3·nH2O, can exist in a number of different forms. These were initially distinguished by their stability, which is dependent upon the presence or absence of water within the structure.19 Although less hydrated ACC has been reported in some systems,20 there is now a consensus that the biologically relevant composition is chemically similar to monohydrocalcite with one water molecule per formula unit (n ∼ 1).21 Hydrated ACC has been observed to persist for days to months at room temperature, while anhydrous ACC readily transforms into one of the final crystalline polymorphs.10,19 Previous analysis by X-ray total scattering showed that both short and medium range order are present within ACC. No correlation, however, in the pair distribution function could be found for distances greater than 10 Å suggesting the absence of long range order.22,23 Ca K-edge extended X-ray absorption spectroscopy has been used to determine the first coordination shell of the calcium ion. Approximately seven oxygen atoms were found in the calcium coordination shell on average, with typical bond lengths between 2.40 and 2.50 Å, but the details proved to be highly dependent on the sample.22,24 Proton solid-state nuclear magnetic resonance showed that two different types of water are present within the structure. One is largely immobile and labelled as structural, but the other showed an increased mobility.22,25,26 The location of this water appears, again, to be dependent on the sample origin. In synthetic samples the mobile water is in contact with the carbonate ions22 while in biogenic samples no mobile water is identified close to the carbonate ions. Instead it was hypothesized by Reeder et al. to be segregated in channels.25
Molecular modelling has also been used to study both anhydrous27–29 and hydrated ACC.24,29–33 Molecular modelling has the great advantage of providing a wealth of molecular-level information about structure and dynamics. The converse of this is that it is limited to short time and length scales. In the context of an amorphous solid—such as ACC, whether with or without water—this must always raise questions about how comprehensively the range of possible molecular configurations is being sampled. Given the experimental evidence that different forms of ACC do exist, this becomes particularly important, and may raise questions about the comparability of different modelling studies. Agreement with the limited amount of structural information is not, in itself, sufficient to guarantee that the proposed structure is correct. For example, not all the proposed ACC structures that are consistent with experimental scattering data prove to be stable in subsequent molecular dynamics simulations.30 It is therefore of considerable importance to characterise the degree of comparability with experiment (and indeed with each other) that may be expected between molecular simulation studies that use different protocols for generating the ACC structures. The purpose of this paper is to provide precisely this comparison. We report results from studies using four different protocols to prepare the ACC, ranging from random initial structures to melting hydrated mineral structures. It is found that all protocols give good agreement with structure factors obtained from diffraction experiments. Some variations are found in the thermodynamic properties, ion coordination environments, and behaviour of water, but these variations are generally modest.
2 Methods
2.1 Simulation methods
We have used classical molecular dynamics (MD) simulations to investigate amorphous CaCO3·H2O. Force fields were selected which are known to predict accurately both the structure and energetics of crystalline CaCO3 polymorphs and the thermodynamics of ion solvation, namely those of Raiteri and Gale29 and Demichelis et al.34 (note that the use of TIP3P35 or SPC/Fw36 for water, respectively, is embedded within these force-fields). The two force-fields differ primarily in that the latter includes intramolecular forces in order to obtain a better comparison to solid state vibrational spectra and to capture the variation in carbonate bond lengths found in vaterite. Within our studies, we found no significant difference between these two force-fields, and so present the results using the Demichelis et al. potential.34All simulations were performed with the DL_POLY code (DL_POLY 4.03.4 and 2.20, and DL_POLY_Classic 1.9),37,38 using the NPT ensemble at T = 300 K and P = 0.1 MPa implemented via a Nosé–Hoover thermostat and barostat with 0.1 ps and 1.0 ps relaxation times respectively. Orthorhombic periodic boundaries conditions were used throughout, except in the case of the monohydrocalcite structure where hexagonal boundary conditions were used due to the unit cell of this mineral. As will be shown later, using different periodic boundary conditions does not affect the results. The cut-off for short-range interactions was set to 9.0 Å, as defined by the chosen force field.34 Calculations were performed with electrostatic interactions treated using either the smooth particle mesh Ewald (SPME) method or the standard Ewald sum. A comparison of the calculations showed no significant difference in any calculated properties; data using SPME electrostatics are reported unless otherwise specified. Production trajectories with a minimum time of 2 ns, though more typically ca. 5 ns, were generated for analysis. The timestep for all the simulations was 1 fs.
2.2 ACC preparation protocols
Four different methods of preparing the initial configuration were used. Two involved random placement of the ions, while the other two melted hydrated crystalline forms of calcium carbonate (monohydrocalcite and ikaite) followed by further steps in the case of ikaite to obtain the required CaCO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratio. Full details are given below.
H2O ratio. Full details are given below.
ACCRLJ: the system was initially prepared by inserting the ions and water molecules at random in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (2880 CaCO3 units and 8640 water molecules). The system was then simulated at 750 K (3 ns, NVT) with all electrostatic interactions switched off, and introducing a Ca–Ca Lennard-Jones interaction (σ = 5.17 Å, ε = 0.00674 eV) since cation repulsion is enforced only via electrostatic interactions in our two chosen force-fields. This produces a random Lennard-Jones (RLJ) analogue of ACC. Subsequently water molecules were removed at random to obtain a composition of CaCO3·H2O, the full published force-field reinstated, and a 5 ns NPT simulation conducted at 300 K to allow the system to relax. Energy and volume were monitored over this time to confirm that relaxation was complete over the 5 ns.
3 (2880 CaCO3 units and 8640 water molecules). The system was then simulated at 750 K (3 ns, NVT) with all electrostatic interactions switched off, and introducing a Ca–Ca Lennard-Jones interaction (σ = 5.17 Å, ε = 0.00674 eV) since cation repulsion is enforced only via electrostatic interactions in our two chosen force-fields. This produces a random Lennard-Jones (RLJ) analogue of ACC. Subsequently water molecules were removed at random to obtain a composition of CaCO3·H2O, the full published force-field reinstated, and a 5 ns NPT simulation conducted at 300 K to allow the system to relax. Energy and volume were monitored over this time to confirm that relaxation was complete over the 5 ns.
ACCRPm: the system was initially prepared using the Packmol package, which randomly inserts molecules or atoms within set boundaries.39 The 486 formula units of CaCO3·H2O were inserted with a tolerance of 2.20 Å (minimum distance between inserted particles). The system was first simulated at 3000 K (2 ns, NVT, V = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111.36 Å3) then cooled down through successive steps (1 ns, ΔT = 300 K, NVT) to 300 K.
111.36 Å3) then cooled down through successive steps (1 ns, ΔT = 300 K, NVT) to 300 K.
ACCIk: a nanocrystal of ikaite (2880 formula units) was embedded in liquid water (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules) and simulated first at 1500 K (1 ns, NVT, V = 221
000 water molecules) and simulated first at 1500 K (1 ns, NVT, V = 221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225.58 Å3) and then at 300 K (5 ns, NPT, P = 0.1 MPa). Water molecules were then removed at random to produce a composition CaCO3·H2O, and the system again simulated at 1500 K (1 ns, NVT, volume taken from the end of the previous simulation) and at 300 K (5 ns, NPT, P = 0.1 MPa) while monitoring energy and volume to confirm relaxation was complete. The ikaite underwent a partial phase separation during the melting phase, with the consequence that the final system contained irregular pores of water, some of which spanned the simulation box; these were not found in the other three systems. This system could appropriately be described as microporous ACC.
225.58 Å3) and then at 300 K (5 ns, NPT, P = 0.1 MPa). Water molecules were then removed at random to produce a composition CaCO3·H2O, and the system again simulated at 1500 K (1 ns, NVT, volume taken from the end of the previous simulation) and at 300 K (5 ns, NPT, P = 0.1 MPa) while monitoring energy and volume to confirm relaxation was complete. The ikaite underwent a partial phase separation during the melting phase, with the consequence that the final system contained irregular pores of water, some of which spanned the simulation box; these were not found in the other three systems. This system could appropriately be described as microporous ACC.
ACCMHC: a nanocrystal of monohydrocalcite (MHC) containing 576 formula units was simulated at 3000 K (2 ns, NVT, a = b = 41.90 Å, c = 30.33 Å, α = β = 90.0°, γ = 120.0°) and then cooled down through successive steps (1 ns, ΔT = 300 K, NVT) to 300 K while retaining the initial volume. A final equilibration simulation was conducted at 300 K (5 ns, NPT, P = 0.1 MPa) while monitoring energy and volume to confirm relaxation was complete.
2.3 Analysis
Where needed for analysis, coordination radii were defined from the first minimum in the appropriate pair distribution function: 2.8 Å for Ca–Oall, 4.01 Å for Ca–C, and 3.8 Å for Ow–Ow (where Ow denotes an oxygen atom that is part of a water molecule; oxygen atoms within the carbonate ions will be denoted Oc, and Oall describes all oxygen atoms). To calculate free volumes and areas a probe method was chosen, namely the Connolly surface.40 This is a method that has been commonly used in the literature to represent regions from which solvent is excluded by measuring the volume accessible to a probe (see, for example its use in analysing microstructure-dependent diffusion by Zhang et al. (2009)41 and mineral-water surfaces by Zeitler et al. (2012)42). The Connolly free volumes and areas were calculated with the Materials Studio package using a probe with a radius of 1.575 Å (corresponds to σ/2 in the water potential), a van der Waals scale factor of 1.0 and the grid interval set to 0.15 (ultra-fine).We have used a perfusion analysis to identify the presence of water channels. Bulk ACC simulation cells were modified by increasing the z component of the simulation box to convert the bulk cell into a slab separated by a vacuum gap that was subsequently filled with argon (gap width, ΔLz = 50.0 Å, density of Ar atoms in the ‘vacuum’ gap, ρargon = 1.203 g cm−3, NVT, Lennard-Jones interactions for argon:43σ = 3.405 Å, ε = 0.991 kJ mol−1) and all water molecules were then removed from the ACC sample. Lorenz–Berthelot mixing rules were used for all the Ar/CaCO3ε terms, while the σ term was chosen to be 2.3 Å for all Ar–X interactions, as this corresponded approximately to the smallest distance observed in the radial distribution function between Ow and Oc. In subsequent MD simulations (1 ns, NVT) the ingress of Ar into the ACC was used to identify potential water-filled channels accessible to the surface.
Diffusion coefficients, D, have been calculated from the long-time slope of the average mean square displacement of atoms and ions over time, following normal procedures and averaging over multiple time origins, t0:44
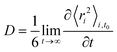 | (1) |
| ri = ∥ ri(t + t0) − ri(t0) ∥ |
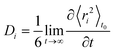 | (2) |
3. Results and discussion
3.1 Pair distribution functions
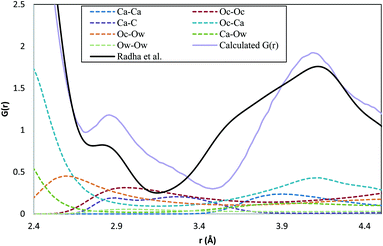
Total distribution functions calculated from the simulated structures are presented in Fig. 1, together with the experimental data of Radha et al.45 It is clear from Fig. 1 that there is good agreement between the experimental and simulated curves, and that the four different protocols lead to essentially identical total distribution functions. Such agreement is a necessary condition for a good ACC model, but is not in itself sufficient. It is only for spherical particles that the radial distribution functions give a complete specification of the thermodynamic and structural properties of the material.46 In general, many configurational ensembles map onto the same total distribution function, and so significant structural differences can still exist between systems that generate the same distribution functions. This point will be considered further in subsequent sections.The large difference observed at 1.3 Å is due to a comparatively rigid C–Oc bond in the force field used for the simulations compared to experimental measurements. Other small differences are apparent between the experimental and simulated curves in the region 2.5–4.0 Å, and it is instructive to consider these in more detail. Because our discussion is focused on this region, we will number the peaks and troughs from the first intermolecular peak, at ca. 2.3 Å. The component pair distribution functions in this region are depicted in Fig. 2. In the total distribution function, the simulated curve shows a second peak at 2.9 Å that is present more as a shoulder to the main peak in the experimental data. The experimental curve also shows a shoulder to the left of the second peak (3.5 Å) that is missing in the simulated curve, with the result that the minimum between these first two peaks shifts from 3.15 Å (experiment) to 3.5 Å (simulation). The dominant pair contributions to this region of the total distribution function come from: Oc–Ca, which is essentially flat across this range; Oc–Ow, which shows a steady monotonic decrease in intensity; and Oc–Oc and Ca–C, both of which peak in the range 2.9–3.5 Å. At the same time, there is very little contribution from Ca–Ow in the range 2.9–3.5 Å, and only a small contribution for 3.5–4.0 Å. Intriguingly, the Ca–C shows two peaks, one coincident with the overstated shoulder at 2.9 Å, and the other near the understated minimum at 3.15 Å.
These small differences between simulation and experiment could be due to subtle deficiencies in the force-field, or to incomplete characterisation of the experimental material at the nanoscale. Recent simulation studies examining the surface organisation of water molecules in carbonates have demonstrated that the force-fields do not perfectly replicate the X-ray reflectivity data,47 and the observations on Fig. 2 would be consistent with a force-field that allowed Ca–C contacts to become too close. On the other hand, nanoscale segregation of the water phases, impurities or non-stoichiometry within the experimental ACC samples cannot be ruled out. Given the potential for differences arising from the large scale structural variability of this phase, the small overall discrepancies between the simulated and experimental total distribution functions, and the coincidence of the major peak positions and heights, we conclude that the major features of ACC are well reproduced within the four series of simulations.
3.2 Thermodynamic properties of ACC
Potential energies and densities for the four ACC systems are shown in Table 1. The densities of the four simulated ACC systems fall between those of monohydrocalcite and vaterite, indicating a more densely packed structure than is found in the hydrated crystalline phase and implying that there is little space for empty pores in these models of ACC.| System | ρ/g cm−3 | U conf/kJ mol−1 | ΔUconf/kJ mol−1 |
|---|---|---|---|
| ACCRLJ | 2.63 | −2908.62 | 3.38 |
| ACCRPm | 2.58 | −2910.45 | 1.55 |
| ACCIk | 2.54 | −2896.44 | 15.56 |
| ACCMHC | 2.62 | −2912.00 | 0 |
| Monohydrocalcite | 2.37 | ||
| Ikaite | 1.77 | ||
| Calcite | 2.76 | ||
| Aragonite | 3.01 | ||
| Vaterite | 2.68 |
Comparison of the densities with experiment is difficult; there are only a few results available and the composition of experimental ACCs is not often analysed. Two studies have analysed the density using SAX measurements and found values of 1.62 and 1.9 g cm−3, respectively.48,49 The main difference between the two experiments was the initial concentration of solutes, which was doubled in the second. In a later study, Faatz et al. also obtained a value of 1.9 g cm−3 using Brillouin spectroscopy for an ACC with 0.5 H2O per formula unit.50 The amount of water in the sample was obtained by thermogravimetric analysis (TGA). However, Michel et al. used the same method as Faatz et al. to prepare their ACC and their TGA analysis showed a water content of 1.29 H2O per formula unit.22 The differences obtained within these studies, and the fact that the same experiments appear to give very different values, suggests that it is very difficult to measure the density accurately for a well-defined composition. Measurements taken at different times and in different environments, give results relating to different compositions and structures. If the density measured by Faatz et al. is assumed to be representative, it suggests that a larger number of void spaces are present in the structure of experimental ACC than for any of the simulated structures. However, such a density could also result from a more highly hydrated ACC (as for Michel et al.22).
ACCIk is the least mechanically stable configuration and shows the maximum variation in configurational energy while the other structures are all within room temperature fluctuations. For the case of ACCIk the difference is 15.56 kJ mol–1, which is only 0.5% of the total energy. However, it is comparable with the dissolution enthalpy of calcite (−12.5 kJ mol−1 experimentally51 and −38.6 kJ mol−1 simulated with the current force field29) and with typical hydrogen bond energies, and so cannot be considered inconsequential. Intriguingly, the energy differences show little correlation with density, which indicates that the variation arises from structural differences and not just from a size-scaling of the Coulombic energy.
3.3 Ion coordination
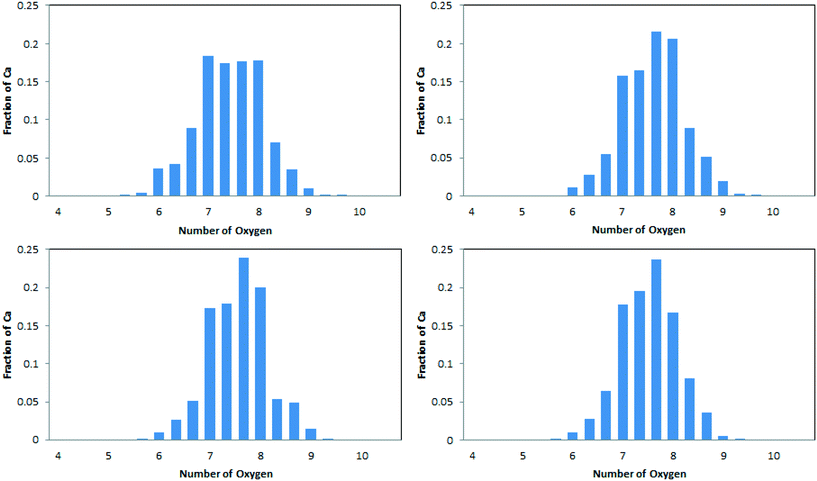
The average coordination numbers for oxygen around calcium have been thoroughly analysed in the literature, and can readily be compared with our results (see Table 2). A more detailed analysis, in terms of the distribution of coordination numbers, is also available from simulation and is depicted in Fig. 3. Values for our simulated ACC are in the range 7.43–7.64. This sits well within the range of experimental results. Extended X-ray absorption fine structure analysis (EXAFS) of synthetic ACCs in different studies showed scattered results between 5 and 9 oxygen atoms in the coordination sphere of calcium.10,19,23,52–54 The distribution of Ca–Oall in Fig. 3 is in agreement with this spread, with Ca2+ ions found to have coordination numbers between 6 and 9. Our simulated data also complies with the analysis of biogenic ACC obtained from the sea-tulip Pyura pachidermatina (7.4 ± 0.5).52| System | C N (Ca–Ox) | C N (Ca–C) | ||
|---|---|---|---|---|
| Oall | Ow | Oc | C | |
| a XAFS data, ref. 8, 10, 19, 23, 52–54. b ACC from Pyura pachidermatina.52 | ||||
| ACCRLJ | 7.64 ± 0.01 | 1.71 ± 0.02 | 5.92 ± 0.02 | 5.17 ± 0.01 |
| ACCRPm | 7.55 ± 0.03 | 1.52 ± 0.05 | 6.03 ± 0.05 | 5.20 ± 0.04 |
| ACCMHC | 7.63 ± 0.02 | 1.58 ± 0.04 | 6.04 ± 0.04 | 5.22 ± 0.03 |
| ACCIk | 7.43 ± 0.01 | 1.21 ± 0.03 | 6.22 ± 0.02 | 5.54 ± 0.02 |
| ACC (expt) | 5–9a | — | — | — |
| 7.4 ± 0.5b | 4.5 ± 2b | |||
| Calcite | 6 | 0 | 6 | 6 |
| Aragonite | 9 | 0 | 9 | 6 |
| Vaterite | 8 | 0 | 8 | 6 |
| Monohydrocalcite | 8 | 2 | 6 | 4 |
| Ikaite | 8 | 6 | 2 | 1 |
The simulated data (Table 2 and Fig. 3) do show some statistically significant differences between the models. In particular, the model derived from ikaite, ACCIk, gives smaller Ca–Oall and larger Ca–C coordination numbers than the other three. Its distribution also shows a more even spread of Ca–Oall coordination numbers in the range 7–8.
The relative contributions of water and carbonate to the calcium coordination shell are also consistent across three of the four ACC systems, with Ow comprising 20–22% of the coordination shell. This value is actually consistent with stoichiometry: the composition of the system, CaCO3·H2O, gives a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio of water
3 ratio of water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) carbonate oxygens; the Oc coordination is 15–16% higher than the C coordination, which indicates that 15% of the carbonate–calcium interactions are bi-dentate; this, in turn, gives a ratio for Ow
carbonate oxygens; the Oc coordination is 15–16% higher than the C coordination, which indicates that 15% of the carbonate–calcium interactions are bi-dentate; this, in turn, gives a ratio for Ow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Oc of 1
Oc of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (3 × 1.15), i.e. 22%, which agrees with the observed ratio of 20% to within the statistical uncertainties. The fourth model is, again, the one derived from ikaite. For this system, only 16% of the calcium coordination shell comes from water. Intriguingly, the bidentate contribution also drops: to 12%. Following the same argument based on stoichiometry, this would predict 23% of the Ca2+ coordination shell to come from water, rather than the 16% found in reality. Thus water appears to be under-represented in the Ca2+ coordination environment for ACCIk. This is consistent with the formation of water micropores within ACCIk but not in the other three models.
(3 × 1.15), i.e. 22%, which agrees with the observed ratio of 20% to within the statistical uncertainties. The fourth model is, again, the one derived from ikaite. For this system, only 16% of the calcium coordination shell comes from water. Intriguingly, the bidentate contribution also drops: to 12%. Following the same argument based on stoichiometry, this would predict 23% of the Ca2+ coordination shell to come from water, rather than the 16% found in reality. Thus water appears to be under-represented in the Ca2+ coordination environment for ACCIk. This is consistent with the formation of water micropores within ACCIk but not in the other three models.
3.4 Water-accessible volume and area
Connolly free volumes and areas,40 or the closely related available volumes and areas,55 are commonly used to probe microporosity and heterogeneity within a material. The available Connolly volumes are calculated by treating atoms in the material as hard spheres and then identifying the regions where it is possible to insert a (hard sphere) probe atom without creating overlap between the material and the probe. Connolly volumes and surface areas are then calculated as the free volume (surface) accessible to the probe atom; as such, the values reported will depend on the probe radius in a way that makes quantitative comparison with experiment ambiguous. If we consider a solid structure, the molecules within it will not pack as perfect spheres, but will form an atomically rough surface. As a result, if we try to obtain a value of the available volume occupied by water molecules using the van der Waals radius of water, 1.575 Å (shown in Table 3) we obtain values that are considerably lower than the average volume of a molecule in liquid water (30.0 Å3), or indeed of that reported for a water molecule within monohydrocalcite:29 14.86 Å3. On the other hand, using a probe radius of zero will overestimate the volume (area), as it overlooks the inefficient packing of spheres in 3D space that happens with real atoms and molecules. In the case of ACC, this uncertainty will be accentuated by strong electrostatic repulsions (Oc–Ow) and attractions (Ca–Ow), which undermine the concept of using a unique probe radius. As a result there is no unique and general way of mapping available volume onto experimental measures. Nevertheless, these measures of volume and surface areas are extremely useful for comparing theoretical models (where probe definitions can be used consistently) and so have been used here to assess the effects of the four ACC preparation protocols. In particular, it is possible to calculate the Connolly volumes accessible to the probe for a series of probe radii to gain much greater detail about the size-dependence of pore space within the material.| ACCRLJ | ACCRPm | ACCMHC | ACCIk | |
|---|---|---|---|---|
| Percentage free volume accessible to the probe after water is removed from structure | 2.69 | 5.36 | 3.57 | 13.621 |
| Free volume (Å3) previously occupied by water accessible to the probe per formula unit | 1.99 ± 0.02 | 4.04 ± 0.11 | 2.66 ± 0.01 | 10.5 ± 0.05 |
| True free volume per formula unit (Å3) for ACC | 0.01 ± 0.00 | 0.00 ± 0.00 | 0.05 ± 0.02 | 0.01 ± 0.01 |
| Area (Å2) of the free surface accessible to the probe when water is removed from the structure | 4.06 ± 0.06 | 7.81 ± 0.11 | 5.88 ± 0.03 | 7.45 ± 0.03 |
The Connolly volumes accessible to the probe have been calculated for all four ACC structures. The calculation has been done for the ACC as formed (to give a measure of the native porosity of the material) and with the water molecules removed (to give a measure of the volume occupied by water). We shall refer to this as “dehydrated ACC” as no relaxation to a stable anhydrous ACC has been allowed. The results are given in Table 3. There is a large variation in the percentage volume occupied by the water molecules between the ACC samples when using a probe radius of 1.575 Å. ACCIk clearly shows the highest water-occupied volume with 13.62%, while the lowest value is observed for ACCMHC with 2.85%.
For the “dehydrated” ACC, we have also calculated the Connolly volume accessible to the probe across a wide range of probe radii (Fig. 4). The probe radius dependence follows the trends in the density identified above. Three of the systems (ACCRLJ, ACCRPm and ACCMHC) give the same curve shape and very similar magnitudes. The ACCRPm curve is shifted up by about 1–2%, which is consistent with its density being about 1% lower than the other two (Table 1). In contrast, the ACCIk system shows consistently higher probe-accessible volumes (about 6% at smaller probe radii, again consistent with its lower density). Much more significantly, however, it shows a much slower decay as the probe radius increases. This is indicative of larger pore sizes (the probe excluded volume effects are confined to the pore surface) and is entirely consistent with the formation of nanoscale channels in the ikaite-derived model.
The maximum Connolly accessible volumes recorded in Fig. 4 are about 30%, and correspond to a volume of 20–23 Å3 per water molecule. This is significantly larger than the value of 14.86 Å3 calculated for monohydrocalcite by Raiteri and Gale (2010). However this should be considered as an upper bound. As mentioned before, this value will include volumes that are not solely occupied by water molecules, such as the effect of small cavities present within the structure due to the inefficient packing of the ions. When the probe radius is increased to 1.575 Å (the approximate van der Waals radius of a water molecule in our model) the accessible volume drops to 2–4 Å3 per water molecule for three of the systems, and 10 Å3 for ACCIk, as shown in Fig. 4; for comparison, the corresponding calculation for ACCMHC with the water removed yields an available volume of just 0.055 Å3. Given the discussion of liquid water free volume above, this indicates that all four ACC systems exhibit a degree of nanoporosity but that this level is again higher for ACCIk. As noted in the Methods section, ACCIk could reasonably be considered microporous.
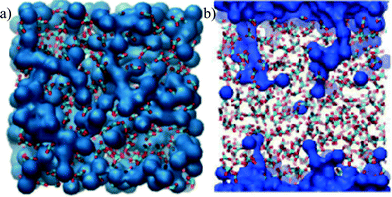
As all the structures were prepared with the same stoichiometry, the difference must arise from the configurations that the water molecules adopt within the different structures. The accessible surface area can be used to investigate some of these differences. Table 3 shows that the surface area available to the probe is approximately equal for all the models for a probe size equivalent to a water molecule, although the corresponding accessible volume is much larger for ACCIk than for the other cases. The smaller surface to volume ratio for ACCIk suggests that the water molecules in that system are more segregated from the ionic framework, forming water channels (here “channel” means a pore large enough to allow translational movement of a water molecule). This may give some of the water in ACCIk properties closer to that of a liquid. On the other hand, ACCMHC, ACCRLJ and ACCRPm models probably form small, individual pores within the structure. This can be seen in Fig. 5 where, in the ACCIk model, the formation of a water layer (in blue) at the centre of the periodic box is clearly visible and a percolating channel appears to be present, whereas the other three structures show a much more homogeneous water distribution throughout the structure.
 | ||
| Fig. 5 Representation of the ACC structure obtained using a surface representation of the Ow from the VMD visualiser using the QuickSurf drawing method (radius scale = 1.1, density isovalue = 1.0, grid spacing = 1.0)56 to show only the water molecules (in blue in the image). Top row: ACCIk (left); ACCRLJ (right). Bottom row: ACCRPm (left); ACCMHC (right). | ||
The change in the total accessible volume occupied by water along the trajectory of the simulation has also been analysed. The total accessible volume changes by approximately 5% over a relatively small amount of time (approximately 0.1 ns) indicating that small scale rearrangements within the system are continually occurring. This mechanism could lead to possible dehydration pathways such as the transient formation of channels.
3.5 Water channels and perfusion of argon
As will be shown below, the CaCO3 framework shows little mobility during any of our simulations. As a result, it is possible to estimate the volume accessible to water by calculating the average 3-dimensional density distribution of water over the simulation; this is akin to visualizing the trajectory with time-lapse photography. The results are depicted in Fig. 6(a). The average volume occupied by water molecules during a simulation, shows chains of water molecules that pervade the whole structure.To explore further whether these chains are in percolating channels, and hence provide a transport network for water within the ACC, anhydrous ACC films were created by removing water from the bulk ACC (see Methods section), and simulated under an Ar atmosphere. Ar-ACC parameters were modified to give Ar an apparent size within the ACC that mimicked water. As mentioned in the method section, the parameters were obtained using the minimum contact distance observed in the radial distribution function between the ions and water. Perfusion of Ar atoms into—and potentially through—the dehydrated ACC film would then identify channels through which water transport was sterically feasible. A snapshot of the distribution of Ar atoms during these perfusion simulations is given in Fig. 6(b). The microporous system, ACCIk, showed the presence of pores that percolated through the system. Pores were also observed for all the other structures. However these were all relatively short, with the longest pore penetrating only 13–15 Å into the slab; this is far less than the width of the slab (33 Å), and demonstrates the absence of stable percolating channels within these three ACC structures. Coupled with the results detailed for Fig. 6(a), this suggests that the water movement is a dynamic process where the water is not segregated from the ions but can jump from one site to the next. The ACCIk structure was the only one to show fully connected channels of water. As shown above (section 3.2 and Table 1), this structure had a higher configurational energy than the other three ACC structures and is therefore likely to exist (if at all) as only a small fraction of the population of the ensemble of structures present in ACC and we would not expect it to contribute significantly to the average structural data.
3.6 Atom and ion mobility
The dynamics of a system is likely to depend strongly on the material structure. Analysing the mobility of the atoms and ions through ACC should therefore be a sensitive test of comparability between the different ACC models. Diffusion coefficients, D, have been calculated from the slope of the ionic/atomic mean square displacements with respect to time (eqn (1)) and results are presented in Table 4. From these values we can see that the only water diffusion coefficients large enough to suggest significant water mobility are those for ACCIk. Moreover, the distribution of single molecule diffusion coefficients (Di, eqn (2)) shows that the molecular diffusion coefficient D in ACCIk is dominated by a comparatively small population of mobile water molecules with Di values in the range 10−11–10−10 m2 s−1 (Fig. 7). This suggests that these water molecules inhabit a different part of the amorphous structure to most of the molecules—the micropores. Water within these micropores should be significantly more mobile than water within an ionic glass, and so gives an average diffusion coefficient that is much larger than for water in the non-microporous ACC systems.| System | 10−15D/m2 s−1 | ||
|---|---|---|---|
| Ca2+ | CO32− | H2O | |
| ACCRLJ | 5.1 | 5.5 | 42 |
| ACCRPm | 13 | 14 | 110 |
| ACCMHC | 6.4 | 5.8 | 48 |
| ACCIk | 32 | 33 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
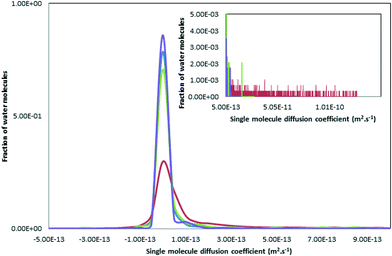 | ||
| Fig. 7 Distribution of single molecule diffusion coefficients Di (see 2.3 and eqn (2)) for the oxygen of the water molecules for the different models. The blue, green, red and purple curves represent ACCRLJ, ACCRPm, ACCIk and ACCMHC respectively. | ||
This is reminiscent of the experimental results obtained by Michel et al.22 and Reeder et al.25 using proton NMR to analyse synthetic ACC. In that work half of the water molecules were largely immobile and were labelled as structural while the rest were capable of restricted motion. If we look at the single molecule diffusion coefficients for the water hydrogen atoms, Hw, (Fig. 8) a much wider spread in the data is found, more in accordance with the proton NMR. This spread of values can be ascribed to rotational motion of the water molecule, giving comparatively large motions of the hydrogen atoms compared with the associated oxygen atoms. Thus some of the water in ACC is translationally free, moving down channels, whereas some is rotationally free, as suggested by the NMR, and some is fully incorporated into the structure of the amorphous solid.
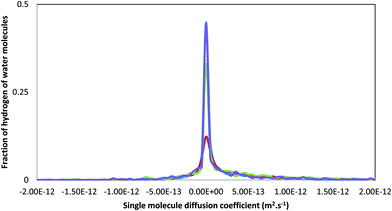 | ||
| Fig. 8 Distribution of single molecule diffusion coefficient, Di (see 2.3 and eqn (2)) for the hydrogens of the water molecules for the different models. The blue, green, red and purple curves represent ACCRLJ, ACCRPm, ACCIk and ACCMHC respectively. | ||
Michel et al. also found that the mobile water was associated with the carbonate ion and the structural water was inferred to be closer to the Ca2+ ions. This is in contrast to a later study looking at biogenic ACC25 where the authors did not find mobile water close to the carbonate ions, but identified segregation of the water molecules within the structure forming channels and pores. Again, when the pair distributions functions were compared, no clear differences were observed between the synthetic and biogenic samples. They hypothesized that in synthetic ACC the water mobility permeated the structure, which could aid ionic transport and ACC restructuring, while in biogenic ACC the water and carbonate are decoupled leading to a more rigid structure, which could explain the increased stability of the sample. However, although our model ACCIk shows the most segregation of water within the structure, it does not give the slowest diffusivity for the ions. While the more mobile water will be more likely to leave the system during dehydration, full dehydration is likely to require further structural changes.26
4. Conclusions
Four different protocols were used in this work to construct models for hydrated ACC with composition CaCO3·H2O. These protocols started from both hydrated crystalline phases and random structures, and employed a wide range of temperatures during the initialisation stages. All four gave materials with very similar pair distribution functions for the hydrated ACC. Associated total distribution functions and ion coordination numbers for all four simulated hydrated ACC systems were also in good agreement with available experimental data. Indeed, none of the simulated ACC structures were inconsistent with the available experimental data for real ACC materials.However, some significant differences in the physical properties of the ACC models were found. Melting and then dehydrating ikaite crystals generated a partial phase separation that gave rise to water-filled micropores within the ACC. This led to a lower overall density and substantially faster diffusion of water within the ACC. It did not, however, increase the mobility of Ca2+ and CO32– ions; nor did it change the coordination environment of the Ca2+ substantially. Interestingly, the phase separation of the water molecule did lead to a structure which was mechanically less stable than the other more homogeneous models.24
In general, the variation between the simulated systems is less than that observed between different experimental studies at compositions comparable to CaCO3·H2O. Greater experimental resolution of the nanoscale structure of real ACC materials would, however, be helpful in developing better models of ACC.
Acknowledgements
Computing facilities were provided by the MESAS group at the University of Sheffield and the Centre for Scientific Computing at the University of Warwick. The work was supported by an EPSRC grant under the MIB project (EP/I001515). This Programme Grant funds the Materials Interface with Biology (MIB) consortium. Further information concerning the underlying data for this work can be obtained by contacting rdm@sheffield.ac.uk and quoting the paper reference.References
- D. A. W. Thompson, On growth and form, Cambridge University Press, New York, 1st edn, 1917 Search PubMed.
- S. Mann, Biomineralization, Oxford University Press, Oxford, 1st edn, 2001 Search PubMed.
- S. Weiner, Y. Levi-Kalisman, S. Raz and L. Addadi, Connect. Tissue Res., 2003, 44, 214–218 CrossRef CAS PubMed.
- I. M. Weiss, N. Tuross, L. Addadi and S. Weiner, J. Exp. Zool., 2002, 293, 478–491 CrossRef CAS PubMed.
- J. Mahamid, A. Sharir, L. Addadi and S. Weiner, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12748–12753 CrossRef CAS PubMed.
- Y. Politi, R. A. Metzler, M. Abrecht, B. Gilbert, F. H. Wilt, I. Sagi, L. Addadi, S. Weiner and P. Gilbert, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17362–17366 CrossRef CAS PubMed.
- N. Nassif, N. Pinna, N. Gehrke, M. Antonietti, C. Jager and H. Colfen, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12653–12655 CrossRef CAS PubMed.
- B. Hasse, H. Ehrenberg, J. C. Marxen, W. Becker and M. Epple, Chem. – Eur. J., 2000, 6, 3679–3685 CrossRef CAS.
- D. Gebauer, P. N. Gunawidjaja, J. Y. P. Ko, Z. Bacsik, B. Aziz, L. J. Liu, Y. F. Hu, L. Bergstrom, C. W. Tai, T. K. Sham, M. Eden and N. Hedin, Angew. Chem., Int. Ed., 2010, 49, 8889–8891 CrossRef CAS PubMed.
- Y. Levi-Kalisman, S. Raz, S. Weiner, L. Addadi and I. Sagi, Adv. Funct. Mater., 2002, 12, 43–48 CrossRef CAS.
- E. Loste, R. M. Wilson, R. Seshadri and F. C. Meldrum, J. Cryst. Growth, 2003, 254, 206–218 CrossRef CAS.
- C. L. Freeman, J. H. Harding, D. Quigley and P. M. Rodger, J. Phys. Chem. C, 2011, 115, 8175–8183 CAS.
- N. Sommerdijk and G. de With, Chem. Rev., 2008, 108, 4499–4550 CrossRef CAS PubMed.
- R. S. K. Lam, J. M. Charnock, A. Lennie and F. C. Meldrum, CrystEngComm, 2007, 9, 1226–1236 RSC.
- C. J. Stephens, S. F. Ladden, F. C. Meldrum and H. K. Christenson, Adv. Funct. Mater., 2010, 20, 2108–2115 CrossRef CAS.
- E. Loste, R. J. Park, J. Warren and F. C. Meldrum, Adv. Funct. Mater., 2004, 14, 1211–1220 CrossRef CAS.
- F. C. Meldrum, Int. Mater. Rev., 2003, 48, 187–224 CrossRef CAS.
- K. Lee, W. Wagermaier, A. Masic, K. P. Kommareddy, M. Bennet, I. Manjubala, S.-W. Lee, S. B. Park, H. Coelfen and P. Fratzl, Nat. Commun., 2012, 3, 725 CrossRef PubMed.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970 CrossRef CAS.
- A. V. Radha, T. Z. Forbes, C. E. Killian, P. U. P. A. Gilbert and A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16438–16443 CrossRef CAS PubMed.
- I. P. Swainson, Am. Mineral., 2008, 93, 1014–1018 CrossRef CAS.
- F. M. Michel, J. MacDonald, J. Feng, B. L. Phillips, L. Ehm, C. Tarabrella, J. B. Parise and R. J. Reeder, Chem. Mater., 2008, 20, 4720–4728 CrossRef CAS.
- A. Becker, U. Bismayer, M. Epple, H. Fabritius, B. Hasse, J. M. Shi and A. Ziegler, Dalton Trans., 2003, 551–555 RSC.
- A. L. Goodwin, F. M. Michel, B. L. Phillips, D. A. Keen, M. T. Dove and R. J. Reeder, Chem. Mater., 2010, 22, 3197–3205 CrossRef CAS.
- R. J. Reeder, Y. Tang, M. P. Schmidt, L. M. Kubista, D. F. Cowan and B. L. Phillips, Cryst. Growth Des., 2013, 13, 1905–1914 CAS.
- M. P. Schmidt, A. J. Ilott, B. L. Phillips and R. J. Reeder, Cryst. Growth Des., 2014, 14, 938–951 CAS.
- D. Quigley and P. M. Rodger, J. Chem. Phys., 2008, 128, 221101 CrossRef CAS PubMed.
- D. Quigley, C. L. Freeman, J. H. Harding and P. M. Rodger, J. Chem. Phys., 2011, 134, 044703 CrossRef CAS PubMed.
- P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2010, 132, 17623–17634 CrossRef CAS PubMed.
- J. W. Singer, A. O. Yazaydin, R. J. Kirkpatrick and G. M. Bowers, Chem. Mater., 2012, 24, 1828–1836 CrossRef CAS.
- M. Saharay and R. J. Kirkpatrick, Chem. Phys. Lett., 2014, 591, 287–291 CrossRef CAS.
- A. R. Finney and P. M. Rodger, Faraday Discuss., 2012, 159, 47–60 RSC.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Science, 2013, 341, 885–889 CrossRef CAS PubMed.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590 CrossRef PubMed.
- D. J. Price and C. L. Brooks, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef CAS PubMed.
- Y. J. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503 CrossRef PubMed.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- M. L. Connolly, Science, 1983, 221, 709–713 CAS.
- Q. G. Zhang, Q. L. Liu, Y. Chen, J. Y. Wu and A. M. Zhu, Chem. Eng. Sci., 2009, 64, 334–340 CrossRef CAS.
- T. R. Zeitler, J. A. Greathouse and R. T. Cygan, Phys. Chem. Chem. Phys., 2012, 14, 1728–1734 RSC.
- L. A. Rowley, D. Nicholson and N. G. Parsonage, J. Comput. Phys., 1975, 17, 401–414 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2nd edn, 2002 Search PubMed.
- A. V. Radha, A. Fernandez-Martinez, Y. Hu, Y.-S. Jun, G. A. Waychunas and A. Navrotsky, Geochim. Cosmochim. Acta, 2012, 90, 83–95 CrossRef CAS.
- D. A. McQuarrie, Statistical Thermodynamics, University Science Books, University of Michigan, 1st edn, 1991 Search PubMed.
- P. Fenter, S. Kerisit, P. Raiteri and J. D. Gale, J. Phys. Chem. C, 2013, 117, 5028–5042 CAS.
- J. Bolze, B. Peng, N. Dingenouts, P. Panine, T. Narayanan and M. Ballauff, Langmuir, 2002, 18, 8364–8369 CrossRef CAS.
- J. Bolze, D. Pontoni, M. Ballauff, T. Narayanan and H. Colfen, J. Colloid Interface Sci., 2004, 277, 84–94 CrossRef CAS PubMed.
- M. Faatz, W. Cheng, G. Wegner, G. Fytas, R. S. Penciu and E. N. Economou, Langmuir, 2005, 21, 6666–6668 CrossRef CAS PubMed.
- B. Raton, Handbook of Chemistry and Physics, 1981 Search PubMed.
- Y. Levi-Kalisman, S. Raz, S. Weiner, L. Addadi and I. Sagi, J. Chem. Soc., Dalton Trans., 2000, 3977–3982 RSC.
- Y. Politi, Y. Levi-Kalisman, S. Raz, F. Wilt, L. Addadi, S. Weiner and I. Sagi, Adv. Funct. Mater., 2006, 16, 1289–1298 CrossRef CAS.
- C. Gunther, A. Becker, G. Wolf and M. Epple, Z. Anorg. Allg. Chem., 2005, 631, 2830–2835 CrossRef.
- B. Lee and F. M. Richards, J. Mol. Biol., 1971, 55, 379–400 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
Footnote |
| † The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript. |
| This journal is © The Royal Society of Chemistry 2016 |