An exploration of the reactivity of singlet oxygen with biomolecular constituents

Abstract

The thermal reaction between biomolecules and singlet oxygen (¹O₂) is important for rendering the genetic material within toxic cells inactive. Here we present results obtained from state-of-the-art multi-reference computational methods that reveal the mechanistic details of the reaction between ¹O₂ and two exemplary biomolecular systems: guanine (Gua) and histidine (His). The results highlight the splitting of the doubly degenerate ¹Δ_g state of O₂ upon complexation and the essentially barrierless potential energy profile of the thermally allowed cycloaddition reaction when the O₂ molecule is in its lower energy ¹Δ_g state.

---

The highest occupied molecular orbitals of the ground state electronic configuration of molecular O₂ (X³Σ_g⁻) are a degenerate pair of π* anti-bonding orbitals, each of which contains an odd electron. This manifests in an uncommon triplet spin multiplicity (henceforth ³O₂) in the electronic ground state. Under ambient conditions, ³O₂ is kinetically inert towards most molecules with the ‘usual’ singlet ground state spin multiplicity – due to non-conservation of spin upon preparing the lowest energy singlet products. In such systems, the reaction path leading to the ultimate spin-preserving triplet product is usually barrierless and endoergic with respect to the reactants and is thus thermodynamically unreactive. The first electronically excited state of O₂, in contrast, has ¹Δ_g symmetry (i.e. singlet spin multiplicity, henceforth ¹O₂) and is highly reactive towards most molecular systems due to its thermodynamically favourable and kinetically facile oxidising ability.¹ Preparation of ¹O₂ is non-trivial, however, since direct electronic excitation from the ground state via, for example, light irradiation is spin-forbidden and therefore improbable. A more viable route for forming ¹O₂ is via indirect photosensitisation using a long-lived chromophore with a photostable triplet state (i.e. via the so-called type II photo-oxidation).^2,3 This is the underlying first step in photodynamic therapy (PDT)⁴ – which has attracted considerable experimental and theoretical attention.^5–8

PDT is a form of medicinal treatment in which light induces the photosensitised formation of cellular ¹O₂. The nascent ¹O₂ has been shown to induce cell death – efficiently killing microbial cells.⁹ PDT has also proved effective for the treatment of some forms of cancer – e.g. squamous cell carcinoma (skin cancer).¹⁰ The mechanisms of PDT have been attributed to ¹O₂-induced oxidation of the molecular structure of cellular DNA that makes up the genetic code – leading to genomic mutations.^11,12 Though the underlying oxidative mechanism has been theoretically proposed and experimentally established for prototypical systems (e.g. small ethene derivatives¹³ and benzene¹⁴), little is mechanistically known about the activity of ¹O₂ on DNA nucleobases and aromatic amino acids. The feasibility of the His + O₂ reaction has previously been detailed using single reference computational methods.¹⁷ Though the study is extremely informative, ref. 17 lacks important information on the details of the multi-reference character of the potential energy profile associated with the thermally allowed cycloaddition reaction. Our present work also provides information on the role of dispersion upon His + O₂ complexation. In DNA, experiments have shown that the ensuing oxidation reaction is exclusively limited to guanine nucleobases – forming three main intermediates, a mixture of endoperoxide and exoperoxide adducts.¹⁵ Through thermal molecular rearrangements, these short-lived intermediates form more stable oxoguanine derivatives. Recent theoretical efforts have attempted to understand the underlying reactivity of ¹O₂-induced DNA oxidation¹⁶ but we are not aware of any prior mechanistic explorations of the topography of the potential energy (PE) profiles involved in the ensuing reaction.

Using highly correlated, multi-reference electronic structure calculations, based on the complete active space with second order perturbation theory (CASPT2),^18–20 we outline the topography of the PE profiles of ¹O₂-induced oxidation of two prototypical biomolecules: Gua and His. Details of the present calculations are provided in the ESI.†Fig. 1 displays the ground state minimum energy geometries of the prototypical π-stacked Gua–O₂ and His–O₂ complexes. These minima were used as the starting points for studying the ensuing [4+2] cycloaddition reaction leading to the endoperoxy intermediate – the thermal reactivity of which is dictated by the Woodward–Hoffmann rules.²¹ Equivalent minima were also located by aligning O₂ such that various hydrogen-bonded complexes were formed. Two such low energy hydrogen-bonded complexes were optimised (see Fig. S1 of the ESI†) but were shown to be less stable than the π-stacked structure – reflecting the dominance of dispersion effects in π-stacking. That said, the cellular environment is likely to comprise a mixture of π-stacked and H-bonded complexes, each of which is likely to lead to reaction of the biomolecule with proximal ¹O₂ dissolved in the cellular solution. Preliminary studies of the lowest energy H-bonded Gua–O₂ complexes suggest the facile formation of an exoperoxy intermediate via a coupled addition and hydrogen abstraction reaction. Though important, the formation of the exoperoxy-adduct is beyond the scope of the present work but will form the basis of a fuller future study.

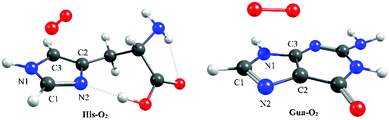Fig. 1 Minimum energy geometries of the π-stacked configurations of His–O₂ (left) and Gua–O₂ (right) in their respective ground states. Molecular depictions and Cartesian coordinates of all optimised structures are presented in Fig. S3 of the ESI.†

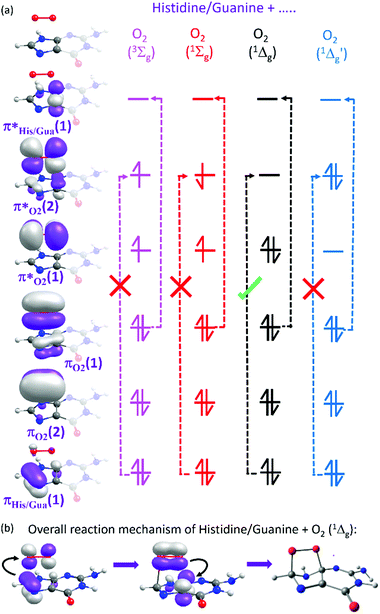
Here we focus on the former reaction in which an endoperoxy-intermediate is formed. Fig. 2(a) and (b) present the PE profiles of the three lowest singlet states and the lowest triplet state of the His–O₂/Gua–O₂ complex along the [4+2] cycloaddition reaction coordinates (henceforth Q_c[4+2]) leading to the respective endoperoxyhistidine and endoperoxyguanine cycloadducts. The orbital promotions involved in preparing these states are displayed in Fig. 3(a). In both Gua and His, the O₂ moiety adds across the C1 and C3 atoms (see Fig. 1 for atomic numberings). The left hand side of Fig. 2(a) and (b) shows the PE profiles linking each state from the respective π-stacked ground state minimum energy geometry towards the optimised lowest energy transition state (TS) along Q_c[4+2]. The right hand panels show results for further calculations, on the lowest singlet potential only, from the TS to the minimum energy configurations of the respective cycloadduct product. The ³Σ_g⁻ and ¹Σ_g⁺ electronic states of O₂ both contain odd electrons in orthogonal π* anti-bonding orbitals, but are distinguishable by the parallel (anti-parallel) arrangement of the respective electron spins (see the molecular orbital diagram in Fig. 3(a)). In isolated O₂, the ³Σ_g⁻ and ¹Σ_g⁺ electronic states are separated by ∼1.6 eV, which the present calculations show to increase upon complexation – highlighting the strong dispersion interaction between O₂ and the π-system of Gua/His. Upon cycloaddition with His/Gua, the PEs of the ³Σ_g⁻ and ¹Σ_g⁺ states of O₂ (i.e. the pink and red curves) both increase as a function of Q_c[4+2] – implying an absence of any driving force towards [4+2] cycloaddition. This can be understood by picturing the Woodward–Hoffmann orbital interactions involved in forming cycloadducts with two C–O bonds between His/Gua and O₂. Since the occupied orbitals of O₂ are the highest energy orbitals in Fig. 3(a), formation of the first C–O bond requires the cleavage of one of the two bonds in the O=O double bond in order to satisfy valency (henceforth step 1). This is achieved by an electron-pair promotion from an occupied π-orbital of His/Gua to an unoccupied π* orbital of O₂ – which within the Woodward–Hoffmann limit are the optimally aligned π_His/Gua(1) and π*_O2(2) orbitals, respectively (see Fig. 3(a)). In much the same way, formation of the second C–O bond required to complete the cycloaddition involves promotion of an electron-pair from an occupied π orbital of O₂ (π_O2(1)) to an unoccupied π* orbital (π*_His/Gua(1)) of His/Gua (henceforth step 2).

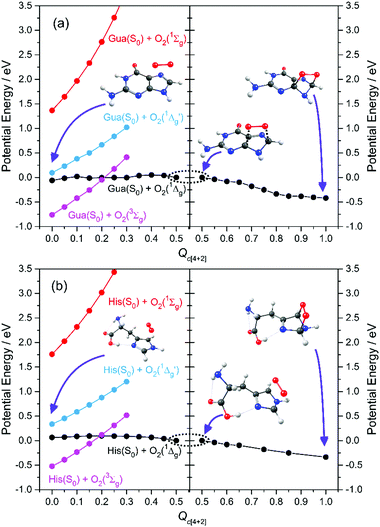Fig. 2 CASPT2 potential energy profiles along the [4+2] cycloaddition coordinate en route to forming the endoperoxy cycloadduct.

Fig. 3 (a) Selected orbitals and orbital promotions associated with the [4+2] cycloaddition reaction. The dashed vertical arrows with (without) the ticks or crosses represent steps 1 (2) of the cycloaddition reaction, with the tick/cross indicating, respectively, an allowed/forbidden electron-pair transfer in step 1. (b) A simplified mechanism summarizing the electron-pair migrations (curly black arrows) associated with the [4+2] cycloaddition reaction with ¹O₂.

The relative ordering of the step 1 and 2 electron-pair transfer processes described here is for illustration purposes only. In practice, steps 1 and 2 could occur in any order and in a concerted or stepwise manner – depending on the reaction conditions. Steps 1 and 2 together comprise the overall [4+2] cycloaddition mechanism summarised in Fig. 3(b). Both π* orbitals of O₂ are already singly occupied in the ³Σ_g⁻ and ¹Σ_g⁺ states, precluding cycloadduct formation between His/Gua and O₂ (see Fig. 3(a)). The ¹Δ_g state, in contrast, has the two electrons spin-paired in one of the two π* orbitals. These π* orbitals are degenerate in an isolated O₂ molecule, and each has the same probability of containing the electron-pair. In isolated O₂, this doubly degenerate ¹Δ_g state is ∼1 eV above that of the ³Σ_g⁻ state. The present calculations show a decrease in the ³Σ_g⁻–¹Δ_g energy gap upon O₂ + His/Gua complexation. Within this complex the degeneracy in the ¹Δ_g state must be lifted, since the two π* orbitals will interact differently when in close proximity to His/Gua. This lifting of the degeneracy is evident in Fig. 2(a) and (b) (as the O₂ moiety approaches His/Gua) – manifesting in two PE curves describing the Gua(S₀)/His(S₀) + O₂(¹Δ_g) configuration (i.e. black and blue curves in Fig. 2 – henceforth ¹Δ_g and ¹Δ_g′) – the lower energy of which (black curve) is reactive with respect to Q_c[4+2].

We also note that the Gua(S₀)/His(S₀) + O₂(¹Δ_g) and Gua(S₀)/His(S₀) + O₂(³Σ_g⁻) potentials cross en route to the lowest energy TS – thereby providing a route by which ¹O₂ could relax to reform ³O₂. This relaxation will be determined by the rate of intersystem crossing (ISC) which is likely to be slower (nanosecond or longer timescale) than the typical thermal (picosecond timescale) motions of the nuclei that are expected to drive the cycloaddition reaction. Thus, though we recognise that some population evolving on the Gua(S₀)/His(S₀) + O₂(¹Δ_g) potential could branch at this crossing, we anticipate that spin–orbit coupling will be relatively weak and that cycloadduct formation would be the dominant process. Notwithstanding, under favourable reaction conditions, the ³O₂ + His/Gua limit could undergo a spin-flipping reaction by ISC to the ¹O₂ + His/Gua state at this crossing.

Beyond the TS, the lower energy Gua(S₀)/His(S₀) + O₂(¹Δ_g) potential continues to decline in energy as it evolves to the endoperoxy cycloadduct. The Gua(S₀)/His(S₀) + O₂(¹Δ_g′) potential (blue curve), in contrast, increases in energy along Q_c[4+2]. This stark difference in the reactivity of the ¹Δ_g and ¹Δ_g′ states of O₂ with Gua/His can also be understood by considering the orbitals involved in preparing the cycloadduct. The favourable driving force for cycloaddition in the lower energy case can be understood by recognising that the optimally aligned π_His/Gua(1) donor and π*_O2(2) acceptor orbitals are, respectively, occupied and unoccupied – as required for the step 1 electron-pair transfer. In the case of the higher energy Gua(S₀)/His(S₀) + O₂(¹Δ_g′) encounter, however, the optimally aligned Woodward–Hoffmann π_His/Gua(1) and π*_O2(2) orbitals are both doubly occupied (see Fig. 3(a)). Hence, the step 1 electron-pair transfer is unfavourable, as shown by the increase in PE along Q_c[4+2].

At this point, we note that the present calculations are limited to the isolated ‘gas phase’ complexes and that we do not attempt to include any of the additional complexities associated with the surrounding cellular environment that would be necessary for a more complete biochemical study. The present topographies of the returned PE profiles may also depend on the electrostatic embedding in the bulk DNA environment. That said, the present calculations are nonetheless very informative, as they illustrate the PE profiles associated with the experimentally observed [4+2] cycloaddition of ¹O₂ to the chosen biomolecular constituent. More specifically, we have used highly correlated multi-reference electronic structure methods to determine PE profiles for the most widely recognised form of biomolecular oxidation via¹O₂: [4+2] cycloaddition of O₂ to His/Gua. In so doing, we have shown that the ¹Δ_g state of isolated O₂ splits into two non-degenerate electronic states when π-stacked with a conjugated biomolecule – the lower of which is the sole state that is reactive towards cycloaddition in the low energy π-stacked configuration shown in Fig. 1. The hitherto neglected higher energy ¹Δ_g′ state of O₂ is unreactive with ground state His/Gua along Q_c[4+2], but this state also possesses a vacant π* orbital that is orthogonal to the coordinate along which His/Gua and O₂ moieties π-stack. The higher energy ¹Δ_g′ state is thus likely to be reactive with proximal aromatic molecules that happen to stack in the correct orientation – highlighting the importance of structure and orientation in the reactivity of ¹O₂ with an associated (bio)molecule.

The cycloadducts shown to the far right of Fig. 2(a) and (b) constitute an intermediate that is likely to undergo further rearrangement to form various more stable products. Recent theoretical studies by Dumont et al.¹⁶ have identified possible products on the ground state potential including 4-hydroxy-8-oxo-deoxyguanine and 8-oxoguanine and spironucleoside derivatives. Most of these products were shown to be very exoergic with respect to the endoperoxy cycloadduct. Within cellular DNA, the eventual formation of such products is likely to lead to irreversible DNA damage – ultimately rendering the normal working functions of the cell inactivated. This is particularly desirable for toxic (e.g. cancerous) cells. As noted, the above experiments have shown that the reactivity of ¹O₂ is exclusively limited to Gua. Comparing the available experiments on the purine and pyrimidine bases, it is clear that the presently studied [4+2] cycloaddition reaction favours the five-membered imidazole constituent of the bicyclic purine systems. This can be simply understood by considering that the five-membered imidazole ring constituent provides an optimal C1–C3 bond distance and π-electron distribution for a thermally allowed [4+2] cycloaddition reaction whilst the six-membered ring constituent does not. With the unavailability of a five-membered ring, the unreactivity of pyrimidine bases is therefore plausibly attributable to the larger C–C bonding distances and, in the case of uracil and thymine, the unfavourable distribution of π-electrons in order to sustain a [4+2] cycloaddition. Notwithstanding, the possibility of a [4+2] cycloaddition between cytosine and ¹O₂ exists – though large reaction barriers hinder this process (see Fig. S2 of the ESI†). Comparing the reactivity of guanine with that of adenine is less trivial since (to first order) both contain an imidazole constituent with an optimal distribution of π-electrons. Dumont et al. went some way to explaining this trend by showing that the reaction barrier associated with the ¹O₂ + adenine cycloaddition reaction was larger than that for guanine – though this too highlights the importance of a mechanistic study of the PE profile.

Therefore, understanding the topography of the PE surface of such oxidative reactions could be insightful not least for studying the effect of other reactive species (oxygen or otherwise) – potentially aiding in the manufacturing of photosensitisers that enhance the formation yield of such species. The present work adds to the small but growing number of reported mechanistic studies on the oxidation of biomolecules by ¹O₂. Given the continued advances in both theoretical and experimental methods, many more such studies can be expected in the near future – involving ¹O₂ or other potentially reactive intermediates with (bio)molecules.

The authors thank Prof. M. N. R. Ashfold (University of Bristol) for fruitful discussions and the EPSRC (EP/L005913) and TUM for funding. The data underpinning the present study has been stored in the University of Bristol research data repository and can be accessed via the following link: DOI: 10.5523/bris.qsf82vq3qbm31kac5ggbn4ldx.

Notes and references

1. R. Y. N. Ho, J. F. Liebman and J. S. Valentine, in Active Oxygen in Chemistry, ed. C. S. Foote, J. S. Valentine, A. Greenberg and J. F. Liebman, Springer Netherlands, Dordrecht, 1995, pp. 1–23.
2. C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1758.
3. A. Greer, Acc. Chem. Res., 2006, 39, 797–804.
4. J. Chen, L. Keltner, J. Christophersen, F. Zheng, M. Krouse, A. Singhal and S-s. Wang, Cancer J., 2002, 8, 154–163.
5. E. Skovsen, J. W. Snyder, J. D. C. Lambert and P. R. Ogilby, J. Phys. Chem. B, 2005, 109, 8570–8573.
6. M. Klaper, W. Fudickar and T. Linker, J. Am. Chem. Soc., 2016, 138, 7024–7029.
7. M. Klaper and T. Linker, J. Am. Chem. Soc., 2015, 137, 13744–13747.
8. S. Kim, T. Tachikawa, M. Fujitsuka and T. Majima, J. Am. Chem. Soc., 2014, 136, 11707–11715.
9. M. R. Hamblin and T. Hasan, Photochem. Photobiol. Sci., 2004, 3, 436–450.
10. J. Chen, L. Keltner, J. Christophersen, F. Zheng, M. Krouse, A. Singhal and S.-s. Wang, Cancer J., 2002, 8, 154–163.
11. T. P. A. Devasagayam, S. Steenken, M. S. W. Obendorf, W. A. Schulz and H. Sies, Biochemistry, 1991, 30, 6283–6289.
12. J. Piette, J. Photochem. Photobiol., B, 1991, 11, 241–260.
13. T. Saito, S. Nishihara, Y. Kataoka, Y. Nakanishi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, J. Phys. Chem. A, 2010, 114, 7967–7974.
14. A. G. Leach and K. N. Houk, Chem. Commun., 2002, 1243–1255.
15. J.-L. Ravanat and J. Cadet, Chem. Res. Toxicol., 1995, 8, 379–388.
16. E. Dumont, R. Grüber, E. Bignon, C. Morell, Y. Moreau, A. Monari and J.-L. Ravanat, Nucleic Acids Res., 2015, 44, 56–62.
17. J. Méndez-Hurtado, R. López, D. Suárez and M. I. Menéndez, Chem. – Eur. J., 2012, 18, 8437–8447.
18. B. O. Roos and K. Andersson, Chem. Phys. Lett., 1995, 245, 215–223.
19. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023.
20. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler and R. D. Amos, et al., MOLPRO, University of Cardiff, Cardiff, U.K., 2010.
21. R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395–397.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cc05392k

---