Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tunnelling in carbonic acid†
J. Philipp
Wagner
a,
Hans Peter
Reisenauer
 a,
Viivi
Hirvonen
a,
Chia-Hua
Wu
b,
Joseph L.
Tyberg
b,
Wesley D.
Allen
*b and
Peter R.
Schreiner
*a
a,
Viivi
Hirvonen
a,
Chia-Hua
Wu
b,
Joseph L.
Tyberg
b,
Wesley D.
Allen
*b and
Peter R.
Schreiner
*a
aInstitute of Organic Chemistry, Justus-Liebig University, Heinrich-Buff-Ring 17, D-35392 Giessen, Germany. E-mail: prs@uni-giessen.de
bCenter for Computational Quantum Chemistry and Department of Chemistry, University of Georgia, Athens, Georgia 30602, USA. E-mail: wdallen@uga.edu
First published on 24th May 2016
Abstract
The cis,trans-conformer of carbonic acid (H2CO3), generated by near-infrared radiation, undergoes an unreported quantum mechanical tunnelling rotamerization with half-lives in cryogenic matrices of 4–20 h, depending on temperature and host material. First-principles quantum chemistry at high levels of theory gives a tunnelling half-life of about 1 h, quite near those measured for the fastest rotamerizations.
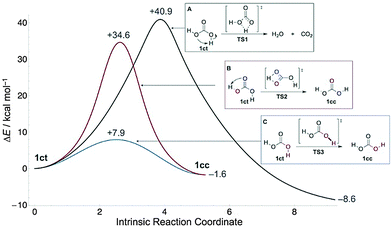
Although carbonic acid (H2CO3, 1, Fig. 1) is constantly on the lips of millions in the form of carbonated beverages, evidence for the molecule in the gas phase was obtained only in 1987 by thermolysis of NH4HCO3 and mass spectrometric detection.1 For many years this profoundly important molecule, which is considered essential for many biological processes,2 escaped unequivocal identification in the gas phase. Indeed, it was vigorously debated whether H2CO3 could persist long enough to be spectroscopically identifiable, as the molecule decomposes readily into CO2 and H2O.3 At the same time, evidence was found for the existence of 1 in atmospheric clouds both on earth and several terrestrial planets.4 Finally, in 20095 and 2011,6 Fourier-transform microwave spectroscopy provided the first spectroscopic characterization of gaseous H2CO3, produced by passing a pulsed electric discharge of CO2 in a supersonic jet through a water reservoir. The cis–trans (1ct)5 and cis–cis (1cc)6 rotamers (Fig. 1) were identified unequivocally, while the trans–trans (1tt) isomer was deemed unattainable because of its high relative energy and small rotational barrier (1.8 kcal mol−1 at CCSD(T)/CBS)7 to 1ct.
Solid carbonic acid was first prepared in 1991 by high-energy irradiation of mixtures of carbon dioxide and water ice.8–10 Shortly thereafter, the protonation of potassium bicarbonate with excess HCl in glassy methanolic solutions led to a solid, later termed the α-H2CO3 polymorph.11 An alternative β-H2CO3 polymorph was generated in an analogous fashion in aqueous glassy solutions in the presence of excess HBr, and conversion of β-H2CO3 to α-H2CO3 was found upon treatment with HCl in methanol.12 Overturning previous understandings, we proved recently7 through comparison of matrix-isolation13,14 infrared (IR) spectra of independently prepared compounds that the substance named α-H2CO3 is in fact carbonic acid monomethyl ester,15,16 while only the β-polymorph17,18 is indeed solid H2CO3.7,19 In doing so, we developed a novel synthetic route to gas-phase H2CO3 utilizing the ester pyrolysis of either Boc2O or di-t-butyl carbonate, a conceptually simpler approach20 generating much higher concentrations in the gas phase than previously achieved.
Carbonic acid is generally considered a fleeting molecule at ambient temperatures due to rapid decomposition into CO2 and H2O in the gas phase3 (Fig. 1) or deprotonation in solution. However, the gas-phase decomposition of 1 has a large barrier in excess of 40 kcal mol−1,21,22 because it is a thermally forbidden [2σ+2π] cycloreversion. In the presence of water, an (auto)catalytic23–25 process appears to be operative instead: computations reveal that complexation of 1 with explicit water molecules allows passage through more favourable cyclic transition states of six or more members that are lower in energy by 16–19 kcal mol−1.21 Here we outline hitherto unreported conformational tunnelling of 1, thereby capturing one of its key reactivities. The detailed delineation of the conformational, reactivity, and spectroscopic landscape of 1 will aid in its identification in the atmosphere and extraterrestrial environments.
Our highly efficient gas-phase preparation of 1via ester pyrolysis (Scheme 1) and its trapping in noble gas matrices under cryogenic conditions allows the unimolecular kinetic behaviour to be probed.7 Di-t-butyl carbonate (2) readily undergoes double ester fragmentation via high vacuum flash pyrolysis (HVFP) with concomitant loss of two isobutene equivalents. Immediately after passing 2 through the pyrolysis tube, the products are trapped in noble gas matrices, kept at low temperatures (3–20 K), and monitored by means of IR spectroscopy. Bimolecular reactions do not occur because the trapped molecules are present in low concentrations and are fully surrounded by noble gas atoms (ratio ca. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103); the solid noble gas matrices do not allow molecular diffusion.
103); the solid noble gas matrices do not allow molecular diffusion.
 | ||
| Scheme 1 High-vacuum flash pyrolysis of di-t-butyl carbonate (2) and trapping of 1 in noble gas matrices. | ||
Infrared bands for most vibrational modes of the two observable isomers of 1 were identified before.7 However, we were able to assign several new absorptions (Tables S16 and S17, ESI†), which assist the detection of 1 in extraterrestrial and other environments. The additional assignments include the νs(O–C–O) symmetric stretching and δ(O–C–O) deformation modes of both conformers, as well as the δ(O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) deformation of 1ct. With decreasing polarizability of the noble gas host from Xe to Ne, we usually observe blue-shifted spectral features that slowly approach the gas-phase values for the vibrational transitions (Fig. S1, ESI†). On this basis it was also possible to assign the very close lying δ(H–O–C) + νas(O–C–O) vibrations of 1cc and 1ct (computed at 1183.8 and 1182.0 cm−1, respectively) in neon in the theoretically predicted ordering.
O) deformation of 1ct. With decreasing polarizability of the noble gas host from Xe to Ne, we usually observe blue-shifted spectral features that slowly approach the gas-phase values for the vibrational transitions (Fig. S1, ESI†). On this basis it was also possible to assign the very close lying δ(H–O–C) + νas(O–C–O) vibrations of 1cc and 1ct (computed at 1183.8 and 1182.0 cm−1, respectively) in neon in the theoretically predicted ordering.
After enrichment of the 1ct conformer by narrow band NIR excitation (see ESI† for details) of matrices containing 1, we observe its decay in solid Ne (3 K), Ar (3, 12.5, 17.5, 20 K), Kr (12.5 K), and Xe (12.5 K) with effective half-lives (τeff) of 4–20 h. During the kinetic measurements a long-pass IR filter cutting off all wavelengths below 4.5 μm (ca. 2200 cm−1) was used to prevent unwanted photochemistry induced by the globar radiation of the IR spectrometer. Decomposition of 1 into CO2 and water (Fig. 1A) can be excluded, as we monitor the concomitant disappearance of 1ct and appearance of 1cc. Since the activation barriers for the other two possible processes (Fig. 1B and C) are too large to be overcome at cryogenic temperatures, quantum mechanical tunnelling (QMT)26 must be responsible for the disappearance of 1ct. The [1,3]H-shift of 1ct to 1cc (Fig. 1B) viaTS2 exhibits a 34.6 kcal mol−1 barrier at the CCSD(T)/CBS level; this compares well with the QCISD(T)/6-311++G(d,p)//MP2(full)/6-31++G(d,p) barrier of 34.3 kcal mol−1 reported earlier.27 Barriers of this magnitude are not too large in principle to prohibit H-tunnelling on the time scales observed here, but in this case the potential energy profile is not “thin”28–34 enough to make hydrogen transfer viable (Fig. 1). Unsurprisingly, we computed a prohibitive half-life of τ = 4.4 × 106 y for this reaction along a CCSD(T)/cc-pVQZ//MP2/aug-cc-pVTZ minimum energy path within a Wenzel–Kramers–Brillouin (WKB) tunnelling model35,36 that has proved very accurate for H-transfer reactions.28,37
The isomerization of 1ct through C–O single bond rotation has a barrier of only 7.9 kcal mol−1 (Fig. 1), which is in the 2–13 kcal mol−1 range typical of carboxylic acids38–44 but still much too large to be overcome thermally at the temperatures of our experiments. Hence, the decay of 1ct to 1cc must occur via tunnelling rotational isomerization, a generic fundamental property of carboxylic acids.38–44 We executed a detailed kinetic analysis of this tunnelling phenomenon in different noble gases and at various temperatures (Table 1).
| Matrix (T/K) | τ 1 | τ 2 | τ eff | X frozen | X slow | X fast |
|---|---|---|---|---|---|---|
| a Standard errors of fits to experimental data in parentheses in units of the last significant digit. b Time required for fitted relative population function to fall half of its descent. | ||||||
| Ar (3) | 19.7(1) | — | 19.7 | 0.61 | 0.39 | 0 |
| Ar (12.5) | 13(2) | 4(9) | 12.5 | 0.29(7) | 0.69(7) | 0.03(9) |
| Ar (17.5) | 12(2) | 4.8(7) | 7.6 | 0 | 0.46(17) | 0.54(17) |
| Ar (20) | 14(3) | 3.0(2) | 4.4 | 0 | 0.31(6) | 0.69(6) |
| Ne (3) | 25.7(4) | 2.0(4) | 19.8 | 0.31 | 0.61 | 0.08 |
| Kr (12.5) | 16(6) | 5(4) | 10.5 | 0.26(23) | 0.57(18) | 0.17(25) |
| Xe (12.5) | 11.2(8) | 2.4(5) | 5.9 | 0.53(2) | 0.36(1) | 0.11(3) |
The intricate kinetic behaviour of matrix-isolated 1 was treated within a multi-exponential model we recently developed to describe a similar conformational tunnelling process in oxalic acid, termed domino tunnelling.45 To achieve high-quality fits of the data within the experimental error bars, the assumption of three classes of matrix-isolated carbonic acid molecules was required: a frozen class, in which tunnelling is entirely precluded by the environment; a slow class with seemingly hindered conformational tunnelling and half-lives (τ1) of 11–26 h; and a fast class, characterized by half-lives (τ2) of 2–5 h, for which the matrix atoms appear to interfere to only a limited extent with the conformational tunnelling. We emphasize here that our three-class model is phenomenological in nature, although it is appealing to interpret the experimental results in terms of a hindering matrix environment that softens at higher temperatures. The final kinetic analysis employed two half-lives (τ1, τ2) and three initial population ratios (1ct fast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) slow, 1ct frozen
slow, 1ct frozen![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) slow, and total 1ct
slow, and total 1ct![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1cc) as fitting parameters in a simultaneous, nonlinear least-squares fit of all suitable infrared spectral bands of both 1ct and 1cc. Complete details of the kinetic analysis are given in the ESI† along with plots of the data and fits. Deuteration completely suppresses the tunnelling isomerization, and we compute τ = 2400 y for monodeuterated 1 (see ESI†); no tunnelling of deuterated 1 was observed over one day at 20 K in Ar.
1cc) as fitting parameters in a simultaneous, nonlinear least-squares fit of all suitable infrared spectral bands of both 1ct and 1cc. Complete details of the kinetic analysis are given in the ESI† along with plots of the data and fits. Deuteration completely suppresses the tunnelling isomerization, and we compute τ = 2400 y for monodeuterated 1 (see ESI†); no tunnelling of deuterated 1 was observed over one day at 20 K in Ar.
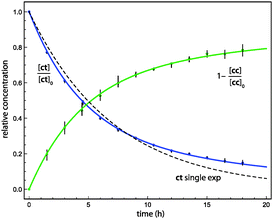
The Ar (20 K) results shown in Fig. 2 are representative of our kinetic analysis of conformational tunnelling. A single-exponential fit to the 1ct decay profile yields an effective half-life of 4.4 h, but the poor quality of the fit demonstrates the multi-exponential character of the kinetics. The initial ratio of fast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) slow sites is near two, and in this case the data do not support the presence of frozen sites (Xfrozen = 0). The slow and fast tunnelling of 1ct exhibits the half-lives τ1 = 14 ± 3 h and τ2 = 3.0 ± 0.2 h, respectively.
slow sites is near two, and in this case the data do not support the presence of frozen sites (Xfrozen = 0). The slow and fast tunnelling of 1ct exhibits the half-lives τ1 = 14 ± 3 h and τ2 = 3.0 ± 0.2 h, respectively.
To theoretically support our experiments, a distinguished reaction path (DRP) was generated for 1ct → 1cc by a series of MP2/aug-cc-pVTZ constrained geometry optimizations, whereby the torsion angle τO![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O–H was varied in 5° increments between 0° and 180° while all other internal coordinates were optimized. Along this path, CCSD(T)/CBS energies were computed to obtain an accurate potential energy curve for the isomerization. Finally, a DRP projected frequency analysis46 was employed to evaluate harmonic vibrational frequencies (ωi) and zero-point vibrational (ZPVE) corrections for each value of τO
C–O–H was varied in 5° increments between 0° and 180° while all other internal coordinates were optimized. Along this path, CCSD(T)/CBS energies were computed to obtain an accurate potential energy curve for the isomerization. Finally, a DRP projected frequency analysis46 was employed to evaluate harmonic vibrational frequencies (ωi) and zero-point vibrational (ZPVE) corrections for each value of τO![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O–H. Tunnelling probabilities (κ) for 1ct → 1cc were computed using exact numerical integration45 and the WKB approximation.35 Tunnelling rates were evaluated as the product of the transmission probability κ and the classical rate (ω0) at which the reactant hits the barrier, assuming that the collision energy under cryogenic conditions is the reaction-mode ZPVE of ω0/2. The computed intrinsic tunnelling half-lives (τ0) for the 1ct → 1cc isomerization in the gas-phase amount to 56 min employing exact numerical integration and to 72 min within the WKB approximation. In support of the methodology underlying these results, a systematic computational study on acid tunnelling has found that “the minimum energy path can be considered as a good approximation for the cis-to-trans tunneling path with maximum transparency”.47 Although our initial tunnelling computations do not incorporate reaction-path curvature effects that would further enhance the rate,48,49 the results compare well with the fast components (τ2) obtained from the multi-exponential kinetic analysis of our experiments. Importantly, the Xfast mole fractions increase toward 1 and the τeff values diminish toward τ0 upon elevating the temperature of the Ar matrix (Table 1 and Fig. 3). While a rigorous assessment of various theoretical methods for computing tunnelling rates is beyond the scope of this communication, we report additional predictions of half-lives obtained with the ZCT and SCT approaches implemented in POLYRATE in the ESI.†50–52
C–O–H. Tunnelling probabilities (κ) for 1ct → 1cc were computed using exact numerical integration45 and the WKB approximation.35 Tunnelling rates were evaluated as the product of the transmission probability κ and the classical rate (ω0) at which the reactant hits the barrier, assuming that the collision energy under cryogenic conditions is the reaction-mode ZPVE of ω0/2. The computed intrinsic tunnelling half-lives (τ0) for the 1ct → 1cc isomerization in the gas-phase amount to 56 min employing exact numerical integration and to 72 min within the WKB approximation. In support of the methodology underlying these results, a systematic computational study on acid tunnelling has found that “the minimum energy path can be considered as a good approximation for the cis-to-trans tunneling path with maximum transparency”.47 Although our initial tunnelling computations do not incorporate reaction-path curvature effects that would further enhance the rate,48,49 the results compare well with the fast components (τ2) obtained from the multi-exponential kinetic analysis of our experiments. Importantly, the Xfast mole fractions increase toward 1 and the τeff values diminish toward τ0 upon elevating the temperature of the Ar matrix (Table 1 and Fig. 3). While a rigorous assessment of various theoretical methods for computing tunnelling rates is beyond the scope of this communication, we report additional predictions of half-lives obtained with the ZCT and SCT approaches implemented in POLYRATE in the ESI.†50–52
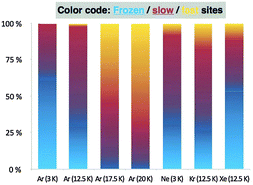 | ||
| Fig. 3 Mole fractions of frozen, slow, and fast tunnelling sites in different noble gas matrices at several temperatures. | ||
The complicated observed tunnelling behaviour is presumably attributable to varying degrees in which the matrix environment hinders the rotamerization of 1. The thermal energy of our highest-temperature experiments (20 K) is not sufficient to significantly excite the C–O torsional vibration (491 cm−1, CCSD(T)/cc-pVTZ) to accelerate the tunnelling rotamerization, which would only become important at about 60 K; however, there is enough thermal energy to excite the solid noble gas host material, whose Debye frequencies are in the range of 40–70 cm−1.53 As the matrix softens at higher temperatures, it can better accommodate the structural changes required for tunnelling of 1ct. Such temperature dependences of conformational tunnelling processes have already been observed experimentally54 and rationalized through a theoretical study of the noble gas environment,55 which showed that the temperature dependence of the tunnelling event is most likely attributable to a reorganization of the matrix environment. The circumstances are very different for the highly exothermic tunnelling of hydroxycarbenes to the corresponding aldehydes.32,37
The intricate dependence of QMT on the noble gas host is currently not fully understood (Fig. 3). Argon seems in this respect well behaved as tunnelling accelerates with increasing temperature in the 3–20 K temperature regime; this corresponds well with a temperature-dependent activation of the noble gas atoms during the QMT rotamerization. Krypton is comparable, while the most polarizable Xe-matrix impedes tunnelling. Comparison with the Ne-matrix is difficult, but its low polarizability is likely to reduce the interaction with the interconverting conformers relative to Ar at the same temperature. Such behaviour has been reported before, e.g., in the conformational tunnelling of formic acid that exhibits increasing tunnelling rates in going from Xe to Ne, while its O-deuterated isotopologue shows the opposite trend.56
In terms of competing tunnelling mechanisms, it is clear that while the two possible pathways from 1ct to 1ccviaTS2 and TS3, respectively, have approximately the same width (Fig. 1), the tunnelling probabilities are primarily determined by barrier height, as found in classic kinetically controlled reactions. This situation is in marked contrast to the phenomenon of tunnelling control,32 where barrier width trumps barrier height in favour of the thermodynamic product. The 26.7 kcal mol−1 activation barrier difference between the two transition structures translates into a tunnelling rate ratio of approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1010, i.e., essential quantitative selectivity.
1010, i.e., essential quantitative selectivity.
We have unveiled a novel conformational tunnelling isomerization of 1 (in the range of 4–20 h) that is supported by high-level quantum chemical computations. The tunnelling process strongly depends on the temperature and nature of the matrix environment. The three phenomenological classes of tunnelling sites demonstrate that tunnelling is affected by the environment and therefore can in principle be controlled externally. On the basis of these findings and the theoretical predictions, we expect the tunnelling half-life for the isomerization of 1ct to 1cc would be even faster in the gas phase.
This work was supported by a collaboration grant from the U.S. National Science Foundation (CHE-1124885) and the Deutsche Forschungsgemeinschaft (Schr 597/18-1) to W. D. A. and P. R. S.; V. H. thanks the Liebig College at Justus-Liebig University, sponsored by the State of Hesse.
Notes and references
- J. K. Terlouw, C. B. Lebrilla and H. Schwarz, Angew. Chem., Int. Ed. Engl., 1987, 26, 354–555 CrossRef.
- K. Adamczyk, M. Prémont-Schwarz, D. Pines, E. Pines and E. T. J. Nibbering, Science, 2009, 326, 1690–1694 CrossRef CAS PubMed.
- S. Ghoshal and M. K. Hazra, RSC Adv., 2015, 5, 17623–17635 RSC.
- C. J. Bennett, C. P. Ennis and R. I. Kaiser, Astrophys. J., 2014, 794, 57 CrossRef.
- T. Mori, K. Suma, Y. Sumiyoshi and Y. Endo, J. Chem. Phys., 2009, 130, 204308 CrossRef PubMed.
- T. Mori, K. Suma, Y. Sumiyoshi and Y. Endo, J. Chem. Phys., 2011, 134, 044319 CrossRef PubMed.
- H. P. Reisenauer, J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2014, 53, 11766–11771 CrossRef CAS PubMed.
- M. H. Moore and R. K. Khanna, Spectrochim. Acta, Part A, 1991, 47, 255–262 CrossRef.
- W. Zheng and R. I. Kaiser, Chem. Phys. Lett., 2007, 450, 55–60 CrossRef CAS.
- M. Garozzo, D. Fulvio, O. Gomis, M. E. Palumbo and G. Strazzulla, Planet. Space Sci., 2008, 56, 1300–1308 CrossRef CAS.
- W. Hage, A. Hallbrucker and E. Mayer, J. Am. Chem. Soc., 1993, 115, 8427–8431 CrossRef CAS.
- W. Hage, A. Hallbrucker and E. Mayer, J. Chem. Soc., Faraday Trans., 1995, 91, 2823–2826 RSC.
- T. Bally, in Reactive Intermediates, ed. R. A. Moss, M. S. Platz and M. Jones Jr., Wiley-Interscience, Hoboken, New Jersey, 2004, pp. 797–845 Search PubMed.
- A. Barnes, W. J. Orville-Thomas, R. Gaufrès and A. Müller, Matrix Isolation Spectroscopy, D. Reidel Publishing Company, Dordrecht, 1981 Search PubMed.
- A. Dibenedetto, M. Aresta, P. Giannoccaro, C. Pastore, I. Pápai and G. Schubert, Eur. J. Inorg. Chem., 2006, 908–913 CrossRef CAS.
- J. Bernard, Faculty of Chemistry and Pharmacy, PhD thesis, University of Innsbruck, Innsbruck, 2014, p. 160 Search PubMed.
- I. Kohl, K. Winkel, M. Bauer, K. R. Liedl, T. Loerting and E. Mayer, Angew. Chem., Int. Ed., 2009, 48, 2690–2694 CrossRef CAS PubMed.
- S. K. Reddy and S. Balasubramanian, Chem. Commun., 2014, 50, 503–514 RSC.
- G. Bucher and W. Sander, Science, 2014, 346, 544–545 CrossRef CAS PubMed.
- G. Bucher, Eur. J. Org. Chem., 2010, 1070–1075 CrossRef CAS.
- T. Loerting, C. Tautermann, R. T. Kroemer, I. Kohl, A. Hallbrucker, E. Mayer and K. R. Liedl, Angew. Chem., Int. Ed., 2000, 39, 891–894 CrossRef.
- B. Jonsson, G. Karlstrom, H. Wennerstrom, S. Forsen, B. Roos and J. Almlof, J. Am. Chem. Soc., 1977, 99, 4628–4632 CrossRef CAS.
- S. Ghoshal and M. K. Hazra, J. Phys. Chem. A, 2014, 118, 2385–2392 CrossRef CAS PubMed.
- M. Kumar, D. H. Busch, B. Subramaniam and W. H. Thompson, J. Phys. Chem. A, 2014, 118, 5020–5028 CrossRef CAS PubMed.
- M. Kumar, D. H. Busch, B. Subramaniam and W. H. Thompson, J. Phys. Chem. A, 2014, 118, 10155–10156 CrossRef CAS.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 158–168 CrossRef.
- C. A. Wight and A. I. Boldyrev, J. Phys. Chem., 1995, 99, 12125–12130 CrossRef CAS.
- J. Kästner, Chem. – Eur. J., 2013, 19, 8207–8212 CrossRef PubMed.
- B. K. Carpenter, J. Am. Chem. Soc., 1983, 105, 1700–1701 CrossRef CAS.
- B. K. Carpenter, Science, 2011, 332, 1269–1270 CrossRef CAS PubMed.
- M. Ertelt, D. A. Hrovat, W. T. Borden and W. Sander, Chem. – Eur. J., 2014, 20, 4713–4720 CrossRef CAS PubMed.
- P. R. Schreiner, H. P. Reisenauer, D. Ley, D. Gerbig, C.-H. Wu and W. D. Allen, Science, 2011, 332, 1300–1303 CrossRef CAS PubMed.
- S. Kozuch, Org. Lett., 2014, 16, 4102–4105 CrossRef CAS PubMed.
- S. Kozuch, Phys. Chem. Chem. Phys., 2014, 16, 7718–7727 RSC.
- H. A. Kramers, Z. Phys., 1926, 39, 828–840 CrossRef.
- M. Razavy, Quantum Theory of Tunneling, World Scientific, Singapore, 2003 Search PubMed.
- P. R. Schreiner, H. P. Reisenauer, F. C. Pickard Iv, A. C. Simmonett, W. D. Allen, E. Matyus and A. G. Császár, Nature, 2008, 453, 906–909 CrossRef CAS PubMed.
- M. Pettersson, E. M. S. Macoas, L. Khriachtchev, J. Lundell, R. Fausto and M. Räsänen, J. Chem. Phys., 2002, 117, 9095–9098 CrossRef CAS.
- E. M. S. Macôas, L. Khriachtchev, R. Fausto and M. Räsänen, J. Phys. Chem. A, 2004, 108, 3380–3389 CrossRef.
- S. Amiri, H. P. Reisenauer and P. R. Schreiner, J. Am. Chem. Soc., 2010, 132, 15902–15904 CrossRef CAS PubMed.
- G. Bazsó, S. Gobi and G. Tarczay, J. Phys. Chem. A, 2012, 116, 4823–4832 CrossRef PubMed.
- G. Bazsó, G. Magyarfalvi and G. Tarczay, J. Phys. Chem. A, 2012, 116, 10539–10547 CrossRef PubMed.
- G. Bazsó, E. E. Najbauer, G. Magyarfalvi and G. Tarczay, J. Phys. Chem. A, 2013, 117, 1952–1962 CrossRef PubMed.
- D. Gerbig and P. R. Schreiner, J. Phys. Chem. B, 2014, 119, 693–703 CrossRef PubMed.
- P. R. Schreiner, J. P. Wagner, H. P. Reisenauer, D. Gerbig, D. Ley, J. Sarka, A. G. Császár, A. Vaughn and W. D. Allen, J. Am. Chem. Soc., 2015, 137, 7828–7834 CrossRef CAS PubMed.
- W. D. Allen, A. Bodi, V. Szalay and A. G. Császár, J. Chem. Phys., 2006, 124, 224310 CrossRef PubMed.
- M. Tsuge and L. Khriachtchev, J. Phys. Chem. A, 2015, 119, 2628–2635 CrossRef CAS PubMed.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- T. V. Albu, B. J. Lynch, D. G. Truhlar, A. C. Goren, D. A. Hrovat, W. T. Borden and R. A. Moss, J. Phys. Chem. A, 2002, 106, 5323–5338 CrossRef CAS.
- A. Kuppermann and D. G. Truhlar, J. Am. Chem. Soc., 1971, 93, 1840–1851 CrossRef CAS.
- R. T. Skodje, D. G. Truhlar and B. C. Garrett, J. Phys. Chem., 1981, 85, 3019–3023 CrossRef CAS.
- J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. F. Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, A. Ratkiewicz, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, POLYRATE 2010-A: Computer Program for the Calculation of Chemical Reaction Rates for Polyatomics., 2010 Search PubMed.
- H. J. Jodl, in Chemistry and Physics of Matrix-Isolated Species, ed. L. Andrews and M. Moskovits, 1989 Search PubMed.
- E. M. S. Macôas, L. Khriachtchev, M. Pettersson, R. Fausto and M. Räsänen, J. Chem. Phys., 2004, 121, 1331–1338 CrossRef PubMed.
- L. I. Trakhtenberg, A. A. Fokeyev, A. S. Zyubin, A. M. Mebel and S. H. Lin, J. Chem. Phys., 2009, 130, 144502 CrossRef PubMed.
- A. Domanskaya, K. Marushkevich, L. Khriachtchev and M. Räsänen, J. Chem. Phys., 2009, 130, 154509 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, detailed matrix isolation spectra, tables of assigned vibrational frequencies, the complete kinetic analysis, the theoretical methods, geometric structures, and electronic and zero-point energies. See DOI: 10.1039/c6cc01756h |
| This journal is © The Royal Society of Chemistry 2016 |