Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dramatic mechanistic switch in Sn/AuI group exchanges: transmetalation vs. oxidative addition†
D.
Carrasco
a,
M.
García-Melchor
*b,
J. A.
Casares
*a and
P.
Espinet
*a
aIU CINQUIMA/Química Inorgánica, Facultad de Ciencias, Universidad de Valladolid, 47071 Valladolid, Spain. E-mail: espinet@qi.uva.es; casares@qi.uva.es
bSUNCAT Center for Interface Science and Catalysis, Department of Chemical Engineering, Stanford University, Stanford, CA 94305, USA
First published on 22nd February 2016
Abstract
The mechanism of Ph/X exchange in reactions involving SnPhnBu3 and [AuXL] complexes switches dramatically from the usual concerted mechanism involving Ar/X mixed bridges when X = Cl, to an unexpected oxidative addition/reductive elimination pathway via an AuIII intermediate when X = vinyl.
Whereas organic-group/halide exchanges operating in cross-coupling catalysis have been studied in detail,1 transmetalations exchanging two carbon groups between metals, often involved in bimetallic catalysis and in formation of unwanted homocoupling products,2 are very little studied.
Recently, transmetalation between gold complexes and organotin derivatives has drawn attention due to its occurrence in multimetallic catalytic processes. For example, we have shown that AuI complexes co-catalyze the coupling of bulky stannanes in the gold co-catalyzed Stille reaction. In this new process a Sn/Au/Pd double transmetalation occurs through successive Sn/Au and Au/Pd transition states with a much lower activation energy than the direct Sn/Pd transmetalation, which allows for coupling of bulky groups.3 Blum has studied the vinyl exchange between gold and tin in the Pd/Au co-catalyzed carbostannylation of alkynes.4 The gold-catalyzed cycloisomerization/stannylation cascade reaction of 1,6-diyne-4-en-3-ols using 2-(furyl)Sn(n-Bu)3 as the primary source of stannane, and leading to stannyl naphthalenes has been reported by Chen.5 Bourissou has communicated examples of transmetalation from vinyl gold complexes to SnBu3(OTf) in the presence of PPh3.6 Furthermore, some of these transmetalations in Au/Pd/Sn systems have been computationally calculated.3a,7 In this work we combine experiments and DFT calculations to study the mechanisms of Sn/Au transmetalation in which a Ph group is exchanged by a halogen or by a vinyl group. Unexpectedly, we find a dramatic mechanistic switch from the first to the second transmetalation process somehow representing the subtle connection between the concepts of acid–base interaction and oxidation–reduction.
First, the thermodynamics of X for R exchange between AuI and Sn was experimentally studied in THF for a number of cases: X = I, Cl, vinyl; L = PMe3, PCy3, PPh3; R = Ph, C6Cl3F2, C6F5, 2Me-naphthyl (eqn (1)).8 The exchange reactions are reasonably fast for X = halide, and the corresponding equilibriums can be reached at 303 K. For X = I, they are strongly shifted to the right, except for R = 3,5-C6Cl2F3 and C6F5: these are slightly shifted to the left due to the stronger Au–C bond for perhaloaryl groups compared to non-halogenated aryls. For X = Cl the equilibria are much more balanced due to the high energy of the Sn–Cl bond, which makes the equilibrium displacement to the right less favourable.3a For X = vinyl, the Caryl/Calkyl exchange is too slow at room temperature, and equilibration is only achieved reasonably fast at 323 K, when an equilibrium slightly displaced to the left is produced.
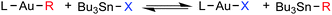 | (1) |
With these data in hand, the exchanges between [AuPh(PMe3)] and SnXBu3 with X = Cl and vinyl were chosen for detailed study, in view of the somewhat unexpectedly large rate difference observed between them. These reactions were monitored in THF and in toluene solutions, using 31P NMR.
The solutions of SnClBu3 and [AuPh(PMe3)] in THF are non-conducting, supporting that the Cl ligand remains coordinated to one metal centre, at least, throughout the reaction. The study of the Ph/Cl transmetalation, using Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au = 20
Au = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in order to simplify the handling of data and to ensure that the equilibrium is established in a reasonable time, affords Keq. = 1.1 at 298 K. Kinetic experiments at 303 K show that the reaction is first order in [AuPh(PMe3)].8 The exchange rates measured in the temperature range 250–330 K afford the activation parameters ΔH‡ = 27(±2) kJ mol−1, ΔS‡ = −223(±23) J K−1 mol−1, ΔG‡298 = 22.3 kcal mol−1. For comparison with experiments and calculations to come, for this reaction ΔG‡323 = 23.7 kcal mol−1. The strongly negative ΔS‡ value clearly supports an associative exchange process. The same reaction was also studied in toluene, resulting in a very similar activation Gibbs energy (ΔG‡298 = 22.0 kcal mol−1), which discards the possible participation of THF as coordinating agent in the first transmetallation.
1 in order to simplify the handling of data and to ensure that the equilibrium is established in a reasonable time, affords Keq. = 1.1 at 298 K. Kinetic experiments at 303 K show that the reaction is first order in [AuPh(PMe3)].8 The exchange rates measured in the temperature range 250–330 K afford the activation parameters ΔH‡ = 27(±2) kJ mol−1, ΔS‡ = −223(±23) J K−1 mol−1, ΔG‡298 = 22.3 kcal mol−1. For comparison with experiments and calculations to come, for this reaction ΔG‡323 = 23.7 kcal mol−1. The strongly negative ΔS‡ value clearly supports an associative exchange process. The same reaction was also studied in toluene, resulting in a very similar activation Gibbs energy (ΔG‡298 = 22.0 kcal mol−1), which discards the possible participation of THF as coordinating agent in the first transmetallation.
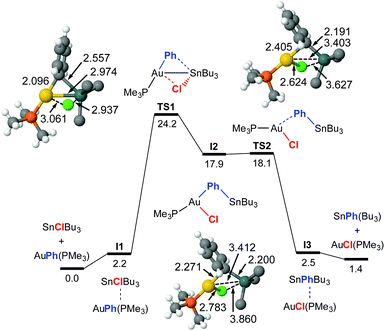
The TS1 energy (ΔG‡323 = 24.2 kcal mol−1) in Fig. 1 matches well the experimental activation energy and the DFT profile predicts a fairly balanced equilibrium, as observed experimentally. The calculations also coincide with the experimental result that the phosphine ligand remains coordinated to gold along the reaction pathway. The mechanism basically consists in a double group exchange via single- or double-bridged intermediates or transition states, as typically found in Pd. At variance with PdII, the transmetalation involving AuI does not require releasing the ancillary ligand, and the coordination number of gold increases from 2 to 3 at the transition state.
The Ph/vinyl exchange was also studied using a 20 fold proportion of Sn(vinyl)Bu3 to produce [Au(vinyl)(PMe3)] and SnPhBu3. As commented above, no conversion was observed at room temperature, but it took place at a low rate of 1.7 (±0.2) × 10−6 L mol−1 s−1 when heated 323 K (ΔG‡323 = 27.5 kcal mol−1). A wide enough temperature range for measuring ΔH‡ and ΔS‡ was not accessible due to partial decomposition to gold upon heating above 333 K, and too slow reaction below 313 K.
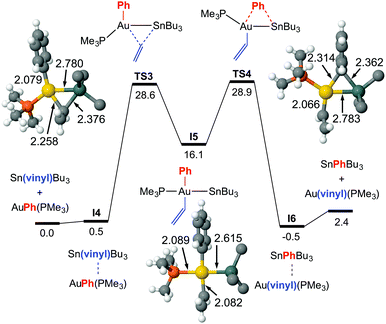
For this exchange DFT calculations prove that the double group exchange mechanism via bridged intermediates, proposed for X = Cl, has to be discarded for X = vinyl because it has a very high energetic barrier (42.1 kcal mol−1) at the rate-determining step.8 Calculations provide instead a reasonable highly symmetrical alternative pathway, much lower in energy, which matches well the experimental ΔG‡ value and uncovers a dramatic mechanistic change (Fig. 3). It involves the oxidative addition of the Sn–Cvinyl bond to Au viaTS3, to produce trans-[Au(SnBu3)(Ph)(vinyl)(PPh3)] (I5), a square-planar gold intermediate from which the Sn–CPh or Sn–Cvinyl reductive elimination viaTS4 can give rise to the respective AuI and Sn products. The calculated ΔG‡323 values are 28.6 kcal mol−1 starting from [AuPh(PMe3)], and 28.9 starting from [Au(vinyl)(PMe3)]. This result prompted us to carry out, as caution, a calculation of the TS energy in an oxidative addition/reductive elimination pathway for Ph/Cl exchange (see ESI,† Fig. S6), which afforded an energetic barrier of 34.2 kcal mol−1, confirming its unlikeliness.
Looking at Fig. 1 and 2, it catches the eye that the closely linear arrangement (P–Au–X ≈ 180°) present in all the starting [AuX(PMe3)] complexes is very differently altered in the transition states. More specifically, TS3 shows a large alteration (P–Au–Ph = 116°) at the initial interaction, wile the change in TS1 is comparatively small (P–Au–Ph = 171°). For the TSs at the right side of the two profiles, both TS2 (P–Au–Cl = 107°), and TS4 (P–Au–vinyl = 118°) show a large alteration from 180°. It is also interesting to note the different Au–Sn distances in the transition states. In TS3 (2.780 Å) and TS4 (2.783 Å), the Au–Sn distance clearly indicates a covalent bond (sum of the covalent radii is 2.75 Å). In TS1, this distance (2.974 Å) clearly indicates a somewhat weaker interaction.9 Finally in TS2 the distance is much longer (3.403 Å) although still shorter than the sum of vdW radii (3.83 Å), supporting at most an extremely weak indication. These distances point to very different orbital implications of the gold fragment at the initial interaction of the reagents in the two pathways.
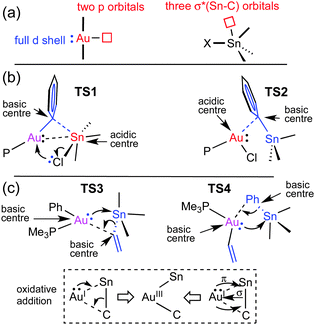
Why are the two pathways so different? It is textbook knowledge that Sn can often expand its coordination number beyond four with common coordinating molecules.10 This can also happen with AuI acting as a metallobase, as nicely shown by Bourissou in a specially designed bimetallic Au/Sn system where Sn becomes pentacoordinated by intramolecular interaction with gold as a donor ligand (experimental Au–Sn bond distance is 2.891 Å).11 The orbital availability in the reagents examined here is schematically shown in Fig. 3a. The low energy unoccupied orbitals available for coordinative expansion in SnXBu3 compounds are the three σ*(Bu–Sn) orbitals (this availability is represented by a small square box). Their acceptor ability depends on the electronegativity of X (highly electronegative X groups will stabilize these orbitals and make them better acceptors) and on how much they are saturated by negative hyperconjugation with the four groups already bonded to tin.10 Hence, tin will be a much better acidic centre and better acceptor of a fifth ligand in SnClBu3 than in Sn(vinyl)Bu3 because vinyl produces much higher hyperconjugation effect. On the other hand, the sp hybridized linear AuI can expand its coordination number to 3 or 4 by involving its empty 6p orbitals in bonding (these are represented by a square box on Au in Fig. 3a). In addition, AuI has the ability to show basicity (metallobasicity) by implicating electron density from its 5d closed shell orbitals in a donor–acceptor interaction with other acidic centres (represented as a lone pair in Fig. 3a, left). This metallobasicity increases with more electron donor groups on Au. Overall, depending on the ligands at Au the potential of our [AuX(PMe3)] complexes as metallobases should follow the trend vinyl > Ph > Cl, whereas the tendency of AuI to increase its coordination number above 2 should be the opposite (Cl > Ph > vinyl).
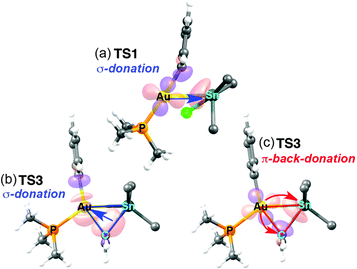
The changes in acidity and basicity of the Au and Sn centres allow us to rationalize the structural variations observed in the transition states and, beyond that, the mechanistic switch observed. To this end the electronic interactions are schematically represented in Fig. 3b and c. For TS2, with a Cl ligand on gold, the metallobasicity of Au is expected to be the lowest, and its acidity the highest. Consistently, the interaction between the two fragments is established by electron donation from the Sn–Ph bond to an empty orbital in the gold centre, which becomes 3-coordinated, while the Sn atom remains 4-coordinated. The observation that the Au–Sn distance is shorter than the sum of vdW radii is not unexpected since the nature of all 3c2e electron deficient Au–C–Sn bridges should produce some degree of Au–Sn bond interaction not needing to invoke metallophilia.12 For TS1, which has the Cl ligand on Sn, this centre becomes very acidic, whereas the Au centre with a good donor Ph group is more basic than in TS2. Consequently, the Au–Ph bond attacks the acidic Sn, which becomes 5-coordinated. This donation from the Au–Ph bond increases the acidity of Au enough as to interact with a lone electron pair from the Cl ligand. Altogether, the metallobasicity of Au in TS1 is likely higher than in TS2, which along with the higher acidity of Sn may contribute to increase the Au–Sn interaction and shorten the distance (Fig. 3b). To investigate in detail the Au–Sn interactions we carried out a second order perturbation theory analysis of the Fock matrices in the Natural Bond Orbital (NBO) basis (details in Table S6 of ESI†).13 For TS1 (Fig. 4a) this analysis reveals an electron donation of 0.08 e from a 5d(Au) orbital to a σ*(Sn–Bu) orbital with 85% Sn character shown in Fig. 4.
The structural features of TS3 and TS4 sharply differ from those of TS1, showing the group being transmetalated almost equidistant from Au and Sn, and displaying a strong Au–Sn bond. The respective highly donor hydrocarbyl group R (R = Ph, vinyl) attached to Sn saturates its potential acidity and the Sn–R moiety behaves as a nucleophile attacking the gold centre with the electron density of the σ(Sn–CR) bond, more participated by the C atom. This leads to an electronically enriched 3-coordinated AuI bearing two hydrocarbyl groups, which markedly enhances its metallobasicity from the 5d(Au) orbitals. In fact, this higher basicity not only favours the interaction with the empty σ*(Sn–CR) orbital of the bridging group (Fig. 3c), but also weakens the Sn–CR bond, eventually leading to the oxidative addition product I5 (Fig. 2).
The NBOs in Fig. 4b and c confirm that there are direct donor–acceptor interactions orbital interaction between the two metal centres in TS3. This analysis can be decomposed into donation and back-donation components. The donation (Fig. 4b) consists in the σ–bond donation from a hybrid sp bonding orbital of the Sn–Cvinyl bond, which has 21% Sn and 79% Cvinyl character, to an empty natural bond orbital constituted mainly by the 6s orbital of Au (78%) and a hybrid sp orbital (22%) from the CPh (Fig. 4b). This interaction eventually results in the formation of the Au–vinyl bond in I5. On the other hand, the back-donation component (Fig. 4c) involves an electron donation of 0.17e from a 5d(Au) orbital to an anti-bonding orbital of the Sn–Cvinyl bond, which has a 79% Sn and 21% Cvinyl character. This interaction eventually results in the formation of the Au–Sn bond in I5. Based on the degree of implication of the 5d(Au) electron density (starting from no implication in TS2 to small implication in TS1 and large implication in TS3) we can say that it is mostly the increasing metallobasicity of AuI that eventually leads to make oxidative addition accessible. Overall, the combination of donation and back-donation components is perfectly consistent with the classical image of a concerted oxidative addition of a X–Y moiety to a metal atom M, where 2 e of the X–Y bond to be broken and 2 e of the metal to be oxidized are shared to form two new X–M and M–Y bonds in a cis arrangement (Fig. 3, bottom). A similar pathway for the hypothetical oxidative addition of Sn(vinyl)H3 to linear Pd(0) complexes was proposed by Matsubara.14
To our knowledge, this is the first time that the oxidative addition of a Sn–C bond to gold has been proposed. The AuIII complexes bearing Au–Sn bonds reported to date have been obtained by oxidative addition of a fairly weak Sn–Sn bond to gold(I).15,16 It is worth mentioning that experimentally we do not detect any Ph–vinyl coupling product by NMR, and only traces by GC. This coupling would require the Ph and vinyl groups to achieve a cis disposition, either directly from the oxidative addition, or by isomerization of I5 to any of the two possible cis-C,C isomers. Calculations show that cis-Ph/vinyl trans-Ph/Sn isomer (the other cis-C,C isomer is expected to have very similar energy) is 8.2 kcal mol−1 less stable than the trans intermediate I5, and the calculated reductive elimination barrier to give Ph–vinyl is prohibitively high (ca. 44 kcal mol−1, see ESI† for details).
Considering the reluctance of Au catalysts to participate in processes that require a difficult oxidation to AuIII, the accessibility of this oxidative addition mechanism is noteworthy, and deserves some comment. Thinking routinely of an oxidation state AuIII for I5 we would infringe the rules to assign oxidation states to a metal. Obeying the formalism, the metal–metal bonds should not count, and gold in I5 should be assigned AuII. This reflects that Au–Sn bonds make gold more electron rich (less “oxidized”) than, for instance, M–X or M–R bonds. For this reason, the oxidative addition process found here is more accessible than those leading to “more authentic” AuIII complexes, from which C–C reductive elimination is fast.17 These considerations help to understand why this Au”III” is more accessible, but also less prone to afford coupling products.
In summary, we find that the Sn/Au transmetalation is very much influenced by the acidity of the tin centre and the metallobasicity of the gold centre. When electron donor groups on tin quench the acidity of the low-lying σ*(Sn–CBu) orbitals by hyperconjugation and the aurobasicity increases in the TS, the transmetalation switches from the classical bridge mechanism to an oxidative addition pathway. This mechanism becomes effective by participation, as acceptor of the electron density from gold, of the σ*(Sn–CR) orbital of the group being transmetalated.
This work was supported by the Spanish MINECO (grants CTQ2013-48406-P, and CTQ2014-52974-REDC) and the Junta de Castilla y León (grant VA256U13).
Notes and references
- Mechanistic studies on transmetalation involving Sn: (a) C. Cordovilla, C. Bartolomé, J. M. Martínez-Ilarduya and P. Espinet, ACS Catal., 2015, 5, 3040 CrossRef CAS; (b) P. Espinet and A. M. Echavarren, Angew. Chem., Int. Ed., 2004, 43, 4704–4734 CAS; (c) M. H. Pérez-Temprano, A. Nova, J. A. Casares and P. Espinet, J. Am. Chem. Soc., 2008, 130, 10518 CrossRef PubMed; (d) M. H. Pérez-Temprano, A. M. Gallego, J. A. Casares and P. Espinet, Organometallics, 2011, 30, 611 CrossRef.
- General review on transmetalation in bimetallic systems: M. H. Pérez-Temprano, J. A. Casares and P. Espinet, Chem. – Eur. J., 2012, 18, 1864 CrossRef PubMed.
- (a) J. delPozo, D. Carrasco, M. H. Pérez-Temprano, M. García-Melchor, R. Álvarez, J. A. Casares and P. Espinet, Angew. Chem., Int. Ed., 2013, 52, 2189 CrossRef CAS PubMed; (b) J. delPozo, J. A. Casares and P. Espinet, Chem. Commun., 2013, 49, 7246 RSC.
- (a) J. J. Hirner, Y. Shi and S. A. Blum, Acc. Chem. Res., 2011, 44, 603 CrossRef CAS PubMed; (b) Y. Shi, S. M. Peterson, W. W. Haberaecker and S. A. Blum, J. Am. Chem. Soc., 2008, 130, 2168 CrossRef CAS PubMed.
- Y. Chen, M. Chen and Y. Liu, Angew. Chem., Int. Ed., 2012, 51, 6181 CrossRef CAS PubMed.
- M. Joost, P. Gualco, S. Mallet-Ladeira, A. Amgoune and D. Bourissou, Angew. Chem., Int. Ed., 2013, 52, 7160 CrossRef CAS PubMed.
- A. Ariafard, N. A. Rajabi, M. J. Atashgah, A. J Canti and B. F. Yates, ACS Catal., 2014, 4, 860 CrossRef CAS.
- Details are given in ESI†.
- For the Sn/Au transmetalation between [AuCl(AsMe3)] and Sn(Naph)Me3 a metal–metal interaction with Au–Sn distance 2.904 Å in the rate determining TS was calculated (ref. 3).
- C. Elschenbroich, Organometallics, Wiley-VCH Verlag GmbH&Co. KGaA, Weinheim, 3rd edn, 2006 Search PubMed.
- P. Gualco, T. P. Lin, M. Sircoglou, M. Mercy, S. Ladeira, G. Bouhadir, L. M. Pérez, A. Amgoune, L. Maron, F. P. Gabbaï and D. Bourissou, Angew. Chem., Int. Ed., 2009, 48, 9892 CrossRef CAS PubMed.
- J. delPozo, E. Gioria, J. A. Casares, R. Álvarez and P. Espinet, Organometallics, 2015, 34, 3120 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013 Search PubMed.
- T. Matsubara, Organometallics, 2003, 22, 4286 CrossRef CAS.
- N. Lassauque, P. Gualco, S. Mallet-Ladeira, K. Miqueu, A. Amgoune and D. Bourissou, J. Am. Chem. Soc., 2013, 135, 13827 CrossRef CAS PubMed.
- Reviews about transition metal-tin chemistry: (a) D. Agustin and M. Ehses, C. R. Chim., 2009, 12, 1189 CrossRef CAS; (b) M. S. Holt, W. L. Wilson and J. H. Nelson, Chem. Rev., 1989, 89, 11 CrossRef CAS.
- W. J. Wolf, M. S. Winston and F. D. Toste, Nat. Chem., 2014, 6, 159 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section and computational details (40 pages). See DOI: 10.1039/c5cc10496c |
| This journal is © The Royal Society of Chemistry 2016 |