Increasing the quantitative bandwidth of NMR measurements

Abstract

The frequency range of quantitative NMR is increased from tens to hundreds of kHz by a new pulse sequence, CHORUS. It uses chirp pulses to excite uniformly over very large bandwidths, yielding accurate integrals even for nuclei such as ¹⁹F that have very wide spectra.

---

¹⁹F NMR is widely used by chemists in the analysis of fluorinated drugs and their impurities. Typical drugs have only one or two fluorine atoms, but many protons. Thus in comparison to ¹H NMR, ¹⁹F NMR offers spectra of greatly reduced complexity, simplifying interpretation while retaining high sensitivity. Quantitative analysis using ¹⁹F, and other nuclei such as ¹³C that have wide chemical shift ranges, requires constant amplitude and constant phase (more strictly, phase with a linear offset dependence) broadband excitation over the full spectral width. This is problematic, since due to the limited radiofrequency power available for pulsed excitation, resonance offset effects distort both signal intensities and signal phases and seriously degrade the accuracy of signal integration.

The scale of the problem can be seen by comparison of the loss in signal intensity towards the edges of the frequency range for narrow bandwidth quantitative experiments (¹H, ±5 ppm) and for much wider bandwidths (¹⁹F, ±300 ppm). On a 500 MHz spectrometer using a 12.5 μs 90° pulse width, the losses are respectively negligible, and almost total (98%). Accurate (±1–2%) quantification with a 90° pulse is restricted to a relatively narrow range of frequencies, about 20 kHz.

In order to circumvent resonance offset effects, current practice in quantifying ¹⁹F spectra¹ is to make a separate measurement for each different region of a spectrum, using a different quantitation standard with an appropriate chemical shift in each case. This is cumbersome, and it can be difficult to find appropriate standards due to problems such as sample instability, insolubility of quantitation standards in the solvent used, and signal overlap between analyte and standard. It would be greatly preferable to find a way to achieve quantitative excitation over the full chemical shift range.

To overcome pulse imperfections and improve the bandwidth of excitation, a variety of composite pulse methods have been developed.^2–7 However even the best of these methods fall well short of the bandwidths required. Pulse sequences generated by optimal control algorithms give more effective results, with small phase errors (<2°) over ±20 kHz, e.g. BEBOP^8,9 and the calibration-free phase modulated sequence PM-BEBOP;¹⁰ however, these methods have yet to be applied to the much wider spectral widths encountered here.

A much larger improvement in excitation bandwidth can be obtained through the use of swept-frequency pulses.^5,11–19 In such pulses the transmitter frequency is rapidly swept over a wide range during the pulse, allowing full signal amplitude to be excited far off resonance even with modest radiofrequency (RF) power. The big disadvantage of such pulses is that the phase of the excitation they produce varies very rapidly, and in a nonlinear fashion, with resonance offset. Much of this phase variation can be refocused by combining 90° and 180° swept-frequency pulses of appropriate relative duration and amplitude^14,17,19 (see ESI,† Fig. S2a), but the remaining signal phase error still varies in a nonlinear fashion with frequency so that less than half of the excitation range is usable (see ESI,† Fig. S2b). Using a nonlinear frequency sweep can improve the phase performance,¹⁷ but there is a further, and less obvious, problem with such double swept-frequency pulse excitation sequences, which is that the signal phase is extremely sensitive to B₁ amplitude.¹⁹ As a result, B₁ inhomogeneity causes large (>30%) losses in signal even with modern probes (see ESI,† Fig. S2b).

In a notably elegant analysis,¹⁹ Cano et al. have shown that the problem of the B₁ sensitivity of the double swept-frequency pulse sequence can be solved by the interpolation of a further 180° element, with a duration equal to that of the 90° pulse, to give the double echo ABSTRUSE (Adjustable, Broadband, Sech/Tanh-Rotation Uniform Selective Excitation) sequence. The ABSTRUSE sequence was derived with the aim of providing a rectangular excitation spectrum, with uniform signal phase and a rapid drop in excitation outside the passband. As the name implies, it is based on hyperbolic secant (“HS” or “sech/tanh”) swept-frequency pulses.²⁰ These have the desirable property of giving close to uniform phase excitation “out of the box” in the double echo, with small phase errors that can be cancelled by co-adding the results of experiments with opposite frequency sweep directions.

The attractive features of the hyperbolic secant pulse for band-selective excitation – a rapid transition between full and zero excitation, and approximate phase uniformity – are not compatible with the aim of exciting very wide bandwidths quantitatively. This requires the best possible phase properties and the widest possible excitation for a given limit on peak radiofrequency power. However, the ABSTRUSE logic can be applied, with one important proviso, to any swept-frequency pulse shape. Where maximum bandwidth for a given duration is the overriding aim, a logical choice of pulse shape is the simple chirp pulse of Bodenhausen et al.,^14–18 leading to a pulse sequence of the form of Fig. 1a. The chirp pulse has uniform RF amplitude, except for smoothed ends, and therefore spreads RF power uniformly over almost the full frequency range. The important proviso is that a basic chirp pulse does not share the benign phase characteristics of the hyperbolic secant pulse, and it is therefore necessary to correct the residual nonlinear dependence of signal phase on excitation frequency.

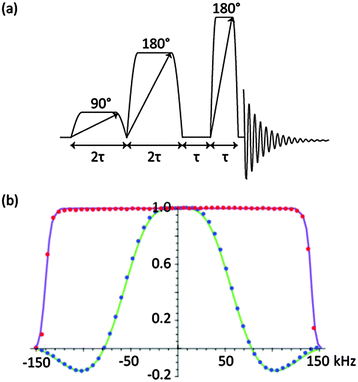Fig. 1 (a) Pulse sequence for CHORUS (CHirped, ORdered pulses for Ultra-broadband Spectroscopy), for B₁-insensitive, broadband, constant-phase excitation. Pulse amplitudes are in the ratio 1 : 0.71 : 0.21, and for best results a 16-step phase cycle (see ESI,† Section S7) should be used. (b) Experimental and calculated ¹⁹F excitation profiles for CHORUS (red dots) and simple 90° excitation (blue dots) using a sample of heavily doped C₆F₆ at 470 MHz with a 90° pulse width of 12.4 μs, corresponding to an RF amplitude of 20.2 kHz. The slight asymmetry (red dots) is caused by the very rapid relaxation (T₂ = 0.05 s). For CHORUS the unit pulse duration τ was 1 ms, chirp frequency range 300 kHz, and RF amplitude 15 kHz; a 64 step phase cycle was used. The frequency of excitation was varied in 6 kHz steps over 300 kHz; the receiver was kept on resonance to eliminate bias caused by the receiver filters. Simulations for CHORUS (purple line) and 90° pulse (green line) were carried out in Mathematica v.9 using compiled analytical solutions of the Bloch equations. For 90° excitation, both experiment and simulation used linearly frequency-dependent phase correction; no correction was needed for CHORUS. Full raw experimental data, pulse sequence code, pulse shape files and analysis software can be downloaded from DOI: http://10.15127/1.276417 and DOI: http://10.15127/1.276419.

This problem of phase variation with frequency can be dealt with by exploiting the one-to-one correspondence between time and frequency in a chirp pulse, which means that a small change in the phase of the pulse at a given time translates to an equal change in phase at the corresponding frequency. Thus calculating the residual phase error as a function of excitation frequency, fitting to a polynomial, and applying the equivalent time-dependent phase correction to the first and second pulses of Fig. 1a (see ESI,† Section S3), leads to a final sequence that achieves constant-phase excitation over a very wide bandwidth, as shown in Fig. 1b. For this CHORUS (CHirped, ORdered pulses for Ultra-broadband Spectroscopy; Fig. 1b) variant on the ABSTRUSE sequence, the experimental data (red dots) shows a very small but discernible asymmetry. This is due to T₂ relaxation, since a heavily doped sample of C₆F₆ of a short T₂ of 0.05 s was used. The size of this error is an artefact of the measurement method; for practical analytes (Fig. 2), the effect is much smaller, and can be reduced further by alternating the sweep direction of the chirp pulses during time averaging.¹⁹

Fig. 2 470 MHz ¹⁹F NMR spectra of a sample containing bicalutamide, SF₆ and C₆F₆ acquired using (a) simple 90° excitation and (b) CHORUS, with simulated excitation profiles in green and purple respectively. For simple 90° excitation, simulation and experiment used a linearly frequency-dependent phase correction. The difference in frequency between the most and least shielded resonances is 104 kHz.

The triple chirp pulse sequence, CHORUS, achieves constant amplitude excitation with constant phase over a 250 kHz bandwidth using a maximum RF amplitude of only 15 kHz, less than that of a typical hard 90° pulse, and shows no undue B₁ sensitivity. For a given RF amplitude, the frequency range over which CHORUS achieves 98% excitation is 5.8 times greater than that for a hard 90° pulse of the same peak RF amplitude, and 4.2 times greater than that for ABSTRUSE (see ESI,† Fig. S4c and d), in both cases after applying the necessary phase correction.

To assess the utility of CHORUS for quantification, tests of repeatability over time and robustness with respect to offset from resonance were made using a sample containing bicalutamide, which has two signals with very different chemical shifts, and the reference material 4-fluoroaniline in DMSO-d₆. ¹⁹F{¹H} data were acquired with 16 scans over a spectral width of 234 ppm (see ESI,† Fig. S5). To test repeatability, two series of thirty spectra of the same sample were acquired consecutively with the spectrometer operating frequency fixed at −100 ppm (see ESI,† Tables S1, S2 and Fig. S6a, b). To test robustness, the spectrometer operating frequency was varied from −20 ppm to −165 ppm, in steps of 5 ppm, to give thirty experiments, with three repetitions (see ESI,† Table S3a–c, and Fig. S7a–c). The percentage relative standard deviations (% RSDs) of the ratios of the integrals of the three peaks in the two tests are shown in Table 1. The repeatability test was carried out on resonance, so is unaffected by any systematic bias introduced by analogue and digital filtration of the signal received, but the robustness test varied the frequencies of the signals measured and hence is affected by the receiver characteristic. Correcting this small fixed error, which shows a quadratic dependence on offset (see ESI,† Fig. S9a and b) leads to a small improvement in the robustness RSD.

Table 1 Percentage relative standard deviations (% RSDs) for the ratios of the integrals of peaks (1 : 2), (1 : 3) and (2 : 3), for a sample of bicalutamide (peaks 1 and 2, at −61.0 ppm and −105.4 ppm, respectively) and reference material 4-fluoroaniline (peak 3 at −129.8 ppm) in DMSO-d₆ (see ESI, Fig. S5). The results for repeatability shown here are for the spectrometer operating frequency set at −100 ppm, and for robustness, the first of the three repetitions. For robustness, the data are shown with and without correction for the effects of the analogue and digital receiver filters on signal amplitude

	Peaks (1 : 2) (%)	Peaks (1 : 3) (%)	Peaks (2 : 3) (%)
Repeatability	0.076	0.028	0.078
Robustness	0.14	0.22	0.12
Robustness (receiver-corrected)	0.070	0.024	0.065

---

A common criterion for the acceptability of an analytical method in the pharmaceutical industry is an RSD ≤ 1%. The % RSDs for both measures of performance obtained with CHORUS are more than an order of magnitude better than this; the very small variations in signal integral that are seen include contributions from noise (lower in the case of the ratio of the two strongest signals, 1 and 3) and from systematic errors caused by environmental factors such as air conditioning. The results show that any contribution from resonance offset effects over the range tested is below the detection limit for these experiments: in other words, well over 99.8% excitation was achieved over the 145 ppm range of offsets used. The linearity of the method was not tested, but the performance of CHORUS should be no different in this respect from that of other NMR excitation methods, since the effect of sample concentration on RF amplitude and phase should be negligible over the concentration range of interest. The influence of such factors such as signal digitisation and signal-to-noise ratio is already well characterised and again their effect on CHORUS spectra should be identical to that on other NMR quantitation methods.

Fig. 2 compares hard pulse and CHORUS ¹⁹F spectra of a sample of bicalutamide (15 mM) in DMSO-d₆, with two reference materials, SF₆ and C₆F₆, giving a wide chemical shift range of 221 ppm (104 kHz). Simulated excitation profiles are superimposed, to show the signal attenuation off resonance that results when a 90° hard pulse is used. The narrow quantitative range for simple 90° excitation is evident, with large losses in signal amplitude seen towards the edges of the frequency range. CHORUS, however, has a much wider usable range, of more than 500 ppm, which extends well beyond the spectral width shown here.

One important limitation of CHORUS (and of its parent ABSTRUSE) is that its relatively long duration leaves it vulnerable to J-modulation if large homonuclear couplings are present. This can be seen in the case of a sample of sodium perfluorooctanoate (NaPFO) in DMSO-d₆, where the 6 ms duration of the CHORUS sequence used is long enough for significant evolution under the ¹⁹F–¹⁹F couplings in the PFO anion, leading to distorted multiplets and reduced integrals (see ESI,† Fig. S8a and b). Analytes of this nature, therefore, are less easy to quantify using CHORUS. A further limitation is that the relatively long duration leads to small losses due to spin–spin relaxation. In both cases it should be possible to improve performance by optimising the sequence, for example using overlapping chirp pulses and/or optimal control theory^8,9 to reduce its duration.

The ABSTRUSE sequence is highly effective at providing pure phase band-selective excitation, and in this role requires no phase correction. In its original form it is however not ideally suited to quantitative excitation of the sorts of spectra described here, first because the hyperbolic secant waveform does not make optimum use of the RF power available, and second because the residual phase errors as a function of frequency reduce excitation slightly towards the edges of the band when opposed sweep acquisitions are combined. Changing from hyperbolic secant to simple chirp pulses sacrifices the appealing simplicity of ABSTRUSE, requiring that time-dependent phase correction be applied to one or more of the component pulses, but allows very accurate constant-amplitude and constant-phase excitation to be achieved over much wider bandwidths.

This CHORUS variant of ABSTRUSE offers a new approach to accurate NMR quantification that for many samples offers a great improvement over the conventional use of a simple 90° pulse. CHORUS uses standard instrumentation and shows excellent reproducibility and robustness in the measurement of signal integrals over very wide frequency ranges (>500 ppm for ¹⁹F at 470 MHz). The radiofrequency energy deposited per transient is still relatively low, so sample heating is not a problem and CHORUS can allow wider bandwidths for excitation than are generally practical for heteronuclear decoupling. All broadband sequences have to address the limitations imposed by resonance offset effects and, to a greater or lesser extent, B₁ inhomogeneity; with the sequence structure introduced with ABSTRUSE and the phase correction added in CHORUS, these limitations are overcome for quantitative excitation. Even greater proportional improvements in bandwidth can result when the same principles are applied to multiple pulse sequences.

This work was funded by the Engineering and Physical Sciences Research Council (grant numbers EP/L018500 and EP/M013820) and by an Industrial CASE award from AstraZeneca and the EPSRC.

Notes and references

1. U. Holzgrabe, eMagRes, 2015, 4, 45–56.
2. R. Tycko, H. M. Cho, E. Schneider and A. Pines, J. Magn. Reson., 1985, 61, 90–101.
3. R. Freeman, S. P. Kempsell and M. H. Levitt, J. Magn. Reson., 1980, 38, 453–479.
4. T. L. Hwang, P. C. M. van Zijl and M. Garwood, J. Magn. Reson., 1997, 124, 250–254.
5. A. Tannús and M. Garwood, NMR Biomed., 1997, 10, 423–434.
6. S. Odedra and S. Wimperis, J. Magn. Reson., 2012, 214, 68–75.
7. S. Odedra, M. J. Thrippleton and S. Wimperis, J. Magn. Reson., 2012, 225, 81–92.
8. K. Kobzar, S. Ehni, T. E. Skinner, S. J. Glaser and B. Luy, J. Magn. Reson., 2012, 225, 142–160.
9. T. E. Skinner, T. O. Reiss, B. Luy, N. Khaneja and S. J. Glaser, J. Magn. Reson., 2004, 167, 68–74.
10. T. E. Skinner, K. Kobzar, B. Luy, M. R. Bendall, W. Bermel, N. Khaneja and S. J. Glaser, J. Magn. Reson., 2006, 179, 241–249.
11. E. Kupče and R. Freeman, J. Magn. Reson., 1994, 108, 268–273.
12. E. Kupče and R. Freeman, J. Magn. Reson., 1995, 117, 246–256.
13. G. Garwood and L. DelaBarre, J. Magn. Reson., 2001, 153, 155–177.
14. J. M. Bohlen, M. Rey and G. Bodenhausen, J. Magn. Reson., 1989, 84, 191–197.
15. J. M. Bohlen, I. Burghardt, M. Rey and G. Bodenhausen, J. Magn. Reson., 1990, 90, 183–191.
16. J. M. Bohlen and G. Bodenhausen, J. Magn. Reson., Ser. A, 1993, 102, 293–301.
17. V. L. Ermakov, J. M. Bohlen and G. Bodenhausen, J. Magn. Reson., Ser. A, 1993, 103, 226–229.
18. V. L. Ermakov and G. Bodenhausen, Chem. Phys. Lett., 1993, 204, 375–380.
19. K. E. Cano, M. A. Smith and A. J. Shaka, J. Magn. Reson., 2002, 155, 131–139.
20. D. G. Norris, Concepts Magn. Reson., 2002, 142, 89–101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cc10206e

---