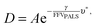Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Porosity in metal–organic framework glasses†
A. W.
Thornton
a,
K. E.
Jelfs
b,
K.
Konstas
a,
C. M.
Doherty
a,
A. J.
Hill
a,
A. K.
Cheetham
c and
T. D.
Bennett
*c
aFuture Industries, Commonwealth Scientific and Industrial Research Organisation, Private Bag 10, Clayton Sth, VIC 3169, Australia
bDepartment of Chemistry, Imperial College London, South Kensington, London SW7 2AZ, UK
cDepartment of Materials Science and Metallurgy, University of Cambridge, CB3 0FS, UK. E-mail: tdb35@cam.ac.uk
First published on 18th January 2016
Abstract
The porosity of a glass formed by melt-quenching a metal–organic framework, has been characterized by positron annihilation lifetime spectroscopy. The results reveal porosity intermediate between the related open and dense crystalline frameworks ZIF-4 and ZIF-zni. A structural model for the glass was constructed using an amorphous polymerization algorithm, providing additional insight into the gas-inaccessible nature of porosity and the possible applications of hybrid glasses.
Metal–organic frameworks (MOFs) remain the subject of intense research across chemistry, engineering, materials and biological domains. Their chemically tunable porosities are intrinsic to the potential for application in, for example, gas storage and separation, drug delivery and catalysis.1,2 The maturing field has seen notable advances in changing the porosity-linked properties of MOFs through utilization of defects,3 and also their physical state of matter. This latter category of non-crystalline or amorphous MOFs4 includes glasses, obtained by melt-quenching of the liquids formed upon melting these hybrid structures.5 The porosity, or ‘free-volume’ within these MOF glasses has not yet been quantified, and is extremely important given the possible application of hybrid glasses in ionic, electronic or thermal conduction,6–8 alongside the more familiar membrane and sieving applications.
Positron Annihilation Lifetime Spectroscopy (PALS) has been used to identify internal porosity in dense polymers,9,10 Nafion,11 microporous polymers,12 porous aromatic frameworks,13 zeolites14 and activated carbons, with good agreement with the cavity sizes measured by small-angle neutron scattering (SANS), ellipso-metric porosimetry (EP) and gas sorption (e.g. BET).15
The technique involves the generation of positrons (the anti-matter counterpart of an electron, with identical mass, spin = 1/2 and charge = +1), with a range of energies able to penetrate dense matter that otherwise would be inaccessible to gas. Positrons slow to thermal energies through inelastic collisions and positron–phonon interactions, and once thermalized, the positron will either annihilate as a free particle, a trapped particle or in a bound state with an electron called positronium. The triplet ground state of positronium, ortho-positronium (o-Ps), annihilates by a mechanism known as pick-off whereby the o-Ps localizes in pockets of free volume and eventually annihilates with an electron from the surrounding matter. The time to annihilation, or o-Ps lifetime, is measured by birth and death gamma rays.9 The lifetime of o-Ps has been directly correlated with the pore size (the lifetime being shortened if the pick-off electron is nearby) while the number of annihilations has been directly correlated with the relative number of pores.16
The application of PALS to crystalline MOF-5 provided both information complimentary to standard gas sorption analysis, but moreover offers unique insights into internal pore structure, including defects.17 PALS has also been used to rationalise the absence of porosity in the theoretically porous Zn-HKUST-1 MOF. In this case, the surface of the activated material was found to be unstable; this collapsed crystal surface formed a barrier which prevented gas molecules from accessing the interior.18 Correlations between gas permeability and the free volume, measured by PALS, in mixed matrix membranes have also been reported.12,19
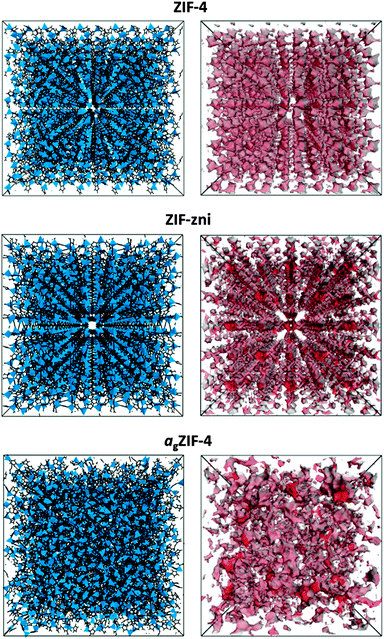
Motivated by the ability to probe the internal structures of the newly reported melt-quenched MOF-glasses,5 here we report the application of PALS to a glass formed by melt-quenching of ZIF-4, a three-dimensional metal–organic framework of composition Zn(C3H3N2)2.20 Prior to melting at 573 °C, recrystallization to a known dense framework of identical chemical composition, ZIF-zni, is observed.5 The porosities of ZIF-4, ZIF-zni and the resultant melt quenched glass (agZIF-4), shown in Fig. 1, were all probed by PALS in this work.
To provide comparison with the experimental data, the Polymatic code21 was used to simulate the atomic structure of agZIF-4, using force fields developed by Hu et al.22 Polymatic is a generalised polymerisation algorithm for amorphous polymers that incorporates automated bond-formation and annealing schemes. Five models were obtained in order to sample different regions of configuration space, and were formed by building an array of Zn(C3H3N2)2 repeat-units and allowing the closest ‘reactive pairs’ to form a bond. An average of 98% of reactions were completed, yielding computationally derived models with an average density of 1.417 g cm−3 (or, in terms of tetrahedral atoms per unit volume, 4.277 Zn nm−3), which is in good agreement with the experimentally determined density of 1.625 g cm−3 (or 4.905 Zn nm−3). The algorithm does not require density as an input and therefore the predicted density is purely an outcome of the dynamics, reactions and equilibration cycles. A representative configuration for agZIF-4, together with the crystallographic unit cells of ZIF-4 and ZIF-zni, is displayed in Fig. 1. The porosity of each structure was generated using BIOVIA based on ‘hard-sphere’ surface mapping across the internal surface.23
Samples of ZIF-4, ZIF-zni and agZIF-4 were synthesized using previously established procedures.522NaCl, which was sealed in a thin mylar envelope, was used as the source of positrons. The samples were packed into a 2 mm thick cell surrounding the positron source. The o-Ps lifetime measurements were taken under vacuum (1 × 10−5 Torr) at 298 K using an EG&G Ortec spectrometer at a rate of 4.5 × 106 counts per sample. The lifetimes are converted to pore sizes by using the quantum-based formulation16 with a spherical pore geometry for ZIF-4 and agZIF4, and a square channel geometry for ZIF-zni based on visual inspection of the structures.
For ZIF-4, two distinct cavity sizes were detected by PALS (Fig. 2). The experimentally determined smaller cavity size of ca. 3.3 Å is in excellent agreement with the value of 3.3 Å calculated from the solved crystal structure, whilst the size of the larger cavity appears slightly overestimated by PALS, at 6.2 Å compared to 5.1 Å. For ZIF-zni, PALS yields pores of 6.6 and 3.8 Å, compared to the crystal structure with pores of 5.5 and 3.0 Å, the latter of which exists in very small quantities.
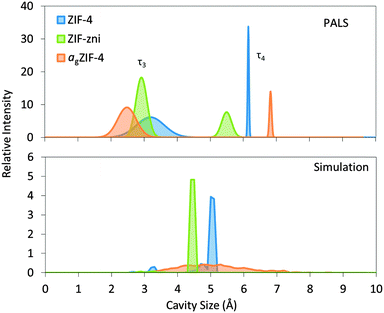 | ||
| Fig. 2 Pore size distributions measured with PALS and simulated with Zeo++24,25 for ZIF-4, ZIF-zni and agZIF-4. PALS results for the third and fourth components (τ3 and τ4) are represented as Gaussian distributions which correspond to the small and large cavities, respectively. | ||
The results from PALS appear to overestimate the pore sizes of the crystalline phases, which perhaps suggests imperfections in the models used for channel geometries.
Such overestimations are however less with agZIF-4, where the distribution of pore sizes is larger than for crystalline ZIF-4 and ZIF-zni. agZIF-4 contains the smallest and the largest pore sizes according to both PALS and simulation. The large and small cavity sizes were detected at 6.9 and 2.6 Å respectively which compare well with the largest and smallest cavities of 6.4 and 2.6 Å from simulation.
Experimental N2 sorption isotherms have demonstrated that ZIF-zni and agZIF-4 show no significant N2 uptake.5 ZIF-4 however, undergoes a phase transition at ca. 35 kPa. This structural change, involving rotation of the imidazolate linkers, facilitates N2 adsorption and is also referred to as a ‘gate-opening’ mechanism.26 The PALS experimental data provide further rationalization of the dense nature of both ZIF-zni and agZIF-4, indicating that the small cavities could prohibit access into the structure by N2 (3.64 Å diameter).
Pore volume fraction as a function of probe size was calculated for the simulated structures (Fig. 3). For a point-size probe, all cavities are accessible which is represented by a pore volume fraction of unity. As the probe diameter increases, a certain amount of cavities become inaccessible which is shown as a drop in pore volume fraction. There is a sharp drop observed for ZIF-4 and ZIF-zni where a large amount of cavities become inaccessible with a slight increase in probe size, a typical feature for crystalline frameworks. agZIF-4 is markedly different with a gradual decline in pore volume fraction highlighting the amorphous nature of the framework. In addition, a tail at large probe diameter is observed for agZIF-4 where there remains a significant fraction of cavities capable of hosting the larger probes up to 7 Å. Considering this adjustment of porosity, agZIF-4 may be a valuable precursor material for fabricating amorphous carbons with a particular morphology. For example, thermally-rearranged (TR) polymers have proven excellent gas and vapour separation membranes due to their optimal combination of large cavities connected with smaller size-selective windows.27
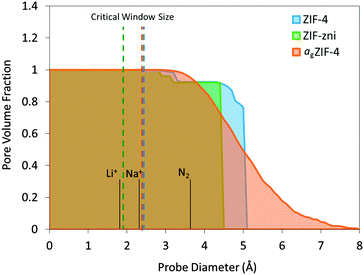 | ||
| Fig. 3 Pore volume fraction calculated for ZIF-4, ZIF-zni and agZIF-4 with a range of probe diameters. Dashed lines represent the critical window size for free transport according to the Voronoi representation using Zeo++.24,25 Note that ZIF-4 undergoes a pressure-induced phase transition, which is not reflected in this scheme. | ||
Critical window size is defined as the maximum probe size that can transport through a unit cell from one side to the other, i.e. the smallest constriction along a connected channel. This is calculated analytically using Zeo++ which can map the pore channels from the nodes of a Voronoi network (a graph representation of the void space for a given arrangement of atoms in a periodic space). This is indicated by dashed lines in Fig. 3. The critical window sizes are smaller than 3 Å, which correspond well with the smallest cavity sizes found by PALS and confirm the expected inaccessibility of N2 (3.64 Å diameter). Given the observed flexibility of the imidazolate linkers in the ZIF family,28 the window sizes may well increase under high pressures but given the restricted degrees of freedom, the expected change is minimal. Even without any flexibility these candidates may be capable of transporting ions such as lithium (1.8 Å diameter) and sodium (2.32 Å diameter), ignoring any electrostatic, physical adsorption and chemical absorption effects.
Whilst the cavity sizes vary slightly upon the sequence of transitions from ZIF-4 to ZIF-zni to agZIF-4, the combination of cavity size and number of cavities can appear significant when compared to the range of materials previously studied by PALS (Fig. 4a). Interestingly, both crystalline materials and agZIF-4 possess cavities of a diameter between those of conventional polymers (e.g. polycarbonate and polysulfone) and classical inorganic zeolites, though lower than open framework MOFs. Such results reflect the hybrid nature of these materials with the possession of both inorganic and organic components.
 | ||
| Fig. 4 (a) Comparison of PALS results for a range of materials including polymers, zeolites, MOFs and the present study of ZIF glasses. Only the cavity diameters for the fourth component (τ4) are displayed where multi-modal distributions exist. (b) Relative diffusivity predicted from Cohen and Turnbull equation with arbitrary penetrant radii of 0.6 and 1.4 Å. Ref. in Table SI-2 (ESI†). | ||
Cohen and Turnbull derived a generalised theory for transport through amorphous materials that was later related to the fractional free volume measured by PALS, here defined as FFVPALS.29–31 Diffusivity (D) can be related to FFVPALS in the following way,
Aside from providing further information on the porosity of MOF glasses, this work has important consequences for the potential applications for glasses made from MOFs, (i.e. in both gas transport and conductive settings). Notably, TR polymers,32 lie close to agZIF-4 in terms of the largest cavity diameter. These TR polymers have been shown to possess free volume structures in the glassy state that enable molecular and ionic transport surpassing that of conventional polymers. Existing literature in the TR domain, which focuses on the effect of chain flexibility on physical and transport properties,33 may provide direction for further research into the potential uses of melt-quenched MOF glasses such as agZIF-4.
AWT and CMD acknowledges the CSIRO Julius Career Award for support. CMD is supported by the Australian Research Council (DE40101359). TDB Acknowledges Trinity Hall (University of Cambridge) for funding.
Notes and references
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 974–986 CrossRef CAS PubMed
.
- J. E. Mondloch, M. J. Katz, W. C. Isley III, P. Ghosh, P. Liao, W. Bury, G. W. Wagner, M. C. Hall, J. B. DeCoste, G. W. Peterson, R. Q. Snurr, C. J. Cramer, J. T. Hupp and O. K. Farha, Nat. Mater., 2015, 14, 512–516 CrossRef CAS PubMed
.
- Z. L. Fang, B. Bueken, D. E. De Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234–7254 CrossRef CAS PubMed
.
- T. D. Bennett and A. K. Cheetham, Acc. Chem. Res., 2014, 47, 1555–1562 CrossRef CAS PubMed
.
- T. D. Bennett, J. C. Tan, Y. Z. Yue, E. Baxter, C. D. Ducati, N. Terril, H. Y. Yeung, Z. Zhou, W. Chen, S. Henke, A. K. Cheetham and G. N. Greaves, Nat. Commun., 2015, 6, 8079 CrossRef CAS PubMed
.
- S. Horike, W. Chen, T. Itakura, M. Inuaki, D. Umeyama, H. Asakura and S. Kitagawa, Chem. Commun., 2014, 50, 10241–10243 RSC
.
- H. Kato and T. Kasuga, Mater. Lett., 2012, 79, 109–111 CrossRef CAS
.
- C. Sanchez, B. Julian, P. Belleville and M. Popall, J. Mater. Chem., 2005, 15, 3559–3592 RSC
.
- M. R. Tant and G. L. Wilkes, Polym. Eng. Sci., 1981, 21, 874–895 CAS
.
- N. Petzetakis, C. M. Doherty, A. W. Thornton, X. C. Chen, P. Cotanda, A. J. Hill and N. P. Balsara, Nat. Commun., 2015, 6, 7529 CrossRef CAS PubMed
.
- Z. Chai, C. Wang, H. Zhang, C. M. Doherty, B. P. Ladewig, A. J. Hill and H. Wang, Adv. Funct. Mater., 2010, 20, 4394–4399 CrossRef CAS
.
- C. H. Lau, P. T. Nguyen, M. R. Hill, A. W. Thornton, K. Konstas, C. M. Doherty, R. J. Mulder, L. Bourgeois, A. C. Y. Liu, D. J. Sprouster, J. P. Sullivan, T. J. Bastow, A. J. Hill, D. L. Gin and R. D. Noble, Angew. Chem., Int. Ed., 2014, 53, 5322–5326 CrossRef CAS PubMed
.
- K. Konstas, K. F. Taupitz, D. R. Turner, D. F. Kennedy and M. R. Hill, CrystEngComm, 2014, 16, 8937–8940 RSC
.
- B. Zhu, C. M. Doherty, X. Hu, A. J. Hill, L. Zou, Y. S. Lin and M. Duke, Microporous Mesoporous Mater., 2013, 173, 78–85 CrossRef CAS
.
- D. W. Gidley, H.-G. Peng and R. S. Vallery, Annu. Rev. Mater. Res., 2006, 36, 49–79 CrossRef CAS
.
- S. J. Tao, J. Chem. Phys., 1972, 56, 5499–5510 CrossRef CAS
.
- M. Liu, A. G. Wong-Foy, R. S. Vallery, W. E. Frieze, J. K. Schnobrich, D. W. Gidley and A. J. Matzger, Adv. Mater., 2010, 22, 1598–1601 CrossRef CAS PubMed
.
- J. I. Feldblyum, M. Liu, D. W. Gidley and A. J. Matzger, J. Am. Chem. Soc., 2011, 133, 18257–18263 CrossRef CAS PubMed
.
- H. Jeazet, T. Koschine, C. Staudt, K. Raetzke and C. Janiak, Membranes, 2013, 3, 331–353 CrossRef CAS PubMed
.
- K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. D. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191 CrossRef CAS PubMed
.
- L. Abbott, K. Hart and C. Colina, Theor. Chem. Acc., 2013, 132, 1–19 CrossRef CAS
.
- Z. Hu, L. Zhang and J. Jiang, J. Chem. Phys., 2012, 136, 244703 CrossRef PubMed
.
- M. L. Greenfield and D. N. Theodorou, Macromolecules, 1993, 26, 5461–5472 CrossRef CAS
.
-
M. Haranczyk, C. H. Rycroft, R. L. Martin and T. F. Willems, Zeo++: High-throughput analysis of crystalline porous materials, v0.2.2, Lawrence Berkeley National Laboratoy, Berkeley, 2012 Search PubMed
.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS
.
- T. D. Bennett, S. Cao, J. C. Tan, D. A. Keen, E. G. Bithell, P. J. Beldon, T. Friscic and A. K. Cheetham, J. Am. Chem. Soc., 2011, 133, 14546–14549 CrossRef CAS PubMed
.
- H. B. Park, C. H. Jung, Y. M. Lee, A. J. Hill, S. J. Pas, S. T. Mudie, E. van Wagner, B. D. Freeman and D. J. Cookson, Science, 2007, 318, 254–258 CrossRef CAS PubMed
.
- E. O. Beake, M. T. Dove, A. E. Phillips, D. A. Keen, M. G. Tucker, A. L. Goodwin, T. D. Bennett and A. K. Cheetham, J. Phys.: Condens. Matter, 2013, 25, 395403 CrossRef CAS PubMed
.
- M. H. Cohen and D. Turnbull, J. Chem. Phys., 1959, 31, 1164–1169 CrossRef CAS
.
- D. Turnbull and M. H. Cohen, J. Chem. Phys., 1961, 34, 120–125 CrossRef CAS
.
-
B. D. Freeman and A. J. Hill, Structure and Properties of Glassy Polymers, American Chemical Society, Washington, DC, 1998 Search PubMed
.
- S. Kim and Y. M. Lee, J. Nanopart. Res., 2012, 14, 949 CrossRef
.
- M. Calle and Y. M. Lee, Macromolecules, 2011, 44, 1156–1165 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: PALS and simulation details. See DOI: 10.1039/c5cc10072k |
| This journal is © The Royal Society of Chemistry 2016 |