Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comparison of techniques for size measurement of nanoparticles in cell culture medium†
Christian
Gollwitzer
*a,
Dorota
Bartczak
b,
Heidi
Goenaga-Infante
b,
Vikram
Kestens
c,
Michael
Krumrey
a,
Caterina
Minelli
d,
Marcell
Pálmai
e,
Yannic
Ramaye
c,
Gert
Roebben
c,
Aneta
Sikora
d and
Zoltán
Varga‡
e
aPhysikalisch-Technische Bundesanstalt (PTB), Abbestr. 2-12, D-10587 Berlin, Germany. E-mail: christian.gollwitzer@ptb.de
bLGC Ltd., Queens Road, Teddington, TW11 0LY, UK
cInstitute for Reference Materials and Measurements (IRMM), Joint Research Centre (JRC), European Commission, Retieseweg 111, 2440 Geel, Belgium
dAnalytical Sciences, National Physical Laboratory, Teddington, TW11 0LW, UK
eBiological Nanochemistry Research Group, Institute of Materials and Environmental Chemistry, Research Centre for Natural Sciences, Hungarian Academy of Sciences, Magyar tudósok körútja 2, 1117 Budapest, Hungary
First published on 8th June 2016
Abstract
Plain and aminated silica nanoparticles dispersed in purified water, in 50 mM Tris–HCl buffer and in cell culture medium were measured using dynamic light scattering (DLS), centrifugal liquid sedimentation (CLS), small-angle X-ray scattering (SAXS), and particle tracking analysis (PTA). The test samples were measured by all methods immediately after dispersion and after incubation at room temperature for 24 h. The effect of the biological dispersion medium on the modal value of the particle size distribution was compared for each method taking into account the estimated uncertainty. For the methods based on light scattering, DLS and PTA, the size distributions obtained were significantly altered due to the formation of a protein corona and induced agglomeration effects. With SAXS and CLS, the measured size of the primary particles was mostly unchanged. While SAXS offers excellent precision and traceability to the SI unit system if the model fitting approach is used for data analysis, CLS provides detailed size distributions from which additional information on the agglomeration state can be deduced.
1 Introduction
Due to the ubiquitous use of nanoparticles in food and consumer products,1,2 human exposure to engineered nanoparticles (ENPs) has recently become an important issue in the field of health and environmental science.3 The potential risks associated with this exposure4 are driving research into the basic physical chemistry of ENPs as well as their interaction with biological materials.5 The effect of ENPs on biological cells, the environment and human health, are under active research and not yet fully understood,6 which also implies regulatory problems.7 Some of these difficulties are related to the limitations of the current size determination techniques used in the field.One of the defining properties of nanomaterials is the mean nanoparticle size, which can be determined with high accuracy by selected techniques for suitable materials.8 For nanoparticles dispersed in plain aqueous media, these techniques can produce results where the reported size is related to the definition of the unit metre in the International System of Units (SI) via an unbroken chain of comparisons, each having a stated uncertainty (SI-traceable results). In complex biological media, however, the determination of the size is challenging not only because the commonly used sizing techniques are less suitable for testing multi-component systems, but also because of the possible interactions between ENPs and the constituents of the biological matrix.9
If ENPs are in contact with biological material, different proteins and other organic molecules can adhere to their surfaces, forming a so-called protein corona. The properties of the corona highly depend on the surface characteristics of the ENPs as well as on the type of the biological matrix.10 The formation of the protein corona determines the biological fate of the ENPs11 and increases the overall size, but usually leaves the size of the solid, dense core intact.12 Measuring the size in a biological medium is therefore more difficult and less well-defined than in plain aqueous media.13 The size determination of ENPs in a biological medium is not only important for human and environmental risk assessment and regulation, but also for the fields of drug delivery, biomedical imaging and toxicology.14
Silica nanoparticles are one of the most frequently used ENPs in consumer products.15 In this study, two well-characterized representative test materials16 (RTMs) based on SiO2 nanoparticles with different surface functionalization, but otherwise very similar properties, were analysed using four common particle size analysis techniques after dispersion in purified water, in a Tris–HCl buffer at a physiological pH, and in a cell culture medium containing 10% fetal bovine serum (FBS). The applied techniques include dynamic light scattering (DLS), centrifugal liquid sedimentation (CLS), small-angle X-ray scattering (SAXS), and particle tracking analysis (PTA). The measurements were complemented by uncertainty analyses, in order to evaluate the significance of the resulting changes in size.
In the next section, a brief description of the preparation of the test materials is followed by the experimental details and the presentation of the results obtained. Different methods are then compared regarding their ability to characterize the particle size distribution (PSD) of the studied ENPs in different media, and finally the advantages and drawbacks of each method are discussed.
2 Materials
The nanomaterials used in this comparison are derived from a commercially available aqueous suspension of plain silica nanoparticles (Klebosol 30R50, 300 g kg−1), supplied by AZ Electronic Materials France SAS (Trosly Breuil, FR).17 One batch was functionalized with amino groups and diluted in purified water (resistivity 18.2 MΩ cm at 25 °C) to a target concentration of 2.5 g kg−1, the other batch was diluted to the same concentration without amination.Throughout the whole processing, the suspensions were kept sterile. This was a precautionary measure, in order to suppress unwanted growth of bacterial contamination, when the nanomaterials come into contact with the cell culture medium.18 An overview of the preparation of NP–NH2 and NP-plain is given in the next paragraph; an in-depth description of the preparation and characterization of these materials (denoted as NanoChOp-06 and NanoChOp-05, respectively) can be found in a separate article.19
For the preparation of the first material (NP–NH2), the base suspension was initially filtered through a Whatman cellulose filter. The amination was carried out using aminopropyl-diethoxy-methylsilane (APDEMS) in an excess amount after changing the solvent to ethanol using dialysis. Finally, the sol was dialysed with a cellulose membrane tubing (D9402 Sigma-Aldrich, Ø 76 mm, nominal molecular weight cut-off 12 kDa) under sterile conditions against autoclaved purified water containing 30 mmol L−1 acetic acid at a pH value of 3 to stop the reaction.
The amination was performed in four batches, which were subsequently mixed and diluted to a final concentration of 2.5 g kg−1. The resulting 1.25 L of NP–NH2 were finally filled into flame-sealed amber glass ampoules with a volume of 2 mL and stored at 4 °C. The second material (NP-plain) was prepared in a similar way, by diluting the initial suspension to the target concentration, but skipping the amination step, and then filled into 9 mL ampoules. These ampoules were stored at 18 °C.
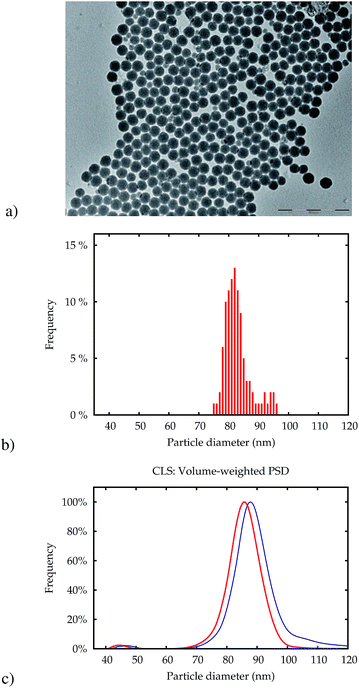
Fig. 1 displays a transmission electron microscopy (TEM) micrograph of NP-plain. The main population of particles has a very low polydispersity with a mean size (area equivalent circle diameter) of around 80 nm (Fig. 1b). A very small number of particles with a mean size of around 40 nm could also be found in the TEM image and in the volume-weighted PSD obtained by CLS (c), which indicates that the particles in this fraction make up about 3% of the total volume of particles. Other basic properties are detailed in Table 1.
| Property | NP–NH2 | NP-plain | Unit |
|---|---|---|---|
| a Obtained with isopycnic sedimentation on the same base colloidal silica. b Tabulated value for SiO2. c Determined by isotope dilution mass spectroscopy. d Obtained with electrophoretic light scattering.19 e Estimated from density, Si mass fraction and mean particle size. | |||
| Surface chemistry | –NH2 | –OH | — |
| Effective particle densitya | 2.0 ± 0.1 | 2.0 ± 0.1 | g cm−3 |
| Particle refractive indexb | 1.46 + 0i | 1.46 + 0i | l |
| Si mass fractionc | 1121 ± 6 | 1108 ± 7 | mg kg−1 |
| ζ-Potentiald | +9 | −48 | mV |
| pH | 3.2 ± 0.5 | 8.4 ± 0.5 | 1 |
| NP concentratione | 5 × 1012 | 5 × 1012 | mL−1 |
Both RTMs were checked for homogeneity (variation between different ampoules) and stability (changes over time). For NP-plain, the standard deviation of the modal size measured with DLS and CLS was less than 1% between samples and with time, when stored at 18 °C. Thus, NP-plain is suitable as a reference material for particle size. For NP–NH2, the modal size measured with SAXS, CLS and DLS varied less than 0.3%. However, whereas the equivalent diameter measured with SAXS was stable within 0.1% over 36 months, the intensity weighted mean diameter obtained by DLS increased slowly with time. To minimize these changes, the NP–NH2 samples were stored at 4 °C.19 These results give the NP–NH2 material the status of a reference material for the equivalent diameters measured with CLS and SAXS, but not for DLS, because of the significant change over time. The measurements reported in this article were performed 4 years after the ampouling of NP-plain and between 6 and 9 months after preparation of NP–NH2.
For the measurements, these two materials were further diluted to a concentration of 1 g kg−1 in purified water, in 50 mM Tris–HCl buffer at a physiological pH, and in a cell culture medium composed of Eagle's Minimum Essential Medium (EMEM, ATCC, Teddington, UK) supplemented with 10% FBS (PAA Laboratories, Dartmouth, USA). Since the measurements were carried out at physically different locations, the FBS was aliquotted from a single batch and distributed to different institutes in frozen form. The dilution of the two materials was performed at each institute following a fixed, written protocol. All measurements were performed immediately after dispersion and after 24 h incubation at room temperature. Thus, in total six different samples were analysed at two points in time, by each method.
3 Measurements
3.1 Dynamic light scattering
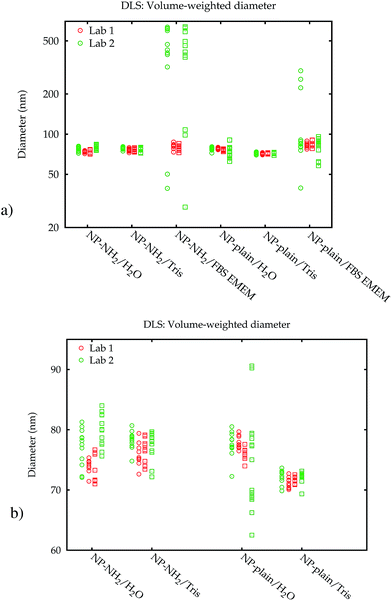
The principle of size measurements by DLS is based on measuring light scattering intensity fluctuations.20 These fluctuations, which are time-related and which occur around a mean intensity value, are caused by the particles that are moving in the suspension under the influence of Brownian motion. The intensity fluctuation recorded is temporally correlated with a delayed value of itself. The result is a decaying intensity autocorrelation function from which the translational diffusion coefficient can be determined. For the computation of a PSD, a non-negative least-squares (NNLS) algorithm21 can be used, which is typically implemented in the vendor's software of the DLS instrument and widely applied for the purpose of analysing DLS data. This algorithm attempts to deduce an intensity-weighted PSD from the raw intensity autocorrelation function by means of an inverse Laplace transform. With the optical properties of the particles, equivalent volume- and number-weighted distributions of a hydrodynamic equivalent spherical diameter are obtained via Mie theory light scattering calculations.As DLS is a widely applied method, two identical instruments (Malvern Zetasizer Nano ZS, Malvern Instruments Ltd., Worcestershire, UK) available at two different laboratories of the authors have been included in this study. This apparatus is equipped with a red light-emitting He–Ne laser (max. 4 mW power and 632.8 nm wavelength) and the scattered light is collected by an avalanche photodiode detector which is located at a backward scattering angle of 173°. To ensure laser stability, the instruments were turned on at least 30 min before each series of measurements.
The measurements were performed in disposable polycarbonate folded capillary cells with gold-plated beryllium-copper electrodes (Malvern DTS1070) in the first laboratory (Lab 1), while the second laboratory (Lab 2) used high-quality glass cells.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nm was used. Because the main fraction of particles of the used materials has a very narrow size distribution (see Fig. 1), the peak of the PSDs is composed of only a very limited number of size classes. In order to determine the mode value with a better resolution than the spacing of the bins, which is around 13 nm near the peak, a parabola was fitted through three datapoints closest to the peak.
000 nm was used. Because the main fraction of particles of the used materials has a very narrow size distribution (see Fig. 1), the peak of the PSDs is composed of only a very limited number of size classes. In order to determine the mode value with a better resolution than the spacing of the bins, which is around 13 nm near the peak, a parabola was fitted through three datapoints closest to the peak.
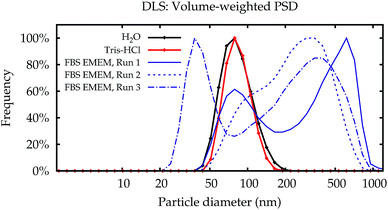
In contrast to the simpler dispersion media, the results in cell culture medium were not reproducible. While some of the PSDs are similar to the dispersions in water and the Tris–HCl buffer, others show multiple modes. Even for repeated measurements performed on a single aliquot in sequence, the results can be completely different (broken lines in Fig. 2).
Fig. 3a shows the modal values of the volume-weighted PSDs for all measurements. Differences between dispersions in purified water and the Tris–HCl buffer are not significant (Fig. 3b). In line with the PSDs in Fig. 2, the modal diameters for the measurements in cell culture medium scatter over a wide range and yield no conclusive or usable result, especially for NP–NH2.
Additionally, the results obtained by Lab 2 seem to be more noisy than those of Lab 1, although all settings of the two identical instruments were exactly the same, the material was split up into aliquots from a single batch and distributed, and the dispersion was carried out according to a written protocol. A blank FBS/EMEM sample, which has been run in one laboratory only, showed that the intensity of the scattered light from the particles is ten times stronger than from the serum proteins. Therefore it is unlikely that the scattering from the medium causes significant shifts of the size distribution. Also, in both labs the instruments are regularly checked using a wide range of reference materials. In order to eliminate the influence of the container material as a possible cause, the measurements for the cell culture medium were repeated in the second laboratory in polycarbonate cells, which had no influence on the results (data shown in the ESI†).
The most likely reason for the strong influence of the cell culture medium on the measurement results is agglomeration.22 The light scattering intensity is much stronger from agglomerates than from the primary particles. The scattered light from all particles in the illuminated sample volume is simultaneously detected with a single detector, therefore even a small number of agglomerates overshadows the scattering of the primary particles. This makes it very difficult to obtain useful results from DLS in complex media.23 This hypothesis is also supported by the fact that the results only tend to larger values in the intensity-weighted data (shown in the ESI†). The smaller modes obtained in the transformed volume-weighted PSD can be explained as artefacts from the transformation of very broad peaks. A sound uncertainty analysis for DLS in the cell culture medium can therefore not be given.
3.2 Centrifugal liquid sedimentation
The line-start incremental CLS method measures the sedimentation time of nanoparticles under increased gravity, and uses the sedimentation time to calculate the so-called Stokes particle diameter.24 Prior to the measurements, a transparent rotating disc is partly filled with a series of liquids of decreasing density, establishing a density gradient. Then few hundred microlitres of nanoparticle suspension are injected into the centre of the rotating disc. If the nanoparticles have a higher density than the density gradient, they will sediment moving radially to the outer edge of the disc. The sedimentation time is monitored by a detector near the outer edge of the disc, which records the loss of light intensity of a laser beam passing through the disc.CLS measurements were performed in two laboratories both using a similar CPS Disc Centrifuge DC 20000 instrument operating at a laser wavelength of 405 nm and a rotational disc speed of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. For both instruments, the disc geometry was measured in order to provide an accurate estimate of the mean density of the gradient crossed by the NPs during sedimentation. Because these instruments cannot control the temperature inside the disc, the temperature of the density gradient after the measurements was measured and shown to have increased by about 7 °C above the ambient temperature of the laboratory (22.5 °C). In Lab 1, the disc was filled with an aqueous sucrose (Amresco LLC, US) solution producing a concentration gradient varying between 40 g kg−1 and 120 g kg−1. In Lab 2, a similar sucrose (Merck KGaA, Darmstadt, DE) gradient was chosen, but with a density varying between 20 g kg−1 and 80 g kg−1.
000 rpm. For both instruments, the disc geometry was measured in order to provide an accurate estimate of the mean density of the gradient crossed by the NPs during sedimentation. Because these instruments cannot control the temperature inside the disc, the temperature of the density gradient after the measurements was measured and shown to have increased by about 7 °C above the ambient temperature of the laboratory (22.5 °C). In Lab 1, the disc was filled with an aqueous sucrose (Amresco LLC, US) solution producing a concentration gradient varying between 40 g kg−1 and 120 g kg−1. In Lab 2, a similar sucrose (Merck KGaA, Darmstadt, DE) gradient was chosen, but with a density varying between 20 g kg−1 and 80 g kg−1.
The instruments were calibrated before each measurement using PVC particles (CPS Instruments, Inc., Prairieville, US) with an assigned modal diameter of 239 nm, and a particle density of 1.385 g cm−3. We note that while the use of these calibrants results in highly consistent Stokes diameter measurements, the SI traceability of the size and particle density values assigned to these calibrants is questioned.25
Different vials of both NanoChop test materials have been measured under repeatability conditions for the three different media. For each measurement, 0.1 mL (Lab 1) or 0.25 mL (Lab 2) of a sample was injected manually. Independent aliquots were prepared from each test sample in 5 mL pyrogenic-free and sterile polypropylene vials. Some of these aliquots were measured immediately after diluting in the dispersing media, the others were measured 24 hours later. Each aliquot was measured in duplicate.
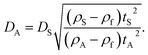 | (1) |
The raw light extinction intensity-weighted PSDs were converted to volume-based PSDs by the manufacturer's instrument software using Mie theory. This requires the complex refractive index values of both the particles and the liquid. The same value for the effective silica particle density was used for both NP-plain and NP–NH2. This density value was measured for the NP-plain base material by isopycnic sedimentation.
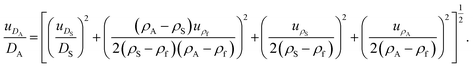 | (2) |
Major contributions to the overall measurement uncertainty of the NP diameters arise from the uncertainties in the density values of the samples and the calibrant, as well as in the size of the calibrant (see Table S1 in the ESI†). This highlights the urgency of well characterised reference materials to be used as calibrant, whose properties are measured with accurate methods and reported with a clear metrological traceability statement. An alternative, top-down approach for the estimation of the uncertainty of the measured Stokes diameters26 is described in the ESI.† Both uncertainty estimation approaches result in similar uncertainty values, thereby mutually increasing their reliability.
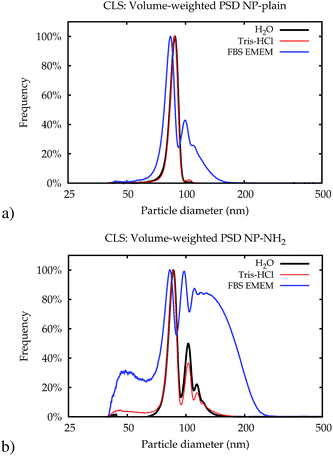 | ||
| Fig. 4 Typical volume-weighted PSDs for NP-plain (a) and NP–NH2 (b) obtained in Lab 1 by CLS immediately after dispersion. | ||
The higher level of agglomeration of the NP–NH2 with respect to NP-plain is most likely driven by the low zeta-potential of the former.27 In addition, in cell culture medium there may be an active bonding of the amine surface groups in NP–NH2 with the serum proteins leading to the significant level of aggregation observed compared to NP-plain in the same medium. Owing to the high resolution of its measured size distribution, CLS also allowed to observe a population of NPs of about 40 nm in diameter in both samples (see ESI†).
The modal values for the peak corresponding to the primary particles are displayed in Fig. 5. Within 24 h, no significant change of the measured Stokes diameters was observed. When measured in the cell culture medium, however, a significant decrease of the Stokes diameter of about 7 nm was observed for NP-plain and NP–NH2 compared with water and the Tris–HCl buffer. This may be explained by the influence of the protein corona on the sedimentation time of the particles. On the one hand the effective particle density decreases due to the low density of the proteins, which increases the sedimentation time, while on the other hand the particle diameter increases, which decreases the sedimentation time. Due to the opposite effects of both mechanisms, the interpretation of the Stokes diameter derived from the sedimentation time is not straightforward. Additional assumptions about the protein density would be required to convert the sedimentation time into a core diameter and shell thickness.28–30
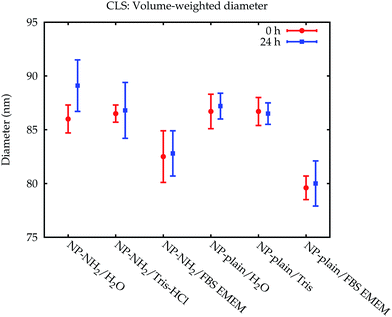 | ||
| Fig. 5 Comparison of the volume-weighted modal diameters of the primary peak from the CLS measurements in Lab 1. The error bars represent the combined standard uncertainty limited to the contributions relevant for comparing between CLS results. The data from Lab 2 can be found in the ESI.† | ||
3.3 Small-angle X-ray scattering
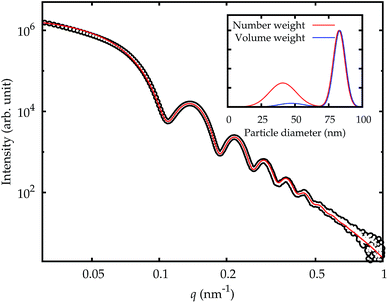
Small-angle X-ray scattering (SAXS) is a method which evaluates the angular distribution of an X-ray beam scattered off the suspended particles in the forward direction under small angles.31 The scattering contrast is caused by electron density differences in the sample. The scattering data is given by the scattering intensity I(q) as a function of the momentum transfer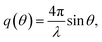 | (3) |
The SAXS experiments were performed at the four-crystal monochromator (FCM) beamline of PTB at BESSY II.32 The samples in suspension were filled into disposable borosilicate glass capillaries with an inner diameter of 1 mm and a wall thickness of 10 μm. The capillaries were closed by welding the upper end in the flame of a propane/oxygen torch. A sample holder containing these capillaries was placed into a vacuum chamber equipped with a six-axes manipulator for sample movement. The synchrotron radiation was collimated using pinholes to a size smaller than 0.5 × 0.5 mm2 and focused on the sample. The incident photon flux was measured using a transparent photodiode located in front of the sample before the guard pinhole. A removable, calibrated diode behind the sample was used to measure the transmission of the sample. The scattered radiation was collected by a PILATUS 1 M detector with a pixel size of p = (172.1 ± 0.2) μm at an adjustable distance between 2 m and 4.5 m behind the sample.33
The measurements were performed at a photon energy of (8000.0 ± 0.8) eV. Each sample was recorded for an integration time of at least 300 s. In addition to the samples, the corresponding dispersion media were measured as a blank. The distance between the sample and the detector was set to (4540.2 ± 0.5) mm.
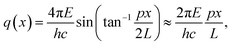 | (4) |
The uncertainty contribution of the model fitting to the number-weighted mean particle diameter was estimated from the residual sum of squares χ2 of this fit by finding the deviation from the best fit diameter at which χ2 exceeds 2χmin2.34
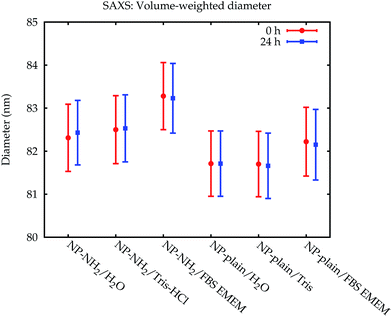 | ||
| Fig. 7 Comparison of the volume-weighted modal diameters from the SAXS measurements. The error bars denote standard uncertainties. | ||
The fraction of smaller particles in the 40 nm size range appeared in the background contribution. Even though the larger primary particles are much stronger scatterers and also more concentrated, this size fraction could be resolved because of the large disparity in size of the two fractions, which causes scattering into different angles. Still, the results were not consistent across the different samples, caused by the vastly different total scattering intensity. Therefore, this fraction was treated as part of the background only and not quantitatively evaluated.
3.4 Particle tracking analysis
Particle tracking analysis (PTA), also known as nanoparticle tracking analysis or NTA, is a method which tracks individual nanoparticles in suspension that are moving under Brownian motion. The sample is illuminated by a laser and a video of the light scattered by the particles is recorded by a light-sensitive camera through a magnifying objective. The Brownian motion of the particles is reconstructed from this video, and the translational diffusion constant and finally the size is inferred from the particle tracks. In order to distinguish the individual particles, the sample must be dilute so that the mean particle distance is larger than the diffraction limit of the microscope. Consequently, the measurements were performed at a much higher dilution (≈1500×) than with the other methods, and, in case of the cell culture medium, a higher concentration of the protein molecules relative to the number of particles.The PTA measurements were carried out with an NS500 instrument, manufactured by NanoSight, Malvern Instruments Ltd. This instrument was equipped with a 405 nm continuous-wave diode laser with a maximum power output of 60 mW. The temperature was set and maintained at (25 ± 1) °C throughout the measurements. The performance of the instrument was checked daily with NIST RM 8013 (Au nanoparticles, nominal mean diameter of 60 nm) diluted ≈ 50× with purified water which was additionally passed through a membrane filter with a nominal pore size of 0.1 μm. Aliquots were taken from the samples with an automatic pipette using a new sterile plastic pipette tip for each aliquot. Prior to analysis, the material was diluted gravimetrically 1500× in the corresponding dispersion medium and vortexed for 15 s. The measurements were performed immediately after sample dispersion (0 h) and following a 24 h incubation at (25 ± 1) °C.
Movies were recorded over 160 s, with 30 s equilibration time prior to each measurement. Camera levels were set to 9. No fluorescence long-pass filters were used.
4 Results and discussion
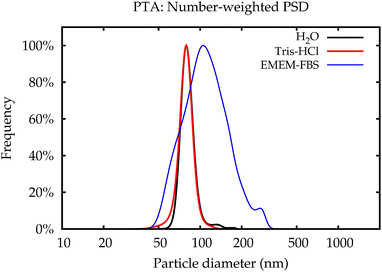
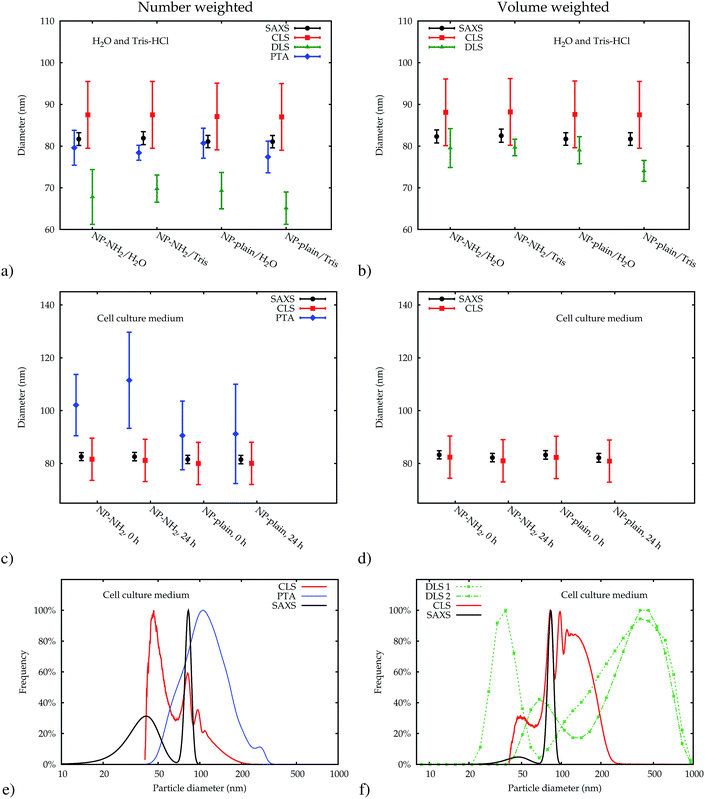
The data which were obtained with the different methods are summarized in Fig. 10. The modal values for the suspensions in water and the Tris–HCl buffer are displayed in number- and volume-weight in Fig. 10a and b, respectively. In number weighting, PTA, CLS and SAXS agree within their expanded (k = 2) uncertainties, whereas DLS gives consistently lower results. Volume-weighted PSDs for PTA are not available, but the other three methods agree on the volume-weighted data, with the exception of NP-plain in the Tris–HCl buffer, where DLS reports a slightly smaller value.As an example of the behaviour of the particle size analysis methods in the cell culture medium, the PSDs for NP–NH2 immediately after dispersion are shown in number- and volume-weight in Fig. 10e and f, respectively. Both SAXS and CLS show a sharp maximum around 80 nm and a broader peak below 50 nm. The CLS volume-weighted distribution contains an additional broader peak between 100 nm and 200 nm, with distinct peaks at 100 nm and 110 nm of the same width approximately as the primary peak, but with a smaller height.
The DLS results in cell culture medium are inconsistent and differ significantly from the other methods. This can be most probably attributed to agglomeration induced by the medium, which can easily distort DLS due to the high sensitivity to larger particles. This effect is amplified by the subsequent conversion to a volume-weighted size distribution (see Fig. 3). Thus, DLS is useful to monitor changes in a sample and to detect agglomeration, but the size results are then completely dominated by the agglomerates. DLS is therefore not considered in the comparison of modal values in Fig. 10c and d.
Like DLS, PTA is based on the detection of Brownian motion and can provide critically important information for assessing the impact of biological systems on the change in the hydrodynamic diameter of the particles and, therefore, also about the thickness of the organic corona upon suspension in serum containing medium.35 Unlike DLS, PTA measurements did not suffer from a severe degradation when applied to the dispersions in the cell culture medium. However, these results could only be obtained using the NTA 3.0 software version. Older algorithms were disturbed by measurements in cell culture media. Only number-weighted PSDs were directly obtained using this method. Volume-weighted PSD data can be computed by the software, but are not shown here, because they were already systematically shifted for reference particles, and no suitable certified matrix reference materials were available, that could be used as calibrants for bias correction.
Due to the physical principle of PTA, it is also not possible to measure the same high concentration of nanoparticles as with the other methods. This means that for the measurements in the cell culture medium, the ratio of the serum proteins to the number of particles is much larger than with the other methods. The serum protein molecules outnumber the nanoparticles also in the dispersions used for the other methods by a factor of 5 × 103, therefore this option was more comparable than the alternative of diluting the incubated particles in purified water.
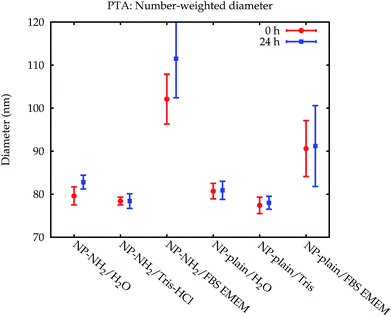
The modal diameters obtained for NP–NH2 and NP-plain in cell culture medium at both points in time are compared in Fig. 10c and d. Due to the very different physical principles behind the methods, the measured modal diameter is influenced differently by the changes in the samples effected by the cell culture medium.36 Meaningful PTA values are only available for the number-weighted distribution. Here, an increase in size was observed which is significant compared to the standard (but not expanded) uncertainty. Since the particle size is inferred from the diffusion constant of the Brownian motion, a protein coating, probably with a rough surface, will lead to a decreased diffusion constant and an increased measured size. Though this increase has a large absolute value, it is not significant within a confidence level of about 95% due to the large uncertainty of the value.
The size of the core of the primary particle fraction is best resolved in the SAXS measurements, which show almost no indication of other fractions (agglomerates and smaller particles). The SAXS technique is sensitive to the electron density of the particles. Since the primary particles are composed of dense silica material, the SAXS results are not affected by or sensitive to the functional amino-groups on NP–NH2 and only minimally by the (light) protein corona on the surface of the particles in cell culture medium. Consequently, all SAXS measurements agree within the standard uncertainties.
The CLS data allow the resolution of different fractions like primary particles and different levels of agglomeration. The interpretation of the measured modal size values, is, however, not straightforward, due to the opposite effects on sedimentation time of the developing protein corona, which changes simultaneously the size and the average density of the particles.22,30 Nevertheless, the size obtained for the primary particle fraction is consistent with the SAXS results within the expanded uncertainties.
5 Conclusion
Plain and amino-functionalized silica nanoparticles were measured using four size characterization techniques based on different physical principles in three different suspending media of increasing complexity, namely water, a Tris–HCl buffer, and a cell culture medium. Using a detailed uncertainty analysis for each method, the values for the main mode of the size distribution could be compared between methods. It was found that there is agreement for simple media (water and Tris buffer). The agglomeration of the nanoparticles induced by the cell culture medium had a significant influence on the DLS measurements, rendering the numerical results unusable, and led to a significant size increase in PTA, whereas the primary particle size remained unchanged for SAXS and CLS measurements. The latter technique can additionally be used to distinguish between agglomerates of different sizes.Acknowledgements
This work was partly funded through a contract with the European Metrology Research Programme (EMRP project NEW 03 NanoChOp). The EMRP is jointly funded by the EMRP participating countries within EURAMET and the European Union. The authors thank Daniel Geißler from Bundesanstalt für Materialforschung und -prüfung (BAM) for carrying out supporting DLS measurements and for help with sample handling.References
- R. Peters, E. Kramer, A. G. Oomen, Z. E. Herrera Rivera, G. Oegema, P. C. Tromp, R. Fokkink, A. Rietveld, H. J. P. Marvin, S. Weigel, A. A. C. M. Peijnenburg and H. Bouwmeester, ACS Nano, 2012, 6, 2441–2451 CrossRef PubMed.
- A. Weir, P. Westerhoff, L. Fabricius, K. Hristovski and N. von Goetz, Environ. Sci. Technol., 2012, 46, 2242–2250 CrossRef PubMed.
- L. Calzolai, D. Gilliland and F. Rossi, Food Addit. Contam., Part A, 2012, 29, 1183–1193 CrossRef PubMed.
- S. Dekkers, P. Krystek, R. J. B. Peters, D. P. K. Lankveld, B. G. H. Bokkers, P. H. van Hoeven-Arentzen, H. Bouwmeester and A. G. Oomen, Nanotoxicology, 2010, 5, 393–405 CrossRef PubMed.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543–557 CrossRef PubMed.
- Compendium of Projects in the European NanoSafety Cluster, 2015, http://www.nanosafetycluster.eu/home/european-nanosafety-cluster-compendium.html.
- European Commission, Recommendation of 18/10/2011 (2011/696/EU), 2011, http://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32011H0696.
- F. Meli, T. Klein, E. Buhr, C. G. Frase, G. Gleber, M. Krumrey, A. Duta, S. Duta, V. Korpelainen, R. Bellotti, G. B. Picotto, R. D. Boyd and A. Cuenat, Meas. Sci. Technol., 2012, 23, 125005 CrossRef.
- M. P. Monopoli, C. Aberg, A. Salvati and K. A. Dawson, Nat. Nanotechnol., 2012, 7, 779–786 CrossRef CAS PubMed.
- M. Lundqvist, J. Stigler, G. Elia, I. Lynch, T. Cedervall and K. A. Dawson, PNAS, 2008, 105, 14265–14270 CrossRef CAS PubMed.
- F. Wang, L. Yu, M. P. Monopoli, P. Sandin, E. Mahon, A. Salvati and K. A. Dawson, Nanomedicine, 2013, 9, 1159–1168 CrossRef CAS PubMed.
- U. Hansen and A. F. Thünemann, Langmuir, 2015, 31, 6842–6852 CrossRef CAS PubMed.
- K. Braeckmans, K. Buyens, W. Bouquet, C. Vervaet, P. Joye, F. D. Vos, L. Plawinski, L. Doeuvre, E. Angles-Cano, N. N. Sanders, J. Demeester and S. C. D. Smedt, Nano Lett., 2010, 10, 4435–4442 CrossRef CAS PubMed.
- G. Orts-Gil, K. Natte and W. Österle, RSC Adv., 2013, 3, 18202–18215 RSC.
- Y.-X. Yang, Z.-M. Song, B. Cheng, K. Xiang, X.-X. Chen, J.-H. Liu, A. Cao, Y. Wang, Y. Liu and H. Wang, J. Appl. Toxicol., 2014, 34, 424–435 CrossRef CAS PubMed.
- G. Roebben, K. Rasmussen, V. Kestens, T. P. J. Linsinger, H. Rauscher, H. Emons and H. Stamm, J. Nanopart. Res., 2013, 15, 1–13 CrossRef.
- Colloidal Silica Products Klebosol, Colloidal silica Particle Size, Silica Content & Stabiliser Type.
- J. S. Gray, J. M. Birmingham and J. I. Fenton, Biologicals, 2010, 38, 273–277 CrossRef CAS PubMed.
- G. Roebben, V. Kestens, Z. Varga, J. Charoud-Got, Y. Ramaye, C. Gollwitzer, D. Bartczak, D. Geißler, J. Noble, S. Mazoua, N. Meeus, P. Corbisier, M. Palmai, J. Mihály, M. Krumrey, J. Davies, U. Resch-Genger, N. Kumarswami, C. Minelli, A. Sikora and H. Goenaga-Infante, Front. Chem., 2015, 56 Search PubMed.
- ISO, Particle Size Analysis – Dynamic Light Scattering (DLS), International Organization for Standardization, ISO 22412, 2008 Search PubMed.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 213–227 CrossRef.
- N. Hondow, R. Brydson, P. Wang, M. D. Holton, M. R. Brown, P. Rees, H. D. Summers and A. Brown, J. Nanopart. Res., 2012, 14, 1–15 CrossRef.
- G. Orts-Gil, K. Natte, D. Drescher, H. Bresch, A. Mantion, J. Kneipp and W. Österle, J. Nanopart. Res., 2010, 13, 1593–1604 CrossRef.
- ISO, Determination of Particle Size Distribution by Centrifugal Liquid Sedimentation Methods – Part 2: Photocentrifuge Method, International Organization for Standardization, ISO 13318-2, 2007 Search PubMed.
- V. Kestens and G. Roebben, The Certification of the Equivalent Spherical Diameters of Silica Nanoparticles in Aqueous Solution, ERM®- FD102, 2014 Search PubMed.
- A. Braun, O. Couteau, K. Franks, V. Kestens, G. Roebben, A. Lamberty and T. P. J. Linsinger, Adv. Powder Technol., 2011, 22, 766–770 CrossRef CAS.
- A. Sikora, D. Bartczak, D. Geißler, V. Kestens, G. Roebben, Y. Ramaye, Z. Varga, M. Palmai, A. G. Shard, H. Goenaga-Infante and C. Minelli, Anal. Methods, 2015, 7, 9835–9843 RSC.
- M. P. Monopoli, D. Walczyk, A. Campbell, G. Elia, I. Lynch, F. Baldelli Bombelli and K. A. Dawson, J. Am. Chem. Soc., 2011, 133, 2525–2534 CrossRef CAS PubMed.
- N. C. Bell, C. Minelli and A. G. Shard, Anal. Methods, 2013, 5, 4591–4601 RSC.
- A. Sikora, A. G. Shard and C. Minelli, Langmuir, 2016, 32, 2216–2224 CrossRef CAS PubMed.
- ISO, Particle Size Analysis – Small-angle X-ray Scattering, International Organization for Standardization, ISO 17867, 2015 Search PubMed.
- M. Krumrey and G. Ulm, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 467–468, 1175–1178 CrossRef CAS.
- J. Wernecke, C. Gollwitzer, P. Müller and M. Krumrey, J. Synchrotron Radiat., 2014, 21, 529–536 CrossRef CAS PubMed.
- I. Hughes and T. P. A. Hase, Measurements and Their Uncertainties: a Practical Guide to Modern Error Analysis, Oxford University Press, Oxford, New York, NY, 2010 Search PubMed.
- D. Bartczak, P. Vincent and H. Goenaga-Infante, Anal. Chem., 2015, 87, 5482–5485 CrossRef CAS PubMed.
- V. Poderys, M. Matulionyte, A. Selskis and R. Rotomskis, Nanoscale Res. Lett., 2010, 6, 9 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.139/c6ay00419a |
| ‡ CG and MK performed and evaluated the SAXS measurements, collected the results and drafted the manuscript. DB performed and evaluated the PTA and TEM measurements. HGI conceived the study in the framework of the NanoChOp project. VK, CM, YR, and AS performed and evaluated DLS and CLS measurements, including a detailed uncertainty analysis. GR organized the production of the test materials. MP and ZV performed the amination of the plain silica particles. All authors read and approved the final manuscript. |
| This journal is © The Royal Society of Chemistry 2016 |