 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thin film depth profiling by ion beam analysis
Chris
Jeynes
 * and
Julien L.
Colaux†
* and
Julien L.
Colaux†
University of Surrey Ion Beam Centre, Guildford, GU2 7XJ, England, UK
First published on 31st August 2016
Abstract
The analysis of thin films is of central importance for functional materials, including the very large and active field of nanomaterials. Quantitative elemental depth profiling is basic to analysis, and many techniques exist, but all have limitations and quantitation is always an issue. We here review recent significant advances in ion beam analysis (IBA) which now merit it a standard place in the analyst's toolbox. Rutherford backscattering spectrometry (RBS) has been in use for half a century to obtain elemental depth profiles non-destructively from the first fraction of a micron from the surface of materials: more generally, “IBA” refers to the cluster of methods including elastic scattering (RBS; elastic recoil detection, ERD; and non-Rutherford elastic backscattering, EBS), nuclear reaction analysis (NRA: including particle-induced gamma-ray emission, PIGE), and also particle-induced X-ray emission (PIXE). We have at last demonstrated what was long promised, that RBS can be used as a primary reference technique for the best traceable accuracy available for non-destructive model-free methods in thin films. Also, it has become clear over the last decade that we can effectively combine synergistically the quite different information available from the atomic (PIXE) and nuclear (RBS, EBS, ERD, NRA) methods. Although it is well known that RBS has severe limitations that curtail its usefulness for elemental depth profiling, these limitations are largely overcome when we make proper synergistic use of IBA methods. In this Tutorial Review we aim to briefly explain to analysts what IBA is and why it is now a general quantitative method of great power. Analysts have got used to the availability of the large synchrotron facilities for certain sorts of difficult problems, but there are many much more easily accessible mid-range IBA facilities also able to address (and often more quantitatively) a wide range of otherwise almost intractable thin film questions.
1 Historical introduction to IBA
What is Ion Beam Analysis (IBA)? We will answer this question implicitly by an historical survey, which will also shed light on the synergies that are central to our subject: modern IBA depth profiling of thin films. IBA has been used by analytical chemists for over half a century, ever since Rubin et al. published their landmark paper in 1957.1 Although in the 1990s IBA methods were rather overtaken by rapid developments in other techniques, in the last decade or so some dramatic developments in IBA have made it significantly more powerful, and it is these we aim to describe and explain here.These developments gathered pace around the turn of the 21st century. Fig. 1 shows a profile through the depth of an antireflection coating which an optics company wished to reverse-engineer. It is an iconic image of far-reaching significance to which we will return repeatedly in this Review, here pointing out merely that the coating is complex and yields an intricate spectrum which we can nevertheless fit very precisely, meaning that very detailed information can be extracted from this single spectrum, non-destructively and with essentially no prior knowledge (it is a “model-free” analysis, although see discussion in §§3.9, 4.2).
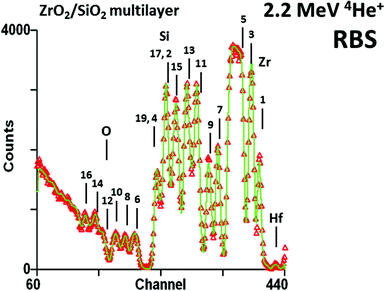 | ||
Fig. 1
Antireflection coating by Rutherford backscattering spectrometry. The coating is a 19 layer silica/zirconia stack on glass: the layer numbers are shown. Layer 1 is zirconia. There is no contrast for layer 18 (silica). The zirconium signals for layers 17 & 19 accidentally overlap the silicon signals for layers 2 & 4. The Zr and Si signals are obvious, Hf and O are also visible: elemental edges are marked. To prevent charging under the beam the sample was coated with gold (channel 445, not shown). The bottom ZrO2 layer thickness was fitted as 14.4 ± 0.5 nm with the other layer thickness measurements having a comparable precision. Redrawn from Fig. 2 of Jeynes et al., Accurate depth profiling of complex optical coatings, Surf. Interface Anal., 30, ©2000,2 with permission from Wiley; and Fig. 11c of Jeynes et al., J. Phys. D: Appl. Phys., 2003![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 © IOP Publishing (reproduced with permission, all rights reserved). 3 © IOP Publishing (reproduced with permission, all rights reserved). | ||
Throughout this Review we will emphasise the importance of the proper use of complementary techniques. This importance is nothing new, but in today's increasingly multidisciplinary science we are finding that even in routine work, for which twenty years ago we might have been satisfied with a single analytical method, we now use multiple complementary methods. It is informative to trace the history of IBA with this in mind, since the various atomic and nuclear excitations that underlie most of the complementary analytical techniques of relevance to thin film analysis (including IBA) were all discovered together at the birth of the new physics.
And central to this Review is the recognition that “IBA” is itself a cluster of complementary techniques that historically were handled separately but which we have recently learned to handle self-consistently in a synergistic way. To refer to this self-consistent use of multiple IBA methods we will use “Total-IBA”, a term proposed by Jeynes et al. in 2012![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 who also provide an annotated Glossary of the “acronym soup” for all the complementary techniques. In this Review we will highlight acronyms as they occur, for ease of reference, expanding them repeatedly as necessary for clarity.
4 who also provide an annotated Glossary of the “acronym soup” for all the complementary techniques. In this Review we will highlight acronyms as they occur, for ease of reference, expanding them repeatedly as necessary for clarity.
High energy nuclear backscattering was first proposed by Ernest Rutherford in 1911![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 to account for the scattering of alpha particles by gold atoms. Also in 1911, Charles Barkla6 recognised that the mysterious effect generated by γ-rays striking matter, which he named “X-ray fluorescence” (XRF), was similar to the atomic emission already familiar to the spectroscopists for half a century. This was immediately followed by Niels Bohr's modelling7 of the Rydberg equation:8–10 hence the first explanation of the characteristic elemental lines that the spectroscopists had never understood. It was Barkla6 in 1911 who established the “K, L, M” nomenclature for the X-ray lines from the atomic shells (before the “Bohr atom”): he started with “K” precisely because he had no reason to believe it was the first!
5 to account for the scattering of alpha particles by gold atoms. Also in 1911, Charles Barkla6 recognised that the mysterious effect generated by γ-rays striking matter, which he named “X-ray fluorescence” (XRF), was similar to the atomic emission already familiar to the spectroscopists for half a century. This was immediately followed by Niels Bohr's modelling7 of the Rydberg equation:8–10 hence the first explanation of the characteristic elemental lines that the spectroscopists had never understood. It was Barkla6 in 1911 who established the “K, L, M” nomenclature for the X-ray lines from the atomic shells (before the “Bohr atom”): he started with “K” precisely because he had no reason to believe it was the first!
Atomic excitation by particles was immediately reported, first for alphas (by James Chadwick11) and then for electrons (by Henry Moseley12,13). Thus, Rutherford backscattering spectrometry (RBS) and particle-induced X-ray emission (PIXE) are classical techniques closely associated with the birth of the new physics. Electron-probe microanalysis (EPMA) eventually followed from Moseley's observation, and he was prescient enough to remark: “The prevalence of [X-ray] lines due to impurities suggests that this may prove a powerful method of chemical analysis”. How right he was!
The first X-ray photoelectron spectra (XPS) were recorded by P. D. Innes in 1907,14 anticipating XRF. Of course, the photoelectric effect was discovered by Hertz in 1887![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 and interpreted by Einstein in 1905
15 and interpreted by Einstein in 1905![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 but Innes was the first to unequivocally energy analyse the emitted electrons, interpreting them as due to ‘nuclear [actually atomic] disintegration’ processes. Pierre Auger observed the eponymous “Auger electron” spectra (AES) in 1925,17 by which time it was clearly understood that XPS was a primary atomic excitation process, and XRF together with AES were the two branches of the secondary relaxation process.
16 but Innes was the first to unequivocally energy analyse the emitted electrons, interpreting them as due to ‘nuclear [actually atomic] disintegration’ processes. Pierre Auger observed the eponymous “Auger electron” spectra (AES) in 1925,17 by which time it was clearly understood that XPS was a primary atomic excitation process, and XRF together with AES were the two branches of the secondary relaxation process.
Nuclear (rather than atomic) processes were of great interest in the early 1920s: the transition from RBS to elastic (non-Rutherford) backscattering (EBS) as the Coulomb barrier is exceeded was first effectively demonstrated by Chadwick & Bieler in 1921 (for alphas on H).18 Of course, in this case the alphas cannot backscatter from H (it is kinematically forbidden) but they can scatter, and the H will recoil with a high energy: such recoils can be detected for analytical purposes and are known as elastic recoil detection (ERD).
Ernest Rutherford first understood that he had observed nuclear reactions in 1922, using the 4.87 MeV α particle from 226Ra on nitrogen gas: the 14N(α,p)17O reaction has a Q-value of −1.19 MeV, so that fast protons were visible.19,20 The so-called “Q-value” of the reaction is determined by the mass difference between the initial and final state (before and after the reaction), and can be readily calculated using Einstein's E = mc2 relation. This reaction is endothermic. Note that the rest mass of the electron is 511 keV. Also see Fig. 8 caption for explanation of this nuclear physics terminology.
Later, Cockcroft and Walton were the first to use an electrostatic ion accelerator to induce nuclear reactions, demonstrating the (exothermic) 7Li(p,α)4He reaction,21 for which the Q-value is an enormous 17.35 MeV, and which has a non-zero cross-section down to very low energies (at 430 keV this is 0.27 mb sr−1).22 We can note here parenthetically that the proton capture reaction 11B(p,γ)12C has its first resonance at an even lower energy: only 163 keV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23–26 (useful both for calibrating ion implanter energies and also for depth profiling boron, with a very high depth resolution implied by the 7 keV resonance width;27 this is discussed below in §3.3 and Fig. 8). This capture reaction also has a huge Q-value of 16 MeV. These sorts of inelastic reactions are used in the so-called nuclear reaction analysis (NRA), which is known as particle-induced gamma emission (PIGE) when it is the resulting γ-rays that are detected. PIGE is the result of nuclear relaxation after an excitation event in exactly the same way that atomic fluorescence (XRF, PIXE, EPMA) is the result of the relaxation of an atom after it has been ionised.
23–26 (useful both for calibrating ion implanter energies and also for depth profiling boron, with a very high depth resolution implied by the 7 keV resonance width;27 this is discussed below in §3.3 and Fig. 8). This capture reaction also has a huge Q-value of 16 MeV. These sorts of inelastic reactions are used in the so-called nuclear reaction analysis (NRA), which is known as particle-induced gamma emission (PIGE) when it is the resulting γ-rays that are detected. PIGE is the result of nuclear relaxation after an excitation event in exactly the same way that atomic fluorescence (XRF, PIXE, EPMA) is the result of the relaxation of an atom after it has been ionised.
Digressing a little, and to complete our whirlwind tour of quantum physics history from an elemental analysis point of view, the wave-mechanical interference between identical scattered and recoil nuclei due to their indistinguishability was pointed out (for electrons) by Nevill Mott in 1930![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 and immediately verified using magnetic spectrometers for proton–proton RBS29 and EBS (measurements30 and theory31).
28 and immediately verified using magnetic spectrometers for proton–proton RBS29 and EBS (measurements30 and theory31).
This has a direct analytical use: extraordinary sensitivity for hydrogen (with a detection limit of 1.4 × 1016 H cm−3) was obtained in 2004 by Reichart et al.32 using proton–proton scattering with detection of the scattered and recoiled particles in coincidence (see Fig. 2). A 3-D analysis of polycrystalline diamond was made with micron-sized voxels using a 17 MeV proton beam focussed by superconducting magnetic lenses: this high energy was needed to penetrate the sample thickness (55 μm) with adequate spatial resolution. Most IBA labs do not have such high energy microbeams, but thinner samples can be measured equally well with lower energies using the same methods.
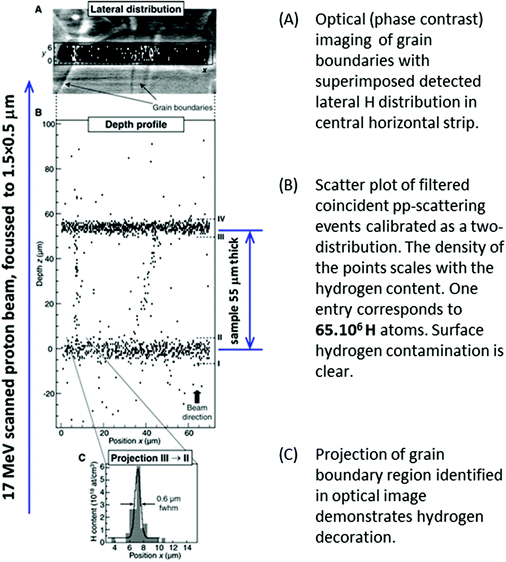 | ||
| Fig. 2 Depth profiling H in polycrystalline diamond with high lateral resolution. From Fig. 3 of Reichart et al., Science, 2004.32 Reprinted with permission from AAAS. | ||
The dramatic advance in the understanding of nuclear processes achieved since Rutherford first directly observed atomic nuclei is beautifully exemplified by the extraordinary and seminal work of Burbidge, Burbidge, Fowler and Hoyle in 1957 on stellar nucleosynthesis (the famous “BBFH” paper33). It is an astounding experience to realise for the first time that we are – literally! – stardust, and not only that but also to see that it is possible for us to grasp the whole of cosmic history, notwithstanding our manifest insignificance.
BBFH was a lifetime ago:34 huge strides have been made since then to obtain an understanding of cosmic chemistry,35 with increasingly well-informed speculations on the origin of life. Curiously, these also have an example using IBA: Howard et al.36 have recently demonstrated that organic molecules can survive a large meteor impact, implying that interstellar organics could possibly be carried intact to earth. This work was initiated from an unambiguous identification by IBA of carbonaceous inclusions in impact glass,37 completely against the expectations of the geologists. We will return to this interesting example below (§4.6 and Fig. 23).
2 Thin film depth profiling methods
The modern analyst is regularly confronted by a wide variety of analytical problems. Of course, in any particular project certain analysis methods become the routinely used workhorses, and in the majority of cases the routine workhorse is either the ideal method or at least well-suited to the problem. But what to do when the routine method fails for the exceptional problems? How to specify appropriate methods for new projects? Which methods should we turn to when we really need absolute model-free fully quantitative analysis?Standard methods for elemental depth profiling of thin films include secondary ion mass spectrometry (SIMS), cross-sectional transmission electron microscopy (XTEM), scanning Auger microscopy (SAM), glow discharge optical emission spectroscopy (GD-OES), X-ray photoelectron spectrometry (XPS), and laser-ablation inductively coupled plasma mass spectrometry (LA-ICP-MS). All of these have very well developed instrumentation and a large analytical literature with very wide applicability, and they (with their variants) are all in widespread use in both industrial and research labs.
In this Review, and in the context of these complementary methods, we will be explaining the strengths and capabilities of ion beam analysis (IBA), which uses an MeV ion beam to probe the sample. Table 1 indicates some of the characteristics of these complementary methods. All analysis methods have strengths and weaknesses, and a wise analyst will have a sensitive appreciation of their complementarity, mixing and matching techniques appropriate to the current analytical problem. Some brief comments here will help the reader to place IBA correctly in context. The strength of one technique is not properly recognised unless the limitations of the others are also understood.
| SIMS | XTEM | SAM | GD-OES | XPS | LA-ICP-MS | IBA | |
|---|---|---|---|---|---|---|---|
| a Auger electrons, photoelectrons and characteristic photons (X-rays or visible) are effects of atomic excitation, which can be by electrons (AES or SAM, EELS), photons (XPS, XRF) or ions (IBA). b SIMS, SAM, XPS, GD-OES use sputtering to obtain depth profiles; XTEM requires special sample preparation; LA-ICP-MS uses laser ablation. IBA is not deliberately destructive, but the probe beam is energetic and may damage the sample. c For SIMS, SAM, XPS the depth resolution depends on control of the sputtering beam; for the LA-ICP-MS the depth resolution depends on control of the laser parameters; for GD-OES the sample is consumed by the plasma; the best IBA surface depth resolution for standard methods is given (rapidly degrades with depth). d For SIMS, SAM, XPS, GD-OES the information depth depends on the sputter time; for IBA the information depth depends on the probe used: 15 μm is a typical value for PIXE excited by a 3 MeV proton beam. For LA-ICP-MS information depth is given by the number of laser pulses at the same spot. e For SIMS, SAM, XPS and IBA the lateral resolution is given by the spot size of the scanned probing beam: respectively keV ions, electrons, photons (X-rays), or MeV ions. f Electron energy loss spectrometry (EELS) of the transmitted primary beam. Reliable elemental characterisation available as an attachment on many higher spec TEMs. See Fig. 23d. Energy-dispersive X-ray analysis (EDX) is usually rather low sensitivity in the TEM because of the very non-optimal geometry. g SIMS is quantitative in particular well-characterised cases, and semi-quantitative in many other cases. Sample-matched standards are always needed. h Elemental sensitivity is expressed in atomic fraction (not mass fraction) for all techniques. i SIMS can be used with excellent relative accuracy but only in specific very well characterised cases. j Three methods have been used as reference methods: only RBS is demonstrated as a primary method. k TEM-EELS, GD-OES and LA-ICP-MS are usually used for elemental depth profiling although in principle all of them could be used to obtain chemical information. l IBA is usually used only for elemental depth profiling, although PIXE-WDX and high energy resolution PIXE-EDX have both been used to obtain chemical information. | |||||||
| Primary beam | keV ions | ∼100 keV electrons | ∼100 keV electrons | Plasma | X-raysa | Pulsed laser | ∼3 MeV light ions |
| ∼30 MeV heavy ions | |||||||
| Detected signal | Sputtered ions | Primary electrons in phase contrast | Augera electrons | Visible photonsh | Photo-electrons | Evaporated ions | X-raysa; nuclear reaction products: scattered primaries, target recoils and γ-rays |
| Destructiveb | Yes | Yes | Yes | Yes | Yes | Yes | No |
| Depth resolutionc | 2 nm | 0.1 nm | 2 nm | 20 nm | 2 nm | 50 nm | 2 nm |
| Information depthd | 500 nm | 100 nm | 500 nm | 50 μm | 500 nm | ∼5 μm | 15 μm |
| Lateral resolutione | 50 nm | 0.1 nm | 2 nm | 1 mm | 3 μm | 10 μm | 500 nm |
| Elemental imaging | Yes | EELS, EDXf | Yes | No | No | No | Yes |
| Molecular information | Yes | No?k | Yes | No?k | Yes | No?k | Nol |
| Ambient analysis | No | No | No | No | No | Yes | Yes |
| Sample preparation | No | Yes | UHV | No | UHV | No | No |
| Quantitative | ?g | No | Yes | Yes | Yes | Yes | Yes |
| Standards needed | Yes | — | Yes | Yes | Yes | Yes | No |
| Elemental sensitivityh | 10−8 | 10−1 | 10−3 | 10−6 | 10−3 | 10−9 | 10−6 |
| Accuracy | —i | — | 10% | 10% | 5% | 5% | 1% |
| Traceabilityj | — | — | — | — | Yes | Yes | primary |
We first (§2.1) describe salient features of the complementary techniques, especially noting the great strengths of each method together with an indication of where alternative methods are needed. We then (§3) briefly sketch the IBA techniques. These will be very incomplete sketches, but should be sufficient for readers to grasp the points in this Review (perhaps with the help of Wikipedia) without being forced to look at other literature. The latter, as we have said before, is voluminous, and we will try to cite it helpfully.
2.1 Standard thin-film depth-profiling methods
• Sputter depth profiling (see Hofmann38 and Taylor et al.39) is used for many methods (SIMS, SAM, and XPS, using an ion gun; and GD-OES, using a plasma). Analysts need to appreciate the various artefacts of sputtering which can be both large and rather intricate, especially in the presence of interfaces; and in particular that the sputter rate (on which the depth scale depends) is usually a strong function of the composition. The surface is also an important interface which is tricky to analyse reliably by sputtering methods.• There are a variety of high-specification SIMS instruments capable of high throughput high reproducibility depth profiling, even at the sample surface. This is a standard workhorse in many labs. SIMS usually has a very high sensitivity, but its problem is that the ionisation probability for secondary ions may vary by orders of magnitude, and the matrix effect is usually huge. This means that quantification is always difficult, and that sample-matched standards are essential for accuracy. Seah et al.40 is a prominent example of an accurate comparison of SIMS and XPS.
• XPS uses beautiful 2-D high resolution (∼0.1 eV) electron energy analysers which are easily good enough to detect chemical shifts in the electron binding energies. This is the reason for the name Kai Siegbahn gave the technique: electron spectroscopy for chemical analysis (ESCA).41 The great value of the technique, apart from the ability to distinguish between (for example) oxidation states of metals, is that the electron mean free path (EMFP) in the sample being analysed is very short (∼5 nm) so that photoelectrons only escape with their characteristic energy intact from the very near surface of the material. XPS is therefore a surface sensitive technique. To use it for depth profiling the sample must be sputtered away, with an XPS analysis for every sputtering increment.
Considering quantitative depth profiling, the weakness of the technique is that the EMFP is a strong function of the material and is not usually known very accurately. Therefore, standards are needed to determine EMFP (which IBA could provide42). Despite this, the method is classed as “traceable” and very considerable effort has gone into developing analysis protocols that allow accreditation of XPS labs to the ISO 17025 standard (Seah & Spencer43). However, the sensitivity of XPS is limited to a fraction of atomic% per layer: thus, it is insensitive to minor or trace elements not concentrated in layers.
XPS benchtop instruments use tube X-ray sources, which can be monochromated: all synchrotron light sources include XPS instrumentation: sy-XPS is very powerful.
• SAM44 uses the non-radiative atomic relaxation AES (Auger electron spectroscopy) process after excitation by an electron beam. The great advantage of AES is that it can be mounted into a (modified) scanning electron microscope (SEM), and the AES signal is used for imaging. Both XPS and AES (and therefore also SAM) are surface sensitive techniques, using the same electron energy analysers and getting depth profiles by sputtering.
• XTEM is an extraordinarily powerful technique, allowing atomic-level structural information by direct phase-contrast imaging of strings of atoms (so-called “high resolution”), and also using selected area diffraction (SAD) to identify the crystal structure, orientation and lattice parameter of nano-crystals. Crystalline defects (dislocations, twins etc.) can be imaged directly, using “dark field” imaging with the primary electron beam oriented crystallographically (but TEM is not sensitive to point defects, for which positron annihilation spectroscopy, PAS,45 is needed). Elemental sensitivity can be obtained either by including an energy dispersive X-ray detector (EDX), or by using the energy-analysed transmitted electrons, so-called electron energy-loss spectrometry (EELS), where the information derives from the effect of target atomic excitation on the primary beam. A recent example is of nano-structured CeO2 thin films,46 and we have discussed another example shown in Fig. 23d.
However, XTEM has a number of weaknesses. Sample preparation is laborious and time consuming, and can be very difficult; also, operating the instrument is very highly skilled and requires great intelligence, including the ability to think in reciprocal space: XTEM is not a fast method for routine use on many samples! The field of view of TEM samples is of the order of 100 nm, so that there is always the question of whether results are representative. Determining quantity of material (fully quantitative EELS or EDX) is usually impossible because sample thickness (on which the EELS or EDX signals depend) is a strong function of the sample preparation, is hard to control, and very difficult to measure. Even the phase contrast images are not entirely straightforward to interpret, so that “simple” film thickness measurements can have much larger errors than expected. This was very clearly demonstrated by Seah et al.47 in an extensive and important multi-technique Intercomparison exercise which established the use of XPS for the very accurate determination of native silicon oxide thicknesses.
• GD-OES is a completely different sort of analysis method with little or no lateral resolution, but rather good at profiling thick (>20 μm) layers. Again, considerable effort has gone into quantification, which always requires sample-matched standards (see the critical review by Winchester & Payling of NIST48).
• LA-ICP-MS is also a completely different sort of analysis involving mass spectrometry where the sample that enters the spectrometer is created by a very well-controlled laser pulse. Even though the lateral and depth resolution of the technique is not usually very good, it can be used very effectively for accurate work (for exceptionally good spatial resolution see Gutiérrez-González et al.49 for a recent use in reference material certification, see Jochum et al.50).
• Multitechnique examples: recently, the EMPIR programme (“European Metrology Programme for Innovation and Research”) has stimulated systematic analytical work on the chalcogenide glasses – in particular “CIGS”, Cu(In,Ga)Se2, which have become important materials for thin film photovoltaics. These are complex materials, and the more powerful analytical methods usually need sample-matched standards for quantification. Abou-Ras et al.51 directly compare 18 techniques (including SIMS, XTEM, XPS, AES, GD-OES, EELS; also RBS, ERD). In a supplementary paper, Abou-Ras et al.52 add “laser-induced breakdown spectroscopy” (an OES variant of LA-ICP-MS) and grazing-incidence X-ray fluorescence (GI-XRF), which is a powerful depth-profiling method used with great delicacy by synchrotron groups for both layered53 and implanted54 samples, and is an interference method analogous to variable-angle spectroscopic ellipsometry (VASE55).
The photovoltaic (PV) efficiency of CIGS materials deposited on plastic (flexible) substrates have been significantly improved (to >20%) by the use of alternates to sodium passivation of grain boundaries. Materials aspects of this development have been described by Reinhard et al. (2015),56 who used SEM, XPS, ICP-MS, ERD, SIMS and PAS in a very thorough analysis. Heavy ion ToF-ERD (13 MeV I, see §3.5) was used to obtain quantitative depth profiles of all elements, including the important light elements.
• Sample charging: it is worth pointing out that the low energy techniques (particularly SIMS, XPS, SAM) cannot be used on insulating samples without very careful attention to charge compensation. As a high energy method IBA is much less sensitive to sample charging, but it is still sometimes a problem.57
2.2 Model-dependent thin film depth profiling methods
Atomic excitation methods (including XRF, PIXE etc.: see Jeynes & Grime58 for a general discussion) usually give integral signals, where depth information affects the signals but cannot usually be extracted from them unambiguously. Important and widely-used methods include X-ray fluorescence (XRF) and electron-induced XRF using a scanning electron microscope (SEM), either with energy-dispersive X-ray spectrometry (SEM-EDX) or with so-called electron-probe microanalysis (EPMA) which also uses wavelength dispersive X-ray spectrometry (WDX). Today the high specification SEMs can operate as EPMA, and here we will use “EPMA” to include “SEM-EDX”.Both XRF and EPMA are now available commercially in very powerful desktop instruments supplied complete with advanced software based on “Fundamental Parameters” methods (see §3.2) which lead the operator through a proper instrument calibration procedure and is then able to validly interpret the spectra on the basis of sample structure information input by the operator without sample-matched standards. Thus, unwary users may think that XRF or EPMA can tell them layer thicknesses: indeed they can, but only if the layer existence and matrix composition are assumed. This is what is meant by “model-dependent” analysis.
Of course, in many cases the sample structure is known quite well in principle, and it is the details that need quantifying: there is no doubt that this sort of information from XRF and EPMA is highly valuable. But analysts need to be aware that the sample structure itself is assumed, and it is frequently difficult or even impossible to critically assess the validity of the assumed sample structure without recourse to other analytical techniques. Indeed, it is not always easy to remember the assumptions that underlie an analysis, and in §3.2 we give one interesting example where perhaps the power of sy-XRF has been rather overstated.
Depth information can be explicitly unfolded from X-ray data without sample structure assumptions using differential methods: the use of sputtering to reveal the depth information is clearly such a (destructive) differential method, and “angular resolved” XPS43 or the analogous “differential” PIXE59,60 are non-destructive differential methods. Karydas et al.61 explicitly compare reference-free sy-GI-XRF with Total-IBA (PIXE + EBS/RBS), where again the application is to CIGS films.
IBA has an entirely different, and model-free, approach to extracting the depth information from the (integral) atomic excitation (PIXE) data: the commensurate methods (most often PIXE + EBS/RBS) mutually interpret each other. This synergy is central to this Review, and we explore it in §4 below.
3 Recent advances in IBA
Ion beam analysis (IBA) is usually done with light ions and quite small accelerators: for example, both Surrey and Namur have a 2 MV “tandem”, and similar machines are common.‡ Such machines inject a negative beam towards the central positively charged (say, 1 MV) terminal; at the terminal the 1 MeV particles are passed through a so-called “stripper” (usually nitrogen stripper gas channel but can be a thin carbon foil) which efficiently strips electrons from the atoms. The particles, now positively charged, are then accelerated away from the terminal. So 1 MV potential on the terminal will give us 2 MeV singly charged particles, 3 MeV doubly charged particles, and so on. A 2 MV machine can deliver 4 MeV protons, 6 MeV alphas, 8 MeV Li3+, etc.Light ion beams (typically protons and alphas) generate backscattered ions (RBS for 1.5 MeV alphas, see §3.1; or EBS for higher energies and protons, see §3.3). They also generate PIXE (see §3.2), and the faster the ions the more X-rays you get. Particle-induced X-rays (PIXE) result from relaxation of inner-shell (core) electron excitations: of course the outer shells are also excited by ion impact but result in lower energy photons (so-called ion-beam-induced luminescence, IBIL) that are much less penetrating, harder to use and much harder to interpret. Still, IBIL is now attracting growing interest; although it is outside the scope of this Review we mention recent work on: damage centres in oxides,62 and demonstrating sub-30 nm imaging (of subcellular structures) using ion-beam-induced upconversion luminescence in lanthanide nano-crystals.63 The latter may prove complementary to (for example) stochastic optical reconstruction microscopy (STORM).64
Light ions at these MeV energies sometimes produce strong nuclear reactions in certain isotopes: this is the basis of NRA (and PIGE). The NRA methods are not emphasised in this Review since they have not significantly improved recently, although the IAEA has sponsored work65 which may yield dramatic improvements in PIGE quite soon.66
These accelerators usually have versatile ion sources which can generate ion beams from essentially the whole Periodic Table. So heavy ion beams are easy to produce, and are very well established for two main analytical uses: accelerator mass spectrometry (AMS) and elastic recoil detection (ERD). In AMS the sample is destroyed in the ion source, and its atoms are mass analysed, with isotope discrimination levels of 10−15 now routine in some cases. One important AMS centre is in Zurich, who have demonstrated outstanding performance with a 600 kV accelerator.67 But this is not a depth profiling method and is outside the scope of this Review. Heavy ion ERD on the other hand is a very important and versatile depth profiling method which has been dramatically improved recently (see §3.5).
IBA depth profiling is based on the energy loss of the probing beam in the target as well as the energy loss of the scattered or recoiled nuclei. It is not deliberately destructive – it does not sputter the sample away to mass-analyse the sputtered atoms as SIMS does, for example – so you get the sample back “intact” after the analysis (although there may still be damage induced by the energetic beam68). But of course there are also mass effects, easily calculated from kinematics. Thus the spectra always convolve mass and depth information and inverting the spectrum to recover the depth profile is a mathematically ill-posed problem: we return to this important issue repeatedly below.
Depth profiling of defects is a classical use of IBA when investigating crystalline materials and their response to various treatments. In particular, ion implantation in semiconductors is an enabling technology for modern electronics, and the implant always introduces crystalline damage (visible in Fig. 3) which must be healed by annealing to activate the impurities (“dopants”) electrically. Annealing is a complex materials problem in which there is still intense interest:69 the related problem of the lattice location of the implanted ion on annealing is also current.70 Channelling is a large and classical topic in its own right which we only mention here, because on the one hand there have not been significant recent advances and on the other hand it is mostly about the nature of the detected defects rather than their position in depth. But Fig. 3 indicates the power and versatility of the technique, showing the integrated damage as a function of lateral position introduced in single-crystal silicon by machining.71 At each point a quantified damage depth profile was obtained, including the contribution of both point and line defects. It is remarkable that silicon can behave plastically in some circumstances despite its extreme brittleness.
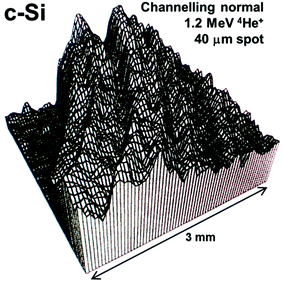 | ||
| Fig. 3 2-D image of crystalline damage introduced in turned silicon. Scanning ion microbeam RBS-channelling image of crystalline damage introduced in single crystal silicon turned on an ultra-stiff lathe using a single-point diamond tool. The displayed signal is integrated down to 350 nm depth: high signal means high integrated damage (silicon atoms off lattice sites). There is also a measurable dislocation density (∼5 × 1010 cm−2). The top left corner is undamaged. Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 118 (Fig. 4 of Jeynes et al., Laterally resolved crystalline damage in single-point-diamond-turned silicon, 431–436, ©1996),71 with permission from Elsevier. | ||
Finally we take up the issue of imaging and tomography. Depth profiling, the subject of this Review, involves 1-D spatial resolution in the direction of the probing beam, where imaging involves 2-D spatial resolution in the plane perpendicular to the probing beam. Focussed MeV ion beams with spot sizes of about 1 μm have been standard for over two decades, and it has proved remarkably difficult to improve on this because of the large off-axis aberrations of magnetic lenses. But recently some dramatic advances have been demonstrated, with spot sizes demonstrated down to 25 nm for very low beam currents. These can be used in scanning transmission ion microscopy (STIM) which is a direct ion analogue of EELS (see Table 1). STIM tomography is now a reality. 3-D imaging also becomes possible if the depth profiling can be put together with imaging. We explore all this in §3.8.
3.1 Accurate Rutherford backscattering spectrometry (RBS): ISO 17025
Stoichiometry is simpler than quantity of material to measure by RBS since only a relative measurement is needed. Even so, the first measurement at 1% accuracy which included a critical evaluation of the uncertainties was only published in 1997.74 This is a classical use of RBS which is still useful even for relatively inexact work where the uncertainty probably approaches only 5%. A recent example of such work is in ligand exchange chemistry (using nuclear magnetic resonance, NMR) in which the power conversion efficiency of optical devices based on semiconductor CdSe nanocrystals was increased from ∼1% to ∼30%! RBS was used to determine the Cd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Se
Se![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl ratios where the ligands were chloride-terminated and the quantity of excess Cd was critical.75
Cl ratios where the ligands were chloride-terminated and the quantity of excess Cd was critical.75
Fig. 4 shows how the ‘quantity of material’ measurement works: the RBS spectrum shown is an energy spectrum, where “channel number” represents the detected energy of the backscattered particle, and the conservation of energy and momentum (kinematics) requires that heavy (or light) target atoms scatter the primary ion beam at high (or low) energies.
 | ||
Fig. 4
Absolute determination of quantity of material by RBS. The sample is the “SPIRIT21” sample used by Jeynes et al.73 from which work this Figure was redrawn: Si nominally implanted with 5 × 1015 As cm−2 at 80 keV (and 3 × 1015 Ar cm−2 at 150 keV to amorphise). Elemental edges (highest backscattered energy) for As, Ar and Si, and the amorphisation depth in the silicon substrate are marked. The inset shows As signals from two RBS detectors plotted on a depth scale, uncorrected for straggle and detector energy resolution. The full energy spectrum is shown for one of these detectors. Note the background under the As signal, due to pulse pileup. Note the logarithmic scale of the ordinate axis. Reproduced from Fig. 1 of Colaux et al., Analyst, 2015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 87 with permission from the Royal Society of Chemistry (RSC). The equations are rearranged from the same paper. 87 with permission from the Royal Society of Chemistry (RSC). The equations are rearranged from the same paper. | ||
Fig. 4 is also an energy loss spectrum where the energy loss mechanism for energetic ions in material is now known fairly well, having been intensively studied since Bragg's76 early work over a century ago. The energy loss is rather insensitive to chemical effects at the 5% level (although larger effects can be observed), and generally energy loss can be estimated for arbitrary materials from a linear combination of elemental energy losses (the so-called “Bragg's rule”) for which a semi-empirical and very widely used database now exists (http://www.srim.org) and has recently been discussed by Ziegler et al.77 The database contains thousands of measurements, but is still sparse and inaccurate; new work is filling gaps,78 using new more efficient methods,79 and achieving very much better accuracy.80
It is the energy loss of the ion beam in material that directly gives depth profile information. The 80 keV arsenic implant in Fig. 4 has a range in silicon of 56 nm with a straggle of 17 nm, consistent with the observed peak and straggle of the As signal shown in the inset of Fig. 4, provided the instrumental function (essentially the detector resolution) is deconvoluted from the signal. This depth sensitivity is a classical use of RBS which remains important: in recent examples thorium diffusion in monazite (important in geochronology),81 the composition of reverse osmosis membranes,82 the stoichiometry of colloidal quantum dots,83 the composition of iron pyrite thin films (for photovoltaic applications),84 and the stoichiometry and thickness of SnO2 thin films85 were all determined using RBS.
RBS spectra are energy spectra that convolve depth and compositional information in a complex way: Fig. 4 is a simple example where all the signals can readily be distinguished, although even in this case the implanted Ar signal partially overlaps the Si substrate signal. In the general case the signals for the various elements of the target mutually overlap (as in Fig. 1): mathematically this turns out to be an ill-posed problem (see Jeynes et al.3), which we discuss further in §§3.4, 3.9.
In Fig. 4, eqn (1) shows the interpretation of the As yield from the measured area AAS of the As signal: AAs is proportional to the number of arsenic atoms fAs, the Rutherford cross-section σ (known analytically), and the charge × solid-angle product QΩ, where QΩ is given (eqn (2)) by the ratio of the (measured) amorphous Si yield Y0,Si and the gain of the spectrometer Δ, provided the energy loss factor [ε0]Si is known (Δ is discussed later with Fig. 6).
Using this method of determining implanted dose from RBS (treating the amorphised substrate signal as an internal reference) the Surrey ion implantation group have carried out a systematic quality assurance exercise to qualify the ion beam fluence, with the retained ion dose absolutely determined by RBS (see Colaux et al.,87 and Fig. 5). This work was a longitudinal study of implanter behaviour over three years, in which the RBS was demonstrated to be reproducible at 0.3% using an analysis of variance (ANOVA) method according to ISO Guide 35,88 and in which both the charge-collection measurement in the ion implanter and the post-implantation electrical characterisation of sheet resistance by four-point-probe (4pp) measurements were separately demonstrated accurate at, respectively, 1.1% and 1.5% (where all numerical error estimates are standard combined uncertainties). To make 4pp measurements the silicon must be annealed to activate the As atoms, that is, to make them substitutional in the Si lattice so they can act as electrical dopants. Thus, 4pp measurements involve further processing.
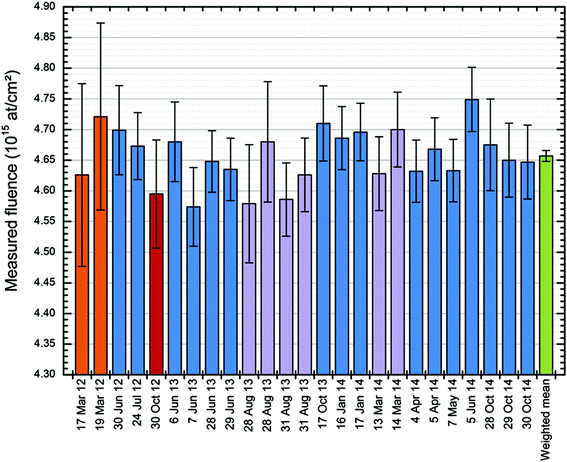 | ||
Fig. 5
RBS repeatability. Repeated independent measurements of the retained 75As dose in the sample measured by Jeynes, Barradas & Szilágyi.73 25 independent fluence measurements of the same sample by RBS over a 31 months period using various incident beams: 9 MeV 12C4+ (in orange); 4 MeV 7Li2+ (in red); 2 MeV 7Li2+ (in purple) and 1.5 MeV 4He+ (in blue). The error bars are given for each measurement as the “Total combined standard uncertainty”. The weighted mean of the measurements (in green) has a precision (standard error on the mean) of 0.19%. The dataset has a standard deviation of 0.93%. ANOVA shows repeatability (the between-bottle variation, in ISO Guide 35 terms) of 0.33%. Reproduced from Fig. 7 of Colaux et al., Analyst, 2015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 87 with permission from the Royal Society of Chemistry (RSC). 87 with permission from the Royal Society of Chemistry (RSC). | ||
This is a remarkable result since three independent measurements of the same quantity (retained ion dose) are shown to be self-consistent, at an accuracy for each which is comparable to (or better than) current best practise. Two of the measurements (RBS and the charge collection in Faraday cups) have full traceability, with the Faraday cup measurements only equivocal because of the possibility of secondary and tertiary electrical currents disturbing the measurement. What we have demonstrated is that the Faraday cup design effectively suppresses these potential auxiliary currents. The third (4pp) shows an excellent relative consistency, with the absolute values depending on a calibration curve (converting sheet resistance to implanted dose: this is VIM terminology89) that is determined by our results. Thus, that the three datasets are demonstrably mutually consistent is itself a fact rich in information.
This accuracy for the 4pp and charge-collection are demonstrable only because both the reproducibility (0.3%) and the accuracy (1%) of the RBS are sufficiently good. The uncertainty of these RBS measurements is thoroughly evaluated through an uncertainty budget (“bottom-up” approach) which has been validated against an analysis of variance (ANOVA; “top-down” approach) of a longitudinal study.87 The RBS accuracy is traceable to an ion implanted certified reference material (CRM) manufactured and certified90,91 by IRMM§ & BAM,¶ through the use of the “stopping power factor” ([ε0]Si in eqn (2) of Fig. 4) of the ion beam in silicon as an intrinsic measurement standard (again using VIM terminology89) whose value was established separately (Colaux & Jeynes92).
RBS is sensitive to the ion beam energy since the Rutherford cross-section goes as 1/E2: we also show how to directly measure this beam energy (at 0.03% accuracy),93 using the well-established nuclear resonance at 3038.1 keV of the 16O(α,α)16O elastic scattering cross-section function as another intrinsic measurement standard. See §3.3 for a discussion of the non-Rutherford scattering cross-sections.
This is the case for the scattering angle of detection which is often (approximately) derived from the schematics of the analysis chamber. That is clearly not good enough for accurate RBS when an error of 0.5° gives a variation of about 1% in the RBS cross-section (σ in eqn (1) of Fig. 4) calculated at a backscattering angle of 150°. For non-Rutherford scattering the effect can be larger (see Fig. 10).
Another very good example is the linearization of the acquisition chain through the use of a proper model of the detector, which always has an entrance dead layer in which the particle loses some energy, with the energy loss being a function of the particle energy. Therefore, the detected pulse height is not a linear function of the incident particle energy: this effect is known as the pulse-height defect (PHD). This seems obvious but historically has only rarely been applied, precisely because RBS is very linear even neglecting this correction. Colaux & Jeynes95 have shown that in their conditions the linearization correction is about 1%, but also that the presence of such an error makes the determination of the spectrometer gain (Δ in eqn (2) of Fig. 4) effectively uncontrollable in detail, so that the precision may easily be worse than 2%. Thus, simple unlinearised RBS works perfectly well at 5% accuracy for a given beam energy, but much more care must be taken to take advantage of its intrinsically high precision (<0.5%). We do this systematically, following a detailed calibration procedure93,95 and using a very well characterised code (discussed below in §3.4).
For a given beam energy the non-linearity of the spectrometer is not so easy to detect, being rather a small effect; Fig. 6 shows an example where it is plainly visible in a simple case where the interpretation of the RBS spectrum is obvious. The maximum scattered energy from Si and N atoms at the sample surface (channel numbers 300 & 160) is readily calculated from the kinematics: assuming linearity this immediately gives the apparent spectrometer gain (in keV per ch). It is when the beam energy is changed that the non-linearity becomes impossible to ignore. The spectrometer gain ought to be a constant if the instrument is undisturbed, but if the PHD is disregarded the gain is apparently not constant against changing energy. Colaux & Jeynes95 calculate that neglecting the PHD when changing the energy from 3 MeV to 1.5 MeV leads to a gain change of 0.3% – a substantial fraction of a channel through most of Fig. 6 and very visible indeed! This is discussed further below (§3.3 and Fig. 11).
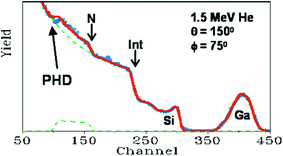 | ||
Fig. 6
Non-linearity of the RBS spectrometer. The sample is a 75 × 1015 Ga cm−2 implant at 75 keV into a 125 nm SiNx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H thin film grown on Si. The detector is placed at a backscattering angle of 150° and the sample normal is at 75° to the beam direction. “Int” labels the SiNx/Si interface as seen in the Si signal. The spectrum (red: calculated assuming linearity) fits the data (blue) perfectly except for the N interface signal (arrowed). “PHD” is the pulse-height defect (see text). Adapted with permission from Fig. 1 of Jeynes et al., Anal. Chem., 2012 H thin film grown on Si. The detector is placed at a backscattering angle of 150° and the sample normal is at 75° to the beam direction. “Int” labels the SiNx/Si interface as seen in the Si signal. The spectrum (red: calculated assuming linearity) fits the data (blue) perfectly except for the N interface signal (arrowed). “PHD” is the pulse-height defect (see text). Adapted with permission from Fig. 1 of Jeynes et al., Anal. Chem., 2012![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73 (©2012, American Chemical Society); after Fig. 6 of Jeynes et al., J. Phys. D: Appl. Phys., 2003.3 © IOP Publishing (reproduced with permission, all rights reserved); and redrawn from Nucl. Instrum. Methods Phys. Res., Sect. B, 148, Barradas et al., RES and ERDA study of ion beam synthesised amorphous gallium nitride, 463–467, (©1999),94 with permission from Elsevier. 73 (©2012, American Chemical Society); after Fig. 6 of Jeynes et al., J. Phys. D: Appl. Phys., 2003.3 © IOP Publishing (reproduced with permission, all rights reserved); and redrawn from Nucl. Instrum. Methods Phys. Res., Sect. B, 148, Barradas et al., RES and ERDA study of ion beam synthesised amorphous gallium nitride, 463–467, (©1999),94 with permission from Elsevier. | ||
At present, the accreditation is for the very limited case of heavy implants in silicon, since we depend on the stopping power factor [ε] (given by the energy loss in silicon; [ε] is accurately known for 1.5 MeV He in Si from a measurement traceable to an Sb-CRM implant92), where [ε] is used as an intrinsic measurement reference standard, thereby removing the need for the difficult measurement of the collected charge and the detector solid angle (QΩ in Fig. 4). However, we have shown that all the parameters of the measurement are well defined (and that the spectrometer is accurately linear when treated correctly), and therefore that the uncertainty budget is very well determined and robust. In particular, the beam energy and the spectrometer gain can now both be determined reliably at very high accuracy.
The case treated so far is rather restrictive, but is actually rather easy to generalise. This can be done at least two ways: by accurate charge measurement (giving QΩ since the detector solid angle Ω is an apparatus constant), or by scanning the beam between the sample to be certified and a standard. Both of these are entirely feasible with present technology (even if the QΩ determination remains notoriously difficult to achieve at better than 5%), and we expect to report high accuracy measurements of thin film foil thicknesses soon: this would be directly relevant for XPS and XRF communities that need reference standards certified at higher accuracy than is currently available to refine the current “Fundamental Parameters” values (see §3.2).
Note that such improvements in knowledge of the FP values would also be directly relevant for the IBA community since they are needed for validly interpreting the PIXE spectra complementary to (accurate) RBS (see Table 3 and §3.4.1) and are always available where an ion beam is used as a primary probe. The cross-sections for X-ray production nevertheless require one to use rather high incident beam energies for which the RBS formalism often breaks down. The knowledge of the (non-Rutherford) elastic backscattering (EBS) cross-sections therefore becomes essential for an accurate analysis of EBS spectra. This is discussed in §3.3.
3.2 EXSA's “Fundamental Parameters Initiative” for XRF methods
Modern analytical methods depend on extensive and detailed knowledge of material parameters. Depth profiling by IBA depends on a single (large) semi-empirical electronic energy-loss database (see §3.1.1). In contrast, the XRF techniques (XRF, PIXE, EPMA) depend on (at least) three large and complex databases of the “Fundamental Parameters” (FP) that enable the accurate calculation of the ionisation, fluorescence and absorption cross-sections; these databases were originally established in the 1980s as a result of a huge quantity of first class work by both theoreticians and experimentalists.But analytical requirements have become much more stringent than a generation ago, with the advent of a clutch of new and relatively complex functional materials (just as one class of examples). And it has become clear that the databases that have served us well for a generation now need revisiting: the European X-ray Spectrometry Association (EXSA) has perceived a “lack of recent reliable values with low associated uncertainties”, and since 2008 has been promoting its “FP Initiative” to address this lack. In this section we briefly introduce the necessity for an FP approach to XRF, and the new work that is improving and underpinning analytical accuracy.
Fig. 7 shows extraordinary data collected on Mars and analysed on Earth to determine Martian geochemistry. This is a tour de force of analysis which depends on very careful calibration and handling of the X-ray data, summarised for the MSL team in a pair of recent Science papers,98,99 where the details of the calibration are explained by Campbell et al. in an important paper in 2012.100
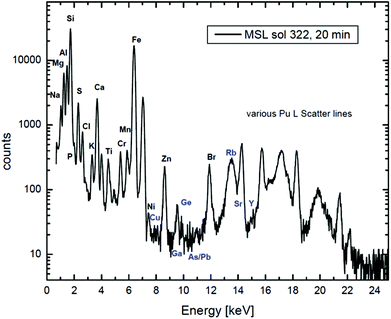 | ||
Fig. 7
XRF + PIXE spectrum collected on Mars. A 20-minute X-ray spectrum of a rock measured by the alpha-particle X-ray spectrometer (“APXS”) on the “Mars Science Laboratory” (MSL) in Gale Crater on the 322nd Martian day of the mission. A 244Cu source on the APXS emits both 5.8 MeV alpha particles and Pu L X-rays (14–20 keV) from the excited daughter products of Cm decay. The low energy lines in the spectrum are generated largely by α-PIXE, and the high energy ones by Pu L-XRF. Large peaks for Rayleigh and Compton (elastic and inelastic) scattering of the incident Pu L X-rays are also present. Reproduced from Fig. 1 of Gellert & Clark, Elements, 2015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 97 by permission of GeoScienceWorld. 97 by permission of GeoScienceWorld. | ||
It is worth noting here that there is an interesting philosophical difference between PIXE and RBS. The abscissa units for Fig. 1 are the instrumental “channel number”, where those for Fig. 7 are in absolute energy units (keV). This is because PIXE spectra show characteristic lines of the elements, where the line energies are natural constants (apart from tiny chemical shifts invisible at this energy resolution): the abscissa calibration is determined by the spectrum. But for the nuclear techniques the spectra show energy loss, and the interpretation of the spectrum depends on the spectrometer calibration, which must be done separately (see §3.1.3 and the discussion for Fig. 6). To give an RBS spectrum with the abscissa in keV interprets the data, whereas a PIXE spectrum in keV is still effectively raw data.
XRF has historically used sample-matched standards for accurate analysis but it was recognised very early that for homogeneous samples the composition could be unfolded from the XRF spectra – provided the appropriate fundamental parameters were known. The problem is that the calculation is complicated; moreover, not only the databases but also their interactions are intricate. A compromise was the use of the semi-empirical approach (the so-called “ZAF correction”, involving the atomic number, the self-absorption of the sample, and the self-fluorescence). In the presence of all these uncertainties, analysts always used sample-matched standards for accurate work: in the absence of such standards it is very difficult to be sure of the reliability of the estimates of uncertainty.
Therefore, this work on Mars data, where “sample-matched standards” are in principle not available, must use a pure Fundamental Parameters (FP) method.101 And the MSL team are explicit that the data reduction is for unknown samples.102
Recent FP work includes obtaining L-shell103 and K-shell104 parameters for germanium, mass attenuation coefficients for silicate minerals105 and aluminium,106 widths of energy levels,107,108 L-shell fluorescence yields,109 the K-shell fluorescence yield of Si,110 and the photo-ionisation cross-sections for light elements.111 Systematic K, L, & M-shell ionisation cross-sections for H+ and 4He2+ beams are now available112,113 and much interesting new information is becoming available (using high energy resolution detectors) on chemical effects on line positions114 (WDX) or intra-shell branching ratios115 (HR-EDX). The latter uses the new transition-edge sensors operating at ∼100 mK which are presently capable of an energy resolution <2 eV at 6 keV but which give the full EDX spectrum. This means that it is easy to obtain good data on the intensity ratios of diagram lines, very difficult for WDX because of the limited energy range of each measurement. There is now intense development of this highly promising technology: see, recently, Palosaari et al.267
We mentioned above (§2.2) that depth information in XRF (or in PIXE by itself) cannot be obtained directly. Strictly speaking the same applies to determining Quantity of Material, since the ZAF correction must always be applied for good quantification, which cannot be done without knowledge of film thicknesses. So, regular EPMA work,116 or commercial XRF quantification using fused glasses117 assume homogeneous samples of infinite thickness. But recent sy-XRF work on biological samples (Turnbull et al.118) makes tacit assumptions which very significantly reduce the information available relative to comparable recent IBA work (Jeynes et al.119), especially since XRF data are not so rich as IBA data.
Turnbull et al. map the elemental distribution using sy-XRF in large numbers (204) of human cancer cells with the aim of counting the number of gold nanoparticles (GNPs) the cells have taken up under different irradiation conditions. Analytically, they identify cells through their Cu content and assign Au L counts per cell through this identification. Experimentally they obtain a high count rate by using the Maia detector, and quantify the XRF through standards in the usual way using the GeoPIXE code (for Maia and GeoPIXE, see §3.4.2: it is “trivial” to add an XRF module to a PIXE code, only the excitation mechanism is different), ignoring absorption effects which are assumed to be small for these relatively high energy X-rays. But because they only roughly determine the spatial extent of the cells, they have no reliable means of normalising the GNP content per cell to the cell size.
On the other hand, Jeynes et al.119 have made a more extensive study using Total-IBA (PIXE + EBS), also on (a different line of) human cancer cells. They map the elemental distribution in large numbers (332) of cells, but obtain a mass closure close to 100% since they measured the light elements (except H) directly. In particular, because the C and P (and S) signals are clearly identifiable, they can weigh each cell individually as well as counting the GNPs per cell. They are therefore able to explore much more thoroughly the inhomogeneity in the GNP uptake that was of interest to Turnbull et al.118 (also obtaining the cell size inhomogeneity directly): and specifically, showing that it conforms to the Hill equation.120
Turnbull et al. measure gold heterogeneity in the cells but this measurement takes no account of cell-size heterogeneity. They measured Cu as a proxy for cell size, but this may be a poor proxy, both because the signal is small (giving large counting statistics uncertainties) and because the Cu concentration in cells is also subject to a large variation (being regulated by external factors). In contrast, Jeynes et al. do not use a proxy for cell size, measuring C (and P + S) directly from the particle spectrum. Such a measurement is not available by XRF. In this case where the sample is known to be thin, the fact that XRF cannot correctly do the ZAF correction in the general case (because it is blind to sample thickness) is not important.
Interestingly, the sy-XRF and the IBA are analytically rather similar, with comparable detection limits for GNPs, and similar spatial resolution. The sy-XRF had much shorter counting times due to the much more sophisticated (and expensive) Maia detector which is so much faster than the standard lithium drifted silicon detector used by the IBA group. Critically, the XRF had neither light element nor depth sensitivity, and therefore could not have corrected for the absorption effects had they been significant. It is notable that Turnbull et al. emphasise the importance of single-cell measurements and therefore the advantage of spatially resolved analysis, but they appear unaware of the prior IBA work, comparing only to bulk analysis methods.
3.3 Evaluated elastic backscattering (EBS) cross-sections
In Rutherford's 1911 treatment, the eponymous RBS assumes point charges in a Coulomb field. But as the beam energy increases, the distance of closest approach of the two nuclei decreases. What happens when this distance becomes comparable to the nuclear size? Clearly “RBS” is always an approximation: the questions are, how good is this approximation? and when does it completely break down? Parenthetically, it is interesting that of course Rutherford himself did a “classical” calculation, but the RBS cross-section also results from a quantum mechanical calculation of Coulomb potential scattering.We mentioned above (§1) the large resonance in the 11B(p,γ)12C nuclear reaction at 163 keV: Fig. 8 shows that this resonance results in a non-zero reaction cross-section down to very low energies. The cross-section functions are given in terms of the astrophysical S factors (in keV·barn) which are effectively normalised to eliminate the exponential decrease of reaction rates at projectile energies below the Coulomb barrier as the beam energy decreases. This normalisation is needed since these reaction rates are dominated by the probability for barrier penetration. The differences between “Solution 1” and “Solution 2” in Fig. 8 are due to the detailed low energy effects of quantum mechanical interferences between higher energy states, and these effects are very sensitive to the details of the calculation, meaning that the low temperature behaviour is very difficult to determine.
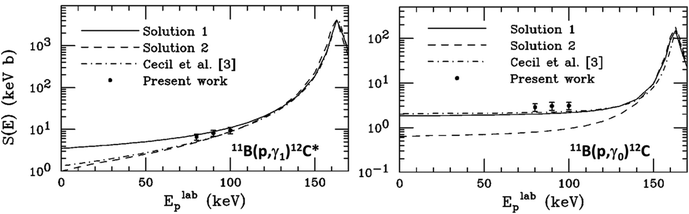 | ||
| Fig. 8 Proton capture cross-sections for 11B, in astrophysical units. Elabp is the proton energy in the laboratory (not “centre of mass”) frame of reference. See text for discussion of “solutions” 1 & 2. Left: Capture to the first excited state of carbon; right: capture to the ground state of carbon. Note on nomenclature: 11B(p,γ)12C means that a proton beam is used on a target containing 11B, and that there is in this case a proton-capture reaction resulting in a 12C atom with the gamma-ray to take away the extra energy. Inside the brackets are the probing and the measured particles, and outside are the target and resulting atoms. Reprinted (Fig. 3b & 5b) from Kelley et al., Phys. Rev. C, 62,121 ©2000, with permission by the American Physical Society. | ||
Recall that the core temperature of the Sun (for example) is surprisingly low: 16 × 106 K is only 1.4 keV! But even at this ridiculously low temperature nuclear reactions still proceed – very slowly! Of course, it is just as well that the reactions are slow, otherwise the Sun would not have been burning steadily without any noticeable change for 4 billion years. And we would not be here to talk about it!
Nevertheless, one might have thought (see §3.1) that it was valid to use Rutherford scattering cross-sections for 1.5 MeV 4He beams because the Coulomb barrier prevents nuclear effects on the cross-section. But this is not the reason, as is shown by Fig. 8 and many other data besides. RBS is valid simply because nuclear tunnelling effects are small. The question of how small they are, and where exactly the boundary lies between effectively Rutherford and measurably non-Rutherford elastic scattering, is still an open question even though much systematic work has been done on measuring the elastic backscattering (EBS) cross-sections in the last decade or so. This work was coordinated by the International Atomic Energy Agency (the IAEA), and was aimed at creating a reliable elastic scattering cross-section database.122
Fig. 9 shows results of this IAEA-sponsored work for protons, and summarises the current rather incomplete knowledge of the Rutherford/non-Rutherford “boundary”. It shows that there remain substantial gaps in the data with some isotopes unmeasured and some measurements not extending to low enough energies. It also shows that there are no easy approximations (such as the “optical model”) that give reliable general estimates of the boundary position, not even for the apparently undemanding “4%” criterion – it is only in the absence of any other information that this “optical model” may sometimes be a useful indicator. The optical model almost always substantially overestimates the boundary energy since it ignores the effect of resonances on the scattering.
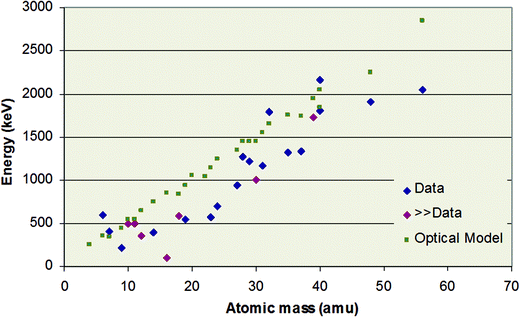 | ||
| Fig. 9 Energy at which proton scattering cross-section deviates from RBS by 4%. “Data”: measured values; “≫Data”: measurements not available, but boundary known to be (much) lower than the point shown; “Optical Model”: semi-classical quantum mechanical calculation of the potential part of the scattering. Data republished with permission of World Scientific Publishing Co., Inc., from Table 1 of “Ion Beam Analysis: A century of exploiting the electronic and nuclear structure of the atom for materials characterisation”, Jeynes, Webb & Lohstroh, Rev. Acceler. Sci. Technol., 2011, 4;123 permission conveyed through Copyright Clearance Center, Inc. | ||
In Fig. 9 the “boundary” is defined as a 4% deviation from Rutherford. A comparable figure for a 1% deviation is not yet possible to draw since, as Fig. 8 shows, the effect of nuclear structure below the Coulomb barrier cannot yet be reliably modelled in the absence of experimental data. Thus, at present we cannot achieve “1% RBS” for a proton beam using the methods of §3.1 above.
Whereas Fig. 9 is for protons, for alphas (with a much higher Coulomb barrier) the Rutherford regime is both larger and better defined. But Fig. 10 shows that nuclear structure can also be probed with alphas at energies easily accessible with a 2 MV tandem accelerator. In particular, there is a very strong resonance at about 3.7 MeV for elastic scattering from nitrogen, where the cross-section is up to 9 times Rutherford: this is often used for extra sensitivity to N.
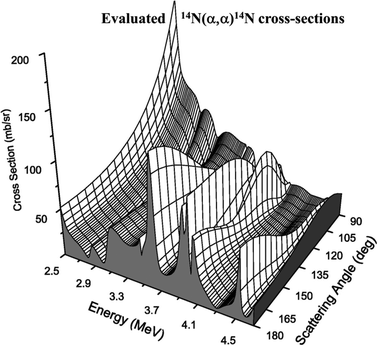 | ||
| Fig. 10 Evaluated EBS cross-sections for alphas on nitrogen. See Fig. 8 caption for explanation of 14N(α,α)14N, the elastic scattering of alphas from 14N. Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 269 (Fig. 4 of A. F. Gurbich et al., Measurements and evaluation of the cross-section for helium elastic scattering from nitrogen, 40–44, ©2011),124 with permission from Elsevier. | ||
Fig. 10 shows that EBS cross-sections can be very strong – and apparently arbitrary – functions of both beam energy and scattering angle. As for the electron mean free path in XPS (see §2.1), these cannot be calculated sufficiently accurately for analytical purposes by the theoretical physicists, and there is at present no reasonable prospect that they will be calculable, even in the medium term. These data must be measured! But from an analytical point of view, measuring this sort of function is a nightmare since repeated measurements with slightly different parameters can give wildly different values, which are completely unpredictable in the absence of a model.
What has changed in this century is the steady increase in the availability of “evaluated” cross-section functions, now available on the “SigmaCalc” website (http://sigmacalc.iate.obnisk.ru/)125. Since there already exists a very well articulated theory of nuclear interactions it is “straightforward” (for skilled nuclear physicists!) to specify a nuclear model accounting for the observed cross-sections. The nuclear model used for the evaluation shown in Fig. 10 is widely agreed (see Bailey et al.126): such models have many parameters, as can be seen from the case of 28Si(α,α)28Si reaction (involving the 32S compound nucleus, see Table 2).127 What is interesting is that constructing a detailed nuclear model sufficiently accurate for analytical purposes usually cannot be done from the existing, apparently comprehensive, compilations of nuclear data. In the 28Si + α case initial data taken from the literature (regarded as authoritative: see Table 2) were significantly changed quantitatively – and even qualitatively in the assignment of quantum numbers – in the effort to accurately fit the observed cross-section data.
| E lab | E x (keV) | J π | Γ (keV) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| keV | NPA1990 | NDS2011 | Surrey | NPA1990 | NDS2011 | Surrey | NPA1990 | NDS2011 | Surrey |
| Potential scattering was calculated by Gurbich (2014) with a Saxon–Woods real potential well requiring additional parameters; the “hard sphere” approximation was not used. The table shows only the parameters for the Breit–Wigner resonances. Elab is the energy of the resonance in the laboratory frame. Ex is the excitation energy of the compound nucleus. Jπ is the spin quantum number and the parity. Γ is the total resonance strength. NPA1990: Endt, Nuclear Physics A (1990);131 NDS2011: Ouellet & Singh, Nuclear Data Sheets (2011)132 relies entirely on Källman, Zeitschrift für Physik A (1996);133 Surrey: Gurbich & Jeynes, Nuclear Data Sheets (2014)127. | |||||||||
| 3876 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 332 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369 369 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
1− | (0+) | 1− | 6.1 | 5.8 | 3.6 |
| 4059 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
0+ | (0+) | 0+ | 1.7 | 1.7 | 1.7 |
| 4139 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 550 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
0 | (0+) | 0+ | 8 | 1.2 | 1.2 |
| 4200 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 701 701 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658 658 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623 623 |
1− | (1−) | 3− | 21 | 2.3 | 1.3 |
| 4309 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 769 769 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 745 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718 718 |
2− | (0+) | 0+ | 5.1 | 8.9 | 8.9 |
| 4381 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 816 816 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 781 781 |
0 | (3−) | 3− | 4.7 | 3.3 | ||
| 4430 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826 826 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868 868 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 824 |
1− | (2+) | 0+ | 22 | 7.7 | 4.7 |
| 4540 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916 916 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956 956 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921 921 |
1− | (0+) | 0+ | 1.6 | 2.9 | 1.9 |
| 4693 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 104 104 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 054 |
0 | (2+) | 0+ | 67.4 | 0.6 | ||
| 4821 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 140 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166 166 |
1+ | (0+) | 5− | 2.6 | 1.8 | 67.0 |
| 4900 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249 249 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 236 236 |
0 | (3−) | 2+ | 1.1 | 2.1 | ||
| 5069 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 410 410 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 383 383 |
0 | (3−) | 5− | 1.9 | 0.6 | ||
Many nuclear model calculations of such low energy data are today done by the astrophysicists (see Fig. 8) who are interested only in estimates of total cross-sections (that is, integrated over all scattering angles). Analysts on the other hand, are interested in accurate values for differential cross-sections (that is, for specific scattering angles). Dramatic and continuing advances in the availability of evaluated cross-sections of sufficient accuracy for analytical purposes are well appreciated from the 2010 review of Gurbich,128 and the summary of the IAEA CRP.122,129
It is clear from Fig. 8 that accuracy is needed for astrophysical calculations to allow extrapolation to the interesting low energy region where measurement is very difficult (since the cross-sections are so small). The “R-matrix” formalism for calculating the resonance part of the reaction cross-section can be adapted successfully to also account for the potential part (using the AZURE code130) even though this is rather arbitrary from a physical point of view: AZURE was not used for Fig. 10 where the potential scattering was calculated in a physically realistic approach, and separately from the resonance scattering (for which a pure R-matrix model was used).
Since fluorine is ubiquitous but notoriously hard to analyse by other methods, the proton-fluorine nuclear reactions are important. But accurate IBA is difficult because so many channels are open at the same time, with 19F, 16O and 20Ne as potential final states. As a multi-channel code, AZURE has been found useful to calculate these cross-sections,134 although these preliminary calculations have so far served only to highlight experimental discrepancies.
Turning from the cross-sections in themselves to their use, Fig. 11 shows a far-reaching example of EBS. We indicated the importance of calibrations above (§3.1.3): this very simple sample can establish both the spectrometer gain (together with its non-linearity) and the accelerator terminal voltage. RBS spectra are exactly self-similar as the beam energy changes, provided the (slow) variation of energy-loss with energy and the spectrometer non-linearity are neglected – both rather small effects. But an EBS spectrum is very sensitive to beam energy where a sharp resonance is excited. In this case there is a strong resonance only 10 keV wide for the 16O(α,α)16O reaction at 3038.1 ± 1.3 keV which we have used to determine the terminal voltage. We have also independently established this reference energy,93 and shown it is consistent with the nuclear physics compilations.135
 | ||
Fig. 11
Energy calibration by resonance EBS. The Si and metal signals are Rutherford at these energies, but the O signal (superimposed on the silicon substrate signal) displays the effect of the 3038 keV resonance of the 16O(α,α)16O reaction. The signals for the elemental “edges” and interface signals are marked. The sample is approximately 20 TFU Au on 50 TFU of Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu = 9 Cu = 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, on 2000 TFU SiO2 on a silicon substrate (3.4 nm Au, 5.5 nm Ni 1, on 2000 TFU SiO2 on a silicon substrate (3.4 nm Au, 5.5 nm Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu, 302 nm SiO2 at 2.2 g cm−3). The Ni Cu, 302 nm SiO2 at 2.2 g cm−3). The Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu ratio is verified by PIXE. Note on thin film units (TFU): 1 TFU ≡ 1015 atoms/cm2. TFUs are density-independent thickness units, equivalent to mass/area. For silicon, 1 TFU is 2 Å. Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 349 (Fig. 1 of Colaux, Terwagne & Jeynes, On the traceably accurate voltage calibration of electrostatic accelerators, 173–183, ©2015),93 with permission from Elsevier. Cu ratio is verified by PIXE. Note on thin film units (TFU): 1 TFU ≡ 1015 atoms/cm2. TFUs are density-independent thickness units, equivalent to mass/area. For silicon, 1 TFU is 2 Å. Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 349 (Fig. 1 of Colaux, Terwagne & Jeynes, On the traceably accurate voltage calibration of electrostatic accelerators, 173–183, ©2015),93 with permission from Elsevier. | ||
3.4 Spectrometry Software for IBA
| Quality | Strong | Weak |
|---|---|---|
| Depth resolution | RBS: direct from energy loss | PIXE: weak indirect (integral) effect |
| Quantification | RBS: analytical, standard-less: readily traceable accuracy to 1% | PIXE: fundamental parameters (∼10%), but best accuracy from sample-matched standards |
| Sensitivity | PIXE: typically a few mg kg−1 | RBS: poor signal/noise due to overlaps |
| Mass resolution | PIXE: spectroscopic technique | RBS: smaller kinematical separation for higher masses, all signals overlap at depth |
In this section we first explain the different codes, emphasising the startling improvements in the last few years. We then describe the – equally startling – recent advances in integrating the atomic and nuclear methods.
GeoPIXE137 (the PIXE program from Melbourne) is designed for mapping geological samples and is now also used not only for PIXE but also for sy-XRF (with “Maia”, a large-solid-angle detector array), again underlining the PIXE/XRF commonality. There are an important pair of recent papers on fluid inclusions (very important indicators of the richness of deposits to the economic geologists), the first by PIXE138 and the second by sy-XRF:139 both using GeoPIXE. Note that in the standard case IBA is richer (and therefore intrinsically superior) to XRF (see §3.2).
We should point out that the Monte Carlo GEANT4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140,141 (“GEometry ANd Tracking”) code developed by CERN is widely used, and not only in the accelerator community: this now also has a PIXE module.142
140,141 (“GEometry ANd Tracking”) code developed by CERN is widely used, and not only in the accelerator community: this now also has a PIXE module.142
We should also mention that there is also an entirely independent multilayer PIXE code from Lisbon143 that has now been incorporated in the nuclear IBA code DataFurnace (see §3.4.4) and is still under vigorous development.144
DataFurnace3,151 is a fitting and simulation program (from Guildford & Lisbon), also well-supported150 and with a very wide applicability, including to the JET programme149 (see §4.5 and Fig. 21, and also Fig. 1, 4, 6, 11 for other examples). These two independent codes (SIMNRA and DataFurnace) have been systematically validated against each other and against other IBA codes in an IAEA-sponsored Intercomparison exercise,152,153 which identifies these two as the “New Generation Codes”. In particular, they agree with each other to better than 0.2% for RBS, with this difference being largely due to rounding errors in the numerical integrations. This could be improved if further advances in the technique accuracy and precision (see §3.1) make it worthwhile. Note that this agreement is not trivial since even RBS, the simplest analytical method, has much subtlety at second and third order.73,92 This is exemplified by Fig. 12 which shows not only that excellent depth resolution is available in the surface 20 nm or so but also that even rather complicated spectra are understood in great detail (Fig. 1 tells the same story!).
 | ||
| Fig. 12 Glancing incidence RBS of a tribological coating on Si. The coating is a TiAlN/Mo multilayer, with a modulation period of 3.9 nm. Second order effects are: pulse pileup (“pup”), multiple scattering (“MS”), double scattering (“DS”), roughness, and low energy yield corrections. Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 266 (Fig. 1 of Barradas & Jeynes, Advanced physics and algorithms in the IBA DataFurnace, 1875–1879, ©2008),150 with permission from Elsevier. | ||
Fig. 12 shows that it is a good approximation to assume single scattering: that is, the incident particle is assumed to travel unperturbed into the material to the reaction site where it scatters off a target atom, and then to travel back out of the material also unperturbed until it exits the material and enters the detector. Thus RBS is qualitatively different from electron backscattering which is used systematically on the SEM for Z-contrast, but which cannot be treated quantitatively due to the intractability of the multiple scattering. But for RBS, even in glancing incidence (θ = 5° in Fig. 12), the single scattering approximation is fairly close to reality, with multiple and double scattering (MS & DS) being second order effects adequately accounted for by analytical approximations. On the other hand, single scattering is no longer a good first approximation for Heavy-Ion Elastic Recoil Detection (HI-ERD) since the MS and DS effects are now large. These can be effectively handled only by Monte Carlo codes, and HI-ERD is now well supported by such a code: CORTEO154 is a new code from Montréal with a good user interface, making HI-ERD accessible to analysts (see §3.5).
Fig. 1 shows a heavy contaminant in the optical multilayer: it is known that Hf is always present with Zr, and Hf fits the observed signal. But PIXE would have positively identified Hf spectroscopically. Again, in Fig. 11 the Ni signal looks strange: it cannot be fitted convincingly with pure Ni. But the PIXE shows that Cu is also present. In these cases we need only the element identification from PIXE, but the PIXE signal is also very well fitted, thus providing an independent confirmation that the interpretation of the data is correct. Grime's OMDAQ code from Oxford157 did this in 1995, using GUPIX for the PIXE data with layer thickness information supplied to GUPIX from a simplified EBS code (see §4.4.2).
Of course, PIXE data on their own are always highly ambiguous for samples not homogeneous in depth (and the same applies to XRF, EPMA and comparable techniques). It should be easy to see that PIXE and RBS spectra can interpret each other so that the depth profile can be obtained from a synergistic analysis where the problem would be intractable if the data were treated separately. We demonstrate that in detail below (§4).
DataFurnace was designed to handle multiple spectra self-consistently, it was always used for multiple detectors, multiple beams and multiple techniques so it was easy to add a PIXE module. SIMNRA was designed to handle only single spectra so a self-consistent analysis of multiple spectra (of any sort) was always troublesome. But this problem has now started to be addressed in a fundamental way (“MultiSIMNRA” from Silva et al.158), although a PIXE module is not yet available.
We should also mention the very new open-source “Virtual IBA lab” (VIBA),159 which is a modular simulation program for PIXE, RBS and other techniques as more modules become available. MultiSIMNRA may well incorporate the PIXE module of VIBA in the future.
Lastly, we point out that with a scanning microbeam the lateral imaging has a spatial resolution given by the ion spot size (deep sub-micron160) and that consequently tomographic methods should give the full 3-D sample composition reconstruction. Tomography seems slightly outside our scope, but it is central in the use of the scanning microbeam and this will be discussed later (§3.8).
3.5 Heavy-ion elastic recoil detection (HI-ERD)
Detection of the elastic recoils in the scattering process has the great advantage that the mass overlaps intrinsic to RBS spectra can largely be avoided. This is because, where in RBS the detected backscattered particles are all necessarily scattered out of the primary incident beam and therefore distinguishable only by their energy (resulting in the mass-depth ambiguity discussed in §3.9), in ERD the detected particles are recoiled from the sample, and can therefore in principle be sorted by mass. Even though exactly the same scattering process is in view, ERD and RBS are qualitatively different since the purpose of the ERD detector is to distinguish the different atoms recoiled out of the sample (and to discriminate the primary scattered beam), where in contrast the RBS detector only sees backscattered primary ions.Classical ERD uses a so-called “range foil” to stop the scattered (high intensity) primary beam161 while being transparent to high energy recoils; a single simple detector sufficed to energy-analyse the recoils. This arrangement has several disadvantages: the range foil necessarily degrades the available depth resolution; the various recoil signals for different masses usually overlap in the simple energy spectrum, degrading the signal/noise; and heavy recoils rapidly damage silicon detectors. However, it does have the enormous advantage of great simplicity, and if it is only sensitivity to hydrogen that is required a standard helium beam can be used (simultaneously with RBS162). In this case only hydrogen isotope recoils have the energy to penetrate the range foil, so the standard silicon detector may be used without damage and there is no signal/noise problem. This simple method remains important163 because hydrogen is otherwise difficult to depth profile quantitatively, and because it is very easy to combine with standard RBS.
However, over the last few years great advances have been made in the instrumentation of more complex detectors able to analyse recoils for mass as well as energy. Fig. 13 shows an example of Kr-ERD compared directly to He-RBS. This explains the dramatic contrast between ERD (Fig. 13a) and RBS (Fig. 13c) in the raw data collected: He-RBS is the energy spectrum of the backscattered ions where the Kr-ERD is a set of energy spectra for each of the recoiled masses, and in this case the (forward) scattered ion is also seen. Of course, there is no Mo recoil signal since it is kinematically forbidden into this recoil angle, but the Mo content is obtained from the scattered primary Kr signal just as for RBS.
 | ||
| Fig. 13 Heavy-ion ERD analysis of a (Cr,Mo)O2 coating on Si. (a) Time-of-flight (ToF) ERD plot using 27.5 MeV 84Kr15+ primary beam incident at 15° grazing angle with the ToF telescope at a recoil (or scattering) angle of 30°. (b) Mass discriminated energy spectra from ToF ERD detector: the raw data (a) are projected onto the X-axis. (c) RBS spectrum with primary beam of 2 MeV 4He2+ in normal incidence, with the detector at 160° scattering angle. (d) Depth profile derived from the HI-ERD data using CORTEO (§3.4.3). The (Cr,Mo)O2 film has thickness ∼2500 TFU or ∼240 nm. See Fig. 11 for “TFU”. Reprinted from Mater. Charact., 70 (Fig. 2, 4, 5, 7 of Khamlich et al., Compositional analysis and depth profiling of thin film CrO2 by heavy ion ERDA and standard RBS: a comparison, 42–47, ©2012),164 with permission from Elsevier. | ||
The great virtues of time-of-flight ERD (ToF-ERD) are the high sensitivity to low-Z contaminants, and also, for relatively low energy primary beams, a very high depth resolution (∼1 nm)165 which is improved for slower beams since it depends on time resolution. But it therefore depends on a reliable energy detector sensitive to these slow ions. The thin window gas ionisation chambers which have only recently become available (§3.6) are a notable detector breakthrough for this application.166
HI-ERD has a high depth resolution because a glancing geometry is used and because the energy loss for heavy ions is high. So ERD is valuable for atomic layer deposition (ALD) among many other applications. Uniform conformal films with excellent thickness controllability can be grown by ALD. As one example, iridium metal is used in optics (Fresnel zone and microchannel plates) and its oxide is biocompatible and also used as an electrode for pH measurement: Ir and IrO2 ALD films between 20 and 50 nm thick were characterised by 8.5 MeV Cl-ERD to directly obtain the Ir/O ratio and the C & H contamination.167 In another example, Nb2O5 (a wide bandgap dielectric material with high permittivity and high refractive index) is an interesting material with a wide range of potential applications: sufficiently high purity of ∼40 nm ALD films of this oxide deposited from three different precursor materials was demonstrated by 6.8 MeV Cl-ERD168 where the required smoothness was determined by atomic force microscopy (AFM). In yet another example, efficient and manufacturable photoelectrochemical cells used a heterostructure of nickel and iron oxides that was depth profiled using XPS and 12 MeV I-ERD.169
3.6 Gas ionisation detectors of energetic particles
The energy loss methods such as RBS with proton or alpha beams have been so powerful because good energy resolution was available using silicon diode detectors. Even cheap photodetector devices work very reliably with a pretty good performance. However, as soon as heavier ions are to be detected the energy resolution becomes quite poor, and the beam rapidly damages the detector, precluding routine analysis.Gas ionisation chambers (GICs) are very well known and widely used as particle detectors: their limitation for the measurement of the energy of fast particles is that the particles have to enter the detector (with its special working gas) through a gas-tight window in which the particles cannot avoid losing energy. The great recent advance is that ultra-strong ultra-thin silicon nitride windows are now available, meaning that these detectors can now be used with high energy resolution for relatively low energy beams.170 And their enormous advantage is that there is no beam damage; this is already very valuable both for HI-ERD (see §3.5) and for STIM (see §3.8). They are also insensitive to light and can have fairly high counting rates which may prove valuable for operando methods (see §3.7).
GICs can be used with more or less complex internal electrode structures to obtain both the mass of the particle (from the spatial distribution of the ionisation) and its entrance position (from the ionisation asymmetry).171 The former means that the GIC by itself can work effectively to discriminate particle mass (essential in a recoil measurement): time of flight (ToF) methods are not required. The latter means that large solid angle detectors can be used without degrading the energy resolution since internal kinematical corrections can be applied.
However, it turns out that for backscattering of particles with relatively low energies, the GICs can be heavily simplified by eliminating most of the internal electrode structure with almost no performance penalty.172 For higher energy particles more attention must be paid to the flow of charge through the detector to the charge collection anode and a more complex electrode structure to shape the field is needed, together with a Frisch grid to improve the charge collection efficiency.173 But the new methods have been used to demonstrate a large solid angle annular backscattering detector which works equally well for heavy and light ion backscattering.174
3.7 “Operando” methods and high volume quantitative analysis
Remarkable recent work that highlights novel and powerful ways of exploring systems with complex chemistry is shown in Fig. 14. Nickel silicides are widely used in making electrical contact to complementary metal–oxide–semiconductor (CMOS) devices in the advanced integrated circuits ubiquitous today. They have been the preferred contacting material since the 2006 “65 nm technology node”, partly because a self-aligned-silicide (“SALICIDE”)175 process is available. However, their high temperature behaviour is complex and, crucially, improved by the presence of platinum. | ||
Fig. 14
Real-time RBS of silicidation of Ni(Pt) thin films. Left (2008 data): contour-plot representation of 125 He-RBS spectra acquired at 2 MeV from a 75 nm layer of Ni: 3%Pt sputter-deposited on Si and annealed at 2 °C min−1 (colour coded counts per channel). For the thick black line at 375 °C, see Centre (2008 data): 2 minute spectrum obtained at 375 °C. Right (2013 data): Activation energy data for formation of the monosilicide for five initial Ni(Pt) film compositions. These data were obtained by single ramped anneals (2 °C min−1) with operando RBS (2 min spectra reduced by artificial neural network) for each case. Below 2 atomic% Pt the activation energy is 1.5 eV, above it is 3 eV. The same values are obtained for ramp rates of 1 °C min−1. Reprinted from Fig. 2 & 3 of Demeulemeester et al., Appl. Phys. Lett., 2008, 93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 176 and Fig. 6 of Demeulemeester et al., J. Appl. Phys., 2013, 113,178 with the permission of AIP Publishing. 176 and Fig. 6 of Demeulemeester et al., J. Appl. Phys., 2013, 113,178 with the permission of AIP Publishing. | ||
Seminal information on the influence of the Pt in limiting the formation of the undesirable Ni2Si phase during annealing was obtained kinetically in 2008 using real-time RBS176 (Fig. 14), where the very large quantity of data resulting is analysed in real-time by an artificial neural network (ANN).177
The Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt/Si system is very complex: the presence of Pt has intricate effects on the interplay between the two phases, Ni2Si and NiSi, as is clear from the operando observation of the complete silicidation process (Fig. 14a), a single spectrum from which is shown in Fig. 14b where the segregation of Pt out of the di-nickel silicide and the onset of the formation of the monosilicide can be seen. Further work by Demeulemeester et al.178 on this important system has shown the sensitivity to the Pt content. They successfully applied real-time RBS (using ANNs) to disentangle the growth kinetics during the complex growth of Ni(Pt) silicides and showed that activation energies can be extracted from a single ramped real-time RBS measurement (see Fig. 14c).
Pt/Si system is very complex: the presence of Pt has intricate effects on the interplay between the two phases, Ni2Si and NiSi, as is clear from the operando observation of the complete silicidation process (Fig. 14a), a single spectrum from which is shown in Fig. 14b where the segregation of Pt out of the di-nickel silicide and the onset of the formation of the monosilicide can be seen. Further work by Demeulemeester et al.178 on this important system has shown the sensitivity to the Pt content. They successfully applied real-time RBS (using ANNs) to disentangle the growth kinetics during the complex growth of Ni(Pt) silicides and showed that activation energies can be extracted from a single ramped real-time RBS measurement (see Fig. 14c).
Complementary work on the same system has included real-time X-ray diffraction179 (XRD) and atom probe tomography180 (APT). RBS allows the phase formation and the redistribution to be followed in situ and thus gives crucial information of the different steps of the redistribution. But RBS has relatively poor depth resolution and, for these nanocrystalline materials, effectively no lateral resolution. APT is a very high resolution (ex situ) tomographic method giving highly detailed structural information. Similar to the complementarity between RBS and TEM, operando RBS gives a (rather detailed) broad overview of the entire process, where APT follows inhomogeneities at the nano-crystalline level.
We should point out that although the spectra in Fig. 14 are fairly simple, they still have a number of intricacies, including sample layer inhomogeneity (which are handled in quite a sophisticated way – see Fig. 12 or 16 for example). But the use of ANNs is not limited to these “simple” cases, or even to RBS. Energy-loss spectrometry (including RBS, EBS, ERD, NRA) is mathematically an “ill-posed” problem3 and this has meant that it has been remarkably difficult to automate. But this work shows that indeed certain sorts of problems can be automated, with the analytical difficulty now being transposed to constructing the proper training and test sets for the ANN. Barradas et al. long ago proposed “RBS without humans”;181,182 policy makers should note that this proposal has now been very well substantiated and that, for a reasonably well-defined application, the marginal cost per analysed spectrum of high-volume IBA can be very low.
We should also point out parenthetically that this work is limited as it stands to only about 600 °C annealing temperatures since semiconductor detectors are light-sensitive, but much higher temperatures could be implemented directly with the gas ionisation detectors (see §3.6).
This is an important example, but only one of many quantitative operando RBS183 observations of diffusion and phase separation during annealing of multilayer samples. What is qualitatively different here is the use of ANNs to handle quantitatively the huge datasets produced. Operando measurements can be extraordinarily efficient; indeed, readily giving details of processes that are hard (or impossible) to obtain conventionally. In situ RBS is an obvious (and old!) technique: see for example Averback et al.184 on the radiation-induced segregation of nickel–silicon alloys, or Rennie et al.185 for the photodissolution of silver in chalcogenide glasses.
In situ IBA can even be used at the liquid–solid interface using an external beam (see §4.7 for cultural heritage applications of this). In situ electrochemical RBS was first published by Kötz et al.186 – both RBS187 and NRA188 still remain of interest and a general patent was published in 2014.189
3.8 Imaging and tomography
We shall highlight the great value in fully quantitative analysis at a high lateral resolution (see §§4.6 and 4.7) and we have already mentioned this in the comparison of μ-XRF and μ-IBA above (§3.2). Le Trequesser et al. also make a similar point in their recent work on gold nanoparticles.190Tomography is now a very well-established technology with X-ray density tomography being widely available (an example is shown in Fig. 23g). Tomography is a 3-D technique that presupposes a 2-D imaging capability, which for the ion and electron beam techniques is usually determined by the probing beam spot size. For MeV ion beams the available ion sources are not very bright, and also the magnetic quadrupole lens aberrations are substantial: it has consequently proved difficult to reduce the spot size below the 1 μm achieved in the 1980s. However, in the last decade or so this had renewed attention and significant improvements in ion source brightness have been obtained.191
Fig. 15 shows the best high resolution imaging currently possible with IBA methods. A cancer cell which has been cultured with gold nanoparticles (GNPs) is being imaged with scanning transmission ion microscopy (STIM)192 using a 1.6 MeV alpha particle (4He2+) beam focussed to 25 nm. “STIM” sounds similar to “STEM” (scanning transmission electron microscopy) but the image is formed entirely differently. It is more analogous to EELS (see Table 1) in that the energy loss of the ion through the material is being imaged, but EELS is a spectroscopy where the characteristic elemental edges are imaged (see Fig. 23d for an example) where STIM is a spectrometry with the energy loss being a proxy for density. This is exactly analogous to X-ray radiography, and the X-ray computed tomography techniques now standard and widespread are equally applicable to STIM. And indeed STIM tomography (STIM-T) has been used in earnest for fusion targets193 (on which see also §4.5).
 | ||
| Fig. 15 1.6 MeV He2+ STIM image of HeLa cell cultured with GNPs. STIM: “scanning transmission ion microscopy”; FSTIM: “forward (off-axis) STIM”; GNP: “gold nanoparticle”; HeLa: immortal cancer cell line cultured from Henrietta Lacks, who died in 1951. STIM beam is focussed to 25 nm. RBS beam is focussed to ∼250 nm. See text. (a) (Top Left): STIM. Colour scale indicates energy loss. (b) (Bottom Left): FSTIM. Colour scale indicates probability of scattering into a large angle. (c) (Right): FSTIM with the GNPs colour coded for depth from the RBS signal. Reprinted from Biophys. J., 104 (Fig. 4b, 5b, 8 of Chen et al., High-resolution 3D imaging and quantification of gold nanoparticles in a whole cell using scanning transmission ion microscopy, 1419–1425, ©2013),197 with permission from Elsevier. | ||
STIM is almost entirely non-destructive: since it is a technique that analyses the energy loss of every transmitted particle only a very few particles are needed (a few thousand per second: ∼fA). But for microbeam RBS or PIXE a larger beam current is required (∼nA), necessitating a larger object aperture which results in an order of magnitude larger spot size. For all focussed ion beams, a high imaging resolution will be controlled by the ion source brightness since a higher brightness allows a smaller object aperture for the same beam current.194
In Fig. 15 we see a combination of techniques: Fig. 15a is classical STIM where the image contrast is most easily understood as representing thickness (with high energy loss due to large sample thickness). This is a well-known technique that was used long ago in conjunction with PIXE imaging in a study of Alzheimers neural plaques195 (as just one influential example). Fig. 15b is dark-field (“off-axis”) STIM196 where the scattering (rather than merely the energy loss) is imaged. This is analogous to the backscattered electron detector in the SEM, which is sensitive to atomic number: Fig. 15b is imaging the GNPs in the cell. Trouble is, we need to distinguish between GNPs inside and outside the cell (the latter are also clearly seen in the top right of Fig. 15b). STIM cannot do this but RBS can: for STIM the energy loss is integrated along the particle path and there is no depth contrast whereas for the (large) RBS beam we look (at lower spatial resolution) for the depth of the GNPs in the cell, which is colour-coded in Fig. 15c.
In Fig. 15 the GNPs cannot unambiguously be identified as gold from the data unless the characteristic X-rays are also collected (PIXE). Clearly, where the RBS signal is collected the PIXE can be too: in this case the PIXE does not carry any further information and is not shown. One might think that if STIM-T is possible then PIXE tomography (PIXE-T) for each element detected is equally possible. This is not the case: in principle they are not equivalent problems. PIXE-T is much more difficult problem than STIM-T because PIXE is a vector, not a scalar method: STIM uses only the energy loss behaviour but the PIXE intensity per element per pixel integrates information from the whole primary beam path and the whole X-ray path to the detector. To do the ZAF correction all of the elemental tomographs need to be known, and they are not independent of each other! However, after much effort PIXE-T is now also a solved problem:198 it has been demonstrated for hair199 (and other targets too: see the useful review of STIM-T and PIXE-T by Michelet et al.200).
The trouble with PIXE-T is that it is very damaging, and only rather robust samples can survive the many slices required.201 We should mention that although simple tomography theory calls for a very large number of slices there are various mathematical ways of dramatically reducing this number and consequently reducing the analysis time (together with sample damage!),202 including maximum likelihood methods.203 Again, Fig. 15 is interesting. The GNPs were located in depth not indirectly by the usual computed tomography methods but directly by RBS.
This example seems to imply a much more efficient method for Total-IBA tomography (Total-IBA-T: another example is discussed in §4.6 and elaborated in Jeynes et al.4). In such a method initial STIM-T would give the 3-D density non-destructively at high spatial resolution, and subsequent Total-IBA (PIXE + EBS) would give the (lower resolution) 3-D elemental composition with far fewer slices than required for PIXE alone since the backscattering signal relieves so much of the depth ambiguity of the PIXE. However, at present Total-IBA-T remains an unsolved problem.
Another approach to the damage problem has a different context. PIXE-T has also been demonstrated for an “animal-sized” model system by Bazalova-Carter et al.204 who use 200 MeV protons for penetration of large targets. They point out that sufficient contrast could be obtained for imaging of GNPs (for example) during clinical irradiations for proton radiotherapy, which has become topical.205
3.9 Estimating the uncertainty of IBA depth profiles
Depth profiling of a thin film sample by nuclear scattering methods depends on a depth scale given by the electronic energy loss of the incident and detected particles in the sample. Because sample composition information is convoluted with depth profile information in the energy spectra of the detected particles, the inversion of the data to yield the depth profile is an ill-posed mathematical problem. By contrast, the composition – but not the depth profile, which has to be assumed – can be extracted analytically from PIXE (or XRF) spectra.There are general mathematical ways to directly solve such ill-posed problems, the IBA case was solved by Kogan et al.206 using Pyt'ev's207 reduction method generalized for this non-linear problem. Unfortunately, this promising approach has not yet been taken up by the community, but Bayesian methods have since been introduced systematically in different ways by both the leading codes (see §3.4.3), either of which allow a general approach to the estimation of uncertainties on the depth profiles extracted from the data.
Maximum Entropy (MaxEnt) methods were used by Fischer et al.208 to improve the effective energy resolution by a factor of about 6 through deconvolving the instrumental function, comparable methods were subsequently used to obtain most probable depth profiles.209 This approach has proved both very computationally intensive, and also cumbersome since it requires detailed knowledge of the instrumental function which is inconveniently unstable. However, Schmid & von Toussaint210 have used similar methods to obtain statistically sound estimates of uncertainties of depth profiles for nuclear fusion applications211 (see §4.5).
Simulated annealing212 was introduced in 1997![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 151 to obtain depth profiles by inverting the RBS spectra; this naturally introduces the Markov-chain Monte Carlo (MCMC) methods used in a Bayesian treatment that allow statistically robust estimates of the depth profile uncertainties to be obtained.213 Dose214 points out that Bayesian methods are useful for all spectrometries, although they are especially useful where the problem is mathematically ill-posed since there are few good alternatives. They have been extensively used: by James et al.215 to determine the uncertainty of polymer diffusion coefficients (see §4.4); and by Jeynes et al.2 (see Fig. 1) and Barradas et al.216 (see §4.2) to determine layer thickness uncertainties in respectively optical multilayers and SiGe superlattices. It is interesting to note that the same mathematical methods can be used on similar data to extract stopping power data79 or even differential scattering cross-sections.217
151 to obtain depth profiles by inverting the RBS spectra; this naturally introduces the Markov-chain Monte Carlo (MCMC) methods used in a Bayesian treatment that allow statistically robust estimates of the depth profile uncertainties to be obtained.213 Dose214 points out that Bayesian methods are useful for all spectrometries, although they are especially useful where the problem is mathematically ill-posed since there are few good alternatives. They have been extensively used: by James et al.215 to determine the uncertainty of polymer diffusion coefficients (see §4.4); and by Jeynes et al.2 (see Fig. 1) and Barradas et al.216 (see §4.2) to determine layer thickness uncertainties in respectively optical multilayers and SiGe superlattices. It is interesting to note that the same mathematical methods can be used on similar data to extract stopping power data79 or even differential scattering cross-sections.217
IBA data can be ambiguous: this was discussed at length in the review by Jeynes et al.3 For RBS the ambiguity comes from the overlap of signals: any particular count could be from a heavy atom deep in the target or a light element close to the surface. There are standard ways of eliminating most (if not all) this ambiguity: in Fig. 1 for example we show only one spectrum with the primary beam normal to the sample, but a second was collected with the primary beam at 45° to the target resulting in a spectrum with a markedly different shape (see Jeynes et al.2). Ambiguity is greatly reduced, but the remnant can be eliminated only by imposing chemical assumptions. In these data O is a small signal with a large background: we impose the assumption that the layer is fully oxidised (that is, it is a zirconia/silica multilayer). Of course, this assumption is fully justified by the optical behaviour of the film. In this early work the fits were only obtained by allowing intermixing of the layers (excluded by the optical properties!), but the same fit quality would be obtained by modelling roughness effects, as for Fig. 12 and 16.
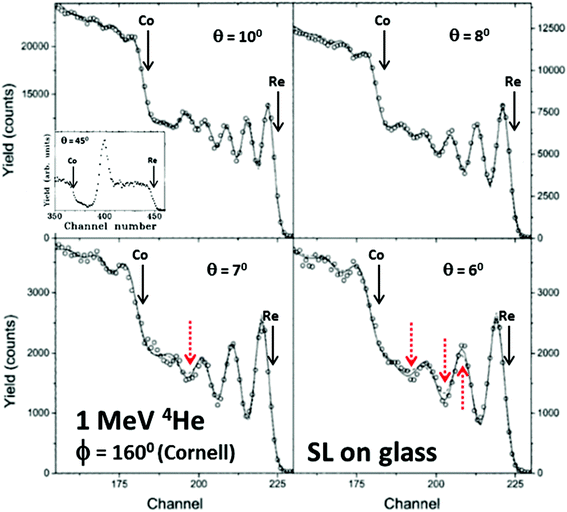 | ||
| Fig. 16 High-resolution RBS of a (Re, Co) superlattice on glass. Glancing incidence RBS at 10°, 8°, 7°, 6° to surface, with detector (in “Cornell” geometry) at a backscattering angle of 160°. See text for red arrows. Sample: Glass substrate/Re(5 nm)/[Co(2.3 nm)/Re(0.5 nm)]15. The Co and Re elemental edges are labelled. Inset: 45° spectrum (courtesy of N. P. Barradas) showing the sample structure including the 5 nm Re interlayer. For the spectra collected at 7° and 6°, the simulated curves calculated for a deformed substrate (dotted line) or a rough substrate (solid line) are shown (see text for details). Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 190 (Fig. 1 of Barradas, Fitting of RBS data including roughness: application to Co/Re multilayers, 247–251, ©2002),232 with permission from Elsevier. | ||
Fitting data sets is done in most cases by simply minimising a χ2 function: multiple spectra each contribute a part of the value and these can be from different detectors (which may be using different techniques) or different data collection runs (different beams or beam energies or geometries). Energy loss spectra are well suited to this treatment since the spectra are histograms with Poisson statistics. However, any “objective function” that represents goodness of fit can be used, and in some cases this is desirable since the χ2 function has some problems. In particular it is unstable for poor fits (with large outlier values), and Dose & von Toussaint218 have pointed out that there are some rather elegant solutions to this.
Another standard statistical approach is to use “robustification”219 where the objective function morphs from χ2 to a ln(χ2) function (for example) as the fit gets poorer. We have found this robustification approach useful for “Total-IBA” with PIXE data because the areas of the characteristic lines that are the input data are neither histogram data nor subject to Poisson statistics. In principle, treating the contribution to the χ2 function from the non-Poisson non-histogram PIXE data uniformly with that from the nuclear scattering data is not mathematically valid: in practice it usually works quite well. But it works better if a robustified χ2 function is used.
4 Quantitative depth profiling: IBA as a reference method
4.1 Introduction: synergy in IBA
In this section we draw together all the threads: many analysts have heard of RBS and many have heard of PIXE but this Review has the purpose of informing analysts of recent developments in Ion Beam Analysis, an effectively new method where the fast ion beam yields rich information when the various signals are treated synergistically. We refer to this “synergistic IBA”, the combining of multiple techniques, as “Total-IBA”, following Jeynes et al.4In Table 3 (§3.4.1) we pointed out that where the performance of PIXE was weak, that of RBS was strong, and vice versa: here we will elaborate on this, with several detailed examples none of which could have been given even a decade ago. These are selected arbitrarily from many possible examples, and demonstrate the great generality of IBA: it is valuable whenever thin films are depth profiled since it is quick, not deliberately destructive (and beam damage is usually limited), model-free and fully quantitative, and has near-100% mass closure.
The systematic use of PIXE is a key because the mass insensitivity (and ambiguity) of RBS is the very well-known drawback that has limited its use. Another important key is the realisation that even noisy spectra may be very informative. This is significant because PIXE typically has very high X-ray generation cross-sections and is often used (with large solid angle X-ray detectors) in imaging (microbeam) applications for which focussed beam currents are limited. For such analyses the backscattered particle signals are traditionally ignored because (a) the counting rates are usually very low, with very noisy spectra; and (b) the spectra usually look intractable anyway, with strongly non-Rutherford scattering cross-sections.
The massive recent work on evaluated cross-sections (summarised above in §3.3) has completely changed the situation: EBS spectra are now usually tractable. And Barradas et al.213 showed in 1999 that even very noisy RBS spectra can enable a qualitatively correct interpretation, allowing PIXE spectra of layered samples to be treated fully quantitatively. The PIXE by itself is blind to whether the films are 20, or 2, or 0.2 microns thick: in this case even a 10% uncertainty due to poor counting statistics of the RBS spectrum contributes negligibly to the PIXE uncertainty. This is something the XRF community knows very well: provided something is known about the sample, the XRF (or PIXE) can tell you much. More recent work has underlined that robust information is available even in the presence of 10% Poisson noise.220
In this final section we will show a series of examples where the nuclear scattering and atomic excitation data, considered separately, are intractable, but where together they mutually interpret each other: self-consistent IBA (“Total-IBA”) is massively more powerful not only than any of the individual IBA techniques taken separately, but also than even the iterated sequential use of the individual IBA techniques, which even where it is successful is acknowledged to be long, clumsy, and uncertain.221
It is now standard practise to collect RBS data with multiple detectors with different geometries to relieve the intrinsic mass-depth ambiguity in the energy-loss spectra. Analysing these multiple spectra self-consistently was first done by Barradas et al.151 and we have already referred to this (Fig. 1 and 4). Strictly, this is not “Total-IBA” since multiple techniques are not in use, but in practise the analysis code is modular and indifferent to which technique is in use for a particular spectrum. So “Total-IBA” was rapidly introduced in 1999 with RBS + ERD,94 RBS + NRA,222 and RBS + EBS + ERD + NRA.223,224
It is clear that Total-IBA is an indispensable tool for quantifying the processes involved in creating novel advanced materials, which of course also need a battery of complementary analytical techniques. For example, Shaw et al.225,226 have synthesised novel porous high strength materials which are promising for energy storage, photovoltaics, and catalysis applications (characterised by nanoimplantation, XRD, SEM, TEM and IBA). They used a process that involved colloidal inorganic nanoparticles manipulated by functionalisation with organic ligands, where the organic material was finally “burnt off” by an oxygen plasma. In this case the IBA was essential to understanding the evolution of the structure during the plasma processing.
In the remainder of this chapter we will first underline how the self-consistent treatment of multiple RBS spectra can be highly informative (§4.2). Then (§4.3) we will explicitly demonstrate how IBA can be used to certify (potential) reference samples in cases that are difficult for alternative methods. §4.4 displays two interesting cases where modern IBA has proved valuably complementary to the big physics facilities: neutron reflectivity at spallation neutron sources and synchrotron X-ray crystallography. §4.5 is an example of an industrial scale analysis, showing that very large numbers of complex samples can be handled effectively with modern techniques. §4.6 shows a “blind” analysis informed by no prior knowledge: this situation is also very frequently found in processed samples where something has gone wrong and the prior knowledge the user thought he had has proven unreliable. We conclude (§4.7) with a celebration of IBA being non-destructive: it can also be used safely and very effectively on valuable and delicate layered samples (such as paintings) using an analysis at atmospheric pressure. Such samples may be rough, and IBA is sensitive to surface roughness – historically neglected but now tractable.
4.2 Self-consistent RBS for ∼1 nm depth resolution
In a Review of IBA depth profiling it would be strange not to underline the very high depth resolution available from rather simple equipment, and here we concentrate on this. However, we should first mention that ultra-high depth resolution is available by RBS using magnetic spectrometers,227,228 which can even be used for liquids;229 liquid surfaces can also be analysed successfully by conventional RBS and grazing incidence geometry.230 Magnetic spectrometers have a rather small energy window (and consequently are often used in conjuction with other detectors – “Total-IBA” is normal for analysts). For example, to measure ultra-thin bilayers of HfO2 and Si oxynitride, Kimura et al.231 compare angular-resolved XPS with high resolution RBS (400 keV He) and HI-ERD (40 MeV Au), where (different) magnetic spectrometers were used for RBS and ERD.Energy straggling of the beam degrades the depth resolution for the deeper layers whichever detector is used: this effect is now thoroughly understood233 and is obvious in Fig. 16, which shows extraordinary data collected by Barradas234 in 1994 but reanalysed in 2002![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232 with the advanced code that handles self-consistent RBS.216 In this analysis standard RBS with the usual silicon diode detector of about 15 keV energy resolution is used. The sample was a magnetic multilayer: the period of the superlattice is less than 3 nm and yet the signal from the top few layers is easily discriminated.
232 with the advanced code that handles self-consistent RBS.216 In this analysis standard RBS with the usual silicon diode detector of about 15 keV energy resolution is used. The sample was a magnetic multilayer: the period of the superlattice is less than 3 nm and yet the signal from the top few layers is easily discriminated.
The questions to be answered were: (a) is the superlattice subject to substrate roughness, or not? and (b) is the roughness behaviour of a silicon substrate (not shown) different from that of the glass substrate (shown in Fig. 16)? Three models of roughness were considered: (i) random layer thickness non-uniformities (excluded by TEM); (ii) a deformed substrate or (iii) a rough substrate, both with conformal films. The difference between a deformed and a rough substrate (models (ii) and (iii)) is that there is correlation for (iii) but not for (ii). It turns out that in fact the data favoured model (iii) since the best fit for model (ii) had misfits marked by the red arrows in Fig. 16. These data are fitted with model (iii) parameters of a correlation length L of the surface asperities and the standard deviation δx of the asperity height distribution.
The high depth resolution RBS data for the superlattices on the two substrates gave fitted roughness parameters of L = 38.2 (39.3) nm and δx = 0.48 (0.61) nm for glass (silicon) substrate. The result that the two substrates actually behave differently was confirmed by other data independently: it surely is amazing that standard RBS is capable of such exquisite sensitivity? The alert reader may object that the arrowed “misfits” are barely significant. But note the ordinate scale: a cold view of the Poisson statistics of the data confirms their significance. The various roughness models affect the energy straggling differently, and therefore we expect effects from the surface layer deeper in the sample (in the second and third layers), which is what we see.
We should point out that Fig. 16 is very remarkable: it is not at all trivial to fit four separate spectra simultaneously and so perfectly. All the experimental parameters have to be correct for this sort of accuracy, and moreover the calculation of the intrinsic energy straggling also has to be correct. We have already pointed to this excellent detailed understanding of RBS in the commentary on Fig. 12; this is another notable demonstration of it.
4.3 The reference sample problem
A leading author from one of Europe's National Metrology Institutes has said: “The quantitation of XRF spectra is, in general, based on the use of appropriate reference materials that are as similar as possible to the sample to be analyzed as the interplay of many often unknown instrumental and fundamental atomic parameters determines the measured element-specific fluorescence countrates in a complex manner”.106 This statement is as true of PIXE as it is of XRF. The work of Beckhoff and co-workers in Berlin to develop and use reference-free XRF (see §3.2 above) is more difficult than for IBA since traceability for nuclear scattering is much easier to establish (see §3.1 above) than for the more complex atomic excitation methods. A recent direct example of this is the characterisation of olivine by IBA to calibrate the IR spectroscopy used in the study.235For validating routine analysis of course we always want comparisons to a reference sample, which should be similar to the sample set of interest: the question invariably is how to certify the reference? And today, with the explosion of interest in new and complex materials, this question is becoming increasingly acute.
The development of “Total-IBA” that we describe in this Review is complementary to reference-free XRF, and may be a better alternative, as we pointed out in §3.2. In particular, accurate RBS (see §3.1) may provide certified reference materials that can be used for establishing the fundamental parameters on which XRF and PIXE depend.
Accurate RBS may also establish reference materials for particular applications. Fig. 17 shows a case where depth profiling by XPS had produced equivocal results and independent validation was required. This is an interesting case since the RBS spectra have large overlaps of the elemental signals and are therefore not entirely trivial to interpret. Careful analysis of the RBS spectrum for the Cd, Zn and S content showed that the spectrum contained no evidence that the S was not a constant 50 atomic% through the depth profile. Therefore we imposed the chemical assumption that the film was a mixture of monosulfides, obtaining the profile shown in Fig. 17. Note that the similar assumption of full oxidation in Fig. 1 does not have independent support from the data (since the direct O signal is so small) but does have independent support from the optical behaviour (as an anti-reflection coating) of the film.
 | ||
| Fig. 17 RBS & PIXE of a 1.1 μm (Cd, Zn)S coating on Si. Data collected at Surrey May 2014 and fitted using NDFv9.6a.150 The fitted layer thickness inhomogeneity is not shown. Left: RBS (below) and PIXE (above: note the logarithmic ordinate scale) spectra collected simultaneously with a 3 MeV alpha beam. The PIXE line groups are labelled, and the overlapping elemental RBS signals, are shown. Note that there is no signal for O. Right: Fitted depth profile derived from the RBS data with the linear depth scale assuming bulk densities for CdS and ZnS. The discontinuities are an artefact of the fitting, representing the ambiguity of the data. | ||
We used a 3070 keV alpha beam to look for surface oxidation, making use of the 16O(α,α)16O resonance at 3038 keV (see §3.3) which gives strongly enhanced sensitivity to O (see Fig. 11). The higher energy beam was also convenient to see the whole film thickness. Oxygen is not detected, but had it been we could have looked for correlations in elemental signals which may have indicated oxidation of one or other of the species present.
There are several advantages of imposing chemical assumptions on the data. The heavy and light element signals are correlated in the analysis, and also the number of free parameters is reduced: both standard noise-reduction techniques. Then, if the profiles are fitted in terms of compounds (sulfides) rather than elements a realistic linear depth scale (in nm) is readily available, using the bulk sulfide densities (in g cm−3). Note that the natural thickness unit for energy loss methods is TFU, since the units of energy loss are eV per TFU: see Fig. 11 caption for “TFU”. This is valuable since the linear film thickness (in nm) can be measured directly with other methods, which then gives information on the actual film density.
Fig. 17 is a good example of a relatively simple coating which could in principle be used as a reference sample for applications work in this mixed sulfide system. The PIXE spectrum shown in Fig. 17 is similar to XRF or EPMA spectra, and is uninterpretable unless the profile is known. But we do know the profile! The RBS gives the profile not only unequivocally but also with rather small uncertainties. Therefore, this is one example where the sample could be certified by RBS, thereby becoming a standard sample for PIXE (or any other technique used), in which case the PIXE (or XRF, XPS, EPMA etc.) can inherit the accuracy of the RBS.
In this case the PIXE was not used to solve the sample structure so that the PIXE simply inherits the accuracy of the RBS. In other cases the PIXE may be needed to solve the structure, and then the RBS would inherit at least some of the uncertainty of the PIXE. In any case a set of detailed Uncertainty Budgets must be constructed separately for each certification analysis.
Fig. 18 is an example of a CIGS (CuInGaSe) sample grown on stainless steel with a Mo electrode (and a thin Cr buffer layer). Such samples are of great current interest for thin film photovoltaic (PV) applications. In this case the RBS is multiply ambiguous because of the systematic elemental overlaps: nevertheless the structure could be unambiguously solved with the addition of the PIXE data. In fact only a selection of the collected (and fitted) data is shown: 15 spectra were used including different beams, and different geometries. Bayesian (Markov chain Monte Carlo, MCMC) methods213 were used to explore the uncertainty of the results given the input assumptions.
 | ||
| Fig. 18 RBS & PIXE of a 1.9 μm CIGS (CuInGaSe) coating. RBS and PIXE data (3 detectors) collected simultaneously at Surrey June 2010 and fitted using NDFv9.3c.150 The fitted CIGS layer thickness inhomogeneity of 5% is not shown. The Mo layer had thickness 322 nm (15% inhomogeneity) and the Cr buffer layer was 70 nm thick. Left (above): RBS with 2 detectors at backscattering angles of 172° and 149°. Data and fits are shown. Left (below): 149° spectrum with fitted partial elemental spectra shown. Right (above): PIXE spectrum with labelled lines (note the logarithmic ordinate scale). Right (below): most probable depth profile derived from MCMC fitting of the RBS + PIXE data. The linear depth scale is in proper thin film units of areal density (μg cm−2). The discontinuities are an artefact of the fitting, representing the depth resolution of the data. | ||
What is interesting is that we can directly compare average IBA with integral XRF results. We obtain CIGS film thickness (assuming 5.8 g cm−3) for IBA (XRF) of 1860 (1900) nm, and average film composition for IBA and XRF respectively of (Cu, In, Ga, Se) = (262, 138, 77, 523) and (219, 133, 90, 558). The purpose of the analysis was specifically to obtain the depth profile which of course is unavailable from XRF.
This analysis has fair agreement between XRF and PIXE. Both methods agree that the Se content is greater than 50 at%, but the Ga content (and profile) is determined from the X-ray data and will be sensitive to the details of the X-ray detector calibration: agreement of XRF and PIXE depend on a consistent calibration protocol. This underlines the point made for the mixed sulfide sample (Fig. 17): an IBA analysis that needs the self-consistent PIXE will have an uncertainty partly inherited from the PIXE.
On the other hand, IBA with accurately calibrated PIXE will yield reliable profile information comparable to that available from sy-GI-XRF and entirely beyond desktop XRF. We therefore expect IBA to be used in future to certify reliable reference samples for desktop XRF.
4.4 Polymers and proteins: IBA as a complementary technique
In this section we show two examples of different complementary analysis methods which have made a significant impact in their fields. We will consider IBA used with neutron reflectivity (NR) for polymer interdiffusion measurements, and with synchrotron X-ray crystallography (sy-XRX) to determine the structure of proteins. In both cases the advances we sketched in §3 have proved crucial to the value of the IBA contribution.In all these cases, to understand the complex thermodynamics driving the development of the structure that gives the functional material its desired properties, a materials science approach following and accounting for this structure is required. Many methods are used, as usual in this multi-disciplinary field, but nuclear reaction analysis (NRA) using the d(3He,p)α reaction237 together with deuteration of one of the mixing components has been found extraordinarily powerful in combination with neutron reflectivity. The NRA method is useful precisely because the isotopic effect due to deuteration is well understood.238
Fig. 19 shows the depth profile of the deuterated component of a conjugated polymer blend which is successfully used in experimental light emitting diodes (LEDs). In this sort of material the exciton diffusion distance is very small (<10 nm) so that nanostructuring is essential to obtain electronic performance. The NRA depth resolution is about 10 nm, which is not good enough to understand the nanostructuring behaviour: for a high resolution measurement the chemists turn to neutron reflectivity, but NR spectra are multiply ambiguous and it is necessary to know the depth profile at low resolution to relieve this ambiguity. The same methods are used to follow depth profiles of surfactant and plasticiser additives in spin-cast polymer films,239 and even to follow nutrient uptake in mycobacteria.240
 | ||
| Fig. 19 NRA of a 70 nm deuterated polymer blend. Volume fraction (ØPFO) of deuterated PFO by nuclear reaction analysis (NRA) in a 70 nm thick spin-coated blend of the conjugated polymers poly(9,9′-dioctylfluorene) (PFO) and poly(9,9′-dioctylfluorene-altbenzothiadiazole) (F8BT). The main graph is uncorrected for energy resolution and cross-section effects, the inset is corrected. Reprinted by permission from Macmillan Publishers Ltd: Nat. Mater. (Fig. 4 of Chappel et al. ©2003).236 | ||
In another recent example215 using the same methods as shown in Fig. 19 (but to understand completely different functional materials), parameters for the surface modification of polyester using incompatible blends of polystyrene additives were obtained. In such cases a surface bilayer is formed with an error function modelling each layer: there are two characteristic lengths for each layer, the layer thickness and the interfacial width. These parameters are obtained directly from a parameterised fit of multiple NRA spectra collected for different glancing beam incident angles, where the absolute (model-free) depth resolution is comparable to about 10 nm and the information depth extends more than a quarter of a micron. Bayesian techniques (see §3.9) give reliable estimates of the uncertainty of these (parameterised) lengths: in this case the thickness of the surface enriched layer is obtained with a precision of about 1 nm, where the interface width between the surface enriched layer and the depleted layer immediately beneath it is obtained with a precision of about 3 Å.
Of course, the neutron reflectivity (NR) also used in this work has a much higher absolute depth resolution than this but a much lower sensitivity to slow changes in concentration. As before, NR and NRA complement each other almost perfectly.
Straightforward RBS is also powerful where one of the polymers is distinguished by a heavy component. In an example of self-assembled transistor structures, sulfur characterises one component.241 Another very recent example of self-assembled photonic structures follows the distribution of gold nanoparticles in polymer mixtures.242
We should point out that neither the use of advanced computational methods243 nor complementary X-ray methods (such as X-ray absorption fine structure, XAFS) to follow the way the metals damage (oxidise) under the photon beam244 can do more than indicate the metal identification: Morshed et al.243 specifically underline the need for complementary methods to both quantify and also unambiguously identify the metals.
We also emphasise that the protein structure (including the location of the metal ions in the structure) is obtained by XRX, not by the IBA which only identifies and quantifies them.
Fig. 20 shows a protein which suppresses tumour growth, but mutations of which are (among other things) the cause of a genetic predisposition to “familial cylindromatosis”, a skin cancer affecting predominantly hair follicles and sweat glands of the head and neck. The main protein structure was determined by XRX but the two Zn atoms, located by XRX, were unambiguously identified by a “Total-IBA” measurement (using OMDAQ and GUPIX, see §3.4.4 and Garman245) using a 2.5 MeV proton beam and both PIXE and EBS, and a special protocol.246 This sort of structural work broadens and deepens our understanding of how cancer works: in this case the gene possessed a previously unknown (and unexpected) type of “B-box domain”. Further work (using sy-XRF) demonstrated that indeed the zinc was a physiological active ligand.
 | ||
| Fig. 20 Structure of one domain of a tumour suppressor gene. The ubiquitin specific protease (USP) domain of the “CYLD” tumour suppressor gene is determined by X-ray crystallography. The “B-box” domain of this USP protein is necessary to retain the CYLD gene in the cytoplasm of cells. The two Zn atoms in the B-box were identified and quantified by IBA. Reprinted from Mol. Cell, 29 (Fig. 1 of Komander et al., The structure of the CYLD USP domain explains its specificity for Lys63-linked polyubiquitin and reveals a B box module, 451–464, ©2008),248 with permission from Elsevier. | ||
There are many other examples of examining important proteins using XRX + IBA, where the metal ligand is essential to the protein function. For example, to expand our understanding of catalysis by the alkaline phosphatase class of enzymes, Yong et al.247 determined the structure of the widely occurring microbial alkaline phosphatase PhoX. These enzymes play a crucial role in phosphate acquisition by micro-organisms. The enzyme contains a complex active-site cofactor comprising two antiferromagnetically coupled ferric iron ions (Fe3+), three calcium ions (Ca2+), and an “oxo” group bridging three of the metal ions. These metal ions were identified and quantified by IBA. The presence of iron in PhoX raises the possibility that iron bioavailability limits microbial phosphate acquisition.
Again, Karkehabadi et al.249 solved the detailed structure of “Cel61A”, one of a significant class of the glycoside hydrolase (GH) “family 61” proteins found in the fungus Hypocrea jecorina. This was the first solution of any of the GH family 61 class. The authors identified a cluster of highly conserved residues on the surface of the Cel61B structure, finding a nickel ion bound within this conserved surface using IBA. The observation of bound Ni is expected to be important for Cel61B activity, stability or function.
In further work on the same fungus H. jecorina, Jacobson et al.250 identified and solved a previously unknown protein, denoted “cellulose induced protein 1” (Cip1) which is thought to be likely to function in biomass degradation. A calcium ion binding site was identified in a sequence-conserved region of Cip1: the presence of this ion was found to have a structural role. The calcium ion was unambiguously identified and quantified by IBA.
4.5 High throughput analysis
In §3.7 we described examples of real-time RBS. Clearly, such analyses generate very large datasets, counting as “high throughput analysis”. Also, at the end of §3.2 we compared a μ-IBA with a μ-XRF analysis: in this case the XRF used a multisegmented detector with a large solid angle capable of a very high total count rate; such a detector could just as easily be used for PIXE. Where the count rate is high the collection time may be small, and again the throughput may be high. So, in Florence the IBA (in this case PIXE) system has been improved to allow dataset collection times of only 30 s,251 meaning that hourly resolved high sensitivity air pollution analyses over continuous periods of a week are easily feasible (and competitive with complementary methods!). This system was used for a large and prominent study.252The problem of collecting enough data is solved by counting for longer; or counting faster, either by increasing the beam current or by increasing the number of detectors (which is equivalent to increasing the solid angle). Technically either is feasible, given appropriate investment. The problem of “high throughput analysis” therefore reduces to the feasibility of handling large datasets involving depth profiling. The air pollution example above is mathematically trivial since only PIXE spectra are handled: these can be inverted with simple minimisation methods. We have already given one example for the non-trivial depth profiling case in §3.7 where the depth profiles were given in real time by an artificial neural network. We give another substantial and interesting example below where the depth profiles are extracted in bulk by standard analytical software used off-line.
The Joint European Torus (JET) and its successor, the International Thermonuclear Experimental Reactor (ITER: this is a pun in Latin, it means the Way), depend on controlling very high temperature plasmas and understanding in detail their interaction with the walls of the reaction chamber. JET is continuing to host experiments aimed at the success of ITER, and these “campaigns” end with the reaction chamber lining tiles being removed for materials analysis. The results of these analyses are buried in the technical literature, but there are a large number of tiles with many analysis points needed per tile: the measurements are very extensive with very large datasets being generated. This is a continuing programme (for example, see Baron-Wiechec et al.149).
Fig. 21 shows just one such analysis. Four different beams are used and many spectra are handled self-consistently per analysis point. This is an example where very large quantities of highly complex data are handled fully quantitatively and entirely automatically in support of an industrial-sized programme.
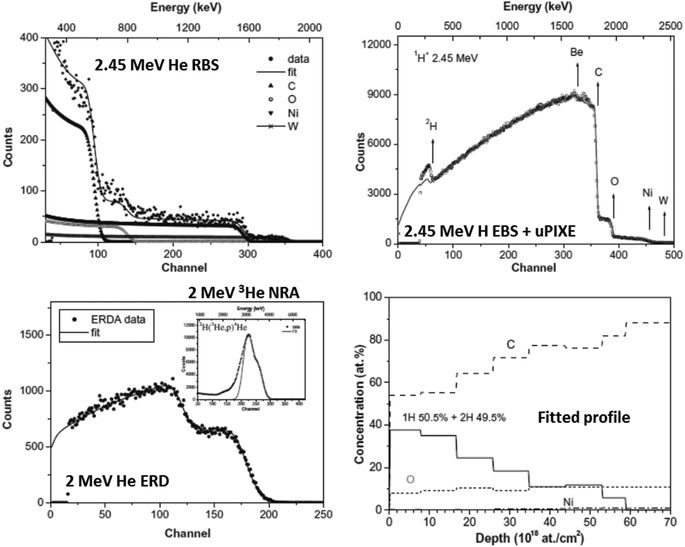 | ||
| Fig. 21 IBA of a diverter tile from the Joint European Torus (JET). IBA of an “outer poloidal limiter” tile from the 2005–2007 JET campaign. He-RBS quantifies heavy impurities (Ni, W), He-ERD quantifies 1H and 2H near the surface, 3He-NRA quantifies 2H down to >5 microns, H-EBS identifies Be and looks much deeper than RBS, and microbeam PIXE (not shown) images the impurity distribution in the tiles and determines minor and trace impurities. Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 268 (Fig. 2 of Alves et al., Erosion and re-deposition processes in JET tiles studied with ion beams, 1991–1996, ©2010),253 with permission from Elsevier. | ||
4.6 Blind analysis – Darwin glass
800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years ago a meteor struck Tasmania, creating a large impact crater (see Fig. 22), with impact glasses (see Fig. 23h) resulting from the condensation of the vaporised rock strewn over 400 km2 around the crater. Some of these glasses have crystalline inclusions – rutile (see Fig. 23e and i) and silica have been detected – which is extraordinarily strange since the rapid quenching of impact glasses ought to have precluded any crystallisation. The geologist accordingly searched for the origin of these unexpected crystals, and found that they resided in inclusions in the glasses (see Fig. 23f). But the composition of these inclusions was completely unknown – standard methods remained equivocal.
000 years ago a meteor struck Tasmania, creating a large impact crater (see Fig. 22), with impact glasses (see Fig. 23h) resulting from the condensation of the vaporised rock strewn over 400 km2 around the crater. Some of these glasses have crystalline inclusions – rutile (see Fig. 23e and i) and silica have been detected – which is extraordinarily strange since the rapid quenching of impact glasses ought to have precluded any crystallisation. The geologist accordingly searched for the origin of these unexpected crystals, and found that they resided in inclusions in the glasses (see Fig. 23f). But the composition of these inclusions was completely unknown – standard methods remained equivocal.
 | ||
| Fig. 22 View of the 1.2 km diameter impact crater at Mount Darwin, Tasmania. Picture courtesy of K. T. Howard. | ||
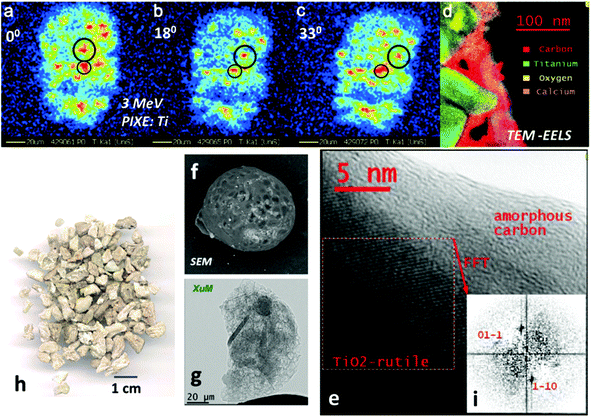 | ||
| Fig. 23 Complementary techniques applied to a Darwin glass inclusion. (a–c) Stereographic Ti maps (PIXE) of the whole inclusion; (d) high resolution TEM-EELS image of a selected area; (e) HR-TEM of fragment of inclusion showing crystalline titania, with inset (i) showing FFT of selected area; (f) SEM of an inclusion extracted from one of the Darwin glasses – see (h); (g) XuM of the inclusion; (h) selection of “white” Darwin glasses. Note the scale markers: 1 cm on (h), 20 μm on (a–c) and (g) – also applies to (f), 100 nm on (d), and 5 nm on (e). HR-TEM: high resolution transmission electron microscopy; FFT: fast Fourier transform; EELS: electron energy-loss spectroscopy; SEM: scanning electron microscope; XuM: X-ray ultramicroscope, an SEM attachment that essentially permits X-ray tomography. PIXE (a–c) is reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 267 (Fig. 2 of Bailey et al., Characterisation of inhomogeneous inclusions in Darwin glass using ion beam analysis, 2219–2224, ©2009),37 with permission from Elsevier; (d–i) are reprinted by permission from Macmillan Publishers Ltd: Nat. Geosci. (EELS (d) is Fig. S9, HR-TEM (e, i) is Fig. S7, (f) is Fig. 1; (g) is a still from the movie, (h) is Fig. S2, all from Howard et al. ©2013).36 | ||
Accordingly, we did IBA imaging of them (see PIXE maps of the Ti signal in Fig. 23a–c), which showed that they were extremely heterogeneous, but contained areas very rich indeed in Si as well as areas rich in Ti (and many other elements as well). Fig. 24 shows an analysis of one of these Si-rich areas, where we deliberately made use of the 12C(p,p)12C EBS resonance at 1734 keV.254,255 These resonances are just as characteristic of nuclear structure as characteristic X-rays are of atomic structure (see §3.2), so that the identification of the carbonaceous matrix of the inclusions was unequivocal, greatly surprising the geologists, for whom the observation of carbon in impact glasses was unprecedented.
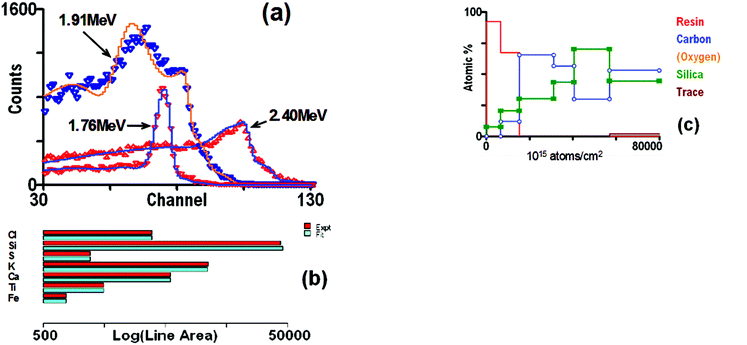 | ||
| Fig. 24 IBA of a Si-rich area of a Darwin glass inclusion. Unambiguous identification of inhomogeneous silica in a carbonaceous matrix by IBA using a proton beam and the 12C(p,p)12C resonance at 1734 keV. (a) EBS spectra of same spot with different proton energies; (b) line areas from PIXE spectrum; (c) derived depth profile where all the O is bound in SiO2 to account for the energy straggling behaviour seen in (a). Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 267 (Fig. 5 of Bailey et al., Characterisation of inhomogeneous inclusions in Darwin glass using ion beam analysis, 2219–2224, ©2009),37 with permission from Elsevier. | ||
Fig. 24 also shows how the carbon can be profiled by increasing the beam energy. Interestingly, the shape of the 1734 keV resonance appears not to be reproduced in the data, but this is due to the structural effect affecting the real energy straggling of the beam as a function of depth. This is a well-known effect256 that has been incorporated into the IBA code: it enables us to reliably model the depth profile in terms of silica inclusions in the carbonaceous matrix. Without this EBS resonance, the IBA would not be sensitive to the structure of the sample: it would only give us average elemental compositions. So the stereo pair for the Ti spatial distribution represented in Fig. 23a–c only localises Ti-rich regions, it does not identify the oxide.
As soon as the geologist understood the general structure of the sample he was able to persuade the microscopist that it was worth preparing a TEM sample to look specifically for the nanocrystals (rutile was positively identified, see Fig. 23e), and he also obtained the density tomograph of the sample (Fig. 23g is a still from the tomograph movie freely available in the supplementary material). He was then able to go on to make a detailed analysis of the chemical state of the carbon, finding a series of organic molecules, which again are unprecedented in impact glasses and indicates that we cannot rule out interstellar organic molecules being carried intact to Earth by meteorites.
4.7 Non-destructive analysis – cultural heritage
There are at least two European IBA labs dedicated to cultural heritage applications: LABEC in Florence257 and the AGLAE lab of the Louvre Museum.258,259 Calligaro & Dran have usefully reviewed this field recently,260 and de Viguerie et al.221 have reviewed IBA for paintings. For cultural heritage the “samples” are frequently priceless treasures that must be treated very carefully: this does not include being cut up and stuffed into vacuum chambers by accelerator physicists. Accordingly, so-called “external beams”261 are usually used, where the samples to be analysed may be arbitrarily large and of any shape: they may also be wet188 or otherwise delicate. Typically, 3 MeV proton beams are used which can exit the vacuum system through a thin (200 nm) silicon nitride window (see §3.6) and travel tens of mm in air. For these applications the sample is brought as close to the exit window as possible to minimise absorption (for X-rays) and energy loss (for particles), and for the same reason a helium atmosphere is often used. The sample is held on a motorised stage, but the ion beam is usually focussed and scanned for fast and convenient imaging, as in the SEM: this is not possible for sy-XRF which is limited to mechanical scanning. The ion beam can be scanned over an area given by the exit window, which can be several mm in diameter.Fig. 25 shows arguably the first photograph, an image of great importance almost 200 years old. It was apparently becoming corroded and was taken to AGLAE for investigation using both alpha and proton beams. Fig. 26 shows the results. In an analysis that would have been inconclusive using obsolete methods, Pascual-Izarra et al.262 were able to synergistically fit the He-RBS and the simultaneously collected H-EBS and H-PIXE to show quantitatively that the tin component of the heliograph was oxidising.
 | ||
| Fig. 25 View from the Window at Le Gras. Heliograph on pewter plate, 162 × 202 mm, by Joseph Niépce (1827). Figure credit: Wikimedia Commons. | ||
 | ||
| Fig. 26 IBA of a corroded spot on Niépce's heliograph. RBS determines Pb/Sn at surface; EBS determines O/metal at surface; PIXE determines (total Pb)/(total Sn). Synergistic fitting of RBS + EBS + PIXE yields the depth profile. Reprinted from Nucl. Instrum. Methods Phys. Res., Sect. B, 261 (Fig. 2 and 3 of Pascual-Izarra et al., Towards truly simultaneous PIXE and RBS analysis of layered objects in cultural heritage, 426–429, ©2007),262 with permission from Elsevier. | ||
Another interesting example of a fully synergistic analysis is of a 19th century copy of La Bohémienne (Frans Hals, 1650).263 These data were also collected at the AGLAE external beam facility to determine the paint layer thickness (as part of an exercise to evaluate the possible beam damage in IBA of paintings). The analysis was completed successfully despite the roughness of the paint, which is large in IBA terms, giving large signal distortions which the analytical codes could not then handle, and which the available codes could not fit and could simulate only if the roughness profile was known.264
Of course in the case of paintings the roughness cannot be determined by the usual contact methods, and in any case is not of intrinsic interest. We only want a way of correctly accounting for the resulting distortions in the backscattering spectra. This is now possible: Molodtsov et al.265 have constructed a generalised parameterisation of roughness that allows the fitting of simple averaged roughness parameters from the backscattering data. They have shown that in the case of this painting the asperities were a reasonable 5 μm high and 5 μm apart, on average. This algorithm has now been incorporated into the standard IBA code and has already been used to correct benchmarking data in scattering cross-section measurements.266
5 Conclusions
Ion Beam Analysis is a collection of analytical techniques which individually have a long history, just as other spectrometries and spectroscopies do. And as for those other complementary methods, IBA has had a series of recent developments that have dramatically increased its power. In particular, we have at last found out how to take advantage of the very well-known synergies between the atomic and nuclear IBA methods. Where the performance of PIXE is weak that of EBS is strong, and vice versa (see Table 3 and §3.4.1).This has resulted in what is effectively a new spectroscopic imaging technique (microbeam scanning “Total-IBA”) which is also fully quantitative (the spectrometries are very well developed). “Total-IBA” has a number of other features very attractive to analytical chemists: its depth resolution can reach ∼1 nm near the sample surface and its lateral resolution depends on the focussed probe size which can be deep sub-micron; there are ways to use it for high-volume routine applications (which may themselves be very demanding); it can be used in real-time; and it requires little or no sample preparation.
The quantitation of “Total-IBA” (usually PIXE + EBS) is model-free in principle since its sensitivity extends from major (matrix) to trace elements; but there are also systematic and well-developed ways to introduce prior knowledge (including chemical information) into the analysis. It is non-destructive, although, as with other nominally “non-destructive” methods, there may be more or less beam damage.
We should emphasise that IBA includes RBS, which has very recently been shown to be a primary direct reference method (using the language of the metrologists), with an absolute traceable accuracy of about 1% easily surpassing any other model-free non-destructive thin film analytical method. We have shown how “Total-IBA” can inherit this new accuracy, and pointed out that it should enable the much easier production of thin film reference standards certified at high accuracy in a very wide variety of materials.
We have shown very varied examples of the power of these modern methods, as well as explaining nine completely different sorts of recent significant advances which together have had such a remarkable result, even if individually they may look incremental to the wider analytical community.
We have stressed the importance of complementary methods throughout this Review, and should now conclude with some observations. XRF and PIXE are competitive methods: they both do very similar things. But XRF and Total-IBA are complementary in that IBA has definite advantages over XRF in quantitation (a specific comparison between sy-XRF and IBA is given in §3.2) where sy-XRF obviously has other advantages over IBA (in chemical imaging for example). GI-XRF is capable of a traceable measurement of quantity of material, just as RBS is: it is very valuable to have independent methods available. On the other hand RBS could certify the thickness of thin film reference samples used for SIMS (and XRF), and for determining Fundamental Parameters (see §3.2), at much higher accuracy than currently available. Such CRMs could also be valuable for determining electron mean free paths for XPS.
Acknowledgements
We are grateful to Rossana Grilli (Surrey), who supplied the (Cd,Zn)S sample analysed in Fig. 16, to Jan Schniebs & Christian Kaufmann (Helmholtz Institute, Berlin) who supplied the CIGS sample analysed in Fig. 17 together with the XRF results, to Nuno Barradas (Lisbon) who provided important elements of the text of §4.5, and to Alexander Gurbich (Obninsk), Richard Thompson (Durham), Max Döbeli (Zurich), Elspeth Garman (Oxford), and Neil Ward (Surrey) for helpful comments.Notes and references
- S. Rubin, T. O. Passell and L. E. Bailey, Chemical analysis of surfaces by nuclear methods, Anal. Chem., 1957, 29, 736–743 CrossRef CAS.
- C. Jeynes, N. P. Barradas, H. Rafla-Yuan, B. P. Hichwa and R. Close, Accurate depth profiling of complex optical coatings, Surf. Interface Anal., 2000, 30, 237–242 CrossRef CAS.
- C. Jeynes, N. P. Barradas, P. K. Marriott, G. Boudreault, M. Jenkin, E. Wendler and R. P. Webb, Elemental thin film depth profiles by ion beam analysis using simulated annealing - a new tool, J. Phys. D: Appl. Phys., 2003, 36, R97–R126 CrossRef CAS.
- C. Jeynes, M. J. Bailey, N. J. Bright, M. E. Christopher, G. W. Grime, B. N. Jones, V. V. Palitsin and R. P. Webb, Total IBA - Where are we?, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 271, 107–118 CrossRef CAS.
- E. Rutherford, The scattering of α and β particles by matter and the structure of the atom, Philos. Mag. Series 6, 1911, 21, 669–688 CrossRef CAS.
- C. G. Barkla, The spectra of the fluorescent Röntgen radiations, Philos. Mag. Series 6, 1911, 22, 396–412 CrossRef CAS.
- N. Bohr, On the Constitution of Atoms and Molecules (this is the first of three papers), Philos. Mag. Series 6, 1913, 26, 1–25 CrossRef CAS.
- J. R. Rydberg, Recherches sur la constitution des spectres d'emission des éléments chimiques, Norstedt, 1890 Search PubMed.
- W. Ritz, Magnetische Atomfelder und Serienspektren, Ann. Phys., 1908, 330, 660–696 CrossRef.
- I. Martinson and L. J. Curtis, Janne Rydberg - his life and work, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 235, 17–22 CrossRef CAS.
- J. Chadwick, The Excitation of gamma Rays by alpha Rays, Philos. Mag. Series 6, 1913, 25, 193–197 CrossRef CAS.
- H. G. J. Moseley, The High-Frequency Spectra of the Elements, Philos. Mag. Series 6, 1913, 26, 1024–1034 CrossRef.
- H. G. J. Moseley, The high-frequency spectra of the elements. Part II, Philos. Mag. Series 6, 1914, 27, 703–713 CrossRef CAS.
- P. D. Innes, On the velocity of the cathode particles emitted by various metals under the influence of Röntgen rays, and its bearing on the theory of atomic disintegration, Proc. R. Soc. London, Ser. A, 1907, 79, 442–462 CrossRef.
- H. Hertz, Ueber einen Einfluss des ultravioletten Lichtes auf die electrische Entladung, Ann. Phys., 1887, 267, 983–1000 CrossRef.
- A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt, Ann. Phys., 1905, 322, 132–148 CrossRef.
- P. Auger, Sur l'effet photoélectrique composé, J. Phys. Radium, 1925, 6, 205–208 CrossRef CAS.
- J. Chadwick and E. S. Bieler, The collisions of alpha particles with hydrogen nuclei, Philos. Mag. Series 6, 1921, 42, 923–940 CrossRef CAS.
- E. Rutherford, Collisions of alpha particles with light atoms. IV. An anomalous effect in nitrogen, Philos. Mag. Series 6, 1919, 37, 581–587 CrossRef CAS.
- E. Rutherford and J. Chadwick, The disintegration of elements by α particles, Philos. Mag. Series 6, 1922, 44, 417–432 CrossRef CAS.
- J. D. Cockcroft and E. T. S. Walton, Disintegration of lithium by swift protons, Nature, 1932, 129, 649–649 CrossRef CAS.
- W. E. Sweeney and J. B. Marion, Gamma-ray transitions involving isobaric-spin mixed states in 8Be, Phys. Rev., 1969, 182, 1007–2021 CrossRef CAS.
- W. Bothe and W. Gentner, Eine Anlage für schnelle Korpuskularstrahlen und einige damit ausgeführte Umwandlungsversuche, Z. Phys., 1937, 104, 685–693 CrossRef CAS.
- W. A. Fowler, E. R. Gaerttner and C. C. Lauritsen, The gamma-radiation from boron bombarded by protons, Phys. Rev., 1938, 53, 628–636 CrossRef CAS.
- B. D. Anderson, M. R. Dwarakanath, J. S. Schweitzer and A. V. Nero, A new determination of the partial widths of the 16.11 MeV state in 12C, Nucl. Phys. A, 1974, 233, 286–296 CrossRef.
- J. M. Davidson, H. L. Berg, M. M. Lowry, M. R. Dwarakanath, A. J. Sierk and P. Batay-Csorba, Low energy cross sections for 11B(p, 3α), Nucl. Phys. A, 1979, 315, 253–268 CrossRef.
- N. P. Barradas, R. Mateus, M. Fonseca, M. A. Reis, K. Lorenz and I. Vickridge, Thin film depth profiling using simultaneous particle backscattering and nuclear resonance profiling, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1829–1832 CrossRef CAS.
- N. F. Mott, The collision between two electrons, Proc. R. Soc. London, Ser. A, 1930, 126, 259–267 CrossRef CAS.
- C. Gerthsen, The dispersion measurements of H-rays in hydrogen as a contribution to the clarification of their wave nature, Ann. Phys., 1931, 401, 769–786 CrossRef.
- M. A. Tuve, N. P. Heydenburg and L. R. Hafstad, The scattering of protons by protons, Phys. Rev., 1936, 50, 806–825 CrossRef CAS.
- G. Breit, E. U. Condon and R. D. Present, Theory of scattering of protons by protons, Phys. Rev., 1936, 50, 825–845 CrossRef CAS.
- P. Reichart, G. Datzmann, A. Hauptner, R. Hertenberger, C. Wild and G. Dollinger, Three-dimensional hydrogen microscopy in diamond, Science, 2004, 306, 1537–1540 CrossRef CAS PubMed.
- E. M. Burbidge, G. R. Burbidge, W. A. Fowler and F. Hoyle, Synthesis of the elements in stars, Rev. Mod. Phys., 1957, 29, 547–650 CrossRef.
- G. Wallerstein, I. Iben, P. Parker, A. M. Boesgaard, G. M. Hale, A. E. Champagne, C. A. Barnes, F. Kappeler, V. V. Smith, R. D. Hoffman, F. X. Timmes, C. Sneden, R. N. Boyd, B. S. Meyer and D. L. Lambert, Synthesis of the elements in stars: Forty years of progress, Rev. Mod. Phys., 1997, 69, 995–1084 CrossRef CAS.
- D. A. Williams and T. W. Hartquist, The Cosmic-Chemical Bond : Chemistry from the Big Bang to Planet Formation, Royal Society of Chemistry, 2013 Search PubMed.
- K. T. Howard, M. J. Bailey, D. Berhanu, P. A. Bland, G. Cressey, L. E. Howard, C. Jeynes, R. Matthewman, Z. Martins, M. A. Sephton, V. Stolojan and S. Verchovsky, Biomass preservation in impact melt ejecta, Nat. Geosci., 2013, 6, 1018–1022 CrossRef CAS.
- M. J. Bailey, K. T. Howard, K. J. Kirkby and C. Jeynes, Characterisation of inhomogeneous inclusions in Darwin glass using ion beam analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 2219–2224 CrossRef CAS.
- S. Hofmann, Compositonal depth profiling by sputtering, Prog. Surf. Sci., 1991, 36, 35–87 CrossRef CAS.
- A. J. Taylor, D. J. Graham and D. G. Castner, Reconstructing accurate ToF-SIMS depth profiles for organic materials with differential sputter rates, Analyst, 2015, 140, 6005–6014 RSC.
- M. P. Seah, S. J. Spencer, R. Havelund, I. S. Gilmore and A. G. Shard, Depth resolution at organic interfaces sputtered by argon gas cluster ions: the effect of energy, angle and cluster size, Analyst, 2015, 140, 6508–6516 RSC.
- K. Siegbahn, Electron spectroscopy for chemical analysis (ESCA), Philos. Trans. R. Soc. London, Ser. A, 1970, 268, 33–57 CrossRef CAS.
- A. C. Simonsen, J. P. Pøhler, C. Jeynes and S. Tougaard, Quantification of Au deposited on Ni: XPS peak shape analysis compared to RES, Surf. Interface Anal., 1999, 27, 52–56 CrossRef CAS.
- M. P. Seah and S. J. Spencer, Ultrathin SiO2 on Si. VII. Angular accuracy in XPS and an accurate attenuation length, Surf. Interface Anal., 2005, 37, 731–736 CrossRef CAS.
- W. Hourani, P. Periwal, F. Bassani, T. Baron, G. Patriarche and E. Martinez, Nanoscale elemental quantification in heterostructured SiGe nanowires, Nanoscale, 2015, 7, 8544–8553 RSC.
- L. A. Tuyen, E. Szilágyi, E. Kótai, K. Lázár, L. Bottyán, T. Q. Dung, L. C. Cuong, D. D. Khiem, P. T. Phuc, L. L. Nguyen, P. T. Hue, N. T. N. Hue, C. V. Tao and H. D. Chuong, Structural effects induced by 2.5 MeV proton beam on zeolite 4A: Positron annihilation and X-ray diffraction study, Radiat. Phys. Chem., 2015, 106, 355–359 CrossRef CAS.
- A. Cavallaro, F. Sandiumenge, J. Gazquez, T. Puig, X. Obradors, J. Arbiol and H. C. Freyhardt, Growth mechanism, microstructure, and surface modification of nanostructured CeO2 films by chemical solution deposition, Adv. Funct. Mater., 2006, 16, 1363–1372 CrossRef CAS.
- M. P. Seah, S. J. Spencer, F. Bensebaa, I. Vickridge, H. Danzebrink, M. Krumrey, T. Gross, W. Oesterle, E. Wendler, B. Rheinländer, Y. Azuma, I. Kojima, N. Suzuki, M. Suzuki, S. Tanuma, D. W. Moon, H. J. Lee, H. M. Cho, H. Y. Chen, A. T. S. Wee, T. Osipowicz, J. S. Pan, W. A. Jordaan, R. Hauert, U. Klotz, C. van der Marel, M. Verheijen, Y. Tarnminga, C. Jeynes, P. Bailey, S. Biswas, U. Falke, N. V. Nguyen, D. Chandler-Horowitz, J. R. Ehrstein, D. Muller and J. A. Dura, Critical review of the current status of thickness measurements for ultrathin SiO2 on Si Part V. Results of a CCQM pilot study, Surf. Interface Anal., 2004, 36, 1269–1303 CrossRef CAS.
- M. R. Winchester and R. Payling, Radio-frequency glow discharge spectrometry: A critical review, Spectrochim. Acta, Part B, 2004, 59, 607–666 CrossRef.
- A. Gutiérrez-González, C. González-Gago, J. Pisonero, N. Tibbetts, A. Menéndez, M. Vélez and N. Bordel, Capabilities and limitations of LA-ICP-MS for depth resolved analysis of CdTe photovoltaic devices, J. Anal. At. Spectrom., 2015, 30, 191–197 RSC.
- K. P. Jochum, U. Weis, B. Stoll, D. Kuzmin, Q. Yang, I. Raczek, D. E. Jacob, A. Stracke, K. Birbaum, D. A. Frick, D. Günther and J. Enzweiler, Determination of Reference Values for NIST SRM 610-617 Glasses Following ISO Guidelines, Geostand. Geoanal. Res., 2011, 35, 397–429 CrossRef CAS.
- D. Abou-Ras, R. Caballero, C. H. Fischer, C. A. Kaufmann, I. Lauermann, R. Mainz, H. Mönig, A. Schöpke, C. Stephan, C. Streeck, S. Schorr, A. Eicke, M. Döbeli, B. Gade, J. Hinrichs, T. Nunney, H. Dijkstra, V. Hoffmann, D. Klemm, V. Efimova, A. Bergmaier, G. Dollinger, T. Wirth, W. Unger, A. A. Rockett, A. Perez-Rodriguez, J. Alvarez-Garcia, V. Izquierdo-Roca, T. Schmid, P. P. Choi, M. Müller, F. Bertram, J. Christen, H. Khatri, R. W. Collins, S. Marsillac and I. Kötschau, Comprehensive Comparison of Various Techniques for the Analysis of Elemental Distributions in Thin Films, Microsc. Microanal., 2011, 17, 728–751 CrossRef CAS PubMed.
- D. Abou-Ras, R. Caballero, C. Streeck, B. Beckhoff, J.-H. In and S. Jeong, Comprehensive Comparison of Various Techniques for the Analysis of Elemental Distributions in Thin Films: Additional Techniques, Microsc. Microanal., 2015, 21, 1644–1648 CrossRef CAS PubMed.
- B. Pollakowski and B. Beckhoff, Nondestructive Speciation Depth Profiling of Complex TiOx Nano layer Structures by Grazing Incidence X-ray Fluorescence Analysis and Near Edge X-ray Absorption Fine Structure Spectroscopy, Anal. Chem., 2015, 87, 7705–7711 CrossRef CAS PubMed.
- Y. Kayser, P. Hoenicke, D. Banas, J.-C. Dousse, J. Hoszowska, P. Jagodzinski, A. Kubala-Kukus, S. H. Nowak and M. Pajek, Depth profiling of low energy ion implantations in Si and Ge by means of micro-focused grazing emission X-ray fluorescence and grazing incidence X-ray fluorescence, J. Anal. At. Spectrom., 2015, 30, 1086–1099 RSC.
- N. P. Barradas, J. L. Keddie and R. Sackin, Bayesian inference analysis of ellipsometry data, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 59, 6138–6151 CrossRef CAS.
- P. Reinhard, B. Bissig, F. Pianezzi, E. Avancini, H. Hagendorfer, D. Keller, P. Fuchs, M. Döbeli, C. Vigo, P. Crivelli, S. Nishiwaki, S. Buecheler and A. N. Tiwari, Features of KF and NaF Postdeposition Treatments of Cu(In,Ga)Se2 Absorbers for High Efficiency Thin Film Solar Cells, Chem. Mater., 2015, 27, 5755–5764 CrossRef CAS.
- K. Gotlib-Vainshtein, O. Girshevitz, V. Richter and C. N. Sukenik, Charging effects in the ion beam analysis of insulating polymers, Polymer, 2015, 72, 59–62 CrossRef CAS.
- C. Jeynes and G. W. Grime, in Common Concepts chapter of “Characterization of Materials”, ed. E. Kaufmann, Wiley-Blackwell, 2nd edn, 2012 Search PubMed.
- M. A. Reis, N. P. Barradas, C. Pascual-Izarra, P. C. Chaves, A. R. Ramos, E. Alves, G. Gonzalez-Aguilar, M. E. V. Costa and I. M. M. Salvado, Holistic RBS-PIXE data reanalysis of SBT thin film samples, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 261, 439–442 CrossRef CAS.
- P. A. Mandò, M. E. Fedi, N. Grassi and A. Migliori, Differential PIXE for investigating the layer structure of paintings, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 239, 71–76 CrossRef.
- A. G. Karydas, C. Streeck, I. B. Radovic, C. Kaufmann, T. Rissom, B. Beckhoff, M. Jaksic and N. P. Barradas, Ion beam analysis of Cu(In,Ga)Se2 thin film solar cells, Appl. Surf. Sci., 2015, 356631–356638 Search PubMed.
- M. L. Crespillo, J. T. Graham, Y. Zhang and W. J. Weber, In situ luminescence monitoring of ion-induced damage evolution in SiO2 and Al2O3, J. Lumin., 2016, 172, 208–218 CrossRef CAS.
- Z. Mi, Y. Zhang, S. K. Vanga, C.-B. Chen, H. Q. Tan, F. Watt, X. Liu and A. A. Bettiol, Subwavelength imaging through ion-beam-induced upconversion, Nat. Commun., 2015, 6, 8832 CrossRef CAS PubMed.
- D. J. Crossman, Y. Hou, I. Jayasinghe, D. Baddeley and C. Soeller, Combining confocal and single molecule localisation microscopy: A correlative approach to multi-scale tissue imaging, Methods, 2015, 88, 98–108 CrossRef CAS PubMed.
- D. Abriola, P. Dimitriou and A. Pedro de Jesus, Development of a Reference Database for Particle-induced Gamma ray Emission (PIGE) Spectroscopy, Summary Report for the 2nd Research Coordination Meeting (RCM) of the IAEA Coordinated Research Project (CRP) (INDC-NDS-0625), List of participants: D. Strivay, A. Lagoyannis, I. B. Radović, A. Z. Kiss, J. Raisanen, O. Kakuee, H.-W. Becker, M. Chiari, A. Pedro de Jesus, A. F. Gurbich, A. Zucchiatti, D. Abriola, S. Utyenkov and P. Dimitriou, IAEA, Vienna, 2013.
- A. F. Gurbich, Evaluation of cross-sections for particle induced gamma-ray emission (PIGE) spectroscopy, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 331, 31–33 CrossRef CAS.
- M. Stocker, M. Döbeli, M. Grajcar, M. Suter, H. A. Synal and L. Wacker, A universal and competitive compact AMS facility, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 240, 483–489 CrossRef CAS.
- D. Benzeggouta and I. Vickridge, Handbook on Best Practice for Minimising Beam Induced Damage during IBA, Cornell University Library, 2013, eprint arXiv:1303.3171 Search PubMed.
- D. N. Faye, E. Wendler, M. Felizardo, S. Magalhães, E. Alves, F. Brunner, M. Weyers and K. Lorenz, Mechanisms of Implantation Damage Formation in AlxGa1-xN Compounds, J. Phys. Chem. C, 2016, 120, 7277–7283 CAS.
- T. Belhabib, P. Desgardin, T. Sauvage, H. Erramli, M. F. Barthe, F. Garrido, G. Carlot, L. Nowicki and P. Garcia, Lattice location and annealing behaviour of helium atoms implanted in uranium dioxide single crystals, J. Nucl. Mater., 2015, 467, 1–8 CrossRef CAS.
- C. Jeynes, K. E. Puttick, L. C. Whitmore, K. Gärtner, A. E. Gee, D. K. Millen, R. P. Webb, R. M. A. Peel and B. J. Sealy, Laterally resolved crystalline damage in single-point-diamond-turned silicon, Nucl. Instrum. Methods Phys. Res., Sect. B, 1996, 118, 431–436 CrossRef CAS.
- A. L. Turkevich, E. J. Franzgrote and J. H. Patterson, Chemical Analysis of Moon at Surveyor V Landing Site, Science, 1967, 158, 635–637 CAS.
- C. Jeynes, N. P. Barradas and E. Szilágyi, Accurate Determination of Quantity of Material in Thin Films by Rutherford Backscattering Spectrometry, Anal. Chem., 2012, 84, 6061–6069 CrossRef CAS PubMed.
- C. Jeynes, Z. H. Jafri, R. P. Webb, A. C. Kimber and M. J. Ashwin, Accurate RBS measurements of the indium content of InGaAs thin films, Surf. Interface Anal., 1997, 25, 254–260 CrossRef CAS.
- N. C. Anderson and J. S. Owen, Soluble, Chloride-Terminated CdSe Nanocrystals: Ligand Exchange Monitored by H-1 and P-31 NMR Spectroscopy, Chem. Mater., 2013, 25, 69–76 CrossRef CAS.
- W. H. Bragg and M. A. Elder, On the alpha particles of radium, and their loss of range in passing through various atoms and molecules, Philos. Mag. Series 6, 1905, 10, 318–340 CrossRef CAS.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, SRIM - The stopping and range of ions in matter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- N. P. Barradas, A. Bergmaier, K. Mizohata, M. Msimanga, J. Raisanen, T. Sajavaara and A. Simon, Determination of molecular stopping cross section of C-12, O-16, Si-28, Cl-35, Ni-58, Br-79, and I-127 in silicon nitride, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 360, 90–96 CrossRef CAS.
- N. P. Barradas, E. Alves, M. Fonseca, Z. Siketić and I. B. Radović, Stopping power of C, O and Cl in tantalum oxide, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 332, 152–155 CrossRef CAS.
- M. V. Moro, T. F. Silva, A. Mangiarotti, Z. O. Guimaraes-Filho, M. A. Rizzutto, N. Added and M. H. Tabacniks, Traceable stopping cross sections of Al and Mo elemental targets for 0.9-3.6-MeV protons, Phys. Rev. A, 2016, 93 CrossRef CAS , 022704.
- D. J. Cherniak and J. M. Pyle, Th diffusion in monazite, Chem. Geol., 2008, 256, 52–61 CrossRef CAS.
- O. Coronell, B. J. Marinas, X. Zhang and D. G. Cahill, Quantification of functional groups and modeling of their ionization behavior in the active layer of FT30 reverse osmosis membrane, Environ. Sci. Technol., 2008, 42, 5260–5266 CrossRef CAS PubMed.
- O. Voznyy, D. Zhitomirsky, P. Stadler, Z. Ning, S. Hoogland and E. H. Sargent, A Charge-Orbital Balance Picture of Doping in Colloidal Quantum Dot Solids, ACS Nano, 2012, 6, 8448–8455 CrossRef CAS PubMed.
- N. Berry, M. Cheng, C. L. Perkins, M. Limpinsel, J. C. Hemminger and M. Law, Atmospheric-Pressure Chemical Vapor Deposition of Iron Pyrite Thin Films, Adv. Energy Mater., 2012, 2, 1124–1135 CrossRef CAS.
- J. Heo, A. S. Hock and R. G. Gordon, Low Temperature Atomic Layer Deposition of Tin Oxide, Chem. Mater., 2010, 22, 4964–4973 CrossRef CAS.
- A. Ghicov, J. M. Macak, H. Tsuchiya, J. Kunze, V. Haeublein, L. Frey and P. Schmuki, Ion implantation and annealing for an efficient N-doping of TiO2 nanotubes, Nano Lett., 2006, 6, 1080–1082 CrossRef CAS.
- J. L. Colaux, C. Jeynes, K. C. Heasman and R. M. Gwilliam, Certified ion implantation fluence by high accuracy RBS, Analyst, 2015, 140, 3251–3261 RSC.
- “ISO Guide 35:1985, Reference materials - General and statistical principles for certification”, International Organization for Standardization, Geneva, Switzerland, 1985.
- “International vocabulary of metrology (VIM: Vocabulaire international de métrologie)”, 3rd edn., Joint Committee for Guides in Metrology (JCGM 200:2012), 2012.
- K. H. Ecker, A. Berger, R. Grötzschel, L. Persson and U. Wätjen, Antimony implanted in silicon - A thin layer reference material for surface analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 2001, 175, 797–801 CrossRef.
- K. H. Ecker, U. Wätjen, A. Berger, R. Grötzschel, L. Persson, W. Pritzkow, M. Radtke, G. Riebe, H. Riesemeier and J. Vogl, “Certification of Antimony Implanted in Silicon Wafer with a Silicon Dioxide Diffusion Barrier, IRMM-302, BAM-L001”, European Commission - Joint Research Centre (European Communities and Bundesanstalt für Materialforschung und -prüfung), 2001.
- J. L. Colaux and C. Jeynes, High accuracy traceable Rutherford backscattering spectrometry of ion implanted samples, Anal. Methods, 2014, 6, 120–129 RSC.
- J. L. Colaux, G. Terwagne and C. Jeynes, On the traceably accurate voltage calibration of electrostatic accelerators, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 349, 173–183 CrossRef CAS.
- N. P. Barradas, S. A. Almeida, C. Jeynes, A. P. Knights, S. R. P. Silva and B. J. Sealy, RES and ERDA study of ion beam synthesised amorphous gallium nitride, Nucl. Instrum. Methods Phys. Res., Sect. B, 1999, 148, 463–467 CrossRef CAS.
- J. L. Colaux and C. Jeynes, Accurate electronics calibration for particle backscattering spectrometry, Anal. Methods, 2015, 7, 3096–3104 RSC.
- UKAS,“http://www.ukas.org/calibration/schedules/actual/8943Calibration%20Single.pdf”.
- R. Gellert, B. C. Clark III and MSL MER Sci Teams, In Situ Compositional Measurements of Rocks and Soils with the Alpha Particle X-ray Spectrometer on Nasa's Mars Rovers, Elements, 2015, 11, 39–44 CrossRef CAS.
- S. M. McLennan, R. B. Anderson, J. F. Bell III, J. C. Bridges, F. Calef III, J. L. Campbell and MSL Sci Team, Elemental Geochemistry of Sedimentary Rocks at Yellowknife Bay, Gale Crater, Mars, Science, 2014, 343 CrossRef CAS PubMed , 1244734.
- D. W. Ming, P. D. Archer Jr., D. P. Glavin, J. L. Eigenbrode, H. B. Franz, B. Sutter, A. E. Brunner, J. C. Stern, C. Freissinet, A. C. McAdam, P. R. Mahaffy, M. Cabane, P. Coll, J. L. Campbell and MSL Sci Team, Volatile and Organic Compositions of Sedimentary Rocks in Yellowknife Bay, Gale Crater, Mars, Science, 2014, 343 CrossRef CAS PubMed , 1245267.
- J. L. Campbell, G. M. Perrett, R. Gellert, S. M. Andrushenko, N. I. Boyd, J. A. Maxwell, P. L. King and C. D. M. Schofield, Calibration of the Mars Science Laboratory Alpha Particle X-ray Spectrometer, Space Sci. Rev., 2012, 170, 319–340 CrossRef CAS.
- C. M. Heirwegh, J. L. Campbell and G. K. Czamanske, Refinement of major- and minor-element PIXE analysis of rocks and minerals, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 366, 40–50 CrossRef CAS.
- J. L. Campbell, S. M. Andrushenko, S. M. Taylor and J. A. Maxwell, A fundamental parameters approach to calibration of the Mars Exploration Rover Alpha Particle X-ray Spectrometer: 2. Analysis of unknown samples, J. Geophys. Res.: Planets, 2010, 115 CAS , E04009.
- M. Guerra, J. M. Sampaio, T. I. Madeira, F. Parente, P. Indelicato, J. P. Marques, J. P. Santos, J. Hoszowska, J. C. Dousse, L. Loperetti, F. Zeeshan, M. Mueller, R. Unterumsberger and B. Beckhoff, Theoretical and experimental determination of L-shell decay rates, line widths, and fluorescence yields in Ge, Phys. Rev. A, 2015, 92 CrossRef CAS , 022507.
- J. M. Sampaio, T. I. Madeira, J. P. Marques, F. Parente, A. M. Costa, P. Indelicato, J. P. Santos, M. C. Lépy and Y. Ménesguen, Approaches for theoretical and experimental determinations of K-shell decay rates and fluorescence yields in Ge, Phys. Rev. A, 2014, 89 CrossRef CAS , 012512.
- C. M. Heirwegh, I. Pradler and J. L. Campbell, Choice of X-ray mass attenuation coefficients for PIXE analysis of silicate minerals and rocks, X-Ray Spectrom., 2015, 44, 63–68 CrossRef CAS.
- B. Beckhoff, Reference-free X-ray spectrometry based on metrology using synchrotron radiation, J. Anal. At. Spectrom., 2008, 23, 845–853 RSC.
- J. L. Campbell and T. Papp, Widths of the atomic K-N7 levels, At. Data Nucl. Data Tables, 2001, 77, 1–56 CrossRef CAS.
- K. Fennane, M. Berset, J. C. Dousse, J. Hoszowska, P. A. Raboud and J. L. Campbell, Reexamination of M2,3 atomic level widths and L1M2,3 transition energies of elements 69≤Z≤95, Phys. Rev. A, 2013, 88 CrossRef CAS , 052506.
- J. L. Campbell, Fluorescence yields and Coster-Kronig probabilities for the atomic L subshells. Part II: The L1 subshell revisited, At. Data Nucl. Data Tables, 2009, 95, 115–124 CrossRef CAS.
- T. L. Hopman, C. M. Heirwegh, J. L. Campbell, M. Krumrey and F. Scholze, An accurate determination of the K-shell X-ray fluorescence yield of silicon, X-Ray Spectrom., 2012, 41, 164–171 CrossRef CAS.
- C. M. Heirwegh, I. Pradler and J. L. Campbell, An accuracy assessment of photo-ionization cross-section datasets for 1-2 keV X-rays in light elements using PIXE, J. Phys. B: At., Mol. Opt. Phys., 2013, 46 CrossRef CAS , 185602.
- A. Taborda, P. C. Chaves, M. L. Carvalho and M. A. Reis, Polynomial approximation to universal M-shell ionisation cross-sections induced by H+ and He2+ ions, X-Ray Spectrom., 2013, 42, 177–182 CrossRef CAS.
- A. Taborda, P. C. Chaves and M. A. Reis, Polynomial approximation to universal ionisation cross-sections of K and L shells induced by H and He ion beams, X-Ray Spectrom., 2011, 40, 127–134 CrossRef CAS.
- M. Petric and M. Kavčič, Chemical speciation via X-ray emission spectroscopy in the tender X-ray range, J. Anal. At. Spectrom., 2016, 31, 450–457 RSC.
- P. C. Chaves, A. Taborda, J. P. Marques and M. A. Reis, H+ and He2+ induced W L X-rays intensity ratios: part I, Si(Li) data and EDS high resolution insight, X-Ray Spectrom., 2013, 42, 141–150 CrossRef CAS.
- B. Stoll, K. P. Jochum, K. Herwig, M. Amini, M. Flanz, B. Kreuzburg, D. Kuzmin, M. Willbold and J. Enzweiler, An automated iridium-strip heater for LA-ICP-MS bulk analysis of geological samples, Geostand. Geoanal. Res., 2008, 32, 5–26 CrossRef CAS.
- M. H. Ramsey, P. J. Potts, P. C. Webb, P. Watkins, J. S. Watson and B. J. Coles, An objective assessment of analytical method precision: comparison of ICP-AES and XRF for the analysis of silicate rocks, Chem. Geol., 1995, 124, 1–19 CrossRef CAS.
- T. Turnbull, M. Douglass, D. Paterson, E. Bezak, B. Thierry and I. Kempson, Relating Intercellular Variability in Nanoparticle Uptake with Biological Consequence: A Quantitative X-ray Fluorescence Study for Radiosensitization of Cells, Anal. Chem., 2015, 87, 10693–10697 CrossRef CAS PubMed.
- J. C. G. Jeynes, C. Jeynes, M. J. Merchant and K. J. Kirkby, Measuring and modelling cell-to-cell variation in uptake of gold nanoparticles, Analyst, 2013, 138, 7070–7074 RSC.
- S. Goutelle, M. Maurin, F. Rougier, X. Barbaut, L. Bourguignon, M. Ducher and P. Maire, The Hill equation: a review of its capabilities in pharmacological modelling, Fundam. Clin. Pharmacol., 2008, 22, 633–648 CrossRef CAS PubMed.
- J. H. Kelley, R. S. Canon, S. J. Gaff, R. M. Prior, B. J. Rice, E. C. Schreiber, M. Spraker, D. R. Tilley, E. A. Wulf and H. R. Weller, The 11B(p,γ)12C reaction below 100 keV, Phys. Rev. C: Nucl. Phys., 2000, 62 CrossRef CAS , 025803.
- A. Abriola and P. Dimitriou, “Development of a Reference Database for Ion Beam Analysis”, Report of a Coordinated Research Project (CRP) on Reference Database for Ion Beam Analysis (IAEA-TECDOC-1780), List of participants: N. P. Barradas, I. B. Radović, M. Chiari, A. F. Gurbich, C. Jeynes, M. Kokkoris, M. Mayer, A. R. Lopes Ramos, E. Rauhala and I. Vickridge, IAEA, Vienna, 2015.
- C. Jeynes, R. P. Webb and A. Lohstroh, Ion Beam Analysis: A Century of Exploiting the Electronic and Nuclear Structure of the Atom for Materials Characterisation, Rev. Acceler. Sci. Technol., 2011, 04, 41–82 CrossRef.
- A. F. Gurbich, I. Bogdanović Radović, Z. Siketić and M. Jaksić, Measurements and evaluation of the cross-section for helium elastic scattering from nitrogen, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 40–44 CrossRef CAS.
- A. F. Gurbich, SigmaCalc recent development and present status of the evaluated cross-sections for IBA, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 371, 27–32 CrossRef CAS.
- S. Bailey, M. Freer, T. Kokalova, S. Cruz, H. Floyd and D. J. Parker, Energy levels of 18F from the 14N+α resonant reaction, Phys. Rev. C: Nucl. Phys., 2014, 90 CrossRef CAS , 024302.
- A. F. Gurbich and C. Jeynes, Evaluation of Non-Rutherford Alpha Elastic Scattering Cross-sections for Silicon, Nucl. Data Sheets, 2014, 119, 270–272 CrossRef CAS.
- A. F. Gurbich, Evaluated differential cross-sections for IBA, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1703–1710 CrossRef CAS.
- D. Abriola, N. P. Barradas, I. Bogdanović-Radović, M. Chiari, A. F. Gurbich, C. Jeynes, M. Kokkoris, M. Mayer, A. R. Ramos, L. Shi and I. Vickridge, Development of a reference database for Ion Beam Analysis and future perspectives, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 2972–2978 CrossRef CAS.
- R. E. Azuma, E. Uberseder, E. C. Simpson, C. R. Brune, H. Costantini, R. J. de Boer, J. Goerres, M. Heil, P. J. LeBlanc, C. Ugalde and M. Wiescher, AZURE: An R-matrix code for nuclear astrophysics, Phys. Rev. C: Nucl. Phys., 2010, 81 CrossRef , 045805.
- P. M. Endt, Energy levels of A=21–44 nuclei (VII), Nucl. Phys. A, 1990, 521, 1–400 CrossRef.
- C. Ouellet and B. Singh, Nuclear Data Sheets for A=32, Nucl. Data Sheets, 2011, 112, 2199–2355 CrossRef CAS.
- K. M. Källman, Low energy scattering of α-particles by 28Si, Z. Phys. A: Hadrons Nucl., 1987, 356, 287–291 CrossRef.
- V. Paneta, A. Gurbich and M. Kokkoris, Theoretical investigation of the 19F(p, p0) differential cross section up to Ep = 2.3 MeV, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 371, 54–58 CrossRef CAS.
- D. R. Tilley, C. M. Cheves, C. H. Kelley, S. Raman and H. R. Weller, Energy levels of light nuclei, A=20, Nucl. Phys. A, 1998, 636, 249–364 CrossRef.
- J. L. Campbell, N. I. Boyd, N. Grassi, P. Bonnick and J. A. Maxwell, The Guelph PIXE software package IV, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 3356–3363 CrossRef CAS.
- C. G. Ryan, J. S. Laird, L. A. Fisher, R. Kirkham and G. F. Moorhead, Improved Dynamic Analysis method for quantitative PIXE and SXRF element imaging of complex materials, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 363, 42–47 CrossRef CAS.
- T. Baker, R. Mustard, B. Fu, P. J. Williams, G. Dong, L. Fisher, G. Mark and C. G. Ryan, Mixed messages in iron oxide-copper-gold systems of the Cloncurry district, Australia: insights from PIXE analysis of halogens and copper in fluid inclusions, Miner. Deposita, 2008, 43, 599–608 CrossRef CAS.
- L. A. Fisher, D. Fougerouse, J. S. Cleverley, C. G. Ryan, S. Micklethwaite, A. Halfpenny, R. M. Hough, M. Gee, D. Paterson, D. L. Howard and K. Spiers, Quantified, multi-scale X-ray fluorescence element mapping using the Maia detector array: application to mineral deposit studies, Miner. Deposita, 2015, 50, 665–674 CrossRef CAS.
- J. Allison, et al., GEANT4 developments and applications, IEEE Trans. Nucl. Sci., 2006, 53, 270–278 CrossRef.
- S. Agostinelli, et al., GEANT4-a simulation toolkit, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 506, 250–303 CrossRef CAS.
- S. Incerti, P. Barberet, G. Deves, C. Michelet, Z. Francis, V. Ivantchenko, A. Mantero, Z. El Bitar, M. A. Bernal, H. N. Tran, M. Karamitros and H. Seznec, Comparison of experimental proton-induced fluorescence spectra for a selection of thin high-Z samples with Geant4 Monte Carlo simulations, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 358, 210–222 CrossRef CAS.
- M. A. Reis and L. C. Alves, DATTPIXE, a computer package for thick target PIXE data analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 1992, 68, 300–304 CrossRef.
- M. A. Reis, P. C. Chaves, A. Taborda, J. P. Marques and N. P. Barradas, Fixed and free line ratio DT2 PIXE fitting and simulation package, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 318, 65–69 CrossRef CAS.
- M. Mayer, SIMNRA User Guide, Technical Report IPP9/113, Max-Planck-Institut für Plasmaphysik, Garching, Germany, 1997 Search PubMed.
- M. Mayer, in chapter of “Application of Accelerators in Research and Industry, Pts 1 and 2”, ed. J. L. Duggan and I. L. Morgan, Amer Inst Physics, Melville, 1999, vol. 475, pp. 541–544 Search PubMed.
- M. Mayer, Improved physics in SIMNRA 7, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 332, 176–180 CrossRef CAS.
- F. Romanelli and JET-EFDA Contributors, Overview of the JET results with the ITER-like wall, Nucl. Fusion, 2013, 53 CrossRef CAS , 104002.
- A. Baron-Wiechec, A. Widdowson, E. Alves, C. F. Ayres, N. P. Barradas, S. Brezinsek, J. P. Coad, N. Catarino, K. Heinola, J. Likonen, G. F. Matthews, M. Mayer, P. Petersson, M. Rubel, W. van Renterghem, I. Uytdenhouwen and JET-EFDA Contributors, Global erosion and deposition patterns in JET with the ITER-like wall, J. Nucl. Mater., 2015, 463, 157–161 CrossRef CAS.
- N. P. Barradas and C. Jeynes, Advanced physics and algorithms in the IBA DataFurnace, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 1875–1879 CrossRef CAS.
- N. P. Barradas, C. Jeynes and R. P. Webb, Simulated annealing analysis of Rutherford backscattering data, Appl. Phys. Lett., 1997, 71, 291–293 CrossRef CAS.
- N. P. Barradas, K. Arstila, G. Battistig, M. Bianconi, N. Dytlewski, C. Jeynes, E. Kotai, G. Lulli, M. Mayer, E. Rauhala, E. Szilágyi and M. Thompson, Summary of “IAEA intercomparison of IBA software”, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 1338–1342 CrossRef CAS.
- N. P. Barradas, K. Arstila, G. Battistig, M. Bianconi, N. Dytlewski, C. Jeynes, E. Kotai, G. Lulli, M. Mayer, E. Rauhala, E. Szilágyi and M. Thompson, International Atomic Energy Agency intercomparison of ion beam analysis software, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 262, 281–303 CrossRef CAS.
- F. Schiettekatte, Fast Monte Carlo for ion beam analysis simulations, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 1880–1885 CrossRef CAS.
- C. Pascual-Izarra, N. P. Barradas and M. A. Reis, LibCPIXE: A PIXE simulation open-source library for multilayered samples, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 249, 820–822 CrossRef CAS.
- C. Pascual-Izarra, M. A. Reis and N. P. Barradas, Simultaneous PIXE and RBS data analysis using Bayesian inference with the DataFurnace code, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 249, 780–783 CrossRef CAS.
- G. W. Grime, The “Q factor” method: Quantitative microPIXE analysis using RBS normalisation, Nucl. Instrum. Methods Phys. Res., Sect. B, 1996, 109, 170–174 CrossRef.
- T. F. Silva, C. L. Rodrigues, M. Mayer, M. V. Moro, G. F. Trindade, F. R. Aguirre, N. Added, M. A. Rizzutto and M. H. Tabacniks, MultiSIMNRA: A computational tool for self-consistent ion beam analysis using SIMNRA, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 371, 86–89 CrossRef CAS.
- I. Orlić, D. Mekterović, I. Mekterović and T. Ivoševic, VIBA-Lab 3.0: Computer program for simulation and semi-quantitative analysis of PIXE and RBS spectra and 2D elemental maps, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 363, 37–41 CrossRef.
- S. Matsuyama, K. Ishii, K. Watanabe, A. Terakawa, Y. Kikuchi, M. Fujiwara, H. Sugai, M. Karahashi, Y. Nozawa, S. Yamauchi, M. Fujisawa, M. Ishiya, T. Nagaya, R. Ortega, A. Carmona and S. Roudeau, Improvement and recent applications of the Tohoku microbeam system, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 318, 32–36 CrossRef CAS.
- J. L'Ecuyer, C. Brassard, C. Cardinal, J. Chabbal, L. Deschênes, J. P. Labrie, B. Terreault, J. G. Martel and R. St.-Jacques, An accurate and sensitive method for the determination of the depth distribution of light elements in heavy materials, J. Appl. Phys., 1976, 47, 381–382 CrossRef.
- G. Boudreault, R. G. Elliman, R. Grötzschel, S. C. Gujrathi, C. Jeynes, W. N. Lennard, E. Rauhala, T. Sajavaara, H. Timmers, Y. Q. Wang and T. D. M. Weijers, Round Robin: measurement of H implantation distributions in Si by elastic recoil detection, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 222, 547–566 CrossRef CAS.
- I. Gouzman, O. Girshevitz, V. Richter, E. S. Avraham, C. N. Sukenik and G. D. Nessim, High Rate of Hydrogen Incorporation in Vertically Aligned Carbon Nanotubes during Initial Stages of Growth Quantified by Elastic Recoil Detection, J. Phys. Chem. C, 2015, 119, 26726–26733 CAS.
- S. Khamlich, M. Msimanga, C. A. Pineda-Vargas, Z. Y. Nuru, R. McCrindle and M. Maaza, Compositional analysis and depth profiling of thin film CrO2 by heavy ion ERDA and standard RBS: a comparison, Mater. Charact., 2012, 70, 42–47 CrossRef CAS.
- M. Laitinen, M. Rossi, J. Julin and T. Sajavaara, Time-of-flight - Energy spectrometer for elemental depth profiling - Jyväskylä design, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 337, 55–61 CrossRef CAS.
- C. Kottler, M. Döbeli, F. Glaus and M. Suter, A spectrometer for low energy heavy ion ERDA, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 248, 155–162 CrossRef CAS.
- J. Hämäläinen, T. Hatanpää, E. Puukilainen, T. Sajavaara, M. Ritala and M. Leskelä, Iridium metal and iridium oxide thin films grown by atomic layer deposition at low temperatures, J. Mater. Chem., 2011, 21, 16488–16493 RSC.
- T. Blanquart, J. Niinisto, M. Heikkila, T. Sajavaara, K. Kukli, E. Puukilainen, C. Xu, W. Hunks, M. Ritala and M. Leskela, Evaluation and Comparison of Novel Precursors for Atomic Layer Deposition of Nb2O5 Thin Films, Chem. Mater., 2012, 24, 975–980 CrossRef CAS.
- D. K. Bora, A. Braun, R. Erni, U. Müller, M. Döbeli and E. C. Constable, Hematite-NiO/α-Ni(OH)2 heterostructure photoanodes with high electrocatalytic current density and charge storage capacity, Phys. Chem. Chem. Phys., 2013, 15, 12648–12659 RSC.
- M. Döbeli, C. Kottler, M. Stocker, S. Weinmann, H. A. Synal, M. Grajcar and M. Suter, Gas ionization chambers with silicon nitride windows for the detection and identification of low energy ions, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 219, 415–419 CrossRef.
- H. Timmers, T. D. M. Weijers and R. G. Elliman, Unique capabilities of heavy ion elastic recoil detection with gas ionization detectors, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 190, 393–396 CrossRef CAS.
- A. M. Müller, M. Döbeli, M. Seiler and H.-A. Synal, A simple Bragg detector design for AMS and IBA applications, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 356, 81–87 CrossRef.
- Z. Siketić, N. Skukan and I. B. Radović, A gas ionisation detector in the axial (Bragg) geometry used for the time-of-flight elastic recoil detection analysis, Rev. Sci. Instrum., 2015, 86 CrossRef PubMed , 083301.
- M. Mallepell, M. Döebeli and M. Suter, Annular gas ionization detector for low energy heavy ion backscattering spectrometry, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 1193–1198 CrossRef CAS.
- P. S. Lee, K. L. Pey, D. Mangelinck, J. Ding, D. Z. Chi and L. Chan, New salicidation technology with Ni(Pt) alloy for MOSFETs, IEEE Electron Device Lett., 2001, 22, 568–570 CrossRef CAS.
- J. Demeulemeester, D. Smeets, C. Van Bockstael, C. Detavernier, C. M. Comrie, N. P. Barradas, A. Vieira and A. Vantomme, Pt redistribution during Ni(Pt) silicide formation, Appl. Phys. Lett., 2008, 93 CrossRef CAS , 261912.
- N. P. Barradas and A. Vieira, Artificial neural network algorithm for analysis of Rutherford backscattering data, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 5818–5829 CrossRef CAS.
- J. Demeulemeester, D. Smeets, C. M. Comrie, N. P. Barradas, A. Vieira, C. Van Bockstael, C. Detavernier, K. Temst and A. Vantomme, On the growth kinetics of Ni(Pt) silicide thin films, J. Appl. Phys., 2013, 113 CrossRef CAS , 234902.
- J. Demeulemeester, D. Smeets, C. M. Comrie, C. Van Bockstael, W. Knaepen, C. Detavernier, K. Temst and A. Vantomme, The influence of Pt redistribution on Ni(1-x)Pt(x)Si growth properties, J. Appl. Phys., 2010, 108 CrossRef CAS , 043505.
- D. Mangelinck, K. Hoummada, A. Portavoce, C. Perrin, R. Daineche, M. Descoins, D. J. Larson and P. H. Clifton, Three-dimensional composition mapping of NiSi phase distribution and Pt diffusion via grain boundaries in Ni2Si, Scr. Mater., 2010, 62, 568–571 CrossRef CAS.
- N. P. Barradas, A. Vieira and R. Patricio, RBS without humans, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 190, 231–236 CrossRef CAS.
- N. P. Barradas, A. Vieira and R. Patricio, Artificial neural networks for automation of Rutherford backscattering spectroscopy experiments and data analysis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65 CrossRef CAS PubMed , 066703.
- J. Demeulemeester, D. Smeets, N. P. Barradas, A. Vieira, C. M. Comrie, K. Temst and A. Vantomme, Artificial neural networks for instantaneous analysis of real-time Rutherford backscattering spectra, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1676–1681 CrossRef CAS.
- R. S. Averback, L. E. Rehn, W. Wagner, H. Wiedersich and P. R. Okamoto, Kinetics of radiation induced segregation in Ni-12.7 at% Si, Phys. Rev. B: Condens. Matter, 1983, 28, 3100–3109 CrossRef CAS.
- J. Rennie, S. R. Elliott and C. Jeynes, Rutherford Backscattering Study of the Photodissolution of Ag in Amorphous Gese2, Appl. Phys. Lett., 1986, 48, 1430–1432 CrossRef CAS.
- R. Kötz, J. Gobrecht, S. Stucki and R. Pixley, In situ rutherford backscattering spectroscopy for electrochemical interphase analysis, Electrochim. Acta, 1986, 31, 169–172 CrossRef.
- A. Hightower, B. Koel and T. Felter, A study of iodine adlayers on polycrystalline gold electrodes by in situ electrochemical Rutherford backscattering (ECRBS), Electrochim. Acta, 2009, 54, 1777–1783 CrossRef CAS.
- A. S. Clough, S. A. Collins, F. E. Gauntlett, M. R. Hodgson, C. Jeynes, M. S. Rihawy, A. M. Todd and R. L. Thompson, In situ water permeation measurement using an external 3He2+ ion beam, J. Membr. Sci., 2006, 285, 137–143 CrossRef CAS.
- X. Y. Yu, B. Liu, L. Yang, Z. Zhu and M. J. Marshall, Microfluidic electrochemical device and process for chemical imaging and electrochemical analysis at the electrode-liquid interface in situ, US2014/0038224A1, 2014, U.S.P.A. Publication Search PubMed.
- Q. Le Trequesser, G. Devès, G. Saez, L. Daudin, P. Barberet, C. Michelet, M.-H. Delville and H. Seznec, Single Cell In Situ Detection and Quantification of Metal Oxide Nanoparticles Using Multimodal Correlative Microscopy, Anal. Chem., 2014, 86, 7311–7319 CrossRef CAS PubMed.
- P. Pelicon, N. C. Podaru, P. Vavpetič, L. Jeromel, N. O. Potocnik, S. Ondračka, A. Gottdang and D. J. M. Mous, A high brightness proton injector for the Tandetron accelerator at Jožef Stefan Institute, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 332, 229–233 CrossRef CAS.
- G. J. F. Legge, C. D. McKenzie, A. P. Mazzolini, R. M. Sealock, D. N. Jamieson, P. M. Obrien, J. C. McCallum, G. L. Allan, R. A. Brown, R. A. Colman, B. J. Kirby, M. A. Lucas, J. Zhu and J. Cerini, Microbeam imaging at micron and submicron resolution, Nucl. Instrum. Methods Phys. Res., Sect. B, 1986, 15, 669–674 CrossRef.
- Y. Q. Li, C. Habchi, X. Liu, Y. Y. Liu, Y. Zheng, X. Y. Li and H. Shen, Scanning transmission ion microscopy computed tomography (STIM-CT) for inertial confinement fusion (ICF) targets, Fusion Eng. Des., 2013, 88, 188–194 CrossRef CAS.
- F. Watt, X. Chen, A. B. De Vera, C. N. B. Udalagama, M. Ren, J. A. van Kan and A. A. Bettiol, The Singapore high resolution single cell imaging facility, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 2168–2174 CrossRef CAS.
- J. P. Landsberg, B. McDonald and F. Watt, Absence of aluminum in neuritic plaque cores in Alzheimers-disease, Nature, 1992, 360, 65–68 CrossRef CAS PubMed.
- I. Orlic, F. Watt, K. K. Loh and S. M. Tang, Nuclear microscopy of single aerosol-particles, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 85, 840–844 CrossRef CAS.
- X. Chen, C.-B. Chen, C. N. B. Udalagama, M. Ren, K. E. Fong, L. Y. L. Yung, P. Giorgia, A. A. Bettiol and F. Watt, High-Resolution 3D Imaging and Quantification of Gold Nanoparticles in a Whole Cell Using Scanning Transmission Ion Microscopy, Biophys. J., 2013, 104, 1419–1425 CrossRef CAS PubMed.
- R. M. S. Schofield and H. W. Lefevre, PIXE-STIM microtomography: zinc and manganese concentrations in a scorpion stinger, Nucl. Instrum. Methods Phys. Res., Sect. B, 1992, 72, 104–110 CrossRef.
- D. Beasley and N. M. Spyrou, Error reduction in simultaneous proton induced X-ray emission tomography and on/off-axis scanning transmission ion microscopy-tomography, J. Radioanal. Nucl. Chem., 2008, 278, 773–776 CrossRef CAS.
- C. Michelet, P. Barberet, P. Moretto and H. Seznec, Development and applications of STIM- and PIXE-tomography: A review, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 363, 55–60 CrossRef CAS.
- D. G. Beasley, L. C. Alves, P. Barberet, S. Bourret, G. Deves, N. Gordillo, C. Michelet, Q. Le Trequesser, A. C. Marques, H. Seznec and R. C. da Silva, A comparison of quantitative reconstruction techniques for PIXE-tomography analysis applied to biological samples, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 331, 248–252 CrossRef CAS.
- T. Andrea, M. Rothermel, R. Werner, T. Butz and T. Reinert, Limited angle STIM and PIXE tomography of single cells, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1884–1888 CrossRef CAS.
- T. Satoh, M. Koka, W. Kada, A. Yokoyama, T. Ohkubo, A. Yamazaki, Y. Ishii, T. Kamiya and N. Kozai, Effectiveness of a combination of ML-EM and STIM-CT in PIXE-CT for biological specimen, Int. J. PIXE, 2012, 22, 73–80 CrossRef CAS.
- M. Bazalova-Carter, M. Ahmad, T. Matsuura, S. Takao, Y. Matsuo, R. Fahrig, H. Shirato, K. Umegaki and L. Xing, Proton-induced x-ray fluorescence CT imaging, Med. Phys., 2015, 42, 900–907 CrossRef CAS PubMed.
- D. Schulz-Ertner and H. Tsujii, Particle radiation therapy using proton and heavier ion beams, J. Clin. Oncol., 2007, 25, 953–964 CrossRef PubMed.
- D. L. Kogan, A. M. Kazancev and L. E. Kuzmin, Beam expert: integrated software for nuclear analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 88, 495–498 CrossRef CAS.
- Y. P. Pyt'ev, Reduction problems in experimental investigations, Math. USSR-Sbornik, 1983, 120, 237–272 Search PubMed ; (in Russian: Trans. Math. USSR Sbornik, 1984, 248, 1237–1372).
- R. Fischer, M. Mayer, W. von der Linden and V. Dose, Enhancement of the energy resolution in ion-beam experiments with the maximum-entropy method, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 6667–6673 CrossRef CAS.
- R. Fischer, Depth profiles and resolution limits in accelerator-based solid state analysis, Anal. Bioanal. Chem., 2002, 374, 619–625 CrossRef CAS PubMed.
- K. Schmid and U. von Toussaint, Statistically sound evaluation of trace element depth profiles by ion beam analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 281, 64–71 CrossRef CAS.
- L. Gao, W. Jacob, G. Meisl, T. Schwarz-Selinger, T. Höschen, U. von Toussaint and T. Dürbeck, Interaction of deuterium plasma with sputter-deposited tungsten nitride films, Nucl. Fusion, 2016, 56 CAS , 016004.
- S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Optimization by simulated annealing, Science, 1983, 220, 671–680 CAS.
- N. P. Barradas, C. Jeynes, M. Jenkin and P. K. Marriott, Bayesian error analysis of Rutherford backscattering spectra, Thin Solid Films, 1999, 343, 31–34 CrossRef.
- V. Dose, Bayesian inference in physics: case studies, Rep. Prog. Phys., 2003, 66, 1421–1461 CrossRef.
- C. D. James, C. Jeynes, N. P. Barradas, L. Clifton, R. M. Dalgliesh, R. F. Smith, S. W. Sankey, L. R. Hutchings and R. L. Thompson, Modifying polyester surfaces with incompatible polymer additives, React. Funct. Polym., 2015, 89, 40–48 CrossRef CAS.
- N. P. Barradas, A. P. Knights, C. Jeynes, O. A. Mironov, T. J. Grasby and E. H. C. Parker, High-depth-resolution Rutherford backscattering data and error analysis of SiGe systems using the simulated annealing and Markov chain Monte Carlo algorithms, Phys. Rev. B: Condens. Matter, 1999, 59, 5097–5105 CrossRef CAS.
- N. P. Barradas, N. Catarino, E. Alves, I. B. Radović and A. F. Gurbich, Measurement and evaluation of the 13C(p,p)13C cross section in the energy range 0.8-2.4 MeV, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 316, 81–87 CrossRef CAS.
- V. Dose and U. von Toussaint, in “Beyond Least Squares” chapter of “Bayesian Inference and Maximum Entropy Methods in Science and Engineering”, ed. U. VonToussaint, AIP Conference Proceedings, 2013, vol. 1553, pp. 92–105 Search PubMed.
- F. Yang-Wallentin, K. G. Joreskog and H. Luo, Confirmatory Factor Analysis of Ordinal Variables With Misspecified Models, Struct. Equat. Model., 2010, 17, 392–423 CrossRef.
- M. M. Li, W. Guo, B. Verma, K. Tickle and J. O'Connor, Intelligent methods for solving inverse problems of backscattering spectra with noise: a comparison between neural networks and simulated annealing, Neural Comput. Appl., 2009, 18, 423–430 CrossRef.
- L. de Viguerie, L. Beck, J. Salomon, L. Pichon and P. Walter, Composition of Renaissance Paint Layers: Simultaneous Particle Induced X-ray Emission and Backscattering Spectrometry, Anal. Chem., 2009, 81, 7960–7966 CrossRef CAS PubMed.
- N. P. Barradas and R. Smith, Simulated annealing analysis of nuclear reaction analysis measurements of polystyrene systems, J. Phys. D: Appl. Phys., 1999, 32, 2964–2971 CrossRef CAS.
- N. P. Barradas, C. Jeynes, R. P. Webb, U. Kreissig and R. Grötzschel, Unambiguous automatic evaluation of multiple Ion Beam Analysis data with Simulated Annealing, Nucl. Instrum. Methods Phys. Res., Sect. B, 1999, 149, 233–237 CrossRef CAS.
- N. P. Barradas, S. Parascandola, B. J. Sealy, R. Grötzschel and U. Kreissig, Simultaneous and consistent analysis of NRA, RES and ERDA data with the IBA DataFurnace, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 161, 308–313 CrossRef.
- S. Shaw, B. Yuan, X. Tian, K. J. Miller, B. M. Cote, J. L. Colaux, A. Migliori, M. G. Panthani and L. Cademartiri, Building Materials from Colloidal Nanocrystal Arrays: Preventing Crack Formation during Ligand Removal by Controlling Structure and Solvation, Adv. Mater., 2016 DOI:10.1002/adma.201601872 , accepted.
- S. Shaw, J. L. Colaux, J. L. Hay, F. C. Peiris and L. Cademartiri, Evolution of the Structure, Composition and Mechanical Properties of Colloidal Nanocrystal Films Upon the Removal of Ligands by O2 Plasma, Adv. Mater., 2016 DOI:10.1002/adma.201601873.
- W. A. Lanford, S. Bedell, S. Amadon, A. Haberl, W. Skala and B. Hjorvarsson, Characteristics of Albany's compact high resolution magnetic spectrometer, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 161, 202–206 CrossRef.
- K. Kimura, S. Joumori, Y. Oota, K. Nakajima and M. Suzuki, High-resolution RBS: a powerful tool for atomic level characterization, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 219, 351–357 CrossRef.
- K. Nakajima, S. Oshima, M. Suzuki and K. Kimura, Surface structures of equimolar mixtures of imidazolium-based ionic liquids using high-resolution Rutherford backscattering spectroscopy, Surf. Sci., 2012, 606, 1693–1699 CrossRef CAS.
- M. Hess, U. K. Krieger, U. Weers, E. Hausammann, T. Peter and W. A. Lanford, Grazing angle 2 MeV RBS on the surface of a liquid with atomic layer depth resolution, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1711–1713 CrossRef CAS.
- K. Kimura, K. Nakajima, T. Conard, W. Vandervorst, A. Bergmaier and G. Dollinger, Analysis of Ultra-Thin HfO2/SiON/Si(001): Comparison of Three Different Techniques, Anal. Sci., 2010, 26, 223–226 CrossRef CAS PubMed.
- N. P. Barradas, Fitting of RBS data including roughness: Application to Co/Re multilayers, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 190, 247–251 CrossRef CAS.
- E. Szilágyi, Energy spread in ion beam analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 161, 37–47 CrossRef.
- N. P. Barradas, J. C. Soares, M. F. da Silva, F. Pászti and E. Szilágyi, Study of multilayer substrate surface roughness using RBS with improved depth resolution, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 94, 266–270 CrossRef CAS.
- A. C. Withers, H. Bureau, C. Raepsaet and M. M. Hirschmann, Calibration of infrared spectroscopy by elastic recoil detection analysis of H in synthetic olivine, Chem. Geol., 2012, 334, 92–98 CrossRef CAS.
- J. Chappell, D. G. Lidzey, P. C. Jukes, A. M. Higgins, R. L. Thompson, S. O'Connor, I. Grizzi, R. Fletcher, J. O'Brien, M. Geoghegan and R. A. L. Jones, Correlating structure with fluorescence emission in phase-separated conjugated-polymer blends, Nat. Mater., 2003, 2, 616–621 CrossRef CAS PubMed.
- R. S. Payne, A. S. Clough, P. Murphy and P. J. Mills, Use of the d(3He,p)4He reaction to study polymer diffusion in polymer melts, Nucl. Instrum. Methods Phys. Res., Sect. B, 1989, 42, 130–134 CrossRef.
- R. A. L. Jones, E. J. Kramer, M. H. Rafailovich, J. Sokolov and S. A. Schwarz, Surface enrichment in an isotopic polymer blend, Phys. Rev. Lett., 1989, 62, 280–283 CrossRef CAS PubMed.
- A. Briddick, P. Li, A. Hughes, F. Courchay, A. Martinez and R. L. Thompson, Surfactant and Plasticizer Segregation in Thin Poly(vinyl alcohol) Films, Langmuir, 2016, 32, 864–872 CrossRef CAS PubMed.
- R. Lowery, M. I. Gibson, R. L. Thompson and E. Fullam, Deuterated carbohydrate probes as ‘label-free’ substrates for probing nutrient uptake in mycobacteria by nuclear reaction analysis, Chem. Commun., 2015, 51, 4838–4841 RSC.
- S. Goffri, C. Müller, N. Stingelin-Stutzmann, D. W. Breiby, C. P. Radano, J. W. Andreasen, R. Thompson, R. A. J. Janssen, M. M. Nielsen, P. Smith and H. Sirringhaus, Multicomponent semiconducting polymer systems with low crystallization-induced percolation threshold, Nat. Mater., 2006, 5, 950–956 CrossRef CAS PubMed.
- A. Utgenannt, R. Maspero, A. Fortini, R. Tumer, M. Florescu, C. Jeynes, A. G. Kanaras, O. L. Muskens, R. P. Sear and J. L. Keddie, Fast Assembly of Gold Nanoparticles in Large-Area 2D Nanogrids Using a One-Step, Near-Infrared Radiation-Assisted Evaporation Process, ACS Nano, 2016, 10, 2232–2242 CrossRef CAS PubMed.
- N. Morshed, N. Echols and P. D. Adams, Using support vector machines to improve elemental ion identification in macromolecular crystal structures, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 1147–1158 CAS.
- S. V. Antonyuk and M. A. Hough, Monitoring and validating active site redox states in protein crystals, Biochim. Biophys. Acta, Proteins Proteomics, 2011, 1814, 778–784 CrossRef CAS PubMed.
- E. Garman, Leaving no element of doubt: analysis of proteins using microPIXE, Struct. Fold. Des., 1999, 7, R291–R299 CrossRef CAS PubMed.
- E. F. Garman and G. W. Grime, Elemental analysis of proteins by microPIXE, Prog. Biophys. Mol. Biol., 2005, 89, 173–205 CrossRef CAS PubMed.
- S. C. Yong, P. Roversi, J. Lillington, F. Rodriguez, M. Krehenbrink, O. B. Zeldin, E. F. Garman, S. M. Lea and B. C. Berks, A complex iron-calcium cofactor catalyzing phosphotransfer chemistry, Science, 2014, 345, 1170–1173 CrossRef CAS PubMed.
- D. Komander, C. J. Lord, H. Scheel, S. Swift, K. Hofmann, A. Ashworth and D. Barford, The structure of the CYLD USP domain explains its specificity for Lys63-linked polyubiquitin and reveals a B box module, Mol. Cell, 2008, 29, 451–464 CrossRef CAS PubMed.
- S. Karkehabadi, H. Hansson, S. Kim, K. Piens, C. Mitchinson and M. Sandgren, The First Structure of a Glycoside Hydrolase Family 61 Member, Cel61B from Hypocrea jecorina, at 1.6 angstrom Resolution, J. Mol. Biol., 2008, 383, 144–154 CrossRef CAS PubMed.
- F. Jacobson, S. Karkehabadi, H. Hansson, F. Goedegebuur, L. Wallace, C. Mitchinson, K. Piens, I. Stals and M. Sandgren, The Crystal Structure of the Core Domain of a Cellulose Induced Protein (Cip1) from Hypocrea jecorina, at 1.5 angstrom Resolution, PLoS One, 2013, 8 CAS , e70562.
- G. Calzolai, F. Lucarelli, M. Chiari, S. Nava, M. Giannoni, L. Carraresi, P. Prati and R. Vecchi, Improvements in PIXE analysis of hourly particulate matter samples, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 363, 99–104 CrossRef CAS.
- S. Nava, F. Lucarelli, F. Amato, S. Becagli, G. Calzolai, M. Chiari, M. Giannoni, R. Traversi and R. Udisti, Biomass burning contributions estimated by synergistic coupling of daily and hourly aerosol composition records, Sci. Total Environ., 2015, 511, 11–20 CrossRef CAS PubMed.
- L. C. Alves, E. Alves, N. P. Barradas, R. Mateus, P. Carvalho, J. P. Coad, A. M. Widdowson, J. Likonen and S. Koivuranta, Erosion and re-deposition processes in JET tiles studied with ion beams, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1991–1996 CrossRef CAS.
- A. F. Gurbich, Evaluation of non-Rutherford proton elastic scattering cross section for carbon, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 136, 60–65 CrossRef.
- D. Abriola, A. F. Gurbich, M. Kokkoris, A. Lagoyannis and V. Paneta, Proton elastic scattering differential cross-sections for 12C, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 2011–2016 CrossRef CAS.
- J. P. Stoquert and T. Szörényi, Determination of the number and size of inhomogeneities in thin films by ion beam analysis, Phys. Rev. B, 2002, 66 CrossRef CAS , 144108.
- S. Calusi, The External Ion Microbeam of the LABEC Laboratory in Florence: Some Applications to Cultural Heritage, Microsc. Microanal., 2011, 17, 661–666 CrossRef CAS PubMed.
- M. Menu, IBA in the museum: Why AGLAE, Nucl. Instrum. Methods Phys. Res., Sect. B, 1990, 45, 597–603 CrossRef.
- L. Pichon, B. Moignard, Q. Lemasson, C. Pacheco and P. Walter, Development of a multi-detector and a systematic imaging system on the AGLAE external beam, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 318(Part A), 27–31 CrossRef CAS.
- T. Calligaro and J.-C. Dran, in Art and Archaeology Applications chapter of “Ion Beam Analysis: Fundamentals and Applications“, ed. M. Nastasi, J. W. Mayer and Y. Wang, CRC Press-Taylor & Francis Group, 2015, pp. 267–307 Search PubMed.
- L. Giuntini, A review of external microbeams for ion beam analyses, Anal. Bioanal. Chem., 2011, 401, 785–793 CrossRef CAS PubMed.
- C. Pascual-Izarra, N. P. Barradas, M. A. Reis, C. Jeynes, M. Menu, B. Lavedrine, J. Jacques Ezrati and S. Roehrs, Towards truly simultaneous PIXE and RBS analysis of layered objects in cultural heritage, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 261, 426–429 CrossRef CAS.
- L. Beck, C. Jeynes and N. P. Barradas, Characterization of paint layers by simultaneous self-consistent fitting of RBS/PIXE spectra using simulated annealing, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 1871–1874 CrossRef CAS.
- M. Mayer, Ion beam analysis of rough thin films, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 194, 177–186 CrossRef CAS.
- S. L. Molodtsov, A. F. Gurbich and C. Jeynes, Accurate ion beam analysis in the presence of surface roughness, J. Phys. D: Appl. Phys., 2008, 41 CrossRef CAS , 205303.
- V. Paneta, J. L. Colaux, A. F. Gurbich, C. Jeynes and M. Kokkoris, Benchmarking experiments for the proton backscattering on Na-23, P-31 and S-nat up to 3.5 MeV, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 328, 1–7 CrossRef CAS.
- M. R. J. Palosaari, M. Käyhkö, K. M. Kinnunen, M. Laitinen, J. Julin, J. Malm, T. Sajavaara, W. B. Doriese, J. Fowler, C. Reintsema, D. Swetz, D. Schmidt, J. N. Ullom and I. J. Maasilta, Phys. Rev. Appl., 2016, 6 Search PubMed , 024002.
Footnotes |
| † Now at University of Namur, Synthesis, Irradiation and Analysis of Materials (SIAM), Namur B-5000, Belgium. |
| ‡ See https://nucleus.iaea.org/sites/accelerators/Pages/default.aspx: the list of accelerator laboratories at the IAEA “Accelerator Knowledge Portal”. |
| § IRMM: Institute for Reference Methods and Materials, Geel. |
| ¶ BAM: Bundesanstalt für Materialforschung und –prüfung, Berlin. |
| This journal is © The Royal Society of Chemistry 2016 |
