Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion mobility mass spectrometry of peptide, protein, and protein complex ions using a radio-frequency confining drift cell†
Samuel J.
Allen
a,
Kevin
Giles
b,
Tony
Gilbert
b and
Matthew F.
Bush
*a
aUniversity of Washington, Department of Chemistry, Box 351700, Seattle, WA 98195-1700, USA. E-mail: mattbush@uw.edu
bWaters Corporation, Stamford Avenue, Altrincham Road, Wilmslow, SK9 4AX, UK
First published on 4th January 2016
Abstract
Ion mobility mass spectrometry experiments enable the characterization of mass, assembly, and shape of biological molecules and assemblies. Here, a new radio-frequency confining drift cell is characterized and used to measure the mobilities of peptide, protein, and protein complex ions. The new drift cell replaced the traveling-wave ion mobility cell in a Waters Synapt G2 HDMS. Methods for operating the drift cell and determining collision cross section values using this experimental set up are presented within the context of the original instrument control software. Collision cross sections for 349 cations and anions are reported, 155 of which are for ions that have not been characterized previously using ion mobility. The values for the remaining ions are similar to those determined using a previous radio-frequency confining drift cell and drift tubes without radial confinement. Using this device under 2 Torr of helium gas and an optimized drift voltage, denatured and native-like ions exhibited average apparent resolving powers of 14.2 and 16.5, respectively. For ions with high mobility, which are also low in mass, the apparent resolving power is limited by contributions from ion gating. In contrast, the arrival-time distributions of low-mobility, native-like ions are not well explained using only contributions from ion gating and diffusion. For those species, the widths of arrival-time distributions are most consistent with the presence of multiple structures in the gas phase.
Introduction
Ion mobility has grown in popularity as a powerful gas-phase technique capable of rapid, efficient separation and structural characterization.1 Ion mobility has been used for the analysis of explosives,2 peptides,3 proteins,4 protein complexes,5–10 and other biomolecules.11 Many variations of this gas-phase technique exist (e.g., differential mobility analysis,12 trapped ion mobility spectrometry,13 and traveling-wave ion mobility spectrometry14) that use different gas compositions, pressures, and electric fields, but are all ultimately designed to leverage differences in gas-phase ion transport that depend on shape and charge. Traditional ion mobility experiments measure the drift times of ions in a neutral background gas (typically helium, nitrogen, or air) under a weak electric field. These ion mobility experiments are usually operated in a low-field regime, in which the mobility of the ion (K, cm2 V−1 s−1) is independent of the applied drift field strength (V cm−1 Torr−1).15Traditional “direct-current-only” (DC-only) ion mobility drift tubes are composed of a series of ring electrodes with an applied DC voltage that changes linearly along the length of the drift tube.16–20 The diffusion-limited resolving power depends on the thermal diffusion along the axis of transmission:21,22
 | (1) |
Here we characterize the performance of, and report methods for, a new RF-confining drift cell that has been integrated into a Waters Synapt G2 HDMS.27 An RF-confining drift cell uses a constant DC potential gradient, similar to a DC-only drift tube, but also applies RF potentials to all electrodes (alternating phases applied to neighboring electrodes), similar to a stacked-ring ion guide. The applied RF potentials radially confine ions across the entire length of the drift cell. Collision cross sections of 349 ions determined using this device are reported. These values can be used to calibrate traveling-wave ion mobility spectrometry experiments28–32 and complement existing reference values available in the literature.4,30,31,33–38 Mobility measurements of peptide, protein, and protein complex ions are compared to those from other devices, demonstrating the accuracy of the values determined using this drift cell. The measured arrival-time distributions enable a critical evaluation of resolving power in these experiments. The apparent resolving powers observed here for peptide ions are significantly limited by contributions from ion gating. The broad arrival-time distributions of native-like protein and protein complex ions are attributed to additional contributions to peak widths that are not accounted for by gating and diffusion alone. Overall, the new RF-confining drift cell was efficiently integrated into the commercial instrument and enables absolute mobility measurements for a broad range of analytes.
Experimental methods
Ionization and sample preparation
Ions were formed by nanoelectrospray using borosilicate capillaries (0.78 mm inner diameter) with a tip at one end (1 to 3 µm inner diameter) pulled using a micropipette puller (Sutter Instruments model P-97, Novato, CA). A platinum wire placed in the open end of the capillary and in contact with the solution was used as the ionization electrode. ESI Table S1† describes the sample preparation. Briefly, peptide and denatured protein analytes were electrosprayed from aqueous or aqueous/organic solutions containing either acid or base for positive or negative ion mode experiments, respectively. Most native-like proteins and protein complexes were electrosprayed from 200 mM ammonium acetate buffer solutions at pH = 7.0.Instrumentation
All measurements were performed using a Synapt G2 HDMS (Waters Corporation, Wilmslow, UK) instrument in which the traveling-wave ion mobility cell was replaced by a new RF-confining drift cell. Voltages for most optics were minimized to reduce ion activation and are reported in the ESI Example Waters Synapt G2 HDMS Parameters File.† Ions are introduced directly from the Trap Cell into the RF-confining drift cell (ESI Fig. S1†). The new RF-confining drift cell is 25.2 cm long and consists of 168 gold-coated ring electrodes that are 0.5 mm thick, have center-to-center spacing of 1.5 mm, and an electrode inner diameter of 7 mm. Entrance and exit plates contain 2 mm apertures for ion transmission. The electrodes are connected to printed circuit boards that contain voltage divider networks consisting of 5 and 10 MΩ resistors that establish a uniform voltage drop (or drift voltage) across the drift cell (ESI Fig. S2†). The circuitry of the printed circuit boards was designed such that the RF-confining drift cell uses the same electrical inputs as the original traveling-wave mobility cell, enabling the control of drift voltage from the original instrument software. The drift voltage is applied using four software parameters, as shown in ESI Fig. S2.† The 25.05 cm drift region spans from the first electrode to the exit plate of the RF-confining drift cell. The peak-to-peak RF amplitude in the RF-confining drift cell was set at 100 V with a frequency of 2.8 MHz.Ion gating and injection was controlled using a mobility trap height of 10 to 15 V and trapping release times ranging from 100 to 200 μs; longer times were used for larger protein and protein complex ions to improve sensitivity. Compared to the analogous traveling-wave ion mobility cell27 the helium cell entrance plate was removed (ESI Fig. S1†), which increases the conductance limit to the helium cell. Buffer gas was introduced using a new gas inlet system (ESI Fig. S3†) that delivers gas to the center of the RF-confining drift cell, rather than the original mobility gas inlet located near the entrance of the drift region. These changes were made to minimize the net flow of gas along the longitudinal axis of the cell.
In this instrument, several factors contribute to obtaining optimal ion transmission and Gaussian-like arrival-time distributions. Ion transmission is improved for large (greater than 60 kDa) proteins and protein complexes when the source backing pressure is raised to 4 to 6 mbar, the Trap Cell flow rate is raised to 10 mL min−1, and the transfer cell exit is set to 0 V. Additionally, the transfer cell wave height is set at 2 to 4 V and the wave velocity is adjusted between 60 to 200 m s−1 to maximize transmission and retain the ion mobility separation.
Determining collision cross section values
Methods for determining ion mobilities in an RF-confining drift cell are analogous to those for a DC-only drift tube. Ion velocities (v) are proportional to the mobility of an ion (K) and the applied electric field (E), which depends on the drift voltage (V) and the length (L) of the drift region: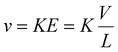 | (2) |
Measured drift times in these experiments depend on the residence time in the drift cell (tD) and the transport time of ions from the exit of the drift cell to the time-of-flight mass analyzer (t0):
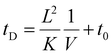 | (3) |
In this system, the drift voltage can be varied up to 354 V (ESI Fig. S2†). The centroid of each arrival-time distribution is estimated by fitting the distribution to a Gaussian function using in-house software.38 For most mobility experiments, drift times were measured at 10 drift voltages ranging from 104 to 354 V. Plotting drift time versus reciprocal drift voltage enables the determination of K from the slopes of the best-fit lines (eqn (3)). Structural information can be obtained from ion mobility experiments by converting measured K into a collision cross section (Ω), which, to a first approximation, describes the orientationally-averaged projection of the ion-neutral interaction area.39,40Ω values were determined using the Mason-Schamp equation:15
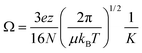 | (4) |
Results & discussion
RF-confining drift cells
Our objective was to develop a new ion mobility device that would enable absolute Ω measurements, while leveraging the broad range of ion selection, activation, and analysis capabilities of the Waters Synapt G2 HDMS. Modifying commercial instrumentation with ion mobility capabilities has been reported previously.30,41–44 The first RF-confining drift cell30 was implemented into a Waters Synapt G1 HDMS and has been used to measure mobilities for a broad range of biomolecules.30,31,37,38,45 An RF-confining drift cell contains RF potentials that radially confine ions in addition to a DC voltage drop that is uniform across all electrodes. Other ion mobility devices that use RF-confinement include segmented quadrupole instruments41,43 and a stacked-ring ion guide containing an axial DC field established by groups of four electrodes.42 Compared to those devices that contain a “staircase-like” DC voltage drop, ions in an RF-confining drift cell experience a uniform voltage drop along the axis of transmission (ESI Fig. S4†). The new RF-confining drift cell described here contains the same physical dimensions and electrical inputs as a Waters Synapt G2 HDMS traveling-wave ion mobility cell, but printed circuits boards now contain a voltage divider network that establishes a uniform voltage drop across the cell, in addition to a capacitor network to couple RF to all electrodes.The main advantage of this device is that it enables direct and absolute Ω measurements with high sensitivity and without using external calibration, which is required for traveling-wave28 and trapped46 ion mobility spectrometry. Implementation using a Synapt G2 HDMS instrument, relative to a Synapt G1 HDMS instrument, takes advantage of access to higher drift voltages and an improved mass analyzer that has higher mass resolving power and dynamic range. Ion mobility measurements using this device can also be used in tandem with other manipulations that are possible on this platform, including collision-induced dissociation,47 ion/ion chemistry,48–50 and surface-induced dissociation.51
Collision cross sections
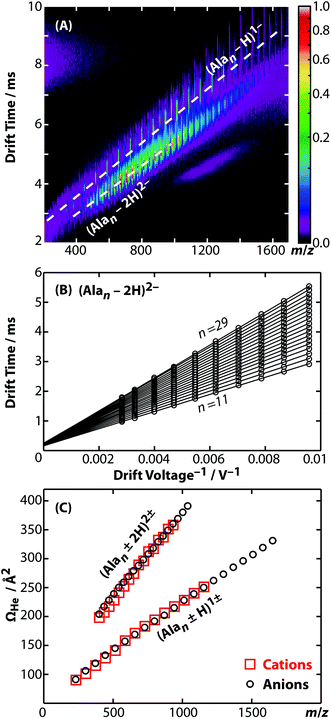
Representative ion mobility data acquired using the new RF-confining drift cell are shown in Fig. 1A. This plot shows separation in drift time and m/z of different charge states (z) and chain lengths (n) of poly-DL-alanine anions, (Alan − zH)z−, in 2 Torr helium gas using a drift voltage of 104 V. Fig. 1B shows drift times acquired for the n = 11 to 29 oligomers of (Alan − 2H)2− measured at 10 drift voltages ranging from 104 to 354 V. This extremely linear response (R2 = 0.9998) enables the determination of K from the slopes of the lines, which are then converted to Ω values. Ω values of singly and doubly charged poly-DL-alanine cations and anions measured in helium gas are shown in Fig. 1C. Cations have Ω values that are up to 5% larger than anions at lower n values, but at higher n values, Ω values between cations and anions are similar. (Alan − H)1− and (Alan − 2H)2−Ω values measured in helium and in nitrogen gas as well as (Alan + H)1+ measured in helium gas are reported in ESI Table S2;† a subset of these values have been reported previously.32,52Ion mobility is also used to investigate the structures and assemblies of native-like proteins and protein complexes.5–10 An example of a mobility separation of the 145 kDa protein complex glyceraldehyde-3-phosphate dehydrogenase using this RF-confining drift cell is shown in Fig. 2A. Here we measured Ω values for cations and anions of 13 native-like proteins and protein complexes (ESI Table S3†), which complement values for 14 proteins and protein complexes that were measured using this drift cell and reported previously.53 Consistent with earlier findings,53 cations and anions had similar Ω values, but anions exhibited lower average charge states than cations. The Ω values for all protein and protein complex cations and anions measured using this cell are shown in Fig. 2B. Values are the averages of Ω values of each observed charge state for a given sample. The data in Fig. 2B show that native-like protein and protein complex mass and Ω values are correlated, suggesting that most of the proteins and protein complexes investigated here are relatively globular.
 | ||
| Fig. 2 (A) Drift time versus m/z plot of native-like glyceraldehyde-3-phosphate dehydrogenase (145 kDa) electrosprayed in positive ion mode from a 200 mM ammonium acetate buffer solution. The projected mass spectrum is shown above and labeled with the assigned charge states. (B) Average collision cross sections with helium gas (〈ΩHe〉) of native-like protein and protein complex cations (red squares) and anions (black circles) ranging in mass from 5.8 to 468 kDa either reported here (open symbols) or previously (closed symbols).53 Values are plotted on log axes and are averages of all charge states for a given polarity of a protein or protein complex (ESI Table S3†). | ||
RF-confining drift cells enable the determination of absolute Ω values for a broad range of biomolecules. ESI Tables S2 and S3† report 349 Ω values measured using this new RF-confining drift cell. Most values are the average of three technical replicate measurements made on separate days, which in all cases differed by less than 1%. These values include small molecules, peptides, denatured proteins, and native-like proteins and protein complexes. ESI Fig. S5† shows all Ω values measured using this device; the data include results for ions that span a wide range of m/z and Ω values. This data adds to a growing body of evidence of the correlations between charge and protein mass53–55 and provide a source of absolute Ω values that can be used for traveling-wave ion mobility calibration.
Comparisons to other ion mobility devices
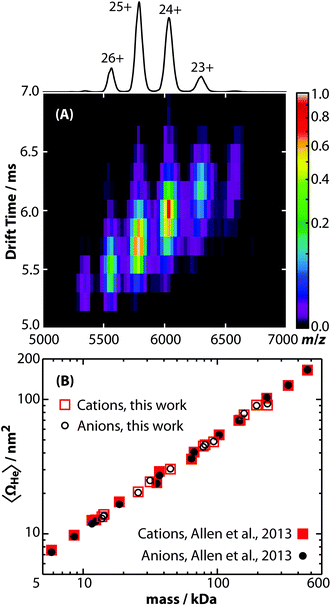
Ω values for a wide mass range of peptide, protein, and protein complex cations measured using this new RF-confining drift cell (ESI Tables S2 and S3†) were compared to those measured using the previous RF-confining drift cell that was implemented in a Waters Synapt G1 HDMS30,31,38 (Fig. 3A). The relative differences between the two sets of data are shown in Fig. 3B. For the 102 ions measured using both cells, 61% have Ω values that are within ±1% of one another and 93% are within ±2% of one another. For comparison, the absolute error in Ω values determined using RF-confining drift cells has been estimated to be <3%, based on propagation of errors in drift times, pressure, and temperature.30 On average, the Ω values measured here are slightly smaller (0.3%) than those measured previously, but this systematic difference is small relative to the standard deviation of the relative Ω values (1.1%). This comparison shows that similar Ω values can be measured using both generations of RF-confining drift cells. | ||
| Fig. 3 (A) Collision cross sections with helium gas measured using the 2nd generation RF-confining drift cell described here (ΩG2He) are compared to those measured using the 1st generation device (ΩG1He).30,31,38 Values are plotted on log axes along with the line ΩG2He = ΩG1He. (B) The ratios of ΩG2He to ΩG1He (red squares) are plotted versus ΩG1He on a log scale (top axis). An overlayed histogram (blue, number of measurements) shows that the ΩG2He and ΩG1He are within ±2% of each other for 93% of the analyte ions. | ||
To further validate the Ω values determined using this RF-confining drift cell, experimental Ω values of peptides and denatured proteins are compared to those measurements made using DC-only drift tubes (ESI Table S4†).4,19,33–36 Note, only ions that have a single reported Ω value from each measurement are compared. Ω values of these analytes measured in helium gas using the new RF-confining drift cell are on average slightly smaller (−0.6% ± 1.5%) than those measured on other devices. In general, comparing Ω values measured here to those measured on the previous RF-confining drift cell and other DC-only drift tubes indicate that Ω values determined using these approaches are statistically similar.
Peak widths and resolving powers
The peptide GRGDS, which has been used previously to characterize the resolving power of several other mobility instruments,19,27,56 was used to characterize the performance of this device. The highest apparent resolving power measured for GRGDS1+ in 2 Torr helium gas was 16.0. This value was calculated by correcting tD for t0 and dividing by the full width at half maximum (Δtexp) determined from fitting a Gaussian function to the experimental arrival-time distribution. Interestingly, the highest apparent resolving power was measured for the lowest drift voltage of 104 V, whereas resolving power increases with drift voltage in eqn (1). To isolate only the contributions of peak widths to resolving power in these experiments, the subsequent analysis focuses on peak width as a function of reciprocal drift voltage. Experimentally measured Δtexp values for GRGDS1+ ranged from 126 to 237 μs for drift voltages from 354 to 104 V, respectively (Fig. 4A). These values are larger than those predicted using diffusion-limited theory (Δtdiff, eqn (1)). This suggests that there are additional contributions to the observed peak width, for example the temporal width of the initial ion population prior to the ion mobility separation (Δtgate). The combined peak width (Δtcombined):21,22| Δtcombined2 = Δtdiff2 + Δtgate2 | (5) |
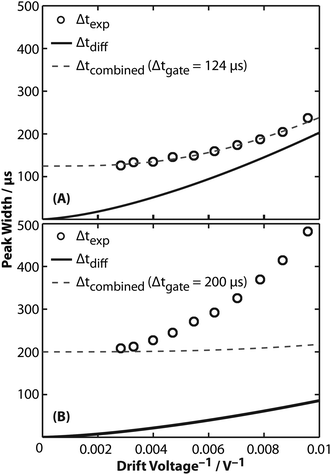 | ||
| Fig. 4 Analysis of full width at half maximum (peak width, Δt) as a function of reciprocal drift voltage. (A) Experimental peak widths (Δtexp, black circles) of GRGDS1+ are greater than those expected using diffusion-limited theory from eqn (1) (Δtdiff, solid line). Instead, the combined peak width (Δtcombined, dashed line) accurately models Δtexp with a Δtgate of 124 μs. (B) Similar to results for GRGDS1+, experimental peak widths (Δtexp, black circles) of the 25+ charge state of glyceraldehyde-3-phosphate dehydrogenase are greater than those expected using diffusion-limited theory from eqn (1) (Δtdiff, solid line). Using a Δtgate of 200 μs to model Δtcombined (dashed line) in these experiments results in good agreement for the highest drift voltage. Significant deviations are exhibited for lower drift voltages, suggesting additional contributions to Δtexp that are not accounted for in eqn (5). | ||
Fig. 4A shows a least-squares minimization of the difference between Δtexp and Δtcombined, which indicates that Δtgate is 124 μs. This value is similar to the trapping release time of 150 μs used for GRGDS experiments. Differences between the two values may be attributable to the assumption in eqn (5) that the initial pulse of ions gated into the drift cell has a Gaussian shape, whereas contributions due to space-charge effects or distortions while gating are also possible. More generally, Δtgate is similar to Δtexp in these experiments, suggesting that the resolving power is significantly limited by contributions from ion gating, but at longer drift times, i.e., low drift voltages, contributions from Δtgate are proportionally less significant. A recent study found that resolving powers that account for gating contributions to peak width compare well to experimental results of the peptide SDGRG (the inverse peptide of GRGDS) using a DC-only drift tube.57
A similar analysis was performed for the 25+ charge state of native-like glyceraldehyde-3-phosphate dehydrogenase, which is a 145 kDa homotetramer. Δtexp values measured under 2 Torr of helium gas are shown in Fig. 4B. Least-squares fitting of Δtcombined to Δtexp results in a Δtgate of 269 μs that does not fit the data appropriately (Fig. S6†). Instead, an upper limit of 200 μs (the trapping release time used in these experiments) was used as Δtgate to calculate Δtcombined. As shown in Fig. 4B, plotting Δtcombined by accounting for Δtgate does not accurately model experimental results. This result suggests that additional contributions, such as an ensemble of conformers with different Ω values, may contribute to the broad peak widths measured in these experiments. This interpretation is consistent with reports that the peak widths for small monomeric protein ions are broader than expected based on diffusion-broadening alone.4,58–60 For example, the arrival-time distributions for ubiquitin have been reported to be greater than that expected for a single conformer60 and using tandem ion mobility methods, these arrival-time distributions have been shown to contain an ensemble of stable conformers.59 Therefore, the peak widths in these current experiments may be better explained using a set of discrete conformers or using semi-empirical peak width theory.61
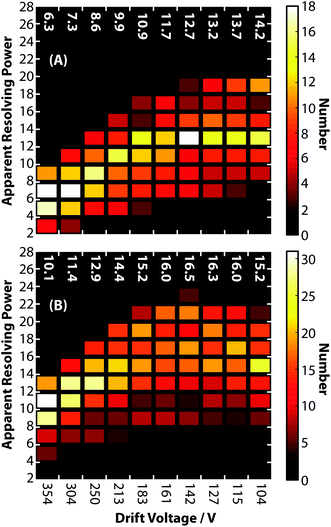
To characterize the peak widths of biomolecular ions more generally, the apparent resolving power was calculated for the cations listed in ESI Tables S2 and S3.† These results were divided into two classes (1) peptides and denatured proteins and (2) native-like proteins and protein complexes. Fig. 5A shows histograms of apparent resolving powers at each drift voltage for peptide and denatured protein ions. Similar to the observation for GRGDS, the lowest drift voltage of 104 V results in the highest average apparent resolving power of 14.2. Measured peak widths at high drift voltages for these ions, which are highly mobile, are attributed predominated to contributions from ion gating, rather than contributions from diffusion. The histograms of apparent resolving powers for native-like protein and protein complex ions are shown in Fig. 5B. In contrast to Fig. 5A, native-like protein and protein complex ions exhibit the highest apparent resolving powers (on average 16.5) at intermediate drift voltages. This is attributable to a balance between contributions from diffusion, gating, and coexisting structural isomers. Note, the apparent resolving power for cations and anions measured using this device are similar. Apparent resolving powers at higher drift voltages could likely be improved by changing ion gating conditions to reduce Δtgate, increasing the drift cell pressure, or using heavier buffer gas molecules in order to decrease the relative contribution of Δtgate to Δtexp.
Conclusions
A new RF-confining drift cell was developed and implemented in a Waters Synapt G2 HDMS. This device has been shown to yield precise and accurate Ω values for a broad mass range of peptide, protein, and protein complex ions. On average, this device yields Ω values that are very similar to those measured using a previous RF-confining drift cell (0.3% average difference) or DC-only drift tubes (0.6% average difference). The apparent resolving power in these experiments is the result of contributions from ion gating, diffusion, and additional factors. For most high-mobility ions, the highest apparent resolving power is observed at the lowest drift voltages for which the relative contributions from ion gating are less prevalent. In contrast, low-mobility proteins and protein complexes yield the highest apparent resolving powers at intermediate drift voltages as a result of more significant contributions to peak widths from relatively broad structural distributions of native-like ions in the gas phase.This broadscale evaluation of apparent resolving powers for native-like protein and protein complex ions provides new insights into the structural diversity of gas-phase ions. In particular, these results provide benchmarks for evaluating the peak widths of analytes of unknown structure. Although improvements in ion mobility instrumentation that increase resolving power (e.g. increased drift voltage and decreased trapping release times) may yield narrower peaks for some ions, this data suggests that the apparent resolving power of native-like ions may be a result of inherent structural diversity that will be difficult to overcome by incremental improvements in instrumentation.
Acknowledgements
This material is based upon work supported by the University of Washington Research Royalty Fund under A70595 (M.F.B), the National Science Foundation under CHE – 1550285 (M.F.B.), and the American Chemical Society, Division of Analytical Chemistry Fellowship, sponsored by Agilent (S.J.A).References
- F. Lanucara, S. W. Holman, C. J. Gray and C. E. Eyers, Nat. Chem., 2014, 6, 281–294 CrossRef CAS PubMed.
- K. M. Roscioli, E. Davis, W. F. Siems, A. Mariano, W. Su, S. K. Guharay and H. H. Hill, Anal. Chem., 2011, 83, 5965–5971 CrossRef CAS PubMed.
- K. Thalassinos, M. Grabenauer, S. E. Slade, G. R. Hilton, M. T. Bowers and J. H. Scrivens, Anal. Chem., 2009, 81, 248–254 CrossRef CAS PubMed.
- K. B. Shelimov, D. E. Clemmer, R. R. Hudgins and M. F. Jarrold, J. Am. Chem. Soc., 1997, 119, 2240–2248 CrossRef CAS.
- U. I. Ekeowa, J. Freeke, E. Miranda, B. Gooptu, M. F. Bush, J. Perez, J. Teckman, C. V. Robinson and D. A. Lomas, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17146–17151 CrossRef CAS PubMed.
- C. Uetrecht, I. M. Barbu, G. K. Shoemaker, E. van Duijn and A. J. R. Heck, Nat. Chem., 2011, 3, 126–132 CrossRef PubMed.
- M. Zhou, A. Politis, R. B. Davies, I. Liko, K.-J. Wu, A. G. Stewart, D. Stock and C. V. Robinson, Nat. Chem., 2014, 6, 208–215 CrossRef CAS PubMed.
- C. A. Scarff, B. Almeida, J. Fraga, S. Macedo-Ribeiro, S. E. Radford and A. E. Ashcroft, Mol. Cell. Proteomics, 2015, 14, 1241–1253 CAS.
- D. Scott, R. Layfield and N. J. Oldham, Protein Sci., 2015, 24, 1257–1263 CrossRef CAS PubMed.
- Y. Zhao, A. Singh, L. Li, R. J. Linhardt, Y. Xu, J. Liu, R. J. Woods and I. J. Amster, Analyst, 2015, 140, 6980–6989 RSC.
- L. S. Fenn, M. Kliman, A. Mahsut, S. R. Zhao and J. A. McLean, Anal. Bioanal. Chem., 2009, 394, 235–244 CrossRef CAS PubMed.
- C. J. Hogan and J. F. de la Mora, J. Am. Soc. Mass Spectrom., 2011, 22, 158–172 CrossRef CAS PubMed.
- J. A. Silveira, M. E. Ridgeway and M. A. Park, Anal. Chem., 2014, 86, 5624–5627 CrossRef CAS PubMed.
- Y. Zhong, S.-J. Hyung and B. T. Ruotolo, Analyst, 2011, 136, 3534 RSC.
- E. A. Mason and E. W. McDaniel, Transport Properties of Ions in Gases, Wiley, New York, 1988 Search PubMed.
- K. Tang, A. A. Shvartsburg, H.-N. Lee, D. C. Prior, M. A. Buschbach, F. Li, A. V. Tolmachev, G. A. Anderson and R. D. Smith, Anal. Chem., 2005, 77, 3330–3339 CrossRef CAS PubMed.
- S. L. Koeniger, S. I. Merenbloom, S. J. Valentine, M. F. Jarrold, H. R. Udseth, R. D. Smith and D. E. Clemmer, Anal. Chem., 2006, 78, 4161–4174 CrossRef CAS PubMed.
- E. S. Baker, B. H. Clowers, F. Li, K. Tang, A. V. Tolmachev, D. C. Prior, M. E. Belov and R. D. Smith, J. Am. Soc. Mass Spectrom., 2007, 18, 1176–1187 CrossRef CAS PubMed.
- P. R. Kemper, N. F. Dupuis and M. T. Bowers, Int. J. Mass Spectrom., 2009, 287, 46–57 CrossRef CAS.
- Y. M. Ibrahim, E. S. Baker, W. F. Danielson III, R. V. Norheim, D. C. Prior, G. A. Anderson, M. E. Belov and R. D. Smith, Int. J. Mass Spectrom., 2015, 377, 655–662 CrossRef CAS PubMed.
- H. E. Revercomb and E. A. Mason, Anal. Chem., 1975, 47, 970–983 CrossRef CAS.
- A. B. Kanu, M. M. Gribb and H. H. Hill, Anal. Chem., 2008, 80, 6610–6619 CrossRef CAS PubMed.
- S. A. Shaffer, A. Tolmachev, D. C. Prior, G. A. Anderson, H. R. Udseth and R. D. Smith, Anal. Chem., 1999, 71, 2957–2964 CrossRef CAS PubMed.
- T. Kim, A. V. Tolmachev, R. Harkewicz, D. C. Prior, G. Anderson, H. R. Udseth, R. D. Smith, T. H. Bailey, S. Rakov and J. H. Futrell, Anal. Chem., 2000, 72, 2247–2255 CrossRef CAS PubMed.
- E. C. Lynn, M. C. Chung and C. C. Han, Rapid Commun. Mass Spectrom., 2000, 14, 2129–2134 CrossRef CAS PubMed.
- Y. Ibrahim, K. Tang, A. V. Tolmachev, A. A. Shvartsburg and R. D. Smith, J. Am. Soc. Mass Spectrom., 2006, 17, 1299–1305 CrossRef CAS PubMed.
- K. Giles, J. P. Williams and I. Campuzano, Rapid Commun. Mass Spectrom., 2011, 25, 1559–1566 CrossRef CAS PubMed.
- B. T. Ruotolo, J. L. P. Benesch, A. M. Sandercock, S.-J. Hyung and C. V. Robinson, Nat. Protoc., 2008, 3, 1139–1152 CrossRef CAS PubMed.
- D. P. Smith, T. W. Knapman, I. Campuzano, R. W. Malham, J. T. Berryman, S. E. Radford and A. E. Ashcroft, Eur. J. Mass Spectrom., 2009, 15, 113–130 CrossRef CAS PubMed.
- M. F. Bush, Z. Hall, K. Giles, J. Hoyes, C. V. Robinson and B. T. Ruotolo, Anal. Chem., 2010, 82, 9557–9565 CrossRef CAS PubMed.
- R. Salbo, M. F. Bush, H. Naver, I. Campuzano, C. V. Robinson, I. Pettersson, T. J. D. Jørgensen and K. F. Haselmann, Rapid Commun. Mass Spectrom., 2012, 26, 1181–1193 CrossRef CAS PubMed.
- J. G. Forsythe, A. S. Petrov, C. A. Walker, S. J. Allen, J. S. Pellissier, M. F. Bush, N. V. Hud and F. M. Fernández, Analyst, 2015, 140, 6853–6861 RSC.
- S. J. Valentine, A. E. Counterman and D. E. Clemmer, J. Am. Soc. Mass Spectrom., 1997, 8, 954–961 CrossRef CAS.
- A. E. Counterman, S. J. Valentine, C. A. Srebalus, S. C. Henderson, C. S. Hoaglund and D. E. Clemmer, J. Am. Soc. Mass Spectrom., 1998, 9, 743–759 CrossRef CAS PubMed.
- S. C. Henderson, J. Li, A. E. Counterman and D. E. Clemmer, J. Phys. Chem. B, 1999, 103, 8780–8785 CrossRef CAS.
- Y. Liu, S. J. Valentine and D. E. Clemmer, unpublished results, http://www.indiana.edu/~clemmer/Research/Cross%20Section%20Database/cs_database.php.
- I. Campuzano, M. F. Bush, C. V. Robinson, C. Beaumont, K. Richardson, H. Kim and H. I. Kim, Anal. Chem., 2012, 84, 1026–1033 CrossRef CAS PubMed.
- M. F. Bush, I. D. G. Campuzano and C. V. Robinson, Anal. Chem., 2012, 84, 7124–7130 CrossRef CAS PubMed.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082–16086 CrossRef CAS.
- T. Wyttenbach, C. Bleiholder and M. T. Bowers, Anal. Chem., 2013, 85, 2191–2199 CrossRef CAS PubMed.
- G. Javahery and B. Thomson, J. Am. Soc. Mass Spectrom., 1997, 8, 697–702 CrossRef CAS.
- K. Thalassinos, S. E. Slade, K. R. Jennings, J. H. Scrivens, K. Giles, J. Wildgoose, J. Hoyes, R. H. Bateman and M. T. Bowers, Int. J. Mass Spectrom., 2004, 236, 55–63 CrossRef CAS.
- Y. Guo, J. Wang, G. Javahery, B. A. Thomson and K. W. M. Siu, Anal. Chem., 2005, 77, 266–275 CrossRef CAS PubMed.
- B. J. McCullough, J. Kalapothakis, H. Eastwood, P. Kemper, D. MacMillan, K. Taylor, J. Dorin and P. E. Barran, Anal. Chem., 2008, 80, 6336–6344 CrossRef CAS PubMed.
- K. Pagel and D. J. Harvey, Anal. Chem., 2013, 85, 5138–5145 CrossRef CAS PubMed.
- D. R. Hernandez, J. D. DeBord, M. E. Ridgeway, D. A. Kaplan, M. A. Park and F. Fernandez-Lima, Analyst, 2014, 139, 1913–1921 RSC.
- J. N. Rabuck, S.-J. Hyung, K. S. Ko, C. C. Fox, M. B. Soellner and B. T. Ruotolo, Anal. Chem., 2013, 85, 6995–7002 CrossRef CAS PubMed.
- R. Pepin, K. J. Laszlo, B. Peng, A. Marek, M. F. Bush and F. Tureček, J. Phys. Chem. A, 2014, 118, 308–324 CrossRef CAS PubMed.
- F. Lermyte, A. Konijnenberg, J. P. Williams, J. M. Brown, D. Valkenborg and F. Sobott, J. Am. Soc. Mass Spectrom., 2014, 25, 343–350 CrossRef CAS PubMed.
- K. J. Laszlo and M. F. Bush, J. Am. Soc. Mass Spectrom., 2015, 26, 2152–2161 CrossRef CAS PubMed.
- M. Zhou, C. M. Jones and V. H. Wysocki, Anal. Chem., 2013, 85, 8262–8267 CrossRef CAS PubMed.
- G. Paglia, J. P. Williams, L. Menikarachchi, J. W. Thompson, R. Tyldesley-Worster, S. Halldórsson, O. Rolfsson, A. Moseley, D. Grant, J. Langridge, B. O. Palsson and G. Astarita, Anal. Chem., 2014, 86, 3985–3993 CrossRef CAS PubMed.
- S. J. Allen, A. M. Schwartz and M. F. Bush, Anal. Chem., 2013, 85, 12055–12061 CrossRef CAS PubMed.
- J. Fernandez de la Mora, Anal. Chim. Acta, 2000, 406, 93–104 CrossRef CAS.
- A. J. R. Heck and R. H. H. van den Heuvel, Mass Spectrom. Rev., 2004, 23, 368–389 CrossRef CAS PubMed.
- C. Wu, W. F. Siems, J. Klasmeier and H. H. Hill, Anal. Chem., 2000, 72, 391–395 CrossRef CAS PubMed.
- J. C. May, J. N. Dodds, R. T. Kurulugama, G. C. Stafford, J. C. Fjeldsted and J. A. McLean, Analyst, 2015, 140, 6824–6833 RSC.
- T. Wyttenbach, P. R. Kemper and M. T. Bowers, Int. J. Mass Spectrom., 2001, 212, 13–23 CrossRef CAS.
- S. L. Koeniger, S. I. Merenbloom and D. E. Clemmer, J. Phys. Chem. B, 2006, 110, 7017–7021 CrossRef CAS PubMed.
- T. Wyttenbach and M. T. Bowers, J. Phys. Chem. B, 2011, 115, 12266–12275 CrossRef CAS PubMed.
- W. F. Siems, C. Wu, E. E. Tarver, H. H. J. Hill, P. R. Larsen and D. G. McMinn, Anal. Chem., 1994, 66, 4195–4201 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5an02107c |
| This journal is © The Royal Society of Chemistry 2016 |