Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High-pressure phase transitions in rubidium and caesium hydroxides†
Andreas
Hermann
*
Centre for Science at Extreme Conditions and SUPA, School of Physics and Astronomy, The University of Edinburgh, Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK. E-mail: a.hermann@ed.ac.uk
First published on 2nd June 2016
Abstract
A computational investigation of the high-pressure phase sequence of the heaviest alkali hydroxides, RbOH and CsOH, shows that the phase diagram of both compounds is richer than hitherto thought. First-principles calculations suggest, based on energetics and comparisons to experimental diffraction and spectroscopy signatures, that the high-pressure phase RbOH-VI, stable above 6 GPa in experiment, should be assigned the KOH-VI structure type, and features localised hydrogen-bonded (OH)4 units. Meanwhile, a new high-pressure phase CsOH-VII is predicted to be stable above 10 GPa in an isosymmetric phase transition that, like RbOH-VI, marks the transition from layered to three-dimensional network structures under increased compression. Both new phases highlight an unexpected flexibility of hydrogen bond network formation in a series of compounds that seemingly only vary in the cation size, and potential consequences for similar systems, such as water-carrying minerals, are discussed briefly.
1 Introduction
Alkali hydroxides, chemical composition MOH with M an alkali metal from lithium to caesium, are intriguing compounds at the interface of ionic and hydrogen bonding. Their crystal structures at high temperatures are driven by ionic interactions between M+ and OH−: just below the melting point, all alkali hydroxides – bar lithium hydroxide, LiOH – form a cubic “rotator” phase in the sodium chloride structure with freely rotating OH− groups on one lattice site, and alkali cations on the other.1–5 Around room temperature, hydrogen bonds between the hydroxyl groups are stabilised, which break the cubic symmetry and result in monoclinic, orthorhombic, or tetragonal phases.6,7 The respective structures are – again, except for LiOH – proton-disordered, and low-temperature proton-ordered modifications have been found in almost all protonated and deuterated compounds (except for NaOH).8–11 Despite these commonalities, microscopic details of the respective compounds' structures differ. For instance, the low-temperature modification of RbOH/D has one-dimensional OH⋯OH chains in overall ferroelectric order, while KOH/D and CsOH/D show antiferroelectric order.12 Fig. S1 in the ESI† provides a schematic overview over this phase sequence.It has been argued that moderate compression at room temperature could induce transitions to the low-temperature modifications in these compounds, and such transitions (below P = 1 GPa) have indeed been found in all alkali hydroxides and deuteroxides.13–16 The compounds' responses to increased density (especially of the hydrogen bond network) are of particular interest. In a sense, alkali hydroxides represent the simplest models of hydrous minerals. Those are complex phases within the MgO–H2O–SiO2 and Al2O3–H2O–SiO2 phase diagrams, and are important carriers and storage materials for water in Earth's mantle.17–19 Water in these minerals is mainly present in hydroxyl form, and can drastically alter the minerals' physical properties. The ladder of interactions that drive the formation and properties of hydrous minerals (ionic, covalent, and hydrogen bonding) is present in the alkali hydroxides as well, and studies of the behaviour of the latter under pressure can give us valuable insight into the behaviour of compressed hydrogen-bonded networks.
Experimental high-pressure studies of the alkali hydroxides have been performed up to P = 15 GPa in some of these compounds, close to mantle transition zone conditions. Phase transitions beyond the presumed low-temperature modifications, resulting in denser non-layered phases, have been reported: NaOH-V, stable above 0.8 GPa, with bifurcated hydrogen bonds;16 KOH-VI, stable above 6.5 GPa, and RbOH-VI, stable above 6.3 GPa, which were both described as taking up a “anti-NaOH” structure, though it was not made clear what that structure is.15 Recently, first-principles calculations together with neutron powder diffraction were able to identify the KOH-VI structure as having an unusual hydrogen-bond network topology, with localised (OH)4 units in a matrix of potassium cations.20 Likewise, the high-pressure phase LiOH-III, stable above 0.7 GPa, was shown in calculations (analysing neutron diffraction patterns, vibrational and energetic properties) to be a new structure type with linear OH⋯OH chains. Calculations also predicted a high-pressure phase LiOH-IV (above 17 GPa) that is structurally identical to NaOH-V.21
Here, the thread of theoretical studies of the compressed alkali hydroxides is continued, and the high-pressure phase transitions exhibited by RbOH and CsOH are examined. It is suggested, on grounds of energetics as well as comparisons to energy-dispersive X-ray (EDX) and spectroscopic data, that RbOH-VI has the same structure as KOH-VI, thus also featuring localised (OH)4 units; and that CsOH undergoes an isosymmetric phase transition to a high-pressure phase at 10 GPa, which has not been detected in previous experiments.
2 Computational methodology
To search for potential high-pressure structures, ground-state crystal structure searches were performed for both RbOH and CsOH, with four formula units per unit cell and at 10 and 20 GPa, respectively. The former is significantly above the onset of RbOH-VI, reported at 6.3 GPa, and the search unit cells correspond to the unit cell size deduced from the EDX data. They would also be able to describe any structure with one or two formula units per cell. Over 1200 structures were optimized in each structure search.The evolutionary algorithm approach as implemented in the XTALOPT package was used in conjunction with scalar relativistic density functional total energy calculations using the Vasp package.22,23 This combined computational approach has proven very fruitful in recent years in computational studies of high-pressure systems, including hydrogen-rich and hydrogen-bonded compounds.24–28 Candidate structures from the crystal structure searches, as well as other structures known in the alkali hydroxides, were optimized across the pressure range P = 1 atm to 20 GPa. Density functional calculations employed the PBE exchange–correlation functional to describe the electron–electron interaction and projector augmented wave (PAW) data sets to model the electron–ion interaction,29,30 using Rb(4s24p65s1) Cs(5s25p66s1) O(2s22p4) and H(1s1) valence spaces, with cutoff radii of 2.5, 2.5, 1.52, and 1.1 aB, respectively. Spin-polarisation and spin–orbit effects were not included, as all systems studied here are effectively closed-shell, wide-gap insulators. A plane wave basis cutoff of 600 eV and regular k-grids of density 20/Å−1 to sample reciprocal space were used to achieve convergence of total energies, and geometries were optimised until remaining force components were below 1 meV Å−1. Phonon calculations used the finite displacement method in conjunction with the supercell approach as implemented in the PHON code to obtain phonon densities of states,31 utilising supercells with up to 144 atoms and symmetry-adapted central displacements of ±0.02 Å. Density functional perturbation theory as implemented in the Quantum-ESPRESSO package was used to ascertain IR and Raman activity of zone-centered modes.32
3 Results and discussion
3.1 RbOH and CsOH at atmospheric pressure
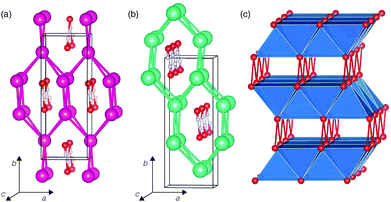
The low-temperature phases of RbOH and CsOH, denoted RbOH-IVb and CsOH-IVc respectively, are very similar: in one interpretation, they feature kinked one-dimensional OH⋯OH chains running through channels of a cation matrix, see Fig. 1. Orthorhombic RbOH-IVb, space group Cmc21, has ferroelectrically ordered chains, while CsOH-IVc, space group P212121, has anti-ferroelectrically ordered chains (in Fig. 1(b), these point along the c axis, alternately into and out of the paper plane). A very common alternative view of both structures is that they are layered compounds, as schematically shown in Fig. 1 (c): (Rb,Cs)O5 polyhedra form layers of edge-sharing square planar pyramids, with their bases connected to adjacent layers through hydrogen bonds. The topology shown in Fig. 1(c) is the same in RbOH-IVb and CsOH-IVc, the two phases only differ in the relative orientations of the inter-layer hydrogen bonds.In the present calculations, the structural parameters of both RbOH-IVb and CsOH-IVc, as determined by neutron powder diffraction at atmospheric pressure are reproduced very well, see Table 1. Lattice constants are mostly in agreement by 0.1 Å, and atomic positions by 0.02 in relative coordinates.
| Phase | Lattice constants [Å] | Atomic positions |
|---|---|---|
| RbOH, this work | a = 4.221, b = 11.100, c = 4.251 | Rb(0, 0.139, 0.257) |
| O(0, 0.398, 0.289) | ||
| H(0, 0.464, 0.135) | ||
| RbOD, 15 K | a = 4.1114, b = 10.991, c = 4.1965 | Rb(0, 0.138, 0.25) |
| O(0, 0.389, 0.282) | ||
| D(0, 0.463, 0.149) | ||
| CsOH, this work | a = 4.446, b = 11.671, c = 4.548 | Cs(0, 0.139, 0.252) |
| O(0, 0.402, 0.292) | ||
| H(0, 0.462, 0.141) | ||
| CsOD, 23 K | a = 4.312, b = 11.514, c = 4.462 | Cs(0.01, 0.14, 0.25) |
| O(0, 0.393, 0.269) | ||
| D(0, 0.462, 0.143) | ||
3.2 High-pressure phase evolution in RbOH
In Fig. 2, the ground state enthalpies of formation (relative to RbOH-IVb) of various RbOH phases are plotted as function of pressure. The figure includes known alkali hydroxide phases (found at atmospheric or higher pressure) as well as results from crystal structure searches at P = 10 GPa. Naturally, the atomistic models here are restricted to proton-ordered phases.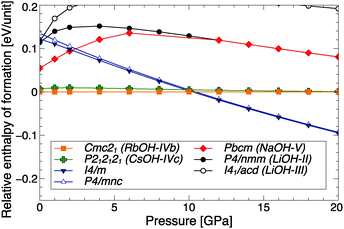 | ||
| Fig. 2 Relative ground state enthalpies of formation per RbOH formula unit, as function of pressure. | ||
The calculations correctly reproduce RbOH-IVb as the ground state of RbOH at low pressures. Only slightly higher in enthalpy is the CsOH-IVc structure type that, as discussed above, only differs in the anti-ferroelectric order of the OH chains, but is otherwise very similar. At P = 10 GPa, two structures very close in enthalpy are found to become more stable than RbOH-IVb. Both are tetragonal, of I4/m and P4/mnc symmetry, and emerged from the crystal structure searches. These are the same structures that were found as high-pressure candidates in potassium hydroxide and that formed the basis of a successful refinement of neutron powder diffraction data of KOH-VI.20 The NaOH-V phase, suggested in EDX experiments, is not energetically competitive at high pressures, and neither is any of the other known alkali hydroxide structure types.
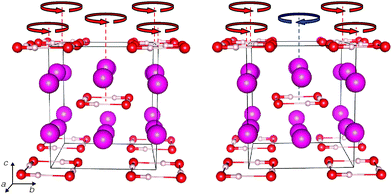
The I4/m and P4/mnc structures are shown in Fig. 3 and their structural details are given in Table 2. Both comprise localised square planar hydrogen-bonded (OH)4 units in a Rb+ matrix; an alternative view is that Rb+(OH−) forms a distorted caesium chloride structure. Both structures have two (OH)4 units per unit cell, but they differ in the relative orientation of their hydroxyl groups: in I4/m, all hydrogen bonds are oriented the same way (say, anticlockwise, as seen down the c axis in Fig. 3), whereas, in P4/mnc, units in adjacent ab planes are oriented in opposite senses (clockwise and anti-clockwise). In Fig. 3, arrows have been added to indicate schematically the sense of orientation of the hydrogen bonds. At room temperature and on a macroscopic scale RbOH-VI might well be proton-disordered (as was found in KOH-VI) – note the small enthalpy difference between I4/m and P4/mnc across the entire pressure range; the true high-pressure phase of RbOH-VI (at room temperature) could then be a more symmetric variant of both structures with partial proton occupancies, for instance with I4/mmm symmetry as found in KOH-VI.20
| Phase | Lattice constants [Å] | Atomic positions |
|---|---|---|
| RbOH-IVb, 10 GPa | ||
| (Cmc21) | a = 3.889, b = 10.119, c = 3.945 | Rb(0, 0.141, 0.279) |
| O(0, 0.408, 0.292) | ||
| H(0, 0.476, 0.110) | ||
| RbOH-VI, 10 GPa | ||
| (I4/m) | a = 6.355, b = 6.355, c = 7.343 | Rb1(0, 0.5, 0.25) |
| Rb2(0, 0, −0.295) | ||
| O(−0.237, −0.211, 0) | ||
| H(0.082, 0.223, 0) | ||
| (P4/mnc) | a = 6.352, b = 6.352, c = 7.346 | Rb1(0, 0.5, 0.25) |
| Rb2(0, 0, −0.295) | ||
| O(−0.234, 0.214, 0) | ||
| H(−0.079, 0.229, 0) | ||
| CsOH-IVc, 10 GPa | ||
| (Pmcn) | a = 4.075, b = 10.064, c = 4.110 | Cs(0, 0.144, 0.251) |
| O(0, 0.416, 0.232) | ||
| H(0, 0.478, 0.416) | ||
| CsOH-VII, 10 GPa | ||
| (P212121) | a = 4.079, b = 5.694, c = 7.662 | Cs(−0.2501, 0.367, 0.179) |
| O(−0.237, −0.101, 0.041) | ||
| H(−0.081, 0.211, −0.489) | ||
| (P21cn) | a = 4.080, b = 5.694, c = 7.662 | Cs(−0.376, 0.117, 0.179) |
| O(−0.392, −0.351, 0.041) | ||
| H(−0.209, −0.460, 0.011) | ||
Without considering such disorder, finite-temperature stability of the new phases was investigated within the quasi-harmonic approximation, i.e. considering vibrational entropy contributions to the free energies of RbOH-IVb and the candidates for RbOH-VI by evaluating
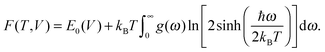 | (1) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) instead of the B1-NaCl structure type (space group Fm
m) instead of the B1-NaCl structure type (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m).
m).
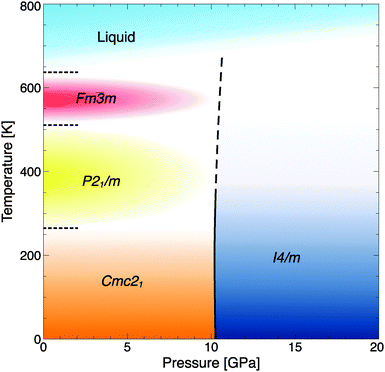 | ||
| Fig. 4 Phase diagram of RbOH, including the calculated transition line RbOH-IVb → VI (solid-dashed line), experimental data at P = 1 atm (dotted lines), and estimates for the high-temperature phases' stability fields (coloured areas).4 | ||
The pressure where RbOH-VI is stabilized in the ground state, about 10 GPa, compares reasonably well to the experimental result of 6.3 GPa, and calculations show a strong enthalpic driving force favoring the phase transition. This result is qualitatively independent of the exchange–correlation functional approximation used: using the local density approximation (LDA),34 the I4/m phase becomes stable at 7.8 GPa, and using the optPBE-vdW functional (which includes dispersion corrections),35–38 the I4/m phase is stabilized at 6.0 GPa, both with respect to the RbOH-IVb phase. However, the two structures found to be suitable candidates are quite different from those proposed in the experimental studies. Note that the diffraction experiments used energy-dispersive X-rays, which make structural refinements quite difficult; and spectroscopic data has not been compared to candidate phases. The lattice parameters obtained in EDX experiments at 8.9 GPa are a = 3.206, b = 6.371, and c = 7.271 Å.15 The orthorhombic deviation from a tetragonal structure with unit cell (2a,b,c) is very small, 2a/b = 1.006, and arguably below the resolution of the EDX experiment. It is hence conceivable that RbOH-VI is tetragonal (the calculated base lattice constant of the I4/m phase at 10 GPa is 6.355 Å), and the top panel of Fig. 5 compares simulated peak positions and intensities of RbOH-VI in the I4/m crystal structure to the EDX data – which give excellent agreement across the entire energy range, except for a small peak at 25 keV (that the experimental structure assignment also could not fully explain).
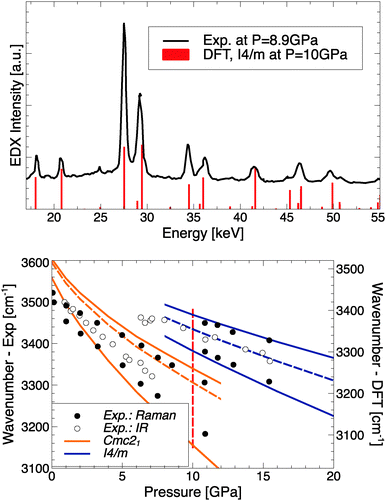 | ||
| Fig. 5 Top: Comparing experimental EDX data from ref. 15 to simulated X-ray intensities of RbOH-I4/m. Bottom: Comparing experimental IR/Raman peak positions from ref. 14 to calculated modes for RbOH-IVb and RbOH-I4/m; solid (dashed) lines indicate Raman (IR) active modes, and the vertical red dashed line indicates the calculated transition pressure. Note calculated frequencies have been offset by 80 cm−1 to account for anharmonicity of the OH stretch mode.33 | ||
In the bottom panel of Fig. 5, the experimental OH stretch frequencies as function of pressure are compared to calculated Raman- and IR-active modes for RbOH-IVb and the proposed RbOH-VI structure. One finds very good agreement for the stretch modes in RbOH-IVb (after an ad hoc shift of 80 cm−1 to account for anharmonic effects not included in the calculations)33 and their decrease with pressure, and an equally good agreement for RbOH-VI, which exhibits a significant blueshift of all stretch modes at the phase transition. This suggests that the hydrogen bonds in RbOH-VI are weaker than in RbOH-IVb, which is in agreement with structural arguments: at P = 10 GPa, the O–H⋯O hydrogen bond lengths in RbOH-IVb are much shorter (1.73 Å) than in RbOH-VI (1.86 Å), even though the latter is overall a much more compact structure.
3.3 Isosymmetric phase transition in CsOH
While there is no known high-pressure phase transition in CsOH, the layered arrangement of CsOH-IVc suggests that a more compact, three-dimensional network structure might become more stable under compression. A crystal structure search at P = 20 GPa provides energetic arguments for a potential isosymmetric phase transition of CsOH around 10 GPa, to a phase one might call CsOH-VII. Fig. 6 shows the relative formation enthalpies of relevant phases. At low pressures, the anti- and ferroelectric structure types of CsOH-IVc and RbOH-IVb are quasi-degenerate as the most stable ground state structures for CsOH. Above 2 GPa, in the calculations, the CsOH-IVc phase, which has P212121 symmetry at atmospheric pressure, optimizes to the higher Pmcn symmetry. One potentially competitive high-pressure phase is a monoclinic P21/a structure that was suggested for NaOH-V,13 but at 10 GPa two other structures become more stable than CsOH-IVc. Note the energy scale in Fig. 6 is smaller by a factor of 20 than the same data shown for RbOH in Fig. 2. There is only a slight enthalpic driving force towards the formation of CsOH-VII, which is due to the relatively subtle structural changes compared to CsOH-IVc. However, the result is qualitatively unaffected by the choice of DFT approximation: using the LDA and optPBE-vdw exchange–correlation functionals, the same high-pressure phase transition is found to occur, respectively, at 4.6 and 6.6 GPa in the ground state; this is reasonable, given that the chemical bonding in CsOH-IVc and CsOH-VII is very similar (see below).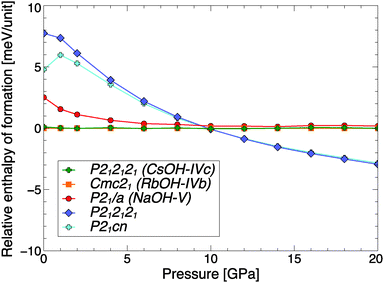 | ||
| Fig. 6 Relative ground state enthalpies of formation per CsOH formula unit, as function of pressure. | ||
Again, the quasi-harmonic approximation gives an indication of the stability of the newly predicted phase at finite temperatures. The phase diagram, as shown in Fig. 7, reveals that the transition to the high-pressure phase should occur around 7 GPa at room temperature. Experimental information5 on the transition temperatures from CsOH-IVc to proton-disordered CsOH-III at 200 K (space group Cmcm), to the “free rotator” phase CsOH-I at 498 K, and eventual melting at 612 K is included in the figure. Note that the underlying calculations only consider the transition CsOH-IVc → VII; in particular, possible stabilisation of a proton-disordered phase CsOH-VII′ at or around room temperature, and its stability relative to CsOH-III, are not included; the phase transition line is drawn as a dashed line to emphasize this uncertainty.
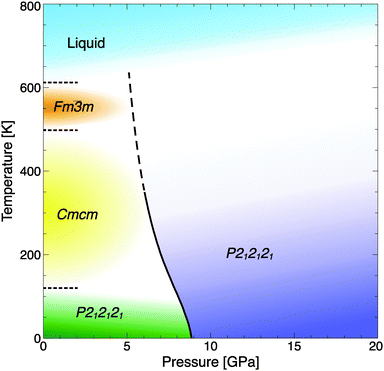 | ||
| Fig. 7 Phase diagram of CsOH, including the calculated transition line CsOH-IVc → VII (solid-dashed line), experimental data at P = 1 atm (dotted lines), and estimates for the high-temperature phases' stability fields (coloured areas).5 | ||
The most stable candidate for CsOH-VII above 10 GPa in the ground state is orthorhombic, of P212121 symmetry, and is shown in Fig. 8. It features kinked hydrogen-bonded OH chains in a cation environment very similar to CsOH-IVc (see Fig. 1(b)), but the cation ‘channels’ are laid out in a herringbone arrangement in the bc plane as opposed to a parallel stacking in CsOH-IVc. This allows for a marginally more compact overall structure: at 10 GPa, the P212121 structure is 0.2% denser per formula unit than CsOH-IVc. If one focuses on the cation coordination and arrangement, the P212121 structure clearly marks the deviation from layered structures, see Fig. 8(b), as edge-sharing CsO5 polyhedra form a three-dimensional network structure. The OH chains in CsOH-VII-P212121 have antiferroelectric order, and a ferroelectric equivalent of space group P21cn is quasi-degenerate with the P212121 phase at the relevant pressure range above 10 GPa, see Fig. 6. The structural details of both phases are given in Table 2. It is conceivable that CsOH-VII will be proton-disordered at room temperature. Its P212121 structure has been found in calculations before, as a metastable high-pressure phase in LiOH.21
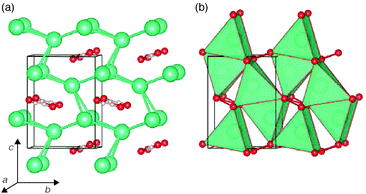 | ||
| Fig. 8 Orthorhombic high-pressure phase of CsOH-VII-P212121, shown at P = 10 GPa. (a) Focus on hydrogen bonds and cation network; (b) focus on CsO5 polyhedral arrangement. | ||
A potential transition from CsOH-IVc to CsOH-VII should be very subtle in terms of equation of state or changes in spectroscopic signatures. Fig. 9 compares the two phases' volume per formula unit: CsOH-VII-P212121 is always more compact than CsOH-IVc, but only marginally so, with both phases approaching very similar molar volumes at high pressures. The equation of state of either phase agrees well with the experimental results by Otto and Holzapfel.15Fig. 9 also shows calculated OH stretch modes as function of pressure, which suggest only minute differences between the two phases; this can be rationalized, because the OH group environments (with kinked one-dimensional hydrogen-bonded chains) are essentially identical. Both facts could explain why a pressure-induced phase transition was not seen in early experiments.14,15
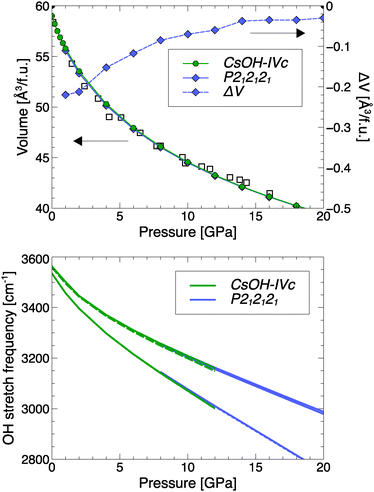 | ||
| Fig. 9 Top: Calculated molar volumes of CsOH-IVc and CsOH-VII, as well as their difference ΔV = V(CsOH-VII) − V(CsOH-IVc). Open symbols denote experimental values.15 Bottom: Calculated OH stretch modes in both phases, as function of pressure. Solid (dashed) lines are Raman + IR (IR only) active. | ||
It should be more straightforward to verify the presence of a transition in diffraction experiments. Fig. 10 compares simulated EDX peak positions and intensities of CsOH-IVc and CsOH-P212121 with the experimental data by Otto and Holzapfel, as well as the evolution of the lattice constants with pressure. One finds that the optimized structure of CsOH-IVc agrees very well with both sets of experimental data. As the top panel of Fig. 10 shows, the predicted P212121 phase has a diffraction pattern very distinct from CsOH-IVc, and its presence in a sample chamber should be noticeable. The experimental pattern shows no sign of additional peaks that would indicate presence of the P212121 phase, and therefore suggests the stability of CsOH-IVc (or, to be precise, CsOH-III) around 10 GPa – while the present calculations predict a phase transition to CsOH-VII (or -VII′, with proton disorder) to occur under the same conditions. However, Otto and Holzapfel noted a broadening of several EDX lines above 10 GPa that might indicate an approach of a structural phase transition. The transition could be unusually sluggish due to the small enthalpic driving force. Higher pressures were only investigated using spectroscopy, which (see above) is unlikely to provide clear evidence of a phase transition.
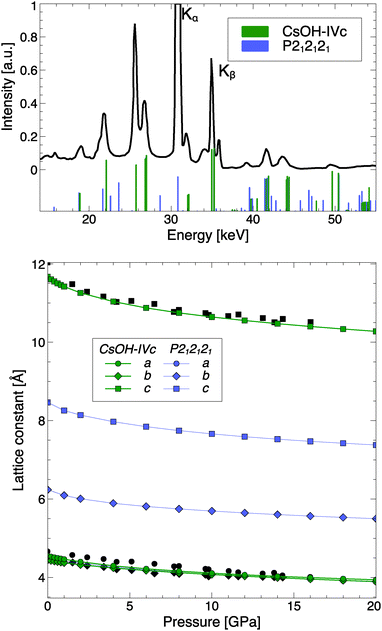 | ||
| Fig. 10 Top: Experimental EDX spectrum at 9.6 GPa, and simulated EDX peaks at 10 GPa, for both CsOH-IVc and CsOH-VII. Bottom: Calculated pressure evolution of lattice constants of both phases. Black symbols are experimental data points.15 | ||
4 Conclusions
In summary, electronic structure calculations combined with crystal structure prediction methodology provide strong hints at hitherto unknown high-pressure phases in both RbOH and CsOH alkali hydroxides. For RbOH, it is suggested that a previously identified high-pressure phase, RbOH-VI, has a completely different structure (which includes the hydrogen bond network) than assumed so far. Instead of being related to NaOH-V, evidence from energetics, simulated EDX patterns and OH vibrons suggests that RbOH-VI has the same structure as KOH-VI, which was recently solved and features localised square-planar (OH)4 units in an overall B2-like Rb+(OH)− arrangement. The structural features of this phase could indicate a different high-temperature “free rotator” phase and even suggest a liquid–liquid phase transition in hot, compressed RbOH.For CsOH, a new high-pressure phase, CsOH-VII, is predicted to be stabilised around 10 GPa. This phase features a more subtle rearrangement of structural features than RbOH-VI, and hence a much smaller enthalpic driving force towards formation under high-pressure conditions. CsOH-VII marks, like RbOH-VI, the departure from layered structural motifs that are so dominant in all alkali hydroxides at atmospheric pressure. While there is no direct experimental evidence for CsOH-VII yet, the phase transition could be sluggish due to the small enthalpy gain upon its formation. Estimates of the finite-temperature phase diagram of either compound show that the proposed new high-pressure phases should be accessible at room temperature, albeit likely in proton-disordered form.
The pressure range of formation for both RbOH-VI and CsOH-VII is accessible by neutron powder diffraction, which should be the best experimental approach to conclusively solve those high-pressure phases. Their formation can probably also be verified using angle-dispersive X-ray diffraction of sufficient quality to enable a refinement. CsOH-VII in particular exhibits a diffraction pattern quite different from CsOH-IVc.
The results presented here yet again extend the range of hydrogen bond networks possible in the alkali hydroxides under suitable conditions. The CsOH-VII phase was seen previously as a metastable candidate for LiOH-III, and with its emergence as a stable phase under compression one now finds hydroxyl hydrogen bond networks of dimensionality zero (KOH-VI and RbOH-VI, with localised (OH)4 units), one (LiOH-III and CsOH-VII, with linear and kinked (OH)∞ chains), and two (LiOH-IV and NaOH-V, with bifurcated hydrogen bonds in OH layers), in a sequence of compounds that arguably do not differ by anything other than the cation size. This flexibility in hydrogen bond topologies could conceivably emerge in other systems as well, such as hydrous minerals, and could significantly influence their ionic conductivity and elasticity. It would be fascinating to study whether similar transitions occur, for instance, in the alkaline earth hydroxides brucite and portlandite, Mg(OH)2 and Ca(OH)2, which also form as layered compounds at atmospheric and low pressures.
Acknowledgements
The author wants to thank John S. Loveday and Roald Hoffmann for fruitful discussions. Computational resources provided by the UK National Supercomputing Service through the UKCP consortium (funded by EPSRC Grant EP/K01465X) and project ID d56, by the Condensed Matter Centre for Doctoral Training (funded by EPSRC Grant EP/L015110/1), and by the Royal Society (Research Grant RG150247) are gratefully acknowledged. Supplementary research data, in compliance with EPSRC research data policy, can be accessed at http://dx.doi.org/10.7488/ds/1413.References
- J. M. Kiat, G. Boemare, B. Rieu and D. Aymes, Solid State Commun., 1998, 108, 241–245 CrossRef CAS.
- H.-J. Bleif and H. Dachs, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1982, 38, 470–476 CrossRef.
- B. Mach, H. Jacobs and W. Schäfer, Z. Anorg. Allg. Chem., 1987, 553, 187–195 CrossRef CAS.
- H. Jacobs, B. Mach, H.-D. Lutz and J. Henning, Z. Anorg. Allg. Chem., 1987, 544, 28–54 CrossRef CAS.
- H. Jacobs, B. Mach, B. Harbrecht, H.-D. Lutz and J. Henning, Z. Anorg. Allg. Chem., 1987, 544, 55–73 CrossRef CAS.
- H. Dachs, Z. Kristall., 1959, 112, 60–67 CrossRef CAS.
- J. A. Ibers, J. Kumamoto and R. G. Snyder, J. Chem. Phys., 1960, 33, 1164 CrossRef CAS.
- T. J. Bastow, M. M. Elcombe and C. J. Howard, Solid State Commun., 1986, 57, 339–341 CrossRef CAS.
- T. J. Bastow, M. M. Elcombe and C. J. Howard, Solid State Commun., 1986, 59, 257–259 CrossRef CAS.
- T. J. Bastow, M. M. Elcombe and C. J. Howard, Solid State Commun., 1987, 62, 149–151 CrossRef CAS.
- T. J. Bastow, S. L. Segel and K. R. Jeffrey, Solid State Commun., 1991, 78, 565–568 CrossRef CAS.
- T. J. Bastow, M. M. Elcombe and C. J. Howard, Ferroelectrics, 1988, 79, 269–271 CrossRef.
- D. M. Adams, A. G. Christy and J. Haines, J. Phys. Chem., 1992, 96, 8173–8176 CrossRef CAS.
- M. P. Krobok and W. B. Holzapfel, J. Phys.: Condens. Matter, 1994, 6, 9789–9806 CrossRef CAS.
- J. W. Otto and W. B. Holzapfel, J. Phys.: Condens. Matter, 1995, 7, 5461–5476 CrossRef CAS.
- J. S. Loveday, W. G. Marshall, R. J. Nelmes, S. Klotz, G. Hamel and J. M. Besson, J. Phys.: Condens. Matter, 1996, 8, L597–L604 CrossRef CAS.
- R. J. Angel, D. J. Frost, N. L. Ross and R. Hemley, Phys. Earth Planet. Inter., 2001, 127, 181–196 CrossRef CAS.
- Q. Williams and R. J. Hemley, Annu. Rev. Earth Planet. Sci., 2001, 29, 365–418 CrossRef CAS.
- R. A. Eggleton, J. N. Boland and A. E. Ringwood, Geochem. J., 1978, 12, 191–194 CrossRef CAS.
- A. Hermann, M. Guthrie, R. J. Nelmes and J. S. Loveday, J. Chem. Phys., 2015, 143, 244706 CrossRef PubMed.
- A. Hermann, N. W. Ashcroft and R. Hoffmann, J. Chem. Phys., 2014, 141, 024505 CrossRef PubMed.
- D. C. Lonie and E. Zurek, Comput. Phys. Commun., 2011, 182, 372–387 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- E. Zurek, R. Hoffmann, N. W. Ashcroft, A. R. Oganov and A. O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17640–17643 CrossRef CAS PubMed.
- A. Hermann, N. W. Ashcroft and R. Hoffmann, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 745–750 CrossRef CAS PubMed.
- A. Hermann, A. Suarez-Alcubilla, I. G. Gurtubay, L.-M. Yang, A. Bergara, N. W. Ashcroft and R. Hoffmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 144110 CrossRef.
- A. Hermann, A. McSorley, N. W. Ashcroft and R. Hoffmann, J. Am. Chem. Soc., 2012, 134, 18606 CrossRef CAS PubMed.
- A. Hermann and P. Schwerdtfeger, J. Phys. Chem. Lett., 2014, 5, 4336–4342 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- D. Alfè, Comput. Phys. Commun., 2009, 180, 2622–2633 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, R. M. Wentzcovitch, A. D. Corso, S. D. Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- K. Hermansson, G. Gajewski and P. D. Mitev, J. Phys. Chem. A, 2008, 112, 13487–13494 CrossRef CAS PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- J. Klimeš, D. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp03203f |
| This journal is © the Owner Societies 2016 |